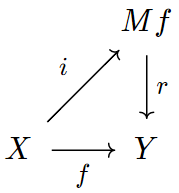अंशांकन: Difference between revisions
(→संदर्भ) |
No edit summary Tag: Manual revert |
| (2 intermediate revisions by 2 users not shown) | |
(No difference)
| |
Latest revision as of 11:03, 10 March 2023
गणित में, विशेष रूप से समरूपता सिद्धांत में, सतत मानचित्रण है-
- ,
जहाँ और टोपोलॉजिकल स्पेस हैं, यदि कोफिब्रेशन मानचित्रण की होमोटॉपी कक्षाऐ प्रदान करता है तब मानचित्रण की होमोटॉपी की कक्षाओं को विस्तारित किया जा सकता है। जब कोई मानचित्रण द्वारा विस्तारित किया जा सकता है। यदि जहाँ , इसलिए उनके संबद्ध होमोटोपी वर्ग समान हैं।
इस प्रकार की संरचना को सभी स्थानों के संबंध में होमोटॉपी एक्सटेंशन संपत्ति होने की तकनीकी स्थिति के साथ को एन्कोड किया जा सकता है। यह परिभाषा कंपन की दोहरी है, जो सभी रिक्त स्थान के संबंध में होमोटॉपी की संपत्ति को संतुष्ट करने के लिए आवश्यक है। इस द्वैत को अनौपचारिक रूप से एकमैन-हिल्टन द्वैत कहा जाता है। सामान्यता के कारण यह तकनीकी स्थिति है, इसका उपयोग मॉडल श्रेणी में किया जा सकता है।
परिभाषा
होमोटॉपी सिद्धांत
निम्नलिखित में, को इकाई अंतराल में निरूपित किया गया है।
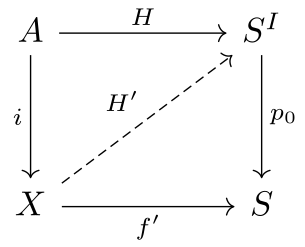
मानचित्रण के टोपोलॉजिकल स्पेस को कोफिब्रेशन कहा जाता है[1]यदि किसी मानचित्र के लिए का विस्तार है, मानचित्रण है। मानचित्रण , द्वारा समरूपता का विस्तार कर सकते हैं। मानचित्रों की समरूपता के लिए , जहां
हम निम्नलिखित क्रमविनिमेय आरेख में इस स्थिति को सांकेतिक शब्दों में परिवर्तित कर सकते है।
जहाँ का पाथ स्पेस कंपन है।
कोफ़िब्रेंट ऑब्जेक्ट
मॉडल श्रेणी के लिए , जैसे पॉइंटेड टोपोलॉजिकल स्पेस के लिए, ऑब्जेक्ट को कोफाइब्रेंट कहा जाता है। यदि मानचित्रण कोफिब्रेशन है। ध्यान दें कि पॉइंटेड टोपोलॉजिकल स्पेस की श्रेणी में, कोफिब्रेशन की धारणा पूर्व परिभाषा के साथ युग्मित होती है, यह मानते हुए कि मानचित्र टोपोलॉजिकल स्पेस हैं।
उदाहरण
टोपोलॉजी में
कम्प्यूटेशनल परिप्रेक्ष्य से कोफिब्रेशन मानचित्र का विचित्र वर्ग है क्योंकि उन्हें औपचारिक तकनीकी उपकरण के रूप में अधिक सरलता से देखा जाता है जो किसी टोपोलॉजिकल रिक्त स्थान के साथ होमोटोपी सैद्धांतिक निर्माण करने में सक्षम बनाता है। सौभाग्य से, किसी भी मानचित्र के लिए-
टोपोलॉजिकल स्पेस में कॉफिब्रेशन जुड़ा होता है, को मैपिंग सिलेंडर कहा जाता है (जहाँ विरूपण वापसी है, इसलिए होमोटोपी इसके समतुल्य है) जिसमें प्रेरित कोफिब्रेशन होता है जिसे कोफिब्रेशन के साथ मानचित्र को परिवर्तित करना कहा जाता है।
मानचित्रण के माध्यम से और कारकों के माध्यम से, जिसका अर्थ है कि क्रमविनिमेय आरेख है-
उदाहरण के अतिरिक्त और भी वर्ग हैं।
- प्रायः उपयोग किया जाने वाला तथ्य यह है कि सेलुलर समावेशन कोफिब्रेशन है (उदाहरण के लिए, यदि सीडब्ल्यू-जोड़ी है, तो कोफिब्रेशन है)। यह पूर्व तथ्य से इस प्रकार है प्रत्येक के लिए कोफिब्रेशन है , और पुशआउट्स ग्लूइंग मानचित्रण हैं स्केलेटन है।
- कोफिब्रेशन को पुशआउट्स और कंपोजीशन के अंतर्गत संरक्षित किया जाता है, जिसे ठीक नीचे बताया गया है।
श्रृंखला परिसरों में
यदि श्रृंखला परिसरों की श्रेणी हैं डिग्री में , मॉडल श्रेणी संरचना है[2]जहां शक्तिहीन समकक्ष अर्ध-समरूपता हैं।
जो एकैकी और कोकर्नेल कॉम्प्लेक्स हैं में प्रक्षेप्य वस्तु का कॉम्प्लेक्स है, इसके अतिरिक्त, कॉफ़िब्रेंट ऑब्जेक्ट वे कॉम्प्लेक्स हैं जिनका प्रक्षेपीय ऑब्जेक्ट हैं।
अर्ध-सरल सेट
श्रेणी के लिए अर्ध-सरलीकृत सेट हैं।[2] (जिसका अर्थ है कि डिग्री में कोई सह-अध: पतन मानचित्र नहीं हैं), कान-फिब्रेशन द्वारा दिए गए फ़िब्रेशन के साथ मॉडल श्रेणी संरचना है, कोफिब्रेशन एकैकी मानचित्रण, और ज्यामितीय प्राप्ति के पश्चात शक्तिहीन समकक्षों का उपयोग किया जाता है।
गुण
- हॉसडॉर्फ रिक्त स्थान के लिए, प्रत्येक कोफिब्रेशन का बंद समावेशन है; परिणाम भी शक्तिहीन हॉउसडॉर्फ रिक्त स्थान के लिए सामान्यीकृत होता है।
- कोफिब्रेशन का पुशआउट (श्रेणी सिद्धांत) कॉफिब्रेशन है। यदि कोई भी (निरंतर) मानचित्रण है (कॉम्पैक्ट रूप से उत्पन्न किए गए रिक्त स्थान के मध्य), और कोफिब्रेशन है, फिर प्रेरित मानचित्रण कोफिब्रेशन है।
- मानचित्रण अनुसार के सिलेंडर को पुशआउट के रूप में जाना जाता है। एम्बेडिंग (इकाई अंतराल का सिरा) . है। अर्थात्, मानचित्रण सिलेंडर को इस प्रकार परिभाषित किया जा सकता है। पुशआउट की सार्वभौमिक संपत्ति द्वारा, कोफिब्रेशन है जब प्रत्येक स्थान X के लिए मानचित्रण सिलेंडर का निर्माण किया जा सकता है।
- मानचित्रण सिलेंडर निर्माण के माध्यम से प्रत्येक मानचित्र को कोफिब्रेशन द्वारा प्रतिस्थापित किया जा सकता है। यही इच्छानुसार (निरंतर) मानचित्रण दिया गया है। (कॉम्पैक्ट रूप से उत्पन्न रिक्त स्थान के मध्य), मानचित्रण सिलेंडर को परिभाषित करता है-
- .
- एक तो विघटित होता है, कोफिब्रेशन और होमोटॉपी तुल्यता के सम्मिश्रण में को मानचित्र के रूप में लिखा जा सकता है-
- साथ , जहाँ समावेशन है, और पर और पर . है।
- कोफिब्रेशन (A, X) है, यदि विरूपण को से पीछे हटना है। चूंकि पुशआउट (श्रेणी सिद्धांत) है और इस प्रकार आरेख में प्रत्येक स्थान के लिए मानचित्र को प्रेरित करता है।
- विरूपण-वापसी जोड़े और अन्तःखंडा विरूपण-वापसी जोड़े के लिए समान समानताएं होती है।
कोफिब्रेशन के साथ निर्माण
कोफ़िब्रेंट प्रतिस्थापन
ध्यान दें कि मॉडल श्रेणी में यदि कोफिब्रेशन नहीं है, तो मानचित्रण सिलेंडर कोफ़िब्रेंट प्रतिस्थापन बनाता है। वास्तव में, यदि हम सिर्फ टोपोलॉजिकल स्पेस की श्रेणी में कार्य करते हैं, तो किसी भी मानचित्र के लिए बिंदु से स्पेस तक कोफिब्रेंट प्रतिस्थापन बनाता है।
कोफाइबर
कोफिब्रेशन के लिए कोफाइबर को प्रेरित भागफल स्थान के रूप में को परिभाषित करते हैं। सामान्यतः, , कोफाइबर[1] को भागफल स्थान के रूप में परिभाषित किया गया है।
जो मानचित्रण शंकु है, होमोटोपिक रूप में कोफाइबर मानचित्र के होमोटॉपी कोकर्नेल के रूप में कार्य करता है। वास्तव में, पॉइंटेड टोपोलॉजिकल स्पेस के लिए, होमोटॉपी कोलिमिट ऑफ़
वास्तव में, मानचित्रण का क्रम कोफाइबर अनुक्रम से सहज है जो त्रिकोणीय श्रेणियों में विशिष्ट त्रिकोण के जैसे कार्य करता है।
यह भी देखें
- कंपन
- होमोटॉपी कोलिमिट
- होमोटॉपी फाइबर
संदर्भ
- ↑ 1.0 1.1 May, J. Peter. (1999). बीजगणितीय टोपोलॉजी में एक संक्षिप्त पाठ्यक्रम. Chicago: University of Chicago Press. ISBN 0-226-51182-0. OCLC 41266205.
- ↑ 2.0 2.1 Quillen, Daniel G. (1967). समरूप बीजगणित. Berlin: Springer-Verlag. ISBN 978-3-540-03914-3. OCLC 294862881.
- Peter May, "A Concise Course in Algebraic Topology" : chapter 6 defines and discusses cofibrations, and they are used throughout
- Brown, Ronald. "7. Cofibrations". Topology and Groupoids. ISBN 978-1-4196-2722-4. Chapter 7 has many results not found elsewhere.