रबर लोच: Difference between revisions
No edit summary |
No edit summary |
||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Property of crosslinked rubber}} | {{Short description|Property of crosslinked rubber}} | ||
रबड़ लोच क्रॉसलिंक्ड रबड़ की संपत्ति को संदर्भित करता है: इसे अपनी मूल लंबाई से 10 के कारक तक बढ़ाया जा सकता है और जब | '''रबड़ लोच''' क्रॉसलिंक्ड रबड़ की संपत्ति को संदर्भित करता है: इसे अपनी मूल लंबाई से 10 के कारक तक बढ़ाया जा सकता है और जब प्रस्तुत किया जाता है, तो इसकी मूल लंबाई के समीपस्थ वापस कर लिया जाता है। इसे कई बार दोहराया जा सकता है और रबर में कोई स्पष्ट कमी नहीं होती है। रबर सामग्री के बड़े वर्ग का सदस्य है जिसे इलास्टोमर्स कहा जाता है और उनके आर्थिक और तकनीकी महत्व को कम आंकना कठिन है। इलास्टोमर्स ने 20वीं सदी में नई विधियों के विकास में महत्वपूर्ण भूमिका है और वैश्विक अर्थव्यवस्था में महत्वपूर्ण योगदान दिया है। रबर लोच कई जटिल आणविक प्रक्रियाओं द्वारा निर्मित होता है और इसकी व्याख्या के लिए उन्नत गणित, रसायन विज्ञान और सांख्यिकीय भौतिकी, विशेष रूप से एन्ट्रापी की अवधारणा के ज्ञान की आवश्यकता होती है। [[एंट्रॉपी]] को तापीय ऊर्जा के माप के रूप में माना जा सकता है जो अणु में संग्रहीत होता है। | ||
सामान्य रबर, जैसे कि पॉलीब्यूटाडाइन और पॉलीसोप्रीन (जिसे प्राकृतिक रबर भी कहा जाता है), पोलीमराइज़ेशन नामक | |||
जैसे ही | सामान्य रबर, जैसे कि पॉलीब्यूटाडाइन और पॉलीसोप्रीन (जिसे प्राकृतिक रबर भी कहा जाता है), [[पोलीमराइज़ेशन]] नामक प्रक्रिया द्वारा निर्मित होते हैं। इस प्रकार बहुत लंबे अणु (बहुलक) रासायनिक प्रतिक्रियाओं के माध्यम से छोटी आणविक रीढ़ की इकाइयों को जोड़कर क्रमिक रूप से निर्मित होते हैं। रबर बहुलक तीन आयामों में यादृच्छिक, ज़िगज़ैग पथ का अनुसरण करता है, जो कई अन्य रबर अणुओं के साथ परस्पर क्रिया करता है। इस प्रकार सल्फर जैसे क्रॉस लिंकिंग अणु के कुछ प्रतिशत को जोड़कर इलास्टोमेर बनाया जाता है। इस स्थिति में गर्म होने पर, क्रॉसलिंकिंग अणु प्रतिक्रिया का कारण बनता है जो रासायनिक रूप से रबर के दो अणुओं को साथ (एक क्रॉसलिंक) साथ जोड़ता है। क्योंकि रबर के अणु इतने लंबे होते हैं, प्रत्येक निरंतर आणविक नेटवर्क बनाने वाले कई अन्य रबर अणुओं के साथ कई क्रॉसलिंक्स में भाग लेता है। | ||
इस प्रकार जैसे ही रबर बैंड को प्रसारित किया जाता हैं, कुछ नेटवर्क चेन को सीधा होने के लिए विवश किया जाता है और इससे उनकी एंट्रॉपी में कमी आ जाती हैं। यह एन्ट्रापी में कमी है जो नेटवर्क श्रृंखलाओं में लोचदार बल को जन्म देती है। | |||
== इतिहास == | == इतिहास == | ||
15वीं शताब्दी के अंत में नई दुनिया से यूरोप में इसकी | 15वीं शताब्दी के अंत में नई दुनिया से यूरोप में इसकी प्रारंभ के बाद, [[प्राकृतिक रबर]] ([[पॉलीसोप्रीन]]) को ज्यादातर आकर्षक जिज्ञासा के रूप में माना जाता था। इसका सबसे उपयोगी अनुप्रयोग कागज पर पेंसिल के निशान को रगड़ कर मिटाने की क्षमता थी, इसलिए इसका यह नाम रखा गया था। इसके सबसे विशिष्ट गुणों में से तापमान में साधारण (लेकिन पता लगाने योग्य) वृद्धि है जो तब होती है जब रबर का नमूना खींचा जाता है। यदि इसे जल्दी से वापस लेने की अनुमति दी जाती है, तो इस प्रकार समान मात्रा में शीतलन देखा जाता है। इस प्रकार इस घटना ने अंग्रेजी भौतिक विज्ञानी [[जॉन गफ (प्राकृतिक दार्शनिक)]] का ध्यान आकर्षित किया हैं। 1805 में उन्होंने इस विशेषता पर कुछ गुणात्मक टिप्पणियों को प्रकाशित किया और यह भी बताया कि तापमान के साथ आवश्यक तनन बल कैसे बढ़ता है।<ref>Proc. Lit. and Phil. Soc., Manchester, 2d ser., 1, 288 (1805)</ref> | ||
उन्नीसवीं शताब्दी के मध्य तक, [[ऊष्मप्रवैगिकी]] के सिद्धांत का विकास हो रहा था और इस ढांचे के भीतर, अंग्रेजी गणितज्ञ और भौतिक विज्ञानी [[लॉर्ड केल्विन]]<ref>Lord Kelvin, Quarterly J. Math., 1, 57 (1857)</ref> दिखाया कि रबर के नमूने को फैलाने के लिए आवश्यक यांत्रिक ऊर्जा में परिवर्तन तापमान में वृद्धि के समानुपाती होना चाहिए। बाद में, यह [[एन्ट्रापी]] में | उन्नीसवीं शताब्दी के मध्य तक, [[ऊष्मप्रवैगिकी]] के सिद्धांत का विकास हो रहा था और इस ढांचे के भीतर, अंग्रेजी गणितज्ञ और भौतिक विज्ञानी [[लॉर्ड केल्विन]]<ref>Lord Kelvin, Quarterly J. Math., 1, 57 (1857)</ref> दिखाया कि रबर के नमूने को फैलाने के लिए आवश्यक यांत्रिक ऊर्जा में परिवर्तन तापमान में वृद्धि के समानुपाती होना चाहिए। बाद में, यह [[एन्ट्रापी]] में परिवर्तन से जुड़ा होगा। ऊष्मप्रवैगिकी का संबंध 1859 में मजबूती से स्थापित हो गया था जब अंग्रेजी भौतिक विज्ञानी [[जेम्स जौल]] ने रबर के नमूने के रूप में होने वाली तापमान वृद्धि का पहला सावधानीपूर्वक माप प्रकाशित किया था।<ref>Joule JP. On thermodynamic properties of solids. Phil Trans R Soc Lond. 1859;149:91–131.</ref> इस कार्य ने लॉर्ड केल्विन की सैद्धांतिक भविष्यवाणियों की पुष्टि की गई हैं। | ||
1838 में अमेरिकी आविष्कारक [[चार्ल्स गुडइयर]] ने पाया कि कुछ प्रतिशत सल्फर मिला कर प्राकृतिक रबर के लोचदार गुणों में अत्यधिक सुधार किया जा सकता है। शॉर्ट सल्फर चेन ने आसन्न पॉलीसोप्रीन अणुओं के बीच रासायनिक क्रॉस-लिंक का निर्माण | 1838 में अमेरिकी आविष्कारक [[चार्ल्स गुडइयर]] ने पाया कि कुछ प्रतिशत सल्फर मिला कर प्राकृतिक रबर के लोचदार गुणों में अत्यधिक सुधार किया जा सकता है। शॉर्ट सल्फर चेन ने आसन्न पॉलीसोप्रीन अणुओं के बीच रासायनिक क्रॉस-लिंक का निर्माण किया था। इससे पहले कि यह क्रॉस-लिंक्ड हो, तरल प्राकृतिक रबर में बहुत लंबे बहुलक अणु होते हैं, जिसमें हजारों [[ आइसोप्रेन |आइसोप्रेन]] बैकबोन इकाइयां होती हैं, जो सिर से पूंछ तक जुड़ी होती हैं जिसमें सामान्यतः चेन के रूप में संदर्भित की गई हैं। प्रत्येक श्रृंखला बहुलक तरल के माध्यम से यादृच्छिक, तीन आयामी पथ का अनुसरण करती है। इस प्रकार हजारों अन्य आस-पास की श्रृंखलाओं के संपर्क में है। जब लगभग 150C तक गर्म किया जाता है, तो प्रतिक्रियाशील क्रॉस-लिंकर अणु, जैसे कि सल्फर या डाइक्यूमिल पेरोक्साइड, विघटित हो सकते हैं और बाद की रासायनिक प्रतिक्रियाएँ आसन्न श्रृंखलाओं के बीच [[रासायनिक बंध]]न उत्पन्न करती हैं। क्रॉसलिंक को 'X' अक्षर के रूप में देखा जा सकता है, लेकिन इसकी कुछ भुजाएँ विमान से बाहर की ओर इंगित करती हैं। परिणामस्वरूप तीन आयामी आण्विक नेटवर्क प्राप्त होते हैं। पॉलीसोप्रीन के सभी अणु इन रासायनिक बंधों (नेटवर्क नोड्स) द्वारा कई बिंदुओं पर साथ जुड़े होते हैं, जिसके परिणामस्वरूप विशाल अणु होता है और इस प्रकार मूल लंबे [[ पॉलीमर |पॉलीमर]] के बारे में सभी जानकारी विलुप्त हो जाती हैं। रबड़ बैंड अणु है, जैसा कि लेटेक्स दस्ताने है, जो दो आसन्न क्रॉस-लिंक्स के बीच पॉलीसोप्रीन के वर्गों को नेटवर्क चेन कहा जाता है और इसमें कई सौ आइसोप्रीन इकाइयां हो सकती हैं। प्राकृतिक रबड़ में, प्रत्येक क्रॉस-लिंक नेटवर्क नोड उत्पन्न करता है जिसमें से चार श्रृंखलाएं निकलती हैं। यह वह नेटवर्क है जो लोचदार गुणों को जन्म देता है। | ||
रबर के विशाल आर्थिक और तकनीकी महत्व के कारण, यह भविष्यवाणी करना कि कैसे | रबर के विशाल आर्थिक और तकनीकी महत्व के कारण, यह भविष्यवाणी करना कि कैसे आणविक नेटवर्क यांत्रिक उपभेदों पर प्रतिक्रिया करता है, वैज्ञानिकों और इंजीनियरों के लिए स्थायी रुचि रही है। रबर के लोचदार गुणों को समझने के लिए, सैद्धांतिक रूप से, आणविक स्तर पर होने वाले दोनों भौतिक तंत्रों को जानना आवश्यक है और बहुलक श्रृंखला की यादृच्छिक-चलना प्रकृति नेटवर्क को कैसे परिभाषित करती है। बहुलक श्रृंखलाओं के छोटे वर्गों के भीतर होने वाले भौतिक तंत्र लोचदार बलों का उत्पादन करते हैं और नेटवर्क आकृति विज्ञान यह निर्धारित करता है कि ये बल मैक्रोस्कोपिक [[तनाव (यांत्रिकी)]] का उत्पादन करने के लिए कैसे गठबंधन करते हैं, जिसे हम रबड़ के नमूने के विकृत होने पर देखते हैं, उदाहरण के लिए इसे [[विरूपण (यांत्रिकी)]] के अधीन माना जाता हैं। | ||
== आण्विक स्तर के मॉडल == | == आण्विक स्तर के मॉडल == | ||
वास्तव में कई भौतिक तंत्र हैं जो नेटवर्क श्रृंखलाओं के भीतर लोचदार बल उत्पन्न करते हैं क्योंकि रबड़ का नमूना फैला हुआ है। इनमें से दो एन्ट्रापी परिवर्तन से उत्पन्न होते हैं और | वास्तव में कई भौतिक तंत्र हैं जो नेटवर्क श्रृंखलाओं के भीतर लोचदार बल उत्पन्न करते हैं क्योंकि रबड़ का नमूना फैला हुआ है। इनमें से दो एन्ट्रापी परिवर्तन से उत्पन्न होते हैं और चेन बैकबोन के साथ आणविक बंधन कोणों की विकृति से जुड़ा होता है। ये तीन तंत्र तुरंत स्पष्ट होते हैं जब मध्यम मोटे रबर के नमूने को मौलिक रूप से खींचा जाता है। प्रारंभ में, रबर अधिक कठोर महसूस होता है, अर्थात तनाव के संबंध में बल को उच्च दर से बढ़ाया जाना चाहिए। मध्यवर्ती उपभेदों पर, समान मात्रा में खिंचाव उत्पन्न करने के लिए बल में आवश्यक वृद्धि बहुत कम होती है। अंत में, जैसे ही नमूना ब्रेकिंग पॉइंट तक पहुंचता है, इसकी कठोरता स्पष्ट रूप से बढ़ जाती है। प्रेक्षक जो देख रहा है वह [[लोच के मापांक]] में परिवर्तन है जो विभिन्न आणविक तंत्रों के कारण होता है। इन क्षेत्रों को चित्र 1 में देखा जा सकता है, [[प्राकृतिक रबर]] के लिए विशिष्ट तनाव की माप की जाती हैं। जिसमें तीन तंत्र (लेबल Ia, Ib और II) मुख्य रूप से भूखंड पर दिखाए गए क्षेत्रों के अनुरूप होते हैं। एंट्रॉपी [[सांख्यिकीय यांत्रिकी]] की अवधारणा हमारे पास गणितीय भौतिकी के क्षेत्र से आती है जिसे सांख्यिकीय यांत्रिकी कहा जाता है जो बड़े तापीय प्रणालियों के अध्ययन से संबंधित है, उदाहरण के लिए कमरे के तापमान पर रबर नेटवर्क इसका मुख्य उदाहरण हैं। यद्यपि घटक श्रृंखलाओं का विस्तृत व्यवहार यादृच्छिक है और व्यक्तिगत रूप से अध्ययन करने के लिए बहुत जटिल है, हम बड़े नमूने के सांख्यिकीय यांत्रिकी विश्लेषण से उनके 'औसत' व्यवहार के बारे में बहुत उपयोगी जानकारी प्राप्त कर सकते हैं। इस प्रकार हमारे दैनिक अनुभवों में एंट्रॉपी परिवर्तन कैसे बल उत्पन्न कर सकते हैं इसका कोई अन्य उदाहरण नहीं है। बहुलक शृंखलाओं में एंट्रोपिक बलों को तापीय टक्करों से उत्पन्न होने वाला माना जा सकता है जो उनके घटक परमाणुओं को इसके समीप की सामग्री के साथ अनुभव करते हैं। यह निरंतर धक्का-मुक्की है जो जंजीरों में प्रतिरोधी (लोचदार) बल उत्पन्न करती है क्योंकि उन्हें सीधा होने के लिए विवश किया जाता है। रबर के नमूने को खींचना लोच का सबसे सरल उदाहरण है, यह तब भी होता है जब रबर को संकुचित किया जाता है। संपीड़न को दो आयामी विस्तार के रूप में माना जा सकता है जब गुब्बारा फुलाया जाता है। लोचदार बल उत्पन्न करने वाले आणविक तंत्र सभी प्रकार के तनाव के लिए समान हैं। | ||
जब इन लोचदार बल मॉडल को नेटवर्क के जटिल आकारिकी के साथ जोड़ दिया जाता है, तो मैक्रोस्कोपिक तनाव की भविष्यवाणी करने के लिए सरल विश्लेषणात्मक सूत्र प्राप्त करना संभव नहीं होता है। यह केवल कंप्यूटरों पर संख्यात्मक सिमुलेशन के माध्यम से है कि रबर के नमूने के तनाव और अंतिम विफलता की भविष्यवाणी करने के लिए आणविक बलों और नेटवर्क आकृति विज्ञान के बीच जटिल | जब इन लोचदार बल मॉडल को नेटवर्क के जटिल आकारिकी के साथ जोड़ दिया जाता है, तो मैक्रोस्कोपिक तनाव की भविष्यवाणी करने के लिए सरल विश्लेषणात्मक सूत्र प्राप्त करना संभव नहीं होता है। यह केवल कंप्यूटरों पर संख्यात्मक सिमुलेशन के माध्यम से है कि रबर के नमूने के तनाव और अंतिम विफलता की भविष्यवाणी करने के लिए आणविक बलों और नेटवर्क आकृति विज्ञान के बीच जटिल वार्तालाभ को पकड़ना संभव है क्योंकि यह तनावपूर्ण है। | ||
=== रबर लोच के लिए आणविक किंक प्रतिमान<ref name=r3>D. E. Hanson and J. L. Barber, Contemporary Physics 56 (3), 319–337 (2015), LAPR-2015-022971</ref>=== | === रबर लोच के लिए आणविक किंक प्रतिमान<ref name=r3>D. E. Hanson and J. L. Barber, Contemporary Physics 56 (3), 319–337 (2015), LAPR-2015-022971</ref>=== | ||
प्राकृतिक रबर नेटवर्क के लिए तनाव तथा तन्यता तनाव के बीच के अन्तर की व्याख्या की जाती हैं। इस प्रकार ट्रेलोअर (ठोस नीला), सैद्धांतिक सिमुलेशन (धराशायी लाल) द्वारा प्रायोगिक डेटा का उपयोग किया जाता हैं। | |||
मॉलिक्यूलर किंक प्रतिमान सहज धारणा से आगे बढ़ता है कि | |||
मॉलिक्यूलर किंक प्रतिमान सहज धारणा से आगे बढ़ता है कि प्राकृतिक रबर (आइसोप्रीन) नेटवर्क बनाने वाली आणविक श्रृंखलाएं 'ट्यूब' के भीतर रहने के लिए आसपास की जंजीरों से विवश हैं। श्रृंखला में उत्पन्न लोचदार बल, कुछ लागू तनाव के परिणामस्वरूप, इस ट्यूब के भीतर श्रृंखला समोच्च के साथ प्रचारित होते हैं। चित्र 2 प्रत्येक छोर पर अतिरिक्त कार्बन परमाणु के साथ चार-कार्बन आइसोप्रीन बैकबोन इकाई का प्रतिनिधित्व दिखाता है, जो श्रृंखला पर आसन्न इकाइयों से इसके कनेक्शन को इंगित करता है। इसमें तीन सिंगल C-C बॉन्ड और डबल बॉन्ड होता है। यह मुख्य रूप से सीसी सिंगल बॉन्ड के बारे में घूर्णन करके है कि पॉलीसोप्रीन श्रृंखला यादृच्छिक रूप से इसकी संभावित अनुरूपताओं की पड़ताल करती है। इस प्रकार दो और तीन आइसोप्रीन इकाइयों के बीच वाली श्रृंखला के खंडों में पर्याप्त लचीलापन है कि उन्हें दूसरे से सांख्यिकीय रूप से असंबद्ध माना जा सकता है। यही है, इस दूरी से अधिक दूरी के लिए श्रृंखला के साथ कोई दिशात्मक संबंध नहीं है, जिसे कुह्न लंबाई कहा जाता है। ये गैर-सीधे क्षेत्र 'किंक्स' की अवधारणा को उद्घाटित करते हैं और वास्तव में रैंडम वॉक हायर डायमेंशन या रैंडम-वॉक प्रकृति की श्रृंखला की अभिव्यक्ति हैं। चूँकि इस प्रकार किंक कई आइसोप्रीन इकाइयों से बना होता है, जिनमें से प्रत्येक में तीन कार्बन-कार्बन सिंगल बॉन्ड होते हैं, किंक के लिए कई संभावित अनुरूपताएँ उपलब्ध होती हैं, जिनमें से प्रत्येक में अलग ऊर्जा और अंत-टू-एंड दूरी होती है। सेकंड से लेकर मिनट तक के समय के पैमाने पर, श्रृंखला के केवल इन अपेक्षाकृत छोटे वर्गों, अर्थात किंक, में उनके संभावित घूर्णी अनुरूपताओं के बीच स्वतंत्र रूप से स्थानांतरित करने के लिए पर्याप्त मात्रा है। ऊष्मीय इंटरैक्शन किंक को निरंतर प्रवाह की स्थिति में रखते हैं, क्योंकि वे अपने सभी संभावित घूर्णी अनुरूपताओं के बीच संक्रमण करते हैं। क्योंकि किंक ऊष्मीय संतुलन में हैं, संभावना है कि किसी घूर्णी रचना में किंक रहता है, बोल्ट्जमान वितरण द्वारा दिया जाता है और हम एंट्रॉपी सांख्यिकीय यांत्रिकी को इसकी एंड-टू-एंड दूरी के साथ जोड़ सकते हैं। कुह्न लंबाई के अंत से अंत तक की दूरी के लिए संभाव्यता वितरण लगभग [[सामान्य वितरण]] है और प्रत्येक स्थिति (घूर्णी रचना) के लिए बोल्ट्जमान संभाव्यता कारकों द्वारा निर्धारित किया जाता है। जैसा कि रबर नेटवर्क फैला हुआ है, कुछ किंक को अधिक से अधिक एंड-टू-एंड दूरी वाले अधिक विस्तारित अनुरूपताओं की सीमित संख्या में विवश किया जाता है और यह एन्ट्रापी में परिणामी कमी है जो श्रृंखला के साथ लोचदार बल उत्पन्न करता है। | |||
तीन अलग-अलग | इस प्रकार इसमें तीन अलग-अलग आण्विक तंत्र होते हैं जो इन बलों का उत्पादन करते हैं, जिनमें से दो एन्ट्रापी में परिवर्तन से उत्पन्न होते हैं जिन्हें हम निम्न श्रृंखला विस्तार प्रणाली, एलए के रूप में संदर्भित किया जाता हैं।<ref name="r4">D. E. Hanson and R. L. Martin, Journal of Chemical Physics 133, 084903 (084908 pp.) (2010)</ref> इस प्रकार मध्यम श्रृंखला विस्तार प्रणाली, आईबी को इसके<ref name="r5">D. E. Hanson, J. L. Barber and G. Subramanian, Journal of Chemical Physics 139 (2013), LAPR-2014-018991</ref> तीसरे तंत्र उच्च श्रृंखला विस्तार पर होता है, क्योंकि इसकी रीढ़ की हड्डी के साथ रासायनिक बंधनों के विरूपण से प्रारंभिक संतुलन समोच्च लंबाई से आगे बढ़ाया जाता है। इस स्थिति में, प्रत्यानयन बल स्प्रिंग जैसा होता है और हम इसे रिजीम II के रूप में संदर्भित करते हैं।<ref name="r6">D. E. Hanson and R. L. Martin, The Journal of Chemical Physics 130, 064903 (2009), LAPR-2009-006764</ref> इस प्रकार तीन बल तंत्र मोटे तौर पर तन्यता तनाव बनाम तनाव प्रयोगों में देखे गए तीन क्षेत्रों के अनुरूप पाए जाते हैं, चित्र 1 में दिखाया गया है। | ||
रासायनिक क्रॉस-लिंकिंग के तुरंत बाद नेटवर्क की प्रारंभिक रूपरेखा दो यादृच्छिक प्रक्रियाओं द्वारा नियंत्रित होती है:<ref name=r7>P. Flory, N. Rabjohn and M. Shaffer, Journal of Polymer Science 4, 435–455 (1949)</ref><ref name=r8>D. E. Hanson, Journal of Chemical Physics 134, 064906 (064906 pp.) (2011)</ref> (1) किसी भी आइसोप्रीन इकाई पर क्रॉस-लिंक होने की संभावना और, (2) श्रृंखला की रचना की यादृच्छिक चलने की | रासायनिक क्रॉस-लिंकिंग के तुरंत बाद नेटवर्क की प्रारंभिक रूपरेखा दो यादृच्छिक प्रक्रियाओं द्वारा नियंत्रित होती है:<ref name="r7">P. Flory, N. Rabjohn and M. Shaffer, Journal of Polymer Science 4, 435–455 (1949)</ref><ref name="r8">D. E. Hanson, Journal of Chemical Physics 134, 064906 (064906 pp.) (2011)</ref> (1) किसी भी आइसोप्रीन इकाई पर क्रॉस-लिंक होने की संभावना और, (2) श्रृंखला की रचना की यादृच्छिक चलने की प्रकृति हैं। निश्चित श्रृंखला लंबाई, अर्थात आइसोप्रीन इकाइयों की निश्चित संख्या के लिए एंड-टू-एंड दूरी संभाव्यता घनत्व फ़ंक्शन, यादृच्छिक चलना द्वारा वर्णित है। इस प्रकार यह नेटवर्क श्रृंखला की लंबाई और उनके क्रॉस-लिंक नोड्स के बीच एंड-टू-एंड दूरी का संयुक्त संभाव्यता वितरण है जो नेटवर्क आकृति विज्ञान की विशेषता है। क्योंकि दोनों आणविक भौतिकी तंत्र जो लोचदार बलों का उत्पादन करते हैं और नेटवर्क के जटिल आकारिकी का साथ उपचार किया जाना चाहिए, सरल विश्लेषणात्मक लोच मॉडल संभव नहीं हैं, इस प्रकार स्पष्ट रूप से यहाँ पर 3-आयामी संख्यात्मक मॉडल<ref name="r9">D. E. Hanson, Polymer 45 (3), 1058–1062 (2004)</ref><ref name="r10">D. E. Hanson, Journal of Chemical Physics 131, 224904 (224905 pp.) (2009)</ref><ref name="r11">D. E. Hanson and J. L. Barber, Modelling and Simulation in Materials Science and Engineering 21 (2013), LAPR-2013-017962</ref> नेटवर्क के प्रतिनिधि वॉल्यूम तत्व पर तनाव के प्रभावों का अनुकरण करना आवश्यक है। | ||
==== कम श्रृंखला विस्तार व्यवस्था, | ==== कम श्रृंखला विस्तार व्यवस्था, एल ए==== | ||
आणविक किंक प्रतिमान | आणविक किंक प्रतिमान प्रतिनिधि नेटवर्क श्रृंखला को वैक्टर की श्रृंखला के रूप में देखता है जो इसकी ट्यूब के भीतर श्रृंखला समोच्च का पालन करता है। प्रत्येक वेक्टर किंक की अंत-टू-एंड संतुलन दूरी का प्रतिनिधित्व करता है। श्रृंखला का वास्तविक 3-आयामी पथ प्रासंगिक नहीं है, क्योंकि सभी लोचदार बलों को श्रृंखला समोच्च के साथ कार्य करने के लिए माना जाता है। इस प्रकार श्रृंखला की समोच्च लंबाई के अतिरिक्त, केवल अन्य महत्वपूर्ण पैरामीटर इसकी टेढ़ी-मेढ़ी है, इस प्रकार इसकी समोच्च लंबाई का अनुपात इसकी एंड-टू-एंड दूरी तक होती है। जैसा कि श्रृंखला को बढ़ाया जाता है, लागू तनाव के उत्तर में, प्रेरित लोचदार बल को इसके समोच्च के साथ समान रूप से फैलाने के लिए माना जाता है। नेटवर्क श्रृंखला पर विचार करें जिसके अंत बिंदु (नेटवर्क नोड) तन्य तनाव अक्ष के साथ कमोबेश संरेखित हैं। जैसे ही रबर के नमूने पर प्रारंभिक तनाव लागू होता है, श्रृंखला के सिरों पर नेटवर्क नोड अलग होने लगते हैं और समोच्च के साथ सभी किंक वैक्टर साथ खिंच जाते हैं। शारीरिक रूप से, लागू किया गया तनाव किंक को उनके बोल्ट्जमैन वितरण के अंत-से-अंत तक की दूरी से आगे बढ़ने के लिए विवश करता है, जिससे उनकी एंट्रॉपी में कमी आती है। इस प्रकार एन्ट्रापी में इस परिवर्तन से जुड़ी मुक्त ऊर्जा में वृद्धि, (रैखिक) लोचदार बल को जन्म देती है जो तनाव का विरोध करती है। कम तनाव प्रणाली के लिए निरंतर बल का अनुमान किंक के [[आणविक गतिशीलता]] (एमडी) प्रक्षेपवक्र के नमूने से लगाया जा सकता है, अर्थात प्रासंगिक तापमान पर 2–3 आइसोप्रीन इकाइयों से बनी छोटी श्रृंखला का उपयोग किया जाता हैं, उदाहरण के लिए 300K इसका मुख्य उदाहरण हैं।<ref name=r4 /> यहाँ पर सिमुलेशन के समय निर्देशांक के कई नमूने लेकर, किंक के लिए एंड-टू-एंड दूरी की संभाव्यता वितरण प्राप्त किया जा सकता है। चूंकि ये वितरण (जो लगभग सामान्य वितरण के रूप में सामने आते हैं) सीधी स्थितियों की संख्या से संबंधित होते हैं, हम उन्हें किसी भी अंत-टू-एंड दूरी पर किंक की एंट्रॉपी से जोड़ सकते हैं। संभाव्यता वितरण को संख्यात्मक रूप से विभेदित करके, एंट्रॉपी में परिवर्तन, और इसलिए [[हेल्महोल्ट्ज़ मुक्त ऊर्जा]], किंक एंड-टू-एंड दूरी के संबंध में पाया जा सकता है। इस व्यवस्था के लिए बल मॉडल को रैखिक और श्रृंखला वक्रता द्वारा विभाजित तापमान के समानुपाती पाया जाता है। | ||
[[File:Fig. 2 Isoprene molecular structure.jpg|thumb| | [[File:Fig. 2 Isoprene molecular structure.jpg|thumb|आइसोप्रीन बैकबोन यूनिट। कार्बन परमाणुओं (गहरा ग्रे) और हाइड्रोजन परमाणुओं (सफेद) से बना है। पॉलिमर श्रृंखला पर '1' और '6' लेबल वाले कार्बन परमाणु आसन्न इकाइयों में हैं।]] | ||
====मध्यम श्रृंखला विस्तार | ====मध्यम श्रृंखला विस्तार प्रणाली, आईबी==== | ||
कम विस्तार व्यवस्था में किसी बिंदु पर, | कम विस्तार व्यवस्था में किसी बिंदु पर, अर्थात श्रृंखला के साथ सभी किंक साथ विस्तारित किए जा रहे हैं, यह श्रृंखला को आगे बढ़ाने के लिए विस्तारित संरचना के लिए किंक संक्रमण के लिए ऊर्जावान रूप से अधिक अनुकूल हो जाता है। लागू तनाव एकल आइसोप्रीन इकाई को विस्तारित संरचना में विस्तारित संरचना में विवश कर सकता है, श्रृंखला की अंत-टू-एंड दूरी को थोड़ा बढ़ा सकता है, और इस प्रकार ऐसा करने के लिए आवश्यक ऊर्जा सभी किंक को साथ विस्तारित करने के लिए आवश्यक ऊर्जा से कम है। इस प्रकार असंख्य प्रयोग<ref name=r12>J. P. Joule, Phil. Trans. R. Soc. London 149, 91–131 (1859)</ref> दृढ़ता से सुझाव देते हैं कि रबर नेटवर्क को फैलाने से एंट्रॉपी में कमी आती है। जैसा कि चित्र 2 में दिखाया गया है, आइसोप्रीन इकाई में तीन एकल सीसी बांड होते हैं और इन बांडों के बारे में दो या तीन पसंदीदा घूर्णी कोण (अभिविन्यास) होते हैं जिनमें न्यूनतम ऊर्जा होती है। इस प्रकार 18 में से अनुमति है<ref name=r5 />घूर्णी अनुरूपता, केवल 6 ने अंत-से-अंत तक दूरी बढ़ाई है और विस्तारित स्थितियों के कुछ सबसेट में रहने के लिए श्रृंखला में आइसोप्रीन इकाइयों को ऊष्मीय गति के लिए उपलब्ध घूर्णी अनुरूपता की संख्या को कम करना चाहिए। यह उपलब्ध स्थितियों की संख्या में कमी है जो एंट्रॉपी को कम करने का कारण बनती है। जैसे-जैसे श्रृंखला सीधी होती जाती है, श्रृंखला की सभी आइसोप्रीन इकाइयाँ अंततः विस्तारित संरूपण में विवश हो जाती हैं और इस प्रकार इस श्रृंखला को 'तना हुआ' माना जाता है। इस एन्ट्रापी परिवर्तन से जुड़े मुक्त ऊर्जा में परिणामी परिवर्तन से श्रृंखला विस्तार के लिए बल स्थिरांक का अनुमान लगाया जा सकता है।<ref name=r5 /> यहाँ पर प्रणाली Ia के साथ, इस प्रणाली के लिए बल मॉडल रैखिक है और श्रृंखला के वक्रता से विभाजित तापमान के समानुपाती है। | ||
==== उच्च श्रृंखला विस्तार | ==== उच्च श्रृंखला विस्तार प्रणाली, II==== | ||
जब | जब नेटवर्क श्रृंखला में सभी आइसोप्रीन इकाइयों को केवल कुछ विस्तारित घूर्णी अनुरूपताओं में रहने के लिए विवश किया जाता है, तो श्रृंखला तना हुआ हो जाता है। चेन समोच्च के साथ सी-सी बांड बनाने वाले ज़िगज़ैग पथ को छोड़कर, इसे समझदारी से सीधा माना जा सकता है। चूंकि, बॉन्ड विकृतियों द्वारा और विस्तार अभी भी संभव है, उदाहरण के लिए, बॉन्ड एंगल बढ़ता है, बॉन्ड स्ट्रेच और [[द्वितल कोण]] रोटेशन होता है। ये बल वसंत की तरह हैं और एंट्रॉपी परिवर्तनों से जुड़े नहीं हैं। इस प्रकार तने हुए चेन केवल लगभग 40% तक बढ़ाया जा सकता है। इस प्रकार इस बिंदु पर श्रृंखला के साथ बल यांत्रिक रूप से सीसी सहसंयोजक बंधन को तोड़ने के लिए पर्याप्त है। इस तन्य बल सीमा की गणना की गई है।<ref name=r6 /> यहाँ पर [[क्वांटम रसायन]] विज्ञान सिमुलेशन के माध्यम से और यह लगभग 7nN है, कम तनाव पर एंट्रोपिक श्रृंखला बलों की तुलना में हजार अधिक कारक के बारे में कही गई हैं। आइसोप्रीन इकाई में आसन्न बैकबोन सी-सी बांड के बीच कोण लगभग 115-120 डिग्री के बीच भिन्न होता है और इन कोणों को बनाए रखने से जुड़े बल अधिक बड़े होते हैं, इसलिए प्रत्येक इकाई के भीतर, चेन बैकबोन सदैव ज़िगज़ैग पथ का अनुसरण करती है, इस प्रकार यहां तक कि बंधन टूटने पर भी इसका अनुसरण करती हैं। यह तंत्र लोचदार तनाव में भारी उतार-चढ़ाव के लिए जिम्मेदार है, जो उच्च उपभेदों (चित्र 1) में देखा गया है। | ||
==== नेटवर्क आकृति विज्ञान ==== | ==== नेटवर्क आकृति विज्ञान ==== | ||
चूंकि नेटवर्क पूरी तरह से केवल दो मापदंडों (प्रति इकाई मात्रा में नेटवर्क नोड्स की संख्या और बहुलक की सांख्यिकीय डी-सहसंबंध लंबाई, कुह्न लंबाई) द्वारा वर्णित है, जिस प्रकार से जंजीरों को जोड़ा जाता है वह वास्तव में अधिक जटिल है। जंजीरों की लंबाई में व्यापक भिन्नता है और उनमें से अधिकतर निकटतम निकटतम नेटवर्क नोड से जुड़े नहीं हैं। इस प्रकार श्रृंखला की लंबाई और इसकी एंड-टू-एंड दूरी दोनों को संभाव्यता वितरण द्वारा वर्णित किया गया है। 'आकृति विज्ञान' शब्द इस जटिलता को दर्शाता है। यदि क्रॉस-लिंकिंग एजेंट पूरी तरह मिश्रित है, तो इस प्रकार किसी भी आइसोप्रीन इकाई के नेटवर्क नोड बनने की समान संभावना है। डाइक्यूमाइल पेरोक्साइड के लिए, प्राकृतिक रबर में क्रॉस लिंकिंग दक्षता एकता है,<ref>L.D. Loan, Pure Appl. Chem. 30 (1972)</ref> लेकिन इस प्रकार सल्फर केस्थितियोंमें ऐसा नहीं है।<ref name=r15>D. E. Hanson and J. L. Barber, Phys. Chem. Chem. Phys. 20, 8460 (2018), LAPR-2018-029488</ref> नेटवर्क की प्रारंभिक आकारिकी दो यादृच्छिक प्रक्रियाओं द्वारा तय की जाती है: किसी भी आइसोप्रीन इकाई पर क्रॉस-लिंक होने की संभावना और श्रृंखला संरचना के मार्कोव यादृच्छिक चलने की प्रकृति के लिए उपयोगी हैं।<ref name=r7 /><ref name=r8 /> इसकी इस श्रृंखला के अंत का छोर दूसरे से कितनी दूर 'भटक' सकता है, इसके लिए प्रायिकता वितरण फ़ंक्शन मार्कोव अनुक्रम द्वारा उत्पन्न होता है।<ref name=r13>A. A. Markov, Izv. Peterb. Akad. 4 (1), 61–80 (1907)</ref> यह [[सशर्त संभाव्यता वितरण]] श्रृंखला की लंबाई से संबंधित है <math>n</math> कुह्न लंबाई की इकाइयों में <math>b</math> एंड-टू-एंड दूरी <math>r</math> के लिए : | |||
{{NumBlk||<math display="block">P(r|n) = 4 \pi r^2\left( \frac{2 n b^2 \pi}{3}\right)^{-{3}/{2}} \exp \left( -\frac{3r^2}{2nb^2} \right) \,</math>|{{EquationRef|1}}}} | {{NumBlk||<math display="block">P(r|n) = 4 \pi r^2\left( \frac{2 n b^2 \pi}{3}\right)^{-{3}/{2}} \exp \left( -\frac{3r^2}{2nb^2} \right) \,</math>|{{EquationRef|1}}}} | ||
संभावना है कि कोई आइसोप्रीन इकाई क्रॉस-लिंक नोड का | संभावना है कि कोई आइसोप्रीन इकाई क्रॉस-लिंक नोड का भाग बन जाती है, क्रॉस-लिंकर अणुओं (जैसे, डाइक्यूमिल-पेरोक्साइड) की सांद्रता के आइसोप्रीन इकाइयों के अनुपात के अनुपात के समानुपाती होती है: <math display="block">p_x = 2 \frac \text{[cross-link]} \text{[isoprene]}</math> इसके दो कारक होते हैं क्योंकि दो आइसोप्रीन इकाइयां (प्रत्येक श्रृंखला से एक) क्रॉस-लिंक में भाग लेती हैं। संभाव्यता वितरण युक्त श्रृंखला खोजने के लिए असतत संभाव्यता वितरण <math>N</math> आइसोप्रीन इकाइयों द्वारा दिया जाता है: | ||
{{NumBlk||<math display="block">P(N) = p_x{\left(1- p_x\right)}^{N-1}\, ,</math>|{{EquationRef|3}}}} | {{NumBlk||<math display="block">P(N) = p_x{\left(1- p_x\right)}^{N-1}\, ,</math>|{{EquationRef|3}}}} | ||
जहाँ <math>N\geq 1</math> | |||
समीकरण को केवल इस संभावना के रूप में समझा जा सकता है कि | |||
समीकरण को केवल इस संभावना के रूप में समझा जा सकता है कि आइसोप्रीन इकाई क्रॉस-लिंक नहीं है (1−p<sub>x</sub>) श्रृंखला के साथ N−1 क्रमिक इकाइयों में किया जाता हैं। चूँकि P(N) N के साथ घटता है, छोटी श्रृंखलाएँ लंबी श्रृंखलाओं की तुलना में अधिक संभावित होती हैं। ध्यान दें कि सांख्यिकीय रूप से स्वतंत्र बैकबोन सेगमेंट की संख्या आइसोप्रीन इकाइयों की संख्या के समान नहीं है। प्राकृतिक रबर नेटवर्क के लिए, कुछ की लंबाई में लगभग 2.2 आइसोप्रीन इकाइयाँ होती हैं, इसलिए <math>N \sim 2.2 n</math>. यह समीकरणों का उत्पाद है ({{EquationNote|1}}) और ({{EquationNote|3}}) ([[संयुक्त संभाव्यता वितरण]]) जो नेटवर्क श्रृंखला लंबाई से संबंधित है (<math>N</math>) और एंड-टू-एंड दूरी (<math>r</math>) इसके समापन क्रॉस-लिंक नोड्स के बीच: | |||
{{NumBlk||<math display="block">P(r, N) \;=\; P(N) P(r|N) \;=\; p_x{\left(1- p_x\right)}^{N-1}\, 4 \pi r^2\left( \frac{2 n b^2 \pi}{3}\right)^{-{3}/{2}} \exp \left( -\frac{3r^2}{2nb^2} \right)</math>|{{EquationRef|4}}}} | {{NumBlk||<math display="block">P(r, N) \;=\; P(N) P(r|N) \;=\; p_x{\left(1- p_x\right)}^{N-1}\, 4 \pi r^2\left( \frac{2 n b^2 \pi}{3}\right)^{-{3}/{2}} \exp \left( -\frac{3r^2}{2nb^2} \right)</math>|{{EquationRef|4}}}} | ||
[[File:Fig_3_Probability_distribution_for_typical_network_chain.jpg|thumb| | [[File:Fig_3_Probability_distribution_for_typical_network_chain.jpg|thumb|माध्य क्रॉस-लिंक नोड रिक्ति (2.9 एनएम) की इकाइयों में औसत नेटवर्क श्रृंखला बनाम एंड-टू-एंड दूरी के लिए संभावना घनत्व, एन = 52, बी = 0.96 एनएम।]] | ||
एक प्राकृतिक रबर नेटवर्क की जटिल आकृति विज्ञान को चित्र 3 में देखा जा सकता है, जो 'औसत' श्रृंखला के लिए प्रायिकता घनत्व बनाम एंड-टू-एंड दूरी (औसत नोड रिक्ति की इकाइयों में) को दर्शाता है। इस प्रकार 4x10<sup>19</sup> सेमी<sup>-3</sup> के सामान्य प्रयोगात्मक क्रॉस-लिंक घनत्व के लिए, औसत श्रृंखला में लगभग 116 आइसोप्रीन इकाइयाँ (52 कुह्न लंबाई) होती हैं, इसकी समोच्च लंबाई लगभग 50 एनएम होती है। चित्र 3 से पता चलता है कि जंजीरों का महत्वपूर्ण अंश कई नोड स्पेसिंग फैलाता है, अर्थात, श्रृंखला समाप्त अन्य नेटवर्क श्रृंखलाओं को ओवरलैप करती है। प्राकृतिक रबर, डाइक्यूमिल पेरोक्साइड के साथ क्रॉस-लिंक्ड, टेट्रा-फंक्शनल क्रॉस-लिंक्स हैं, अर्थात प्रत्येक क्रॉस-लिंक नोड में 4 नेटवर्क चेन निकलती हैं। इस प्रकार तनाव अक्ष के संबंध में उनकी प्रारंभिक वक्रता और उनके समापन बिंदुओं के उन्मुखीकरण के आधार पर, सक्रिय क्रॉस-लिंक नोड से जुड़ी प्रत्येक श्रृंखला में अलग लोचदार हुक का नियम हो सकता है क्योंकि यह लागू तनाव का विरोध करता है। प्रत्येक क्रॉस-लिंक नोड पर बल संतुलन (शून्य शुद्ध बल) को संरक्षित करने के लिए, नोड को श्रृंखला विस्तार के लिए उच्चतम बल स्थिरांक वाली श्रृंखला के साथ मिलकर चलने के लिए विवश किया जा सकता है। इस प्रकार यह जटिल नोड गति है, जो नेटवर्क आकृति विज्ञान की यादृच्छिक प्रकृति से उत्पन्न होती है, जो रबर नेटवर्क के यांत्रिक गुणों के अध्ययन को इतना कठिन बना देती है। जैसे-जैसे नेटवर्क तनावपूर्ण होता है, इन अधिक विस्तारित श्रृंखलाओं से बने पथ उभर कर सामने आते हैं जो पूरे नमूने को फैलाते हैं, और यही वे रास्ते हैं जो अधिकांश तनाव को उच्च तनाव में ले जाते हैं। | |||
==== संख्यात्मक नेटवर्क सिमुलेशन मॉडल ==== | ==== संख्यात्मक नेटवर्क सिमुलेशन मॉडल ==== | ||
रबर के नमूने की लोचदार प्रतिक्रिया की गणना करने के लिए, तीन श्रृंखला बल मॉडल ( | रबर के नमूने की लोचदार प्रतिक्रिया की गणना करने के लिए, तीन श्रृंखला बल मॉडल (प्रणाली Ia, Ib और II) और नेटवर्क आकृति विज्ञान को सूक्ष्म-यांत्रिक नेटवर्क मॉडल में जोड़ा जाना चाहिए।<ref name=r9 /><ref name=r10 /><ref name=r11 />समीकरण में संयुक्त संभाव्यता वितरण का उपयोग करना ({{EquationNote|4}}) और बल विस्तार मॉडल, नेटवर्क के वफादार प्रतिनिधि वॉल्यूम तत्व का निर्माण करने और परिणामी यांत्रिक तनाव को अनुकरण करने के लिए संख्यात्मक एल्गोरिदम तैयार करना संभव है क्योंकि यह तनाव के अधीन है। तनाव लगाए जाने पर प्रत्येक नेटवर्क नोड पर अनुमानित बल संतुलन बनाए रखने के लिए पुनरावृत्त विश्राम एल्गोरिदम का उपयोग किया जाता है। जब संख्यात्मक सिमुलेशन में 2 या 3 आइसोप्रीन इकाइयों (लगभग कुह्न लंबाई) वाले किंक के लिए प्राप्त बल स्थिरांक का उपयोग किया जाता है, तो अनुमानित तनाव प्रयोगों के अनुरूप पाया जाता है। ऐसी गणना के परिणाम<ref name=r15/>सल्फर क्रॉस-लिंक्ड प्राकृतिक रबर के लिए चित्र 1 (धराशायी लाल रेखा) में दिखाया गया है और प्रयोगात्मक डेटा के साथ तुलना की गई है <ref name=r14>{{cite journal|last=Treloar|first=L.R.G.|title=विभिन्न प्रकार के विरूपण के तहत वल्केनाइज्ड रबर के लिए तनाव-तनाव डेटा|journal=Trans. Faraday Soc.|volume=40|pages=0059|year=1944|doi=10.5254/1.3546701}}</ref> (ठोस नीली रेखा)। ये सिमुलेशन भी तनाव में तेजी से वृद्धि की भविष्यवाणी करते हैं क्योंकि नेटवर्क श्रृंखलाएं तंग हो जाती हैं और अंत में, बंधन टूटने के कारण भौतिक विफलता होती है। इसमें उपस्थित सल्फर क्रॉस-लिंक्ड प्राकृतिक रबर की विभिन्न स्थितियों में, क्रॉस-लिंक में एसएस बांड चेन बैकबोन पर सीसी बांड की तुलना में बहुत कमजोर होती हैं और नेटवर्क की विफलता के बिंदु पर केंद्रित रहती हैं। इस प्रकार सिम्युलेटेड तनाव में पठार, लगभग 7 के तनाव से प्रारंभ होकर, नेटवर्क के लिए सीमित मूल्य है। लगभग 7 एमपीए से अधिक के तनाव का समर्थन नहीं किया जा सकता है और नेटवर्क विफल हो जाता है। इस प्रकार इस तनाव सीमा के पास, सिमुलेशन भविष्यवाणी करते हैं<ref name=r11/>कि 10% से कम जंजीरें तनी हुई हैं, अर्थात उच्च श्रृंखला विस्तार व्यवस्था में और 0.1% से कम जंजीरें फट गई हैं। जबकि बहुत कम टूटना अंश आश्चर्यजनक लग सकता है, यह रबर बैंड को तब तक खींचने के हमारे अनुभव के साथ असंगत नहीं है जब तक कि यह टूट न जाए इस बात का ध्यान रखना आवश्यक होता हैं। इसके टूटने के बाद रबर की लोचदार प्रतिक्रिया मूल से अलग नहीं होती हैं। | ||
== प्रयोग == | == प्रयोग == | ||
===तापमान के साथ तनन तनाव का परिवर्तन=== | ===तापमान के साथ तनन तनाव का परिवर्तन=== | ||
तनाव के रूप में तापमान के साथ तन्य तनाव का परिवर्तन चार मानों (100%, 200%, 300% और 380%) पर स्थिर रहता है।<ref name=r18>{{cite journal|last1=Anthony|first1=R.L.|last2=Caston|first2=R.H.|last3=Guth|first3=E.|title=प्राकृतिक और सिंथेटिक रबर जैसी सामग्री के लिए राज्य के समीकरण। I. गैर-त्वरित प्राकृतिक नरम रबर|journal=J. Phys. Chem.|volume=46|pages=826-840|year=1942|doi=10.5254/1.3540117}}</ref> ऊष्मीय संतुलन में आणविक प्रणालियों के लिए, ऊर्जा का जोड़ इ जी यांत्रिक कार्य द्वारा, एंट्रॉपी में परिवर्तन का कारण बन सकता है। यह ऊष्मप्रवैगिकी और सांख्यिकीय यांत्रिकी के सिद्धांतों से जाना जाता है। इस प्रकार विशेष रूप से, दोनों सिद्धांतों का प्रमाण है कि ऊर्जा में परिवर्तन एंट्रॉपी परिवर्तन समय के पूर्ण तापमान के समानुपाती होना चाहिए। यह नियम तभी तक मान्य है जब तक कि ऊर्जा अणुओं की ऊष्मीय अवस्थाओं तक ही सीमित है। यदि रबर के नमूने को अधिक दूर तक खींचा जाता है, तो इस प्रकार ऊर्जा गैर-तापीय अवस्थाओं में रह सकती है जैसे कि रासायनिक बंधों का विरूपण और नियम लागू नहीं होता है। इस प्रकार निम्न से मध्यम उपभेदों पर, सिद्धांत भविष्यवाणी करता है कि आवश्यक खिंचाव बल नेटवर्क श्रृंखलाओं में एन्ट्रॉपी में परिवर्तन के कारण होता है। यदि यह सही है, तो हम अपेक्षा करते हैं कि किसी नमूने को तनाव के कुछ मान तक खींचने के लिए आवश्यक बल नमूने के तापमान के समानुपाती होना चाहिए। तापमान के साथ तन्यता तनाव कैसे भिन्न होता है, इस प्रकार यह दिखाते हुए माप चित्र 4 में दिखाए गए हैं। इस प्रकार इन प्रयोगों में,<ref name=r18/> खींचे गए रबर के नमूने का तनाव स्थिर रखा गया था क्योंकि तापमान 10 से 70 डिग्री सेल्सियस के बीच भिन्न था। निश्चित तनाव के प्रत्येक मूल्य के लिए, यह देखा जाता है कि तन्य तनाव रैखिक रूप से भिन्न होता है। ये प्रयोग सबसे सम्मोहक साक्ष्य प्रदान करते हैं कि रबर लोच के लिए एन्ट्रापी परिवर्तन मूलभूत तंत्र हैं। | |||
तापमान के साथ तनाव का सकारात्मक रैखिक व्यवहार कभी-कभी गलत धारणा की ओर ले जाता है कि रबर में | |||
तापमान के साथ तनाव का सकारात्मक रैखिक व्यवहार कभी-कभी गलत धारणा की ओर ले जाता है कि रबर में ऊष्मीय विस्तार का ऋणात्मक गुणांक होता है, अर्थात गर्म होने पर नमूने की लंबाई सिकुड़ जाती है। प्रयोगों<ref>L. A. Wood and G. Martin, Journal of Research of the National Bureau of Standards-A. Physics and Chemistry Vol 68A, No. 3 (1964).</ref> ने निर्णायक रूप से दिखाया है कि, लगभग सभी अन्य सामग्रियों की तरह, ऊष्मीय विस्तार का गुणांक प्राकृतिक रबर सकारात्मक है। | |||
=== स्नैप-बैक वेग === | === स्नैप-बैक वेग === | ||
रबड़ के नमूने बनाम समय के अंत और मध्य बिंदु का विस्थापन क्योंकि यह उच्च विस्तार से वापस आ जाता है।<ref name=r20>{{cite journal|last1=Mrowca|first1=B.A.|last2=Dart|first2=S.L.|last3=Guth|first3=E.|title=तनावग्रस्त रबर की वापसी|journal=Phys. Rev.|volume=66|pages=30|year=1944|doi=10.1103/PhysRev.66.30.2}}</ref> जब हम रबड़ के टुकड़े को खींचते हैं, उदाहरण के लिए रबर बैंड, हम देखते हैं कि यह लंबाई में समान रूप से विकृत होता है। इसकी लंबाई के साथ प्रत्येक तत्व पूरे नमूने के समान विस्तार कारक का अनुभव करता है। इस प्रकार यदि हम छोर को छोड़ देते हैं, तो नमूना बहुत तेजी से अपनी मूल लंबाई पर वापस आ जाता है, प्रक्रिया को हल करने के लिए हमारी आंख के लिए बहुत तेजी से। हमारी सहज अपेक्षा यह है कि यह अपनी मूल लंबाई पर उसी तरह लौटता है। जैसे कि जब इसे खींचा गया था, अर्थात। इ। समान रूप से। चूंकि, ऐसा नहीं होता है। म्रोव्का एट एल द्वारा प्रायोगिक अवलोकन किया जाता हैं।<ref name=r20 /> इसके आश्चर्यजनक परिणाम प्राप्त होते हैं। इस प्रकार अत्यधिक तेज़ प्रत्यावर्तन गतिकी को पकड़ने के लिए, उन्होंने एक्सनर और स्टीफ़न द्वारा तैयार की गई चतुर प्रयोगात्मक विधि का उपयोग किया गया था।<ref>G. S. Whitby, "Plantation Rubber and the Testing of Rubber", Longmans and Green, London, 1920. p 461</ref> इस प्रकार 1874 में, उच्च गति वाले इलेक्ट्रॉनिक मापने वाले उपकरणों का आविष्कार होने से पहले। उनकी पद्धति में तेजी से घूमने वाला कांच का सिलेंडर सम्मिलित था, जिसे लैंप ब्लैक के साथ लेपित करने के बाद, फैलाए गए रबड़ के नमूने के बगल में रखा गया था। इस प्रकार रबर के नमूने के मध्य-बिंदु और मुक्त सिरे से जुड़ी स्टाइलि को ग्लास सिलेंडर के संपर्क में रखा गया था। फिर, जैसे ही रबर का मुक्त सिरा वापस टूटा, स्टाइली ने घूर्णन सिलेंडर के लैंप ब्लैक कोटिंग में पेचदार रास्तों का पता लगाया था। सिलेंडर की घूर्णन गति को समायोजित करके, वे से कम पूर्ण रोटेशन में स्टाइली की स्थिति रिकॉर्ड कर सकते थे। नम ब्लोटर पेपर के टुकड़े पर सिलेंडर को रोल करके प्रक्षेपवक्र को ग्राफ में स्थानांतरित कर दिया गया था। इस लेखनी द्वारा छोड़े गए निशान कागज पर सफेद रेखा (कोई दीपक काला नहीं) के रूप में दिखाई देते हैं। | |||
उनका डेटा, चित्र 5 में ग्राफ के रूप में प्लॉट किया गया है, अंत और मध्यबिंदु स्टाइलि की स्थिति दिखाता है क्योंकि नमूना तेजी से अपनी मूल लंबाई में वापस आ जाता है। नमूना | |||
उच्च विस्तार पर फैली हुई नेटवर्क श्रृंखला में संग्रहीत कुछ ऊर्जा इसकी एन्ट्रापी में परिवर्तन के कारण होती है, लेकिन अधिकांश ऊर्जा बांड विकृतियों (उपरोक्त | उनका डेटा, चित्र 5 में ग्राफ के रूप में प्लॉट किया गया है, अंत और मध्यबिंदु स्टाइलि की स्थिति दिखाता है क्योंकि नमूना तेजी से अपनी मूल लंबाई में वापस आ जाता है। नमूना प्रारंभ में अपनी अप्रशिक्षित लंबाई से 9.5” ऊपर खींचा गया और फिर छोड़ दिया गया। स्टाइलि 6 एमएस से थोड़ा अधिक समय में अपनी मूल स्थिति (0 का विस्थापन) पर लौट आया। विस्थापन बनाम समय का रैखिक व्यवहार इंगित करता है कि, संक्षिप्त त्वरण के बाद, नमूने का अंत और मध्य बिंदु दोनों लगभग 50 मी/से या 112 मील प्रति घंटे के निरंतर वेग से वापस आ गए। चूंकि, अंत प्रस्तुत होने के बाद लगभग 3 एमएस तक मिडपॉइंट स्टाइलस चलना प्रारंभ नहीं हुआ। प्रकट है, वापसी की प्रक्रिया लहर के रूप में यात्रा करती है, मुक्त छोर से प्रारंभ होती है। | ||
उच्च विस्तार पर फैली हुई नेटवर्क श्रृंखला में संग्रहीत कुछ ऊर्जा इसकी एन्ट्रापी में परिवर्तन के कारण होती है, लेकिन अधिकांश ऊर्जा बांड विकृतियों (उपरोक्त प्रणाली II, ऊपर) में संग्रहीत होती है, जिसमें एन्ट्रापी परिवर्तन सम्मिलित नहीं होता है। यदि कोई मानता है कि सभी संग्रहीत ऊर्जा गतिज ऊर्जा में परिवर्तित हो जाती है, तो प्रत्यावर्तन वेग की गणना सीधे परिचित संरक्षण समीकरण E ={{1/2}} mv<sup>2 से की जा सकती है। इस प्रकार संख्यात्मक सिमुलेशन,<ref name="r10" />आणविक किंक प्रतिमान के आधार पर, इस प्रयोग के अनुरूप वेगों की भविष्यवाणी करेता हैं। | |||
== लोच सिद्धांत के लिए ऐतिहासिक दृष्टिकोण == | == लोच सिद्धांत के लिए ऐतिहासिक दृष्टिकोण == | ||
[[यूजीन गुथ]] और ह्यूबर्ट एम। जेम्स ने 1941 में रबर लोच की एन्ट्रोपिक उत्पत्ति का प्रस्ताव | [[यूजीन गुथ]] और ह्यूबर्ट एम। जेम्स ने 1941 में रबर लोच की एन्ट्रोपिक उत्पत्ति का प्रस्ताव रखा था।<ref name="James and Guth 1941">{{cite journal |last1=Guth|first1=Eugene| last2=James|first2=Hubert M.| title=रबर जैसी सामग्री के लोचदार और थर्मोइलास्टिक गुण| journal=Ind. Eng. Chem.|date=May 1941|volume=33 |issue=5| pages=624–629| doi=10.1021/ie50377a017}}</ref> | ||
=== ऊष्मप्रवैगिकी === | === ऊष्मप्रवैगिकी === | ||
तापमान असामान्य | तापमान असामान्य विधि से इलास्टोमर्स की लोच को प्रभावित करता है। जब इलास्टोमेर को फैला हुआ अवस्था में माना जाता है, तो हीटिंग उन्हें अनुबंधित करने का कारण बनता है। इसके विपरीत, ठंडा करने से विस्तार हो सकता है।<ref>{{Citation | ||
|title= Thermodynamics of a Rubber Band | |title= Thermodynamics of a Rubber Band | ||
|journal=American Journal of Physics | |journal=American Journal of Physics | ||
| Line 83: | Line 89: | ||
|page= 397 | |page= 397 | ||
|doi= 10.1119/1.1969535|bibcode = 1963AmJPh..31..397T }}</ref> | |doi= 10.1119/1.1969535|bibcode = 1963AmJPh..31..397T }}</ref> | ||
यह | |||
इसका परिणाम यह होता है कि | यह साधारण [[रबर बैंड]] के साथ देखा जा सकता है। रबर बैंड को खींचने से यह गर्मी छोड़ेगा (इसे अपने होठों के विरुद्ध दबाएं), जबकि इसे खींचे जाने के पश्चात इसे प्रस्तुत करने से यह गर्मी को अवशोषित कर लेगा, जिससे इसका परिवेश ठंडा हो जाएगा। इस परिघटना को [[गिब्स मुक्त ऊर्जा]] द्वारा समझाया जा सकता है। ΔG=ΔH−TΔS को पुनर्व्यवस्थित करने पर, जहाँ G मुक्त ऊर्जा है, H [[तापीय धारिता]] है, और S एन्ट्रॉपी है, हमें मिलता है {{math|1=''T'' Δ''S'' = Δ''H'' − Δ''G''}}. चूंकि खिंचाव सहज नहीं है, क्योंकि इस प्रकार इसके लिए बाहरी कार्य की आवश्यकता होती है, TΔS ऋणात्मक होना चाहिए। चूँकि T सदैव धनात्मक होता है (यह कभी भी पूर्ण शून्य तक नहीं पहुँच सकता है), ΔS को ऋणात्मक होना चाहिए, जिसका अर्थ है कि रबर अपनी प्राकृतिक अवस्था में अधिक उलझा हुआ है (अधिक [[माइक्रोस्टेट (सांख्यिकीय यांत्रिकी)]] के साथ) जब यह तनाव में होता है। इस प्रकार, जब तनाव हटा दिया जाता है, तो प्रतिक्रिया सहज होती है, जिससे ΔG ऋणात्मक हो जाती है। जिसके परिणाम स्वरुप , शीतलन प्रभाव का परिणाम सकारात्मक ΔH होना चाहिए, इसलिए ΔS वहां धनात्मक प्राप्त होगा।<ref>Rubber Bands and Heat, http://scifun.chem.wisc.edu/HomeExpts/rubberband.html {{Webarchive|url=https://web.archive.org/web/20190613204939/http://scifun.chem.wisc.edu/HOMEEXPTS/rubberband.html |date=2019-06-13 }}, citing {{Harvtxt|Shakhashiri|1983}}</ref><ref>{{Citation |title=Chemical Demonstrations: A Handbook for Teachers of Chemistry |volume=1 |first=Bassam Z. |last= Shakhashiri |year= 1983 |publisher= The University of Wisconsin Press |location= Madison, WI |isbn= 978-0-299-08890-3 }}</ref> | ||
इसका परिणाम यह होता है कि इलास्टोमर कुछ हद तक आदर्श मोनोएटोमिक गैस की तरह व्यवहार करता है, क्योंकि (अच्छे सन्निकटन के लिए) इलास्टिक पॉलीमर किसी भी संभावित ऊर्जा को स्ट्रेच्ड केमिकल बॉन्ड्स या स्ट्रेचिंग मॉलिक्यूल्स में किए गए इलास्टिक वर्क में स्टोर नहीं करते हैं, जब उन पर कार्य किया जाता है। इसके अतिरिक्त, रबर पर किए गए सभी कार्य प्रस्तुत (संग्रहीत नहीं) होते हैं और तुरंत बहुलक में तापीय ऊर्जा के रूप में दिखाई देते हैं। इस प्रकार इस प्रकार कार्य करने के लिए इलास्टिक द्वारा आसपास के वातावरण में किए जाने वाले सभी कार्य तापीय ऊर्जा के विलुप्त होने का कारण बनती हैं (इलास्टिक बैंड विस्तारित गैस की तरह ठंडा हो जाता है)। यह अंतिम घटना महत्वपूर्ण सुराग है कि कार्य करने के लिए इलास्टोमर की क्षमता (एक आदर्श गैस के साथ) केवल एन्ट्रापी-परिवर्तन के विचारों पर निर्भर करती है, न कि बहुलक बांडों के भीतर किसी संग्रहीत (अर्थात, संभावित) ऊर्जा पर प्राप्त किया जाता हैं। इसके अतिरिक्त, कार्य करने के लिए ऊर्जा पूरी तरह से तापीय ऊर्जा से आती है, और (जैसा कि विस्तारित आदर्श गैस केस्थितियोंमें) बहुलक का केवल सकारात्मक एन्ट्रापी परिवर्तन इसकी आंतरिक तापीय ऊर्जा को कुशलता से परिवर्तित करने की अनुमति देता है इस प्रकार इस सिद्धांत में 100 प्रतिशत कार्य में उपयोग किया जाता हैं। | |||
=== पॉलिमर श्रृंखला सिद्धांत === | === पॉलिमर श्रृंखला सिद्धांत === | ||
रबर लोच के सिद्धांत का आह्वान करते हुए, | रबर लोच के सिद्धांत का आह्वान करते हुए, क्रॉस-लिंक्ड नेटवर्क में बहुलक श्रृंखला को [[एंट्रोपिक बल]] के रूप में मानता है। जब श्रृंखला को बढ़ाया जाता है, तो एंट्रॉपी बड़े मार्जिन से कम हो जाती है क्योंकि कम अनुरूपताएं उपलब्ध होती हैं।<ref>{{Citation | ||
|author=L.R.G. Treloar | |author=L.R.G. Treloar | ||
|title= Physics of Rubber Elasticity | |title= Physics of Rubber Elasticity | ||
|year= 1975 | |year= 1975 | ||
|publisher=Oxford University Press | |publisher=Oxford University Press | ||
|isbn= 9780198570271}}</ref> इसलिए, | |isbn= 9780198570271}}</ref> इसलिए, प्रत्यानयन बल होता है, जो बार बाहरी बल हटा दिए जाने पर, बहुलक श्रृंखला को उसके संतुलन या अविस्तारित अवस्था में लौटने का कारण बनता है, इस प्रकार जैसे कि उच्च एन्ट्रापी यादृच्छिक कुंडल विन्यास। यही कारण है कि रबर बैंड अपनी मूल स्थिति में लौट आते हैं। रबर लोच के लिए दो सामान्य मॉडल स्वतंत्र रूप से जुड़े श्रृंखला मॉडल और वर्म-जैसी श्रृंखला मॉडल हैं। | ||
==== स्वतंत्र रूप से जुड़ा हुआ चेन मॉडल ==== | ==== स्वतंत्र रूप से जुड़ा हुआ चेन मॉडल ==== | ||
{{Main| | {{Main|स्वतंत्र रूप से संयुक्त श्रृंखला}} | ||
स्वतंत्र रूप से जुड़ी हुई श्रृंखला, जिसे | स्वतंत्र रूप से जुड़ी हुई श्रृंखला, जिसे आदर्श श्रृंखला भी कहा जाता है, [[रैंडम वॉक मॉडल]] का अनुसरण करती है। सूक्ष्म रूप से, बहुलक श्रृंखला का 3-डी यादृच्छिक चलना एक्स, वाई और जेड दिशाओं के संदर्भ में समग्र अंत-टू-एंड दूरी को व्यक्त करता है: | ||
[[File:FJCpolymer.JPG|स्वतंत्र रूप से जुड़ी हुई श्रृंखला का मॉडल|alt=|thumb|265x265px]] | [[File:FJCpolymer.JPG|स्वतंत्र रूप से जुड़ी हुई श्रृंखला का मॉडल|alt=|thumb|265x265px]] | ||
<math display="block">\vec{R} = R_x\hat{x} + R_y\hat{y} + R_z\hat{z}</math> | <math display="block">\vec{R} = R_x\hat{x} + R_y\hat{y} + R_z\hat{z}</math> | ||
मॉडल में, <math>b </math> कठोर खंड की लंबाई है, <math>N </math> लंबाई के खंडों की संख्या है <math>b </math>, <math>R </math> निश्चित और मुक्त सिरों के बीच की दूरी है, और <math>L_\text{c} </math> समोच्च लंबाई है या <math>Nb</math>. कांच के संक्रमण तापमान के ऊपर, बहुलक श्रृंखला दोलन करती है और <math>r</math> समय के साथ | मॉडल में, <math>b </math> कठोर खंड की लंबाई है, <math>N </math> लंबाई के खंडों की संख्या है <math>b </math>, <math>R </math> निश्चित और मुक्त सिरों के बीच की दूरी है, और <math>L_\text{c} </math> समोच्च लंबाई है या <math>Nb</math>. कांच के संक्रमण तापमान के ऊपर, बहुलक श्रृंखला दोलन करती है और <math>r</math> समय के साथ परिवर्तित होती हैं। इस श्रृंखला का संभाव्यता वितरण व्यक्तिगत घटकों के संभाव्यता वितरण का उत्पाद है, जो निम्नलिखित गॉसियन वितरण द्वारा दिया गया है: | ||
<math display="block">P(\vec{R}) = P(R_x) P(R_y) P(R_z) = \left( \frac{2 n b^2 \pi}{3}\right)^{-{3}/{2}} \exp \left( \frac{-3R^2}{2Nb^2} \right)</math> | <math display="block">P(\vec{R}) = P(R_x) P(R_y) P(R_z) = \left( \frac{2 n b^2 \pi}{3}\right)^{-{3}/{2}} \exp \left( \frac{-3R^2}{2Nb^2} \right)</math> | ||
इसलिए, पहनावा औसत एंड-टू-एंड दूरी सभी जगहों पर संभाव्यता वितरण का मानक अभिन्न अंग है। ध्यान दें कि आंदोलन पीछे या आगे हो सकता है, इसलिए शुद्ध औसत <math>\langle R\rangle</math> शून्य होगा। | इसलिए, पहनावा औसत एंड-टू-एंड दूरी सभी जगहों पर संभाव्यता वितरण का मानक अभिन्न अंग है। इस प्रकार ध्यान दें कि आंदोलन पीछे या आगे हो सकता है, इसलिए शुद्ध औसत <math>\langle R\rangle</math> शून्य होगा। चूंकि, रूट माध्य वर्ग का उपयोग दूरी के उपयोगी माप के रूप में किया जा सकता है।<math display="block">\begin{align} | ||
<math display="block">\begin{align} | |||
\langle R\rangle &= 0 \\ | \langle R\rangle &= 0 \\ | ||
\langle R^2\rangle &= \int_0^\infty R^24\pi R^2 P(\vec{R})dR = Nb^2 \\ | \langle R^2\rangle &= \int_0^\infty R^24\pi R^2 P(\vec{R})dR = Nb^2 \\ | ||
\langle R^2\rangle^\frac{1}{2} &= \sqrt{N} b | \langle R^2\rangle^\frac{1}{2} &= \sqrt{N} b | ||
\end{align}</math> | \end{align}</math> | ||
हम फ्लोरी सिद्धांत को | |||
रबर लोच के फ्लोरी सिद्धांत ने बताया है कि रबर लोच में मुख्य रूप से एन्ट्रोपिक उत्पत्ति होती है। हेल्महोल्ट्ज़ मुक्त ऊर्जा के लिए निम्नलिखित बुनियादी समीकरणों का उपयोग करके और एन्ट्रापी के बारे में इसकी चर्चा करके, रबर श्रृंखला के विरूपण से उत्पन्न बल को उसके मूल गैर-विस्तारित संरूपण से प्राप्त किया जा सकता है। इस प्रकार यहाँ पर <math>\Omega</math> h> बहुलक श्रृंखला के अनुरूपताओं की संख्या है। चूँकि विकृति में एन्थैल्पी परिवर्तन सम्मिलित नहीं है, मुक्त ऊर्जा में परिवर्तन की गणना एंट्रॉपी में परिवर्तन के रूप <math>-T\Delta S</math> में की जा सकती है। इस प्रकार यह देखा जा सकता है कि बल समीकरण वसंत के व्यवहार जैसा दिखता है और हुक के नियम का पालन करता है: <math>F = kx</math>, जहां F बल है, k वसंत स्थिरांक और x दूरी है। सामान्यतः, [[नव-हुकियन ठोस]] या नव-हुकियन मॉडल का उपयोग उनके तनाव के संबंधों की भविष्यवाणी करने के लिए क्रॉस-लिंक्ड पॉलिमर पर किया जा सकता है:<math display="block">\Omega = C \exp \left ( \frac{-3\vec{R}^2}{2Nb^2} \right ) | |||
</math><math display="block">S = k_\text{B} \ln \Omega \, \approx \frac{-3k_\text{B} \vec{R}^2}{2Nb^2} </math><math display="block">\Delta F(\vec{R}) \approx -T\Delta S_d(\vec{R}^2) = C+\frac{3 k_\text{B} T}{N b^2} \vec{R}^2</math><math display="block">f =\frac{dF(\vec{R})}{d\vec{R}} = \frac{d}{d\vec{R}}\left(\frac{3k_\text{B}T\vec{R}^2}{2Nb^2}\right) = \frac{3k_\text{B}T}{Nb^2} \vec{R}</math> | |||
ध्यान दें कि लोचदार गुणांक <math>3 k_\text{B} T/N b</math> तापमान पर निर्भर है। यदि हम रबर का तापमान बढ़ाते हैं, तो लोचदार गुणांक भी बढ़ जाता है। यही कारण है कि क्रम में होने वाले तनाव में रहने वाला रबर तापमान बढ़ने पर सिकुड़ जाता है। | |||
हम फ्लोरी सिद्धांत को मैक्रोस्कोपिक दृश्य में आगे बढ़ा सकते हैं, जहां बल्क रबर सामग्री पर चर्चा की जाती है। इस प्रकार मान लें कि रबर सामग्री का मूल आयाम है <math>L_x</math>, <math>L_y</math> और <math>L_z</math>, विकृत आकार को व्यक्तिगत विस्तार अनुपात लागू करके <math>\lambda_i</math> लंबाई तक (<math>\lambda_x L_x</math>, <math>\lambda_y L_y</math>, <math>\lambda_z L_z</math>). तक व्यक्त किया जा सकता है, तो इस प्रकार सूक्ष्म रूप से, विकृत बहुलक श्रृंखला को विस्तार अनुपात के साथ भी व्यक्त किया जा सकता है: <math>\lambda_x R_x</math>, <math>\lambda_y R_y</math>, <math>\lambda_z R_z</math>. विरूपण के कारण मुक्त ऊर्जा परिवर्तन को निम्नानुसार व्यक्त किया जा सकता है: | |||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 133: | Line 139: | ||
प्रति आयतन मुक्त ऊर्जा परिवर्तन बस है: | प्रति आयतन मुक्त ऊर्जा परिवर्तन बस है: | ||
<math display="block">\Delta f_\text{def} = \frac{\Delta F_\text{def}(\vec{R})}{V} = -\frac{k_\text{B}T v_s \beta \left(\lambda_x^2 + \lambda_y^2 + \lambda_z^2 - 3\right)}{2}</math> | <math display="block">\Delta f_\text{def} = \frac{\Delta F_\text{def}(\vec{R})}{V} = -\frac{k_\text{B}T v_s \beta \left(\lambda_x^2 + \lambda_y^2 + \lambda_z^2 - 3\right)}{2}</math> | ||
जहाँ <math>n_s</math> नेटवर्क में स्ट्रैंड्स की संख्या है, सबस्क्रिप्ट डीफ़ का मतलब विरूपण <math>v_s = n_s / V</math> है , जो बहुलक शृंखलाओं का प्रति आयतन संख्या घनत्व <math>\beta = \langle R^2\rangle / R_0^2</math> है, इस प्रकार जो श्रृंखला के अंत से अंत तक की दूरी और यादृच्छिक चलने के आंकड़ों का पालन करने वाली सैद्धांतिक दूरी के बीच का अनुपात है। यदि हम असम्पीड्यता मान लेते हैं, तो विस्तार अनुपात का गुणनफल 1 होता है, जिसका अर्थ है आयतन में कोई परिवर्तन नहीं: <math>\lambda_x \lambda_y \lambda_z = 1</math>. | |||
<u>केस स्टडी: | <u>केस स्टडी: अक्षीय विरूपण:</u> | ||
इस प्रकार अक्षीय विकृत रबर में, क्योंकि <math>\lambda_x \lambda_y \lambda_z = 1</math> हम यह मानते है कि <math>\lambda_x = \lambda_y = \lambda_z^{-1/2}</math>. तो पिछली मुक्त ऊर्जा प्रति आयतन समीकरण है:<math display="block">\Delta f_\text{def} = \frac{\Delta F_\text{def}(\vec{R})}{V} = -\frac{k_\text{B}T v_s \beta \left(\lambda_x^2 + \lambda_y^2 + \lambda_z^2 - 3\right)}{2} | |||
<math display="block">\Delta f_\text{def} = \frac{\Delta F_\text{def}(\vec{R})}{V} = -\frac{k_\text{B}T v_s \beta \left(\lambda_x^2 + \lambda_y^2 + \lambda_z^2 - 3\right)}{2} | = \frac{k_\text{B}T v_s\beta}{2} \left(\lambda_z^2 + \frac{2}{\lambda_z}-3\right)</math>विस्तार अनुपात के संदर्भ में [[इंजीनियरिंग तनाव]] (परिभाषा के अनुसार) ऊर्जा का पहला व्युत्पन्न है, जो तनाव की अवधारणा के बराबर है:<math display="block">\sigma_\text{eng}=\frac{d(\Delta f_\text{def})}{\lambda_z} = k_\text{B}T v_s \beta\left(\lambda_z-\frac{1}{\lambda_z^2}\right)</math>और यंग का मापांक|यंग का मापांक <math>E</math> तनाव के संबंध में तनाव के व्युत्पन्न के रूप में परिभाषित किया गया है, जो प्रयोगशाला प्रयोगों में रबर की [[कठोरता]] को मापता है।<math display="block">E=\frac{d(\sigma_\text{eng})}{d\lambda_z}=k_\text{B}T v_s \beta \left.\left(1+ \frac{2}{\lambda_z^3}\right)\right|_{\lambda_z=1} | ||
= \frac{k_\text{B}T v_s\beta}{2} \left(\lambda_z^2 + \frac{2}{\lambda_z}-3\right)</math> | = 3 k_\text{B}T v_s\beta = \frac{3\rho \beta RT}{M_s}</math> | ||
विस्तार अनुपात के संदर्भ में [[इंजीनियरिंग तनाव]] (परिभाषा के अनुसार) ऊर्जा का पहला व्युत्पन्न है, जो तनाव की अवधारणा के बराबर है: | |||
<math display="block">\sigma_\text{eng}=\frac{d(\Delta f_\text{def})}{\lambda_z} = k_\text{B}T v_s \beta\left(\lambda_z-\frac{1}{\lambda_z^2}\right)</math> | |||
और यंग का मापांक|यंग का मापांक <math>E</math> तनाव के संबंध में तनाव के व्युत्पन्न के रूप में परिभाषित किया गया है, जो प्रयोगशाला प्रयोगों में रबर की [[कठोरता]] को मापता है। | |||
जहाँ <math>v_s = \rho N_a / M_s</math>, <math>\rho</math> श्रृंखला का द्रव्यमान घनत्व है, इस प्रकार <math>M_s</math> क्रॉसलिंक्स के बीच नेटवर्क स्ट्रैंड का नंबर औसत आणविक भार है। यहाँ, इस प्रकार का विश्लेषण<ref name="BS">{{cite journal|last1=Buche|first1=M.R.|last2=Silberstein|first2=M.N.|title=Statistical mechanical constitutive theory of polymer networks: The inextricable links between distribution, behavior, and ensemble|journal=Phys. Rev. E|volume=102|pages=012501|year=2020|doi=10.1103/PhysRevE.102.012501|arxiv=2004.07874}}</ref> रबर लोच के थर्मोडायनामिक सिद्धांत को प्रायोगिक रूप से मापने योग्य मापदंडों से जोड़ता है। इस प्रकार इसके अतिरिक्त, यह सामग्री की क्रॉस-लिंकिंग स्थिति में जगहें देता है। | |||
====कीड़ा जैसा चेन मॉडल==== | ====कीड़ा जैसा चेन मॉडल==== | ||
वर्म-लाइक चेन मॉडल (WLC) | वर्म-लाइक चेन मॉडल (WLC) अणु को खाते में मोड़ने के लिए आवश्यक ऊर्जा लेता है। इस प्रकार इसके अतिरिक्त चर <math>L_\text{p}</math> समान हैं, पर्सिस्टेंस लेंथ <math>b </math> रिप्लेस करता है . फिर, बल इस समीकरण का अनुसरण करता है:<math display="block">F \approx \frac{k_\text{B} T}{L_\text{p}} \left ( \frac{1}{4 \left( 1- \frac{r}{L_{\rm c}} \right )^2} - \frac{1}{4} + \frac{r}{L_\text{c}} \right ) </math> | ||
<math display="block">F \approx \frac{k_\text{B} T}{L_\text{p}} \left ( \frac{1}{4 \left( 1- \frac{r}{L_{\rm c}} \right )^2} - \frac{1}{4} + \frac{r}{L_\text{c}} \right ) </math> | |||
इसलिए, जब श्रृंखला के सिरों (r = 0) के बीच कोई दूरी नहीं होती है, तो ऐसा करने के लिए आवश्यक बल शून्य होता है, और बहुलक श्रृंखला को पूरी तरह से विस्तारित करने के लिए (<math> r = L_\text{c} </math>), | |||
इसलिए, जब श्रृंखला के सिरों (r = 0) के बीच कोई दूरी नहीं होती है, तो ऐसा करने के लिए आवश्यक बल शून्य होता है, और बहुलक श्रृंखला को पूरी तरह से विस्तारित करने के लिए (<math> r = L_\text{c} </math>), अनंत बल की आवश्यकता होती है, जो सहज ज्ञान युक्त है। इस प्रकार रेखांकन के अनुसार, बल मूल बिंदु से प्रारंभ होता है और इस प्रकार प्रारंभ में रैखिक रूप <math>r</math>. से बढ़ता है तथा यहाँ पर बल तब पठार होता है लेकिन अंततः फिर से बढ़ जाता है और श्रृंखला <math>L_\text{c}</math> की लंबाई के समीप पहुंचने पर अनंत तक पहुंच जाता है। | |||
== यह भी देखें == | == यह भी देखें == | ||
| Line 160: | Line 164: | ||
==संदर्भ== | ==संदर्भ== | ||
{{Reflist}} | {{Reflist}} | ||
[[Category:All articles with unsourced statements]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category: | [[Category:Articles with invalid date parameter in template]] | ||
[[Category:Articles with unsourced statements from August 2021]] | |||
[[Category:Created On 24/02/2023]] | [[Category:Created On 24/02/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:ऊष्मप्रवैगिकी]] | |||
[[Category:यांत्रिकी]] | |||
[[Category:रबड़ के गुण]] | |||
Latest revision as of 11:09, 10 March 2023
रबड़ लोच क्रॉसलिंक्ड रबड़ की संपत्ति को संदर्भित करता है: इसे अपनी मूल लंबाई से 10 के कारक तक बढ़ाया जा सकता है और जब प्रस्तुत किया जाता है, तो इसकी मूल लंबाई के समीपस्थ वापस कर लिया जाता है। इसे कई बार दोहराया जा सकता है और रबर में कोई स्पष्ट कमी नहीं होती है। रबर सामग्री के बड़े वर्ग का सदस्य है जिसे इलास्टोमर्स कहा जाता है और उनके आर्थिक और तकनीकी महत्व को कम आंकना कठिन है। इलास्टोमर्स ने 20वीं सदी में नई विधियों के विकास में महत्वपूर्ण भूमिका है और वैश्विक अर्थव्यवस्था में महत्वपूर्ण योगदान दिया है। रबर लोच कई जटिल आणविक प्रक्रियाओं द्वारा निर्मित होता है और इसकी व्याख्या के लिए उन्नत गणित, रसायन विज्ञान और सांख्यिकीय भौतिकी, विशेष रूप से एन्ट्रापी की अवधारणा के ज्ञान की आवश्यकता होती है। एंट्रॉपी को तापीय ऊर्जा के माप के रूप में माना जा सकता है जो अणु में संग्रहीत होता है।
सामान्य रबर, जैसे कि पॉलीब्यूटाडाइन और पॉलीसोप्रीन (जिसे प्राकृतिक रबर भी कहा जाता है), पोलीमराइज़ेशन नामक प्रक्रिया द्वारा निर्मित होते हैं। इस प्रकार बहुत लंबे अणु (बहुलक) रासायनिक प्रतिक्रियाओं के माध्यम से छोटी आणविक रीढ़ की इकाइयों को जोड़कर क्रमिक रूप से निर्मित होते हैं। रबर बहुलक तीन आयामों में यादृच्छिक, ज़िगज़ैग पथ का अनुसरण करता है, जो कई अन्य रबर अणुओं के साथ परस्पर क्रिया करता है। इस प्रकार सल्फर जैसे क्रॉस लिंकिंग अणु के कुछ प्रतिशत को जोड़कर इलास्टोमेर बनाया जाता है। इस स्थिति में गर्म होने पर, क्रॉसलिंकिंग अणु प्रतिक्रिया का कारण बनता है जो रासायनिक रूप से रबर के दो अणुओं को साथ (एक क्रॉसलिंक) साथ जोड़ता है। क्योंकि रबर के अणु इतने लंबे होते हैं, प्रत्येक निरंतर आणविक नेटवर्क बनाने वाले कई अन्य रबर अणुओं के साथ कई क्रॉसलिंक्स में भाग लेता है।
इस प्रकार जैसे ही रबर बैंड को प्रसारित किया जाता हैं, कुछ नेटवर्क चेन को सीधा होने के लिए विवश किया जाता है और इससे उनकी एंट्रॉपी में कमी आ जाती हैं। यह एन्ट्रापी में कमी है जो नेटवर्क श्रृंखलाओं में लोचदार बल को जन्म देती है।
इतिहास
15वीं शताब्दी के अंत में नई दुनिया से यूरोप में इसकी प्रारंभ के बाद, प्राकृतिक रबर (पॉलीसोप्रीन) को ज्यादातर आकर्षक जिज्ञासा के रूप में माना जाता था। इसका सबसे उपयोगी अनुप्रयोग कागज पर पेंसिल के निशान को रगड़ कर मिटाने की क्षमता थी, इसलिए इसका यह नाम रखा गया था। इसके सबसे विशिष्ट गुणों में से तापमान में साधारण (लेकिन पता लगाने योग्य) वृद्धि है जो तब होती है जब रबर का नमूना खींचा जाता है। यदि इसे जल्दी से वापस लेने की अनुमति दी जाती है, तो इस प्रकार समान मात्रा में शीतलन देखा जाता है। इस प्रकार इस घटना ने अंग्रेजी भौतिक विज्ञानी जॉन गफ (प्राकृतिक दार्शनिक) का ध्यान आकर्षित किया हैं। 1805 में उन्होंने इस विशेषता पर कुछ गुणात्मक टिप्पणियों को प्रकाशित किया और यह भी बताया कि तापमान के साथ आवश्यक तनन बल कैसे बढ़ता है।[1]
उन्नीसवीं शताब्दी के मध्य तक, ऊष्मप्रवैगिकी के सिद्धांत का विकास हो रहा था और इस ढांचे के भीतर, अंग्रेजी गणितज्ञ और भौतिक विज्ञानी लॉर्ड केल्विन[2] दिखाया कि रबर के नमूने को फैलाने के लिए आवश्यक यांत्रिक ऊर्जा में परिवर्तन तापमान में वृद्धि के समानुपाती होना चाहिए। बाद में, यह एन्ट्रापी में परिवर्तन से जुड़ा होगा। ऊष्मप्रवैगिकी का संबंध 1859 में मजबूती से स्थापित हो गया था जब अंग्रेजी भौतिक विज्ञानी जेम्स जौल ने रबर के नमूने के रूप में होने वाली तापमान वृद्धि का पहला सावधानीपूर्वक माप प्रकाशित किया था।[3] इस कार्य ने लॉर्ड केल्विन की सैद्धांतिक भविष्यवाणियों की पुष्टि की गई हैं।
1838 में अमेरिकी आविष्कारक चार्ल्स गुडइयर ने पाया कि कुछ प्रतिशत सल्फर मिला कर प्राकृतिक रबर के लोचदार गुणों में अत्यधिक सुधार किया जा सकता है। शॉर्ट सल्फर चेन ने आसन्न पॉलीसोप्रीन अणुओं के बीच रासायनिक क्रॉस-लिंक का निर्माण किया था। इससे पहले कि यह क्रॉस-लिंक्ड हो, तरल प्राकृतिक रबर में बहुत लंबे बहुलक अणु होते हैं, जिसमें हजारों आइसोप्रेन बैकबोन इकाइयां होती हैं, जो सिर से पूंछ तक जुड़ी होती हैं जिसमें सामान्यतः चेन के रूप में संदर्भित की गई हैं। प्रत्येक श्रृंखला बहुलक तरल के माध्यम से यादृच्छिक, तीन आयामी पथ का अनुसरण करती है। इस प्रकार हजारों अन्य आस-पास की श्रृंखलाओं के संपर्क में है। जब लगभग 150C तक गर्म किया जाता है, तो प्रतिक्रियाशील क्रॉस-लिंकर अणु, जैसे कि सल्फर या डाइक्यूमिल पेरोक्साइड, विघटित हो सकते हैं और बाद की रासायनिक प्रतिक्रियाएँ आसन्न श्रृंखलाओं के बीच रासायनिक बंधन उत्पन्न करती हैं। क्रॉसलिंक को 'X' अक्षर के रूप में देखा जा सकता है, लेकिन इसकी कुछ भुजाएँ विमान से बाहर की ओर इंगित करती हैं। परिणामस्वरूप तीन आयामी आण्विक नेटवर्क प्राप्त होते हैं। पॉलीसोप्रीन के सभी अणु इन रासायनिक बंधों (नेटवर्क नोड्स) द्वारा कई बिंदुओं पर साथ जुड़े होते हैं, जिसके परिणामस्वरूप विशाल अणु होता है और इस प्रकार मूल लंबे पॉलीमर के बारे में सभी जानकारी विलुप्त हो जाती हैं। रबड़ बैंड अणु है, जैसा कि लेटेक्स दस्ताने है, जो दो आसन्न क्रॉस-लिंक्स के बीच पॉलीसोप्रीन के वर्गों को नेटवर्क चेन कहा जाता है और इसमें कई सौ आइसोप्रीन इकाइयां हो सकती हैं। प्राकृतिक रबड़ में, प्रत्येक क्रॉस-लिंक नेटवर्क नोड उत्पन्न करता है जिसमें से चार श्रृंखलाएं निकलती हैं। यह वह नेटवर्क है जो लोचदार गुणों को जन्म देता है।
रबर के विशाल आर्थिक और तकनीकी महत्व के कारण, यह भविष्यवाणी करना कि कैसे आणविक नेटवर्क यांत्रिक उपभेदों पर प्रतिक्रिया करता है, वैज्ञानिकों और इंजीनियरों के लिए स्थायी रुचि रही है। रबर के लोचदार गुणों को समझने के लिए, सैद्धांतिक रूप से, आणविक स्तर पर होने वाले दोनों भौतिक तंत्रों को जानना आवश्यक है और बहुलक श्रृंखला की यादृच्छिक-चलना प्रकृति नेटवर्क को कैसे परिभाषित करती है। बहुलक श्रृंखलाओं के छोटे वर्गों के भीतर होने वाले भौतिक तंत्र लोचदार बलों का उत्पादन करते हैं और नेटवर्क आकृति विज्ञान यह निर्धारित करता है कि ये बल मैक्रोस्कोपिक तनाव (यांत्रिकी) का उत्पादन करने के लिए कैसे गठबंधन करते हैं, जिसे हम रबड़ के नमूने के विकृत होने पर देखते हैं, उदाहरण के लिए इसे विरूपण (यांत्रिकी) के अधीन माना जाता हैं।
आण्विक स्तर के मॉडल
वास्तव में कई भौतिक तंत्र हैं जो नेटवर्क श्रृंखलाओं के भीतर लोचदार बल उत्पन्न करते हैं क्योंकि रबड़ का नमूना फैला हुआ है। इनमें से दो एन्ट्रापी परिवर्तन से उत्पन्न होते हैं और चेन बैकबोन के साथ आणविक बंधन कोणों की विकृति से जुड़ा होता है। ये तीन तंत्र तुरंत स्पष्ट होते हैं जब मध्यम मोटे रबर के नमूने को मौलिक रूप से खींचा जाता है। प्रारंभ में, रबर अधिक कठोर महसूस होता है, अर्थात तनाव के संबंध में बल को उच्च दर से बढ़ाया जाना चाहिए। मध्यवर्ती उपभेदों पर, समान मात्रा में खिंचाव उत्पन्न करने के लिए बल में आवश्यक वृद्धि बहुत कम होती है। अंत में, जैसे ही नमूना ब्रेकिंग पॉइंट तक पहुंचता है, इसकी कठोरता स्पष्ट रूप से बढ़ जाती है। प्रेक्षक जो देख रहा है वह लोच के मापांक में परिवर्तन है जो विभिन्न आणविक तंत्रों के कारण होता है। इन क्षेत्रों को चित्र 1 में देखा जा सकता है, प्राकृतिक रबर के लिए विशिष्ट तनाव की माप की जाती हैं। जिसमें तीन तंत्र (लेबल Ia, Ib और II) मुख्य रूप से भूखंड पर दिखाए गए क्षेत्रों के अनुरूप होते हैं। एंट्रॉपी सांख्यिकीय यांत्रिकी की अवधारणा हमारे पास गणितीय भौतिकी के क्षेत्र से आती है जिसे सांख्यिकीय यांत्रिकी कहा जाता है जो बड़े तापीय प्रणालियों के अध्ययन से संबंधित है, उदाहरण के लिए कमरे के तापमान पर रबर नेटवर्क इसका मुख्य उदाहरण हैं। यद्यपि घटक श्रृंखलाओं का विस्तृत व्यवहार यादृच्छिक है और व्यक्तिगत रूप से अध्ययन करने के लिए बहुत जटिल है, हम बड़े नमूने के सांख्यिकीय यांत्रिकी विश्लेषण से उनके 'औसत' व्यवहार के बारे में बहुत उपयोगी जानकारी प्राप्त कर सकते हैं। इस प्रकार हमारे दैनिक अनुभवों में एंट्रॉपी परिवर्तन कैसे बल उत्पन्न कर सकते हैं इसका कोई अन्य उदाहरण नहीं है। बहुलक शृंखलाओं में एंट्रोपिक बलों को तापीय टक्करों से उत्पन्न होने वाला माना जा सकता है जो उनके घटक परमाणुओं को इसके समीप की सामग्री के साथ अनुभव करते हैं। यह निरंतर धक्का-मुक्की है जो जंजीरों में प्रतिरोधी (लोचदार) बल उत्पन्न करती है क्योंकि उन्हें सीधा होने के लिए विवश किया जाता है। रबर के नमूने को खींचना लोच का सबसे सरल उदाहरण है, यह तब भी होता है जब रबर को संकुचित किया जाता है। संपीड़न को दो आयामी विस्तार के रूप में माना जा सकता है जब गुब्बारा फुलाया जाता है। लोचदार बल उत्पन्न करने वाले आणविक तंत्र सभी प्रकार के तनाव के लिए समान हैं।
जब इन लोचदार बल मॉडल को नेटवर्क के जटिल आकारिकी के साथ जोड़ दिया जाता है, तो मैक्रोस्कोपिक तनाव की भविष्यवाणी करने के लिए सरल विश्लेषणात्मक सूत्र प्राप्त करना संभव नहीं होता है। यह केवल कंप्यूटरों पर संख्यात्मक सिमुलेशन के माध्यम से है कि रबर के नमूने के तनाव और अंतिम विफलता की भविष्यवाणी करने के लिए आणविक बलों और नेटवर्क आकृति विज्ञान के बीच जटिल वार्तालाभ को पकड़ना संभव है क्योंकि यह तनावपूर्ण है।
रबर लोच के लिए आणविक किंक प्रतिमान[4]
प्राकृतिक रबर नेटवर्क के लिए तनाव तथा तन्यता तनाव के बीच के अन्तर की व्याख्या की जाती हैं। इस प्रकार ट्रेलोअर (ठोस नीला), सैद्धांतिक सिमुलेशन (धराशायी लाल) द्वारा प्रायोगिक डेटा का उपयोग किया जाता हैं।
मॉलिक्यूलर किंक प्रतिमान सहज धारणा से आगे बढ़ता है कि प्राकृतिक रबर (आइसोप्रीन) नेटवर्क बनाने वाली आणविक श्रृंखलाएं 'ट्यूब' के भीतर रहने के लिए आसपास की जंजीरों से विवश हैं। श्रृंखला में उत्पन्न लोचदार बल, कुछ लागू तनाव के परिणामस्वरूप, इस ट्यूब के भीतर श्रृंखला समोच्च के साथ प्रचारित होते हैं। चित्र 2 प्रत्येक छोर पर अतिरिक्त कार्बन परमाणु के साथ चार-कार्बन आइसोप्रीन बैकबोन इकाई का प्रतिनिधित्व दिखाता है, जो श्रृंखला पर आसन्न इकाइयों से इसके कनेक्शन को इंगित करता है। इसमें तीन सिंगल C-C बॉन्ड और डबल बॉन्ड होता है। यह मुख्य रूप से सीसी सिंगल बॉन्ड के बारे में घूर्णन करके है कि पॉलीसोप्रीन श्रृंखला यादृच्छिक रूप से इसकी संभावित अनुरूपताओं की पड़ताल करती है। इस प्रकार दो और तीन आइसोप्रीन इकाइयों के बीच वाली श्रृंखला के खंडों में पर्याप्त लचीलापन है कि उन्हें दूसरे से सांख्यिकीय रूप से असंबद्ध माना जा सकता है। यही है, इस दूरी से अधिक दूरी के लिए श्रृंखला के साथ कोई दिशात्मक संबंध नहीं है, जिसे कुह्न लंबाई कहा जाता है। ये गैर-सीधे क्षेत्र 'किंक्स' की अवधारणा को उद्घाटित करते हैं और वास्तव में रैंडम वॉक हायर डायमेंशन या रैंडम-वॉक प्रकृति की श्रृंखला की अभिव्यक्ति हैं। चूँकि इस प्रकार किंक कई आइसोप्रीन इकाइयों से बना होता है, जिनमें से प्रत्येक में तीन कार्बन-कार्बन सिंगल बॉन्ड होते हैं, किंक के लिए कई संभावित अनुरूपताएँ उपलब्ध होती हैं, जिनमें से प्रत्येक में अलग ऊर्जा और अंत-टू-एंड दूरी होती है। सेकंड से लेकर मिनट तक के समय के पैमाने पर, श्रृंखला के केवल इन अपेक्षाकृत छोटे वर्गों, अर्थात किंक, में उनके संभावित घूर्णी अनुरूपताओं के बीच स्वतंत्र रूप से स्थानांतरित करने के लिए पर्याप्त मात्रा है। ऊष्मीय इंटरैक्शन किंक को निरंतर प्रवाह की स्थिति में रखते हैं, क्योंकि वे अपने सभी संभावित घूर्णी अनुरूपताओं के बीच संक्रमण करते हैं। क्योंकि किंक ऊष्मीय संतुलन में हैं, संभावना है कि किसी घूर्णी रचना में किंक रहता है, बोल्ट्जमान वितरण द्वारा दिया जाता है और हम एंट्रॉपी सांख्यिकीय यांत्रिकी को इसकी एंड-टू-एंड दूरी के साथ जोड़ सकते हैं। कुह्न लंबाई के अंत से अंत तक की दूरी के लिए संभाव्यता वितरण लगभग सामान्य वितरण है और प्रत्येक स्थिति (घूर्णी रचना) के लिए बोल्ट्जमान संभाव्यता कारकों द्वारा निर्धारित किया जाता है। जैसा कि रबर नेटवर्क फैला हुआ है, कुछ किंक को अधिक से अधिक एंड-टू-एंड दूरी वाले अधिक विस्तारित अनुरूपताओं की सीमित संख्या में विवश किया जाता है और यह एन्ट्रापी में परिणामी कमी है जो श्रृंखला के साथ लोचदार बल उत्पन्न करता है।
इस प्रकार इसमें तीन अलग-अलग आण्विक तंत्र होते हैं जो इन बलों का उत्पादन करते हैं, जिनमें से दो एन्ट्रापी में परिवर्तन से उत्पन्न होते हैं जिन्हें हम निम्न श्रृंखला विस्तार प्रणाली, एलए के रूप में संदर्भित किया जाता हैं।[5] इस प्रकार मध्यम श्रृंखला विस्तार प्रणाली, आईबी को इसके[6] तीसरे तंत्र उच्च श्रृंखला विस्तार पर होता है, क्योंकि इसकी रीढ़ की हड्डी के साथ रासायनिक बंधनों के विरूपण से प्रारंभिक संतुलन समोच्च लंबाई से आगे बढ़ाया जाता है। इस स्थिति में, प्रत्यानयन बल स्प्रिंग जैसा होता है और हम इसे रिजीम II के रूप में संदर्भित करते हैं।[7] इस प्रकार तीन बल तंत्र मोटे तौर पर तन्यता तनाव बनाम तनाव प्रयोगों में देखे गए तीन क्षेत्रों के अनुरूप पाए जाते हैं, चित्र 1 में दिखाया गया है।
रासायनिक क्रॉस-लिंकिंग के तुरंत बाद नेटवर्क की प्रारंभिक रूपरेखा दो यादृच्छिक प्रक्रियाओं द्वारा नियंत्रित होती है:[8][9] (1) किसी भी आइसोप्रीन इकाई पर क्रॉस-लिंक होने की संभावना और, (2) श्रृंखला की रचना की यादृच्छिक चलने की प्रकृति हैं। निश्चित श्रृंखला लंबाई, अर्थात आइसोप्रीन इकाइयों की निश्चित संख्या के लिए एंड-टू-एंड दूरी संभाव्यता घनत्व फ़ंक्शन, यादृच्छिक चलना द्वारा वर्णित है। इस प्रकार यह नेटवर्क श्रृंखला की लंबाई और उनके क्रॉस-लिंक नोड्स के बीच एंड-टू-एंड दूरी का संयुक्त संभाव्यता वितरण है जो नेटवर्क आकृति विज्ञान की विशेषता है। क्योंकि दोनों आणविक भौतिकी तंत्र जो लोचदार बलों का उत्पादन करते हैं और नेटवर्क के जटिल आकारिकी का साथ उपचार किया जाना चाहिए, सरल विश्लेषणात्मक लोच मॉडल संभव नहीं हैं, इस प्रकार स्पष्ट रूप से यहाँ पर 3-आयामी संख्यात्मक मॉडल[10][11][12] नेटवर्क के प्रतिनिधि वॉल्यूम तत्व पर तनाव के प्रभावों का अनुकरण करना आवश्यक है।
कम श्रृंखला विस्तार व्यवस्था, एल ए
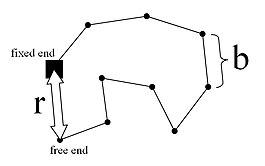
आणविक किंक प्रतिमान प्रतिनिधि नेटवर्क श्रृंखला को वैक्टर की श्रृंखला के रूप में देखता है जो इसकी ट्यूब के भीतर श्रृंखला समोच्च का पालन करता है। प्रत्येक वेक्टर किंक की अंत-टू-एंड संतुलन दूरी का प्रतिनिधित्व करता है। श्रृंखला का वास्तविक 3-आयामी पथ प्रासंगिक नहीं है, क्योंकि सभी लोचदार बलों को श्रृंखला समोच्च के साथ कार्य करने के लिए माना जाता है। इस प्रकार श्रृंखला की समोच्च लंबाई के अतिरिक्त, केवल अन्य महत्वपूर्ण पैरामीटर इसकी टेढ़ी-मेढ़ी है, इस प्रकार इसकी समोच्च लंबाई का अनुपात इसकी एंड-टू-एंड दूरी तक होती है। जैसा कि श्रृंखला को बढ़ाया जाता है, लागू तनाव के उत्तर में, प्रेरित लोचदार बल को इसके समोच्च के साथ समान रूप से फैलाने के लिए माना जाता है। नेटवर्क श्रृंखला पर विचार करें जिसके अंत बिंदु (नेटवर्क नोड) तन्य तनाव अक्ष के साथ कमोबेश संरेखित हैं। जैसे ही रबर के नमूने पर प्रारंभिक तनाव लागू होता है, श्रृंखला के सिरों पर नेटवर्क नोड अलग होने लगते हैं और समोच्च के साथ सभी किंक वैक्टर साथ खिंच जाते हैं। शारीरिक रूप से, लागू किया गया तनाव किंक को उनके बोल्ट्जमैन वितरण के अंत-से-अंत तक की दूरी से आगे बढ़ने के लिए विवश करता है, जिससे उनकी एंट्रॉपी में कमी आती है। इस प्रकार एन्ट्रापी में इस परिवर्तन से जुड़ी मुक्त ऊर्जा में वृद्धि, (रैखिक) लोचदार बल को जन्म देती है जो तनाव का विरोध करती है। कम तनाव प्रणाली के लिए निरंतर बल का अनुमान किंक के आणविक गतिशीलता (एमडी) प्रक्षेपवक्र के नमूने से लगाया जा सकता है, अर्थात प्रासंगिक तापमान पर 2–3 आइसोप्रीन इकाइयों से बनी छोटी श्रृंखला का उपयोग किया जाता हैं, उदाहरण के लिए 300K इसका मुख्य उदाहरण हैं।[5] यहाँ पर सिमुलेशन के समय निर्देशांक के कई नमूने लेकर, किंक के लिए एंड-टू-एंड दूरी की संभाव्यता वितरण प्राप्त किया जा सकता है। चूंकि ये वितरण (जो लगभग सामान्य वितरण के रूप में सामने आते हैं) सीधी स्थितियों की संख्या से संबंधित होते हैं, हम उन्हें किसी भी अंत-टू-एंड दूरी पर किंक की एंट्रॉपी से जोड़ सकते हैं। संभाव्यता वितरण को संख्यात्मक रूप से विभेदित करके, एंट्रॉपी में परिवर्तन, और इसलिए हेल्महोल्ट्ज़ मुक्त ऊर्जा, किंक एंड-टू-एंड दूरी के संबंध में पाया जा सकता है। इस व्यवस्था के लिए बल मॉडल को रैखिक और श्रृंखला वक्रता द्वारा विभाजित तापमान के समानुपाती पाया जाता है।
मध्यम श्रृंखला विस्तार प्रणाली, आईबी
कम विस्तार व्यवस्था में किसी बिंदु पर, अर्थात श्रृंखला के साथ सभी किंक साथ विस्तारित किए जा रहे हैं, यह श्रृंखला को आगे बढ़ाने के लिए विस्तारित संरचना के लिए किंक संक्रमण के लिए ऊर्जावान रूप से अधिक अनुकूल हो जाता है। लागू तनाव एकल आइसोप्रीन इकाई को विस्तारित संरचना में विस्तारित संरचना में विवश कर सकता है, श्रृंखला की अंत-टू-एंड दूरी को थोड़ा बढ़ा सकता है, और इस प्रकार ऐसा करने के लिए आवश्यक ऊर्जा सभी किंक को साथ विस्तारित करने के लिए आवश्यक ऊर्जा से कम है। इस प्रकार असंख्य प्रयोग[13] दृढ़ता से सुझाव देते हैं कि रबर नेटवर्क को फैलाने से एंट्रॉपी में कमी आती है। जैसा कि चित्र 2 में दिखाया गया है, आइसोप्रीन इकाई में तीन एकल सीसी बांड होते हैं और इन बांडों के बारे में दो या तीन पसंदीदा घूर्णी कोण (अभिविन्यास) होते हैं जिनमें न्यूनतम ऊर्जा होती है। इस प्रकार 18 में से अनुमति है[6]घूर्णी अनुरूपता, केवल 6 ने अंत-से-अंत तक दूरी बढ़ाई है और विस्तारित स्थितियों के कुछ सबसेट में रहने के लिए श्रृंखला में आइसोप्रीन इकाइयों को ऊष्मीय गति के लिए उपलब्ध घूर्णी अनुरूपता की संख्या को कम करना चाहिए। यह उपलब्ध स्थितियों की संख्या में कमी है जो एंट्रॉपी को कम करने का कारण बनती है। जैसे-जैसे श्रृंखला सीधी होती जाती है, श्रृंखला की सभी आइसोप्रीन इकाइयाँ अंततः विस्तारित संरूपण में विवश हो जाती हैं और इस प्रकार इस श्रृंखला को 'तना हुआ' माना जाता है। इस एन्ट्रापी परिवर्तन से जुड़े मुक्त ऊर्जा में परिणामी परिवर्तन से श्रृंखला विस्तार के लिए बल स्थिरांक का अनुमान लगाया जा सकता है।[6] यहाँ पर प्रणाली Ia के साथ, इस प्रणाली के लिए बल मॉडल रैखिक है और श्रृंखला के वक्रता से विभाजित तापमान के समानुपाती है।
उच्च श्रृंखला विस्तार प्रणाली, II
जब नेटवर्क श्रृंखला में सभी आइसोप्रीन इकाइयों को केवल कुछ विस्तारित घूर्णी अनुरूपताओं में रहने के लिए विवश किया जाता है, तो श्रृंखला तना हुआ हो जाता है। चेन समोच्च के साथ सी-सी बांड बनाने वाले ज़िगज़ैग पथ को छोड़कर, इसे समझदारी से सीधा माना जा सकता है। चूंकि, बॉन्ड विकृतियों द्वारा और विस्तार अभी भी संभव है, उदाहरण के लिए, बॉन्ड एंगल बढ़ता है, बॉन्ड स्ट्रेच और द्वितल कोण रोटेशन होता है। ये बल वसंत की तरह हैं और एंट्रॉपी परिवर्तनों से जुड़े नहीं हैं। इस प्रकार तने हुए चेन केवल लगभग 40% तक बढ़ाया जा सकता है। इस प्रकार इस बिंदु पर श्रृंखला के साथ बल यांत्रिक रूप से सीसी सहसंयोजक बंधन को तोड़ने के लिए पर्याप्त है। इस तन्य बल सीमा की गणना की गई है।[7] यहाँ पर क्वांटम रसायन विज्ञान सिमुलेशन के माध्यम से और यह लगभग 7nN है, कम तनाव पर एंट्रोपिक श्रृंखला बलों की तुलना में हजार अधिक कारक के बारे में कही गई हैं। आइसोप्रीन इकाई में आसन्न बैकबोन सी-सी बांड के बीच कोण लगभग 115-120 डिग्री के बीच भिन्न होता है और इन कोणों को बनाए रखने से जुड़े बल अधिक बड़े होते हैं, इसलिए प्रत्येक इकाई के भीतर, चेन बैकबोन सदैव ज़िगज़ैग पथ का अनुसरण करती है, इस प्रकार यहां तक कि बंधन टूटने पर भी इसका अनुसरण करती हैं। यह तंत्र लोचदार तनाव में भारी उतार-चढ़ाव के लिए जिम्मेदार है, जो उच्च उपभेदों (चित्र 1) में देखा गया है।
नेटवर्क आकृति विज्ञान
चूंकि नेटवर्क पूरी तरह से केवल दो मापदंडों (प्रति इकाई मात्रा में नेटवर्क नोड्स की संख्या और बहुलक की सांख्यिकीय डी-सहसंबंध लंबाई, कुह्न लंबाई) द्वारा वर्णित है, जिस प्रकार से जंजीरों को जोड़ा जाता है वह वास्तव में अधिक जटिल है। जंजीरों की लंबाई में व्यापक भिन्नता है और उनमें से अधिकतर निकटतम निकटतम नेटवर्क नोड से जुड़े नहीं हैं। इस प्रकार श्रृंखला की लंबाई और इसकी एंड-टू-एंड दूरी दोनों को संभाव्यता वितरण द्वारा वर्णित किया गया है। 'आकृति विज्ञान' शब्द इस जटिलता को दर्शाता है। यदि क्रॉस-लिंकिंग एजेंट पूरी तरह मिश्रित है, तो इस प्रकार किसी भी आइसोप्रीन इकाई के नेटवर्क नोड बनने की समान संभावना है। डाइक्यूमाइल पेरोक्साइड के लिए, प्राकृतिक रबर में क्रॉस लिंकिंग दक्षता एकता है,[14] लेकिन इस प्रकार सल्फर केस्थितियोंमें ऐसा नहीं है।[15] नेटवर्क की प्रारंभिक आकारिकी दो यादृच्छिक प्रक्रियाओं द्वारा तय की जाती है: किसी भी आइसोप्रीन इकाई पर क्रॉस-लिंक होने की संभावना और श्रृंखला संरचना के मार्कोव यादृच्छिक चलने की प्रकृति के लिए उपयोगी हैं।[8][9] इसकी इस श्रृंखला के अंत का छोर दूसरे से कितनी दूर 'भटक' सकता है, इसके लिए प्रायिकता वितरण फ़ंक्शन मार्कोव अनुक्रम द्वारा उत्पन्न होता है।[16] यह सशर्त संभाव्यता वितरण श्रृंखला की लंबाई से संबंधित है कुह्न लंबाई की इकाइयों में एंड-टू-एंड दूरी के लिए :
|
(1) |
संभावना है कि कोई आइसोप्रीन इकाई क्रॉस-लिंक नोड का भाग बन जाती है, क्रॉस-लिंकर अणुओं (जैसे, डाइक्यूमिल-पेरोक्साइड) की सांद्रता के आइसोप्रीन इकाइयों के अनुपात के अनुपात के समानुपाती होती है:
|
(3) |
जहाँ
समीकरण को केवल इस संभावना के रूप में समझा जा सकता है कि आइसोप्रीन इकाई क्रॉस-लिंक नहीं है (1−px) श्रृंखला के साथ N−1 क्रमिक इकाइयों में किया जाता हैं। चूँकि P(N) N के साथ घटता है, छोटी श्रृंखलाएँ लंबी श्रृंखलाओं की तुलना में अधिक संभावित होती हैं। ध्यान दें कि सांख्यिकीय रूप से स्वतंत्र बैकबोन सेगमेंट की संख्या आइसोप्रीन इकाइयों की संख्या के समान नहीं है। प्राकृतिक रबर नेटवर्क के लिए, कुछ की लंबाई में लगभग 2.2 आइसोप्रीन इकाइयाँ होती हैं, इसलिए . यह समीकरणों का उत्पाद है (1) और (3) (संयुक्त संभाव्यता वितरण) जो नेटवर्क श्रृंखला लंबाई से संबंधित है () और एंड-टू-एंड दूरी () इसके समापन क्रॉस-लिंक नोड्स के बीच:
|
(4) |
एक प्राकृतिक रबर नेटवर्क की जटिल आकृति विज्ञान को चित्र 3 में देखा जा सकता है, जो 'औसत' श्रृंखला के लिए प्रायिकता घनत्व बनाम एंड-टू-एंड दूरी (औसत नोड रिक्ति की इकाइयों में) को दर्शाता है। इस प्रकार 4x1019 सेमी-3 के सामान्य प्रयोगात्मक क्रॉस-लिंक घनत्व के लिए, औसत श्रृंखला में लगभग 116 आइसोप्रीन इकाइयाँ (52 कुह्न लंबाई) होती हैं, इसकी समोच्च लंबाई लगभग 50 एनएम होती है। चित्र 3 से पता चलता है कि जंजीरों का महत्वपूर्ण अंश कई नोड स्पेसिंग फैलाता है, अर्थात, श्रृंखला समाप्त अन्य नेटवर्क श्रृंखलाओं को ओवरलैप करती है। प्राकृतिक रबर, डाइक्यूमिल पेरोक्साइड के साथ क्रॉस-लिंक्ड, टेट्रा-फंक्शनल क्रॉस-लिंक्स हैं, अर्थात प्रत्येक क्रॉस-लिंक नोड में 4 नेटवर्क चेन निकलती हैं। इस प्रकार तनाव अक्ष के संबंध में उनकी प्रारंभिक वक्रता और उनके समापन बिंदुओं के उन्मुखीकरण के आधार पर, सक्रिय क्रॉस-लिंक नोड से जुड़ी प्रत्येक श्रृंखला में अलग लोचदार हुक का नियम हो सकता है क्योंकि यह लागू तनाव का विरोध करता है। प्रत्येक क्रॉस-लिंक नोड पर बल संतुलन (शून्य शुद्ध बल) को संरक्षित करने के लिए, नोड को श्रृंखला विस्तार के लिए उच्चतम बल स्थिरांक वाली श्रृंखला के साथ मिलकर चलने के लिए विवश किया जा सकता है। इस प्रकार यह जटिल नोड गति है, जो नेटवर्क आकृति विज्ञान की यादृच्छिक प्रकृति से उत्पन्न होती है, जो रबर नेटवर्क के यांत्रिक गुणों के अध्ययन को इतना कठिन बना देती है। जैसे-जैसे नेटवर्क तनावपूर्ण होता है, इन अधिक विस्तारित श्रृंखलाओं से बने पथ उभर कर सामने आते हैं जो पूरे नमूने को फैलाते हैं, और यही वे रास्ते हैं जो अधिकांश तनाव को उच्च तनाव में ले जाते हैं।
संख्यात्मक नेटवर्क सिमुलेशन मॉडल
रबर के नमूने की लोचदार प्रतिक्रिया की गणना करने के लिए, तीन श्रृंखला बल मॉडल (प्रणाली Ia, Ib और II) और नेटवर्क आकृति विज्ञान को सूक्ष्म-यांत्रिक नेटवर्क मॉडल में जोड़ा जाना चाहिए।[10][11][12]समीकरण में संयुक्त संभाव्यता वितरण का उपयोग करना (4) और बल विस्तार मॉडल, नेटवर्क के वफादार प्रतिनिधि वॉल्यूम तत्व का निर्माण करने और परिणामी यांत्रिक तनाव को अनुकरण करने के लिए संख्यात्मक एल्गोरिदम तैयार करना संभव है क्योंकि यह तनाव के अधीन है। तनाव लगाए जाने पर प्रत्येक नेटवर्क नोड पर अनुमानित बल संतुलन बनाए रखने के लिए पुनरावृत्त विश्राम एल्गोरिदम का उपयोग किया जाता है। जब संख्यात्मक सिमुलेशन में 2 या 3 आइसोप्रीन इकाइयों (लगभग कुह्न लंबाई) वाले किंक के लिए प्राप्त बल स्थिरांक का उपयोग किया जाता है, तो अनुमानित तनाव प्रयोगों के अनुरूप पाया जाता है। ऐसी गणना के परिणाम[15]सल्फर क्रॉस-लिंक्ड प्राकृतिक रबर के लिए चित्र 1 (धराशायी लाल रेखा) में दिखाया गया है और प्रयोगात्मक डेटा के साथ तुलना की गई है [17] (ठोस नीली रेखा)। ये सिमुलेशन भी तनाव में तेजी से वृद्धि की भविष्यवाणी करते हैं क्योंकि नेटवर्क श्रृंखलाएं तंग हो जाती हैं और अंत में, बंधन टूटने के कारण भौतिक विफलता होती है। इसमें उपस्थित सल्फर क्रॉस-लिंक्ड प्राकृतिक रबर की विभिन्न स्थितियों में, क्रॉस-लिंक में एसएस बांड चेन बैकबोन पर सीसी बांड की तुलना में बहुत कमजोर होती हैं और नेटवर्क की विफलता के बिंदु पर केंद्रित रहती हैं। इस प्रकार सिम्युलेटेड तनाव में पठार, लगभग 7 के तनाव से प्रारंभ होकर, नेटवर्क के लिए सीमित मूल्य है। लगभग 7 एमपीए से अधिक के तनाव का समर्थन नहीं किया जा सकता है और नेटवर्क विफल हो जाता है। इस प्रकार इस तनाव सीमा के पास, सिमुलेशन भविष्यवाणी करते हैं[12]कि 10% से कम जंजीरें तनी हुई हैं, अर्थात उच्च श्रृंखला विस्तार व्यवस्था में और 0.1% से कम जंजीरें फट गई हैं। जबकि बहुत कम टूटना अंश आश्चर्यजनक लग सकता है, यह रबर बैंड को तब तक खींचने के हमारे अनुभव के साथ असंगत नहीं है जब तक कि यह टूट न जाए इस बात का ध्यान रखना आवश्यक होता हैं। इसके टूटने के बाद रबर की लोचदार प्रतिक्रिया मूल से अलग नहीं होती हैं।
प्रयोग
तापमान के साथ तनन तनाव का परिवर्तन
तनाव के रूप में तापमान के साथ तन्य तनाव का परिवर्तन चार मानों (100%, 200%, 300% और 380%) पर स्थिर रहता है।[18] ऊष्मीय संतुलन में आणविक प्रणालियों के लिए, ऊर्जा का जोड़ इ जी यांत्रिक कार्य द्वारा, एंट्रॉपी में परिवर्तन का कारण बन सकता है। यह ऊष्मप्रवैगिकी और सांख्यिकीय यांत्रिकी के सिद्धांतों से जाना जाता है। इस प्रकार विशेष रूप से, दोनों सिद्धांतों का प्रमाण है कि ऊर्जा में परिवर्तन एंट्रॉपी परिवर्तन समय के पूर्ण तापमान के समानुपाती होना चाहिए। यह नियम तभी तक मान्य है जब तक कि ऊर्जा अणुओं की ऊष्मीय अवस्थाओं तक ही सीमित है। यदि रबर के नमूने को अधिक दूर तक खींचा जाता है, तो इस प्रकार ऊर्जा गैर-तापीय अवस्थाओं में रह सकती है जैसे कि रासायनिक बंधों का विरूपण और नियम लागू नहीं होता है। इस प्रकार निम्न से मध्यम उपभेदों पर, सिद्धांत भविष्यवाणी करता है कि आवश्यक खिंचाव बल नेटवर्क श्रृंखलाओं में एन्ट्रॉपी में परिवर्तन के कारण होता है। यदि यह सही है, तो हम अपेक्षा करते हैं कि किसी नमूने को तनाव के कुछ मान तक खींचने के लिए आवश्यक बल नमूने के तापमान के समानुपाती होना चाहिए। तापमान के साथ तन्यता तनाव कैसे भिन्न होता है, इस प्रकार यह दिखाते हुए माप चित्र 4 में दिखाए गए हैं। इस प्रकार इन प्रयोगों में,[18] खींचे गए रबर के नमूने का तनाव स्थिर रखा गया था क्योंकि तापमान 10 से 70 डिग्री सेल्सियस के बीच भिन्न था। निश्चित तनाव के प्रत्येक मूल्य के लिए, यह देखा जाता है कि तन्य तनाव रैखिक रूप से भिन्न होता है। ये प्रयोग सबसे सम्मोहक साक्ष्य प्रदान करते हैं कि रबर लोच के लिए एन्ट्रापी परिवर्तन मूलभूत तंत्र हैं।
तापमान के साथ तनाव का सकारात्मक रैखिक व्यवहार कभी-कभी गलत धारणा की ओर ले जाता है कि रबर में ऊष्मीय विस्तार का ऋणात्मक गुणांक होता है, अर्थात गर्म होने पर नमूने की लंबाई सिकुड़ जाती है। प्रयोगों[19] ने निर्णायक रूप से दिखाया है कि, लगभग सभी अन्य सामग्रियों की तरह, ऊष्मीय विस्तार का गुणांक प्राकृतिक रबर सकारात्मक है।
स्नैप-बैक वेग
रबड़ के नमूने बनाम समय के अंत और मध्य बिंदु का विस्थापन क्योंकि यह उच्च विस्तार से वापस आ जाता है।[20] जब हम रबड़ के टुकड़े को खींचते हैं, उदाहरण के लिए रबर बैंड, हम देखते हैं कि यह लंबाई में समान रूप से विकृत होता है। इसकी लंबाई के साथ प्रत्येक तत्व पूरे नमूने के समान विस्तार कारक का अनुभव करता है। इस प्रकार यदि हम छोर को छोड़ देते हैं, तो नमूना बहुत तेजी से अपनी मूल लंबाई पर वापस आ जाता है, प्रक्रिया को हल करने के लिए हमारी आंख के लिए बहुत तेजी से। हमारी सहज अपेक्षा यह है कि यह अपनी मूल लंबाई पर उसी तरह लौटता है। जैसे कि जब इसे खींचा गया था, अर्थात। इ। समान रूप से। चूंकि, ऐसा नहीं होता है। म्रोव्का एट एल द्वारा प्रायोगिक अवलोकन किया जाता हैं।[20] इसके आश्चर्यजनक परिणाम प्राप्त होते हैं। इस प्रकार अत्यधिक तेज़ प्रत्यावर्तन गतिकी को पकड़ने के लिए, उन्होंने एक्सनर और स्टीफ़न द्वारा तैयार की गई चतुर प्रयोगात्मक विधि का उपयोग किया गया था।[21] इस प्रकार 1874 में, उच्च गति वाले इलेक्ट्रॉनिक मापने वाले उपकरणों का आविष्कार होने से पहले। उनकी पद्धति में तेजी से घूमने वाला कांच का सिलेंडर सम्मिलित था, जिसे लैंप ब्लैक के साथ लेपित करने के बाद, फैलाए गए रबड़ के नमूने के बगल में रखा गया था। इस प्रकार रबर के नमूने के मध्य-बिंदु और मुक्त सिरे से जुड़ी स्टाइलि को ग्लास सिलेंडर के संपर्क में रखा गया था। फिर, जैसे ही रबर का मुक्त सिरा वापस टूटा, स्टाइली ने घूर्णन सिलेंडर के लैंप ब्लैक कोटिंग में पेचदार रास्तों का पता लगाया था। सिलेंडर की घूर्णन गति को समायोजित करके, वे से कम पूर्ण रोटेशन में स्टाइली की स्थिति रिकॉर्ड कर सकते थे। नम ब्लोटर पेपर के टुकड़े पर सिलेंडर को रोल करके प्रक्षेपवक्र को ग्राफ में स्थानांतरित कर दिया गया था। इस लेखनी द्वारा छोड़े गए निशान कागज पर सफेद रेखा (कोई दीपक काला नहीं) के रूप में दिखाई देते हैं।
उनका डेटा, चित्र 5 में ग्राफ के रूप में प्लॉट किया गया है, अंत और मध्यबिंदु स्टाइलि की स्थिति दिखाता है क्योंकि नमूना तेजी से अपनी मूल लंबाई में वापस आ जाता है। नमूना प्रारंभ में अपनी अप्रशिक्षित लंबाई से 9.5” ऊपर खींचा गया और फिर छोड़ दिया गया। स्टाइलि 6 एमएस से थोड़ा अधिक समय में अपनी मूल स्थिति (0 का विस्थापन) पर लौट आया। विस्थापन बनाम समय का रैखिक व्यवहार इंगित करता है कि, संक्षिप्त त्वरण के बाद, नमूने का अंत और मध्य बिंदु दोनों लगभग 50 मी/से या 112 मील प्रति घंटे के निरंतर वेग से वापस आ गए। चूंकि, अंत प्रस्तुत होने के बाद लगभग 3 एमएस तक मिडपॉइंट स्टाइलस चलना प्रारंभ नहीं हुआ। प्रकट है, वापसी की प्रक्रिया लहर के रूप में यात्रा करती है, मुक्त छोर से प्रारंभ होती है।
उच्च विस्तार पर फैली हुई नेटवर्क श्रृंखला में संग्रहीत कुछ ऊर्जा इसकी एन्ट्रापी में परिवर्तन के कारण होती है, लेकिन अधिकांश ऊर्जा बांड विकृतियों (उपरोक्त प्रणाली II, ऊपर) में संग्रहीत होती है, जिसमें एन्ट्रापी परिवर्तन सम्मिलित नहीं होता है। यदि कोई मानता है कि सभी संग्रहीत ऊर्जा गतिज ऊर्जा में परिवर्तित हो जाती है, तो प्रत्यावर्तन वेग की गणना सीधे परिचित संरक्षण समीकरण E =1⁄2 mv2 से की जा सकती है। इस प्रकार संख्यात्मक सिमुलेशन,[11]आणविक किंक प्रतिमान के आधार पर, इस प्रयोग के अनुरूप वेगों की भविष्यवाणी करेता हैं।
लोच सिद्धांत के लिए ऐतिहासिक दृष्टिकोण
यूजीन गुथ और ह्यूबर्ट एम। जेम्स ने 1941 में रबर लोच की एन्ट्रोपिक उत्पत्ति का प्रस्ताव रखा था।[22]
ऊष्मप्रवैगिकी
तापमान असामान्य विधि से इलास्टोमर्स की लोच को प्रभावित करता है। जब इलास्टोमेर को फैला हुआ अवस्था में माना जाता है, तो हीटिंग उन्हें अनुबंधित करने का कारण बनता है। इसके विपरीत, ठंडा करने से विस्तार हो सकता है।[23]
यह साधारण रबर बैंड के साथ देखा जा सकता है। रबर बैंड को खींचने से यह गर्मी छोड़ेगा (इसे अपने होठों के विरुद्ध दबाएं), जबकि इसे खींचे जाने के पश्चात इसे प्रस्तुत करने से यह गर्मी को अवशोषित कर लेगा, जिससे इसका परिवेश ठंडा हो जाएगा। इस परिघटना को गिब्स मुक्त ऊर्जा द्वारा समझाया जा सकता है। ΔG=ΔH−TΔS को पुनर्व्यवस्थित करने पर, जहाँ G मुक्त ऊर्जा है, H तापीय धारिता है, और S एन्ट्रॉपी है, हमें मिलता है T ΔS = ΔH − ΔG. चूंकि खिंचाव सहज नहीं है, क्योंकि इस प्रकार इसके लिए बाहरी कार्य की आवश्यकता होती है, TΔS ऋणात्मक होना चाहिए। चूँकि T सदैव धनात्मक होता है (यह कभी भी पूर्ण शून्य तक नहीं पहुँच सकता है), ΔS को ऋणात्मक होना चाहिए, जिसका अर्थ है कि रबर अपनी प्राकृतिक अवस्था में अधिक उलझा हुआ है (अधिक माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) के साथ) जब यह तनाव में होता है। इस प्रकार, जब तनाव हटा दिया जाता है, तो प्रतिक्रिया सहज होती है, जिससे ΔG ऋणात्मक हो जाती है। जिसके परिणाम स्वरुप , शीतलन प्रभाव का परिणाम सकारात्मक ΔH होना चाहिए, इसलिए ΔS वहां धनात्मक प्राप्त होगा।[24][25]
इसका परिणाम यह होता है कि इलास्टोमर कुछ हद तक आदर्श मोनोएटोमिक गैस की तरह व्यवहार करता है, क्योंकि (अच्छे सन्निकटन के लिए) इलास्टिक पॉलीमर किसी भी संभावित ऊर्जा को स्ट्रेच्ड केमिकल बॉन्ड्स या स्ट्रेचिंग मॉलिक्यूल्स में किए गए इलास्टिक वर्क में स्टोर नहीं करते हैं, जब उन पर कार्य किया जाता है। इसके अतिरिक्त, रबर पर किए गए सभी कार्य प्रस्तुत (संग्रहीत नहीं) होते हैं और तुरंत बहुलक में तापीय ऊर्जा के रूप में दिखाई देते हैं। इस प्रकार इस प्रकार कार्य करने के लिए इलास्टिक द्वारा आसपास के वातावरण में किए जाने वाले सभी कार्य तापीय ऊर्जा के विलुप्त होने का कारण बनती हैं (इलास्टिक बैंड विस्तारित गैस की तरह ठंडा हो जाता है)। यह अंतिम घटना महत्वपूर्ण सुराग है कि कार्य करने के लिए इलास्टोमर की क्षमता (एक आदर्श गैस के साथ) केवल एन्ट्रापी-परिवर्तन के विचारों पर निर्भर करती है, न कि बहुलक बांडों के भीतर किसी संग्रहीत (अर्थात, संभावित) ऊर्जा पर प्राप्त किया जाता हैं। इसके अतिरिक्त, कार्य करने के लिए ऊर्जा पूरी तरह से तापीय ऊर्जा से आती है, और (जैसा कि विस्तारित आदर्श गैस केस्थितियोंमें) बहुलक का केवल सकारात्मक एन्ट्रापी परिवर्तन इसकी आंतरिक तापीय ऊर्जा को कुशलता से परिवर्तित करने की अनुमति देता है इस प्रकार इस सिद्धांत में 100 प्रतिशत कार्य में उपयोग किया जाता हैं।
पॉलिमर श्रृंखला सिद्धांत
रबर लोच के सिद्धांत का आह्वान करते हुए, क्रॉस-लिंक्ड नेटवर्क में बहुलक श्रृंखला को एंट्रोपिक बल के रूप में मानता है। जब श्रृंखला को बढ़ाया जाता है, तो एंट्रॉपी बड़े मार्जिन से कम हो जाती है क्योंकि कम अनुरूपताएं उपलब्ध होती हैं।[26] इसलिए, प्रत्यानयन बल होता है, जो बार बाहरी बल हटा दिए जाने पर, बहुलक श्रृंखला को उसके संतुलन या अविस्तारित अवस्था में लौटने का कारण बनता है, इस प्रकार जैसे कि उच्च एन्ट्रापी यादृच्छिक कुंडल विन्यास। यही कारण है कि रबर बैंड अपनी मूल स्थिति में लौट आते हैं। रबर लोच के लिए दो सामान्य मॉडल स्वतंत्र रूप से जुड़े श्रृंखला मॉडल और वर्म-जैसी श्रृंखला मॉडल हैं।
स्वतंत्र रूप से जुड़ा हुआ चेन मॉडल
स्वतंत्र रूप से जुड़ी हुई श्रृंखला, जिसे आदर्श श्रृंखला भी कहा जाता है, रैंडम वॉक मॉडल का अनुसरण करती है। सूक्ष्म रूप से, बहुलक श्रृंखला का 3-डी यादृच्छिक चलना एक्स, वाई और जेड दिशाओं के संदर्भ में समग्र अंत-टू-एंड दूरी को व्यक्त करता है:
रबर लोच के फ्लोरी सिद्धांत ने बताया है कि रबर लोच में मुख्य रूप से एन्ट्रोपिक उत्पत्ति होती है। हेल्महोल्ट्ज़ मुक्त ऊर्जा के लिए निम्नलिखित बुनियादी समीकरणों का उपयोग करके और एन्ट्रापी के बारे में इसकी चर्चा करके, रबर श्रृंखला के विरूपण से उत्पन्न बल को उसके मूल गैर-विस्तारित संरूपण से प्राप्त किया जा सकता है। इस प्रकार यहाँ पर h> बहुलक श्रृंखला के अनुरूपताओं की संख्या है। चूँकि विकृति में एन्थैल्पी परिवर्तन सम्मिलित नहीं है, मुक्त ऊर्जा में परिवर्तन की गणना एंट्रॉपी में परिवर्तन के रूप में की जा सकती है। इस प्रकार यह देखा जा सकता है कि बल समीकरण वसंत के व्यवहार जैसा दिखता है और हुक के नियम का पालन करता है: , जहां F बल है, k वसंत स्थिरांक और x दूरी है। सामान्यतः, नव-हुकियन ठोस या नव-हुकियन मॉडल का उपयोग उनके तनाव के संबंधों की भविष्यवाणी करने के लिए क्रॉस-लिंक्ड पॉलिमर पर किया जा सकता है:
ध्यान दें कि लोचदार गुणांक तापमान पर निर्भर है। यदि हम रबर का तापमान बढ़ाते हैं, तो लोचदार गुणांक भी बढ़ जाता है। यही कारण है कि क्रम में होने वाले तनाव में रहने वाला रबर तापमान बढ़ने पर सिकुड़ जाता है।
हम फ्लोरी सिद्धांत को मैक्रोस्कोपिक दृश्य में आगे बढ़ा सकते हैं, जहां बल्क रबर सामग्री पर चर्चा की जाती है। इस प्रकार मान लें कि रबर सामग्री का मूल आयाम है , और , विकृत आकार को व्यक्तिगत विस्तार अनुपात लागू करके लंबाई तक (, , ). तक व्यक्त किया जा सकता है, तो इस प्रकार सूक्ष्म रूप से, विकृत बहुलक श्रृंखला को विस्तार अनुपात के साथ भी व्यक्त किया जा सकता है: , , . विरूपण के कारण मुक्त ऊर्जा परिवर्तन को निम्नानुसार व्यक्त किया जा सकता है:
केस स्टडी: अक्षीय विरूपण:
इस प्रकार अक्षीय विकृत रबर में, क्योंकि हम यह मानते है कि . तो पिछली मुक्त ऊर्जा प्रति आयतन समीकरण है:
जहाँ , श्रृंखला का द्रव्यमान घनत्व है, इस प्रकार क्रॉसलिंक्स के बीच नेटवर्क स्ट्रैंड का नंबर औसत आणविक भार है। यहाँ, इस प्रकार का विश्लेषण[27] रबर लोच के थर्मोडायनामिक सिद्धांत को प्रायोगिक रूप से मापने योग्य मापदंडों से जोड़ता है। इस प्रकार इसके अतिरिक्त, यह सामग्री की क्रॉस-लिंकिंग स्थिति में जगहें देता है।
कीड़ा जैसा चेन मॉडल
वर्म-लाइक चेन मॉडल (WLC) अणु को खाते में मोड़ने के लिए आवश्यक ऊर्जा लेता है। इस प्रकार इसके अतिरिक्त चर समान हैं, पर्सिस्टेंस लेंथ रिप्लेस करता है . फिर, बल इस समीकरण का अनुसरण करता है:
इसलिए, जब श्रृंखला के सिरों (r = 0) के बीच कोई दूरी नहीं होती है, तो ऐसा करने के लिए आवश्यक बल शून्य होता है, और बहुलक श्रृंखला को पूरी तरह से विस्तारित करने के लिए (), अनंत बल की आवश्यकता होती है, जो सहज ज्ञान युक्त है। इस प्रकार रेखांकन के अनुसार, बल मूल बिंदु से प्रारंभ होता है और इस प्रकार प्रारंभ में रैखिक रूप . से बढ़ता है तथा यहाँ पर बल तब पठार होता है लेकिन अंततः फिर से बढ़ जाता है और श्रृंखला की लंबाई के समीप पहुंचने पर अनंत तक पहुंच जाता है।
यह भी देखें
- लोच (भौतिकी)
- हाइपरलास्टिक सामग्री
- पॉलिमर
- ऊष्मप्रवैगिकी
संदर्भ
- ↑ Proc. Lit. and Phil. Soc., Manchester, 2d ser., 1, 288 (1805)
- ↑ Lord Kelvin, Quarterly J. Math., 1, 57 (1857)
- ↑ Joule JP. On thermodynamic properties of solids. Phil Trans R Soc Lond. 1859;149:91–131.
- ↑ D. E. Hanson and J. L. Barber, Contemporary Physics 56 (3), 319–337 (2015), LAPR-2015-022971
- ↑ 5.0 5.1 D. E. Hanson and R. L. Martin, Journal of Chemical Physics 133, 084903 (084908 pp.) (2010)
- ↑ 6.0 6.1 6.2 D. E. Hanson, J. L. Barber and G. Subramanian, Journal of Chemical Physics 139 (2013), LAPR-2014-018991
- ↑ 7.0 7.1 D. E. Hanson and R. L. Martin, The Journal of Chemical Physics 130, 064903 (2009), LAPR-2009-006764
- ↑ 8.0 8.1 P. Flory, N. Rabjohn and M. Shaffer, Journal of Polymer Science 4, 435–455 (1949)
- ↑ 9.0 9.1 D. E. Hanson, Journal of Chemical Physics 134, 064906 (064906 pp.) (2011)
- ↑ 10.0 10.1 D. E. Hanson, Polymer 45 (3), 1058–1062 (2004)
- ↑ 11.0 11.1 11.2 D. E. Hanson, Journal of Chemical Physics 131, 224904 (224905 pp.) (2009)
- ↑ 12.0 12.1 12.2 D. E. Hanson and J. L. Barber, Modelling and Simulation in Materials Science and Engineering 21 (2013), LAPR-2013-017962
- ↑ J. P. Joule, Phil. Trans. R. Soc. London 149, 91–131 (1859)
- ↑ L.D. Loan, Pure Appl. Chem. 30 (1972)
- ↑ 15.0 15.1 D. E. Hanson and J. L. Barber, Phys. Chem. Chem. Phys. 20, 8460 (2018), LAPR-2018-029488
- ↑ A. A. Markov, Izv. Peterb. Akad. 4 (1), 61–80 (1907)
- ↑ Treloar, L.R.G. (1944). "विभिन्न प्रकार के विरूपण के तहत वल्केनाइज्ड रबर के लिए तनाव-तनाव डेटा". Trans. Faraday Soc. 40: 0059. doi:10.5254/1.3546701.
- ↑ 18.0 18.1 Anthony, R.L.; Caston, R.H.; Guth, E. (1942). "प्राकृतिक और सिंथेटिक रबर जैसी सामग्री के लिए राज्य के समीकरण। I. गैर-त्वरित प्राकृतिक नरम रबर". J. Phys. Chem. 46: 826–840. doi:10.5254/1.3540117.
- ↑ L. A. Wood and G. Martin, Journal of Research of the National Bureau of Standards-A. Physics and Chemistry Vol 68A, No. 3 (1964).
- ↑ 20.0 20.1 Mrowca, B.A.; Dart, S.L.; Guth, E. (1944). "तनावग्रस्त रबर की वापसी". Phys. Rev. 66: 30. doi:10.1103/PhysRev.66.30.2.
- ↑ G. S. Whitby, "Plantation Rubber and the Testing of Rubber", Longmans and Green, London, 1920. p 461
- ↑ Guth, Eugene; James, Hubert M. (May 1941). "रबर जैसी सामग्री के लोचदार और थर्मोइलास्टिक गुण". Ind. Eng. Chem. 33 (5): 624–629. doi:10.1021/ie50377a017.
- ↑ "Thermodynamics of a Rubber Band", American Journal of Physics, 31 (5): 397, May 1963, Bibcode:1963AmJPh..31..397T, doi:10.1119/1.1969535
- ↑ Rubber Bands and Heat, http://scifun.chem.wisc.edu/HomeExpts/rubberband.html Archived 2019-06-13 at the Wayback Machine, citing Shakhashiri (1983)
- ↑ Shakhashiri, Bassam Z. (1983), Chemical Demonstrations: A Handbook for Teachers of Chemistry, vol. 1, Madison, WI: The University of Wisconsin Press, ISBN 978-0-299-08890-3
- ↑ L.R.G. Treloar (1975), Physics of Rubber Elasticity, Oxford University Press, ISBN 9780198570271
- ↑ Buche, M.R.; Silberstein, M.N. (2020). "Statistical mechanical constitutive theory of polymer networks: The inextricable links between distribution, behavior, and ensemble". Phys. Rev. E. 102: 012501. arXiv:2004.07874. doi:10.1103/PhysRevE.102.012501.