संरचनात्मक समीकरण मॉडलिंग: Difference between revisions
No edit summary |
No edit summary |
||
| (18 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Form of causal modeling that fit networks of constructs to data}} | {{short description|Form of causal modeling that fit networks of constructs to data}}[[File:Example Structural equation model.svg|alt= An example structural equation model|thumb|336x336px|चित्रा 1. अनुमान के पश्चात उदाहरण संरचनात्मक समीकरण मॉडलिंग है। अव्यक्त चर सामान्य रूप से अंडाकार के साथ दर्शाए जाते हैं और देखे गए चर आयतों में दिखाए जाते हैं। अवशिष्ट और प्रसरण दो सिरों वाले तीरों (यहां दिखाए गए) या एकल तीरों और वृत्त (यहां उपयोग नहीं किए गए) के रूप में खींचे गए हैं। मॉडलिंग को माप प्रदान करने के लिए अव्यक्त IQ विचरण 1 पर तय किया गया है। चित्र 1 गुप्त बुद्धि के प्रत्येक संकेतक को प्रभावित करने वाली माप त्रुटियों को दर्शाता है। न तो संकेतकों और न ही संकेतकों की माप त्रुटियों को अव्यक्त चरों को प्रभावित करने के रूप में प्रतिरूपित किया जाता है, किन्तु यदि शोधकर्ता उन्हें मॉडलिंग करने का विकल्प का चयन करते हैं तो वे ऐसा कर सकते हैं।]] | ||
[[File:Example | [[File:Example SEM of Human Intelligence.png|alt=An example structural equation model pre-estimation|thumb|336x336px|चित्रा 2. अनुमान से पूर्व का उदाहरण संरचनात्मक समीकरण मॉडलिंग है। चित्र 1 के समान किन्तु मानकीकृत मूल्यों और अल्प वस्तुओं के बिना होता है। क्योंकि बुद्धि और शैक्षणिक प्रदर्शन केवल कल्पना या सिद्धांत-पोस्ट किए गए चर हैं, उनके त्रुटिहीन स्तर के मूल्य अज्ञात हैं, चूँकि मॉडलिंग निर्दिष्ट करता है कि प्रत्येक अव्यक्त चर के मूल्यों को संकेतकों में से देखे जाने योग्य स्तर के साथ कहीं गिरना चाहिए। अव्यक्त को संकेतक से जोड़ने वाला 1.0 प्रभाव निर्दिष्ट करता है कि प्रत्येक वास्तविक इकाई में अव्यक्त चर के मूल्य में वृद्धि या अल्पता के परिणामस्वरूप संबंधित इकाई में वृद्धि या संकेतक के मूल्य में अल्पता होती है। यह आशा की जाती है कि प्रत्येक अव्यक्त के लिए उत्तम संकेतक का चयन किया गया है, किन्तु 1.0 मान सही माप का संकेत नहीं देते हैं क्योंकि यह मॉडलिंग बताता है कि अन्य अनिर्दिष्ट संस्थाएं हैं जो प्रेक्षित संकेतक मापों को कारणात्मक रूप से प्रभावित करती हैं, जिससे माप त्रुटि का परिचय मिलता है। यह मॉडलिंग बताता है कि भिन्न-भिन्न माप त्रुटियां गुप्त बुद्धि के दो संकेतकों में से प्रत्येक को प्रभावित करती हैं, और गुप्त उपलब्धि के प्रत्येक संकेतक को प्रभावित करती हैं। शैक्षणिक प्रदर्शन की ओर संकेत करते हुए बिना लेबल वाला तीर स्वीकार करता है कि बुद्धिमत्ता के अतिरिक्त अन्य शैक्षणिक प्रदर्शन को प्रभावित कर सकती हैं।]]संरचनात्मक समीकरण मॉडलिंग सेम (SEM) वैज्ञानिकों द्वारा प्रयोग किए जाने वाले विधि के समूह के लिए लेबल करते है, जो विज्ञान में प्रयोगात्मक और अवलोकन अनुसंधान दोनों में उपयोग किया जाता है,<ref name="Boslaugh2008" />जैसे- व्यवसाय,<ref>{{cite book|last1=Shelley|first1=Mack C|title=शैक्षिक नेतृत्व और प्रशासन का विश्वकोश|year=2006|isbn=978-0-7619-3087-7|chapter=Structural Equation Modeling|doi=10.4135/9781412939584.n544}}</ref> और अन्य क्षेत्र है। इसका उपयोग सामाजिक और व्यवहार विज्ञान में सबसे अधिक किया जाता है। अत्यधिक प्रौद्योगिकी भाषा के संदर्भ के बिना सेम की परिभाषा कठिन है, किन्तु उत्तम प्रारम्भ का स्थान नाम ही है। | ||
[[ | सेम में मॉडलिंग का निर्माण सम्मलित है, यह दर्शाने के लिए कि कैसे अवलोकनीय या सैद्धांतिक घटना के विभिन्न पार्श्व को दूसरे से [[संरचना|संरचनात्मक]] रूप से संबंधित माना जाता है। मॉडल का संरचनात्मक उन चरों के मध्य सैद्धांतिक संघों को दर्शाता है जो अन्वेषण के अंतर्गत घटना का प्रतिनिधित्व करते हैं। अनुमानित कारण संरचना को अधिकांशतः चर के मध्य कारण का प्रतिनिधित्व करने वाले तीरों के साथ चित्रित किया जाता है (जैसा कि [[आंकड़े]] 1 और 2 में) किन्तु इस कारण सम्बन्ध को समान रूप से [[समीकरण]] के रूप में दर्शाया जा सकता है। संरचनाओं का अर्थ है कि सम्बन्ध के विशिष्ट पैटर्न चर के मूल्यों के मध्य दिखाई देने चाहिए, और चर के मूल्यों के मध्य देखे गए सम्बन्ध का उपयोग कारण प्रभाव के परिमाण का अनुमान लगाने के लिए किया जाता है, और यह अनुसंधान के लिए मनाया गया डेटा संगत है या नहीं अनुमानित कारण संरचना सेम में समीकरण गणित और सांख्यिकी गुण हैं जो मॉडल और इसकी संरचनात्मक विशेषताओं द्वारा निहित हैं, और प्रायोगिक या अवलोकन संबंधी डेटा पर चलने वाले सांख्यिकीय एल्गोरिदम (सामान्यतः [[मैट्रिक्स कैलकुलस|आव्यूह गणना]] और [[सामान्यीकृत रैखिक मॉडल|सामान्यीकृत रैखिक]] मॉडलिंग पर आधारित) के साथ अनुमानित हैं। | ||
संरचनात्मक समीकरण मॉडल क्या है और क्या नहीं है, के मध्य सीमा में सदैव की स्पष्टता नहीं होती है, किन्तु एसई मॉडल में अधिकांशतः अव्यक्त चर के समूह के मध्य अनुमानित कारण जुड़े होते हैं और पोस्ट किए गए को जोड़ने वाले कारण सम्बंधित अव्यक्त चर जिन्हें देखा जा सकता है और जिनके मान कुछ डेटा समूह में उपलब्ध हैं। अव्यक्त कारण की शैलियों के मध्य भिन्नता, अव्यक्त चर को मापने वाले प्रेक्षित चर के मध्य भिन्नता, और सांख्यिकीय अनुमान रणनीतियों में भिन्नता के परिणामस्वरूप सेम उपकरण किट में [[पुष्टि कारक विश्लेषण]], पुष्टिकरण समग्र विश्लेषण, [[पथ विश्लेषण (सांख्यिकी)]], बहु-समूह मॉडलिंग सम्मलित हैं। अनुदैर्ध्य मॉडलिंग, [[आंशिक न्यूनतम वर्ग पथ मॉडलिंग]], [[अव्यक्त विकास मॉडलिंग|अव्यक्त विकास]] मॉडलिंग और श्रेणीबद्ध या बहुस्तरीय मॉडलिंग हैं।<ref name="kline_2016" /><ref>{{Cite book |last=Bollen |first=Kenneth A. |title=गुप्त चरों के साथ स्ट्रक्चरल समीकरण|date=1989 |publisher=Wiley |isbn=0-471-01171-1 |location=New York |oclc=18834634}}</ref><ref>{{Cite book |last=Kaplan |first=David |title=Structural equation modeling: foundations and extensions |date=2009 |publisher=SAGE |isbn=978-1-4129-1624-0 |edition=2nd |location=Los Angeles |oclc=225852466}}</ref> | |||
एसईएम का उपयोग सामान्यतः उचित है क्योंकि यह उन अव्यक्त चरों की पहचान करने में सहायता करता है जिनके बारे में माना जाता है कि वे उपस्तिथ हैं, किन्तु उन्हें सरलता से नहीं देखा जा सकता है। चूँकि एसईएम क्या है और क्या नहीं है, इसकी सदैव स्पष्ट सीमाएं नहीं होती हैं,<ref>{{Cite journal|last=Curran|first=Patrick J.|date=2003-10-01|title=Have Multilevel Models Been Structural Equation Models All Along?|journal=Multivariate Behavioral Research|volume=38|issue=4|pages=529–569|doi=10.1207/s15327906mbr3804_5|issn=0027-3171|pmid=26777445|s2cid=7384127}}</ref> इसमें सामान्यतः पथ मॉडल सम्मलित होते हैं (पथ विश्लेषण भी देखें) और माप मॉडल ([[कारक विश्लेषण]] भी देखें) में डेटा से लिए गए वास्तविक चर के अंतर्निहित चर के मध्य संरचनात्मक सम्बन्ध की अन्वेषण करने के लिए सदैव सांख्यिकीय मॉडल और कंप्यूटर प्रोग्राम को नियोजित करते हैं।<ref name="kline_2016"><nowiki>{{Cite book|last=Kline|first=Rex B. |title=आधारभूत समीकरण मोडलिंग के सिद्धांत एवं व्यवहार|date=2016 |isbn=978-1-4625-2334-4|edition=4th |location=New York|oclc=934184322}</nowiki></ref> एसईएम का उपयोग करने वाले शोधकर्ता प्रत्येक मॉडल किए गए तीर (उदाहरण के लिए चित्र 1 में दिखाए गए नंबर) गुणांक की शक्ति और संकेत का अनुमान लगाने के लिए सॉफ्टवेयर प्रोग्राम का उपयोग करते हैं, और डायग्नोस्टिक प्रदान करने के लिए विचार देते हैं कि कौन से संकेतक या मॉडल घटक के मध्य असंगतता उत्पन्न कर सकते हैं। एसईएम विधियों की आलोचना गणितीय सूत्रीकरण समस्याओं, बाहरी वैधता स्थापित किए बिना मॉडल को स्वीकार करने की प्रवृत्ति और संभावित दार्शनिक पूर्वाग्रह की ओर संकेत करती है। | |||
सेम | सेम विचार देता है कि बुद्धि (जैसा कि चार प्रश्नों द्वारा मापा जाता है) शैक्षणिक प्रदर्शन की भविष्यवाणी कर सकता है (जैसा कि सैट, एक्ट, और हाई स्कूल जीपीए द्वारा मापा जाता है) चित्र 1 में दिखाया गया है। [[मानव बुद्धि]] की अवधारणा को सरलता से उस प्रकार नहीं मापा जा सकता है जिससे व्यक्ति की ऊंचाई या भार मापें जाते है। इसके अतिरिक्त, शोधकर्ताओं के निकट बुद्धि का सिद्धांत और अवधारणा है और फिर प्रश्नावली या परीक्षण जैसे [[माप उपकरण]] को डिजाइन करते हैं जो उन्हें बुद्धि के कई संकेतक प्रदान करते हैं। इन संकेतों को मॉडल में संयोजित किया जाता है जिससे कि संकेतों से अव्यक्त चर (चित्र 1 में बुद्धि के लिए वृत्त) के रूप में बुद्धिमत्ता को मापने का प्रशंसनीय विधि बनाया जा सके (चित्र 1 में स्केल 1-4 के साथ वर्गाकार बक्से)।<ref name="Salkind2007" />चित्र 1 को अंतिम मॉडल के रूप में प्रस्तुत किया गया है, इसे चलाने और सभी अनुमानों (तीरों पर संख्या) को प्राप्त करने के पश्चात सेम का प्रतिनिधित्व करने के लिए सबसे उत्तम प्रतीकात्मक संकेतन पर कोई सहमति नहीं है, उदाहरण के लिए चित्र 2 और 1 के समान मॉडल का प्रतिनिधित्व करता है, बिना कई तीरों के प्रारूप में जो मॉडल को चलाने से पूर्व हो सकता है। | ||
एसईएम का | एसईएम का बड़ा लाभ यह है कि ये सभी माप और परीक्षण के साथ सांख्यिकीय अनुमान प्रक्रिया में होते हैं, जहां मॉडल से सभी जानकारी का उपयोग करके पूर्ण मॉडल में त्रुटियों की गणना की जाती है। इसका तात्पर्य यह है कि त्रुटियां अधिक त्रुटिहीन होती हैं यदि शोधकर्ता को मॉडलिंग के प्रत्येक भाग की भिन्न-भिन्न गणना करनी होती है।{{sfn|MacCallum|Austin|2000|p=209}} | ||
== इतिहास == | == इतिहास == | ||
संरचनात्मक | संरचनात्मक समीकरण मॉडलिंग सेम की जड़ें सेवेल राइट के कार्य में हैं, जिन्होंने जनसंख्या आनुवंशिकी में देखे गए चर के प्रत्यक्ष और अप्रत्यक्ष प्रभावों के आधार पर प्रतिगमन समीकरणों के लिए स्पष्ट कारण व्याख्याएं प्रारम्भ कीं।<ref>{{Cite journal|last=Wright|first=S.|date=1920-06-01|title=गिनी-सूअरों के पाइबल्ड पैटर्न का निर्धारण करने में आनुवंशिकता और पर्यावरण का सापेक्ष महत्व|journal=Proceedings of the National Academy of Sciences|language=en|volume=6|issue=6|pages=320–332|doi=10.1073/pnas.6.6.320|issn=0027-8424|pmc=1084532|pmid=16576506|bibcode=1920PNAS....6..320W|doi-access=free}}</ref><ref>{{Cite journal|last=Wright|first=Sewall|date=1921|title=जर्नल ऑफ एग्रीकल्चरल रिसर्च|url=https://naldc.nal.usda.gov/download/IND43966364/PDF|journal=जर्नल ऑफ एग्रीकल्चरल रिसर्च|volume=20|issue=1|pages=557–585|via=USDA}}</ref> ली एम. वोल्फले ने सिवाल राइट की पथ गुणांक पद्धति का व्याख्यात्मक ग्रंथ सूची इतिहास संकलित किया जिसे पथ विश्लेषण (सांख्यिकी) के रूप में जानते हैं।<ref>{{Cite journal|last=Wolfle|first=Lee M.|date=1999|title=Sewall wright on the method of path coefficients: An annotated bibliography|url=http://www.tandfonline.com/doi/abs/10.1080/10705519909540134|journal=Structural Equation Modeling|language=en|volume=6|issue=3|pages=280–291|doi=10.1080/10705519909540134|issn=1070-5511}}</ref> राइट ने परिणाम की भविष्यवाणी करने के लिए प्रतिगमन का उपयोग करने के मानक अभ्यास में दो महत्वपूर्ण तत्व जोड़े। (1) अधिक समाश्रयण समीकरणों की जानकारी को संयोजित करने के लिए (2) प्रतिगमन मॉडलिंग के लिए केवल पूर्वानुमान के अतिरिक्त कारणात्मक दृष्टिकोण का उपयोग करना। सीवेल राइट ने अपने 1934 के लेख में द मेथड ऑफ पाथ गुणांकों में पथ विश्लेषण की पद्धति को समेकित किया।<ref>{{Cite journal|last=Wright|first=Sewall|date=1934|title=पथ गुणांक की विधि|journal=The Annals of Mathematical Statistics|volume=5|issue=3|pages=161–215|doi=10.1214/aoms/1177732676|jstor=2957502|issn=0003-4851|doi-access=free}}</ref> | ||
1970 के दशक | ओटिस डुडले डंकन ने 1975 में सेम को सामाजिक विज्ञान में प्रस्तुत किया<ref>{{Cite book|last=Duncan|first=Otis Dudley|url=https://www.worldcat.org/oclc/1175858|title=संरचनात्मक समीकरण मॉडल का परिचय|date=1975|publisher=Academic Press|isbn=0-12-224150-9|location=New York|oclc=1175858}}</ref> और यह 1970 और 80 के दशक में अधिक विस्तारित हुआ। मनोविज्ञान, समाजशास्त्र और अर्थशास्त्र में विकसित विभिन्न गणितीय रूप से संबंधित मॉडलिंग दृष्टिकोण का उपयोग किया जाता है। इनमें से दो विकासात्मक धाराओं (मनोविज्ञान से कारक विश्लेषण, और डंकन के माध्यम से समाजशास्त्र से पथ विश्लेषण) के अभिसरण ने सेम के वर्तमान कोर का उत्पादन किया, चूँकि समीकरणों और बहिर्जात को नियोजित करने वाले अर्थमितीय प्रथाओं के साथ अधिक ओवरलैप है।<ref>{{Cite journal|last=Christ|first=Carl F.|date=1994|title=The Cowles Commission's Contributions to Econometrics at Chicago, 1939-1955|url=https://www.jstor.org/stable/2728422|journal=Journal of Economic Literature|volume=32|issue=1|pages=30–59|jstor=2728422|issn=0022-0515}}</ref><ref name="Westland2015" /> | ||
1970 के दशक के प्रारम्भ में शिक्षात्मक परिक्षण सेवाएं लिस्रेल ([[LISREL]]) में विकसित कई कार्यक्रमों में से कार्ल गुस्ताव बल स्कॉग पथ-विश्लेषण-शैली समीकरणों के भीतर अंतर्निहित अव्यक्त चर (जिसे मनोवैज्ञानिक कारक विश्लेषण से अव्यक्त कारकों के रूप में जानते थे) में विकसित हुए।)<ref name=":0">{{Cite journal|last1=Jöreskog|first1=Karl Gustav|last2=van Thillo|first2=Mariella|date=1972|title=LISREL: A General Computer Program for Estimating a Linear Structural Equation System Involving Multiple Indicators of Unmeasured Variables|url=https://files.eric.ed.gov/fulltext/ED073122.pdf|journal=Research Bulletin: Office of Education|volume=ETS-RB-72-56|via=US Government}}</ref> मॉडल के कारक-संरचित भाग में माप त्रुटियां सम्मलित थीं और इस प्रकार अव्यक्त चरों को जोड़ने वाले प्रभावों के माप-त्रुटि-समायोजित अनुमान की अनुमति दी गई थी। | |||
विधि में शक्तिहीनता को अस्पष्ट करने के लिए अव्यवस्थित और भ्रामक शब्दावली का उपयोग किया गया है। विशेष रूप से, पीएलएस-पीए को आंशिक न्यूनतम वर्ग प्रतिगमन पीएलएसआर (PLSR) के साथ मिला दिया गया है, जो साधारण न्यूनतम वर्ग प्रतिगमन का विकल्प है और इसका पथ विश्लेषण से कोई लेना-देना नहीं है। पीएलएस-पीए को त्रुटिपूर्ण विधि के रूप में प्रचारित किया गया है जो छोटे डेटा समूह के साथ कार्य करता है जब अन्य अनुमान विफल हो जाते हैं; वास्तव में, यह दिखाया गया है कि इस पद्धति के लिए न्यूनतम आवश्यक आकार कई प्रतिगमन के अनुरूप हैं।<ref>{{cite journal | url=https://onlinelibrary.wiley.com/doi/full/10.1111/isj.12131 | doi=10.1111/isj.12131 | title=Minimum sample size estimation in PLS-SEM: The inverse square root and gamma-exponential methods | year=2018 | last1=Kock | first1=Ned | last2=Hadaya | first2=Pierre | journal=Information Systems Journal | volume=28 | pages=227–261 | s2cid=3733557 }}</ref> | |||
लिस्रेल और पीएलएस-पीए दोनों की परिकल्पना पुनरावृत्त कंप्यूटर एल्गोरिदम के रूप में की गई थी, जिसमें प्रारंभ से ही सुलभ ग्राफिकल और डेटा प्रविष्टि इंटरफ़ेस बनाने और राइट के (1921) पथ विश्लेषण के विस्तार पर बल दिया गया था। अर्ली [[काउल्स फाउंडेशन]] समीकरणों के आकलन पर कार्य करता है, कोपमैन और हूड्स (1953) के एल्गोरिदम पर [[परिवहन अर्थशास्त्र]] और इष्टतम रूटिंग पर केंद्रित है, [[अधिकतम संभावना अनुमान]] के साथ, और बंद फॉर्म बीजगणितीय गणना, क्योंकि पुनरावृत्त समाधान परीक्षण प्रौद्योगिकी कंप्यूटर से पूर्व के दिनों में सीमित थी। | |||
एंडरसन और रुबिन (1949, 1950) ने एकल संरचनात्मक समीकरण के मापदंडों के लिए सीमित जानकारी अधिकतम संभावना अनुमानक विकसित किया, जिसमें अप्रत्यक्ष रूप से दो-चरण न्यूनतम वर्ग अनुमानक और इसके स्पर्शोन्मुख वितरण (एंडरसन, 2005) (फेयरब्रदर, 1999) सम्मलित थे। [[हेनरी थेल]] (1953a, 1953b, 1961) द्वारा प्रस्तुत किए गए रैखिक युगपत समीकरणों की प्रणाली में एकल संरचनात्मक समीकरण के मापदंडों का अनुमान लगाने की विधि के रूप में [[दो-चरण कम से कम वर्ग|दो-चरण अल्प से अल्प वर्गों]] को मूल रूप से प्रस्तावित किया गया था और [[ रॉबर्ट बसमैन |रॉबर्ट बसमैन]] (1957) द्वारा कमोबेश स्वतंत्र रूप से प्रस्तुत किया गया था।) और [[ सरगन टेनिस |सरगन टेनिस]] (1958) ने एंडरसन की सीमित जानकारी की, अधिकतम संभावना का अनुमान अंततः अविष्कार एल्गोरिथ्म में प्रारम्भ किया गया था, जहां यह अन्य पुनरावृत्त सेम एल्गोरिदम के साथ प्रतिस्पर्धा करता था। इनमें से, 1960 के दशक और 1970 के दशक के प्रारम्भ में दो-चरण न्यूनतम वर्ग अब तक सबसे व्यापक रूप से उपयोग की जाने वाली विधि थी। | |||
1950 के दशक से काउल्स आयोग में प्रतिगमन समीकरण दृष्टिकोण की प्रणालियाँ विकसित की गईं, जो तजालिंग कोपमैन्स के परिवहन मॉडलिंग का विस्तार करती हैं। सीवेल राइट और अन्य सांख्यिकी विदों ने काउल्स (तब [[शिकागो विश्वविद्यालय]] में) में पथ विश्लेषण विधियों को विस्तारित करने का प्रयास किया। शिकागो विश्वविद्यालय के सांख्यिकी विदों ने सामाजिक विज्ञानों के पथ विश्लेषण अनुप्रयोगों के साथ कई दोषों की पहचान की; दोष जो राइट के संदर्भ में जीन संचरण की पहचान करने के लिए महत्वपूर्ण समस्याएँ उत्पन्न नहीं करते थे, किन्तु जिन्होंने सामाजिक विज्ञानों में पीएलएस-पीए और लिस्रेल जैसी पथ विधियों को समस्याग्रस्त बना दिया। फ्रीडमैन (1987) ने पथ विश्लेषण में इन आपत्तियों को संक्षेप में प्रस्तुत किया: सामाजिक विज्ञानों में मात्रात्मक विधि के संदेह और भ्रम के मुख्य कारणों में से धारणाओं, सांख्यिकीय निहितार्थों और नीतिगत आशयों के मध्य अंतर करने में विफलता रही है (वोल्ड्स (1987) भी देखें)। राइट के पथ विश्लेषण ने अमेरिकी अर्थशास्त्रियों के मध्य कभी भी बड़ा अनुसरण नहीं किया, किन्तु [[हरमन वॉल्ड]] और उनके छात्र कार्ल जोरेस्कोग को प्रभावित करने में सफल रहे। जोरेस्कोग के छात्र क्लेस फोर्नेल ने अमेरिका में एलआईएसआरएल को विस्तारित किया। | |||
कंप्यूटर में प्रगति ने अप्रशिक्षित के लिए जटिल, असंरचित समस्याओं में बड़े डेटासमूह के कंप्यूटर-गहन विश्लेषण में संरचनात्मक समीकरण विधियों को प्रारम्भ करना सरल बना दिया। सबसे लोकप्रिय समाधान प्रविधि एल्गोरिदम के तीन वर्गों में आती हैं: (1) सामान्य न्यूनतम वर्ग एल्गोरिदम प्रत्येक पथ पर स्वतंत्र रूप से प्रारम्भ होते हैं, जैसे तथाकथित पीएलएस पथ विश्लेषण पैकेज में प्रारम्भ होते हैं जो ओएलएस के साथ अनुमान लगाते हैं; (2) वोल्ड और उनके छात्र कार्ल जोरेस्कॉग द्वारा एलआईएसआरएल, एएमओएस और ईक्यूएस में प्रारम्भ किए गए मौलिक कार्य से विकसित सहप्रसरण विश्लेषण एल्गोरिदम; और (3) समीकरण प्रतिगमन एल्गोरिदम काउल्स आयोग में तजालिंग कोपमैन्स द्वारा विकसित किया गया। | |||
पर्ल <ref name=Pearl />सेम को रैखिक से गैर पैरामीट्रिक मॉडलिंग तक विस्तारित किया है, और समीकरणों के कारण और प्रतितथ्यात्मक व्याख्याओं का प्रस्ताव दिया है। उदाहरण के लिए, समीकरण के तर्कों से चर Z को त्याग कर यह प्रमाणित करता है कि आश्रित चर बहिष्कृत चर पर हस्तक्षेप से स्वतंत्र है, जब हम शेष तर्कों को स्थिर रखते हैं। गैर पैरामीट्रिक सेम (Nonparametric SEMs) समीकरणों के रूप में या त्रुटि के वितरण के लिए कोई प्रतिबद्धता किए बिना कुल, प्रत्यक्ष और अप्रत्यक्ष प्रभावों के अनुमान की अनुमति देते हैं। यह गैर-रेखीय अंतःक्रियाओं की उपस्थिति में श्रेणीबद्ध चरों को सम्मलित करने वाली प्रणालियों के लिए मध्यस्थता विश्लेषण का विस्तार करता है। बोलेन और पर्ल<ref name="bollen-pearl2013" />एसईएम के कारण व्याख्या के इतिहास का सर्वेक्षण करें और यह क्यों भ्रम और विवादों का स्रोत बन गया है। | |||
सेम पथ विश्लेषण विधियाँ अपनी पहुँच के कारण सामाजिक विज्ञानों में लोकप्रिय हैं; पैक किए गए कंप्यूटर प्रोग्राम शोधकर्ताओं को प्रयोगात्मक डिजाइन और नियंत्रण, प्रभाव और मॉडलिंग आकार, और कई अन्य कारकों को समझने की असुविधा के बिना परिणाम प्राप्त करने की अनुमति देते हैं जो उत्तम शोध डिजाइन का भाग हैं।{{Citation needed|date=January 2023}} समर्थकों का कहना है कि यह प्राकृतिक विज्ञानों में अपनाए जाने की तुलना में विशेष रूप से मनोविज्ञान और सामाजिक संपर्क में कई वास्तविक विश्व की घटनाओं की समग्र, और अल्प स्पष्ट रूप से कारण, व्याख्या को दर्शाता है; आलोचकों का विचार है कि प्रयोगात्मक नियंत्रण की इस अल्पता के कारण कई त्रुटिपूर्ण निष्कर्ष निकाले गए हैं।{{Citation needed|date=January 2023}} | |||
सेम के निर्देशित नेटवर्क मॉडलिंग में दिशा वास्तविकता के बारे में अनुमानित कारण-प्रभाव धारणाओं से उत्पन्न होती है। सामाजिक संपर्क और कलाकृतियाँ अधिकांशतः एपिफेनोमेना होती हैं, द्वितीयक घटनाएँ जो सरलता के कारण कारकों से जुड़ती हैं। फिजियोलॉजिकल एपिफेनोमेनन का उदाहरण है- 100 मीटर वेग को पूर्ण करने का समय है। व्यक्ति अपनी वेग गति को 12 सेकंड से 11 सेकंड तक सुधारने में सक्षम हो सकता है, किन्तु आहार, दृष्टिकोण, मौसम इत्यादि जैसे किसी भी प्रत्यक्ष कारकों में सुधार को श्रेय देना जटिल होगा। वेग समय में 1 सेकंड का सुधार है एपिफेनोमेनन कई भिन्न-भिन्न कारकों का समग्र उत्पाद हैं। | |||
== सेम के लिए सामान्य दृष्टिकोण == | |||
चूँकि सेम परिवार में प्रत्येक प्रौद्योगिकी भिन्न है, निम्नलिखित स्वरूप कई सेम विधियों के लिए सामान्य हैं, क्योंकि इसे [[एलेक्स लियू]] जैसे कई सेम विद्वानों द्वारा 4E के रूप में संक्षेपित किया जा सकता है, जो कि 1) समीकरण (मॉडलिंग या समीकरण विनिर्देश), 2 ) मुक्त मापदंडों का अनुमान, 3) मॉडलिंग का मूल्यांकन, 4) स्पष्टीकरण और संचार, साथ ही परिणामों का निष्पादन है। | |||
=== मॉडलिंग विनिर्देश === | |||
सेम में मॉडलिंग के दो मुख्य घटक प्रतिष्ठित हैं: अंतर्जात और बहिर्जात चर के मध्य संभावित कारण निर्भरता दिखाने वाला संरचनात्मक प्रतिरूप, और अव्यक्त चर और उनके संकेतकों के मध्य संबंध दिखाने वाला माप मॉडलिंग हैं। अन्वेषी और पुष्टि कारक विश्लेषण प्रतिरूप, उदाहरण के लिए, केवल माप के भाग होते हैं, जबकि पथ विश्लेषण (सांख्यिकी) को एसईएम के रूप में देखा जा सकता है जिसमें केवल संरचनात्मक भाग होता है। | |||
पहचाना गया | मॉडलिंग में पथों को निर्दिष्ट करने में, मॉडलिंग दो प्रकार के संबंधों को प्रस्तुत कर सकता है: (1) मुक्त मार्ग, जिसमें परिकल्पित कारण (वास्तव में प्रतितथ्यात्मक) चर के मध्य संबंधों का परीक्षण किया जाता है, और इसलिए भिन्नता के लिए 'मुक्त' त्याग दिया जाता है, और (2) ) चर के मध्य संबंध जिनका पूर्व से ही अनुमानित संबंध है, सामान्यतः पूर्व अध्ययनों पर आधारित होते हैं, जो मॉडलिंग में 'निश्चित' होते हैं। | ||
मॉडलिंग अधिकांशतः सैद्धांतिक रूप से प्रशंसनीय मॉडलिंग का समूह निर्दिष्ट करेगा जिससे कि यह आकलन किया जा सके कि प्रस्तावित मॉडलिंग संभावित मॉडलिंग के समूह में सबसे उत्तम है या नहीं। मॉडलिंग को न केवल मॉडलिंग के निर्माण के लिए सैद्धांतिक कारणों के लिए होना चाहिए, जबकि मॉडलिंग को [[डेटा बिंदु|डेटा बिंदुओं]] की संख्या और मॉडलिंग की पहचान करने के लिए अनुमान लगाने वाले मापदंडों की संख्या को भी ध्यान में रखना चाहिए। | |||
पहचाना गया मॉडलिंग वह है जहां विशिष्ट पैरामीटर मान विशिष्ट रूप से मॉडलिंग ([[पुनरावर्ती परिभाषा]]) की पहचान करता है, और कोई भिन्न पैरामीटर मान द्वारा कोई अन्य समकक्ष सूत्रीकरण नहीं दिया जा सकता है। डेटा बिंदु देखे गए अंकों वाला चर है, जैसे चर जिसमें किसी प्रश्न पर स्कोर होता है या उत्तरदाताओं द्वारा कार अनुचित की संख्या होती है। पैरामीटर ब्याज का मूल्य है, जो बहिर्जात और अंतर्जात चर या कारक लोडिंग (संकेतक और उसके कारक के मध्य प्रतिगमन गुणांक) के मध्य प्रतिगमन गुणांक हो सकता है। यदि अनुमानित मापदंडों की संख्या से अल्प डेटा बिंदु हैं, तो परिणामी मॉडलिंग अज्ञात है, क्योंकि मॉडलिंग में सभी भिन्नताओं के लिए अधिक अल्प संदर्भ बिंदु हैं। समाधान पथों में से शून्य तक सीमित करना है, जिसका अर्थ है कि यह अब मॉडलिंग का भाग नहीं है। | |||
=== मुक्त मापदंडों का अनुमान === | === मुक्त मापदंडों का अनुमान === | ||
पैरामीटर अनुमान वास्तविक | पैरामीटर अनुमान वास्तविक सह-प्रसरण आव्यूह की तुलना करके किया जाता है जो चर और सर्वोत्तम उपयुक्त मॉडलिंग के अनुमानित सह-प्रसरण आव्यूह के मध्य संबंधों का प्रतिनिधित्व करता है। यह अपेक्षा-अधिकतमकरण एल्गोरिथ्म के माध्यम से संख्यात्मक अधिकतमकरण के माध्यम से प्राप्त किया जाता है। अपेक्षा-अधिकतम मानदंड का अधिकतमकरण जैसा कि अधिकतम संभावना अनुमान, [[अर्ध-अधिकतम संभावना]] अनुमान, भारित अल्प से अल्प वर्ग या असमान रूप से वितरण-मुक्त विधियों द्वारा प्रदान किया जाता है। यह अधिकांशतः विशेष एसईएम विश्लेषण कार्यक्रम का उपयोग करके पूर्ण किया जाता है, जिनमें से कई उपस्तिथ हैं। | ||
=== | === मॉडलिंग और मॉडलिंग उपयुक्त का मूल्यांकन === | ||
मॉडलिंग का अनुमान लगाने के पश्चात, विश्लेषक मॉडलिंग की व्याख्या करना। अनुमानित पथों को पथ मॉडलिंग के रूप में सारणीबद्ध या रेखांकन के रूप में प्रस्तुत किया जा सकता है। पथ विश्लेषण (सांख्यिकी) पथ अनुरेखण नियमों (पथ विश्लेषण (सांख्यिकी) देखें) का उपयोग करके चरों के प्रभाव का आकलन किया जाता है। | |||
यह निर्धारित करने के लिए अनुमानित | यह निर्धारित करने के लिए अनुमानित मॉडलिंग के उपयुक्त की अन्वेषण करना महत्वपूर्ण है कि यह डेटा को कितना उत्तम प्रकार का मॉडलिंग करता है। एसईएम मॉडलिंग में यह आधारभूत कार्य है, मॉडलिंग को स्वीकार या अस्वीकार करने के लिए आधार तैयार करना और अधिक सामान्यतः, प्रतिस्पर्धी मॉडलिंग को दूसरे पर स्वीकार करना। एसईएम कार्यक्रमों के आउटपुट में मॉडलिंग में चरों के मध्य अनुमानित संबंधों के आव्यूह सम्मलित हैं। उपयुक्त आकलन अनिवार्य रूप से गणना करता है कि अनुमानित डेटा वास्तविक डेटा में संबंधों वाले मैट्रिसेस के समान कैसे हैं। | ||
इन उद्देश्यों के लिए औपचारिक सांख्यिकीय परीक्षण और | इन उद्देश्यों के लिए औपचारिक सांख्यिकीय परीक्षण और उपयुक्त अनुक्रमणिका विकसित किए गए हैं। अनुमानित मॉडलिंग के भीतर मॉडलिंग के व्यक्तिगत मापदंडों की भी अन्वेषण की जा सकती है जिससे कि यह देखा जा सके कि प्रस्तावित मॉडलिंग ड्राइविंग सिद्धांत में कितना उत्तम प्रकार उपयुक्त है। अधिकांश, चूँकि सभी, आकलन विधियां मॉडलिंग के ऐसे परीक्षणों को संभव नहीं बनाती हैं। | ||
निश्चित रूप से जैसा कि सभी [[सांख्यिकीय परिकल्पना परीक्षण]] में होता है, | निश्चित रूप से जैसा कि सभी [[सांख्यिकीय परिकल्पना परीक्षण]] में होता है, सेम मॉडलिंग परीक्षण इस धारणा पर आधारित होते हैं कि उत्तम और पूर्ण प्रासंगिक डेटा को मॉडलिंग किया गया है। सेम साहित्य में, उपयुक्त विचार ने विभिन्न सूचकांकों और परिकल्पना परीक्षणों के त्रुटिहीन अनुप्रयोग पर विभिन्न अनुशंसाओं को उद्गम किया है। | ||
उपयुक्त का आकलन करने के लिए भिन्न-भिन्न दृष्टिकोण हैं। मॉडलिंग के लिए पारंपरिक दृष्टिकोण अशक्त परिकल्पना से प्रारंभ होता है, अधिक उदार मॉडलिंग (अर्थात अल्प मुक्त मापदंडों वाले) को पुरस्कृत करते हुए, अन्य जैसे कि [[एकैके सूचना मानदंड|सूचना मानदंड]] जो इस बात पर ध्यान केंद्रित करते हैं कि संतृप्त मॉडलिंग से उपयुक्त किए गए मान कितने अल्प हैं। {{Citation needed|date=November 2009}} (अर्थात वे कितनी उत्तम प्रकार से मूल्यों को पुन: उत्पन्न करते हैं), उपयोग किए गए मुक्त मापदंडों की संख्या को ध्यान में रखते हुए। क्योंकि उपयुक्त के विभिन्न उपाय मॉडलिंग के विभिन्न तत्वों का उपयोग करते है, इसलिए विभिन्न उपयुक्त उपायों के चयन की रिपोर्ट करना उचित है। उपयुक्त उपायों की व्याख्या के लिए दिशानिर्देश (अर्थात, कटऑफ स्कोर), के नीचे सूचीबद्ध लोगों सहित, सेम शोधकर्ताओं के मध्य अधिक विवश का विषय हैं।{{sfn|MacCallum|Austin|2000|p=218-219}} | |||
उपयुक्त के कुछ अधिक सामान्य रूप से उपयोग किए जाने वाले उपायों में सम्मलित हैं | |||
* [[ची-स्क्वेर्ड परीक्षण]] | * [[ची-स्क्वेर्ड परीक्षण]] | ||
** कई अन्य | ** कई अन्य उपायों की गणना में उपयोग किए जाने वाले उपयुक्त मौलिक उपाय है। संकल्पनात्मक रूप से मॉडलिंग आकार का कार्य है और देखे गए सह-प्रसरण मैट्रिक्स और मॉडलिंग सहप्रसरण मैट्रिक्स के मध्य का अंतर है। | ||
* | * एकैके सूचना मानदंड (एआईसी) | ||
** | ** संबंधी मॉडलिंग उपयुक्त का परीक्षण: रुचिकर मॉडलिंग सबसे अल्प एआईसी मूल्य वाला है। | ||
** <math>\mathit{AIC} = 2k - 2\ln(L)\,</math> | ** <math>\mathit{AIC} = 2k - 2\ln(L)\,</math> | ||
** जहां k [[सांख्यिकीय मॉडल]] में मापदंडों की संख्या है, और L | ** जहां k [[सांख्यिकीय मॉडल|सांख्यिकीय]] मॉडलिंग में मापदंडों की संख्या है, और L मॉडलिंग की [[संभावना]] का अधिकतम मूल्य है। | ||
* [[सन्निकटन का मूल माध्य वर्ग त्रुटि]] (RMSEA) | * [[सन्निकटन का मूल माध्य वर्ग त्रुटि|समीप का मूल माध्य वर्ग त्रुटि]] (RMSEA) | ||
** | **उपयुक्त अनुक्रमणिका जहां शून्य का मान सर्वोत्तम उपयुक्त प्रदर्शित करता है।{{sfn|Kline|2011|p=205}} जबकि आरएमएसईए का उपयोग करके समीप उपयुक्त का निर्धारण करने के लिए दिशानिर्देश अत्यधिक विवादित है,{{sfn|Kline|2011|p=206}} अधिकांश शोधकर्ता इस बात से सहमत हैं कि .1 या अधिक का आरएमएसईए दुर्गति उपयुक्त प्रदर्शित करता है।{{sfn|Hu|Bentler|1999|p=11}}<ref name="Browne1993" /> | ||
** | **[[मानकीकृत रूट माध्य चुकता अवशिष्ट]] (SRMR) | ||
* तुलनात्मक | ** एसआरएमआर लोकप्रिय संपूर्ण उपयुक्त संकेतक है। हू और बेंटलर (1999) ने उत्तम उपयुक्त के लिए दिशानिर्देश के रूप में .08 या उससे छोटे का विचार दिया।{{sfn|Hu|Bentler|1999|p=27}} क्लाइन (2011) ने उत्तम उपयुक्त के लिए दिशानिर्देश के रूप में .1 या उससे अल्प का विचार दिया। | ||
**बेसलाइन तुलनाओं की | * तुलनात्मक उपयुक्त अनुक्रमणिका (सीएफआई) | ||
**बेसलाइन तुलनाओं की अन्वेषण में, सीएफआई डेटा में सह-संबंधों के औसत आकार पर बड़े भाग पर निर्भर करता है। यदि चरों के मध्य औसत सह-संबंध अधिक नहीं है, तो सीएफआई (CFI) अधिक नहीं होगा। .95 या उच्चतर का सीएफआई मूल्य वांछनीय है।{{sfn|Hu|Bentler|1999|p=27}} | |||
उपयुक्त के प्रत्येक माप के लिए, मॉडलिंग और डेटा के मध्य उत्तम-पर्याप्त उपयुक्त का प्रतिनिधित्व करने वाले निर्णय को अन्य प्रासंगिक कारकों जैसे मॉडलिंग आकार, कारकों के संकेतों का अनुपात और मॉडलिंग की समग्र जटिलता को प्रतिबिंबित करना चाहिए। उदाहरण के लिए, अधिक बड़े मॉडलिंग ची-स्क्वेर्ड परीक्षण को अत्यधिक संवेदनशील बनाते हैं और प्रतिरूप-डेटा उपयुक्त की अल्पता का संकेत देने की अधिक संभावना रखते हैं। {{sfn|Kline|2011|p=201}} | |||
=== | === मॉडलिंग संशोधन === | ||
उपयुक्त को उत्तम बनाने के लिए मॉडलिंग को संशोधित करने की आवश्यकता हो सकती है, जिससे चर के मध्य सबसे अधिक संभावित संबंधों का अनुमान लगाया जा सके। कई कार्यक्रम संशोधन सूचकांक प्रदान करते हैं जो सामान्य संशोधनों का मार्गदर्शन कर सकते हैं। संशोधन सूचकांक χ² में परिवर्तन की रिपोर्ट करते हैं जो निश्चित मापदंडों को मुक्त करने के परिणामस्वरूप होता है: सामान्यतः, इसलिए मॉडलिंग के लिए पथ जोड़ना जो वर्तमान में शून्य पर समूह है। मॉडलिंग उपयुक्त में सुधार करने वाले संशोधनों को मॉडलिंग में किए जा सकने वाले संभावित परिवर्तनों के रूप में फ़्लैग किया जा सकता है। मॉडलिंग में संशोधन, विशेष रूप से संरचनात्मक प्रतिरूप, उचित होने का प्रमाणित करने वाले सिद्धांत में परिवर्तन हैं। इसलिए संशोधनों का परीक्षण किए जा रहे सिद्धांत के संदर्भ में समझ में आना चाहिए, या उस सिद्धांत की सीमाओं के रूप में स्वीकार किया जाना चाहिए। माप मॉडलिंग में परिवर्तन प्रभावी रूप से प्रमाणित करते हैं कि डेटा सिद्धांत द्वारा निर्दिष्ट अव्यक्त चर के अशुद्ध संकेतक हैं।<ref name="Loehlin2004" /> | |||
मॉडलिंग को संशोधन सूचकांकों द्वारा नेतृत्व नहीं किया जाना चाहिए, जैसा कि मैककलम (1986) ने प्रदर्शित किया: अनुकूल परिस्थितियों में भी, विनिर्देश अविष्कार से उत्पन्न होने वाले मॉडलिंग को सावधानी के साथ देखा जाना चाहिए।<ref name="MacCallum1986" /> | |||
=== | === मॉडलिंग आकार और शक्ति === | ||
जब शोधकर्ता इस बात से सहमत हैं कि सेम का उपयोग करके पर्याप्त [[सांख्यिकीय शक्ति]] और त्रुटिहीन अनुमान प्रदान करने के लिए बड़े मॉडलिंग आकार की आवश्यकता होती है, पर्याप्त मॉडलिंग आकार निर्धारित करने के लिए उपयुक्त विधि पर कोई साधारण सहमति नहीं है।{{sfn|Quintana|Maxwell|1999|p=499}} <ref name="Westland" />सामान्यतः, मॉडलिंग आकार निर्धारित करने के लिए विचारों में प्रति पैरामीटर टिप्पणियों की संख्या, उपयुक्त अनुक्रमणिका के लिए पर्याप्त रूप से प्रदर्शन करने के लिए आवश्यक टिप्पणियों की संख्या और स्वतंत्रता की प्रति डिग्री टिप्पणियों की संख्या सम्मलित होती है।{{sfn|Quintana|Maxwell|1999|p=499}} शोधकर्ताओं ने सिमुलेशन अध्ययन, व्यवसायी अनुभव, और गणितीय सूत्रों के आधार पर दिशानिर्देश प्रस्तावित किए हैं।<ref name="Chou1995" /><ref name="Bentler2016" /><ref name="Westland"/><ref name="MacCallum1996" /> | |||
सेम परिकल्पना परीक्षण में विशेष महत्व और शक्ति प्राप्त करने के लिए मॉडलिंग आकार की आवश्यकताएं उसी मॉडलिंग के लिए समान होती हैं जब परीक्षण के लिए तीन एल्गोरिदम (पीएलएस-पीए, लिस्रेल या प्रतिगमन समीकरणों की प्रणाली) का उपयोग किया जाता है।{{Citation needed|date=January 2015}} | |||
=== स्पष्टीकरण और संचार === | === स्पष्टीकरण और संचार === | ||
इसके | इसके पश्चात मॉडलिंग के समूह की व्याख्या की जाती है जिससे कि सर्वोत्तम उपयुक्त मॉडलिंग के आधार पर निर्माण के बारे में प्रमाणित किया जा सके। | ||
प्रयोग या समय-आदेशित अध्ययन किए जाने पर भी कारणता का प्रमाणित | प्रयोग या समय-आदेशित अध्ययन किए जाने पर भी कारणता का प्रमाणित करते समय सदैव सावधानी बरतनी चाहिए। शब्द कारणात्मक मॉडलिंग को ऐसे मॉडलिंग के रूप में समझा जाना चाहिए जो कारण संबंधी मान्यताओं को व्यक्त करता है, आवश्यक नहीं कि ऐसा मॉडलिंग हो जो मान्य कारण निष्कर्ष उत्पन्न करता हो। कई समय बिंदुओं पर डेटा एकत्र करना और प्रायोगिक या अर्ध-प्रायोगिक डिजाइन का उपयोग करने से कुछ प्रतिद्वंद्वी परिकल्पनाओं को दूर करने में सहायता मिल सकती है, किन्तु यादृच्छिक प्रयोग भी ऐसे सभी आशंका से इंकार नहीं कर सकता है। कारण परिकल्पना के अनुरूप मॉडलिंग द्वारा उत्तम उपयुक्त अनिवार्य रूप से विरोधी कारण परिकल्पना के अनुरूप दूसरे मॉडलिंग द्वारा समान रूप से उत्तम उपयुक्त होता है। कोई भी शोध डिजाइन, चाहे कितना भी निपुण क्यों न हो, इस प्रकार की प्रतिद्वंद्वी परिकल्पनाओं को भिन्न करने में सहायता कर सकता हैI<ref name="Pearl" /> | ||
किसी भी विज्ञान | किसी भी विज्ञान के जैसे, पश्चात की प्रतिकृति और संभवतः संशोधन प्रारंभिक अविष्कार से विस्तारित होंगे। | ||
== उन्नत उपयोग == | == उन्नत उपयोग == | ||
* [[मापन व्युत्क्रम]] | * [[मापन व्युत्क्रम]] | ||
* | *एकाधिक समूह प्रतिरूप: यह ऐसी प्रौद्योगिकी है जो कई मॉडलिंग के संयुक्त अनुमान की अनुमति देती है, प्रत्येक भिन्न-भिन्न उप-समूहों के साथ अनुप्रयोगों में [[व्यवहार आनुवंशिकी]], और समूहों के मध्य मतभेदों का विश्लेषण सम्मलित है (जैसे, लिंग, संस्कृतियां, विभिन्न भाषाओं में लिखे गए परीक्षण प्रपत्र आदि)। | ||
* अव्यक्त विकास | * अव्यक्त विकास प्रतिरूप | ||
* [[अरैखिक मिश्रित प्रभाव मॉडल]] | * [[अरैखिक मिश्रित प्रभाव मॉडल|अरैखिक मिश्रित प्रभाव प्रतिरूप]] | ||
* श्रेणीबद्ध/[[बहुस्तरीय मॉडल]]; [[आइटम प्रतिक्रिया सिद्धांत]] | * श्रेणीबद्ध/[[बहुस्तरीय मॉडल|बहुस्तरीय प्रतिरूप]] ; [[आइटम प्रतिक्रिया सिद्धांत|डेटा प्रतिक्रिया सिद्धांत]] प्रतिरूप | ||
* [[मिश्रण मॉडल]] (अव्यक्त वर्ग) | * [[मिश्रण मॉडल|मिश्रण]] मॉडलिंग (अव्यक्त वर्ग) सेम | ||
* वैकल्पिक अनुमान और परीक्षण | * वैकल्पिक अनुमान और परीक्षण प्रौद्योगिकी | ||
* दृढ़ अनुमान | * दृढ़ अनुमान | ||
* सर्वेक्षण | * सर्वेक्षण मॉडलिंग विश्लेषण | ||
* मल्टी-मेथड मल्टी-ट्रेट | * मल्टी-मेथड मल्टी-ट्रेट प्रतिरूप | ||
* संरचनात्मक समीकरण | * संरचनात्मक समीकरण मॉडलिंग ट्रीज | ||
== एसईएम-विशिष्ट सॉफ़्टवेयर == | == एसईएम-विशिष्ट सॉफ़्टवेयर == | ||
संरचनात्मक समीकरण | संरचनात्मक समीकरण मॉडलिंग को उपयुक्त करने के लिए कई सॉफ़्टवेयर पैकेज उपस्तिथ हैं। लिस्रेल ऐसा प्रथम सॉफ्टवेयर था, जो प्रारम्भ में 1970 के दशक में निरंतर उपयोग किया गया था।<ref name=":0" />शोधकर्ताओं के मध्य अधिकांशतः उपयोग किए जाने वाले सॉफ्टवेयर कार्यान्वयन में [[एमप्लस]] (Mplus),[[ आर (प्रोग्रामिंग भाषा) | आर (R) (प्रोग्रामिंग भाषा)]] पैकेज सम्मलित हैं<ref name="lavaan"/>और सेम, लिस्रेल, ओपनएमएक्स ([[OpenMx]]), एसपीएसएस ([[SPSS]]) अमोस (AMOS), और स्टाटा ([[Stata]]) इत्यादि।<ref>{{Cite journal |last=Narayanan |first=A. |date=2012-05-01 |title=स्ट्रक्चरल इक्वेशन मॉडलिंग के लिए आठ सॉफ्टवेयर पैकेज की समीक्षा|url=https://doi.org/10.1080/00031305.2012.708641 |journal=The American Statistician |volume=66 |issue=2 |pages=129–138 |doi=10.1080/00031305.2012.708641 |s2cid=59460771 |issn=0003-1305}}</ref> बारबरा एम बायरन ने [[बहुभिन्नरूपी प्रायोगिक मनोविज्ञान का समाज]] के बहुभिन्नरूपी एप्लीकेशन बुक सीरीज के भाग के रूप में इन सॉफ्टवेयरों का उपयोग करने के लिए कई निर्देशात्मक पुस्तकें प्रकाशित कीं।<ref>{{Cite web |title=Barbara Byrne Award for Outstanding Book or Edited Volume {{!}} SMEP |url=https://smep.org/barbara-byrne-award |access-date=2022-10-25 |website=smep.org}}</ref> | ||
विद्वान इसे रिपोर्ट करने के लिए | |||
विद्वान द्वारा इसे रिपोर्ट करने के लिए उत्तम अभ्यास मानते हैं कि एसईएम विश्लेषण के लिए कौन से सॉफ़्टवेयर पैकेज और संस्करण का उपयोग किया गया था क्योंकि उनके निकट भिन्न -भिन्न क्षमताएं हैं और समान नामित प्रौद्योगिकी को करने के लिए थोड़ा भिन्न विधि का उपयोग कर सकते हैं।{{sfn|Kline|2011|p=79-88}} | |||
== यह भी देखें == | == यह भी देखें == | ||
* [[कारण मॉडल]] | * [[कारण मॉडल|कारण प्रतिरूप]] | ||
* [[ग्राफिकल मॉडल]] | * [[ग्राफिकल मॉडल|चित्रमय प्रतिरूप]] | ||
* [[बहुभिन्नरूपी आँकड़े]] | * [[बहुभिन्नरूपी आँकड़े]] | ||
* आंशिक न्यूनतम वर्ग पथ | * आंशिक न्यूनतम वर्ग पथ प्रतिरूप | ||
* [[आंशिक न्यूनतम वर्ग प्रतिगमन]] | * [[आंशिक न्यूनतम वर्ग प्रतिगमन]] | ||
* साथ समीकरण | * साथ समीकरण प्रतिरूप | ||
* [[गुप्त चरों के साथ स्ट्रक्चरल समीकरण|गुप्त चरों के साथ संरचनात्मक समीकरण]] | * [[गुप्त चरों के साथ स्ट्रक्चरल समीकरण|गुप्त चरों के साथ संरचनात्मक समीकरण]] | ||
* [[कारण मानचित्र]] | * [[कारण मानचित्र]] | ||
| Line 179: | Line 181: | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* [http://archive.wikiwix.com/cache/20110707224407/http://www2.chass.ncsu.edu/garson/pa765/structur.htm Structural equation modeling page under David Garson's StatNotes, NCSU] | * [http://archive.wikiwix.com/cache/20110707224407/http://www2.chass.ncsu.edu/garson/pa765/structur.htm Structural equation modeling page under David Garson's StatNotes, NCSU] | ||
* [http://disc-nt.cba.uh.edu/chin/ais/ Issues and Opinion on Structural Equation Modeling], | * [http://disc-nt.cba.uh.edu/chin/ais/ Issues and Opinion on Structural Equation Modeling], सेमin IS Research | ||
* [http://bayes.cs.ucla.edu/BOOK-2K/jw.html The causal interpretation of structural equations (or | * [http://bayes.cs.ucla.edu/BOOK-2K/jw.html The causal interpretation of structural equations (or सेमsurvival kit) by Judea Pearl 2000.] | ||
* [http://archive.wikiwix.com/cache/20110707224414/http://www.upa.pdx.edu/IOA/newsom/semrefs.htm Structural Equation Modeling Reference List by Jason Newsom]: journal articles and book chapters on structural equation models | * [http://archive.wikiwix.com/cache/20110707224414/http://www.upa.pdx.edu/IOA/newsom/semrefs.htm Structural Equation Modeling Reference List by Jason Newsom]: journal articles and book chapters on structural equation models | ||
* [[Wikibooks:Handbook of Management Scales|Handbook of Management Scales]], a collection of previously used multi-item scales to measure constructs for SEM | * [[Wikibooks:Handbook of Management Scales|Handbook of Management Scales]], a collection of previously used multi-item scales to measure constructs for SEM | ||
{{Authority control}} | {{Authority control}} | ||
[[Category: | [[Category:All articles with unsourced statements]] | ||
[[Category:Articles with unsourced statements from January 2015]] | |||
[[Category:Articles with unsourced statements from January 2023]] | |||
[[Category:Articles with unsourced statements from November 2009]] | |||
[[Category:CS1]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:Created On 24/02/2023]] | [[Category:Created On 24/02/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:अव्यक्त चर मॉडल]] | |||
[[Category:ग्राफिकल मॉडल]] | |||
[[Category:प्रतिगमन मॉडल]] | |||
[[Category:संरचनात्मक समीकरण मॉडल]] | |||
Latest revision as of 12:52, 12 March 2023

संरचनात्मक समीकरण मॉडलिंग सेम (SEM) वैज्ञानिकों द्वारा प्रयोग किए जाने वाले विधि के समूह के लिए लेबल करते है, जो विज्ञान में प्रयोगात्मक और अवलोकन अनुसंधान दोनों में उपयोग किया जाता है,[1]जैसे- व्यवसाय,[2] और अन्य क्षेत्र है। इसका उपयोग सामाजिक और व्यवहार विज्ञान में सबसे अधिक किया जाता है। अत्यधिक प्रौद्योगिकी भाषा के संदर्भ के बिना सेम की परिभाषा कठिन है, किन्तु उत्तम प्रारम्भ का स्थान नाम ही है।
सेम में मॉडलिंग का निर्माण सम्मलित है, यह दर्शाने के लिए कि कैसे अवलोकनीय या सैद्धांतिक घटना के विभिन्न पार्श्व को दूसरे से संरचनात्मक रूप से संबंधित माना जाता है। मॉडल का संरचनात्मक उन चरों के मध्य सैद्धांतिक संघों को दर्शाता है जो अन्वेषण के अंतर्गत घटना का प्रतिनिधित्व करते हैं। अनुमानित कारण संरचना को अधिकांशतः चर के मध्य कारण का प्रतिनिधित्व करने वाले तीरों के साथ चित्रित किया जाता है (जैसा कि आंकड़े 1 और 2 में) किन्तु इस कारण सम्बन्ध को समान रूप से समीकरण के रूप में दर्शाया जा सकता है। संरचनाओं का अर्थ है कि सम्बन्ध के विशिष्ट पैटर्न चर के मूल्यों के मध्य दिखाई देने चाहिए, और चर के मूल्यों के मध्य देखे गए सम्बन्ध का उपयोग कारण प्रभाव के परिमाण का अनुमान लगाने के लिए किया जाता है, और यह अनुसंधान के लिए मनाया गया डेटा संगत है या नहीं अनुमानित कारण संरचना सेम में समीकरण गणित और सांख्यिकी गुण हैं जो मॉडल और इसकी संरचनात्मक विशेषताओं द्वारा निहित हैं, और प्रायोगिक या अवलोकन संबंधी डेटा पर चलने वाले सांख्यिकीय एल्गोरिदम (सामान्यतः आव्यूह गणना और सामान्यीकृत रैखिक मॉडलिंग पर आधारित) के साथ अनुमानित हैं।
संरचनात्मक समीकरण मॉडल क्या है और क्या नहीं है, के मध्य सीमा में सदैव की स्पष्टता नहीं होती है, किन्तु एसई मॉडल में अधिकांशतः अव्यक्त चर के समूह के मध्य अनुमानित कारण जुड़े होते हैं और पोस्ट किए गए को जोड़ने वाले कारण सम्बंधित अव्यक्त चर जिन्हें देखा जा सकता है और जिनके मान कुछ डेटा समूह में उपलब्ध हैं। अव्यक्त कारण की शैलियों के मध्य भिन्नता, अव्यक्त चर को मापने वाले प्रेक्षित चर के मध्य भिन्नता, और सांख्यिकीय अनुमान रणनीतियों में भिन्नता के परिणामस्वरूप सेम उपकरण किट में पुष्टि कारक विश्लेषण, पुष्टिकरण समग्र विश्लेषण, पथ विश्लेषण (सांख्यिकी), बहु-समूह मॉडलिंग सम्मलित हैं। अनुदैर्ध्य मॉडलिंग, आंशिक न्यूनतम वर्ग पथ मॉडलिंग, अव्यक्त विकास मॉडलिंग और श्रेणीबद्ध या बहुस्तरीय मॉडलिंग हैं।[3][4][5]
एसईएम का उपयोग सामान्यतः उचित है क्योंकि यह उन अव्यक्त चरों की पहचान करने में सहायता करता है जिनके बारे में माना जाता है कि वे उपस्तिथ हैं, किन्तु उन्हें सरलता से नहीं देखा जा सकता है। चूँकि एसईएम क्या है और क्या नहीं है, इसकी सदैव स्पष्ट सीमाएं नहीं होती हैं,[6] इसमें सामान्यतः पथ मॉडल सम्मलित होते हैं (पथ विश्लेषण भी देखें) और माप मॉडल (कारक विश्लेषण भी देखें) में डेटा से लिए गए वास्तविक चर के अंतर्निहित चर के मध्य संरचनात्मक सम्बन्ध की अन्वेषण करने के लिए सदैव सांख्यिकीय मॉडल और कंप्यूटर प्रोग्राम को नियोजित करते हैं।[3] एसईएम का उपयोग करने वाले शोधकर्ता प्रत्येक मॉडल किए गए तीर (उदाहरण के लिए चित्र 1 में दिखाए गए नंबर) गुणांक की शक्ति और संकेत का अनुमान लगाने के लिए सॉफ्टवेयर प्रोग्राम का उपयोग करते हैं, और डायग्नोस्टिक प्रदान करने के लिए विचार देते हैं कि कौन से संकेतक या मॉडल घटक के मध्य असंगतता उत्पन्न कर सकते हैं। एसईएम विधियों की आलोचना गणितीय सूत्रीकरण समस्याओं, बाहरी वैधता स्थापित किए बिना मॉडल को स्वीकार करने की प्रवृत्ति और संभावित दार्शनिक पूर्वाग्रह की ओर संकेत करती है।
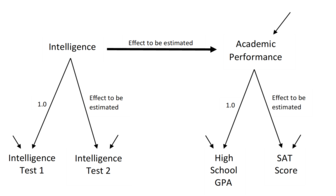
सेम विचार देता है कि बुद्धि (जैसा कि चार प्रश्नों द्वारा मापा जाता है) शैक्षणिक प्रदर्शन की भविष्यवाणी कर सकता है (जैसा कि सैट, एक्ट, और हाई स्कूल जीपीए द्वारा मापा जाता है) चित्र 1 में दिखाया गया है। मानव बुद्धि की अवधारणा को सरलता से उस प्रकार नहीं मापा जा सकता है जिससे व्यक्ति की ऊंचाई या भार मापें जाते है। इसके अतिरिक्त, शोधकर्ताओं के निकट बुद्धि का सिद्धांत और अवधारणा है और फिर प्रश्नावली या परीक्षण जैसे माप उपकरण को डिजाइन करते हैं जो उन्हें बुद्धि के कई संकेतक प्रदान करते हैं। इन संकेतों को मॉडल में संयोजित किया जाता है जिससे कि संकेतों से अव्यक्त चर (चित्र 1 में बुद्धि के लिए वृत्त) के रूप में बुद्धिमत्ता को मापने का प्रशंसनीय विधि बनाया जा सके (चित्र 1 में स्केल 1-4 के साथ वर्गाकार बक्से)।[7]चित्र 1 को अंतिम मॉडल के रूप में प्रस्तुत किया गया है, इसे चलाने और सभी अनुमानों (तीरों पर संख्या) को प्राप्त करने के पश्चात सेम का प्रतिनिधित्व करने के लिए सबसे उत्तम प्रतीकात्मक संकेतन पर कोई सहमति नहीं है, उदाहरण के लिए चित्र 2 और 1 के समान मॉडल का प्रतिनिधित्व करता है, बिना कई तीरों के प्रारूप में जो मॉडल को चलाने से पूर्व हो सकता है।
एसईएम का बड़ा लाभ यह है कि ये सभी माप और परीक्षण के साथ सांख्यिकीय अनुमान प्रक्रिया में होते हैं, जहां मॉडल से सभी जानकारी का उपयोग करके पूर्ण मॉडल में त्रुटियों की गणना की जाती है। इसका तात्पर्य यह है कि त्रुटियां अधिक त्रुटिहीन होती हैं यदि शोधकर्ता को मॉडलिंग के प्रत्येक भाग की भिन्न-भिन्न गणना करनी होती है।[8]
इतिहास
संरचनात्मक समीकरण मॉडलिंग सेम की जड़ें सेवेल राइट के कार्य में हैं, जिन्होंने जनसंख्या आनुवंशिकी में देखे गए चर के प्रत्यक्ष और अप्रत्यक्ष प्रभावों के आधार पर प्रतिगमन समीकरणों के लिए स्पष्ट कारण व्याख्याएं प्रारम्भ कीं।[9][10] ली एम. वोल्फले ने सिवाल राइट की पथ गुणांक पद्धति का व्याख्यात्मक ग्रंथ सूची इतिहास संकलित किया जिसे पथ विश्लेषण (सांख्यिकी) के रूप में जानते हैं।[11] राइट ने परिणाम की भविष्यवाणी करने के लिए प्रतिगमन का उपयोग करने के मानक अभ्यास में दो महत्वपूर्ण तत्व जोड़े। (1) अधिक समाश्रयण समीकरणों की जानकारी को संयोजित करने के लिए (2) प्रतिगमन मॉडलिंग के लिए केवल पूर्वानुमान के अतिरिक्त कारणात्मक दृष्टिकोण का उपयोग करना। सीवेल राइट ने अपने 1934 के लेख में द मेथड ऑफ पाथ गुणांकों में पथ विश्लेषण की पद्धति को समेकित किया।[12]
ओटिस डुडले डंकन ने 1975 में सेम को सामाजिक विज्ञान में प्रस्तुत किया[13] और यह 1970 और 80 के दशक में अधिक विस्तारित हुआ। मनोविज्ञान, समाजशास्त्र और अर्थशास्त्र में विकसित विभिन्न गणितीय रूप से संबंधित मॉडलिंग दृष्टिकोण का उपयोग किया जाता है। इनमें से दो विकासात्मक धाराओं (मनोविज्ञान से कारक विश्लेषण, और डंकन के माध्यम से समाजशास्त्र से पथ विश्लेषण) के अभिसरण ने सेम के वर्तमान कोर का उत्पादन किया, चूँकि समीकरणों और बहिर्जात को नियोजित करने वाले अर्थमितीय प्रथाओं के साथ अधिक ओवरलैप है।[14][15]
1970 के दशक के प्रारम्भ में शिक्षात्मक परिक्षण सेवाएं लिस्रेल (LISREL) में विकसित कई कार्यक्रमों में से कार्ल गुस्ताव बल स्कॉग पथ-विश्लेषण-शैली समीकरणों के भीतर अंतर्निहित अव्यक्त चर (जिसे मनोवैज्ञानिक कारक विश्लेषण से अव्यक्त कारकों के रूप में जानते थे) में विकसित हुए।)[16] मॉडल के कारक-संरचित भाग में माप त्रुटियां सम्मलित थीं और इस प्रकार अव्यक्त चरों को जोड़ने वाले प्रभावों के माप-त्रुटि-समायोजित अनुमान की अनुमति दी गई थी।
विधि में शक्तिहीनता को अस्पष्ट करने के लिए अव्यवस्थित और भ्रामक शब्दावली का उपयोग किया गया है। विशेष रूप से, पीएलएस-पीए को आंशिक न्यूनतम वर्ग प्रतिगमन पीएलएसआर (PLSR) के साथ मिला दिया गया है, जो साधारण न्यूनतम वर्ग प्रतिगमन का विकल्प है और इसका पथ विश्लेषण से कोई लेना-देना नहीं है। पीएलएस-पीए को त्रुटिपूर्ण विधि के रूप में प्रचारित किया गया है जो छोटे डेटा समूह के साथ कार्य करता है जब अन्य अनुमान विफल हो जाते हैं; वास्तव में, यह दिखाया गया है कि इस पद्धति के लिए न्यूनतम आवश्यक आकार कई प्रतिगमन के अनुरूप हैं।[17]
लिस्रेल और पीएलएस-पीए दोनों की परिकल्पना पुनरावृत्त कंप्यूटर एल्गोरिदम के रूप में की गई थी, जिसमें प्रारंभ से ही सुलभ ग्राफिकल और डेटा प्रविष्टि इंटरफ़ेस बनाने और राइट के (1921) पथ विश्लेषण के विस्तार पर बल दिया गया था। अर्ली काउल्स फाउंडेशन समीकरणों के आकलन पर कार्य करता है, कोपमैन और हूड्स (1953) के एल्गोरिदम पर परिवहन अर्थशास्त्र और इष्टतम रूटिंग पर केंद्रित है, अधिकतम संभावना अनुमान के साथ, और बंद फॉर्म बीजगणितीय गणना, क्योंकि पुनरावृत्त समाधान परीक्षण प्रौद्योगिकी कंप्यूटर से पूर्व के दिनों में सीमित थी।
एंडरसन और रुबिन (1949, 1950) ने एकल संरचनात्मक समीकरण के मापदंडों के लिए सीमित जानकारी अधिकतम संभावना अनुमानक विकसित किया, जिसमें अप्रत्यक्ष रूप से दो-चरण न्यूनतम वर्ग अनुमानक और इसके स्पर्शोन्मुख वितरण (एंडरसन, 2005) (फेयरब्रदर, 1999) सम्मलित थे। हेनरी थेल (1953a, 1953b, 1961) द्वारा प्रस्तुत किए गए रैखिक युगपत समीकरणों की प्रणाली में एकल संरचनात्मक समीकरण के मापदंडों का अनुमान लगाने की विधि के रूप में दो-चरण अल्प से अल्प वर्गों को मूल रूप से प्रस्तावित किया गया था और रॉबर्ट बसमैन (1957) द्वारा कमोबेश स्वतंत्र रूप से प्रस्तुत किया गया था।) और सरगन टेनिस (1958) ने एंडरसन की सीमित जानकारी की, अधिकतम संभावना का अनुमान अंततः अविष्कार एल्गोरिथ्म में प्रारम्भ किया गया था, जहां यह अन्य पुनरावृत्त सेम एल्गोरिदम के साथ प्रतिस्पर्धा करता था। इनमें से, 1960 के दशक और 1970 के दशक के प्रारम्भ में दो-चरण न्यूनतम वर्ग अब तक सबसे व्यापक रूप से उपयोग की जाने वाली विधि थी।
1950 के दशक से काउल्स आयोग में प्रतिगमन समीकरण दृष्टिकोण की प्रणालियाँ विकसित की गईं, जो तजालिंग कोपमैन्स के परिवहन मॉडलिंग का विस्तार करती हैं। सीवेल राइट और अन्य सांख्यिकी विदों ने काउल्स (तब शिकागो विश्वविद्यालय में) में पथ विश्लेषण विधियों को विस्तारित करने का प्रयास किया। शिकागो विश्वविद्यालय के सांख्यिकी विदों ने सामाजिक विज्ञानों के पथ विश्लेषण अनुप्रयोगों के साथ कई दोषों की पहचान की; दोष जो राइट के संदर्भ में जीन संचरण की पहचान करने के लिए महत्वपूर्ण समस्याएँ उत्पन्न नहीं करते थे, किन्तु जिन्होंने सामाजिक विज्ञानों में पीएलएस-पीए और लिस्रेल जैसी पथ विधियों को समस्याग्रस्त बना दिया। फ्रीडमैन (1987) ने पथ विश्लेषण में इन आपत्तियों को संक्षेप में प्रस्तुत किया: सामाजिक विज्ञानों में मात्रात्मक विधि के संदेह और भ्रम के मुख्य कारणों में से धारणाओं, सांख्यिकीय निहितार्थों और नीतिगत आशयों के मध्य अंतर करने में विफलता रही है (वोल्ड्स (1987) भी देखें)। राइट के पथ विश्लेषण ने अमेरिकी अर्थशास्त्रियों के मध्य कभी भी बड़ा अनुसरण नहीं किया, किन्तु हरमन वॉल्ड और उनके छात्र कार्ल जोरेस्कोग को प्रभावित करने में सफल रहे। जोरेस्कोग के छात्र क्लेस फोर्नेल ने अमेरिका में एलआईएसआरएल को विस्तारित किया।
कंप्यूटर में प्रगति ने अप्रशिक्षित के लिए जटिल, असंरचित समस्याओं में बड़े डेटासमूह के कंप्यूटर-गहन विश्लेषण में संरचनात्मक समीकरण विधियों को प्रारम्भ करना सरल बना दिया। सबसे लोकप्रिय समाधान प्रविधि एल्गोरिदम के तीन वर्गों में आती हैं: (1) सामान्य न्यूनतम वर्ग एल्गोरिदम प्रत्येक पथ पर स्वतंत्र रूप से प्रारम्भ होते हैं, जैसे तथाकथित पीएलएस पथ विश्लेषण पैकेज में प्रारम्भ होते हैं जो ओएलएस के साथ अनुमान लगाते हैं; (2) वोल्ड और उनके छात्र कार्ल जोरेस्कॉग द्वारा एलआईएसआरएल, एएमओएस और ईक्यूएस में प्रारम्भ किए गए मौलिक कार्य से विकसित सहप्रसरण विश्लेषण एल्गोरिदम; और (3) समीकरण प्रतिगमन एल्गोरिदम काउल्स आयोग में तजालिंग कोपमैन्स द्वारा विकसित किया गया।
पर्ल [18]सेम को रैखिक से गैर पैरामीट्रिक मॉडलिंग तक विस्तारित किया है, और समीकरणों के कारण और प्रतितथ्यात्मक व्याख्याओं का प्रस्ताव दिया है। उदाहरण के लिए, समीकरण के तर्कों से चर Z को त्याग कर यह प्रमाणित करता है कि आश्रित चर बहिष्कृत चर पर हस्तक्षेप से स्वतंत्र है, जब हम शेष तर्कों को स्थिर रखते हैं। गैर पैरामीट्रिक सेम (Nonparametric SEMs) समीकरणों के रूप में या त्रुटि के वितरण के लिए कोई प्रतिबद्धता किए बिना कुल, प्रत्यक्ष और अप्रत्यक्ष प्रभावों के अनुमान की अनुमति देते हैं। यह गैर-रेखीय अंतःक्रियाओं की उपस्थिति में श्रेणीबद्ध चरों को सम्मलित करने वाली प्रणालियों के लिए मध्यस्थता विश्लेषण का विस्तार करता है। बोलेन और पर्ल[19]एसईएम के कारण व्याख्या के इतिहास का सर्वेक्षण करें और यह क्यों भ्रम और विवादों का स्रोत बन गया है।
सेम पथ विश्लेषण विधियाँ अपनी पहुँच के कारण सामाजिक विज्ञानों में लोकप्रिय हैं; पैक किए गए कंप्यूटर प्रोग्राम शोधकर्ताओं को प्रयोगात्मक डिजाइन और नियंत्रण, प्रभाव और मॉडलिंग आकार, और कई अन्य कारकों को समझने की असुविधा के बिना परिणाम प्राप्त करने की अनुमति देते हैं जो उत्तम शोध डिजाइन का भाग हैं।[citation needed] समर्थकों का कहना है कि यह प्राकृतिक विज्ञानों में अपनाए जाने की तुलना में विशेष रूप से मनोविज्ञान और सामाजिक संपर्क में कई वास्तविक विश्व की घटनाओं की समग्र, और अल्प स्पष्ट रूप से कारण, व्याख्या को दर्शाता है; आलोचकों का विचार है कि प्रयोगात्मक नियंत्रण की इस अल्पता के कारण कई त्रुटिपूर्ण निष्कर्ष निकाले गए हैं।[citation needed]
सेम के निर्देशित नेटवर्क मॉडलिंग में दिशा वास्तविकता के बारे में अनुमानित कारण-प्रभाव धारणाओं से उत्पन्न होती है। सामाजिक संपर्क और कलाकृतियाँ अधिकांशतः एपिफेनोमेना होती हैं, द्वितीयक घटनाएँ जो सरलता के कारण कारकों से जुड़ती हैं। फिजियोलॉजिकल एपिफेनोमेनन का उदाहरण है- 100 मीटर वेग को पूर्ण करने का समय है। व्यक्ति अपनी वेग गति को 12 सेकंड से 11 सेकंड तक सुधारने में सक्षम हो सकता है, किन्तु आहार, दृष्टिकोण, मौसम इत्यादि जैसे किसी भी प्रत्यक्ष कारकों में सुधार को श्रेय देना जटिल होगा। वेग समय में 1 सेकंड का सुधार है एपिफेनोमेनन कई भिन्न-भिन्न कारकों का समग्र उत्पाद हैं।
सेम के लिए सामान्य दृष्टिकोण
चूँकि सेम परिवार में प्रत्येक प्रौद्योगिकी भिन्न है, निम्नलिखित स्वरूप कई सेम विधियों के लिए सामान्य हैं, क्योंकि इसे एलेक्स लियू जैसे कई सेम विद्वानों द्वारा 4E के रूप में संक्षेपित किया जा सकता है, जो कि 1) समीकरण (मॉडलिंग या समीकरण विनिर्देश), 2 ) मुक्त मापदंडों का अनुमान, 3) मॉडलिंग का मूल्यांकन, 4) स्पष्टीकरण और संचार, साथ ही परिणामों का निष्पादन है।
मॉडलिंग विनिर्देश
सेम में मॉडलिंग के दो मुख्य घटक प्रतिष्ठित हैं: अंतर्जात और बहिर्जात चर के मध्य संभावित कारण निर्भरता दिखाने वाला संरचनात्मक प्रतिरूप, और अव्यक्त चर और उनके संकेतकों के मध्य संबंध दिखाने वाला माप मॉडलिंग हैं। अन्वेषी और पुष्टि कारक विश्लेषण प्रतिरूप, उदाहरण के लिए, केवल माप के भाग होते हैं, जबकि पथ विश्लेषण (सांख्यिकी) को एसईएम के रूप में देखा जा सकता है जिसमें केवल संरचनात्मक भाग होता है।
मॉडलिंग में पथों को निर्दिष्ट करने में, मॉडलिंग दो प्रकार के संबंधों को प्रस्तुत कर सकता है: (1) मुक्त मार्ग, जिसमें परिकल्पित कारण (वास्तव में प्रतितथ्यात्मक) चर के मध्य संबंधों का परीक्षण किया जाता है, और इसलिए भिन्नता के लिए 'मुक्त' त्याग दिया जाता है, और (2) ) चर के मध्य संबंध जिनका पूर्व से ही अनुमानित संबंध है, सामान्यतः पूर्व अध्ययनों पर आधारित होते हैं, जो मॉडलिंग में 'निश्चित' होते हैं।
मॉडलिंग अधिकांशतः सैद्धांतिक रूप से प्रशंसनीय मॉडलिंग का समूह निर्दिष्ट करेगा जिससे कि यह आकलन किया जा सके कि प्रस्तावित मॉडलिंग संभावित मॉडलिंग के समूह में सबसे उत्तम है या नहीं। मॉडलिंग को न केवल मॉडलिंग के निर्माण के लिए सैद्धांतिक कारणों के लिए होना चाहिए, जबकि मॉडलिंग को डेटा बिंदुओं की संख्या और मॉडलिंग की पहचान करने के लिए अनुमान लगाने वाले मापदंडों की संख्या को भी ध्यान में रखना चाहिए।
पहचाना गया मॉडलिंग वह है जहां विशिष्ट पैरामीटर मान विशिष्ट रूप से मॉडलिंग (पुनरावर्ती परिभाषा) की पहचान करता है, और कोई भिन्न पैरामीटर मान द्वारा कोई अन्य समकक्ष सूत्रीकरण नहीं दिया जा सकता है। डेटा बिंदु देखे गए अंकों वाला चर है, जैसे चर जिसमें किसी प्रश्न पर स्कोर होता है या उत्तरदाताओं द्वारा कार अनुचित की संख्या होती है। पैरामीटर ब्याज का मूल्य है, जो बहिर्जात और अंतर्जात चर या कारक लोडिंग (संकेतक और उसके कारक के मध्य प्रतिगमन गुणांक) के मध्य प्रतिगमन गुणांक हो सकता है। यदि अनुमानित मापदंडों की संख्या से अल्प डेटा बिंदु हैं, तो परिणामी मॉडलिंग अज्ञात है, क्योंकि मॉडलिंग में सभी भिन्नताओं के लिए अधिक अल्प संदर्भ बिंदु हैं। समाधान पथों में से शून्य तक सीमित करना है, जिसका अर्थ है कि यह अब मॉडलिंग का भाग नहीं है।
मुक्त मापदंडों का अनुमान
पैरामीटर अनुमान वास्तविक सह-प्रसरण आव्यूह की तुलना करके किया जाता है जो चर और सर्वोत्तम उपयुक्त मॉडलिंग के अनुमानित सह-प्रसरण आव्यूह के मध्य संबंधों का प्रतिनिधित्व करता है। यह अपेक्षा-अधिकतमकरण एल्गोरिथ्म के माध्यम से संख्यात्मक अधिकतमकरण के माध्यम से प्राप्त किया जाता है। अपेक्षा-अधिकतम मानदंड का अधिकतमकरण जैसा कि अधिकतम संभावना अनुमान, अर्ध-अधिकतम संभावना अनुमान, भारित अल्प से अल्प वर्ग या असमान रूप से वितरण-मुक्त विधियों द्वारा प्रदान किया जाता है। यह अधिकांशतः विशेष एसईएम विश्लेषण कार्यक्रम का उपयोग करके पूर्ण किया जाता है, जिनमें से कई उपस्तिथ हैं।
मॉडलिंग और मॉडलिंग उपयुक्त का मूल्यांकन
मॉडलिंग का अनुमान लगाने के पश्चात, विश्लेषक मॉडलिंग की व्याख्या करना। अनुमानित पथों को पथ मॉडलिंग के रूप में सारणीबद्ध या रेखांकन के रूप में प्रस्तुत किया जा सकता है। पथ विश्लेषण (सांख्यिकी) पथ अनुरेखण नियमों (पथ विश्लेषण (सांख्यिकी) देखें) का उपयोग करके चरों के प्रभाव का आकलन किया जाता है।
यह निर्धारित करने के लिए अनुमानित मॉडलिंग के उपयुक्त की अन्वेषण करना महत्वपूर्ण है कि यह डेटा को कितना उत्तम प्रकार का मॉडलिंग करता है। एसईएम मॉडलिंग में यह आधारभूत कार्य है, मॉडलिंग को स्वीकार या अस्वीकार करने के लिए आधार तैयार करना और अधिक सामान्यतः, प्रतिस्पर्धी मॉडलिंग को दूसरे पर स्वीकार करना। एसईएम कार्यक्रमों के आउटपुट में मॉडलिंग में चरों के मध्य अनुमानित संबंधों के आव्यूह सम्मलित हैं। उपयुक्त आकलन अनिवार्य रूप से गणना करता है कि अनुमानित डेटा वास्तविक डेटा में संबंधों वाले मैट्रिसेस के समान कैसे हैं।
इन उद्देश्यों के लिए औपचारिक सांख्यिकीय परीक्षण और उपयुक्त अनुक्रमणिका विकसित किए गए हैं। अनुमानित मॉडलिंग के भीतर मॉडलिंग के व्यक्तिगत मापदंडों की भी अन्वेषण की जा सकती है जिससे कि यह देखा जा सके कि प्रस्तावित मॉडलिंग ड्राइविंग सिद्धांत में कितना उत्तम प्रकार उपयुक्त है। अधिकांश, चूँकि सभी, आकलन विधियां मॉडलिंग के ऐसे परीक्षणों को संभव नहीं बनाती हैं।
निश्चित रूप से जैसा कि सभी सांख्यिकीय परिकल्पना परीक्षण में होता है, सेम मॉडलिंग परीक्षण इस धारणा पर आधारित होते हैं कि उत्तम और पूर्ण प्रासंगिक डेटा को मॉडलिंग किया गया है। सेम साहित्य में, उपयुक्त विचार ने विभिन्न सूचकांकों और परिकल्पना परीक्षणों के त्रुटिहीन अनुप्रयोग पर विभिन्न अनुशंसाओं को उद्गम किया है।
उपयुक्त का आकलन करने के लिए भिन्न-भिन्न दृष्टिकोण हैं। मॉडलिंग के लिए पारंपरिक दृष्टिकोण अशक्त परिकल्पना से प्रारंभ होता है, अधिक उदार मॉडलिंग (अर्थात अल्प मुक्त मापदंडों वाले) को पुरस्कृत करते हुए, अन्य जैसे कि सूचना मानदंड जो इस बात पर ध्यान केंद्रित करते हैं कि संतृप्त मॉडलिंग से उपयुक्त किए गए मान कितने अल्प हैं।[citation needed] (अर्थात वे कितनी उत्तम प्रकार से मूल्यों को पुन: उत्पन्न करते हैं), उपयोग किए गए मुक्त मापदंडों की संख्या को ध्यान में रखते हुए। क्योंकि उपयुक्त के विभिन्न उपाय मॉडलिंग के विभिन्न तत्वों का उपयोग करते है, इसलिए विभिन्न उपयुक्त उपायों के चयन की रिपोर्ट करना उचित है। उपयुक्त उपायों की व्याख्या के लिए दिशानिर्देश (अर्थात, कटऑफ स्कोर), के नीचे सूचीबद्ध लोगों सहित, सेम शोधकर्ताओं के मध्य अधिक विवश का विषय हैं।[20]
उपयुक्त के कुछ अधिक सामान्य रूप से उपयोग किए जाने वाले उपायों में सम्मलित हैं
- ची-स्क्वेर्ड परीक्षण
- कई अन्य उपायों की गणना में उपयोग किए जाने वाले उपयुक्त मौलिक उपाय है। संकल्पनात्मक रूप से मॉडलिंग आकार का कार्य है और देखे गए सह-प्रसरण मैट्रिक्स और मॉडलिंग सहप्रसरण मैट्रिक्स के मध्य का अंतर है।
- एकैके सूचना मानदंड (एआईसी)
- संबंधी मॉडलिंग उपयुक्त का परीक्षण: रुचिकर मॉडलिंग सबसे अल्प एआईसी मूल्य वाला है।
- जहां k सांख्यिकीय मॉडलिंग में मापदंडों की संख्या है, और L मॉडलिंग की संभावना का अधिकतम मूल्य है।
- समीप का मूल माध्य वर्ग त्रुटि (RMSEA)
- उपयुक्त अनुक्रमणिका जहां शून्य का मान सर्वोत्तम उपयुक्त प्रदर्शित करता है।[21] जबकि आरएमएसईए का उपयोग करके समीप उपयुक्त का निर्धारण करने के लिए दिशानिर्देश अत्यधिक विवादित है,[22] अधिकांश शोधकर्ता इस बात से सहमत हैं कि .1 या अधिक का आरएमएसईए दुर्गति उपयुक्त प्रदर्शित करता है।[23][24]
- मानकीकृत रूट माध्य चुकता अवशिष्ट (SRMR)
- एसआरएमआर लोकप्रिय संपूर्ण उपयुक्त संकेतक है। हू और बेंटलर (1999) ने उत्तम उपयुक्त के लिए दिशानिर्देश के रूप में .08 या उससे छोटे का विचार दिया।[25] क्लाइन (2011) ने उत्तम उपयुक्त के लिए दिशानिर्देश के रूप में .1 या उससे अल्प का विचार दिया।
- तुलनात्मक उपयुक्त अनुक्रमणिका (सीएफआई)
- बेसलाइन तुलनाओं की अन्वेषण में, सीएफआई डेटा में सह-संबंधों के औसत आकार पर बड़े भाग पर निर्भर करता है। यदि चरों के मध्य औसत सह-संबंध अधिक नहीं है, तो सीएफआई (CFI) अधिक नहीं होगा। .95 या उच्चतर का सीएफआई मूल्य वांछनीय है।[25]
उपयुक्त के प्रत्येक माप के लिए, मॉडलिंग और डेटा के मध्य उत्तम-पर्याप्त उपयुक्त का प्रतिनिधित्व करने वाले निर्णय को अन्य प्रासंगिक कारकों जैसे मॉडलिंग आकार, कारकों के संकेतों का अनुपात और मॉडलिंग की समग्र जटिलता को प्रतिबिंबित करना चाहिए। उदाहरण के लिए, अधिक बड़े मॉडलिंग ची-स्क्वेर्ड परीक्षण को अत्यधिक संवेदनशील बनाते हैं और प्रतिरूप-डेटा उपयुक्त की अल्पता का संकेत देने की अधिक संभावना रखते हैं। [26]
मॉडलिंग संशोधन
उपयुक्त को उत्तम बनाने के लिए मॉडलिंग को संशोधित करने की आवश्यकता हो सकती है, जिससे चर के मध्य सबसे अधिक संभावित संबंधों का अनुमान लगाया जा सके। कई कार्यक्रम संशोधन सूचकांक प्रदान करते हैं जो सामान्य संशोधनों का मार्गदर्शन कर सकते हैं। संशोधन सूचकांक χ² में परिवर्तन की रिपोर्ट करते हैं जो निश्चित मापदंडों को मुक्त करने के परिणामस्वरूप होता है: सामान्यतः, इसलिए मॉडलिंग के लिए पथ जोड़ना जो वर्तमान में शून्य पर समूह है। मॉडलिंग उपयुक्त में सुधार करने वाले संशोधनों को मॉडलिंग में किए जा सकने वाले संभावित परिवर्तनों के रूप में फ़्लैग किया जा सकता है। मॉडलिंग में संशोधन, विशेष रूप से संरचनात्मक प्रतिरूप, उचित होने का प्रमाणित करने वाले सिद्धांत में परिवर्तन हैं। इसलिए संशोधनों का परीक्षण किए जा रहे सिद्धांत के संदर्भ में समझ में आना चाहिए, या उस सिद्धांत की सीमाओं के रूप में स्वीकार किया जाना चाहिए। माप मॉडलिंग में परिवर्तन प्रभावी रूप से प्रमाणित करते हैं कि डेटा सिद्धांत द्वारा निर्दिष्ट अव्यक्त चर के अशुद्ध संकेतक हैं।[27]
मॉडलिंग को संशोधन सूचकांकों द्वारा नेतृत्व नहीं किया जाना चाहिए, जैसा कि मैककलम (1986) ने प्रदर्शित किया: अनुकूल परिस्थितियों में भी, विनिर्देश अविष्कार से उत्पन्न होने वाले मॉडलिंग को सावधानी के साथ देखा जाना चाहिए।[28]
मॉडलिंग आकार और शक्ति
जब शोधकर्ता इस बात से सहमत हैं कि सेम का उपयोग करके पर्याप्त सांख्यिकीय शक्ति और त्रुटिहीन अनुमान प्रदान करने के लिए बड़े मॉडलिंग आकार की आवश्यकता होती है, पर्याप्त मॉडलिंग आकार निर्धारित करने के लिए उपयुक्त विधि पर कोई साधारण सहमति नहीं है।[29] [30]सामान्यतः, मॉडलिंग आकार निर्धारित करने के लिए विचारों में प्रति पैरामीटर टिप्पणियों की संख्या, उपयुक्त अनुक्रमणिका के लिए पर्याप्त रूप से प्रदर्शन करने के लिए आवश्यक टिप्पणियों की संख्या और स्वतंत्रता की प्रति डिग्री टिप्पणियों की संख्या सम्मलित होती है।[29] शोधकर्ताओं ने सिमुलेशन अध्ययन, व्यवसायी अनुभव, और गणितीय सूत्रों के आधार पर दिशानिर्देश प्रस्तावित किए हैं।[31][32][30][33]
सेम परिकल्पना परीक्षण में विशेष महत्व और शक्ति प्राप्त करने के लिए मॉडलिंग आकार की आवश्यकताएं उसी मॉडलिंग के लिए समान होती हैं जब परीक्षण के लिए तीन एल्गोरिदम (पीएलएस-पीए, लिस्रेल या प्रतिगमन समीकरणों की प्रणाली) का उपयोग किया जाता है।[citation needed]
स्पष्टीकरण और संचार
इसके पश्चात मॉडलिंग के समूह की व्याख्या की जाती है जिससे कि सर्वोत्तम उपयुक्त मॉडलिंग के आधार पर निर्माण के बारे में प्रमाणित किया जा सके।
प्रयोग या समय-आदेशित अध्ययन किए जाने पर भी कारणता का प्रमाणित करते समय सदैव सावधानी बरतनी चाहिए। शब्द कारणात्मक मॉडलिंग को ऐसे मॉडलिंग के रूप में समझा जाना चाहिए जो कारण संबंधी मान्यताओं को व्यक्त करता है, आवश्यक नहीं कि ऐसा मॉडलिंग हो जो मान्य कारण निष्कर्ष उत्पन्न करता हो। कई समय बिंदुओं पर डेटा एकत्र करना और प्रायोगिक या अर्ध-प्रायोगिक डिजाइन का उपयोग करने से कुछ प्रतिद्वंद्वी परिकल्पनाओं को दूर करने में सहायता मिल सकती है, किन्तु यादृच्छिक प्रयोग भी ऐसे सभी आशंका से इंकार नहीं कर सकता है। कारण परिकल्पना के अनुरूप मॉडलिंग द्वारा उत्तम उपयुक्त अनिवार्य रूप से विरोधी कारण परिकल्पना के अनुरूप दूसरे मॉडलिंग द्वारा समान रूप से उत्तम उपयुक्त होता है। कोई भी शोध डिजाइन, चाहे कितना भी निपुण क्यों न हो, इस प्रकार की प्रतिद्वंद्वी परिकल्पनाओं को भिन्न करने में सहायता कर सकता हैI[18]
किसी भी विज्ञान के जैसे, पश्चात की प्रतिकृति और संभवतः संशोधन प्रारंभिक अविष्कार से विस्तारित होंगे।
उन्नत उपयोग
- मापन व्युत्क्रम
- एकाधिक समूह प्रतिरूप: यह ऐसी प्रौद्योगिकी है जो कई मॉडलिंग के संयुक्त अनुमान की अनुमति देती है, प्रत्येक भिन्न-भिन्न उप-समूहों के साथ अनुप्रयोगों में व्यवहार आनुवंशिकी, और समूहों के मध्य मतभेदों का विश्लेषण सम्मलित है (जैसे, लिंग, संस्कृतियां, विभिन्न भाषाओं में लिखे गए परीक्षण प्रपत्र आदि)।
- अव्यक्त विकास प्रतिरूप
- अरैखिक मिश्रित प्रभाव प्रतिरूप
- श्रेणीबद्ध/बहुस्तरीय प्रतिरूप ; डेटा प्रतिक्रिया सिद्धांत प्रतिरूप
- मिश्रण मॉडलिंग (अव्यक्त वर्ग) सेम
- वैकल्पिक अनुमान और परीक्षण प्रौद्योगिकी
- दृढ़ अनुमान
- सर्वेक्षण मॉडलिंग विश्लेषण
- मल्टी-मेथड मल्टी-ट्रेट प्रतिरूप
- संरचनात्मक समीकरण मॉडलिंग ट्रीज
एसईएम-विशिष्ट सॉफ़्टवेयर
संरचनात्मक समीकरण मॉडलिंग को उपयुक्त करने के लिए कई सॉफ़्टवेयर पैकेज उपस्तिथ हैं। लिस्रेल ऐसा प्रथम सॉफ्टवेयर था, जो प्रारम्भ में 1970 के दशक में निरंतर उपयोग किया गया था।[16]शोधकर्ताओं के मध्य अधिकांशतः उपयोग किए जाने वाले सॉफ्टवेयर कार्यान्वयन में एमप्लस (Mplus), आर (R) (प्रोग्रामिंग भाषा) पैकेज सम्मलित हैं[34]और सेम, लिस्रेल, ओपनएमएक्स (OpenMx), एसपीएसएस (SPSS) अमोस (AMOS), और स्टाटा (Stata) इत्यादि।[35] बारबरा एम बायरन ने बहुभिन्नरूपी प्रायोगिक मनोविज्ञान का समाज के बहुभिन्नरूपी एप्लीकेशन बुक सीरीज के भाग के रूप में इन सॉफ्टवेयरों का उपयोग करने के लिए कई निर्देशात्मक पुस्तकें प्रकाशित कीं।[36]
विद्वान द्वारा इसे रिपोर्ट करने के लिए उत्तम अभ्यास मानते हैं कि एसईएम विश्लेषण के लिए कौन से सॉफ़्टवेयर पैकेज और संस्करण का उपयोग किया गया था क्योंकि उनके निकट भिन्न -भिन्न क्षमताएं हैं और समान नामित प्रौद्योगिकी को करने के लिए थोड़ा भिन्न विधि का उपयोग कर सकते हैं।[37]
यह भी देखें
- कारण प्रतिरूप
- चित्रमय प्रतिरूप
- बहुभिन्नरूपी आँकड़े
- आंशिक न्यूनतम वर्ग पथ प्रतिरूप
- आंशिक न्यूनतम वर्ग प्रतिगमन
- साथ समीकरण प्रतिरूप
- गुप्त चरों के साथ संरचनात्मक समीकरण
- कारण मानचित्र
संदर्भ
- ↑ Boslaugh, Sarah; McNutt, Louise-Anne (2008). "Structural Equation Modeling". Encyclopedia of Epidemiology. doi:10.4135/9781412953948.n443. hdl:2022/21973. ISBN 978-1-4129-2816-8.
- ↑ Shelley, Mack C (2006). "Structural Equation Modeling". शैक्षिक नेतृत्व और प्रशासन का विश्वकोश. doi:10.4135/9781412939584.n544. ISBN 978-0-7619-3087-7.
- ↑ 3.0 3.1 {{Cite book|last=Kline|first=Rex B. |title=आधारभूत समीकरण मोडलिंग के सिद्धांत एवं व्यवहार|date=2016 |isbn=978-1-4625-2334-4|edition=4th |location=New York|oclc=934184322}
- ↑ Bollen, Kenneth A. (1989). गुप्त चरों के साथ स्ट्रक्चरल समीकरण. New York: Wiley. ISBN 0-471-01171-1. OCLC 18834634.
- ↑ Kaplan, David (2009). Structural equation modeling: foundations and extensions (2nd ed.). Los Angeles: SAGE. ISBN 978-1-4129-1624-0. OCLC 225852466.
- ↑ Curran, Patrick J. (2003-10-01). "Have Multilevel Models Been Structural Equation Models All Along?". Multivariate Behavioral Research. 38 (4): 529–569. doi:10.1207/s15327906mbr3804_5. ISSN 0027-3171. PMID 26777445. S2CID 7384127.
- ↑ Salkind, Neil J. (2007). "Intelligence Tests". Encyclopedia of Measurement and Statistics. doi:10.4135/9781412952644.n220. ISBN 978-1-4129-1611-0.
- ↑ MacCallum & Austin 2000, p. 209.
- ↑ Wright, S. (1920-06-01). "गिनी-सूअरों के पाइबल्ड पैटर्न का निर्धारण करने में आनुवंशिकता और पर्यावरण का सापेक्ष महत्व". Proceedings of the National Academy of Sciences (in English). 6 (6): 320–332. Bibcode:1920PNAS....6..320W. doi:10.1073/pnas.6.6.320. ISSN 0027-8424. PMC 1084532. PMID 16576506.
- ↑ Wright, Sewall (1921). "जर्नल ऑफ एग्रीकल्चरल रिसर्च". जर्नल ऑफ एग्रीकल्चरल रिसर्च. 20 (1): 557–585 – via USDA.
- ↑ Wolfle, Lee M. (1999). "Sewall wright on the method of path coefficients: An annotated bibliography". Structural Equation Modeling (in English). 6 (3): 280–291. doi:10.1080/10705519909540134. ISSN 1070-5511.
- ↑ Wright, Sewall (1934). "पथ गुणांक की विधि". The Annals of Mathematical Statistics. 5 (3): 161–215. doi:10.1214/aoms/1177732676. ISSN 0003-4851. JSTOR 2957502.
- ↑ Duncan, Otis Dudley (1975). संरचनात्मक समीकरण मॉडल का परिचय. New York: Academic Press. ISBN 0-12-224150-9. OCLC 1175858.
- ↑ Christ, Carl F. (1994). "The Cowles Commission's Contributions to Econometrics at Chicago, 1939-1955". Journal of Economic Literature. 32 (1): 30–59. ISSN 0022-0515. JSTOR 2728422.
- ↑ Westland, J. Christopher (2015). Structural Equation Modeling: From Paths to Networks. New York: Springer.
- ↑ 16.0 16.1 Jöreskog, Karl Gustav; van Thillo, Mariella (1972). "LISREL: A General Computer Program for Estimating a Linear Structural Equation System Involving Multiple Indicators of Unmeasured Variables" (PDF). Research Bulletin: Office of Education. ETS-RB-72-56 – via US Government.
- ↑ Kock, Ned; Hadaya, Pierre (2018). "Minimum sample size estimation in PLS-SEM: The inverse square root and gamma-exponential methods". Information Systems Journal. 28: 227–261. doi:10.1111/isj.12131. S2CID 3733557.
- ↑ 18.0 18.1 Pearl, Judea (2000). Causality: Models, Reasoning, and Inference. Cambridge University Press. ISBN 978-0-521-77362-1.
- ↑ Bollen, Kenneth A; Pearl, Judea (2013). "Eight Myths About Causality and Structural Equation Models". Handbook of Causal Analysis for Social Research. Handbooks of Sociology and Social Research. pp. 301–28. doi:10.1007/978-94-007-6094-3_15. ISBN 978-94-007-6093-6.
- ↑ MacCallum & Austin 2000, p. 218-219.
- ↑ Kline 2011, p. 205.
- ↑ Kline 2011, p. 206.
- ↑ Hu & Bentler 1999, p. 11.
- ↑ Browne, M. W.; Cudeck, R. (1993). "Alternative ways of assessing model fit". In Bollen, K. A.; Long, J. S. (eds.). Testing structural equation models. Newbury Park, CA: Sage.
- ↑ 25.0 25.1 Hu & Bentler 1999, p. 27.
- ↑ Kline 2011, p. 201.
- ↑ Loehlin, J. C. (2004). Latent Variable Models: An Introduction to Factor, Path, and Structural Equation Analysis. Psychology Press.
- ↑ MacCallum, Robert (1986). "Specification searches in covariance structure modeling". Psychological Bulletin. 100: 107–120. doi:10.1037/0033-2909.100.1.107.
- ↑ 29.0 29.1 Quintana & Maxwell 1999, p. 499.
- ↑ 30.0 30.1 Westland, J. Christopher (2010). "Lower bounds on sample size in structural equation modeling". Electron. Comm. Res. Appl. 9 (6): 476–487. doi:10.1016/j.elerap.2010.07.003.
- ↑ Chou, C. P.; Bentler, Peter (1995). "Estimates and tests in structural equation modeling". In Hoyle, Rick (ed.). Structural equation modeling: Concepts, issues, and applications. Thousand Oaks, CA: Sage. pp. 37–55.
- ↑ Bentler, P. M; Chou, Chih-Ping (2016). "Practical Issues in Structural Modeling". Sociological Methods & Research. 16 (1): 78–117. doi:10.1177/0049124187016001004. S2CID 62548269.
- ↑ MacCallum, Robert C; Browne, Michael W; Sugawara, Hazuki M (1996). "Power analysis and determination of sample size for covariance structure modeling". Psychological Methods. 1 (2): 130–49. doi:10.1037/1082-989X.1.2.130.
- ↑ Rosseel, Yves (2012-05-24). "lavaan: An R Package for Structural Equation Modeling". Journal of Statistical Software. 48 (2): 1–36. doi:10.18637/jss.v048.i02. Retrieved 27 January 2021.
- ↑ Narayanan, A. (2012-05-01). "स्ट्रक्चरल इक्वेशन मॉडलिंग के लिए आठ सॉफ्टवेयर पैकेज की समीक्षा". The American Statistician. 66 (2): 129–138. doi:10.1080/00031305.2012.708641. ISSN 0003-1305. S2CID 59460771.
- ↑ "Barbara Byrne Award for Outstanding Book or Edited Volume | SMEP". smep.org. Retrieved 2022-10-25.
- ↑ Kline 2011, p. 79-88.
ग्रन्थसूची
- Hu, Li‐tze; Bentler, Peter M (1999). "Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives". Structural Equation Modeling. 6: 1–55. doi:10.1080/10705519909540118. hdl:2027.42/139911.
- Kaplan, D. (2008). Structural Equation Modeling: Foundations and Extensions (2nd ed.). SAGE. ISBN 978-1412916240.
- Kline, Rex (2011). Principles and Practice of Structural Equation Modeling (Third ed.). Guilford. ISBN 978-1-60623-876-9.
- MacCallum, Robert; Austin, James (2000). "Applications of Structural Equation Modeling in Psychological Research" (PDF). Annual Review of Psychology. 51: 201–226. doi:10.1146/annurev.psych.51.1.201. PMID 10751970. Retrieved 25 January 2015.
- Quintana, Stephen M.; Maxwell, Scott E. (1999). "Implications of Recent Developments in Structural Equation Modeling for Counseling Psychology". The Counseling Psychologist. 27 (4): 485–527. doi:10.1177/0011000099274002. S2CID 145586057.
अग्रिम पठन
- Bagozzi, Richard P; Yi, Youjae (2011). "Specification, evaluation, and interpretation of structural equation models". Journal of the Academy of Marketing Science. 40 (1): 8–34. doi:10.1007/s11747-011-0278-x. S2CID 167896719.
- Bartholomew, D. J., and Knott, M. (1999) Latent Variable Models and Factor Analysis Kendall's Library of Statistics, vol. 7, Edward Arnold Publishers, ISBN 0-340-69243-X
- Bentler, P.M. & Bonett, D.G. (1980), "Significance tests and goodness of fit in the analysis of covariance structures", Psychological Bulletin, 88, 588–606.
- Bollen, K. A. (1989). Structural Equations with Latent Variables. Wiley, ISBN 0-471-01171-1
- Byrne, B. M. (2001) Structural Equation Modeling with AMOS - Basic Concepts, Applications, and Programming.LEA, ISBN 0-8058-4104-0
- Goldberger, A. S. (1972). Structural equation models in the social sciences. Econometrica 40, 979- 1001.
- Haavelmo, Trygve (January 1943). "The Statistical Implications of a System of Simultaneous Equations". Econometrica. 11 (1): 1–12. doi:10.2307/1905714. JSTOR 1905714.
- Hoyle, R H (ed) (1995) Structural Equation Modeling: Concepts, Issues, and Applications. SAGE, ISBN 0-8039-5318-6
- Jöreskog, Karl G.; Yang, Fan (1996). "Non-linear structural equation models: The Kenny-Judd model with interaction effects". In Marcoulides, George A.; Schumacker, Randall E. (eds.). Advanced structural equation modeling: Concepts, issues, and applications. Thousand Oaks, CA: Sage Publications. pp. 57–88. ISBN 978-1-317-84380-1.
- Lewis-Beck, Michael; Bryman, Alan E.; Bryman, Emeritus Professor Alan; Liao, Tim Futing (2004). "Structural Equation Modeling". The SAGE Encyclopedia of Social Science Research Methods. doi:10.4135/9781412950589.n979. hdl:2022/21973. ISBN 978-0-7619-2363-3.
- Schermelleh-Engel, K.; Moosbrugger, H.; Müller, H. (2003), "Evaluating the fit of structural equation models" (PDF), Methods of Psychological Research, 8 (2): 23–74.
बाहरी संबंध
- Structural equation modeling page under David Garson's StatNotes, NCSU
- Issues and Opinion on Structural Equation Modeling, सेमin IS Research
- The causal interpretation of structural equations (or सेमsurvival kit) by Judea Pearl 2000.
- Structural Equation Modeling Reference List by Jason Newsom: journal articles and book chapters on structural equation models
- Handbook of Management Scales, a collection of previously used multi-item scales to measure constructs for SEM