प्रतिच्छेदन ग्राफ: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{short description|Graph representing intersections between given sets}} | {{short description|Graph representing intersections between given sets}} | ||
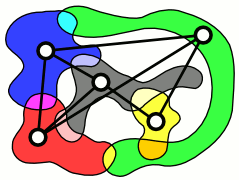
[[Image:Intersection graph.gif|thumb|इंटरसेक्टिंग सेट कैसे एक ग्राफ को परिभाषित करता है इसका एक उदाहरण।]][[ग्राफ सिद्धांत]] में, एक | [[Image:Intersection graph.gif|thumb|इंटरसेक्टिंग सेट कैसे एक ग्राफ को परिभाषित करता है इसका एक उदाहरण।]][[ग्राफ सिद्धांत]] में, एक प्रतिच्छेदन ग्राफ एक [[ग्राफ (असतत गणित)|ग्राफ]] है जो [[सेट (गणित)|सेट]] के एक परिवार के प्रतिच्छेदन '''(सेट सिद्धांत)''' के पैटर्न का प्रतिनिधित्व करता है। किसी भी ग्राफ़ को एक प्रतिच्छेदन ग्राफ़ के रूप में दर्शाया जा सकता है, लेकिन ग्राफ़ के कुछ महत्वपूर्ण विशेष वर्गों को उन सेटों के प्रकारों द्वारा परिभाषित किया जा सकता है, जिनका उपयोग उनका एक प्रतिच्छेदन प्रतिनिधित्व करने के लिए किया जाता है। | ||
== औपचारिक परिभाषा == | == औपचारिक परिभाषा == | ||
औपचारिक रूप से, एक | औपचारिक रूप से, एक प्रतिच्छेदन ग्राफ {{mvar|G}} सेट के परिवार से बना एक [[अप्रत्यक्ष ग्राफ]] है | ||
: <math>S_i, \,\,\, i = 0, 1, 2, \dots</math> | : <math>S_i, \,\,\, i = 0, 1, 2, \dots</math> | ||
एक शीर्ष | प्रत्येक सेट {{mvar|S{{sub|i}}}} के लिए एक शीर्ष {{mvar|v{{sub|i}}}} बनाकर '''प्रत्येक सेट {{mvar|S{{sub|i}}}} के लिए''' , और दो शीर्षों {{mvar|v{{sub|i}}}} और {{mvar|v{{sub|j}}}} को एक किनारे से जोड़कर जब भी संगत दो सेटों में एक [[खाली सेट|गैर-रिक्त प्रतिच्छेदन '''े''']] '''प्रतिच्छेदन''' होता है, अर्थात | ||
: <math>E(G) = \{ \{ v_i, v_j \} \mid i \neq j, S_i \cap S_j \neq \empty \}.</math> | : <math>E(G) = \{ \{ v_i, v_j \} \mid i \neq j, S_i \cap S_j \neq \empty \}.</math> | ||
== सभी रेखांकन प्रतिच्छेदन रेखांकन हैं == | == सभी रेखांकन प्रतिच्छेदन रेखांकन हैं == | ||
कोई भी अप्रत्यक्ष ग्राफ {{mvar|G}} को प्रतिच्छेदन ग्राफ के रूप में दर्शाया जा सकता है। प्रत्येक शीर्ष | कोई भी अप्रत्यक्ष ग्राफ {{mvar|G}} को प्रतिच्छेदन ग्राफ के रूप में दर्शाया जा सकता है। {{mvar|G}} के प्रत्येक शीर्ष {{mvar|v<sub>i</sub>}} के लिए '''का''' , एक सेट {{mvar|S<sub>i</sub>}} बनाएं जिसमें किनारे {{mvar|v<sub>i</sub>}} से जुड़े हों; तो दो ऐसे सेटों में एक गैर-रिक्त प्रतिच्छेदन होता है यदि और केवल यदि संबंधित कोने किनारे साझा करते हैं। इसलिए, {{mvar|G}} सेट {{mvar|S<sub>i</sub>}} का प्रतिच्छेदन ग्राफ है। | ||
{{harvtxt| | {{harvtxt|एर्डोस|गुडमैन|पोसा|1966}} एक ऐसा निर्माण प्रदान करते हैं जो अधिक कुशल है, इस अर्थ में कि इसके लिए सभी सेट {{mvar|S<sub>i</sub>}} संयुक्त में तत्वों की एक छोटी संख्या की आवश्यकता होती है। इसके लिए, सेट तत्वों की कुल संख्या अधिक से अधिक {{math|{{sfrac|''n''<sup>2</sup>|4}}}}, जहां {{mvar|n}} ग्राफ में शीर्षों की संख्या है। वे इस अवलोकन का श्रेय {{harvtxt|स्ज़पिलराजन-मार्क्ज़वेस्की|1945}} को देते हैं कि सभी ग्राफ़ प्रतिच्छेदन ग्राफ़ हैं , लेकिन {{harvtxt|कुलिक|1964}} इसे देखने के लिए भी कहते है। किसी ग्राफ़ का प्रतिच्छेदन संख्या ग्राफ़ के किसी भी प्रतिच्छेदन प्रतिनिधित्व में तत्वों की न्यूनतम कुल संख्या है। | ||
== प्रतिच्छेदन रेखांकन की कक्षाएं == | == प्रतिच्छेदन रेखांकन की कक्षाएं == | ||
| Line 38: | Line 38: | ||
== संबंधित अवधारणाएं == | == संबंधित अवधारणाएं == | ||
इंटरसेक्शन ग्राफ़ के लिए ऑर्डर-सैद्धांतिक एनालॉग शामिल किए जाने के ऑर्डर हैं। उसी तरह जिस तरह एक ग्राफ का एक प्रतिच्छेदन प्रतिनिधित्व प्रत्येक शीर्ष को एक सेट के साथ लेबल करता है ताकि कोने आसन्न हों यदि और केवल अगर उनके सेट में गैर-रिक्त चौराहा है, ताकि पोसेट में किसी भी x और y के लिए, x ≤ y अगर और केवल अगर f(x) ⊆ f(y)। | |||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 10:31, 11 March 2023
ग्राफ सिद्धांत में, एक प्रतिच्छेदन ग्राफ एक ग्राफ है जो सेट के एक परिवार के प्रतिच्छेदन (सेट सिद्धांत) के पैटर्न का प्रतिनिधित्व करता है। किसी भी ग्राफ़ को एक प्रतिच्छेदन ग्राफ़ के रूप में दर्शाया जा सकता है, लेकिन ग्राफ़ के कुछ महत्वपूर्ण विशेष वर्गों को उन सेटों के प्रकारों द्वारा परिभाषित किया जा सकता है, जिनका उपयोग उनका एक प्रतिच्छेदन प्रतिनिधित्व करने के लिए किया जाता है।
औपचारिक परिभाषा
औपचारिक रूप से, एक प्रतिच्छेदन ग्राफ G सेट के परिवार से बना एक अप्रत्यक्ष ग्राफ है
प्रत्येक सेट Si के लिए एक शीर्ष vi बनाकर प्रत्येक सेट Si के लिए , और दो शीर्षों vi और vj को एक किनारे से जोड़कर जब भी संगत दो सेटों में एक गैर-रिक्त प्रतिच्छेदन े प्रतिच्छेदन होता है, अर्थात
सभी रेखांकन प्रतिच्छेदन रेखांकन हैं
कोई भी अप्रत्यक्ष ग्राफ G को प्रतिच्छेदन ग्राफ के रूप में दर्शाया जा सकता है। G के प्रत्येक शीर्ष vi के लिए का , एक सेट Si बनाएं जिसमें किनारे vi से जुड़े हों; तो दो ऐसे सेटों में एक गैर-रिक्त प्रतिच्छेदन होता है यदि और केवल यदि संबंधित कोने किनारे साझा करते हैं। इसलिए, G सेट Si का प्रतिच्छेदन ग्राफ है।
एर्डोस, गुडमैन & पोसा (1966) एक ऐसा निर्माण प्रदान करते हैं जो अधिक कुशल है, इस अर्थ में कि इसके लिए सभी सेट Si संयुक्त में तत्वों की एक छोटी संख्या की आवश्यकता होती है। इसके लिए, सेट तत्वों की कुल संख्या अधिक से अधिक n2/4, जहां n ग्राफ में शीर्षों की संख्या है। वे इस अवलोकन का श्रेय स्ज़पिलराजन-मार्क्ज़वेस्की (1945) को देते हैं कि सभी ग्राफ़ प्रतिच्छेदन ग्राफ़ हैं , लेकिन कुलिक (1964) इसे देखने के लिए भी कहते है। किसी ग्राफ़ का प्रतिच्छेदन संख्या ग्राफ़ के किसी भी प्रतिच्छेदन प्रतिनिधित्व में तत्वों की न्यूनतम कुल संख्या है।
प्रतिच्छेदन रेखांकन की कक्षाएं
कई महत्वपूर्ण ग्राफ़ परिवारों को अधिक प्रतिबंधित प्रकार के सेट परिवारों के प्रतिच्छेदन ग्राफ़ के रूप में वर्णित किया जा सकता है, उदाहरण के लिए किसी प्रकार के ज्यामितीय विन्यास से प्राप्त सेट:
- एक अंतराल ग्राफ को वास्तविक रेखा पर अंतरालों के प्रतिच्छेदन ग्राफ, या एक पथ ग्राफ के जुड़े हुए सबग्राफ के रूप में परिभाषित किया जाता है।
- एक उदासीनता ग्राफ को वास्तविक रेखा पर इकाई अंतरालों के प्रतिच्छेदन ग्राफ के रूप में परिभाषित किया जा सकता है
- एक वृत्ताकार चाप ग्राफ को वृत्ताकार चाप के प्रतिच्छेदन ग्राफ के रूप में परिभाषित किया जाता है।
- एक बहुभुज-वृत्त ग्राफ़ को एक वृत्त पर कोनों वाले बहुभुजों के प्रतिच्छेदन के रूप में परिभाषित किया जाता है।
- कॉर्डल ग्राफ का एक लक्षण एक पेड़ (ग्राफ थ्योरी) के जुड़े सबग्राफ के इंटरसेक्शन ग्राफ के रूप में है।
- समलम्बाकार ग्राफ को दो समांतर रेखाओं से बने समलम्बाकार के प्रतिच्छेदन ग्राफ के रूप में परिभाषित किया जाता है। वे क्रमचय ग्राफ की धारणा का एक सामान्यीकरण हैं, बदले में वे तुलनात्मकता ग्राफ के पूरक के परिवार का एक विशेष मामला हैं, जिसे सह-तुलनीयता ग्राफ के रूप में जाना जाता है।
- [[यूनिट डिस्क ग्राफ]] को प्लेन में यूनिट डिस्क के इंटरसेक्शन ग्राफ के रूप में परिभाषित किया गया है।
- एक वृत्त ग्राफ एक वृत्त की जीवाओं के समूह का प्रतिच्छेदन ग्राफ है।
- सर्कल पैकिंग प्रमेय में कहा गया है कि प्लेनर ग्राफ गैर-क्रॉसिंग सर्किलों से घिरे विमान में बंद डिस्क के परिवारों के बिल्कुल प्रतिच्छेदन ग्राफ हैं।
- स्कीनरमैन के अनुमान (अब एक प्रमेय) में कहा गया है कि प्रत्येक प्लानर ग्राफ को विमान में रेखा खंडों के एक प्रतिच्छेदन ग्राफ के रूप में भी दर्शाया जा सकता है। हालाँकि, रेखा खंडों के प्रतिच्छेदन रेखांकन गैर-योजनाबद्ध भी हो सकते हैं, और रेखा खंडों के प्रतिच्छेदन रेखांकन को पहचानना वास्तविक के अस्तित्वगत सिद्धांत के लिए पूर्ण (जटिलता) है (Schaefer 2010).
- ग्राफ़ G के लाइन ग्राफ को G के किनारों के प्रतिच्छेदन ग्राफ़ के रूप में परिभाषित किया गया है, जहाँ हम प्रत्येक किनारे को उसके दो समापन बिंदुओं के सेट के रूप में दर्शाते हैं।
- एक स्ट्रिंग ग्राफ समतल वक्र का प्रतिच्छेदन ग्राफ है।
- एक ग्राफ़ में बॉक्सिसिटी k है यदि यह आयाम k के बहुआयामी अतिआयत का प्रतिच्छेदन ग्राफ़ है, लेकिन किसी छोटे आयाम का नहीं है।
- एक ग्राफ क्लिक करें दूसरे ग्राफ के अधिकतम क्लिक्स का प्रतिच्छेदन ग्राफ है
- क्लिक ट्री का एक ब्लॉक ग्राफ दूसरे ग्राफ के द्विसंबद्ध घटकों का प्रतिच्छेदन ग्राफ है
Scheinerman (1985) रेखांकन के प्रतिच्छेदन वर्गों की विशेषता है, परिमित रेखांकन के परिवार जिन्हें सेट के दिए गए परिवार से तैयार किए गए सेट के प्रतिच्छेदन ग्राफ के रूप में वर्णित किया जा सकता है। यह आवश्यक और पर्याप्त है कि परिवार में निम्नलिखित गुण हों:
- परिवार में एक ग्राफ का प्रत्येक प्रेरित सबग्राफ भी परिवार में होना चाहिए।
- परिवार में एक शीर्ष को क्लिक (ग्राफ सिद्धांत) द्वारा प्रतिस्थापित करके परिवार में एक ग्राफ से गठित प्रत्येक ग्राफ भी परिवार से संबंधित होना चाहिए।
- परिवार में रेखांकन का एक अनंत अनुक्रम मौजूद है, जिनमें से प्रत्येक अनुक्रम में अगले ग्राफ का एक प्रेरित सबग्राफ है, संपत्ति के साथ कि परिवार में प्रत्येक ग्राफ अनुक्रम में एक ग्राफ का एक प्रेरित सबग्राफ है।
यदि प्रतिच्छेदन ग्राफ अभ्यावेदन की अतिरिक्त आवश्यकता है कि अलग-अलग सिरों को अलग-अलग सेटों द्वारा दर्शाया जाना चाहिए, तो क्लिक विस्तार संपत्ति को छोड़ा जा सकता है।
संबंधित अवधारणाएं
इंटरसेक्शन ग्राफ़ के लिए ऑर्डर-सैद्धांतिक एनालॉग शामिल किए जाने के ऑर्डर हैं। उसी तरह जिस तरह एक ग्राफ का एक प्रतिच्छेदन प्रतिनिधित्व प्रत्येक शीर्ष को एक सेट के साथ लेबल करता है ताकि कोने आसन्न हों यदि और केवल अगर उनके सेट में गैर-रिक्त चौराहा है, ताकि पोसेट में किसी भी x और y के लिए, x ≤ y अगर और केवल अगर f(x) ⊆ f(y)।
यह भी देखें
संदर्भ
- Čulík, K. (1964), "Applications of graph theory to mathematical logic and linguistics", Theory of Graphs and its Applications (Proc. Sympos. Smolenice, 1963), Prague: Publ. House Czechoslovak Acad. Sci., pp. 13–20, MR 0176940.
- Erdős, Paul; Goodman, A. W.; Pósa, Louis (1966), "The representation of a graph by set intersections" (PDF), Canadian Journal of Mathematics, 18 (1): 106–112, doi:10.4153/CJM-1966-014-3, MR 0186575, S2CID 646660.
- Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press, ISBN 0-12-289260-7.
- McKee, Terry A.; McMorris, F. R. (1999), Topics in Intersection Graph Theory, SIAM Monographs on Discrete Mathematics and Applications, vol. 2, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 0-89871-430-3, MR 1672910.
- Szpilrajn-Marczewski, E. (1945), "Sur deux propriétés des classes d'ensembles", Fund. Math., 33: 303–307, doi:10.4064/fm-33-1-303-307, MR 0015448.
- Schaefer, Marcus (2010), "Complexity of some geometric and topological problems" (PDF), Graph Drawing, 17th International Symposium, GS 2009, Chicago, IL, USA, September 2009, Revised Papers, Lecture Notes in Computer Science, vol. 5849, Springer-Verlag, pp. 334–344, doi:10.1007/978-3-642-11805-0_32, ISBN 978-3-642-11804-3.
- Scheinerman, Edward R. (1985), "Characterizing intersection classes of graphs", Discrete Mathematics, 55 (2): 185–193, doi:10.1016/0012-365X(85)90047-0, MR 0798535.
अग्रिम पठन
- For an overview of both the theory of intersection graphs and important special classes of intersection graphs, see McKee & McMorris (1999).
बाहरी संबंध
- Jan Kratochvíl, A video lecture on intersection graphs (June 2007)
- E. Prisner, A Journey through Intersection Graph County