भौतिकी में समय: Difference between revisions
No edit summary |
No edit summary Tag: Manual revert |
||
| (18 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Time sidebar| | {{Time sidebar|विज्ञान}} | ||
[[File:Pendule de Foucault.jpg|thumb|right|पेंथियन, [[पेरिस]] में लियोन फौकॉल्ट का [[फौकॉल्ट पेंडुलम]]|पेरिस का पैन्थियन [[समय]] को माप सकता है और साथ ही पृथ्वी के घूर्णन को प्रदर्शित कर सकता है।]]'''भौतिकी में समय''' को इसकी क्रियात्मक परिभाषा द्वारा परिभाषित किया जाता है। समय वह है जो [[घड़ी]] पढ़ती है।<ref>{{cite book | [[File:Pendule de Foucault.jpg|thumb|right|पेंथियन, [[पेरिस]] में लियोन फौकॉल्ट का [[फौकॉल्ट पेंडुलम]]|पेरिस का पैन्थियन [[समय]] को माप सकता है और साथ ही पृथ्वी के घूर्णन को प्रदर्शित कर सकता है।]]'''भौतिकी में समय''' को इसकी क्रियात्मक परिभाषा द्वारा परिभाषित किया जाता है। समय वह है जो [[घड़ी]] पढ़ती है।<ref>{{cite book | ||
| Line 12: | Line 12: | ||
|isbn=0-07-012436-1 | |isbn=0-07-012436-1 | ||
|pages=18–61 | |pages=18–61 | ||
|url=https://books.google.com/books?id=kt1UAAAAMAAJ}}</ref> | |url=https://books.google.com/books?id=kt1UAAAAMAAJ}}</ref> चिरसम्मत सापेक्ष भौतिकी में यह [[अदिश (भौतिकी)]] मात्रा है, अधिकांशतः प्रतीक (<math>t</math> ) द्वारा निरूपित [[लंबाई]], [[द्रव्यमान]] और विद्युत आवेश के प्रकार सामान्यतः [[मौलिक मात्रा]] के रूप में वर्णित किया जाता है। [[गति (भौतिकी)]], [[गतिज ऊर्जा]] और समय पर निर्भर [[क्षेत्र (भौतिकी)]] जैसी अन्य अवधारणाओं के [[औपचारिक प्रमाण]] के लिए समय को गणितीय रूप से अन्य भौतिक राशियों के साथ जोड़ा जा सकता है। समयनिर्धारक और [[रिकॉर्ड रखना]] प्राविधिक वैज्ञानिक समस्याएँ की नींव का जटिल भाग है। | ||
== समय के निशान == | == समय के निशान == | ||
| Line 30: | Line 30: | ||
अंततः <ref>The Mesopotamian (modern-day Iraq) astronomers recorded astronomical observations with the naked eye, more than 3500 years ago. [[P. W. Bridgman]] defined his [[operational definition]] in the twentieth c.</ref><ref>[[Naked-eye stars|Naked eye astronomy]] became obsolete in 1609 with Galileo's observations with a telescope. Galileo Galilei Linceo, [http://www.rarebookroom.org/Control/galsid/index.html ''Sidereus Nuncius''] (''[[Starry Messenger]]'') 1610.</ref> परिचालन परिभाषाओं का उपयोग करते हुए, साधनविनियोग के साथ समय बीतने को चिह्नित करना संभव हो गया। इसके साथ ही समय की हमारी अवधारणा विकसित हुई है, जैसा कि नीचे दिखाया गया है।<ref>http://tycho.usno.navy.mil/gpstt.html http://www.phys.lsu.edu/mog/mog9/node9.html Today, automated astronomical observations from satellites and spacecraft require relativistic corrections of the reported positions.</ref> | अंततः <ref>The Mesopotamian (modern-day Iraq) astronomers recorded astronomical observations with the naked eye, more than 3500 years ago. [[P. W. Bridgman]] defined his [[operational definition]] in the twentieth c.</ref><ref>[[Naked-eye stars|Naked eye astronomy]] became obsolete in 1609 with Galileo's observations with a telescope. Galileo Galilei Linceo, [http://www.rarebookroom.org/Control/galsid/index.html ''Sidereus Nuncius''] (''[[Starry Messenger]]'') 1610.</ref> परिचालन परिभाषाओं का उपयोग करते हुए, साधनविनियोग के साथ समय बीतने को चिह्नित करना संभव हो गया। इसके साथ ही समय की हमारी अवधारणा विकसित हुई है, जैसा कि नीचे दिखाया गया है।<ref>http://tycho.usno.navy.mil/gpstt.html http://www.phys.lsu.edu/mog/mog9/node9.html Today, automated astronomical observations from satellites and spacecraft require relativistic corrections of the reported positions.</ref> | ||
== समय की माप की इकाई: [[दूसरा]] == | == समय की माप की इकाई: [[दूसरा]] == | ||
[[इकाइयों की अंतर्राष्ट्रीय प्रणाली]] (एसआई) में, समय की इकाई दूसरी है (प्रतीक: <math>\mathrm{s}</math>)। यह एसआई आधार इकाई है और 1967 से इसकी अवधि के रूप में परिभाषित किया गया है।{{nowrap|9,192,631,770}} [[सीज़ियम]] 133 परमाणु की | [[इकाइयों की अंतर्राष्ट्रीय प्रणाली]] (एसआई) में, समय की इकाई दूसरी है (प्रतीक: <math>\mathrm{s}</math>)। यह एसआई आधार इकाई है और 1967 से इसकी अवधि के रूप में परिभाषित किया गया है। {{nowrap|9,192,631,770}} [[सीज़ियम]] 133 परमाणु की मूलभूत अवस्था के दो [[हाइपरफाइन संरचना|अति सूक्ष्म संरचना]] के बीच संक्रमण के अनुरूप [[विकिरण]] का चक्र।<ref>{{cite web | ||
|url=http://www.bipm.org/en/si/si_brochure/chapter2/2-1/second.html | |url=http://www.bipm.org/en/si/si_brochure/chapter2/2-1/second.html | ||
|title=Unit of time (second) | |title=Unit of time (second) | ||
| Line 38: | Line 38: | ||
|publisher=[[International Bureau of Weights and Measures]] (BIPM) | |publisher=[[International Bureau of Weights and Measures]] (BIPM) | ||
}} | }} | ||
</ref> यह परिभाषा सीज़ियम [[परमाणु घड़ी]] के संचालन पर आधारित है। ये घड़ियाँ लगभग 1955 के बाद प्राथमिक संदर्भ मानकों के रूप में उपयोग के लिए व्यावहारिक हो गईं | </ref> यह परिभाषा सीज़ियम [[परमाणु घड़ी]] के संचालन पर आधारित है। ये घड़ियाँ लगभग 1955 के बाद प्राथमिक संदर्भ मानकों के रूप में उपयोग के लिए व्यावहारिक हो गईं और तब से उपयोग में हैं। | ||
=== समयनिर्धारक में कला की स्थिति === | === समयनिर्धारक में कला की स्थिति === | ||
| Line 58: | Line 58: | ||
==== यांत्रिक घड़ियाँ ==== | ==== यांत्रिक घड़ियाँ ==== | ||
वॉलिंगफोर्ड के रिचर्ड (1292–1336), सेंट अल्बंस एब्बे के मठाधीश, प्रसिद्ध रूप से 1330 के आसपास खगोलीय कक्ष के रूप में घड़ी पूरी | वॉलिंगफोर्ड के रिचर्ड (1292–1336), सेंट अल्बंस एब्बे के मठाधीश, प्रसिद्ध रूप से 1330 के आसपास खगोलीय कक्ष के रूप में घड़ी पूरी प्रकार से यांत्रिक बनाया।<ref>North, J. (2004) ''God's Clockmaker: Richard of Wallingford and the Invention of Time''. Oxbow Books. {{ISBN|1-85285-451-0}}</ref><ref>Watson, E (1979) "The St Albans Clock of Richard of Wallingford". ''Antiquarian Horology'' 372-384.</ref>वालिंगफोर्ड के रिचर्ड के समय तक, [[शाफ़्ट (उपकरण)]] और [[गियर]] के उपयोग ने यूरोप के शहरों को अपने संबंधित शहर की घड़ियों पर समय प्रदर्शित करने के लिए तंत्र बनाने की अनुमति दी। वैज्ञानिक क्रांति के समय तक घड़ियाँ इतनी छोटी हो गईं कि परिवार व्यक्तिगत घड़ी, संभवतः जेब घड़ी साझा कर सकें। पहले केवल राजा ही उन्हें वहन कर सकते थे। 18वीं और 19वीं शताब्दी में पेंडुलम घड़ियों का व्यापक रूप से उपयोग किया जाता था। वे सामान्य उपयोग में बड़े पैमाने पर क्वार्ट्ज-घड़ी और डिजिटल घड़ियों द्वारा प्रतिस्थापित किए गए हैं। [[परमाणु घड़ियाँ]] सैद्धांतिक रूप से लाखों वर्षों तक सटीक समय रख सकती हैं। वे [[मानकीकरण]] और वैज्ञानिक उपयोग के लिए उपयुक्त हैं। | ||
=== गैलीलियो: समय का प्रवाह === | === गैलीलियो: समय का प्रवाह === | ||
{{main|पुनः उत्पादकता}} | {{main|पुनः उत्पादकता}} | ||
1583 में, [[गैलीलियो गैलीली]] (1564-1642) ने पाया कि हार्मोनिक ऑसिलेटर पेंडुलम की हार्मोनिक गति की निरंतर अवधि होती है, जिसे उन्होंने [[पीसा]] के कैथेड्रल में [[ मास (लिटुरजी) |मास (लिटुरजी)]] में सरल हार्मोनिक गति में लहराते दीपक की गति के समय उसकी नाड़ी के साथ से सीखा।<ref>Jo Ellen Barnett, ''Time's Pendulum'' {{ISBN|0-306-45787-3}} p.99.</ref>अपने [[दो नए विज्ञान]] (1638) में गैलीलियो गैलीली ने झुकाव वाले विमान के नीचे ज्ञात दूरी को रोल करने के लिए कांस्य गेंद के लिए लगने वाले समय को मापने के लिए पानी की घड़ी का उपयोग किया, यह घड़ी थी।<ref name="galileo">[[Galileo]] 1638 ''Discorsi e dimostrazioni matematiche, intorno á due nuoue scienze'' '''213''', Leida, Appresso gli Elsevirii (Louis Elsevier), or ''Mathematical discourses and demonstrations, relating to [[Two New Sciences]]'', English translation by Henry Crew and Alfonso de Salvio 1914. Section '''213''' is reprinted on pages 534-535 of ''On the Shoulders of Giants'':The Great Works of Physics and Astronomy (works by [[Copernicus]], [[Johannes Kepler|Kepler]], [[Galileo]], [[Isaac Newton|Newton]], and [[Albert Einstein|Einstein]]). [[Stephen Hawking]], ed. 2002 {{ISBN|0-7624-1348-4}}</ref> | 1583 में, [[गैलीलियो गैलीली]] (1564-1642) ने पाया कि हार्मोनिक ऑसिलेटर पेंडुलम की हार्मोनिक गति की निरंतर अवधि होती है, जिसे उन्होंने [[पीसा]] के कैथेड्रल में [[ मास (लिटुरजी) |मास (लिटुरजी)]] में सरल हार्मोनिक गति में लहराते दीपक की गति के समय उसकी नाड़ी के साथ से सीखा।<ref>Jo Ellen Barnett, ''Time's Pendulum'' {{ISBN|0-306-45787-3}} p.99.</ref>अपने [[दो नए विज्ञान]] (1638) में गैलीलियो गैलीली ने झुकाव वाले विमान के नीचे ज्ञात दूरी को रोल करने के लिए कांस्य गेंद के लिए लगने वाले समय को मापने के लिए पानी की घड़ी का उपयोग किया, यह घड़ी थी।<ref name="galileo">[[Galileo]] 1638 ''Discorsi e dimostrazioni matematiche, intorno á due nuoue scienze'' '''213''', Leida, Appresso gli Elsevirii (Louis Elsevier), or ''Mathematical discourses and demonstrations, relating to [[Two New Sciences]]'', English translation by Henry Crew and Alfonso de Salvio 1914. Section '''213''' is reprinted on pages 534-535 of ''On the Shoulders of Giants'':The Great Works of Physics and Astronomy (works by [[Copernicus]], [[Johannes Kepler|Kepler]], [[Galileo]], [[Isaac Newton|Newton]], and [[Albert Einstein|Einstein]]). [[Stephen Hawking]], ed. 2002 {{ISBN|0-7624-1348-4}}</ref> | ||
<blockquote>पानी का बड़ा पात्र जिसे ऊँचे स्थान पर रखा गया है, इस बर्तन के तल में पानी की पतली धारा देने वाले छोटे व्यास का पाइप मिलाप किया गया था, जिसे हमने प्रत्येक वंश के समय छोटे गिलास में | <blockquote>पानी का बड़ा पात्र जिसे ऊँचे स्थान पर रखा गया है, इस बर्तन के तल में पानी की पतली धारा देने वाले छोटे व्यास का पाइप मिलाप किया गया था, जिसे हमने प्रत्येक वंश के समय छोटे गिलास में एकत्र किया। चाहे वह चैनल की पूरी लंबाई के लिए हो या उसकी लंबाई के भागों के लिए इस प्रकार त्र किए गए पानी को प्रत्येक अवतरण के बाद बहुत ही सटीक संतुलन पर तौला गया था। इन भारों के अंतर और अनुपात ने हमें समय के अंतर और अनुपात दिए और यह इतनी त्रुटिहीन के साथ कि चूंकि ऑपरेशन को कई बार दोहराया गया, परिणामों में कोई सराहनीय विसंगति नहीं थी।</blockquote> | ||
शाब्दिक दो नए विज्ञानों को मापने के लिए गैलीलियो का प्रायोगिक परिस्थिति समय का प्रवाह, गेंद की गति का वर्णन करने के लिए है। इसहाक न्यूटन के अपने फिलोसोफी नेचुरेलिस प्रिन्सिपिया मैथेमेटिका में बयान से पहले, मैं समय, [[स्थान (भूगोल)]] और को परिभाषित नहीं करता गति (भौतिकी), जैसा कि सभी जानते हैं।<ref name="galileo2">[[Isaac Newton|Newton]] 1687 ''[[Philosophiae Naturalis Principia Mathematica]]'', Londini, Jussu Societatis Regiae ac Typis J. Streater, or '''''[[The Mathematical Principles of Natural Philosophy]]''''', [[London]], English translation by [[Andrew Motte]] 1700s. From part of the Scholium, reprinted on page 737 of ''On the Shoulders of Giants'':The Great Works of Physics and Astronomy (works by [[Copernicus]], [[Johannes Kepler|Kepler]], [[Galileo]], [[Isaac Newton|Newton]], and [[Albert Einstein|Einstein]]). [[Stephen Hawking]], ed. 2002 {{ISBN|0-7624-1348-4}}</ref>गैलिलियन परिवर्तन मानते हैं कि संदर्भ के सभी | शाब्दिक दो नए विज्ञानों को मापने के लिए गैलीलियो का प्रायोगिक परिस्थिति समय का प्रवाह, गेंद की गति का वर्णन करने के लिए है। इसहाक न्यूटन के अपने फिलोसोफी नेचुरेलिस प्रिन्सिपिया मैथेमेटिका में बयान से पहले, मैं समय, [[स्थान (भूगोल)]] और को परिभाषित नहीं करता गति (भौतिकी), जैसा कि सभी जानते हैं।<ref name="galileo2">[[Isaac Newton|Newton]] 1687 ''[[Philosophiae Naturalis Principia Mathematica]]'', Londini, Jussu Societatis Regiae ac Typis J. Streater, or '''''[[The Mathematical Principles of Natural Philosophy]]''''', [[London]], English translation by [[Andrew Motte]] 1700s. From part of the Scholium, reprinted on page 737 of ''On the Shoulders of Giants'':The Great Works of Physics and Astronomy (works by [[Copernicus]], [[Johannes Kepler|Kepler]], [[Galileo]], [[Isaac Newton|Newton]], and [[Albert Einstein|Einstein]]). [[Stephen Hawking]], ed. 2002 {{ISBN|0-7624-1348-4}}</ref>गैलिलियन परिवर्तन मानते हैं कि संदर्भ के सभी निर्माण के लिए समय समान है। | ||
=== न्यूटन की भौतिकी: रैखिक समय === | === न्यूटन की भौतिकी: रैखिक समय === | ||
| Line 72: | Line 72: | ||
1665 में उसके आसपास जब आइजैक न्यूटन (1643-1727) ने [[गुरुत्वाकर्षण]] के अनुसार गिरने वाली वस्तुओं की गति को व्युत्पन्न किया, समय के उपचार के [[गणितीय भौतिकी]] के लिए पहला स्पष्ट सूत्रीकरण प्रारंभ हुआ। रैखिक समय, सार्वभौमिक घड़ी के रूप में माना गया। | 1665 में उसके आसपास जब आइजैक न्यूटन (1643-1727) ने [[गुरुत्वाकर्षण]] के अनुसार गिरने वाली वस्तुओं की गति को व्युत्पन्न किया, समय के उपचार के [[गणितीय भौतिकी]] के लिए पहला स्पष्ट सूत्रीकरण प्रारंभ हुआ। रैखिक समय, सार्वभौमिक घड़ी के रूप में माना गया। | ||
<blockquote>निरपेक्ष, सत्य और गणितीय समय, स्वयं का और अपनी प्रकृति से समान रूप से बहता है अतिरिक्त किसी बाहरी चीज़ की | <blockquote>निरपेक्ष, सत्य और गणितीय समय, स्वयं का और अपनी प्रकृति से समान रूप से बहता है अतिरिक्त किसी बाहरी चीज़ की देख-भाल किए और दूसरे नाम से अवधि कहा जाता है। सापेक्ष, स्पष्ट और सामान्य समय कुछ समझदार और बाहरी है चाहे सटीक या असमान गति के माध्यम से अवधि का माप, जो सामान्यतः वास्तविक समय के अतिरिक्त प्रयोग किया जाता है। जैसे घंटा, दिन, महीना, साल।<ref name="newton">[[Isaac Newton|Newton]] 1687 page 738.</ref> | ||
गैलीलियो द्वारा वर्णित जल घड़ी तंत्र को प्रयोगों के पर्यन्त पानी के लामिनार प्रवाह प्रदान करने के लिए अभियंता किया गया था, इस प्रकार प्रयोगों की अवधि के लिए पानी का निरंतर प्रवाह प्रदान किया गया था और जिसे न्यूटन ने अवधि कहा था। | गैलीलियो द्वारा वर्णित जल घड़ी तंत्र को प्रयोगों के पर्यन्त पानी के लामिनार प्रवाह प्रदान करने के लिए अभियंता किया गया था, इस प्रकार प्रयोगों की अवधि के लिए पानी का निरंतर प्रवाह प्रदान किया गया था और जिसे न्यूटन ने अवधि कहा था। | ||
| Line 79: | Line 79: | ||
=== ऊष्मप्रवैगिकी और अपरिवर्तनीयता का विरोधाभास === | === ऊष्मप्रवैगिकी और अपरिवर्तनीयता का विरोधाभास === | ||
{{main|समय का तीर}} | {{main|समय का तीर}} | ||
1798 तक, [[बेंजामिन थॉम्पसन]] (1753-1814) ने पता लगाया था कि काम को अतिरिक्त किसी सीमा के [[गर्मी]] में बदला जा सकता है - ऊर्जा के संरक्षण का अग्रदूत या | 1798 तक, [[बेंजामिन थॉम्पसन]] (1753-1814) ने पता लगाया था कि काम को अतिरिक्त किसी सीमा के [[गर्मी]] में बदला जा सकता है - ऊर्जा के संरक्षण का अग्रदूत या ऊर्जा संरक्षण | ||
*[[ | *[[ऊष्मप्रवैगिकी|ऊष्मप्रवैगिकी का पहला नियम]] | ||
1824 में निकोलस लेओनार्ड साडी कार्नोट (1796-1832) ने वैज्ञानिक रूप से अपने कार्नोट चक्र, सार इंजन के साथ भाप इंजन का विश्लेषण किया। [[रुडोल्फ क्लॉसियस]] (1822-1888) ने विकार | 1824 में निकोलस लेओनार्ड साडी कार्नोट (1796-1832) ने वैज्ञानिक रूप से अपने कार्नोट चक्र, सार इंजन के साथ भाप इंजन का विश्लेषण किया। [[रुडोल्फ क्लॉसियस]] (1822-1888) ने विकार [[एन्ट्रापी]] का उपाय नोट किया, जो मुक्त ऊर्जा की लगातार घटती मात्रा को प्रभावित करता है जो कार्नाट इंजन के लिए उपलब्ध है। | ||
* | * [[ऊष्मप्रवैगिकी का दूसरा नियम]] | ||
इस प्रकार, किसी दिए गए तापमान पर | इस प्रकार, किसी दिए गए तापमान पर कम से अधिक [[एन्ट्रापी]] की ओर ऊष्मप्रवैगिकी प्रणाली का निरंतर मार्च, समय के तीर को परिभाषित करता है। विशेष रूप से [[स्टीफन हॉकिंग]] समय के तीन तीरों की पहचान करते हैं।<ref name="einstein2">pp. 182–195. [[Stephen Hawking]] 1996. ''The Illustrated Brief History of Time'': updated and expanded edition {{ISBN|0-553-10374-1}}</ref> | ||
* समय का मनोवैज्ञानिक तीर - कठोर प्रवाह की हमारी धारणा। | * समय का मनोवैज्ञानिक तीर - कठोर प्रवाह की हमारी धारणा। | ||
*समय का ऊष्मप्रवैगिकी तीर - एन्ट्रापी के विकास द्वारा प्रतिष्ठित। | *समय का ऊष्मप्रवैगिकी तीर - एन्ट्रापी के विकास द्वारा प्रतिष्ठित। | ||
*समय का ब्रह्माण्ड संबंधी तीर - ब्रह्मांड के विस्तार द्वारा प्रतिष्ठित। | *समय का ब्रह्माण्ड संबंधी तीर - ब्रह्मांड के विस्तार द्वारा प्रतिष्ठित। | ||
समय के साथ, पृथक | समय के साथ, पृथक ऊष्मप्रवैगिकी प्रणाली में एन्ट्रापी बढ़ जाती है। इसके विपरीत, इरविन श्रोडिंगर (1887-1961) ने बताया कि जीवन नकारात्मक एन्ट्रॉपी प्रवाह पर निर्भर करता है।<ref>[[Erwin Schrödinger]] (1945) ''What is Life?''</ref> [[इल्या प्रिझोगिन]] (1917-2003) ने कहा कि जीवन की प्रकार अन्य ऊष्मप्रवैगिकी प्रणालियां भी संतुलन से बहुत दूर हैं, वे भी स्थिर अनुपात-लौकिक संरचनाओं को प्रदर्शित कर सकती हैं जो जीवन की याद दिलाती हैं। इसके तुरंत बाद बेलौसोव-झाबोटिंस्की प्रतिक्रियाएं<ref>G. Nicolis and I. Prigogine (1989), ''Exploring Complexity''</ref> प्रतिवेदन किए गए, जो रासायनिक समाधान में दोलनशील रंगों को प्रदर्शित करते हैं।<ref>R. Kapral and K. Showalter, eds. (1995), ''Chemical Waves and Patterns''</ref> ये संतुलन उष्मागतिक शाखाएं [[द्विभाजन सिद्धांत]] तक पहुंचती हैं, जो अस्थिर है और अन्य ऊष्मप्रवैगिकी शाखा इसके स्थान पर स्थिर हो जाती है।<ref>Ilya Prigogine (1996) ''The End of Certainty'' pp. 63–71</ref> | ||
===विद्युत चुंबकत्व और प्रकाश की गति=== | ===विद्युत चुंबकत्व और प्रकाश की गति=== | ||
{{main| | {{main|मैक्सवेल के समीकरण}} | ||
1864 में, [[जेम्स क्लर्क मैक्सवेल]] (1831-1879) ने [[बिजली]] और [[चुंबकत्व]] का संयुक्त सिद्धांत प्रस्तुत किया। उन्होंने उन दो घटनाओं से संबंधित सभी कानूनों को चार समीकरणों में जोड़ दिया। इन समीकरणों को [[विद्युत]] चुंबकत्व के लिए मैक्सवेल के समीकरण के रूप में जाना जाता है | 1864 में, [[जेम्स क्लर्क मैक्सवेल]] (1831-1879) ने [[बिजली]] और [[चुंबकत्व]] का संयुक्त सिद्धांत प्रस्तुत किया। उन्होंने उन दो घटनाओं से संबंधित सभी कानूनों को चार समीकरणों में जोड़ दिया। इन समीकरणों को [[विद्युत]] चुंबकत्व के लिए मैक्सवेल के समीकरण के रूप में जाना जाता है, वे विद्युत चुम्बकीय तरंगों के रूप में समाधानों की अनुमति देते हैं और उन्हें उत्पन्न करने वाले विद्युत आवेश के वेग की देख-भाल किए अतिरिक्त निश्चित गति, c पर प्रचार करते हैं। | ||
तथ्य यह है कि प्रकाश को | तथ्य यह है कि प्रकाश को सदैव गति c पर यात्रा करने की भविष्यवाणी की जाती है। यदि मैक्सवेल के समीकरणों को किसी [[जड़त्वीय फ्रेम|जड़त्वीय निर्माण]] स्थिर वेग के साथ संदर्भ निर्माण में धारण करने के लिए माना जाता है, तो गैलिलियन सापेक्षता के साथ असंगत होगा। क्योंकि गैलीलियन परिवर्तन गति को कम करके बढ़ाने की भविष्यवाणी करते हैं। प्रकाश के समानांतर विरोधी समानांतर यात्रा करने वाले पर्यवेक्षक के संदर्भ निर्माण में है। | ||
यह उम्मीद की गई थी कि निरपेक्ष संदर्भ ढांचा था, जो [[चमकदार ईथर]] का था, जिसमें मैक्सवेल के समीकरण ज्ञात रूप में असंशोधित थे। | यह उम्मीद की गई थी कि निरपेक्ष संदर्भ ढांचा था, जो [[चमकदार ईथर]] का था, जिसमें मैक्सवेल के समीकरण ज्ञात रूप में असंशोधित थे। | ||
मिशेलसन-मॉर्ले प्रयोग चमकदार एथर के सापेक्ष पृथ्वी की गति के कारण प्रकाश की सापेक्ष गति में किसी भी अंतर का पता लगाने में विफल रहा, यह सुझाव देते हुए कि मैक्सवेल के समीकरण वास्तव में सभी | मिशेलसन-मॉर्ले प्रयोग चमकदार एथर के सापेक्ष पृथ्वी की गति के कारण प्रकाश की सापेक्ष गति में किसी भी अंतर का पता लगाने में विफल रहा, यह सुझाव देते हुए कि मैक्सवेल के समीकरण वास्तव में सभी निर्माण में उपस्तिथ थे। 1875 में, [[हेंड्रिक लोरेंत्ज़]] (1853-1928) ने [[लोरेंत्ज़ परिवर्तन]] की खोज की, जिसने मैक्सवेल के समीकरणों को अपरिवर्तित छोड़ दिया, जिससे माइकलसन और मॉर्ले के नकारात्मक परिणाम की व्याख्या की जा सके। हेनरी पॉइनकेयर (1854-1912) ने लोरेंत्ज़ के परिवर्तन के महत्व को नोट किया और इसे लोकप्रिय बनाया। विशेष रूप से रेलमार्ग कार का विवरण [[विज्ञान और परिकल्पना]] में पाया जा सकता है,<ref>Henri Poincaré, (1902). ''[[Science and Hypothesis]]'' [http://spartan.ac.brocku.ca/~lward/Poincare/Poincare_1905_toc.html Eprint] {{Webarchive|url=https://web.archive.org/web/20061004103729/http://spartan.ac.brocku.ca/~lward/Poincare/Poincare_1905_toc.html |date=2006-10-04 }}</ref> जो 1905 के आइंस्टीन के लेखों से पहले प्रकाशित हुआ था। | ||
लोरेंत्ज़ परिवर्तन ने [[अंतरिक्ष संकुचन]] और समय के फैलाव की भविष्यवाणी की | लोरेंत्ज़ परिवर्तन ने [[अंतरिक्ष संकुचन]] और समय के फैलाव की भविष्यवाणी की, 1905 तक, पूर्व की व्याख्या आणविक बलों के विद्युत प्रकृति के संशोधन के कारण ईथर के संबंध में गतिमान वस्तुओं के भौतिक संकुचन के रूप में की गई थी, जबकि बाद वाले को केवल गणितीय शर्त माना गया था। | ||
===आइंस्टीन की भौतिकी: | ===आइंस्टीन की भौतिकी: अंतरिक्ष समय=== | ||
{{main| | {{main|विशेष सापेक्षता|सामान्य सापेक्षता}} | ||
अल्बर्ट आइंस्टीन की 1905 की [[विशेष सापेक्षता]] ने निरपेक्ष समय की धारणा को चुनौती दी | अल्बर्ट आइंस्टीन की 1905 की [[विशेष सापेक्षता]] ने निरपेक्ष समय की धारणा को चुनौती दी और केवल उन घड़ियों के लिए तुल्यकालन की परिभाषा तैयार की जो समय के रैखिक प्रवाह को चिह्नित करती हैं। | ||
{{Quote| | {{Quote|यदि अंतरिक्ष के बिंदु ए पर एक घड़ी है, तो ए पर एक पर्यवेक्षक इन घटनाओं के साथ-साथ हाथों की स्थिति को ढूंढकर ए के तत्काल निकटता में घटनाओं के समय मूल्यों को निर्धारित कर सकता है। यदि अंतरिक्ष के बिंदु B पर एक और घड़ी है जो सभी प्रकार से A के समान है, तो B पर एक पर्यवेक्षक के लिए B के तत्काल सन्निकट घटनाओं के समय मूल्यों को निर्धारित करना संभव है। | ||
लेकिन आगे की धारणा के बिना, समय के संबंध में, बी में एक घटना के साथ ए में एक घटना की तुलना करना संभव नहीं है। हमने अभी तक केवल "A टाइम" और "B टाइम" परिभाषित किया है। | |||
हमने A और B के लिए एक सामान्य "समय" को परिभाषित नहीं किया है, क्योंकि बाद वाले को तब तक परिभाषित नहीं किया जा सकता जब तक कि हम ''परिभाषा के अनुसार'' स्थापित नहीं करते हैं कि A से B तक यात्रा करने के लिए प्रकाश द्वारा आवश्यक "समय" के बराबर होता है। इसे B से A तक यात्रा करने की आवश्यकता है। प्रकाश की किरण को A से B की तरफ "A टाइम" ''T''<sub>A</sub> पर शुरू होने दें, इसे "B टाइम" ''T पर जाने दें ''<sub>B</sub> A की दिशा में B पर परिलक्षित होता है, और फिर से A पर "A time" ''t''′<sub>A</sub> पर पहुंचता है। | |||
परिभाषा के अनुसार दो घड़ियां अगर सिंक्रनाइज़ होती हैं | |||
: <math>t_\text{B} - t_\text{A} = t'_\text{A} - t_\text{B}\text{.}\,\!</math> | : <math>t_\text{B} - t_\text{A} = t'_\text{A} - t_\text{B}\text{.}\,\!</math> | ||
हम मानते हैं कि समकालिकता की यह परिभाषा विरोधाभासों से मुक्त है, और किसी भी बिंदु के लिए संभव है; और यह कि निम्नलिखित संबंध सार्वभौमिक रूप से मान्य हैं:- | |||
# | # यदि B की घड़ी A की घड़ी के साथ तालमेल बिठाती है, तो A की घड़ी B की घड़ी के साथ तालमेल बिठाती है। | ||
# | # यदि A की घड़ी B की घड़ी के साथ और C की घड़ी के साथ भी सिंक्रनाइज़ होती है, तो B और C की घड़ियाँ भी एक दूसरे के साथ सिंक्रनाइज़ होती हैं।|अल्बर्ट आइंस्टीन|"मूविंग बॉडीज के इलेक्ट्रोडायनामिक्स पर"<ref name="एरो_ऑफ_टाइम">[[अल्बर्ट आइंस्टीन|आइंस्टीन]] 1905, ''जुर एलेक्ट्रोडायनेमिक बेवेग्टर कोपर'' [ऑन द इलेक्ट्रोडायनामिक्स ऑफ मूविंग बॉडीज] 1922 में ''[[विशेष सापेक्षता |Das Relativitätsprinzip]]'', बी.जी. टेबनेर, लीपज़िग। '''''[[विशेष सापेक्षता|सापेक्षता के सिद्धांत]]: सापेक्षता के विशेष सिद्धांत पर मूल पत्रों का संग्रह'''', एच.ए. लॉरेंत्ज़, ए. आइंस्टीन, एच. मिन्कोव्स्की, और डब्ल्यू. एच. वेइल, मोनोग्राफियन, हेफ़्ट 2 में ''फ़ोर्टस्क्रिट डेर मैथेमेटिसचेन विसेनशाफ्टन'' का हिस्सा हैं। अंग्रेजी अनुवाद डब्ल्यू पेरेट और जी.बी. जेफरी, 'ऑन द शोल्डर ऑफ जायंट्स': द ग्रेट वर्क्स ऑफ फिजिक्स एंड एस्ट्रोनॉमी के पृष्ठ 1169 पर पुनर्मुद्रित ([[कॉपरनिकस]], [[जोहान्स केप्लर|केप्लर]], [[गैलीलियो]], [[गैलीलियो]] द्वारा काम करता है। आइजैक न्यूटन|न्यूटन]], और [[अल्बर्ट आइंस्टीन|आइंस्टीन]])। [[स्टीफन हॉकिंग]], एड। 2002 {{ISBN|0-7624-1348-4}}</ref>}} आइंस्टीन ने दिखाया कि यदि संदर्भ निर्माण के बीच प्रकाश की गति नहीं बदल रही है, तो स्थान और समय ऐसा होना चाहिए कि गतिमान पर्यवेक्षक प्रकाश की उसी गति को स्थिर के रूप में मापेगा क्योंकि वेग को अंतरिक्ष और समय द्वारा परिभाषित किया गया है: | ||
| | |||
:<math>\mathbf{v}={d\mathbf{r}\over dt} \text{,}</math> जहाँ r स्थिति है और ''t'' समय है। | :<math>\mathbf{v}={d\mathbf{r}\over dt} \text{,}</math> जहाँ r स्थिति है और ''t'' समय है। | ||
वास्तव में, लोरेंत्ज़ परिवर्तन | वास्तव में, लोरेंत्ज़ परिवर्तन सापेक्ष गति में दो संदर्भ निर्माण के लिए, जिसका ''x'' अक्ष सापेक्ष वेग की दिशा में निर्देशित है। | ||
:<math>\begin{cases} | :<math>\begin{cases} | ||
| Line 131: | Line 130: | ||
z' &= z | z' &= z | ||
\end{cases}</math> | \end{cases}</math> | ||
कहा जा सकता है कि अंतरिक्ष और समय को | कहा जा सकता है कि अंतरिक्ष और समय को प्रकार से मिश्रित किया जा सकता है जिस प्रकार से जेड अक्ष के चारों ओर एक यूक्लिडियन घूर्णन और वाई निर्देशांक को मिलाता है। इसके परिणामों में साथ सापेक्षता सम्मलित है। [[File:Relativity of Simultaneity.svg|thumb|घटना बी हरे रंग के संदर्भ निर्माण में ए के साथ-साथ है, किन्तु ऐसा हुआ | ||
पहले नीले | पहले नीले निर्माण में, और बाद में लाल निर्माण में होगा।]]अधिक विशेष रूप से लोरेंत्ज़ परिवर्तन अतिशयोक्तिपूर्ण घुमाव है <math> | ||
\begin{pmatrix} | \begin{pmatrix} | ||
ct' \\ | ct' \\ | ||
| Line 147: | Line 146: | ||
x | x | ||
\end{pmatrix} \text{ where } \phi = \operatorname{artanh}\,\frac{v}{c} \text{,} | \end{pmatrix} \text{ where } \phi = \operatorname{artanh}\,\frac{v}{c} \text{,} | ||
</math> जो कि चार-आयामी मिन्कोव्स्की अंतरिक्ष में निर्देशांक का परिवर्तन है, जिसका आयाम सीटी है। | </math> जो कि चार-आयामी मिन्कोव्स्की अंतरिक्ष में निर्देशांक का परिवर्तन है, जिसका आयाम सीटी है। [[यूक्लिडियन अंतरिक्ष]] में साधारण घुमाव <math> | ||
\begin{pmatrix} | \begin{pmatrix} | ||
x' \\ | x' \\ | ||
| Line 162: | Line 161: | ||
y | y | ||
\end{pmatrix} | \end{pmatrix} | ||
</math> निर्देशांक का संगत परिवर्तन है। | </math> निर्देशांक का संगत परिवर्तन है। प्रकाश की गति को केवल रूपांतरण कारक के रूप में देखा जा सकता है, क्योंकि हम अलग-अलग इकाइयों में अंतरिक्ष समय के आयामों को मापते हैं, चूँकि वर्तमान में [[मीटर]] को सेकंड के संदर्भ में परिभाषित किया गया है। इसका सटीक मान है {{nowrap|299 792 458 m/s}}. यूक्लिडियन अंतरिक्ष में हमें समान कारक की आवश्यकता होगी। उदाहरण के लिए, हमने समुद्री मील में चौड़ाई और पैरों में गहराई मापी। भौतिक विज्ञान में कभी-कभी प्राकृतिक इकाइयाँ माप की इकाइयाँ जिनमें c = 1 का उपयोग समीकरणों को सरल बनाने के लिए किया जाता है। | ||
गतिमान संदर्भ | गतिमान संदर्भ निर्माण में समय को स्थिर की तुलना में निम्न संबंध द्वारा अधिक धीमी गति से चलाने के लिए दिखाया गया है, जो लोरेंत्ज़ परिवर्तन द्वारा ∆x′ = 0, ∆τ = ∆t′ डालकर प्राप्त किया जा सकता है। | ||
:<math>\Delta t= {{\Delta \tau}\over\sqrt{1 - v^2/c^2}}</math> | :<math>\Delta t= {{\Delta \tau}\over\sqrt{1 - v^2/c^2}}</math> | ||
जहाँ, | |||
*∆τ दो घटनाओं के बीच का समय है जैसा कि चलती संदर्भ | *∆τ दो घटनाओं के बीच का समय है जैसा कि चलती संदर्भ निर्माण में मापा जाता है जिसमें वे ही स्थान पर होते हैं, उदाहरण के लिए चलती घड़ी पर दो टिक, इसे दो घटनाओं के बीच का [[उचित समय]] कहा जाता है। | ||
*∆t इन दो घटनाओं के बीच का समय है, किन्तु स्थिर संदर्भ | *∆t इन दो घटनाओं के बीच का समय है, किन्तु स्थिर संदर्भ निर्माण में मापा जाता है। | ||
*v गतिमान संदर्भ | *v गतिमान संदर्भ निर्माण की गति स्थिर के सापेक्ष है। | ||
*c [[प्रकाश की गति]] है। | *c [[प्रकाश की गति]] है। | ||
इसलिए कहा जाता है कि गतिमान वस्तुएँ समय की धीमी गति दर्शाती हैं। इसे समय फैलाव के रूप में जाना जाता है। | इसलिए कहा जाता है कि गतिमान वस्तुएँ समय की धीमी गति दर्शाती हैं। इसे समय फैलाव के रूप में जाना जाता है। | ||
ये परिवर्तन केवल दो | ये परिवर्तन केवल दो निर्माण के लिए निरंतर सापेक्ष वेग पर मान्य हैं। भोलेपन से उन्हें अन्य स्थितियों में लागू करने से जुड़वाँ [[विरोधाभास]] जैसे विरोधाभास उत्पन्न होते हैं। | ||
उस विरोधाभास को उदाहरण के लिए आइंस्टीन के सापेक्षता के सामान्य सिद्धांत का उपयोग करके हल किया जा सकता है, जो रिमेंनियन ज्यामिति का उपयोग करता है, त्वरित, अ-जड़त्वीय संदर्भ | उस विरोधाभास को उदाहरण के लिए आइंस्टीन के सापेक्षता के सामान्य सिद्धांत का उपयोग करके हल किया जा सकता है, जो रिमेंनियन ज्यामिति का उपयोग करता है, त्वरित, अ-जड़त्वीय संदर्भ निर्माण में ज्यामिति। मिंकोव्स्की स्थान का वर्णन करने वाले [[मीट्रिक टेंसर]] को नियोजित करना। | ||
:<math>\left[(dx^1)^2+(dx^2)^2+(dx^3)^2-c(dt)^2)\right],</math> | :<math>\left[(dx^1)^2+(dx^2)^2+(dx^3)^2-c(dt)^2)\right],</math> | ||
आइंस्टीन ने लोरेंत्ज़ के परिवर्तन के लिए ज्यामितीय समाधान विकसित किया जो मैक्सवेल के समीकरणों को संरक्षित करता है। उनके आइंस्टीन के क्षेत्र समीकरण दिक्-काल के दिए गए क्षेत्र में स्थान और समय के मापन और उस क्षेत्र के ऊर्जा घनत्व के बीच सटीक संबंध देते हैं। | आइंस्टीन ने लोरेंत्ज़ के परिवर्तन के लिए ज्यामितीय समाधान विकसित किया, जो मैक्सवेल के समीकरणों को संरक्षित करता है। उनके आइंस्टीन के क्षेत्र समीकरण दिक्-काल के दिए गए क्षेत्र में स्थान और समय के मापन और उस क्षेत्र के ऊर्जा घनत्व के बीच सटीक संबंध देते हैं। | ||
आइंस्टीन के समीकरण भविष्यवाणी करते हैं कि [[गुरुत्वाकर्षण क्षेत्र]] | आइंस्टीन के समीकरण भविष्यवाणी करते हैं कि [[गुरुत्वाकर्षण क्षेत्र]] की उपस्थिति से समय को बदलना चाहिए ([[श्वार्जस्चिल्ड मीट्रिक]] देखें): | ||
:<math>T=\frac{dt}{\sqrt{\left( 1 - \frac{2GM}{rc^2} \right ) dt^2 - \frac{1}{c^2}\left ( 1 - \frac{2GM}{rc^2} \right )^{-1} dr^2 - \frac{r^2}{c^2} d\theta^2 - \frac{r^2}{c^2} \sin^2 \theta \; d\phi^2}}</math> | :<math>T=\frac{dt}{\sqrt{\left( 1 - \frac{2GM}{rc^2} \right ) dt^2 - \frac{1}{c^2}\left ( 1 - \frac{2GM}{rc^2} \right )^{-1} dr^2 - \frac{r^2}{c^2} d\theta^2 - \frac{r^2}{c^2} \sin^2 \theta \; d\phi^2}}</math> | ||
जहाँ, | |||
:<math>T</math> की दूरी पर किसी वस्तु का गुरुत्वीय समय फैलाव है <math>r</math> | :<math>T</math> की दूरी पर किसी वस्तु का गुरुत्वीय समय फैलाव है <math>r</math> | ||
:<math>dt</math> समन्वय समय में परिवर्तन है, या समन्वय समय का अंतराल है। | :<math>dt</math> समन्वय समय में परिवर्तन है, या समन्वय समय का अंतराल है। | ||
| Line 196: | Line 195: | ||
:<math>\sqrt{\left( 1 - \frac{2GM}{rc^2} \right ) dt^2 - \frac{1}{c^2}\left ( 1 - \frac{2GM}{rc^2} \right )^{-1} dr^2 - \frac{r^2}{c^2} d\theta^2 - \frac{r^2}{c^2} \sin^2 \theta \; d\phi^2}</math> उचित समय में परिवर्तन है <math>d\tau</math>, या उचित समय का अंतराल। | :<math>\sqrt{\left( 1 - \frac{2GM}{rc^2} \right ) dt^2 - \frac{1}{c^2}\left ( 1 - \frac{2GM}{rc^2} \right )^{-1} dr^2 - \frac{r^2}{c^2} d\theta^2 - \frac{r^2}{c^2} \sin^2 \theta \; d\phi^2}</math> उचित समय में परिवर्तन है <math>d\tau</math>, या उचित समय का अंतराल। | ||
कोई निम्नलिखित सरल सन्निकटन का उपयोग कर सकता है। | |||
:<math>\frac{dt}{d\tau} = \frac{1}{ \sqrt{1 - \left( \frac{2GM}{rc^2} \right)}}. </math> | :<math>\frac{dt}{d\tau} = \frac{1}{ \sqrt{1 - \left( \frac{2GM}{rc^2} \right)}}. </math> | ||
अर्थात्, गुरुत्वाकर्षण क्षेत्र जितना मजबूत होता है | अर्थात्, गुरुत्वाकर्षण क्षेत्र जितना मजबूत होता है और इस प्रकार, [[त्वरण]] जितना बड़ा होता है, उतना ही धीरे-धीरे समय चलता है। [[कण त्वरक]] प्रयोगों और ब्रह्मांडीय किरण साक्ष्य द्वारा समय फैलाव की भविष्यवाणियों की पुष्टि की जाती है, जहां गतिमान कण अपने कम ऊर्जावान समकक्षों की तुलना में क्षय होते हैं। गुरुत्वीय समय फैलाव गुरुत्वाकर्षण लाल बदलाव की घटना को जन्म देता है और शापिरो सूरज जैसे बड़े पैमाने पर वस्तुओं के पास देरी करता है। [[ग्लोबल पोजिशनिंग सिस्टम|वैश्विक स्थिति निर्धारण प्रणाली]] को इस प्रभाव को ध्यान में रखते हुए संकेतों को भी समायोजित करना चाहिए। | ||
आइंस्टीन के सापेक्षता के सामान्य सिद्धांत के अनुसार, स्वतंत्र रूप से चलने वाला कण अंतरिक्ष-समय में ऐसे इतिहास का पता लगाता है जो अपने उचित समय को अधिकतम करता है। इस घटना को अधिकतम उम्र बढ़ने के सिद्धांत के रूप में भी जाना जाता है | आइंस्टीन के सापेक्षता के सामान्य सिद्धांत के अनुसार, स्वतंत्र रूप से चलने वाला कण अंतरिक्ष-समय में ऐसे इतिहास का पता लगाता है जो अपने उचित समय को अधिकतम करता है। इस घटना को अधिकतम उम्र बढ़ने के सिद्धांत के रूप में भी जाना जाता है और [[टेलर श्रृंखला|एडविन एफ टेलर]] और [[ जॉन आर्चीबाल्ड व्हीलर |जॉन आर्चीबाल्ड व्हीलर]] द्वारा वर्णित किया गया था।<ref>{{cite web | ||
|url=http://www.eftaylor.com/pub/chapter1.pdf | |url=http://www.eftaylor.com/pub/chapter1.pdf | ||
|last=Taylor | |last=Taylor | ||
| Line 210: | Line 209: | ||
}} | }} | ||
</ref> | </ref> | ||
:: | :: चरम जरण का सिद्धांत: अंतरिक्ष समय में दो घटनाओं के बीच मुक्त वस्तु जिस पथ को लेता है, वह वह पथ है जिसके लिए ऑब्जेक्ट की कलाई घड़ी पर अंकित इन घटनाओं के बीच का समय समाप्त हो जाता है। | ||
आइंस्टीन का सिद्धांत इस धारणा से प्रेरित था कि ब्रह्मांड में हर बिंदु को 'केंद्र' के रूप में माना जा सकता है | आइंस्टीन का सिद्धांत इस धारणा से प्रेरित था कि ब्रह्मांड में हर बिंदु को 'केंद्र' के रूप में माना जा सकता है और तदनुसार, भौतिकी को सभी संदर्भ निर्माण में समान कार्य करना चाहिए। उनके सरल और सुरुचिपूर्ण सिद्धांत से पता चलता है कि समय जड़त्वीय निर्माण के सापेक्ष है। जड़त्वीय निर्माण में न्यूटन का पहला नियम लागू होता है, इसकी अपनी स्थानीय ज्यामिति होती है और इसलिए स्थान और समय के अपने माप, कोई 'सार्वभौमिक घड़ी' नहीं है। कम से कम दो प्रणालियों के बीच तुल्यकालन का कार्य किया जाना चाहिए। | ||
=== क्वांटम यांत्रिकी में समय === | === क्वांटम यांत्रिकी में समय === | ||
{{see also| | {{see also|क्वांटम यांत्रिकी}} | ||
[[क्वांटम यांत्रिकी]] के समीकरणों में समय पैरामीटर है। श्रोडिंगर समीकरण<ref name="schrodinger">{{cite journal | last=Schrödinger | first=E. | author-link=Erwin Schrödinger| title=परमाणुओं और अणुओं के यांत्रिकी का एक लहरदार सिद्धांत| journal=[[Physical Review]] | publisher=American Physical Society (APS) | volume=28 | issue=6 | date=1 November 1926 | issn=0031-899X | doi=10.1103/physrev.28.1049 | pages=1049–1070| bibcode=1926PhRv...28.1049S }}</ref> है | [[क्वांटम यांत्रिकी]] के समीकरणों में समय पैरामीटर है। श्रोडिंगर समीकरण<ref name="schrodinger">{{cite journal | last=Schrödinger | first=E. | author-link=Erwin Schrödinger| title=परमाणुओं और अणुओं के यांत्रिकी का एक लहरदार सिद्धांत| journal=[[Physical Review]] | publisher=American Physical Society (APS) | volume=28 | issue=6 | date=1 November 1926 | issn=0031-899X | doi=10.1103/physrev.28.1049 | pages=1049–1070| bibcode=1926PhRv...28.1049S }}</ref> है | ||
| Line 222: | Line 221: | ||
उपाय हो सकता है | उपाय हो सकता है | ||
:<math> | \psi_e(t) \rangle = e^{-iHt / \hbar} | \psi_e(0) \rangle </math>. | :<math> | \psi_e(t) \rangle = e^{-iHt / \hbar} | \psi_e(0) \rangle </math>. | ||
जहाँ, <math> e^{-iHt / \hbar} </math>[[ समय विकास ऑपरेटर | समय विकास प्रचालक]] और एच [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] कहा जाता है। | |||
[[ समय विकास ऑपरेटर | समय विकास | |||
किन्तु ऊपर दिखाया गया श्रोडिंगर चित्र [[हाइजेनबर्ग चित्र]] के समतुल्य है, जो मौलिक यांत्रिकी के पॉइसन कोष्ठक के समान है। पोइसन कोष्ठकों को अ-शून्य [[कम्यूटेटर]] द्वारा अधिगृहीत किया जाता है, कहते हैं [एच, ए] देखने योग्य ए और हैमिल्टनियन एच के | किन्तु ऊपर दिखाया गया श्रोडिंगर चित्र [[हाइजेनबर्ग चित्र]] के समतुल्य है, जो मौलिक यांत्रिकी के पॉइसन कोष्ठक के समान है। पोइसन कोष्ठकों को अ-शून्य [[कम्यूटेटर]] द्वारा अधिगृहीत किया जाता है, कहते हैं [एच, ए] देखने योग्य ए और हैमिल्टनियन एच के लिए। | ||
:<math>\frac{d}{dt}A=(i\hbar)^{-1}[A,H]+\left(\frac{\partial A}{\partial t}\right)_\mathrm{classical}.</math> | :<math>\frac{d}{dt}A=(i\hbar)^{-1}[A,H]+\left(\frac{\partial A}{\partial t}\right)_\mathrm{classical}.</math> | ||
यह समीकरण क्वांटम भौतिकी में अनिश्चितता के सिद्धांत को दर्शाता है। उदाहरण के लिए, समय के साथ (देखने योग्य ए), | यह समीकरण क्वांटम भौतिकी में अनिश्चितता के सिद्धांत को दर्शाता है। उदाहरण के लिए, समय के साथ (देखने योग्य ए), ई हैमिल्टनियन एच से ऊर्जा देता है। | ||
:<math>\Delta E \Delta T \ge \frac{\hbar}{2} </math> | :<math>\Delta E \Delta T \ge \frac{\hbar}{2} </math> | ||
: | :जहाँ, | ||
:<math>\Delta E</math> ऊर्जा में अनिश्चितता है | :<math>\Delta E</math> ऊर्जा में अनिश्चितता है | ||
:<math>\Delta T</math> समय में अनिश्चितता है | :<math>\Delta T</math> समय में अनिश्चितता है | ||
:<math>\hbar</math> काष्ठफलक नियतांक है | :<math>\hbar</math> काष्ठफलक नियतांक है | ||
घटना की अवधि जितनी अधिक त्रुटिहीन और त्रुटिहीन से मापी जाती है, उतनी ही कम त्रुटिहीन से उस क्रम से जुड़ी ऊर्जा को मापा जा सकता है | घटना की अवधि जितनी अधिक त्रुटिहीन और त्रुटिहीन से मापी जाती है, उतनी ही कम त्रुटिहीन से उस क्रम से जुड़ी ऊर्जा को मापा जा सकता है और इसके विपरीत। यह समीकरण मानक अनिश्चितता सिद्धांत से भिन्न है, क्योंकि क्वांटम यांत्रिकी में समय [[ऑपरेटर (भौतिकी)|प्रचालक (भौतिकी)]] नहीं है। | ||
संबंधित कम्यूटेटर संबंध गति पी और स्थिति क्यू के लिए भी हैं, जो दूसरे के संयुग्मित चर हैं, साथ ही गति और स्थिति में इसी अनिश्चितता सिद्धांत के साथ, उपरोक्त ऊर्जा और समय संबंध के समान। | संबंधित कम्यूटेटर संबंध गति पी और स्थिति क्यू के लिए भी हैं, जो दूसरे के संयुग्मित चर हैं, साथ ही गति और स्थिति में इसी अनिश्चितता सिद्धांत के साथ, उपरोक्त ऊर्जा और समय संबंध के समान। | ||
क्वांटम यांत्रिकी [[रासायनिक तत्व]] की [[आवर्त सारणी]] के गुणों की व्याख्या करती है। चुंबकीय क्षेत्र में आणविक बीम के साथ [[ओटो स्टर्न]] और [[वाल्टर गेरलाच]] के प्रयोग से प्रारंभ, [[ इसीडोर रबी |इसीडोर रबी]] (1898-1988), बीम के चुंबकीय अनुनाद को संशोधित करने में सक्षम था। 1945 में रबी ने सुझाव दिया कि यह तकनीक घड़ी का आधार हो<ref name= sternGerlachRabi>[http://tf.nist.gov/timefreq/cesium/atomichistory.htm A Brief History of Atomic Clocks at NIST] {{Webarchive|url=https://web.archive.org/web/20090214125707/http://tf.nist.gov/timefreq/cesium/atomichistory.htm |date=2009-02-14 }}</ref> परमाणु किरण की [[गुंजयमान आवृत्ति]] का उपयोग | क्वांटम यांत्रिकी [[रासायनिक तत्व]] की [[आवर्त सारणी]] के गुणों की व्याख्या करती है। चुंबकीय क्षेत्र में आणविक बीम के साथ [[ओटो स्टर्न]] और [[वाल्टर गेरलाच]] के प्रयोग से प्रारंभ, [[ इसीडोर रबी |इसीडोर रबी]] (1898-1988), बीम के चुंबकीय अनुनाद को संशोधित करने में सक्षम था। 1945 में रबी ने सुझाव दिया कि यह तकनीक घड़ी का आधार हो<ref name= sternGerlachRabi>[http://tf.nist.gov/timefreq/cesium/atomichistory.htm A Brief History of Atomic Clocks at NIST] {{Webarchive|url=https://web.archive.org/web/20090214125707/http://tf.nist.gov/timefreq/cesium/atomichistory.htm |date=2009-02-14 }}</ref> परमाणु किरण की [[गुंजयमान आवृत्ति]] का उपयोग करना।बोल्डर कोलोराडो में जेआईएलए के 2021 जून में, ये स्ट्रोंटियम परमाणुओं के बादल के शीर्ष पर प्रकाशीय जाली घड़ी की टिक की दर में अंतर में [[समय फैलाव]] देखा गया, उस बादल के नीचे की तुलना में मिलीमीटर लंबा स्तंभ प्रभाव के अनुसार गुरुत्वाकर्षण है।<ref name= jilaYe> [https://science.slashdot.org/story/21/10/25/1646249/an-ultra-precise-clock-shows-how-to-link-the-quantum-world-with-gravity Slashdot (25 Oct 2021) An Ultra-Precise Clock Shows How To Link the Quantum World With Gravity] Jun Ye's work at JILA</ref> | ||
| Line 246: | Line 243: | ||
[[[[गतिशील प्रणाली]] और [[अराजकता सिद्धांत]]]], [[ विघटनकारी संरचनाएं |विघटनकारी संरचनाएं]] देखें | [[[[गतिशील प्रणाली]] और [[अराजकता सिद्धांत]]]], [[ विघटनकारी संरचनाएं |विघटनकारी संरचनाएं]] देखें | ||
कोई कह सकता है कि समय गतिशील प्रणाली का [[मानकीकरण]] है जो | कोई कह सकता है कि समय गतिशील प्रणाली का [[मानकीकरण]] है, जो प्रणाली की ज्यामिति को प्रकट और संचालित करने की अनुमति देता है। यह प्रमाणित किया गया है कि समय कैओस सिद्धांत अर्थात अ-रैखिकता/[[अपरिवर्तनीयता]] का निहित परिणाम है। प्रणाली की [[विशेषता समय]], [[सूचना एन्ट्रापी]] उत्पादन की दर बेनोइट मंडेलब्रॉट ने अपनी पुस्तक बहु भग्नऔर 1/f शोर में [[आंतरिक समय]] का परिचय दिया। | ||
=== समय क्रिस्टल === | === समय क्रिस्टल === | ||
{{See| | {{See|समय क्रिस्टल}} | ||
खेमानी, मोएसनर और सोंधी समय क्रिस्टल को स्थिर, रूढ़िवादी, स्थूल घड़ी के रूप में परिभाषित करते हैं।<ref name=kms2019>Vedika Khemani, Roderich Moessner, and S. L. Sondhi [https://arxiv.org/pdf/1910.10745.pdf (23 Oct 2019) A Brief History of Time Crystals]</ref> | खेमानी, मोएसनर और सोंधी समय क्रिस्टल को स्थिर, रूढ़िवादी, स्थूल घड़ी के रूप में परिभाषित करते हैं।<ref name=kms2019>Vedika Khemani, Roderich Moessner, and S. L. Sondhi [https://arxiv.org/pdf/1910.10745.pdf (23 Oct 2019) A Brief History of Time Crystals]</ref> | ||
== | == संकेतन == | ||
संकेतन ऊपर वर्णित [[विद्युत चुम्बकीय तरंग]] का अनुप्रयोग है। सामान्यतः, संकेत पार्टियों और स्थानों के बीच [[संचार]] का भाग होता है। उदाहरण पेड़ से बंधा [[पीला रिबन]], [[चर्च की घंटी]] बजना हो सकता है। संकेत [[बातचीत]] का भाग हो सकता है, जिसमें [[संचार प्रोटोकॉल|संचार प्रोटोपुकारना]] सम्मलित होता है और संकेत शहर की घड़ी, रेलवे स्टेशन पर घंटे की सुई की स्थिति हो सकती है। इच्छुक पार्टी समय जानने के लिए उस घड़ी को देखने की इच्छा कर सकती है। देखें: समय [[टाइम बॉल|बॉल]], [[ समय संकेत |समय संकेत]] का प्रारंभिक रूप। | |||
[[File:Lorentz transform of world line.gif|thumb|left|त्वरित विशाल कण की विश्व रेखा का विकास। यह विश्व रेखा इस दिक्-समय के आंकड़े के समय-समान शीर्ष और निचले वर्गों तक ही सीमित है; यह विश्व रेखा शीर्ष ([[भविष्य]]) या नीचे ([[अतीत]]) [[प्रकाश शंकु]] को पार नहीं कर सकती है। बाएँ और दाएँ खंड (जो प्रकाश शंकु के बाहर हैं) [[ spacelike |spacelike]] हैं।]]जब तक हम उनके पिछले प्रकाश शंकु के भीतर रहते हैं, तब तक हम पर्यवेक्षक के रूप में विभिन्न दलों और स्थानों को संकेत दे सकते हैं। किन्तु हम अपने पिछले प्रकाश शंकु के बाहर उन दलों और स्थानों से संकेत प्राप्त नहीं कर सकते। | [[File:Lorentz transform of world line.gif|thumb|left|त्वरित विशाल कण की विश्व रेखा का विकास। यह विश्व रेखा इस दिक्-समय के आंकड़े के समय-समान शीर्ष और निचले वर्गों तक ही सीमित है; यह विश्व रेखा शीर्ष ([[भविष्य]]) या नीचे ([[अतीत]]) [[प्रकाश शंकु]] को पार नहीं कर सकती है। बाएँ और दाएँ खंड (जो प्रकाश शंकु के बाहर हैं) [[ spacelike |spacelike]] हैं।]]जब तक हम उनके पिछले प्रकाश शंकु के भीतर रहते हैं, तब तक हम पर्यवेक्षक के रूप में विभिन्न दलों और स्थानों को संकेत दे सकते हैं। किन्तु हम अपने पिछले प्रकाश शंकु के बाहर उन दलों और स्थानों से संकेत प्राप्त नहीं कर सकते। | ||
विद्युत चुम्बकीय तरंग के लिए समीकरणों के निर्माण के साथ-साथ [[दूरसंचार]] के क्षेत्र की स्थापना की जा सकती है। | विद्युत चुम्बकीय तरंग के लिए समीकरणों के निर्माण के साथ-साथ [[दूरसंचार]] के क्षेत्र की स्थापना की जा सकती है। | ||
19वीं शताब्दी में [[टेलीग्राफी]], विद्युत परिपथ, कुछ फैले हुए [[महाद्वीप]] और [[महासागर]], [[कोड]] - सरल बिंदु, डैश और रिक्त स्थान संचारित कर सकते थे। इससे, | 19वीं शताब्दी में [[टेलीग्राफी]], विद्युत परिपथ, कुछ फैले हुए [[महाद्वीप]] और [[महासागर]], [[कोड]] - सरल बिंदु, डैश और रिक्त स्थान संचारित कर सकते थे। इससे, प्राविधिक समस्याएँ की श्रृंखला सामने आई है, देखें :श्रेणी वर्णनात्मकता। किन्तु यह कहना सुरक्षित है कि हमारे संकेतन प्रणाली केवल लगभग समकालीकरण हो सकते हैं, [[प्लेसिओक्रोनस]] स्थिति, जिससे घबराहट को समाप्त करने की आवश्यकता होती है। | ||
उस ने कहा, [[ GPS | | उस ने कहा, [[ GPS |जीपीएस]] जैसी तकनीकों का उपयोग करके प्रणाली को समकालीकरण किया जा सकता है। अभियंतािंग सन्निकटन पर जीपीएस उपग्रहों को उनके सर्किटरी में गुरुत्वाकर्षण और अन्य सापेक्ष कारकों के प्रभाव के लिए जिम्मेदार होना चाहिए। देखें: [[सेल्फ क्लॉकिंग सिग्नल|स्व घड़ी संकेत]] | ||
== समयनिर्धारक मानकों के लिए प्रौद्योगिकी == | == समयनिर्धारक मानकों के लिए प्रौद्योगिकी == | ||
अमेरिका में [[प्राथमिक समय मानक]] वर्तमान में [[NIST-F1]] | अमेरिका में [[प्राथमिक समय मानक]] वर्तमान में [[NIST-F1|एनआईएसटी-एफ1]] है। [[लेजर]]-ठंडा सीज़ियम फव्वारा है।<ref>D. M. Meekhof, S. R. Jefferts, M. Stepanovíc, and T. E. Parker (2001) "Accuracy Evaluation of a Cesium Fountain Primary Frequency Standard at NIST", ''IEEE Transactions on Instrumentation and Measurement''. '''50''', no. 2, (April 2001) pp. 507-509</ref> [[अमोनिया]]-आधारित परमाणु घड़ी (1949) से सीज़ियम-आधारित एनबीएस-1 (1952) से एनआईएसटी-7 (1993) तक, समय और आवृत्ति मानकों की श्रृंखला में नवीनतम। संबंधित घड़ी की अनिश्चितता 5 दशकों में प्रति दिन 10,000 नैनोसेकंड से घटकर 0.5 नैनोसेकंड प्रति दिन हो गई।<ref>James Jespersen and Jane Fitz-Randolph (1999). ''From sundials to atomic clocks : understanding time and frequency''. Washington, D.C. : U.S. Dept. of Commerce, Technology Administration, National Institute of Standards and Technology. 308 p. : ill. ; 28 cm. | ||
{{ISBN|0-16-050010-9}}</ref> 2001 में | {{ISBN|0-16-050010-9}}</ref> 2001 में एनआईएसटी-एफ1 के लिए घड़ी की अनिश्चितता 0.1 नैनोसेकंड/दिन थी। तेजी से सटीक आवृत्ति मानकों का विकास चल रहा है। | ||
इस समय [[और]] आवृत्ति मानक में, सीज़ियम परमाणुओं की आबादी को [[माइक्रोकेल्विन]] के तापमान तक लेज़र- | इस समय [[और]] आवृत्ति मानक में, सीज़ियम परमाणुओं की आबादी को [[माइक्रोकेल्विन]] के तापमान तक लेज़र-ठंडा किया जाता है। परमाणु छह लेज़रों द्वारा आकार की गेंद में त्रित होते हैं, प्रत्येक स्थानिक आयाम के लिए दो, लंबवत (ऊपर/नीचे), क्षैतिज (बाएं/दाएं) और आगे/पीछे ऊर्ध्वाधर लेज़र सीज़ियम बॉल को माइक्रोवेव गुहा के माध्यम से धकेलते हैं। जैसे ही गेंद को ठंडा किया जाता है, सीज़ियम की आबादी अपनी मूलभूत अवस्था में ठंडी हो जाती है और ऊपर की दूसरी परिभाषा में बताई गई अपनी प्राकृतिक आवृत्ति पर प्रकाश का उत्सर्जन करती है। सीज़ियम आबादी से उत्सर्जन में ग्यारह भौतिक प्रभावों का हिसाब लगाया जाता है, जिन्हें एनआईएसटी-एफ1 घड़ी में नियंत्रित किया जाता है। ये परिणाम [[ बीपं |बीपं]] को प्रतिवेदन किए गए हैं। | ||
इसके अतिरिक्त, संदर्भ मेसर | इसके अतिरिक्त, संदर्भ मेसर हाइड्रोजन मेसर भी [[अंतर्राष्ट्रीय परमाणु समय]] के लिए आवृत्ति मानक के रूप में बीआईपीएम को प्रतिवेदन किया जाता है। | ||
सेवरेस, फ्रांस में स्थित बीआईपीएम ( | सेवरेस, फ्रांस में स्थित बीआईपीएम (अंतरराष्ट्रीय विभाग डेस पॉयड्स एट मेसर्स) द्वारा समय की माप की देखरेख की जाती है, जो माप की रूपता और दुनिया भर में अंतरराष्ट्रीय प्रणाली इकाइयों से बाहर (एसआई) के लिए उनकी पता लगाने की क्षमता सुनिश्चित करता है। बीआईपीएम परामर्शदात्री समितियों की श्रृंखला के माध्यम से, इक्यावन देशों, सम्मेलन के सदस्य राज्यों के बीच राजनयिक संधि, [[मीटर कन्वेंशन|मीटर सम्मेलनन]] के अधिकार के अनुसार संचालित होता है, जिसके सदस्य संबंधित राष्ट्रीय [[ मैट्रोलोजी |मैट्रोलोजी]] प्रयोगशालाएं हैं। | ||
== ब्रह्माण्ड विज्ञान में समय == | == ब्रह्माण्ड विज्ञान में समय == | ||
{{main| | {{main|भौतिक ब्रह्मांड विज्ञान}} | ||
[[सामान्य सापेक्षता]] के समीकरण गैर स्थैतिक ब्रह्मांड की भविष्यवाणी करते हैं। चूंकि, आइंस्टीन ने केवल स्थिर ब्रह्मांड को स्वीकार किया | [[सामान्य सापेक्षता]] के समीकरण गैर स्थैतिक ब्रह्मांड की भविष्यवाणी करते हैं। चूंकि, आइंस्टीन ने केवल स्थिर ब्रह्मांड को स्वीकार किया और ब्रह्मांडीय स्थिरांक को जोड़कर इसे प्रतिबिंबित करने के लिए आइंस्टीन क्षेत्र समीकरण को संशोधित किया, जिसे उन्होंने बाद में अपने जीवन की सबसे बड़ी गलती बताया। किन्तु 1927 में, जॉर्जेस लेमेत्रे (1894-1966) ने सामान्य सापेक्षता के आधार पर तर्क दिया कि ब्रह्मांड की उत्पत्ति प्रारंभिक विस्फोट में हुई थी। उस साल पांचवें सॉल्वे सम्मेलन में, आइंस्टीन ने उन्हें खारिज कर दिया <ref>John C. Mather and John Boslough (1996), ''The Very First Light'' {{ISBN|0-465-01575-1}} p. 41.</ref> "आपका गणित सही है, किन्तु आपका भौतिकी घृणित है"। 1929 में, [[एडविन हबल]] (1889-1953) ने विस्तारित ब्रह्मांड की अपनी खोज की घोषणा की। वर्तमान सामान्यतः स्वीकृत ब्रह्माण्ड संबंधी मॉडल, [[लैम्ब्डा-सीडीएम मॉडल]] में सकारात्मक ब्रह्माण्ड संबंधी स्थिरांक है और इस प्रकार न केवल विस्तारित ब्रह्मांड बल्कि त्वरित विस्तार करने वाला ब्रह्मांड है। | ||
यदि ब्रह्मांड का विस्तार हो रहा था, तो यह अतीत में बहुत छोटा और इसलिए अधिक गर्म और सघन रहा होगा। [[जॉर्ज गैमोव]] (1904-1968) ने परिकल्पना की कि तत्वों की आवर्त सारणी में तत्वों की प्रचुरता, गर्म घने ब्रह्मांड में परमाणु प्रतिक्रियाओं के कारण हो सकती है। वह [[फ्रेड हॉयल]] (1915-2001) द्वारा विवादित था, जिसने इसे नापसंद करने के लिए 'बिग बैंग' शब्द का आविष्कार किया था। [[एनरिको फर्मी]] और अन्य ने नोट किया कि केवल प्रकाश तत्वों के बनने के बाद ही यह प्रक्रिया बंद हो गई होगी | यदि ब्रह्मांड का विस्तार हो रहा था, तो यह अतीत में बहुत छोटा और इसलिए अधिक गर्म और सघन रहा होगा। [[जॉर्ज गैमोव]] (1904-1968) ने परिकल्पना की कि तत्वों की आवर्त सारणी में तत्वों की प्रचुरता, गर्म घने ब्रह्मांड में परमाणु प्रतिक्रियाओं के कारण हो सकती है। वह [[फ्रेड हॉयल]] (1915-2001) द्वारा विवादित था, जिसने इसे नापसंद करने के लिए 'बिग बैंग' शब्द का आविष्कार किया था। [[एनरिको फर्मी]] और अन्य ने नोट किया कि केवल प्रकाश तत्वों के बनने के बाद ही यह प्रक्रिया बंद हो गई होगी और इस प्रकार भारी तत्वों की प्रचुरता का हिसाब नहीं दिया। | ||
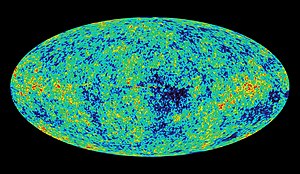
[[File:WMAP.jpg|thumb|right|[[ब्रह्मांडीय माइक्रोवेव पृष्ठभूमि विकिरण]] के [[WMAP]] उतार-चढ़ाव<ref>[[George Smoot]] and Keay Davidson (1993) ''[[Wrinkles in Time]]'' {{ISBN|0-688-12330-9}} A memoir of the experiment program for detecting the predicted fluctuations in the [[cosmic microwave background radiation]].</ref>]]विस्तार के पर्यन्त ठंडा होने के बाद, गैमो की भविष्यवाणी ब्रह्मांड के लिए 5-10-[[केल्विन]] [[ श्याम पिंडों से उत्पन्न विकिरण |श्याम पिंडों से उत्पन्न विकिरण]] तापमान थी। [[ब्रह्मांडीय माइक्रोवेव पृष्ठभूमि विकिरण की खोज]] की खोज द्वारा इसकी पुष्टि की गई थी। इसके बाद के प्रयोग 2.7 केल्विन तापमान पर पहुंचे, जो कि बिग बैंग के 13.8 बिलियन वर्ष बाद [[ब्रह्मांड की आयु]] के अनुरूप है। | [[File:WMAP.jpg|thumb|right|[[ब्रह्मांडीय माइक्रोवेव पृष्ठभूमि विकिरण]] के [[WMAP]] उतार-चढ़ाव<ref>[[George Smoot]] and Keay Davidson (1993) ''[[Wrinkles in Time]]'' {{ISBN|0-688-12330-9}} A memoir of the experiment program for detecting the predicted fluctuations in the [[cosmic microwave background radiation]].</ref>]]विस्तार के पर्यन्त ठंडा होने के बाद, गैमो की भविष्यवाणी ब्रह्मांड के लिए 5-10-[[केल्विन]] [[ श्याम पिंडों से उत्पन्न विकिरण |श्याम पिंडों से उत्पन्न विकिरण]] तापमान थी। [[ब्रह्मांडीय माइक्रोवेव पृष्ठभूमि विकिरण की खोज]] की खोज द्वारा इसकी पुष्टि की गई थी। इसके बाद के प्रयोग 2.7 केल्विन तापमान पर पहुंचे, जो कि बिग बैंग के 13.8 बिलियन वर्ष बाद [[ब्रह्मांड की आयु]] के अनुरूप है। | ||
इस नाटकीय परिणाम ने | इस नाटकीय परिणाम ने समस्याएँ को उठाया है। बिग बैंग और काष्ठफलक समय की विलक्षणता के बीच क्या हुआ, जो कि सबसे छोटा अवलोकन योग्य समय है। जब [[स्पेसटाइम फोम|अंतरिक्ष समय फोम]] से समय अलग हो सकता है,<ref>[[Martin Rees]] (1997), ''Before the Beginning'' {{ISBN|0-201-15142-1}} p. 210.</ref> केवल टूटी हुई समरूपता पर आधारित संकेत हैं (देखें स्वतःस्फूर्त समरूपता ब्रेकिंग, [[बिग बैंग की समयरेखा]], और लेख:श्रेणी:भौतिक ब्रह्मांड विज्ञान)। | ||
सामान्य सापेक्षता ने हमें विस्तारित ब्रह्मांड की हमारी आधुनिक धारणा दी जो बिग बैंग में प्रारंभ हुई थी। सापेक्षता और क्वांटम सिद्धांत का उपयोग करके हम मोटे तौर पर ब्रह्मांड के इतिहास का पुनर्निर्माण करने में सक्षम हुए हैं। ब्रह्मांड के हमारे युग में | सामान्य सापेक्षता ने हमें विस्तारित ब्रह्मांड की हमारी आधुनिक धारणा दी जो बिग बैंग में प्रारंभ हुई थी। सापेक्षता और क्वांटम सिद्धांत का उपयोग करके हम मोटे तौर पर ब्रह्मांड के इतिहास का पुनर्निर्माण करने में सक्षम हुए हैं। ब्रह्मांड के हमारे युग में जिसके पर्यन्त विद्युत चुम्बकीय तरंगें संवाहक आवेशों द्वारा परेशान किए अतिरिक्त फैल सकती हैं, हम रात के आकाश में हमसे बड़ी दूरी पर तारे देख सकते हैं। इस युग से पहले बिग बैंग के लगभग 377,000 वर्षों के बाद, इलेक्ट्रॉनों और नाभिकों को परमाणुओं में संयोजित करने के लिए ब्रह्मांड के पर्याप्त ठंडा होने से पहले समय था, जिसके पर्यन्त बड़ी दूरी पर तारों का प्रकाश दिखाई नहीं देता था। | ||
== रीप्राइज़ == | == रीप्राइज़ == | ||
इल्या प्रोगोगाइन का आश्चर्य समय से पहले का [[अस्तित्व]] है। न्यूटन, आइंस्टीन और क्वांटम भौतिकी के विचारों के विपरीत | इल्या प्रोगोगाइन का आश्चर्य समय से पहले का [[अस्तित्व]] है। न्यूटन, आइंस्टीन और क्वांटम भौतिकी के विचारों के विपरीत जो समय के सममित दृष्टिकोण की प्रस्तुत करते हैं, जैसा कि ऊपर चर्चा की गई है। प्रोगोगाइन बताते हैं कि सांख्यिकीय और ऊष्मप्रवैगिकी भौतिकी [[अपरिवर्तनीय प्रक्रिया]] के साथ ही समय का तीर और बिग बैंग की व्याख्या कर सकते हैं।<ref>Prigogine, Ilya (1996), ''The End of Certainty: Time, Chaos and the New Laws of Nature''. {{ISBN|0-684-83705-6}} On pages 163 and 182.</ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[सापेक्ष गतिकी]] | * [[सापेक्ष गतिकी]] | ||
* [[खगोल विज्ञान में समय]] | * [[खगोल विज्ञान में समय]] | ||
| Line 306: | Line 302: | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
*{{Commonscat-inline}} | *{{Commonscat-inline}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Commons category link is the pagename]] | |||
[[Category: | |||
[[Category:Created On 02/03/2023]] | [[Category:Created On 02/03/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Translated in Hindi]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:भौतिक विज्ञान में समय| भौतिक विज्ञान में समय ]] | |||
[[Category:भौतिकी का दर्शन]] | |||
Latest revision as of 10:22, 15 March 2023
| Time |
|---|
 |
| Current time (update) |
| 07:01, 23 November 2024 (UTC) |

भौतिकी में समय को इसकी क्रियात्मक परिभाषा द्वारा परिभाषित किया जाता है। समय वह है जो घड़ी पढ़ती है।[1] चिरसम्मत सापेक्ष भौतिकी में यह अदिश (भौतिकी) मात्रा है, अधिकांशतः प्रतीक ( ) द्वारा निरूपित लंबाई, द्रव्यमान और विद्युत आवेश के प्रकार सामान्यतः मौलिक मात्रा के रूप में वर्णित किया जाता है। गति (भौतिकी), गतिज ऊर्जा और समय पर निर्भर क्षेत्र (भौतिकी) जैसी अन्य अवधारणाओं के औपचारिक प्रमाण के लिए समय को गणितीय रूप से अन्य भौतिक राशियों के साथ जोड़ा जा सकता है। समयनिर्धारक और रिकॉर्ड रखना प्राविधिक वैज्ञानिक समस्याएँ की नींव का जटिल भाग है।
समय के निशान
घड़ियाँ होने से पहले समय को उन भौतिक प्रक्रियाओं द्वारा मापा जाता था,[2] जो सभ्यता के प्रत्येक युग के लिए समझ में आते थे।[3]
प्रत्येक वर्ष नील नदी में आई बाढ़ को चिह्नित करने के लिए सीरियस की पहली उपस्थिति देखें: हेलियाकल बढ़ रहा है ।[3]
- रात और दिन का आवधिक उत्तराधिकार, अनंत काल तक प्रतीत होता है[4]
- भोर में सूर्य की पहली उपस्थिति के क्षितिज पर स्थिति[5]
- आकाश में सूर्य की स्थिति[6]
- दिन के पर्यन्त दोपहर के क्षण का अंकन[7]
- सूक्ति द्वारा डाली गई छाया की लंबाई [8]
अंततः [9][10] परिचालन परिभाषाओं का उपयोग करते हुए, साधनविनियोग के साथ समय बीतने को चिह्नित करना संभव हो गया। इसके साथ ही समय की हमारी अवधारणा विकसित हुई है, जैसा कि नीचे दिखाया गया है।[11]
समय की माप की इकाई: दूसरा
इकाइयों की अंतर्राष्ट्रीय प्रणाली (एसआई) में, समय की इकाई दूसरी है (प्रतीक: )। यह एसआई आधार इकाई है और 1967 से इसकी अवधि के रूप में परिभाषित किया गया है। 9,192,631,770 सीज़ियम 133 परमाणु की मूलभूत अवस्था के दो अति सूक्ष्म संरचना के बीच संक्रमण के अनुरूप विकिरण का चक्र।[12] यह परिभाषा सीज़ियम परमाणु घड़ी के संचालन पर आधारित है। ये घड़ियाँ लगभग 1955 के बाद प्राथमिक संदर्भ मानकों के रूप में उपयोग के लिए व्यावहारिक हो गईं और तब से उपयोग में हैं।
समयनिर्धारक में कला की स्थिति
दुनिया भर में उपयोग में आने वाला समन्वित सार्वभौमिक समय टाइम स्टैम्प परमाणु समय मानक है। ऐसे समय मानक की सापेक्ष त्रुटिहीन वर्तमान में 10-15 के क्रम में है[13] लगभग 30 मिलियन वर्षों में 1 सेकंड के अनुरूप। सैद्धांतिक रूप से देखने योग्य माना जाने वाला सबसे छोटा समय चरण काष्ठफलक समय कहलाता है, जो लगभग 5.391×10 है−44 सेकेंड - वर्तमान समय मानकों के संकल्प के नीचे परिमाण के कई आदेश है।
1950 के बाद सीज़ियम परमाणु घड़ी व्यावहारिक हो गई, जब इलेक्ट्रॉनिक्स में प्रगति ने इसे उत्पन्न होने वाली माइक्रोवेव आवृत्तियों के विश्वसनीय माप को सक्षम किया। जैसे-जैसे आगे की प्रगति हुई। परमाणु घड़ी अनुसंधान उच्च-उच्च आवृत्तियों की ओर बढ़ गया है, जो उच्च त्रुटिहीन और उच्च त्रुटिहीन प्रदान कर सकता है। इन तकनीकों पर आधारित घड़ियाँ विकसित की गई हैं, किन्तु अभी तक प्राथमिक संदर्भ मानकों के रूप में उपयोग में नहीं हैं।
समय की अवधारणा

गैलीलियो, आइजैक न्यूटन और 20वीं शताब्दी तक अधिकांश लोगों का मानना था कि समय हर किसी के लिए समान है। यह श्रेणी: समयबद्धता का आधार है, जहां समय पैरामीटर है। समय की आधुनिक समझ अल्बर्ट आइंस्टीन के सापेक्षता के सिद्धांत पर आधारित है, जिसमें समय की दरें सापेक्ष गति के आधार पर अलग-अलग चलती हैं और अंतरिक्ष और समय को अंतरिक्ष समय में मिला दिया जाता है, जहां हम समयरेखा के अतिरिक्त विश्व रेखा पर रहते हैं। इस दृष्टि से समय समन्वय है। प्रचलित भौतिक ब्रह्माण्ड विज्ञान के अनुसार महा विस्फोट सिद्धांत के वैज्ञानिक प्रतिरूपण के अनुसार लगभग 13.8 अरब वर्ष पहले पूरे ब्रह्मांड के भागों के रूप में समय की प्रारंभिक हुई।
प्रकृति में नियमितता
समय को मापने के लिए कोई आवधिक कार्य घटना की घटनाओं की संख्या रिकॉर्ड कर सकता है। ऋतुओं की नियमित पुनरावृत्ति, सूर्य, चंद्रमा और तारों की गति भौतिकी को सहस्राब्दी के लिए नोट किया गया और सारणीबद्ध किया गया। इससे पहले कि भौतिकी के नियम तैयार किए गए। सूर्य समय के प्रवाह का मध्यस्थ था, किन्तु सहस्राब्दी के लिए समय केवल घंटे के लिए जाना जाता था, इसलिए सूक्ति का उपयोग दुनिया के अधिकांश भागों में विशेष रूप से यूरेशिया और कम से कम दक्षिण की ओर जंगलों के रूप में जाना जाता था। दक्षिण - पूर्व एशिया[15]विशेष रूप से धार्मिक उद्देश्यों के लिए बनाए गए खगोलीय वेधशालाएं सितारों और यहां तक कि कुछ ग्रहों की नियमित गति का पता लगाने के लिए पर्याप्त सटीक हो गईं।
सबसे पहले पुजारियों द्वारा समय-निर्धारण हाथ से किया जाता था और फिर वाणिज्य के लिए पहरेदारों के साथ अपने कर्तव्यों के भागों के रूप में समय नोट करने के लिए। विषुव, समुद्री बालूघड़ी और जल घड़ी का सारणीकरण अधिक से अधिक सटीक और अंत में विश्वसनीय हो गया। समुद्र में जहाजों के लिए लड़कों का उपयोग समुद्री बालूघड़ी को घुमाने और घंटों को पुकारना करने के लिए किया जाता था।
यांत्रिक घड़ियाँ
वॉलिंगफोर्ड के रिचर्ड (1292–1336), सेंट अल्बंस एब्बे के मठाधीश, प्रसिद्ध रूप से 1330 के आसपास खगोलीय कक्ष के रूप में घड़ी पूरी प्रकार से यांत्रिक बनाया।[16][17]वालिंगफोर्ड के रिचर्ड के समय तक, शाफ़्ट (उपकरण) और गियर के उपयोग ने यूरोप के शहरों को अपने संबंधित शहर की घड़ियों पर समय प्रदर्शित करने के लिए तंत्र बनाने की अनुमति दी। वैज्ञानिक क्रांति के समय तक घड़ियाँ इतनी छोटी हो गईं कि परिवार व्यक्तिगत घड़ी, संभवतः जेब घड़ी साझा कर सकें। पहले केवल राजा ही उन्हें वहन कर सकते थे। 18वीं और 19वीं शताब्दी में पेंडुलम घड़ियों का व्यापक रूप से उपयोग किया जाता था। वे सामान्य उपयोग में बड़े पैमाने पर क्वार्ट्ज-घड़ी और डिजिटल घड़ियों द्वारा प्रतिस्थापित किए गए हैं। परमाणु घड़ियाँ सैद्धांतिक रूप से लाखों वर्षों तक सटीक समय रख सकती हैं। वे मानकीकरण और वैज्ञानिक उपयोग के लिए उपयुक्त हैं।
गैलीलियो: समय का प्रवाह
1583 में, गैलीलियो गैलीली (1564-1642) ने पाया कि हार्मोनिक ऑसिलेटर पेंडुलम की हार्मोनिक गति की निरंतर अवधि होती है, जिसे उन्होंने पीसा के कैथेड्रल में मास (लिटुरजी) में सरल हार्मोनिक गति में लहराते दीपक की गति के समय उसकी नाड़ी के साथ से सीखा।[18]अपने दो नए विज्ञान (1638) में गैलीलियो गैलीली ने झुकाव वाले विमान के नीचे ज्ञात दूरी को रोल करने के लिए कांस्य गेंद के लिए लगने वाले समय को मापने के लिए पानी की घड़ी का उपयोग किया, यह घड़ी थी।[19]
पानी का बड़ा पात्र जिसे ऊँचे स्थान पर रखा गया है, इस बर्तन के तल में पानी की पतली धारा देने वाले छोटे व्यास का पाइप मिलाप किया गया था, जिसे हमने प्रत्येक वंश के समय छोटे गिलास में एकत्र किया। चाहे वह चैनल की पूरी लंबाई के लिए हो या उसकी लंबाई के भागों के लिए इस प्रकार त्र किए गए पानी को प्रत्येक अवतरण के बाद बहुत ही सटीक संतुलन पर तौला गया था। इन भारों के अंतर और अनुपात ने हमें समय के अंतर और अनुपात दिए और यह इतनी त्रुटिहीन के साथ कि चूंकि ऑपरेशन को कई बार दोहराया गया, परिणामों में कोई सराहनीय विसंगति नहीं थी।
शाब्दिक दो नए विज्ञानों को मापने के लिए गैलीलियो का प्रायोगिक परिस्थिति समय का प्रवाह, गेंद की गति का वर्णन करने के लिए है। इसहाक न्यूटन के अपने फिलोसोफी नेचुरेलिस प्रिन्सिपिया मैथेमेटिका में बयान से पहले, मैं समय, स्थान (भूगोल) और को परिभाषित नहीं करता गति (भौतिकी), जैसा कि सभी जानते हैं।[20]गैलिलियन परिवर्तन मानते हैं कि संदर्भ के सभी निर्माण के लिए समय समान है।
न्यूटन की भौतिकी: रैखिक समय
1665 में उसके आसपास जब आइजैक न्यूटन (1643-1727) ने गुरुत्वाकर्षण के अनुसार गिरने वाली वस्तुओं की गति को व्युत्पन्न किया, समय के उपचार के गणितीय भौतिकी के लिए पहला स्पष्ट सूत्रीकरण प्रारंभ हुआ। रैखिक समय, सार्वभौमिक घड़ी के रूप में माना गया।
निरपेक्ष, सत्य और गणितीय समय, स्वयं का और अपनी प्रकृति से समान रूप से बहता है अतिरिक्त किसी बाहरी चीज़ की देख-भाल किए और दूसरे नाम से अवधि कहा जाता है। सापेक्ष, स्पष्ट और सामान्य समय कुछ समझदार और बाहरी है चाहे सटीक या असमान गति के माध्यम से अवधि का माप, जो सामान्यतः वास्तविक समय के अतिरिक्त प्रयोग किया जाता है। जैसे घंटा, दिन, महीना, साल।[21]
गैलीलियो द्वारा वर्णित जल घड़ी तंत्र को प्रयोगों के पर्यन्त पानी के लामिनार प्रवाह प्रदान करने के लिए अभियंता किया गया था, इस प्रकार प्रयोगों की अवधि के लिए पानी का निरंतर प्रवाह प्रदान किया गया था और जिसे न्यूटन ने अवधि कहा था।
इस खंड में नीचे सूचीबद्ध संबंध समय को पैरामीटर के रूप में मानते हैं, जो विचाराधीन भौतिक प्रणाली के व्यवहार के लिए सूचकांक के रूप में कार्य करता है। क्योंकि न्यूटन के धाराप्रवाह (गणित) समय के रैखिक प्रवाह जिसे उन्होंने गणितीय समय कहा जाता है, समय को रैखिक रूप से भिन्न पैरामीटर माना जा सकता है। घड़ी के चेहरे पर घंटों के मार्च का सार कैलेंडर और जहाज के लॉग को घंटे, दिन, महीने, साल और सदियों के मार्च में मानचित्र किया जा सकता है।
ऊष्मप्रवैगिकी और अपरिवर्तनीयता का विरोधाभास
1798 तक, बेंजामिन थॉम्पसन (1753-1814) ने पता लगाया था कि काम को अतिरिक्त किसी सीमा के गर्मी में बदला जा सकता है - ऊर्जा के संरक्षण का अग्रदूत या ऊर्जा संरक्षण
1824 में निकोलस लेओनार्ड साडी कार्नोट (1796-1832) ने वैज्ञानिक रूप से अपने कार्नोट चक्र, सार इंजन के साथ भाप इंजन का विश्लेषण किया। रुडोल्फ क्लॉसियस (1822-1888) ने विकार एन्ट्रापी का उपाय नोट किया, जो मुक्त ऊर्जा की लगातार घटती मात्रा को प्रभावित करता है जो कार्नाट इंजन के लिए उपलब्ध है।
इस प्रकार, किसी दिए गए तापमान पर कम से अधिक एन्ट्रापी की ओर ऊष्मप्रवैगिकी प्रणाली का निरंतर मार्च, समय के तीर को परिभाषित करता है। विशेष रूप से स्टीफन हॉकिंग समय के तीन तीरों की पहचान करते हैं।[22]
- समय का मनोवैज्ञानिक तीर - कठोर प्रवाह की हमारी धारणा।
- समय का ऊष्मप्रवैगिकी तीर - एन्ट्रापी के विकास द्वारा प्रतिष्ठित।
- समय का ब्रह्माण्ड संबंधी तीर - ब्रह्मांड के विस्तार द्वारा प्रतिष्ठित।
समय के साथ, पृथक ऊष्मप्रवैगिकी प्रणाली में एन्ट्रापी बढ़ जाती है। इसके विपरीत, इरविन श्रोडिंगर (1887-1961) ने बताया कि जीवन नकारात्मक एन्ट्रॉपी प्रवाह पर निर्भर करता है।[23] इल्या प्रिझोगिन (1917-2003) ने कहा कि जीवन की प्रकार अन्य ऊष्मप्रवैगिकी प्रणालियां भी संतुलन से बहुत दूर हैं, वे भी स्थिर अनुपात-लौकिक संरचनाओं को प्रदर्शित कर सकती हैं जो जीवन की याद दिलाती हैं। इसके तुरंत बाद बेलौसोव-झाबोटिंस्की प्रतिक्रियाएं[24] प्रतिवेदन किए गए, जो रासायनिक समाधान में दोलनशील रंगों को प्रदर्शित करते हैं।[25] ये संतुलन उष्मागतिक शाखाएं द्विभाजन सिद्धांत तक पहुंचती हैं, जो अस्थिर है और अन्य ऊष्मप्रवैगिकी शाखा इसके स्थान पर स्थिर हो जाती है।[26]
विद्युत चुंबकत्व और प्रकाश की गति
1864 में, जेम्स क्लर्क मैक्सवेल (1831-1879) ने बिजली और चुंबकत्व का संयुक्त सिद्धांत प्रस्तुत किया। उन्होंने उन दो घटनाओं से संबंधित सभी कानूनों को चार समीकरणों में जोड़ दिया। इन समीकरणों को विद्युत चुंबकत्व के लिए मैक्सवेल के समीकरण के रूप में जाना जाता है, वे विद्युत चुम्बकीय तरंगों के रूप में समाधानों की अनुमति देते हैं और उन्हें उत्पन्न करने वाले विद्युत आवेश के वेग की देख-भाल किए अतिरिक्त निश्चित गति, c पर प्रचार करते हैं।
तथ्य यह है कि प्रकाश को सदैव गति c पर यात्रा करने की भविष्यवाणी की जाती है। यदि मैक्सवेल के समीकरणों को किसी जड़त्वीय निर्माण स्थिर वेग के साथ संदर्भ निर्माण में धारण करने के लिए माना जाता है, तो गैलिलियन सापेक्षता के साथ असंगत होगा। क्योंकि गैलीलियन परिवर्तन गति को कम करके बढ़ाने की भविष्यवाणी करते हैं। प्रकाश के समानांतर विरोधी समानांतर यात्रा करने वाले पर्यवेक्षक के संदर्भ निर्माण में है।
यह उम्मीद की गई थी कि निरपेक्ष संदर्भ ढांचा था, जो चमकदार ईथर का था, जिसमें मैक्सवेल के समीकरण ज्ञात रूप में असंशोधित थे।
मिशेलसन-मॉर्ले प्रयोग चमकदार एथर के सापेक्ष पृथ्वी की गति के कारण प्रकाश की सापेक्ष गति में किसी भी अंतर का पता लगाने में विफल रहा, यह सुझाव देते हुए कि मैक्सवेल के समीकरण वास्तव में सभी निर्माण में उपस्तिथ थे। 1875 में, हेंड्रिक लोरेंत्ज़ (1853-1928) ने लोरेंत्ज़ परिवर्तन की खोज की, जिसने मैक्सवेल के समीकरणों को अपरिवर्तित छोड़ दिया, जिससे माइकलसन और मॉर्ले के नकारात्मक परिणाम की व्याख्या की जा सके। हेनरी पॉइनकेयर (1854-1912) ने लोरेंत्ज़ के परिवर्तन के महत्व को नोट किया और इसे लोकप्रिय बनाया। विशेष रूप से रेलमार्ग कार का विवरण विज्ञान और परिकल्पना में पाया जा सकता है,[27] जो 1905 के आइंस्टीन के लेखों से पहले प्रकाशित हुआ था।
लोरेंत्ज़ परिवर्तन ने अंतरिक्ष संकुचन और समय के फैलाव की भविष्यवाणी की, 1905 तक, पूर्व की व्याख्या आणविक बलों के विद्युत प्रकृति के संशोधन के कारण ईथर के संबंध में गतिमान वस्तुओं के भौतिक संकुचन के रूप में की गई थी, जबकि बाद वाले को केवल गणितीय शर्त माना गया था।
आइंस्टीन की भौतिकी: अंतरिक्ष समय
अल्बर्ट आइंस्टीन की 1905 की विशेष सापेक्षता ने निरपेक्ष समय की धारणा को चुनौती दी और केवल उन घड़ियों के लिए तुल्यकालन की परिभाषा तैयार की जो समय के रैखिक प्रवाह को चिह्नित करती हैं।
यदि अंतरिक्ष के बिंदु ए पर एक घड़ी है, तो ए पर एक पर्यवेक्षक इन घटनाओं के साथ-साथ हाथों की स्थिति को ढूंढकर ए के तत्काल निकटता में घटनाओं के समय मूल्यों को निर्धारित कर सकता है। यदि अंतरिक्ष के बिंदु B पर एक और घड़ी है जो सभी प्रकार से A के समान है, तो B पर एक पर्यवेक्षक के लिए B के तत्काल सन्निकट घटनाओं के समय मूल्यों को निर्धारित करना संभव है।
लेकिन आगे की धारणा के बिना, समय के संबंध में, बी में एक घटना के साथ ए में एक घटना की तुलना करना संभव नहीं है। हमने अभी तक केवल "A टाइम" और "B टाइम" परिभाषित किया है।
हमने A और B के लिए एक सामान्य "समय" को परिभाषित नहीं किया है, क्योंकि बाद वाले को तब तक परिभाषित नहीं किया जा सकता जब तक कि हम परिभाषा के अनुसार स्थापित नहीं करते हैं कि A से B तक यात्रा करने के लिए प्रकाश द्वारा आवश्यक "समय" के बराबर होता है। इसे B से A तक यात्रा करने की आवश्यकता है। प्रकाश की किरण को A से B की तरफ "A टाइम" TA पर शुरू होने दें, इसे "B टाइम" T पर जाने दें B A की दिशा में B पर परिलक्षित होता है, और फिर से A पर "A time" t′A पर पहुंचता है।
परिभाषा के अनुसार दो घड़ियां अगर सिंक्रनाइज़ होती हैं
हम मानते हैं कि समकालिकता की यह परिभाषा विरोधाभासों से मुक्त है, और किसी भी बिंदु के लिए संभव है; और यह कि निम्नलिखित संबंध सार्वभौमिक रूप से मान्य हैं:-
- यदि B की घड़ी A की घड़ी के साथ तालमेल बिठाती है, तो A की घड़ी B की घड़ी के साथ तालमेल बिठाती है।
- यदि A की घड़ी B की घड़ी के साथ और C की घड़ी के साथ भी सिंक्रनाइज़ होती है, तो B और C की घड़ियाँ भी एक दूसरे के साथ सिंक्रनाइज़ होती हैं।
— अल्बर्ट आइंस्टीन, "मूविंग बॉडीज के इलेक्ट्रोडायनामिक्स पर"[28]आइंस्टीन ने दिखाया कि यदि संदर्भ निर्माण के बीच प्रकाश की गति नहीं बदल रही है, तो स्थान और समय ऐसा होना चाहिए कि गतिमान पर्यवेक्षक प्रकाश की उसी गति को स्थिर के रूप में मापेगा क्योंकि वेग को अंतरिक्ष और समय द्वारा परिभाषित किया गया है:
- जहाँ r स्थिति है और t समय है।
वास्तव में, लोरेंत्ज़ परिवर्तन सापेक्ष गति में दो संदर्भ निर्माण के लिए, जिसका x अक्ष सापेक्ष वेग की दिशा में निर्देशित है।
कहा जा सकता है कि अंतरिक्ष और समय को प्रकार से मिश्रित किया जा सकता है जिस प्रकार से जेड अक्ष के चारों ओर एक यूक्लिडियन घूर्णन और वाई निर्देशांक को मिलाता है। इसके परिणामों में साथ सापेक्षता सम्मलित है।
अधिक विशेष रूप से लोरेंत्ज़ परिवर्तन अतिशयोक्तिपूर्ण घुमाव है जो कि चार-आयामी मिन्कोव्स्की अंतरिक्ष में निर्देशांक का परिवर्तन है, जिसका आयाम सीटी है। यूक्लिडियन अंतरिक्ष में साधारण घुमाव निर्देशांक का संगत परिवर्तन है। प्रकाश की गति को केवल रूपांतरण कारक के रूप में देखा जा सकता है, क्योंकि हम अलग-अलग इकाइयों में अंतरिक्ष समय के आयामों को मापते हैं, चूँकि वर्तमान में मीटर को सेकंड के संदर्भ में परिभाषित किया गया है। इसका सटीक मान है 299 792 458 m/s. यूक्लिडियन अंतरिक्ष में हमें समान कारक की आवश्यकता होगी। उदाहरण के लिए, हमने समुद्री मील में चौड़ाई और पैरों में गहराई मापी। भौतिक विज्ञान में कभी-कभी प्राकृतिक इकाइयाँ माप की इकाइयाँ जिनमें c = 1 का उपयोग समीकरणों को सरल बनाने के लिए किया जाता है।
गतिमान संदर्भ निर्माण में समय को स्थिर की तुलना में निम्न संबंध द्वारा अधिक धीमी गति से चलाने के लिए दिखाया गया है, जो लोरेंत्ज़ परिवर्तन द्वारा ∆x′ = 0, ∆τ = ∆t′ डालकर प्राप्त किया जा सकता है।
जहाँ,
- ∆τ दो घटनाओं के बीच का समय है जैसा कि चलती संदर्भ निर्माण में मापा जाता है जिसमें वे ही स्थान पर होते हैं, उदाहरण के लिए चलती घड़ी पर दो टिक, इसे दो घटनाओं के बीच का उचित समय कहा जाता है।
- ∆t इन दो घटनाओं के बीच का समय है, किन्तु स्थिर संदर्भ निर्माण में मापा जाता है।
- v गतिमान संदर्भ निर्माण की गति स्थिर के सापेक्ष है।
- c प्रकाश की गति है।
इसलिए कहा जाता है कि गतिमान वस्तुएँ समय की धीमी गति दर्शाती हैं। इसे समय फैलाव के रूप में जाना जाता है।
ये परिवर्तन केवल दो निर्माण के लिए निरंतर सापेक्ष वेग पर मान्य हैं। भोलेपन से उन्हें अन्य स्थितियों में लागू करने से जुड़वाँ विरोधाभास जैसे विरोधाभास उत्पन्न होते हैं।
उस विरोधाभास को उदाहरण के लिए आइंस्टीन के सापेक्षता के सामान्य सिद्धांत का उपयोग करके हल किया जा सकता है, जो रिमेंनियन ज्यामिति का उपयोग करता है, त्वरित, अ-जड़त्वीय संदर्भ निर्माण में ज्यामिति। मिंकोव्स्की स्थान का वर्णन करने वाले मीट्रिक टेंसर को नियोजित करना।
आइंस्टीन ने लोरेंत्ज़ के परिवर्तन के लिए ज्यामितीय समाधान विकसित किया, जो मैक्सवेल के समीकरणों को संरक्षित करता है। उनके आइंस्टीन के क्षेत्र समीकरण दिक्-काल के दिए गए क्षेत्र में स्थान और समय के मापन और उस क्षेत्र के ऊर्जा घनत्व के बीच सटीक संबंध देते हैं।
आइंस्टीन के समीकरण भविष्यवाणी करते हैं कि गुरुत्वाकर्षण क्षेत्र की उपस्थिति से समय को बदलना चाहिए (श्वार्जस्चिल्ड मीट्रिक देखें):
जहाँ,
- की दूरी पर किसी वस्तु का गुरुत्वीय समय फैलाव है
- समन्वय समय में परिवर्तन है, या समन्वय समय का अंतराल है।
- द्रव्यमान उत्पन्न करने वाला क्षेत्र है
- उचित समय में परिवर्तन है , या उचित समय का अंतराल।
कोई निम्नलिखित सरल सन्निकटन का उपयोग कर सकता है।
अर्थात्, गुरुत्वाकर्षण क्षेत्र जितना मजबूत होता है और इस प्रकार, त्वरण जितना बड़ा होता है, उतना ही धीरे-धीरे समय चलता है। कण त्वरक प्रयोगों और ब्रह्मांडीय किरण साक्ष्य द्वारा समय फैलाव की भविष्यवाणियों की पुष्टि की जाती है, जहां गतिमान कण अपने कम ऊर्जावान समकक्षों की तुलना में क्षय होते हैं। गुरुत्वीय समय फैलाव गुरुत्वाकर्षण लाल बदलाव की घटना को जन्म देता है और शापिरो सूरज जैसे बड़े पैमाने पर वस्तुओं के पास देरी करता है। वैश्विक स्थिति निर्धारण प्रणाली को इस प्रभाव को ध्यान में रखते हुए संकेतों को भी समायोजित करना चाहिए।
आइंस्टीन के सापेक्षता के सामान्य सिद्धांत के अनुसार, स्वतंत्र रूप से चलने वाला कण अंतरिक्ष-समय में ऐसे इतिहास का पता लगाता है जो अपने उचित समय को अधिकतम करता है। इस घटना को अधिकतम उम्र बढ़ने के सिद्धांत के रूप में भी जाना जाता है और एडविन एफ टेलर और जॉन आर्चीबाल्ड व्हीलर द्वारा वर्णित किया गया था।[29]
- चरम जरण का सिद्धांत: अंतरिक्ष समय में दो घटनाओं के बीच मुक्त वस्तु जिस पथ को लेता है, वह वह पथ है जिसके लिए ऑब्जेक्ट की कलाई घड़ी पर अंकित इन घटनाओं के बीच का समय समाप्त हो जाता है।
आइंस्टीन का सिद्धांत इस धारणा से प्रेरित था कि ब्रह्मांड में हर बिंदु को 'केंद्र' के रूप में माना जा सकता है और तदनुसार, भौतिकी को सभी संदर्भ निर्माण में समान कार्य करना चाहिए। उनके सरल और सुरुचिपूर्ण सिद्धांत से पता चलता है कि समय जड़त्वीय निर्माण के सापेक्ष है। जड़त्वीय निर्माण में न्यूटन का पहला नियम लागू होता है, इसकी अपनी स्थानीय ज्यामिति होती है और इसलिए स्थान और समय के अपने माप, कोई 'सार्वभौमिक घड़ी' नहीं है। कम से कम दो प्रणालियों के बीच तुल्यकालन का कार्य किया जाना चाहिए।
क्वांटम यांत्रिकी में समय
क्वांटम यांत्रिकी के समीकरणों में समय पैरामीटर है। श्रोडिंगर समीकरण[30] है
उपाय हो सकता है
- .
जहाँ, समय विकास प्रचालक और एच हैमिल्टनियन (क्वांटम यांत्रिकी) कहा जाता है।
किन्तु ऊपर दिखाया गया श्रोडिंगर चित्र हाइजेनबर्ग चित्र के समतुल्य है, जो मौलिक यांत्रिकी के पॉइसन कोष्ठक के समान है। पोइसन कोष्ठकों को अ-शून्य कम्यूटेटर द्वारा अधिगृहीत किया जाता है, कहते हैं [एच, ए] देखने योग्य ए और हैमिल्टनियन एच के लिए।
यह समीकरण क्वांटम भौतिकी में अनिश्चितता के सिद्धांत को दर्शाता है। उदाहरण के लिए, समय के साथ (देखने योग्य ए), ई हैमिल्टनियन एच से ऊर्जा देता है।
- जहाँ,
- ऊर्जा में अनिश्चितता है
- समय में अनिश्चितता है
- काष्ठफलक नियतांक है
घटना की अवधि जितनी अधिक त्रुटिहीन और त्रुटिहीन से मापी जाती है, उतनी ही कम त्रुटिहीन से उस क्रम से जुड़ी ऊर्जा को मापा जा सकता है और इसके विपरीत। यह समीकरण मानक अनिश्चितता सिद्धांत से भिन्न है, क्योंकि क्वांटम यांत्रिकी में समय प्रचालक (भौतिकी) नहीं है।
संबंधित कम्यूटेटर संबंध गति पी और स्थिति क्यू के लिए भी हैं, जो दूसरे के संयुग्मित चर हैं, साथ ही गति और स्थिति में इसी अनिश्चितता सिद्धांत के साथ, उपरोक्त ऊर्जा और समय संबंध के समान।
क्वांटम यांत्रिकी रासायनिक तत्व की आवर्त सारणी के गुणों की व्याख्या करती है। चुंबकीय क्षेत्र में आणविक बीम के साथ ओटो स्टर्न और वाल्टर गेरलाच के प्रयोग से प्रारंभ, इसीडोर रबी (1898-1988), बीम के चुंबकीय अनुनाद को संशोधित करने में सक्षम था। 1945 में रबी ने सुझाव दिया कि यह तकनीक घड़ी का आधार हो[31] परमाणु किरण की गुंजयमान आवृत्ति का उपयोग करना।बोल्डर कोलोराडो में जेआईएलए के 2021 जून में, ये स्ट्रोंटियम परमाणुओं के बादल के शीर्ष पर प्रकाशीय जाली घड़ी की टिक की दर में अंतर में समय फैलाव देखा गया, उस बादल के नीचे की तुलना में मिलीमीटर लंबा स्तंभ प्रभाव के अनुसार गुरुत्वाकर्षण है।[32]
गतिशील प्रणाली
[[गतिशील प्रणाली और अराजकता सिद्धांत]], विघटनकारी संरचनाएं देखें
कोई कह सकता है कि समय गतिशील प्रणाली का मानकीकरण है, जो प्रणाली की ज्यामिति को प्रकट और संचालित करने की अनुमति देता है। यह प्रमाणित किया गया है कि समय कैओस सिद्धांत अर्थात अ-रैखिकता/अपरिवर्तनीयता का निहित परिणाम है। प्रणाली की विशेषता समय, सूचना एन्ट्रापी उत्पादन की दर बेनोइट मंडेलब्रॉट ने अपनी पुस्तक बहु भग्नऔर 1/f शोर में आंतरिक समय का परिचय दिया।
समय क्रिस्टल
खेमानी, मोएसनर और सोंधी समय क्रिस्टल को स्थिर, रूढ़िवादी, स्थूल घड़ी के रूप में परिभाषित करते हैं।[33]
संकेतन
संकेतन ऊपर वर्णित विद्युत चुम्बकीय तरंग का अनुप्रयोग है। सामान्यतः, संकेत पार्टियों और स्थानों के बीच संचार का भाग होता है। उदाहरण पेड़ से बंधा पीला रिबन, चर्च की घंटी बजना हो सकता है। संकेत बातचीत का भाग हो सकता है, जिसमें संचार प्रोटोपुकारना सम्मलित होता है और संकेत शहर की घड़ी, रेलवे स्टेशन पर घंटे की सुई की स्थिति हो सकती है। इच्छुक पार्टी समय जानने के लिए उस घड़ी को देखने की इच्छा कर सकती है। देखें: समय बॉल, समय संकेत का प्रारंभिक रूप।
 त्वरित विशाल कण की विश्व रेखा का विकास। यह विश्व रेखा इस दिक्-समय के आंकड़े के समय-समान शीर्ष और निचले वर्गों तक ही सीमित है; यह विश्व रेखा शीर्ष (भविष्य) या नीचे (अतीत) प्रकाश शंकु को पार नहीं कर सकती है। बाएँ और दाएँ खंड (जो प्रकाश शंकु के बाहर हैं) spacelike हैं।
त्वरित विशाल कण की विश्व रेखा का विकास। यह विश्व रेखा इस दिक्-समय के आंकड़े के समय-समान शीर्ष और निचले वर्गों तक ही सीमित है; यह विश्व रेखा शीर्ष (भविष्य) या नीचे (अतीत) प्रकाश शंकु को पार नहीं कर सकती है। बाएँ और दाएँ खंड (जो प्रकाश शंकु के बाहर हैं) spacelike हैं।जब तक हम उनके पिछले प्रकाश शंकु के भीतर रहते हैं, तब तक हम पर्यवेक्षक के रूप में विभिन्न दलों और स्थानों को संकेत दे सकते हैं। किन्तु हम अपने पिछले प्रकाश शंकु के बाहर उन दलों और स्थानों से संकेत प्राप्त नहीं कर सकते।
विद्युत चुम्बकीय तरंग के लिए समीकरणों के निर्माण के साथ-साथ दूरसंचार के क्षेत्र की स्थापना की जा सकती है।
19वीं शताब्दी में टेलीग्राफी, विद्युत परिपथ, कुछ फैले हुए महाद्वीप और महासागर, कोड - सरल बिंदु, डैश और रिक्त स्थान संचारित कर सकते थे। इससे, प्राविधिक समस्याएँ की श्रृंखला सामने आई है, देखें :श्रेणी वर्णनात्मकता। किन्तु यह कहना सुरक्षित है कि हमारे संकेतन प्रणाली केवल लगभग समकालीकरण हो सकते हैं, प्लेसिओक्रोनस स्थिति, जिससे घबराहट को समाप्त करने की आवश्यकता होती है।
उस ने कहा, जीपीएस जैसी तकनीकों का उपयोग करके प्रणाली को समकालीकरण किया जा सकता है। अभियंतािंग सन्निकटन पर जीपीएस उपग्रहों को उनके सर्किटरी में गुरुत्वाकर्षण और अन्य सापेक्ष कारकों के प्रभाव के लिए जिम्मेदार होना चाहिए। देखें: स्व घड़ी संकेत
समयनिर्धारक मानकों के लिए प्रौद्योगिकी
अमेरिका में प्राथमिक समय मानक वर्तमान में एनआईएसटी-एफ1 है। लेजर-ठंडा सीज़ियम फव्वारा है।[34] अमोनिया-आधारित परमाणु घड़ी (1949) से सीज़ियम-आधारित एनबीएस-1 (1952) से एनआईएसटी-7 (1993) तक, समय और आवृत्ति मानकों की श्रृंखला में नवीनतम। संबंधित घड़ी की अनिश्चितता 5 दशकों में प्रति दिन 10,000 नैनोसेकंड से घटकर 0.5 नैनोसेकंड प्रति दिन हो गई।[35] 2001 में एनआईएसटी-एफ1 के लिए घड़ी की अनिश्चितता 0.1 नैनोसेकंड/दिन थी। तेजी से सटीक आवृत्ति मानकों का विकास चल रहा है।
इस समय और आवृत्ति मानक में, सीज़ियम परमाणुओं की आबादी को माइक्रोकेल्विन के तापमान तक लेज़र-ठंडा किया जाता है। परमाणु छह लेज़रों द्वारा आकार की गेंद में त्रित होते हैं, प्रत्येक स्थानिक आयाम के लिए दो, लंबवत (ऊपर/नीचे), क्षैतिज (बाएं/दाएं) और आगे/पीछे ऊर्ध्वाधर लेज़र सीज़ियम बॉल को माइक्रोवेव गुहा के माध्यम से धकेलते हैं। जैसे ही गेंद को ठंडा किया जाता है, सीज़ियम की आबादी अपनी मूलभूत अवस्था में ठंडी हो जाती है और ऊपर की दूसरी परिभाषा में बताई गई अपनी प्राकृतिक आवृत्ति पर प्रकाश का उत्सर्जन करती है। सीज़ियम आबादी से उत्सर्जन में ग्यारह भौतिक प्रभावों का हिसाब लगाया जाता है, जिन्हें एनआईएसटी-एफ1 घड़ी में नियंत्रित किया जाता है। ये परिणाम बीपं को प्रतिवेदन किए गए हैं।
इसके अतिरिक्त, संदर्भ मेसर हाइड्रोजन मेसर भी अंतर्राष्ट्रीय परमाणु समय के लिए आवृत्ति मानक के रूप में बीआईपीएम को प्रतिवेदन किया जाता है।
सेवरेस, फ्रांस में स्थित बीआईपीएम (अंतरराष्ट्रीय विभाग डेस पॉयड्स एट मेसर्स) द्वारा समय की माप की देखरेख की जाती है, जो माप की रूपता और दुनिया भर में अंतरराष्ट्रीय प्रणाली इकाइयों से बाहर (एसआई) के लिए उनकी पता लगाने की क्षमता सुनिश्चित करता है। बीआईपीएम परामर्शदात्री समितियों की श्रृंखला के माध्यम से, इक्यावन देशों, सम्मेलन के सदस्य राज्यों के बीच राजनयिक संधि, मीटर सम्मेलनन के अधिकार के अनुसार संचालित होता है, जिसके सदस्य संबंधित राष्ट्रीय मैट्रोलोजी प्रयोगशालाएं हैं।
ब्रह्माण्ड विज्ञान में समय
सामान्य सापेक्षता के समीकरण गैर स्थैतिक ब्रह्मांड की भविष्यवाणी करते हैं। चूंकि, आइंस्टीन ने केवल स्थिर ब्रह्मांड को स्वीकार किया और ब्रह्मांडीय स्थिरांक को जोड़कर इसे प्रतिबिंबित करने के लिए आइंस्टीन क्षेत्र समीकरण को संशोधित किया, जिसे उन्होंने बाद में अपने जीवन की सबसे बड़ी गलती बताया। किन्तु 1927 में, जॉर्जेस लेमेत्रे (1894-1966) ने सामान्य सापेक्षता के आधार पर तर्क दिया कि ब्रह्मांड की उत्पत्ति प्रारंभिक विस्फोट में हुई थी। उस साल पांचवें सॉल्वे सम्मेलन में, आइंस्टीन ने उन्हें खारिज कर दिया [36] "आपका गणित सही है, किन्तु आपका भौतिकी घृणित है"। 1929 में, एडविन हबल (1889-1953) ने विस्तारित ब्रह्मांड की अपनी खोज की घोषणा की। वर्तमान सामान्यतः स्वीकृत ब्रह्माण्ड संबंधी मॉडल, लैम्ब्डा-सीडीएम मॉडल में सकारात्मक ब्रह्माण्ड संबंधी स्थिरांक है और इस प्रकार न केवल विस्तारित ब्रह्मांड बल्कि त्वरित विस्तार करने वाला ब्रह्मांड है।
यदि ब्रह्मांड का विस्तार हो रहा था, तो यह अतीत में बहुत छोटा और इसलिए अधिक गर्म और सघन रहा होगा। जॉर्ज गैमोव (1904-1968) ने परिकल्पना की कि तत्वों की आवर्त सारणी में तत्वों की प्रचुरता, गर्म घने ब्रह्मांड में परमाणु प्रतिक्रियाओं के कारण हो सकती है। वह फ्रेड हॉयल (1915-2001) द्वारा विवादित था, जिसने इसे नापसंद करने के लिए 'बिग बैंग' शब्द का आविष्कार किया था। एनरिको फर्मी और अन्य ने नोट किया कि केवल प्रकाश तत्वों के बनने के बाद ही यह प्रक्रिया बंद हो गई होगी और इस प्रकार भारी तत्वों की प्रचुरता का हिसाब नहीं दिया।
विस्तार के पर्यन्त ठंडा होने के बाद, गैमो की भविष्यवाणी ब्रह्मांड के लिए 5-10-केल्विन श्याम पिंडों से उत्पन्न विकिरण तापमान थी। ब्रह्मांडीय माइक्रोवेव पृष्ठभूमि विकिरण की खोज की खोज द्वारा इसकी पुष्टि की गई थी। इसके बाद के प्रयोग 2.7 केल्विन तापमान पर पहुंचे, जो कि बिग बैंग के 13.8 बिलियन वर्ष बाद ब्रह्मांड की आयु के अनुरूप है।
इस नाटकीय परिणाम ने समस्याएँ को उठाया है। बिग बैंग और काष्ठफलक समय की विलक्षणता के बीच क्या हुआ, जो कि सबसे छोटा अवलोकन योग्य समय है। जब अंतरिक्ष समय फोम से समय अलग हो सकता है,[38] केवल टूटी हुई समरूपता पर आधारित संकेत हैं (देखें स्वतःस्फूर्त समरूपता ब्रेकिंग, बिग बैंग की समयरेखा, और लेख:श्रेणी:भौतिक ब्रह्मांड विज्ञान)।
सामान्य सापेक्षता ने हमें विस्तारित ब्रह्मांड की हमारी आधुनिक धारणा दी जो बिग बैंग में प्रारंभ हुई थी। सापेक्षता और क्वांटम सिद्धांत का उपयोग करके हम मोटे तौर पर ब्रह्मांड के इतिहास का पुनर्निर्माण करने में सक्षम हुए हैं। ब्रह्मांड के हमारे युग में जिसके पर्यन्त विद्युत चुम्बकीय तरंगें संवाहक आवेशों द्वारा परेशान किए अतिरिक्त फैल सकती हैं, हम रात के आकाश में हमसे बड़ी दूरी पर तारे देख सकते हैं। इस युग से पहले बिग बैंग के लगभग 377,000 वर्षों के बाद, इलेक्ट्रॉनों और नाभिकों को परमाणुओं में संयोजित करने के लिए ब्रह्मांड के पर्याप्त ठंडा होने से पहले समय था, जिसके पर्यन्त बड़ी दूरी पर तारों का प्रकाश दिखाई नहीं देता था।
रीप्राइज़
इल्या प्रोगोगाइन का आश्चर्य समय से पहले का अस्तित्व है। न्यूटन, आइंस्टीन और क्वांटम भौतिकी के विचारों के विपरीत जो समय के सममित दृष्टिकोण की प्रस्तुत करते हैं, जैसा कि ऊपर चर्चा की गई है। प्रोगोगाइन बताते हैं कि सांख्यिकीय और ऊष्मप्रवैगिकी भौतिकी अपरिवर्तनीय प्रक्रिया के साथ ही समय का तीर और बिग बैंग की व्याख्या कर सकते हैं।[39]
यह भी देखें
संदर्भ
- ↑ Considine, Douglas M.; Considine, Glenn D. (1985). Process instruments and controls handbook (3 ed.). McGraw-Hill. pp. 18–61. ISBN 0-07-012436-1.
- ↑ For example, Galileo measured the period of a simple harmonic oscillator with his pulse.
- ↑ 3.0 3.1 Otto Neugebauer The Exact Sciences in Antiquity. Princeton: Princeton University Press, 1952; 2nd edition, Brown University Press, 1957; reprint, New York: Dover publications, 1969. Page 82.
- ↑ See, for example William Shakespeare Hamlet: " ... to thine own self be true, And it must follow, as the night the day, Thou canst not then be false to any man."
- ↑ "Heliacal/Dawn Risings". Solar-center.stanford.edu. Retrieved 2012-08-17.
- ↑ Farmers have used the sun to mark time for thousands of years, as the most ancient method of telling time. Archived 2010-07-26 at the Wayback Machine
- ↑ Eratosthenes, On the measure of the Earth calculated the circumference of Earth, based on the measurement of the length of the shadow cast by a gnomon in two different places in Egypt, with an error of -2.4% to +0.8%
- ↑ Fred Hoyle (1962), Astronomy: A history of man's investigation of the universe, Crescent Books, Inc., London LC 62-14108, p.31
- ↑ The Mesopotamian (modern-day Iraq) astronomers recorded astronomical observations with the naked eye, more than 3500 years ago. P. W. Bridgman defined his operational definition in the twentieth c.
- ↑ Naked eye astronomy became obsolete in 1609 with Galileo's observations with a telescope. Galileo Galilei Linceo, Sidereus Nuncius (Starry Messenger) 1610.
- ↑ http://tycho.usno.navy.mil/gpstt.html http://www.phys.lsu.edu/mog/mog9/node9.html Today, automated astronomical observations from satellites and spacecraft require relativistic corrections of the reported positions.
- ↑ "Unit of time (second)". SI brochure. International Bureau of Weights and Measures (BIPM). pp. Section 2.1.1.3. Retrieved 2008-06-08.
- ↑ S. R. Jefferts et al., "Accuracy evaluation of NIST-F1".
- ↑ Fred Adams and Greg Laughlin (1999), Five Ages of the Universe ISBN 0-684-86576-9 p.35.
- ↑ Charles Hose and William McDougall (1912) The Pagan Tribes of Borneo, Plate 60. Kenyahs measuring the Length of the Shadow at Noon to determine the Time for sowing PADI p. 108. This photograph is reproduced as plate B in Fred Hoyle (1962), Astronomy: A history of man's investigation of the universe, Crescent Books, Inc., London LC 62-14108, p.31. The measurement process is explained by: Gene Ammarell (1997), "Astronomy in the Indo-Malay Archipelago", p.119, Encyclopaedia of the history of science, technology, and medicine in non-western cultures, Helaine Selin, ed., which describes Kenyah Tribesmen of Borneo measuring the shadow cast by a gnomon, or tukar do with a measuring scale, or aso do.
- ↑ North, J. (2004) God's Clockmaker: Richard of Wallingford and the Invention of Time. Oxbow Books. ISBN 1-85285-451-0
- ↑ Watson, E (1979) "The St Albans Clock of Richard of Wallingford". Antiquarian Horology 372-384.
- ↑ Jo Ellen Barnett, Time's Pendulum ISBN 0-306-45787-3 p.99.
- ↑ Galileo 1638 Discorsi e dimostrazioni matematiche, intorno á due nuoue scienze 213, Leida, Appresso gli Elsevirii (Louis Elsevier), or Mathematical discourses and demonstrations, relating to Two New Sciences, English translation by Henry Crew and Alfonso de Salvio 1914. Section 213 is reprinted on pages 534-535 of On the Shoulders of Giants:The Great Works of Physics and Astronomy (works by Copernicus, Kepler, Galileo, Newton, and Einstein). Stephen Hawking, ed. 2002 ISBN 0-7624-1348-4
- ↑ Newton 1687 Philosophiae Naturalis Principia Mathematica, Londini, Jussu Societatis Regiae ac Typis J. Streater, or The Mathematical Principles of Natural Philosophy, London, English translation by Andrew Motte 1700s. From part of the Scholium, reprinted on page 737 of On the Shoulders of Giants:The Great Works of Physics and Astronomy (works by Copernicus, Kepler, Galileo, Newton, and Einstein). Stephen Hawking, ed. 2002 ISBN 0-7624-1348-4
- ↑ Newton 1687 page 738.
- ↑ pp. 182–195. Stephen Hawking 1996. The Illustrated Brief History of Time: updated and expanded edition ISBN 0-553-10374-1
- ↑ Erwin Schrödinger (1945) What is Life?
- ↑ G. Nicolis and I. Prigogine (1989), Exploring Complexity
- ↑ R. Kapral and K. Showalter, eds. (1995), Chemical Waves and Patterns
- ↑ Ilya Prigogine (1996) The End of Certainty pp. 63–71
- ↑ Henri Poincaré, (1902). Science and Hypothesis Eprint Archived 2006-10-04 at the Wayback Machine
- ↑ आइंस्टीन 1905, जुर एलेक्ट्रोडायनेमिक बेवेग्टर कोपर [ऑन द इलेक्ट्रोडायनामिक्स ऑफ मूविंग बॉडीज] 1922 में Das Relativitätsprinzip, बी.जी. टेबनेर, लीपज़िग। सापेक्षता के सिद्धांत: सापेक्षता के विशेष सिद्धांत पर मूल पत्रों का संग्रह', एच.ए. लॉरेंत्ज़, ए. आइंस्टीन, एच. मिन्कोव्स्की, और डब्ल्यू. एच. वेइल, मोनोग्राफियन, हेफ़्ट 2 में फ़ोर्टस्क्रिट डेर मैथेमेटिसचेन विसेनशाफ्टन का हिस्सा हैं। अंग्रेजी अनुवाद डब्ल्यू पेरेट और जी.बी. जेफरी, 'ऑन द शोल्डर ऑफ जायंट्स': द ग्रेट वर्क्स ऑफ फिजिक्स एंड एस्ट्रोनॉमी के पृष्ठ 1169 पर पुनर्मुद्रित (कॉपरनिकस, केप्लर, गैलीलियो, गैलीलियो द्वारा काम करता है। आइजैक न्यूटन|न्यूटन]], और आइंस्टीन)। स्टीफन हॉकिंग, एड। 2002 ISBN 0-7624-1348-4
- ↑ Taylor (2000). "Exploring Black Holes: Introduction to General Relativity" (PDF). Addison Wesley Longman.
- ↑ Schrödinger, E. (1 November 1926). "परमाणुओं और अणुओं के यांत्रिकी का एक लहरदार सिद्धांत". Physical Review. American Physical Society (APS). 28 (6): 1049–1070. Bibcode:1926PhRv...28.1049S. doi:10.1103/physrev.28.1049. ISSN 0031-899X.
- ↑ A Brief History of Atomic Clocks at NIST Archived 2009-02-14 at the Wayback Machine
- ↑ Slashdot (25 Oct 2021) An Ultra-Precise Clock Shows How To Link the Quantum World With Gravity Jun Ye's work at JILA
- ↑ Vedika Khemani, Roderich Moessner, and S. L. Sondhi (23 Oct 2019) A Brief History of Time Crystals
- ↑ D. M. Meekhof, S. R. Jefferts, M. Stepanovíc, and T. E. Parker (2001) "Accuracy Evaluation of a Cesium Fountain Primary Frequency Standard at NIST", IEEE Transactions on Instrumentation and Measurement. 50, no. 2, (April 2001) pp. 507-509
- ↑ James Jespersen and Jane Fitz-Randolph (1999). From sundials to atomic clocks : understanding time and frequency. Washington, D.C. : U.S. Dept. of Commerce, Technology Administration, National Institute of Standards and Technology. 308 p. : ill. ; 28 cm. ISBN 0-16-050010-9
- ↑ John C. Mather and John Boslough (1996), The Very First Light ISBN 0-465-01575-1 p. 41.
- ↑ George Smoot and Keay Davidson (1993) Wrinkles in Time ISBN 0-688-12330-9 A memoir of the experiment program for detecting the predicted fluctuations in the cosmic microwave background radiation.
- ↑ Martin Rees (1997), Before the Beginning ISBN 0-201-15142-1 p. 210.
- ↑ Prigogine, Ilya (1996), The End of Certainty: Time, Chaos and the New Laws of Nature. ISBN 0-684-83705-6 On pages 163 and 182.
अग्रिम पठन
- Boorstein, Daniel J., The Discoverers. Vintage. February 12, 1985. ISBN 0-394-72625-1
- Dieter Zeh, H., The physical basis of the direction of time. Springer. ISBN 978-3-540-42081-1
- Kuhn, Thomas S., The Structure of Scientific Revolutions. ISBN 0-226-45808-3
- Mandelbrot, Benoît, Multifractals and 1/f noise. Springer Verlag. February 1999. ISBN 0-387-98539-5
- Prigogine, Ilya (1984), Order out of Chaos. ISBN 0-394-54204-5
- Serres, Michel, et al., "Conversations on Science, Culture, and Time (Studies in Literature and Science)". March, 1995. ISBN 0-472-06548-3
- Stengers, Isabelle, and Ilya Prigogine, Theory Out of Bounds. University of Minnesota Press. November 1997. ISBN 0-8166-2517-4
बाहरी संबंध
Media related to भौतिकी में समय at Wikimedia Commons