प्रत्यक्ष सीमा: Difference between revisions
(→उदाहरण) |
|||
| Line 44: | Line 44: | ||
प्रत्यक्ष सीमाएँ व्युत्क्रम सीमाओं से जुड़ी होती हैं | प्रत्यक्ष सीमाएँ व्युत्क्रम सीमाओं से जुड़ी होती हैं | ||
: | : | ||
एक महत्वपूर्ण संपत्ति यह | एक महत्वपूर्ण संपत्ति यह हैप्रमापीय ्रेण में प्रत्यक्ष सीमाएं लेना एक सटीक फ़ैक्सीधा खंड लघु सटीकअर्थों की एक निर्देशित प्खंड़ोंीके से शुरू करते हैं <math>0 \to A_i \to B_i \to C_i \to 0</math> और प्रत्यक्ष सीमाएँ ब तो आपको संक्षिप्त सटीक क्र प्राप्त होता है <math>0 \to \varinjlim A_i \to \varinjlim B_i \to \varinjlim C_i \to 0</math>. | ||
== | कए | ||
== ित निर्माण और सामान्यीकरण == | |||
हम ध्यान दें कि एक श्रेणी में एक प्रत्यक्ष प्रणाली <math>\mathcal{C}</math> [[functor]]s के संदर्भ में एक वैकल्पिक विवरण स्वीकार करता है। कोई निर्देशित सेट <math>\langle I,\le \rangle</math> एक [[छोटी श्रेणी]] के रूप में माना जा सकता है <math>\mathcal{I}</math> जिनकी वस्तुएं तत्व हैं <math>I</math> और एक morphisms है <math>i\rightarrow j</math> [[अगर और केवल अगर]] <math>i\le j</math>. एक सीधा सिस्टम खत्म <math>I</math> तब एक सहसंयोजक फ़ंक्टर के समान है <math>\mathcal{I}\rightarrow \mathcal{C}</math>. इस फ़ैक्टर की सीमा (श्रेणी सिद्धांत) मूल प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा के समान है। | हम ध्यान दें कि एक श्रेणी में एक प्रत्यक्ष प्रणाली <math>\mathcal{C}</math> [[functor]]s के संदर्भ में एक वैकल्पिक विवरण स्वीकार करता है। कोई निर्देशित सेट <math>\langle I,\le \rangle</math> एक [[छोटी श्रेणी]] के रूप में माना जा सकता है <math>\mathcal{I}</math> जिनकी वस्तुएं तत्व हैं <math>I</math> और एक morphisms है <math>i\rightarrow j</math> [[अगर और केवल अगर]] <math>i\le j</math>. एक सीधा सिस्टम खत्म <math>I</math> तब एक सहसंयोजक फ़ंक्टर के समान है <math>\mathcal{I}\rightarrow \mathcal{C}</math>. इस फ़ैक्टर की सीमा (श्रेणी सिद्धांत) मूल प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा के समान है। | ||
| Line 56: | Line 58: | ||
== शब्दावली == | == शब्दावली == | ||
साहित्य में | साहित्य में परिभाषित प्रत्यक्ष सीमा की अवधारणा के लिए निर्देशित सीमा प्रत्यक्ष आगमनात्मक सीमा, निर्देशित परिचालक, प्रत्यक्ष परिचालक और आगमनात्मक सीमा शब्द मिलते हैं आगमनात्मक सीमा शब्द अस्पष्ट है क्योंकि कुछ लेखक इसे परिचालक की सामान्य अवधारणा के लिए उपयोग करते हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[समूहों की प्रत्यक्ष सीमा]] | * [[समूहों की प्रत्यक्ष सीमा|समूहों की सीधी सीमा।]] | ||
* | |||
== टिप्पणियाँ == | == टिप्पणियाँ == | ||
Revision as of 09:15, 15 March 2023
| Algebraic structure → Ring theory Ring theory |
|---|
 |
गणित में सीधी सीमा में कई छोटी वस्तुओं को एक बड़ी वस्तु में बदलने का तरीका है जो एक विशिष्ट तरीके से एक साथ रखी जाती है। ये वस्तुएँ समूह , वलय, सदिश स्थल या सामान्य रूप से किसी भी श्रेणी की वस्तुएँ हो सकती हैं जिस तरह से उन्हें एक साथ रखा जाता है वह उन छोटी वस्तुओं के बीच होमोमोर्फिज्म समूह समरूपता, वलय समरूपता या श्रेणी में सामान्य आकार की एक प्रणाली द्वारा निर्दिष्ट किया जाता है। वस्तुओं की सीधी सीमा , कहाँ कुछ निर्देशित सेट पर पर्वतमाला, द्वारा निरूपित किया गया है क्योंकि यह समरूपता की प्रणाली को दबा देता है जो कि सीमा की संरचना के लिए महत्वपूर्ण है।
प्रत्यक्ष सीमा श्रेणी सिद्धांत में सीमा श्रेणी सिद्धांतकी अवधारणा की एक विशेष स्थिति है। प्रत्यक्ष सीमाएं दोहरी श्रेणी सिद्धांत की व्युत्क्रम सीमा तक हैं जो श्रेणी सिद्धांत में सीमा श्रेणी सिद्धांत की एक विशेष स्थिति है।
औपचारिक परिभाषा
हम पहले समूह और प्रमापीय गणित जैसी बीजगणितीय संरचना की परिभाषा देंगे और फिर सामान्य परिभाषा देते हैं जिसका उपयोग किसी भी श्रेणी में किया जा सकता है।
बीजगणितीय वस्तुओं की प्रत्यक्ष सीमा
इस खंड में वस्तुओं को एक दिए गए बीजगणितीय संरचना से तैयार अंतर्निहित सेट से मिलकर समझा जाता है जैसे कि समूह गणित, वलय गणित, प्रमापीय गणित एक निश्चित वलय पर तथा एक क्षेत्र पर बीजगणित का एक निश्चित क्षेत्र होता है इसे ध्यान में रखते हुए कि समूह समरूपता से संबंधित समूह को समझा जाता है।
माना एक निर्देशित समूह हो तथा वस्तुएँ अनुक्रमणिका द्वारा निर्धारित परिवार बनें और सभी के लिए एक समरूपता निम्नलिखित गुणों के साथ हो-
फिर जोड़ी डायरेक्ट सिस्टम ओवर कहा जाता है .
प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा को आई द्वारा निरूपित किया जाता है और निम्नानुसार परिभाषित भी किया गया है। इसके अंतर्निहित समूह का असंयुक्त संघ है {{{1}}}:
एक मनमानी श्रेणी में प्रत्यक्ष सीमा
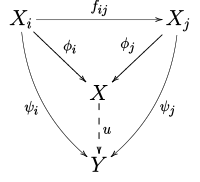
प्रत्यक्ष सीमा को मनमानी श्रेणी से परिभाषित किया जा सकता है एक सार्वभौमिक संपत्ति के माध्यम से वस्तुओं और आकारिता की एक सीधी प्रणाली बनें जैसा कि ऊपर परिभाषित किया गया है कि एक लक्ष्य एक जोड़ी है जहाँ एक्स एक वस्तु है और फाई तथा एक्स आकारिता हैं कि जब कभी भी प्रत्यक्ष प्रणाली की एक सीधी सीमा एक सार्वभौमिक रूप से विकर्षक लक्ष्य है तथी एक अद्वितीय आकारिता का आरेख इस प्रकार है
तब सभी आई जे के लिए क्रमविनिमेय आरेख होगा।
प्रत्यक्ष सीमा को अधिकतर
- दवा्रा निरूपित किया जाता है
प्रत्यक्ष प्रणाली को विहित रूपवाद समझा जा रहा है।
बीजगणितीय वस्तुओं के विपरीत मनमानी श्रेणी में प्रत्येक प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा नहीं होती है अगर ऐसा होता है तो प्रत्यक्ष सीमा एक मजबूत अर्थ में अद्वितीय है एक और सीधी सीमा एक्स दी गई है वहां एक अद्वितीय समरूपता एक्स' स्थित है जो विहित आकारिकी के साथ संचार करता है।
उदाहरण
- उपसमुच्चयों का संग्रह एम एक समूह है जिसमें एम सम्मिलित करके आंशिक आदेश हो सकता है यदि संग्रह निर्देशित है तो इसकी सीधी सीमा संघ है यूनियन एम आई किसी दिए गए समूह के उपसमूह के निर्देशित करके संग्रहित किया जाता है या किसी दिए गए वलय के सब्रिंग का निर्देशित संग्रह है।
- सीडब्ल्यू परिसर की कमजोर टोपोलॉजी को प्रत्यक्ष सीमा के रूप में परिभाषित किया गया है।
- इसमें एक्स बड़े तत्व के साथ कोई भी निर्देशित समूह हो एम किसी भी प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा आइसोमोर्फिक है और विहित आकारिता की एक समरूपता है।
- माना के एक क्षेत्र धनात्मक पूर्णांक एन के लिए सामान्य रैखिक समूह जिसमें उलटा प्रविष्टियों के साथ आव्यूह हमारे पास एक समूह समरूपता का विस्तार करता है निचले दाएं कोने में एक और अंतिम पंक्ति और कॉलम में शून्य लगाकर आव्यूह इस प्रणाली की प्रत्यक्ष सीमा के का सामान्य रैखिक समूह है जिसे जी एल के रूप में लिखा जाता है जीएल (के) के एक तत्व को अनंत व्युत्क्रमणीय आव्यूह के रूप में माना जा सकता है जो अनंत पहचान आव्यूह से केवल बहुत ही सूक्ष्म प्रविष्टियों में भिन्न होता है जो बीजगणितीय सिद्धांत में समूह का महत्व है।
- माना पी एक अविभाज्य संख्या है भागफल समूह से बनी प्रत्यक्ष प्रणाली पर विचार करें और समरूपता द्वारा प्रेरित इस प्रणाली की प्रत्यक्ष सीमा में आदेश की एकता की कुछ शक्ति की सभी जड़ें सम्मिलित हैं और इसे सुझाव समूह कहा जाता है .
- सममित बहुपद के वलय से एक गैर-स्पष्ट अंतःक्षेपी वलय समरूपता है सममित बहुपदों के वलय के लिए चर पद इस प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा बनाने से सममित कार्यों का वलय उत्पन्न करते हैं।
- यहाँ एफ एक व्याकुलता अंतरिछ एक्स पर एक सी-मूल्यवान समूह (गणित) हो एक्स में एक बिंदु एक्स है तथा एक्स के खुले एक निर्देशित समूह को समावेशन द्वारा आदेशित करते हैं संबंधित प्रत्यक्ष प्रणाली में एफ,आर जहां आर प्रतिबंध मानचित्र है इस प्रणाली की सीधी सीमा को एक्स पर एफ का भाग है जिसे एफ निरूपित किया जाता है एक्स के प्रत्येक यू के लिए विहित आकारिकी एफ (यू) पर एफ के एक खंड एस से संबद्ध है एक्स पर एस का रोगाणु गणित कहलाता है।
- अंतर्निहित सेट-सैद्धांतिक प्रत्यक्ष सीमा पर अंतिम टोपोलॉजी रखकर संस्स्थित रिक्त स्थान की श्रेणी में प्रत्यक्ष सीमाएं दी गई हैं।
- आखिरी योजना की आगमनात्मक सीमा है।
गुण
प्रत्यक्ष सीमाएँ व्युत्क्रम सीमाओं से जुड़ी होती हैं
एक महत्वपूर्ण संपत्ति यह हैप्रमापीय ्रेण में प्रत्यक्ष सीमाएं लेना एक सटीक फ़ैक्सीधा खंड लघु सटीकअर्थों की एक निर्देशित प्खंड़ोंीके से शुरू करते हैं और प्रत्यक्ष सीमाएँ ब तो आपको संक्षिप्त सटीक क्र प्राप्त होता है .
कए
ित निर्माण और सामान्यीकरण
हम ध्यान दें कि एक श्रेणी में एक प्रत्यक्ष प्रणाली functors के संदर्भ में एक वैकल्पिक विवरण स्वीकार करता है। कोई निर्देशित सेट एक छोटी श्रेणी के रूप में माना जा सकता है जिनकी वस्तुएं तत्व हैं और एक morphisms है अगर और केवल अगर . एक सीधा सिस्टम खत्म तब एक सहसंयोजक फ़ंक्टर के समान है . इस फ़ैक्टर की सीमा (श्रेणी सिद्धांत) मूल प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा के समान है।
प्रत्यक्ष सीमा से निकटता से जुड़ी एक धारणा फ़िल्टर्ड श्रेणी है। यहां हम एक सहसंयोजक फ़नकार के साथ शुरू करते हैं फ़िल्टर की गई श्रेणी से किसी वर्ग को और इस फ़ैक्टर का कोलिमिट बनाएं। कोई यह दिखा सकता है कि किसी श्रेणी की सभी निर्देशित सीमाएँ हैं यदि और केवल यदि उसके पास सभी फ़िल्टर किए गए कोलिमिट्स हैं, और ऐसी श्रेणी पर परिभाषित फ़ंक्टर सभी प्रत्यक्ष सीमाओं के साथ संचार करता है और यदि वह सभी फ़िल्टर किए गए कोलिमिट्स के साथ संचार करता है।[1] एक मनमानी श्रेणी दी गई , में डायरेक्ट सिस्टम हो सकते हैं जिसकी कोई सीधी सीमा नहीं है (उदाहरण के लिए परिमित समुच्चयों की श्रेणी, या परिमित रूप से उत्पन्न एबेलियन समूहों की श्रेणी पर विचार करें)। इस मामले में, हम हमेशा एम्बेड कर सकते हैं एक श्रेणी में जिसमें सभी प्रत्यक्ष सीमाएँ मौजूद हैं; की वस्तुएं कहलाते हैं इंडस्ट्रीज़ वस्तु | और-ऑब्जेक्ट्स ऑफ़ .
प्रत्यक्ष सीमा के दोहरे (श्रेणी सिद्धांत) को व्युत्क्रम सीमा कहा जाता है। जैसा कि ऊपर बताया गया है, व्युत्क्रम सीमाओं को कुछ फ़ैक्टरों की सीमाओं के रूप में देखा जा सकता है और ये सह-फ़िल्टर्ड श्रेणियों की सीमाओं से निकटता से संबंधित हैं।
शब्दावली
साहित्य में परिभाषित प्रत्यक्ष सीमा की अवधारणा के लिए निर्देशित सीमा प्रत्यक्ष आगमनात्मक सीमा, निर्देशित परिचालक, प्रत्यक्ष परिचालक और आगमनात्मक सीमा शब्द मिलते हैं आगमनात्मक सीमा शब्द अस्पष्ट है क्योंकि कुछ लेखक इसे परिचालक की सामान्य अवधारणा के लिए उपयोग करते हैं।
यह भी देखें
टिप्पणियाँ
- ↑ Adamek, J.; Rosicky, J. (1994). स्थानीय रूप से प्रस्तुत करने योग्य और सुलभ श्रेणियां (in English). Cambridge University Press. p. 15. ISBN 9780521422611.
संदर्भ
- Bourbaki, Nicolas (1968), Elements of mathematics. Theory of sets, Translated from French, Paris: Hermann, MR 0237342
- Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics, vol. 5 (2nd ed.), Springer-Verlag