प्रत्यक्ष सीमा

Template:प्रत्यक्ष सीमागणित की सीधी सीमा में कई छोटी वस्तुओं को एक बड़ी वस्तु से बदलने का एक सार्थक तरीका है जो एक विशिष्ट तरीके से एक साथ रखी जाती है। ये वस्तुएँ समूह , वलय, सदिश स्थल या सामान्य रूप से किसी भी श्रेणी की वस्तुएँ हो सकती हैं क्योंकि जिस तरह से उन्हें एक साथ रखा जाता है तो वह उन छोटी वस्तुओं के बीच होमोमोर्फिज्म समूह समरूपता, वलय समरूपता या श्रेणी में सामान्य आकार की एक प्रणाली द्वारा निर्दिष्ट किया जाता है। वस्तुओं की सीधी सीमा में कुछ निर्देशित समूह पर पर्वतमाला आई द्वारा निरूपित किया गया है क्योंकि यह समरूपता की प्रणाली को दबा देता है जो कि सीमा की संरचना के लिए महत्वपूर्ण है।

प्रत्यक्ष सीमा श्रेणी सिद्धांत में सीमा श्रेणी सिद्धांतकी अवधारणा की एक विशेष स्थिति है। प्रत्यक्ष सीमाएं दोहरी श्रेणी सिद्धांत की व्युत्क्रम सीमा तक हैं जो श्रेणी सिद्धांत में सीमा श्रेणी सिद्धांत की एक विशेष स्थिति है।

औपचारिक परिभाषा

हम पहले समूह और प्रमापीय गणित बीजगणितीय संरचना की परिभाषा देते हैं। फिर सामान्य परिभाषा देते हैं जिसका उपयोग किसी भी श्रेणी में किया जा सकता है।

बीजगणितीय वस्तुओं की प्रत्यक्ष सीमा

इस खंड में वस्तुओं को एक दिए गए बीजगणितीय संरचना से तैयार अंतर्निहित समूह से मिलाकर समझा जाता है जैसे कि समूह गणित, वलय गणित, प्रमापीय गणित एक निश्चित वलय पर तथा एक क्षेत्र पर बीजगणित का एक निश्चित क्षेत्र होता है जबकि समूह समरूपता से संबंधित समूह को समझा जाता है।

माना एक निर्देशित समूह तथा वस्तुएँ अनुक्रमणिका द्वारा निर्धारित परिवार बनें और सभी के लिए एक समरूपता निम्नलिखित गुणों के साथ हो-

फिर जोड़ी को सीधी प्रणाली कहा जाता है।

प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा को आई द्वारा निरूपित किया जाता है और निम्नानुसार परिभाषित भी किया गया है। इसके अंतर्निहित समूह में एक असंयुक्त संघ भी सम्मिलित है।

{{{1}}}:

एक मनमानी श्रेणी में प्रत्यक्ष सीमा

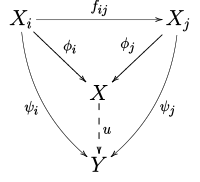
प्रत्यक्ष सीमा को मनमानी श्रेणी से परिभाषित किया जा सकता है एक सार्वभौमिक संपत्ति के माध्यम से वस्तुओं और आकारिता की एक सीधी प्रणाली बनें जैसा कि ऊपर परिभाषित किया गया है कि एक लक्ष्य एक जोड़ी है जहाँ एक्स एक वस्तु है और फाई तथा एक्स आकारिता हैं कि जब कभी भी प्रत्यक्ष प्रणाली की एक सीधी सीमा एक सार्वभौमिक रूप से विकर्षक लक्ष्य है तथी एक अद्वितीय आकारिता का आरेख इस प्रकार है

तब सभी आई जे के लिए क्रमविनिमेय आरेख होगा।

प्रत्यक्ष सीमा को अधिकतर

$X=\varinjlim X_{i}$ दवा्रा निरूपित किया जाता है

प्रत्यक्ष प्रणाली को विहित रूपवाद समझा जा रहा है।

बीजगणितीय वस्तुओं के विपरीत मनमानी श्रेणी में प्रत्येक प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा नहीं होती है अगर ऐसा होता है तो प्रत्यक्ष सीमा एक मजबूत अर्थ में अद्वितीय है एक और सीधी सीमा एक्स दी गई है वहां एक अद्वितीय समरूपता एक्स' स्थित है जो विहित आकारिकी के साथ संचार करता है।

उदाहरण

• उपसमुच्चयों का संग्रह एम एक समूह है जिसमें एम सम्मिलित करके आंशिक आदेश हो सकता है यदि संग्रह निर्देशित है तो इसकी सीधी सीमा संघ है यूनियन एम आई किसी दिए गए समूह के उपसमूह के निर्देशित करके संग्रहित किया जाता है या किसी दिए गए वलय के सब्रिंग का निर्देशित संग्रह है।
• सीडब्ल्यू परिसर की कमजोर टोपोलॉजी को प्रत्यक्ष सीमा के रूप में परिभाषित किया गया है।
• इसमें एक्स बड़े तत्व के साथ कोई भी निर्देशित समूह हो एम किसी भी प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा आइसोमोर्फिक है और विहित आकारिता की एक समरूपता है।
• माना के एक क्षेत्र धनात्मक पूर्णांक एन के लिए सामान्य रैखिक समूह जिसमें उलटा प्रविष्टियों के साथ आव्यूह हमारे पास एक समूह समरूपता का विस्तार करता है निचले दाएं कोने में एक और अंतिम पंक्ति और कॉलम में शून्य लगाकर आव्यूह इस प्रणाली की प्रत्यक्ष सीमा के का सामान्य रैखिक समूह है जिसे जी एल के रूप में लिखा जाता है जीएल (के) के एक तत्व को अनंत व्युत्क्रमणीय आव्यूह के रूप में माना जा सकता है जो अनंत पहचान आव्यूह से केवल बहुत ही सूक्ष्म प्रविष्टियों में भिन्न होता है जो बीजगणितीय सिद्धांत में समूह का महत्व है।
• माना पी एक अविभाज्य संख्या है भागफल समूह से बनी प्रत्यक्ष प्रणाली पर विचार करें और समरूपता द्वारा प्रेरित इस प्रणाली की प्रत्यक्ष सीमा में आदेश की एकता की कुछ शक्ति की सभी जड़ें सम्मिलित हैं और इसे सुझाव समूह कहा जाता है .
• सममित बहुपद के वलय से एक गैर-स्पष्ट अंतःक्षेपी वलय समरूपता है सममित बहुपदों के वलय के लिए चर पद इस प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा बनाने से सममित कार्यों का वलय उत्पन्न करते हैं।
• यहाँ एफ एक व्याकुलता अंतरिछ एक्स पर एक सी-मूल्यवान समूह (गणित) हो और एक्स में एक बिंदु एक्स है तथा एक्स के खुले एक निर्देशित समूह को समावेशन द्वारा प्रदर्शित करते हैं संबंधित प्रत्यक्ष प्रणाली में एफ,आर है जहां आर प्रतिबंध मानचित्र है इस प्रणाली की सीधी सीमा को एक्स पर एफ का भाग है जिसे एफ द्वारा निरूपित किया जाता है एक्स के प्रत्येक यू के लिए विहित आकारिकी एफ (यू) पर एफ के एक खंड एस से संबद्ध है एक्स पर एस का रोगाणु गणित कहलाता है।
• अंतर्निहित सेट-सैद्धांतिक प्रत्यक्ष सीमा पर अंतिम टोपोलॉजी रखकर संस्स्थित रिक्त स्थान की श्रेणी में प्रत्यक्ष सीमाएं दी गई हैं।
• आखिरी योजना की आगमनात्मक सीमा है।

गुण

प्रत्यक्ष सीमाएँ व्युत्क्रम सीमाओं से जुड़ी होती हैं

एक महत्वपूर्ण संपत्ति यह है कि प्रमापीय में प्रत्यक्ष सीमाएं लेना एक सीधा संक्षिप्त खंड प्राप्त होता है

प्रत्यक्ष निर्माण और सामान्यीकरण

यदि एक श्रेणी में एक प्रत्यक्ष प्रणाली सी खंड के संदर्भ में एक वैकल्पिक विवरण स्वीकार करता है तो निर्देशित सेट एक छोटी श्रेणी के रूप में माना जा सकता है आई जिनकी वस्तुएं हैं और एक्स आकारिता हैं एक सीधी प्रणाली के समान है इस खंड की सीमा मूल प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा के समान है।

शब्दावली

साहित्य में परिभाषित प्रत्यक्ष सीमा की अवधारणा के लिए निर्देशित सीमा प्रत्यक्ष आगमनात्मक सीमा, निर्देशित परिचालक, प्रत्यक्ष परिचालक और आगमनात्मक सीमा शब्द मिलते हैं आगमनात्मक सीमा शब्द अस्पष्ट है क्योंकि कुछ लेखक इसे परिचालक की सामान्य अवधारणा के लिए उपयोग करते हैं।

यह भी देखें

• समूहों की सीधी सीमा।

संदर्भ

• Bourbaki, Nicolas (1968), Elements of mathematics. Theory of sets, Translated from French, Paris: Hermann, MR 0237342
• Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics, vol. 5 (2nd ed.), Springer-Verlag