प्रत्यक्ष सीमा: Difference between revisions

From Vigyanwiki
No edit summary
No edit summary
 
(15 intermediate revisions by 4 users not shown)
Line 1: Line 1:
{{Short description|Special case of colimit in category theory}}
{{Short description|Special case of colimit in category theory}}
{{Ring theory sidebar}}
गणित की सीधी सीमा में कई छोटी वस्तुओं को एक बड़ी वस्तु से बदलने का एक सार्थक तरीका है जो एक विशिष्ट स्थान में एक साथ रखी जाती है। ये वस्तुएँ [[समूह (गणित)|समूह]] , वलय, [[ सदिश स्थल |सदिश स्थल]] या सामान्य रूप से किसी भी [[श्रेणी (गणित)|श्रेणी]] की वस्तुएँ हो सकती हैं क्योंकि जिस तरह से उन्हें एक साथ रखा जाता है तो वह उन छोटी वस्तुओं के बीच होमोमोर्फिज्म समूह [[समरूपता]], [[रिंग समरूपता|वलय समरूपता]] या श्रेणी में सामान्य आकार की एक प्रणाली द्वारा निर्दिष्ट किया जाता है। वस्तुओं की सीधी सीमा में कुछ [[निर्देशित सेट|निर्देशित समूह]] पर पर्वतमाला आई द्वारा निरूपित किया गया है क्योंकि यह समरूपता की प्रणाली को दबा देता है जो कि सीमा की संरचना के लिए महत्वपूर्ण है।
गणित में सीधी सीमा में कई छोटी वस्तुओं को एक बड़ी वस्तु में बदलने का तरीका है जो एक विशिष्ट तरीके से एक साथ रखी जाती है। ये वस्तुएँ [[समूह (गणित)|समूह]] , वलय, [[ सदिश स्थल |सदिश स्थल]] या सामान्य रूप से किसी भी [[श्रेणी (गणित)|श्रेणी]] की वस्तुएँ हो सकती हैं जिस तरह से उन्हें एक साथ रखा जाता है वह उन छोटी वस्तुओं के बीच होमोमोर्फिज्म समूह [[समरूपता]], [[रिंग समरूपता|वलय समरूपता]] या श्रेणी में सामान्य आकार की एक प्रणाली द्वारा निर्दिष्ट किया जाता है। वस्तुओं की सीधी सीमा <math>A_i</math>, कहाँ <math>i</math> कुछ [[निर्देशित सेट]] पर पर्वतमाला<math>I</math>, द्वारा निरूपित किया गया है <math>\varinjlim A_i </math> क्योंकि यह समरूपता की प्रणाली को दबा देता है जो कि सीमा की संरचना के लिए महत्वपूर्ण है।


प्रत्यक्ष सीमा [[श्रेणी सिद्धांत]] में [[सीमा (श्रेणी सिद्धांत)|सीमा श्रेणी सिद्धांत]]की अवधारणा की एक विशेष स्थिति है। प्रत्यक्ष सीमाएं [[दोहरी (श्रेणी सिद्धांत)|दोहरी श्रेणी सिद्धांत]] की व्युत्क्रम सीमा तक हैं जो श्रेणी सिद्धांत में सीमा श्रेणी सिद्धांत की एक विशेष स्थिति है।
प्रत्यक्ष सीमा [[श्रेणी सिद्धांत]] में [[सीमा (श्रेणी सिद्धांत)|सीमा श्रेणी सिद्धांत]]की अवधारणा की एक विशेष स्थिति है। प्रत्यक्ष सीमाएं [[दोहरी (श्रेणी सिद्धांत)|दोहरी श्रेणी सिद्धांत]] की व्युत्क्रम सीमा तक हैं जो श्रेणी सिद्धांत में सीमा श्रेणी सिद्धांत की एक विशेष स्थिति है।


== औपचारिक परिभाषा ==
== औपचारिक परिभाषा ==
हम पहले समूह (गणित) और [[मॉड्यूल (गणित)]] जैसी [[बीजगणितीय संरचना]] की परिभाषा देंगे, और फिर सामान्य परिभाषा, जिसका उपयोग किसी भी श्रेणी (गणित) में किया जा सकता है।
हम पहले समूह और [[मॉड्यूल (गणित)|प्रमापीय गणि]]त  [[बीजगणितीय संरचना]] की परिभाषा देते हैं। फिर सामान्य परिभाषा देते हैं जिसका उपयोग किसी भी श्रेणी में किया जा सकता है।


=== बीजगणितीय वस्तुओं की प्रत्यक्ष सीमा ===
=== बीजगणितीय वस्तुओं की प्रत्यक्ष सीमा ===
इस खंड में वस्तुओं को एक दिए गए बीजगणितीय संरचना से लैस अंतर्निहित [[सेट (गणित)]] से मिलकर समझा जाता है, जैसे कि समूह (गणित), वलय (गणित), मॉड्यूल (गणित) (एक निश्चित वलय पर), [[एक क्षेत्र पर बीजगणित]] (ऊपर) एक निश्चित [[क्षेत्र (गणित)]]), आदि। इसे ध्यान में रखते हुए, समरूपता को संबंधित सेटिंग (समूह समरूपता, आदि) में समझा जाता है।
इस खंड में वस्तुओं को एक दिए गए बीजगणितीय संरचना से तैयार अंतर्निहित [[सेट (गणित)|समूह]] से मिलाकर समझा जाता है जैसे कि समूह गणित, वलय गणित, प्रमापीय गणित एक निश्चित वलय पर तथा [[एक क्षेत्र पर बीजगणित]] का एक निश्चित [[क्षेत्र (गणित)|क्षेत्र]] होता है जबकि समूह समरूपता से संबंधित समूह को समझा जाता है।


होने देना <math>\langle I,\le\rangle</math> एक निर्देशित सेट हो। होने देना <math>\{A_i : i\in I\}</math> ऑब्जेक्ट इंडेक्स द्वारा निर्धारित परिवार बनें <math>I\,</math> और <math> f_{ij}\colon A_i \rightarrow A_j </math> सभी के लिए एक समरूपता हो <math>i \le j</math> निम्नलिखित गुणों के साथ:
माना एक निर्देशित समूह तथा वस्तुएँ अनुक्रमणिका द्वारा निर्धारित परिवार बनें और   सभी के लिए एक समरूपता निम्नलिखित गुणों के साथ हो-
# <math>f_{ii}\,</math> की पहचान है <math>A_i\,</math>, और
#
# <math>f_{ik}= f_{jk}\circ f_{ij}</math> सभी के लिए <math>i\le j\le k</math>.
फिर जोड़ी को  सीधी प्रणाली कहा जाता है।
फिर जोड़ी <math>\langle A_i,f_{ij}\rangle</math> डायरेक्ट सिस्टम ओवर कहा जाता है <math>I</math>.


प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा <math>\langle A_i,f_{ij}\rangle</math> द्वारा निरूपित किया जाता है <math>\varinjlim A_i</math> और निम्नानुसार परिभाषित किया गया है। इसका अंतर्निहित सेट का असंयुक्त संघ है <math>A_i</math>का मोडुलो (शब्दजाल) एक निश्चित {{nowrap|[[equivalence relation]] <math>\sim\,</math>}}:
प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा को आई द्वारा निरूपित किया जाता है और निम्नानुसार परिभाषित भी किया गया है। इसके अंतर्निहित समूह में एक असंयुक्त संघ भी सम्मिलित है।


:<math>\varinjlim A_i = \bigsqcup_i A_i\bigg/\sim.</math>
{{nowrap}}:
यहाँ, अगर <math>x_i\in A_i</math> और <math>x_j\in A_j</math>, तब <math>x_i\sim\, x_j</math> अगर और केवल अगर कुछ है <math>k\in I</math> साथ <math>i \le k</math> और <math>j \le k</math> ऐसा है कि <math>f_{ik}(x_i) = f_{jk}(x_j)\,</math>.
सहज रूप से, असंयुक्त संघ में दो तत्व समान होते हैं यदि और केवल यदि वे अंततः प्रत्यक्ष प्रणाली में समान हो जाते हैं। एक समतुल्य सूत्रीकरण जो द्वैत को व्युत्क्रम सीमा तक उजागर करता है, वह यह है कि एक तत्व प्रत्यक्ष प्रणाली के नक्शे के तहत अपनी सभी छवियों के बराबर है, अर्थात। <math>x_i\sim\, f_{ij}(x_i)</math> जब कभी भी <math>i \le j</math>.


कोई इस परिभाषा से कैनोनिकल फ़ंक्शंस प्राप्त करता है <math>\phi_j \colon A_j\rightarrow \varinjlim A_i</math> प्रत्येक तत्व को उसके तुल्यता वर्ग में भेजना। बीजगणितीय संक्रियाएँ चालू हैं <math>\varinjlim A_i\,</math> इस प्रकार परिभाषित किया जाता है कि ये मानचित्र समाकारिता बन जाते हैं। औपचारिक रूप से, प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा <math>\langle A_i,f_{ij}\rangle</math> वस्तु से मिलकर बनता है <math>\varinjlim A_i</math> एक साथ विहित समरूपता के साथ <math>\phi_j \colon A_j\rightarrow \varinjlim A_i</math>.
:


=== एक मनमानी श्रेणी में प्रत्यक्ष सीमा ===
=== एक मनमानी श्रेणी में प्रत्यक्ष सीमा ===
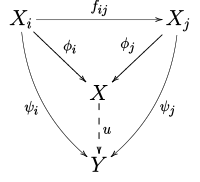
प्रत्यक्ष सीमा को मनमानी श्रेणी (गणित) में परिभाषित किया जा सकता है <math>\mathcal{C}</math> एक [[सार्वभौमिक संपत्ति]] के माध्यम से। होने देना <math>\langle X_i, f_{ij}\rangle</math> वस्तुओं और morphisms की एक सीधी प्रणाली बनें <math>\mathcal{C}</math> (जैसा कि ऊपर परिभाषित किया गया है)। एक लक्ष्य एक जोड़ी है <math>\langle X, \phi_i\rangle</math> कहाँ <math>X\,</math> में एक वस्तु है <math>\mathcal{C}</math> और <math>\phi_i\colon X_i\rightarrow X</math> प्रत्येक के लिए morphisms हैं <math>i\in I</math> ऐसा है कि <math>\phi_i =\phi_j \circ f_{ij}</math> जब कभी भी <math>i \le j</math>. प्रत्यक्ष प्रणाली की एक सीधी सीमा <math>\langle X_i, f_{ij}\rangle</math> एक सार्वभौमिक रूप से विकर्षक लक्ष्य है <math>\langle X, \phi_i\rangle</math> इस अर्थ में कि <math>\langle X, \phi_i\rangle</math> एक लक्ष्य है और प्रत्येक लक्ष्य के लिए <math>\langle Y, \psi_i\rangle</math>, एक अद्वितीय morphism है <math> u\colon X\rightarrow Y</math> ऐसा है कि <math>u\circ \phi_i=\psi_i</math> प्रत्येक मैं के लिए निम्नलिखित आरेख
प्रत्यक्ष सीमा को मनमानी श्रेणी से परिभाषित किया जा सकता है एक [[सार्वभौमिक संपत्ति]] के माध्यम से वस्तुओं और आकारिता की एक सीधी प्रणाली बनें जैसा कि ऊपर परिभाषित किया गया है कि एक लक्ष्य एक जोड़ी है जहाँ एक्स एक वस्तु है और फाई तथा एक्स आकारिता हैं कि जब कभी भी प्रत्यक्ष प्रणाली की एक सीधी सीमा एक सार्वभौमिक रूप से विकर्षक लक्ष्य है तथी एक अद्वितीय आकारिता का आरेख इस प्रकार है
<div शैली = पाठ-संरेखण: केंद्र; >[[Image:Direct limit category.svg]]</div>
<div शैली = पाठ-संरेखण: केंद्र; >[[Image:Direct limit category.svg]]</div>
तब सभी i, j के लिए [[क्रमविनिमेय आरेख]] होगा।
तब सभी आई जे के लिए [[क्रमविनिमेय आरेख]] होगा।


प्रत्यक्ष सीमा को अक्सर निरूपित किया जाता है
प्रत्यक्ष सीमा को अधिकतर
:<math>X = \varinjlim X_i</math>
:<math>X = \varinjlim X_i</math> दवा्रा निरूपित किया जाता है
प्रत्यक्ष प्रणाली के साथ <math>\langle X_i, f_{ij}\rangle</math> और विहित morphisms <math>\phi_i</math> समझा जा रहा है।
प्रत्यक्ष प्रणाली को विहित रूपवाद समझा जा रहा है।


बीजगणितीय वस्तुओं के विपरीत, मनमानी श्रेणी में प्रत्येक प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा नहीं होती है। अगर ऐसा होता है, हालांकि, प्रत्यक्ष सीमा एक मजबूत अर्थ में अद्वितीय है: एक और सीधी सीमा एक्स' दी गई है, वहां एक अद्वितीय समरूपता एक्स' → एक्स मौजूद है जो कैनोनिकल आकारिकी के साथ संचार करता है।
बीजगणितीय वस्तुओं के विपरीत मनमानी श्रेणी में प्रत्येक प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा नहीं होती है अगर ऐसा होता है तो प्रत्यक्ष सीमा एक मजबूत अर्थ में अद्वितीय है एक और सीधी सीमा एक्स दी गई है वहां एक अद्वितीय समरूपता एक्स' स्थित है जो विहित आकारिकी के साथ संचार करता है।


== उदाहरण ==
== उदाहरण ==
*उपसमुच्चयों का संग्रह <math>M_i</math> एक सेट का <math>M</math> शामिल करके [[आंशिक आदेश]] हो सकता है। यदि संग्रह निर्देशित है, तो इसकी सीधी सीमा संघ है <math>\bigcup M_i</math>. किसी दिए गए समूह के [[उपसमूह]] के निर्देशित संग्रह के लिए भी यही सच है, या किसी दिए गए अंगूठी के [[सब्रिंग]] का निर्देशित संग्रह आदि।
*उपसमुच्चयों का संग्रह एम एक समूह है जिसमें एम सम्मिलित करके [[आंशिक आदेश]] हो सकता है यदि संग्रह निर्देशित है तो इसकी सीधी सीमा संघ है यूनियन एम आई किसी दिए गए समूह के [[उपसमूह]] के निर्देशित करके संग्रहित किया जाता है या किसी दिए गए वलय के [[सब्रिंग]] का निर्देशित संग्रह है।
* [[सीडब्ल्यू कॉम्प्लेक्स]] की [[कमजोर टोपोलॉजी]] को प्रत्यक्ष सीमा के रूप में परिभाषित किया गया है।
* [[सीडब्ल्यू कॉम्प्लेक्स|सीडब्ल्यू परिसर]] की [[कमजोर टोपोलॉजी]] को प्रत्यक्ष सीमा के रूप में परिभाषित किया गया है।
*होने देना <math>X</math> सबसे बड़े तत्व के साथ कोई भी निर्देशित सेट हो <math>m</math>. किसी भी प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा आइसोमोर्फिक है <math>X_m</math> और विहित morphism <math>\phi_m: X_m \rightarrow X</math> एक समरूपता है।
*इसमें एक्स बड़े तत्व के साथ कोई भी निर्देशित समूह हो एम किसी भी प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा आइसोमोर्फिक है और विहित आकारिता की एक समरूपता है।
*मान लीजिए K एक क्षेत्र है। एक धनात्मक पूर्णांक n के लिए, [[सामान्य रैखिक समूह]] GL(n;K) पर विचार करें जिसमें उलटा n x n - K से प्रविष्टियों के साथ मेट्रिसेस शामिल हैं। हमारे पास एक समूह समरूपता GL(n;K) → GL(n+1;K) है जो विस्तार करता है निचले दाएं कोने में 1 और अंतिम पंक्ति और कॉलम में कहीं और शून्य लगाकर मैट्रिसेस। इस प्रणाली की प्रत्यक्ष सीमा K का सामान्य रैखिक समूह है, जिसे GL(K) के रूप में लिखा जाता है। जीएल (के) के एक तत्व को अनंत व्युत्क्रमणीय मैट्रिक्स के रूप में माना जा सकता है जो अनंत पहचान मैट्रिक्स से केवल बहुत ही सूक्ष्म प्रविष्टियों में भिन्न होता है। बीजगणितीय K-सिद्धांत में समूह GL(K) का महत्वपूर्ण महत्व है।
*माना के एक क्षेत्र धनात्मक पूर्णांक एन के लिए [[सामान्य रैखिक समूह]] जिसमें उलटा प्रविष्टियों के साथ आव्यूह हमारे पास एक समूह समरूपता का विस्तार करता है निचले दाएं कोने में एक और अंतिम पंक्ति और कॉलम में शून्य लगाकर आव्यूह इस प्रणाली की प्रत्यक्ष सीमा के का सामान्य रैखिक समूह है जिसे जी एल के रूप में लिखा जाता है जीएल (के) के एक तत्व को अनंत व्युत्क्रमणीय आव्यूह के रूप में माना जा सकता है जो अनंत पहचान आव्यूह से केवल बहुत ही सूक्ष्म प्रविष्टियों में भिन्न होता है जो बीजगणितीय सिद्धांत में समूह का महत्व है।
*माना पी एक अविभाज्य संख्या है। भागफल समूह से बनी प्रत्यक्ष प्रणाली पर विचार करें <math>\mathbb{Z}/p^n\mathbb{Z}</math> और समरूपता <math>\mathbb{Z}/p^n\mathbb{Z} \rightarrow \mathbb{Z}/p^{n+1}\mathbb{Z}</math> गुणा द्वारा प्रेरित <math>p</math>. इस प्रणाली की प्रत्यक्ष सीमा में आदेश की एकता की कुछ शक्ति की सभी जड़ें शामिल हैं <math>p</math>, और इसे प्रूफ़र समूह कहा जाता है <math>\mathbb{Z}(p^\infty)</math>.
*माना पी एक अविभाज्य संख्या है भागफल समूह से बनी प्रत्यक्ष प्रणाली पर विचार करें और समरूपता द्वारा प्रेरित इस प्रणाली की प्रत्यक्ष सीमा में आदेश की एकता की कुछ शक्ति की सभी जड़ें सम्मिलित हैं और इसे सुझाव समूह कहा जाता है .
* [[सममित बहुपद]] के वलय से एक (गैर-स्पष्ट) अंतःक्षेपी वलय समरूपता है <math>n</math> सममित बहुपदों की अंगूठी के लिए चर <math>n + 1</math> चर। इस प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा बनाने से सममित कार्यों की अंगूठी उत्पन्न होती है।
* [[सममित बहुपद]] के वलय से एक गैर-स्पष्ट अंतःक्षेपी वलय समरूपता है सममित बहुपदों के वलय के लिए चर पद इस प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा बनाने से सममित कार्यों का वलय उत्पन्न करते हैं।
*चलो एफ एक [[टोपोलॉजिकल स्पेस]] एक्स पर एक सी-मूल्यवान [[शीफ (गणित)]] हो। एक्स में एक बिंदु एक्स को ठीक करें। एक्स के खुले पड़ोस एक निर्देशित सेट को समावेशन द्वारा आदेशित करते हैं (यू ≤ वी अगर और केवल अगर यू में वी होता है)। संबंधित प्रत्यक्ष प्रणाली है (एफ(यू), आर<sub>''U'',''V''</sub>) जहां r प्रतिबंध मानचित्र है। इस प्रणाली की सीधी सीमा को एक्स पर एफ का [[डंठल (गणित)]] कहा जाता है, जिसे एफ निरूपित किया जाता है<sub>''x''</sub>. एक्स के प्रत्येक पड़ोस यू के लिए, विहित आकारिकी एफ (यू) → एफ<sub>''x''</sub> यू के एक तत्व एस पर एफ के एक खंड एस से संबद्ध है<sub>''x''</sub> डंठल की एफ<sub>''x''</sub> x पर s का [[रोगाणु (गणित)]] कहलाता है।
*यहाँ एफ एक [[टोपोलॉजिकल स्पेस|व्याकुलता अंतरिछ]] एक्स पर एक सी-मूल्यवान [[शीफ (गणित)|समूह (गणित)]] हो और एक्स में एक बिंदु एक्स है तथा एक्स के खुले एक निर्देशित समूह को समावेशन द्वारा प्रदर्शित करते हैं संबंधित प्रत्यक्ष प्रणाली में एफ,आर है जहां आर प्रतिबंध मानचित्र है इस प्रणाली की सीधी सीमा को एक्स पर एफ का भाग है जिसे एफ द्वारा निरूपित किया जाता है एक्स के प्रत्येक यू के लिए विहित आकारिकी एफ (यू) पर एफ के एक खंड एस से संबद्ध है एक्स पर एस का [[रोगाणु (गणित)|रोगाणु गणित]] कहलाता है।
*अंतर्निहित सेट-सैद्धांतिक प्रत्यक्ष सीमा पर [[अंतिम टोपोलॉजी]] रखकर टोपोलॉजिकल रिक्त स्थान की श्रेणी में प्रत्यक्ष सीमाएं दी गई हैं।
*अंतर्निहित सेट-सैद्धांतिक प्रत्यक्ष सीमा पर [[अंतिम टोपोलॉजी]] रखकर संस्स्थित रिक्त स्थान की श्रेणी में प्रत्यक्ष सीमाएं दी गई हैं।
*इंड-स्कीम, स्कीमों की आगमनात्मक सीमा है।
*आखिरी योजना की आगमनात्मक सीमा है।


== गुण ==
== गुण ==
प्रत्यक्ष सीमाएँ व्युत्क्रम सीमाओं से जुड़ी होती हैं
प्रत्यक्ष सीमाएँ व्युत्क्रम सीमाओं से जुड़ी होती हैं


:<math>\mathrm{Hom} (\varinjlim X_i, Y) = \varprojlim \mathrm{Hom} (X_i, Y).</math>
:
एक महत्वपूर्ण संपत्ति यह है कि मॉड्यूल (गणित) की श्रेणी में प्रत्यक्ष सीमाएं लेना एक सटीक फ़ैक्टर है। इसका मतलब यह है कि यदि आप लघु सटीक अनुक्रमों की एक निर्देशित प्रणाली से शुरू करते हैं <math>0 \to A_i \to B_i \to C_i \to 0</math> और प्रत्यक्ष सीमाएँ बनाते हैं, तो आपको एक संक्षिप्त सटीक क्रम प्राप्त होता है <math>0 \to \varinjlim A_i \to \varinjlim B_i \to \varinjlim C_i \to 0</math>.
एक महत्वपूर्ण संपत्ति यह है कि प्रमापीय में प्रत्यक्ष सीमाएं लेना एक सीधा संक्षिप्त खंड प्राप्त होता है  


== संबंधित निर्माण और सामान्यीकरण ==
== प्रत्यक्ष निर्माण और सामान्यीकरण ==
हम ध्यान दें कि एक श्रेणी में एक प्रत्यक्ष प्रणाली <math>\mathcal{C}</math> [[functor]]s के संदर्भ में एक वैकल्पिक विवरण स्वीकार करता है। कोई निर्देशित सेट <math>\langle I,\le \rangle</math> एक [[छोटी श्रेणी]] के रूप में माना जा सकता है <math>\mathcal{I}</math> जिनकी वस्तुएं तत्व हैं <math>I</math> और एक morphisms है  <math>i\rightarrow j</math> [[अगर और केवल अगर]] <math>i\le j</math>. एक सीधा सिस्टम खत्म <math>I</math> तब एक सहसंयोजक फ़ंक्टर के समान है <math>\mathcal{I}\rightarrow \mathcal{C}</math>. इस फ़ैक्टर की सीमा (श्रेणी सिद्धांत) मूल प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा के समान है।
यदि एक श्रेणी में एक प्रत्यक्ष प्रणाली सी खंड के संदर्भ में एक वैकल्पिक विवरण स्वीकार करता है तो निर्देशित सेट एक [[छोटी श्रेणी]] के रूप में माना जा सकता है आई जिनकी वस्तुएं हैं और एक्स आकारिता हैं एक सीधी प्रणाली के समान है इस खंड की सीमा मूल प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा के समान है।
 
प्रत्यक्ष सीमा से निकटता से जुड़ी एक धारणा फ़िल्टर्ड श्रेणी है। यहां हम एक सहसंयोजक फ़नकार के साथ शुरू करते हैं <math>\mathcal J \to \mathcal C</math> फ़िल्टर की गई श्रेणी से <math>\mathcal J</math> किसी वर्ग को <math>\mathcal{C}</math> और इस फ़ैक्टर का कोलिमिट बनाएं। कोई यह दिखा सकता है कि किसी श्रेणी की सभी निर्देशित सीमाएँ हैं यदि और केवल यदि उसके पास सभी फ़िल्टर किए गए कोलिमिट्स हैं, और ऐसी श्रेणी पर परिभाषित फ़ंक्टर सभी प्रत्यक्ष सीमाओं के साथ संचार करता है और यदि वह सभी फ़िल्टर किए गए कोलिमिट्स के साथ संचार करता है।<ref>{{Cite book|url=https://books.google.com/books?id=iXh6rOd7of0C|title=स्थानीय रूप से प्रस्तुत करने योग्य और सुलभ श्रेणियां|last1=Adamek|first1=J.|last2=Rosicky|first2=J.|publisher=Cambridge University Press|year=1994|location=|pages=15|isbn=9780521422611|language=en}}</ref>
एक मनमानी श्रेणी दी गई <math>\mathcal{C}</math>, में डायरेक्ट सिस्टम हो सकते हैं <math>\mathcal{C}</math> जिसकी कोई सीधी सीमा नहीं है <math>\mathcal{C}</math> (उदाहरण के लिए परिमित समुच्चयों की श्रेणी, या परिमित रूप से उत्पन्न एबेलियन समूहों की श्रेणी पर विचार करें)। इस मामले में, हम हमेशा एम्बेड कर सकते हैं <math>\mathcal{C}</math> एक श्रेणी में <math>\text{Ind}(\mathcal{C})</math> जिसमें सभी प्रत्यक्ष सीमाएँ मौजूद हैं; की वस्तुएं  <math>\text{Ind}(\mathcal{C})</math> कहलाते हैं [[इंडस्ट्रीज़ वस्तु]] | और-ऑब्जेक्ट्स ऑफ़  <math>\mathcal{C}</math>.
 
प्रत्यक्ष सीमा के दोहरे (श्रेणी सिद्धांत) को व्युत्क्रम सीमा कहा जाता है। जैसा कि ऊपर बताया गया है, व्युत्क्रम सीमाओं को कुछ फ़ैक्टरों की सीमाओं के रूप में देखा जा सकता है और ये सह-फ़िल्टर्ड श्रेणियों की सीमाओं से निकटता से संबंधित हैं।


== शब्दावली ==
== शब्दावली ==
साहित्य में, ऊपर परिभाषित प्रत्यक्ष सीमा की अवधारणा के लिए निर्देशित सीमा, प्रत्यक्ष आगमनात्मक सीमा, निर्देशित कोलिमिट, प्रत्यक्ष कोलिमिट और आगमनात्मक सीमा शब्द मिलते हैं। आगमनात्मक सीमा शब्द अस्पष्ट है, क्योंकि कुछ लेखक इसे कोलिमिट की सामान्य अवधारणा के लिए उपयोग करते हैं।
साहित्य में परिभाषित प्रत्यक्ष सीमा की अवधारणा के लिए निर्देशित सीमा प्रत्यक्ष आगमनात्मक सीमा, निर्देशित परिचालक, प्रत्यक्ष परिचालक और आगमनात्मक सीमा शब्द मिलते हैं आगमनात्मक सीमा शब्द अस्पष्ट है क्योंकि कुछ लेखक इसे परिचालक की सामान्य अवधारणा के लिए उपयोग करते हैं।


== यह भी देखें ==
== यह भी देखें ==


* [[समूहों की प्रत्यक्ष सीमा]]
* [[समूहों की प्रत्यक्ष सीमा|समूहों की सीधी सीमा।]]
*


== टिप्पणियाँ ==
== टिप्पणियाँ ==
Line 75: Line 67:
* {{Citation |last=Mac Lane |first=Saunders |authorlink=Saunders Mac Lane |year=1998 |title=[[Categories for the Working Mathematician]] |edition=2nd |series=[[Graduate Texts in Mathematics]] |volume=5 |publisher=Springer-Verlag}}
* {{Citation |last=Mac Lane |first=Saunders |authorlink=Saunders Mac Lane |year=1998 |title=[[Categories for the Working Mathematician]] |edition=2nd |series=[[Graduate Texts in Mathematics]] |volume=5 |publisher=Springer-Verlag}}


{{Category theory}}
[[Category:Collapse templates|Direct Limit]]
 
[[Category:Created On 03/03/2023|Direct Limit]]
{{DEFAULTSORT:Direct Limit}}[[Category: सीमाएं (श्रेणी सिद्धांत)]] [[Category: सार बीजगणित]]  
[[Category:Lua-based templates]]
 
[[Category:Machine Translated Page|Direct Limit]]
 
[[Category:Navigational boxes| ]]
 
[[Category:Navigational boxes without horizontal lists|Direct Limit]]
[[Category: Machine Translated Page]]
[[Category:Pages with script errors|Direct Limit]]
[[Category:Created On 03/03/2023]]
[[Category:Short description with empty Wikidata description|Direct Limit]]
[[Category:Sidebars with styles needing conversion|Direct Limit]]
[[Category:Template documentation pages|Documentation/doc]]
[[Category:Templates Vigyan Ready|Direct Limit]]
[[Category:Templates that add a tracking category]]
[[Category:Templates that generate short descriptions]]
[[Category:Templates using TemplateData]]

Latest revision as of 07:17, 19 March 2023

गणित की सीधी सीमा में कई छोटी वस्तुओं को एक बड़ी वस्तु से बदलने का एक सार्थक तरीका है जो एक विशिष्ट स्थान में एक साथ रखी जाती है। ये वस्तुएँ समूह , वलय, सदिश स्थल या सामान्य रूप से किसी भी श्रेणी की वस्तुएँ हो सकती हैं क्योंकि जिस तरह से उन्हें एक साथ रखा जाता है तो वह उन छोटी वस्तुओं के बीच होमोमोर्फिज्म समूह समरूपता, वलय समरूपता या श्रेणी में सामान्य आकार की एक प्रणाली द्वारा निर्दिष्ट किया जाता है। वस्तुओं की सीधी सीमा में कुछ निर्देशित समूह पर पर्वतमाला आई द्वारा निरूपित किया गया है क्योंकि यह समरूपता की प्रणाली को दबा देता है जो कि सीमा की संरचना के लिए महत्वपूर्ण है।

प्रत्यक्ष सीमा श्रेणी सिद्धांत में सीमा श्रेणी सिद्धांतकी अवधारणा की एक विशेष स्थिति है। प्रत्यक्ष सीमाएं दोहरी श्रेणी सिद्धांत की व्युत्क्रम सीमा तक हैं जो श्रेणी सिद्धांत में सीमा श्रेणी सिद्धांत की एक विशेष स्थिति है।

औपचारिक परिभाषा

हम पहले समूह और प्रमापीय गणित बीजगणितीय संरचना की परिभाषा देते हैं। फिर सामान्य परिभाषा देते हैं जिसका उपयोग किसी भी श्रेणी में किया जा सकता है।

बीजगणितीय वस्तुओं की प्रत्यक्ष सीमा

इस खंड में वस्तुओं को एक दिए गए बीजगणितीय संरचना से तैयार अंतर्निहित समूह से मिलाकर समझा जाता है जैसे कि समूह गणित, वलय गणित, प्रमापीय गणित एक निश्चित वलय पर तथा एक क्षेत्र पर बीजगणित का एक निश्चित क्षेत्र होता है जबकि समूह समरूपता से संबंधित समूह को समझा जाता है।

माना एक निर्देशित समूह तथा वस्तुएँ अनुक्रमणिका द्वारा निर्धारित परिवार बनें और सभी के लिए एक समरूपता निम्नलिखित गुणों के साथ हो-

फिर जोड़ी को सीधी प्रणाली कहा जाता है।

प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा को आई द्वारा निरूपित किया जाता है और निम्नानुसार परिभाषित भी किया गया है। इसके अंतर्निहित समूह में एक असंयुक्त संघ भी सम्मिलित है।

{{{1}}}:

एक मनमानी श्रेणी में प्रत्यक्ष सीमा

प्रत्यक्ष सीमा को मनमानी श्रेणी से परिभाषित किया जा सकता है एक सार्वभौमिक संपत्ति के माध्यम से वस्तुओं और आकारिता की एक सीधी प्रणाली बनें जैसा कि ऊपर परिभाषित किया गया है कि एक लक्ष्य एक जोड़ी है जहाँ एक्स एक वस्तु है और फाई तथा एक्स आकारिता हैं कि जब कभी भी प्रत्यक्ष प्रणाली की एक सीधी सीमा एक सार्वभौमिक रूप से विकर्षक लक्ष्य है तथी एक अद्वितीय आकारिता का आरेख इस प्रकार है

Direct limit category.svg

तब सभी आई जे के लिए क्रमविनिमेय आरेख होगा।

प्रत्यक्ष सीमा को अधिकतर

दवा्रा निरूपित किया जाता है

प्रत्यक्ष प्रणाली को विहित रूपवाद समझा जा रहा है।

बीजगणितीय वस्तुओं के विपरीत मनमानी श्रेणी में प्रत्येक प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा नहीं होती है अगर ऐसा होता है तो प्रत्यक्ष सीमा एक मजबूत अर्थ में अद्वितीय है एक और सीधी सीमा एक्स दी गई है वहां एक अद्वितीय समरूपता एक्स' स्थित है जो विहित आकारिकी के साथ संचार करता है।

उदाहरण

  • उपसमुच्चयों का संग्रह एम एक समूह है जिसमें एम सम्मिलित करके आंशिक आदेश हो सकता है यदि संग्रह निर्देशित है तो इसकी सीधी सीमा संघ है यूनियन एम आई किसी दिए गए समूह के उपसमूह के निर्देशित करके संग्रहित किया जाता है या किसी दिए गए वलय के सब्रिंग का निर्देशित संग्रह है।
  • सीडब्ल्यू परिसर की कमजोर टोपोलॉजी को प्रत्यक्ष सीमा के रूप में परिभाषित किया गया है।
  • इसमें एक्स बड़े तत्व के साथ कोई भी निर्देशित समूह हो एम किसी भी प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा आइसोमोर्फिक है और विहित आकारिता की एक समरूपता है।
  • माना के एक क्षेत्र धनात्मक पूर्णांक एन के लिए सामान्य रैखिक समूह जिसमें उलटा प्रविष्टियों के साथ आव्यूह हमारे पास एक समूह समरूपता का विस्तार करता है निचले दाएं कोने में एक और अंतिम पंक्ति और कॉलम में शून्य लगाकर आव्यूह इस प्रणाली की प्रत्यक्ष सीमा के का सामान्य रैखिक समूह है जिसे जी एल के रूप में लिखा जाता है जीएल (के) के एक तत्व को अनंत व्युत्क्रमणीय आव्यूह के रूप में माना जा सकता है जो अनंत पहचान आव्यूह से केवल बहुत ही सूक्ष्म प्रविष्टियों में भिन्न होता है जो बीजगणितीय सिद्धांत में समूह का महत्व है।
  • माना पी एक अविभाज्य संख्या है भागफल समूह से बनी प्रत्यक्ष प्रणाली पर विचार करें और समरूपता द्वारा प्रेरित इस प्रणाली की प्रत्यक्ष सीमा में आदेश की एकता की कुछ शक्ति की सभी जड़ें सम्मिलित हैं और इसे सुझाव समूह कहा जाता है .
  • सममित बहुपद के वलय से एक गैर-स्पष्ट अंतःक्षेपी वलय समरूपता है सममित बहुपदों के वलय के लिए चर पद इस प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा बनाने से सममित कार्यों का वलय उत्पन्न करते हैं।
  • यहाँ एफ एक व्याकुलता अंतरिछ एक्स पर एक सी-मूल्यवान समूह (गणित) हो और एक्स में एक बिंदु एक्स है तथा एक्स के खुले एक निर्देशित समूह को समावेशन द्वारा प्रदर्शित करते हैं संबंधित प्रत्यक्ष प्रणाली में एफ,आर है जहां आर प्रतिबंध मानचित्र है इस प्रणाली की सीधी सीमा को एक्स पर एफ का भाग है जिसे एफ द्वारा निरूपित किया जाता है एक्स के प्रत्येक यू के लिए विहित आकारिकी एफ (यू) पर एफ के एक खंड एस से संबद्ध है एक्स पर एस का रोगाणु गणित कहलाता है।
  • अंतर्निहित सेट-सैद्धांतिक प्रत्यक्ष सीमा पर अंतिम टोपोलॉजी रखकर संस्स्थित रिक्त स्थान की श्रेणी में प्रत्यक्ष सीमाएं दी गई हैं।
  • आखिरी योजना की आगमनात्मक सीमा है।

गुण

प्रत्यक्ष सीमाएँ व्युत्क्रम सीमाओं से जुड़ी होती हैं

एक महत्वपूर्ण संपत्ति यह है कि प्रमापीय में प्रत्यक्ष सीमाएं लेना एक सीधा संक्षिप्त खंड प्राप्त होता है

प्रत्यक्ष निर्माण और सामान्यीकरण

यदि एक श्रेणी में एक प्रत्यक्ष प्रणाली सी खंड के संदर्भ में एक वैकल्पिक विवरण स्वीकार करता है तो निर्देशित सेट एक छोटी श्रेणी के रूप में माना जा सकता है आई जिनकी वस्तुएं हैं और एक्स आकारिता हैं एक सीधी प्रणाली के समान है इस खंड की सीमा मूल प्रत्यक्ष प्रणाली की प्रत्यक्ष सीमा के समान है।

शब्दावली

साहित्य में परिभाषित प्रत्यक्ष सीमा की अवधारणा के लिए निर्देशित सीमा प्रत्यक्ष आगमनात्मक सीमा, निर्देशित परिचालक, प्रत्यक्ष परिचालक और आगमनात्मक सीमा शब्द मिलते हैं आगमनात्मक सीमा शब्द अस्पष्ट है क्योंकि कुछ लेखक इसे परिचालक की सामान्य अवधारणा के लिए उपयोग करते हैं।

यह भी देखें

टिप्पणियाँ


संदर्भ

  • Bourbaki, Nicolas (1968), Elements of mathematics. Theory of sets, Translated from French, Paris: Hermann, MR 0237342
  • Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics, vol. 5 (2nd ed.), Springer-Verlag
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=प्रत्यक्ष_सीमा&oldid=113172’