तिर्यक रेखा (ज्यामिति): Difference between revisions
| Line 59: | Line 59: | ||
===क्रमागत आंतरिक कोण=== | ===क्रमागत आंतरिक कोण=== | ||
[[File:Transverzala parallel.svg|250px|thumb|right|क्रमागत कोणों का एक युग्म। समानांतर रेखाओं के साथ, वे दो समकोणों तक | [[File:Transverzala parallel.svg|250px|thumb|right|क्रमागत कोणों का एक युग्म। समानांतर रेखाओं के साथ, वे दो समकोणों तक का कुल योग होते हैं।]]क्रमागत आंतरिक कोण कोणों के दो युग्म हैं जिसमे:<ref name=Oxford>{{cite web | url=http://web.cortland.edu/matresearch/OxfordDictionaryMathematics.pdf |title=गणित का ऑक्सफोर्ड संक्षिप्त शब्दकोश| author=C.Clapham, J.Nicholson | publisher =Addison-Wesley | year =2009| page=582 }}</ref><ref name=MathisFun>{{cite web | url=http://www.mathsisfun.com/geometry/parallel-lines.html |title=समानांतर रेखाएं| author=Rod Pierce | publisher =MathisFun | year=2011}} (interactive)</ref> | ||
*पृथक शीर्ष बिंदु हैं, | *पृथक शीर्ष बिंदु हैं, | ||
*तिर्यक रेखा के एक ही दिशा में स्थित होते हैं और | *तिर्यक रेखा के एक ही दिशा में स्थित होते हैं और | ||
| Line 82: | Line 82: | ||
यूक्लिड का प्रस्तावना 28 इस परिणाम को दो तरह से विस्तारित करता है। सर्वप्रथम, यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार परिच्छेद करती है कि संगत कोण सर्वांगसम हों, तो रेखाएँ समानांतर होती हैं। दूसरा, यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार परिच्छेद करती है कि तिर्यक रेखा के एक ही भुजा के आंतरिक कोण संपूरक हों, तो रेखाएँ समानांतर होती हैं। ये पूर्ववर्ती प्रस्ताव से इस तथ्य को अनप्रयुक्त करते हैं कि प्रतिच्छेदी रेखाओं के विपरीत कोण समान होते हैं (प्रस्तावना 15) और एक रेखा पर आसन्न कोण पूरक होते हैं (प्रस्तावना 13)। जैसा कि प्रोक्लस ने उल्लेख किया है , यूक्लिड समानांतर रेखाओं के लिए संभावित छह में से केवल तीन मानदंड दिए है।{{r|heath1908|pp=309-310}}{{r|holgate1901|at=Art. 89-90}} | यूक्लिड का प्रस्तावना 28 इस परिणाम को दो तरह से विस्तारित करता है। सर्वप्रथम, यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार परिच्छेद करती है कि संगत कोण सर्वांगसम हों, तो रेखाएँ समानांतर होती हैं। दूसरा, यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार परिच्छेद करती है कि तिर्यक रेखा के एक ही भुजा के आंतरिक कोण संपूरक हों, तो रेखाएँ समानांतर होती हैं। ये पूर्ववर्ती प्रस्ताव से इस तथ्य को अनप्रयुक्त करते हैं कि प्रतिच्छेदी रेखाओं के विपरीत कोण समान होते हैं (प्रस्तावना 15) और एक रेखा पर आसन्न कोण पूरक होते हैं (प्रस्तावना 13)। जैसा कि प्रोक्लस ने उल्लेख किया है , यूक्लिड समानांतर रेखाओं के लिए संभावित छह में से केवल तीन मानदंड दिए है।{{r|heath1908|pp=309-310}}{{r|holgate1901|at=Art. 89-90}} | ||
यूक्लिड का प्रस्तावना 29 पूर्ववर्ती दोनों के विपरित है। सर्वप्रथम, यदि एक तिर्यक रेखा दो समानांतर रेखाओं को परिच्छेद करती है, तो एकांतर आंतरिक कोण सर्वांगसम होते हैं। यदि नहीं, तो पहला दूसरे से बड़ा है, जिसका अर्थ है कि इसका पूरक दूसरे कोण के पूरक से कम है। इसका तात्पर्य यह है कि तिर्यक रेखा के एक ही भुजा के आंतरिक कोण होते हैं जो दो समकोणों से कम होते हैं, जो पांचवें अभिधारणा के विपरीत हैं। प्रस्ताव निरंतर यह अभिव्यक्त करता है कि दो समानांतर रेखाओं के तिर्यक रेखा पर, संगत कोण सर्वांगसम होते हैं और एक ही भुजा के आंतरिक कोण दो समकोण के समान होते हैं। ये कथन उसी तरह अनुसरण करते हैं जैसे प्रस्तावना 28 प्रस्तावना 27 का अनुसरण करता है।{{r|heath1908|pp=311-312}}{{r|holgate1901|at=Art. 93-95}} | यूक्लिड का प्रस्तावना 29 पूर्ववर्ती दोनों के विपरित है। सर्वप्रथम, यदि एक तिर्यक रेखा दो समानांतर रेखाओं को परिच्छेद करती है, तो एकांतर आंतरिक कोण सर्वांगसम होते हैं। यदि नहीं, तो पहला दूसरे से बड़ा है, जिसका अर्थ है कि इसका पूरक दूसरे कोण के पूरक से कम है। इसका तात्पर्य यह है कि तिर्यक रेखा के एक ही भुजा के आंतरिक कोण होते हैं जो दो समकोणों से कम होते हैं, जो पांचवें अभिधारणा के विपरीत हैं। प्रस्ताव निरंतर यह अभिव्यक्त करता है कि दो समानांतर रेखाओं के तिर्यक रेखा पर, संगत कोण सर्वांगसम होते हैं और एक ही भुजा के आंतरिक कोण दो समकोण के समान होते हैं। ये कथन उसी तरह अनुसरण करते हैं जैसे प्रस्तावना 28, प्रस्तावना 27 का अनुसरण करता है।{{r|heath1908|pp=311-312}}{{r|holgate1901|at=Art. 93-95}} | ||
यूक्लिड का प्रमाण पाँचवीं अभिधारणा का आवश्यक उपयोग करता है, यद्यपि, ज्यामिति के आधुनिक उपचार इसके अलावा प्लेफेयर के स्वयंसिद्ध का उपयोग करते हैं। प्लेफेयर के स्वयंसिद्ध को मानते हुए प्रस्ताव 29 को सिद्ध करने के लिए, एक तिर्यक रेखा को दो समानांतर रेखाओं को परिच्छिद्द करने दें और अनुमान कर लें कि एकांतर आंतरिक कोण समान नहीं हैं। उस बिंदु से एक तीसरी रेखा खींचें जहां तिर्यक रेखा पहली रेखा को परिच्छेद करती है, लेकिन तिर्यक रेखा द्वारा दूसरी रेखा के साथ बनाए गए कोण के समान कोण के साथ। यह एक बिंदु के माध्यम से दो विभिन्न रेखाएँ उत्पन्न करती है, दोनों दूसरी रेखा के समानांतर, स्वयंसिद्ध के विपरीत।{{r|heath1908|p=313}}<ref>A similar proof is given in Holgate 1901, Art. 93</ref> | यूक्लिड का प्रमाण पाँचवीं अभिधारणा का आवश्यक उपयोग करता है, यद्यपि, ज्यामिति के आधुनिक उपचार इसके अलावा प्लेफेयर के स्वयंसिद्ध का उपयोग करते हैं। प्लेफेयर के स्वयंसिद्ध को मानते हुए प्रस्ताव 29 को सिद्ध करने के लिए, एक तिर्यक रेखा को दो समानांतर रेखाओं को परिच्छिद्द करने दें और अनुमान कर लें कि एकांतर आंतरिक कोण समान नहीं हैं। उस बिंदु से एक तीसरी रेखा खींचें जहां तिर्यक रेखा पहली रेखा को परिच्छेद करती है, लेकिन तिर्यक रेखा द्वारा दूसरी रेखा के साथ बनाए गए कोण के समान कोण के साथ। यह एक बिंदु के माध्यम से दो विभिन्न रेखाएँ उत्पन्न करती है, दोनों दूसरी रेखा के समानांतर, स्वयंसिद्ध के विपरीत।{{r|heath1908|p=313}}<ref>A similar proof is given in Holgate 1901, Art. 93</ref> | ||
Revision as of 20:46, 16 March 2023
| Types of angles |
|---|
| 2D angles |
| Exterior |
| 2D angle pairs |
|
Adjacent |
| 3D angles |
| Dihedral |
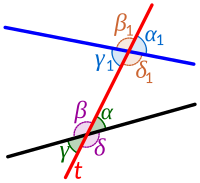
ज्यामिति में, एक तिर्यक रेखा एक रेखा (गणित) है जो रेखा-रेखा दो रेखाओं को एक ही तल (ज्यामिति) में दो भिन्न बिंदु (ज्यामिति) पर काटती है। तिर्यक रेखाएँ यह स्थापित करने में एक भूमिका निभाते हैं कि यूक्लिडियन समतल में दो या दो से अधिक अन्य रेखाएं समानांतर (ज्यामिति) हैं या नहीं। दो रेखाओं के साथ एक तिर्यक रेखा के प्रतिच्छेदन विभिन्न प्रकार के कोणों के जोड़े निरन्तर आंतरिक कोण, बाहरी कोण, संगत कोण और वैकल्पिक कोण बनाते हैं। यूक्लिड के समानांतर अभिधारणा यदि दो रेखाएँ समानांतर हैं, तो क्रमागत आंतरिक कोण संपूरक होते हैं, संगत कोण और एकांतर कोण समान होते हैं।
|

|

| |
| तिर्यक रेखा के आठ कोण। (ऊर्ध्वाधर कोण जैसे और सदैव सर्वांगसम होते हैं।) |
गैर-समानांतर रेखाओं के बीच तिर्यक रेखा।
क्रमागत कोण संपूरक नहीं होते हैं। |
समानांतर रेखाओं के बीच तिर्यक रेखा।
क्रमागत कोण संपूरक होते हैं। |
तिर्यक रेखा के कोण
एक तिर्यक रेखा 8 कोण बनाती है, जैसा कि ऊपर बाईं ओर ग्राफ में दिखाया गया है:
- α, β, γ और δ और फिर α1, β1, γ1 और δ1 नामक दो पंक्तियों में से प्रत्येक के साथ 4; और
- जिनमें से 4 आंतरिक हैं (दो पंक्तियों के बीच) अर्थात् α, β, γ1 और δ1 और जिनमें से 4 बाहरी अर्थात् α1, β1, γ और δ हैं।
एक तिर्यक रेखा जो दो समान्तर रेखाओं को समकोण पर विभाजित करती है, लंबवत् तिर्यक रेखा कहलाती है। इस स्थिति में सभी 8 कोण समकोण हैं [1]
जब रेखाएँ समानांतर होती हैं, एक ऐसी स्थिति जिसे प्रायः माना जाता है, एक तिर्यक रेखा कई सर्वांगसम (ज्यामिति) पूरक कोण उत्पन्न करती है। इनमें से कुछ कोण युग्मों के विशिष्ट नाम हैं और नीचे उनकी चर्चा की गई है: संगत कोण, एकांतर कोण और क्रमागत कोण।[2][3]: Art. 87
एकांतर कोण
एकांतर कोण कोणों के चार युग्म हैं जिसमे:
- पृथक शीर्ष (ज्यामिति) बिंदु हैं,
- तिर्यक रेखा के विपरीत दिशा में स्थित होते हैं और
- दोनों कोण आंतरिक या दोनों कोण बाहरी हैं।
यह गणित का एक बहुत ही उपयोगी विषय है
यदि एक युग्म के दो कोण सर्वांगसम (माप में बराबर) हैं तो अन्य युग्मों में से प्रत्येक के कोण भी सर्वांगसम होते हैं।
यूक्लिड के तत्वों के कथन 1.27 के अंतर्गत निरपेक्ष ज्यामिति का एक प्रमेय (अतः अतिपरवलीय ज्यामिति और यूक्लिडियन ज्यामिति दोनों में मान्य) यह प्रमाणित करता है कि यदि एक तिर्यक रेखा के एकांतर कोणों की एक युग्म के कोण सर्वांगसम हैं तो दो रेखाएँ समानांतर (गैर-प्रतिच्छेदन) हैं।
यूक्लिड के तत्वों की प्रस्तावना 1.29 के अंतर्गत यह यूक्लिड के समानांतर अभिधारणा से अनुसरण करता है कि यदि दो रेखाएँ समानांतर हैं, तो एक तिर्यक रेखा के एकांतर कोणों के एक युग्म के कोण सर्वांगसम होते हैं।
संगत कोण
संगत कोण कोणों के चार युग्म हैं जिसमे:
- पृथक शीर्ष बिंदु हैं,
- तिर्यक रेखा के एक ही दिशा में स्थित होते हैं और
- एक कोण आंतरिक और दूसरा बाहरी है।
दो रेखाएँ समानांतर होती हैं यदि केवल किसी तिर्यक रेखा के संगत कोणों के किसी युग्म के दो कोण सर्वांगसम (मापक में समान) हैं।
यूक्लिड के तत्वों का प्रस्ताव 1.28 के अंतर्गत, निरपेक्ष ज्यामिति का एक प्रमेय (इसलिए अतिपरवलीय और यूक्लिडियन ज्यामिति दोनों में मान्य ), यह प्रमाणित करता है कि यदि एक तिर्यक रेखा के संगत कोणों की एक युग्म के कोण सर्वांगसम हैं तो दो रेखाएँ समानांतर (गैर-प्रतिच्छेदन) हैं।
यूक्लिड के तत्वों की प्रस्तावना 1.29 के अंतर्गत यह यूक्लिड के समानांतर अभिधारणा से अनुसरण करता है कि यदि दो रेखाएँ समानांतर हैं, तो एक तिर्यक रेखा के संगत कोणों के एक युग्म के कोण सर्वांगसम होते हैं
यदि संगत कोणों के एक युग्म के कोण सर्वांगसम हैं, तो अन्य युग्मों के प्रत्येक कोण भी सर्वांगसम होते हैं। इस पृष्ठ पर समानांतर रेखाओं वाली विभिन्न छवियों में, संगत कोण युग्म α=α1, β=β1, γ=γ1 और δ=δ1 हैं।
क्रमागत आंतरिक कोण
क्रमागत आंतरिक कोण कोणों के दो युग्म हैं जिसमे:[4][2]
- पृथक शीर्ष बिंदु हैं,
- तिर्यक रेखा के एक ही दिशा में स्थित होते हैं और
- दोनों आंतरिक हैं।
दो रेखाएँ समानांतर होती हैं यदि केवल किसी तिर्यक रेखा के क्रमागत आंतरिक कोणों के किसी भी युग्म के दो कोण संपूरक हैं(योग 180° तक)।
यूक्लिड के तत्वों की प्रस्तावना 1.28 के अंतर्गत, निरपेक्ष ज्यामिति का एक प्रमेय (इसलिए अतिपरवलीय और यूक्लिडियन ज्यामिति दोनों में मान्य ), यह प्रमाणित करता है कि यदि क्रमागत आंतरिक कोणों की एक युग्म के कोण पूरक हैं तो दो रेखाएँ समानांतर (गैर-प्रतिच्छेदन) हैं।
यूक्लिड के तत्वों का प्रस्तावना 1.29 के अंतर्गत, यह यूक्लिड के समानांतर अभिधारणा से अनुसरण करता है कि यदि दो रेखाएँ समानांतर हैं, तो एक तिर्यक रेखा के क्रमागत आंतरिक कोणों की एक युग्म के कोण पूरक होते हैं।
यदि क्रमागत आंतरिक कोणों का एक युग्म संपूरक है, तो दूसरा युग्म भी संपूरक है।
तिर्यक रेखाओं की अन्य विशेषताएं
यदि सामान्य स्थिति में तीन रेखाएँ एक त्रिभुज बनाती हैं और फिर एक तिर्यक रेखा द्वारा काटी जाती हैं, तो छह परिणामी खंडों की लंबाई मेनेलॉस प्रमेय को संतुष्ट करती है।
संबंधित प्रमेय
समानांतर अभिधारणा के यूक्लिड के सूत्रीकरण को एक तिर्यक रेखा के रूप में बताया जा सकता है। विशेष रूप से, यदि तिर्यक रेखा के एक ही भुजा के आंतरिक कोण दो समकोणों से कम हैं तो रेखाओं को प्रतिच्छेद करना चाहिए। वास्तव में, यूक्लिड ग्रीक में उसी वाक्यांश का उपयोग करता है जिसे सामान्यतः "ट्रांसवर्सल या तिर्यक रेखा" के रूप में अनुवादित किया जाता है।[5]: 308, nfote 1
यूक्लिड के प्रस्तावना 27 में कहा गया है कि यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार काटती है कि एकांतर आंतरिक कोण सर्वांगसम हों, तो रेखाएँ समानांतर होती हैं। यूक्लिड इसे विरोधाभास द्वारा सिद्ध करता है: यदि रेखाएँ समानांतर नहीं हैं तो उन्हें प्रतिच्छेद करना आवश्यक हैं और एक त्रिभुज रूपांकित होता है। तब इनमे से एक एकांतर कोण अन्य कोण के बाहरी कोण के समान होता है जो त्रिभुज में एक विपरीत आंतरिक कोण होता है। यह प्रस्ताव 16 का खंडन करता है जिसमें कहा गया है कि त्रिभुज का एक बाहरी कोण विपरीत आंतरिक कोणों से सदैव बड़ा होता है।[5]: 307 [3]: Art. 88
यूक्लिड का प्रस्तावना 28 इस परिणाम को दो तरह से विस्तारित करता है। सर्वप्रथम, यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार परिच्छेद करती है कि संगत कोण सर्वांगसम हों, तो रेखाएँ समानांतर होती हैं। दूसरा, यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार परिच्छेद करती है कि तिर्यक रेखा के एक ही भुजा के आंतरिक कोण संपूरक हों, तो रेखाएँ समानांतर होती हैं। ये पूर्ववर्ती प्रस्ताव से इस तथ्य को अनप्रयुक्त करते हैं कि प्रतिच्छेदी रेखाओं के विपरीत कोण समान होते हैं (प्रस्तावना 15) और एक रेखा पर आसन्न कोण पूरक होते हैं (प्रस्तावना 13)। जैसा कि प्रोक्लस ने उल्लेख किया है , यूक्लिड समानांतर रेखाओं के लिए संभावित छह में से केवल तीन मानदंड दिए है।[5]: 309–310 [3]: Art. 89-90
यूक्लिड का प्रस्तावना 29 पूर्ववर्ती दोनों के विपरित है। सर्वप्रथम, यदि एक तिर्यक रेखा दो समानांतर रेखाओं को परिच्छेद करती है, तो एकांतर आंतरिक कोण सर्वांगसम होते हैं। यदि नहीं, तो पहला दूसरे से बड़ा है, जिसका अर्थ है कि इसका पूरक दूसरे कोण के पूरक से कम है। इसका तात्पर्य यह है कि तिर्यक रेखा के एक ही भुजा के आंतरिक कोण होते हैं जो दो समकोणों से कम होते हैं, जो पांचवें अभिधारणा के विपरीत हैं। प्रस्ताव निरंतर यह अभिव्यक्त करता है कि दो समानांतर रेखाओं के तिर्यक रेखा पर, संगत कोण सर्वांगसम होते हैं और एक ही भुजा के आंतरिक कोण दो समकोण के समान होते हैं। ये कथन उसी तरह अनुसरण करते हैं जैसे प्रस्तावना 28, प्रस्तावना 27 का अनुसरण करता है।[5]: 311–312 [3]: Art. 93-95
यूक्लिड का प्रमाण पाँचवीं अभिधारणा का आवश्यक उपयोग करता है, यद्यपि, ज्यामिति के आधुनिक उपचार इसके अलावा प्लेफेयर के स्वयंसिद्ध का उपयोग करते हैं। प्लेफेयर के स्वयंसिद्ध को मानते हुए प्रस्ताव 29 को सिद्ध करने के लिए, एक तिर्यक रेखा को दो समानांतर रेखाओं को परिच्छिद्द करने दें और अनुमान कर लें कि एकांतर आंतरिक कोण समान नहीं हैं। उस बिंदु से एक तीसरी रेखा खींचें जहां तिर्यक रेखा पहली रेखा को परिच्छेद करती है, लेकिन तिर्यक रेखा द्वारा दूसरी रेखा के साथ बनाए गए कोण के समान कोण के साथ। यह एक बिंदु के माध्यम से दो विभिन्न रेखाएँ उत्पन्न करती है, दोनों दूसरी रेखा के समानांतर, स्वयंसिद्ध के विपरीत।[5]: 313 [6]
उच्च आयामों में
उच्च परिमापी स्थानों में, एक रेखा जो विभिन्न बिंदुओं में रेखाओं के प्रत्येक समुच्चय को प्रतिच्छेद करती है, वह रेखाओं के उस समुच्चय का तिर्यक रेखा है। द्वि-परिमापी (समतल) स्थिति के विपरीत, दो से अधिक रेखाओं के समुच्चय के लिए तिर्यक रेखा के होने की प्रत्याभूत नहीं है।
यूक्लिडियन 3-समष्टि में, रेगुलस (ज्यामिति) एक रेगुलस तिरछी रेखाओं का एक समुच्चय है ,आर, जैसे कि आर की प्रत्येक रेखा पर प्रत्येक बिंदु के माध्यम से, आर का एक तिर्यक रेखा पारित होता है और आर के तिर्यक रेखा के प्रत्येक बिंदु के माध्यम से आर की एक रेखा पारित होती है। रेगुलस आर के तिर्यक रेखा का समुच्चय भी एक रेगुलस है, जिसे विपरीत रेगुलस Ro कहा जाता है, इस समष्टि में, तीन परस्पर तिरछी रेखाओं को सदैव एक रेगुलस तक विस्तृत किया जा सकता है।
संदर्भ
- ↑ "आड़ा". Math Open Reference. 2009. (interactive)
- ↑ 2.0 2.1 Rod Pierce (2011). "समानांतर रेखाएं". MathisFun. (interactive)
- ↑ 3.0 3.1 3.2 3.3 Holgate, Thomas Franklin (1901). Elementary Geometry. Macmillan.
- ↑ C.Clapham, J.Nicholson (2009). "गणित का ऑक्सफोर्ड संक्षिप्त शब्दकोश" (PDF). Addison-Wesley. p. 582.
- ↑ 5.0 5.1 5.2 5.3 5.4 Heath, T.L. (1908). The thirteen books of Euclid's Elements. Vol. 1. The University Press.
- ↑ A similar proof is given in Holgate 1901, Art. 93


