अनुप्रस्थ तरंग: Difference between revisions
No edit summary |
No edit summary |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Moving wave whose oscillations are perpendicular to the direction of the wave}} | {{short description|Moving wave whose oscillations are perpendicular to the direction of the wave}} | ||
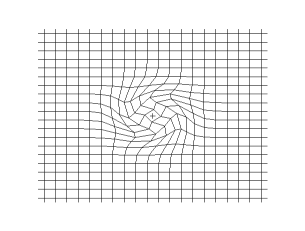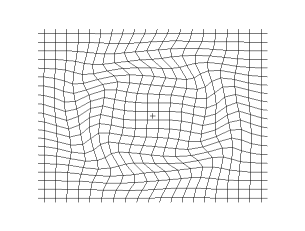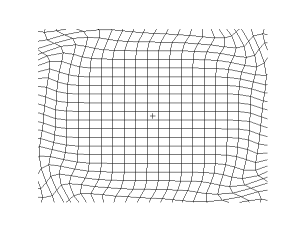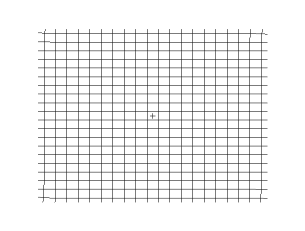
[[File:Onde cisaillement impulsion 1d 30 petit.gif|thumb|305px|क्षैतिज दिशा में एक लोचदार माध्यम के माध्यम से फैलने वाली एक सरल (समतल) अनुप्रस्थ तरंग का चित्रण, जिसमें कण ऊर्ध्वाधर दिशा में विस्थापित होते हैं। सामग्री की केवल एक परत दिखाई गई है]] | [[File:Onde cisaillement impulsion 1d 30 petit.gif|thumb|305px|क्षैतिज दिशा में एक लोचदार माध्यम के माध्यम से फैलने वाली एक सरल (समतल) अनुप्रस्थ तरंग का चित्रण, जिसमें कण ऊर्ध्वाधर दिशा में विस्थापित होते हैं। सामग्री की केवल एक परत दिखाई गई है]] | ||
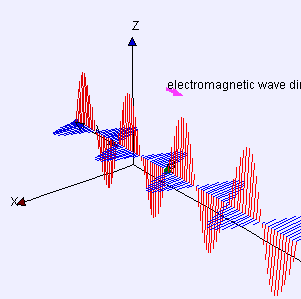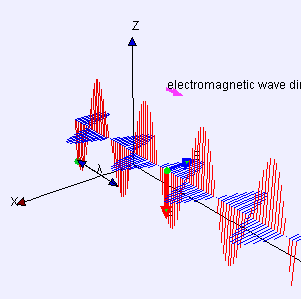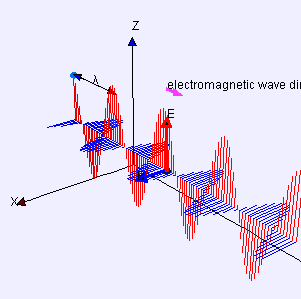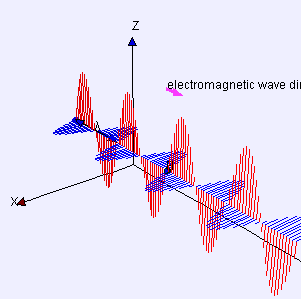
[[File:Electromagneticwave3D.gif|thumb|305px|एक साधारण प्रकाश तरंग में एक किरण के साथ विद्युत (लाल) और चुंबकीय (नीला) क्षेत्रों का चित्रण। किरण के लंबवत किसी भी समतल के लिए, प्रत्येक क्षेत्र का मान हमेशा समतल के सभी बिंदुओं पर समान होता है।]] | [[File:Electromagneticwave3D.gif|thumb|305px|एक साधारण प्रकाश तरंग में एक किरण के साथ विद्युत (लाल) और चुंबकीय (नीला) क्षेत्रों का चित्रण। किरण के लंबवत किसी भी समतल के लिए, प्रत्येक क्षेत्र का मान हमेशा समतल के सभी बिंदुओं पर समान होता है।]] | ||
| Line 82: | Line 83: | ||
[[Category:CS1 maint]] | [[Category:CS1 maint]] | ||
[[Category:Pages with script errors | [[Category:Lua-based templates]] | ||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | [[Category:Short description with empty Wikidata description]] | ||
[[Category:Templates Vigyan Ready]] | [[Category:Templates Vigyan Ready]] | ||
[[Category:Templates that add a tracking category]] | [[Category:Templates that add a tracking category]] | ||
[[Category:Templates that generate short descriptions]] | [[Category:Templates that generate short descriptions]] | ||
[[Category:Templates using TemplateData]] | [[Category:Templates using TemplateData]] | ||
Latest revision as of 13:07, 24 March 2023
भौतिकी में, एक अनुप्रस्थ तरंग एक तरंग के रूप में होती है जिसका दोलन तरंग की अग्रिम दिशा में लंबवत रूप में होता है। यह अनुदैर्ध्य तरंग के विपरीत होती है, जो इसके दोलनों की दिशा में घूमता है। और पानी की तरंगें अनुप्रस्थ तरंग का उदाहरण है।
एक छोर को ऊपर-नीचे रखकर और दूसरे छोर को ऊपर-नीचे घुमाकर तारों की क्षैतिज लंबाई में निर्मित तरंगो द्वारा एक सरल उदाहरण दिया जा सकता है। इसका एक अन्य उदाहरण लहर तरंगें हैं जो एक ड्रम की झिल्ली पर निर्मित होती हैं। तरंगें झिल्ली के समतल के समान्तर दिशा में अपना प्रसार करती हैं, लेकिन झिल्ली में प्रत्येक बिंदु स्वयं उस तल के लंबवत ऊपर और नीचे विस्थापित हो जाता है।उसी तल के लम्बवत प्रकाश एक अनुप्रस्थ तरंग का अन्य उदाहरण है, जहां दोलन विद्युत क्षेत्र और चुंबकीय क्षेत्र हैं, जो प्रसार की दिशा का वर्णन करने वाली आदर्श प्रकाश किरणों के समकोण पर इंगित करते हैं।
अनुप्रस्थ तरंगें सामान्यतः कतरनी तनाव उत्पन्न होने के कारण लोचदार (भौतिकी) ठोस रूप में होती हैं, इस स्थिति में दोलन तरंग के लम्बवत दिशा में निदेशन में ठोस कणों का उनकी शिथिल स्थिति से दूर विस्थापन होता है। ये विस्थापन सामग्री के स्थानीय कतरनी विरूपण के अनुरूप होते हैं। अतः इस प्रकार की अनुप्रस्थ तरंग को कतरनी तरंग कहा जाता है। चूंकि तरल पदार्थ गतिहीन के समय अपरूपण बलों का विरोध नहीं कर सकता हैं, तरल पदार्थों के बल्क के अंदर अनुप्रस्थ तरंगों का प्रसार संभव नहीं होता है।[1] भूकंप विज्ञान में, कतरनी तरंगों को द्वितीयक तरंगें या एस-तरंगें भी कहा जाता है।
अनुप्रस्थ तरंगें अनुदैर्ध्य तरंगों के विपरीत होती हैं, जहां तरंग की दिशा में दोलन होते हैं। अनुदैर्ध्य तरंग का मानक उदाहरण गैसों, तरल पदार्थों या ठोस पदार्थों में एक ध्वनि तरंग या दबाव तरंग के रूप में होता है, जिसके दोलनों के कारण उस सामग्री का संपीड़न और विस्तार होता है, जिसके माध्यम से तरंग फैलती है। दबाव तरंगों को भूभौतिकी में प्राथमिक तरंगें या पी-तरंगें कहा जाता है।
गणितीय सूत्रीकरण
गणितीय रूप से, सबसे सरल प्रकार की अनुप्रस्थ तरंग एक समतल रैखिक रूप से ध्रुवीकृत ज्यावक्रीय रूप में होती है। यहाँ समतल का अर्थ है कि प्रसार की दिशा अपरिवर्तित होती है और पूरे माध्यम में समान रूप में होती है; ध्रुवीकरण (तरंगों) का अर्थ है कि विस्थापन की दिशा भी अपरिवर्तनीय होती है और पूरे माध्यम में समान और विस्थापन का परिमाण प्रसार की दिशा में केवल समय और स्थिति का एक ज्यावक्रीय फलन होता है ।
ऐसी तरंग की गति को गणितीय रूप में इस प्रकार व्यक्त किया जा सकता है। डी प्रसार की दिशा एक इकाई लंबाई के साथ एक वेक्टर (गणित) और माध्यम में किसी भी संदर्भ बिंदु के रूप में हो सकते है। मान लीजिए कि आप दोलनों की दिशा डी के लंबवत एक अन्य इकाई लंबाई सदिश के रूप में होती है। किसी कण का माध्यम के किसी बिंदु p पर और किसी भी समय t सेकंड में विस्थापन होता है।
इस समीकरण से, तरंग d दिशा में घूमती है और दोलन दिशा u के साथ आगे और पीछे होती है। लहर को यू दिशा में रैखिक रूप से ध्रुवीकृत किया जाता है।
एक निश्चित बिंदु पी पर देखने वाला एक प्रेक्षक टी सेकेंड के साथ साधारण हार्मोनिक ( ज्यावक्रीय) गति को देखता है, जिसमें प्रत्येक अर्थ में अधिकतम कण विस्थापन ए के साथ दिखाई देता है; अर्थात्, प्रति सेकंड f = 1/T पूर्ण दोलन चक्र की 'आवृत्ति' के साथ हर दूसरे निश्चित समय t पर सभी कणों का एक स्नैपशॉट, d के लम्बवत् प्रत्येक तल पर सभी कणों के लिए समान विस्थापन प्रदर्शित करता है, जिसमें क्रमिक तलों में विस्थापन के साथ एक ज्यावक्रीय पैटर्न बनाते है। तथा प्रत्येक पूर्ण चक्र तरंग दैर्ध्य λ = v T = v / f द्वारा d के साथ विस्तारित होता है। और पूरा पैटर्न गति V के साथ दिशा d में चलता है।
समान समीकरण समतलीय रूप से ध्रुवीकृत ज्यावक्रीय प्रकाश तरंग का वर्णन करता है, इसके अतिरिक्त विस्थापन S(p, t) बिंदु p और समय t पर विद्युत क्षेत्र का वर्णन करता है। चुंबकीय क्षेत्र को समान समीकरण द्वारा वर्णित किया जाता है, लेकिन विस्थापन दिशा के साथ जो कि d और u दोनों के लंबवत होते है और एक भिन्न आयाम के रूप में होते है।
लहर सुपरपोजिशन सिद्धांत
एक सजातीय रैखिक संयोजन माध्यम में, जटिल दोलनों सामग्री या प्रकाश प्रवाह में कंपन को कई सरल ज्यावक्रीय तरंगों की तरंग सुपरपोजिशन के रूप में वर्णित किया जा सकता है या तो अनुप्रस्थ या अनुदैर्ध्य के रूप में वर्णित किया जा सकता है।
उदाहरण के लिए, एक वायलिन स्ट्रिंग के कंपन का विश्लेषण विभिन्न आवृत्तियों की कई अनुप्रस्थ तरंगों के योग के रूप में किया जाता है, जो स्ट्रिंग को या तो ऊपर या नीचे या बाएं से दाएं विस्थापित करती हैं। एक तालाब में तरंगों का विश्लेषण अनुप्रस्थ और अनुदैर्ध्य तरंगों (गुरुत्वाकर्षण तरंगों) के संयोजन के रूप में किया जाता है,जो एक साथ फैलती हैं।
परिपत्र ध्रुवीकरण
यदि माध्यम रैखिक रूप में होता है और एक ही दिशा d के लिए कई स्वतंत्र विस्थापन दिशाओं की अनुमति देता है, तो हम ध्रुवीकरण की दो परस्पर लंबवत दिशाओं को चुन सकते हैं और किसी भी दिशा में रैखिक रूप से ध्रुवीकृत किसी भी तरंग को उन दो तरंगों के रैखिक संयोजन (मिश्रण) के रूप में व्यक्त कर सकते हैं।
दो तरंगों को एक ही आवृत्ति, वेग और यात्रा की दिशा के साथ संयोजित किया जाता है, लेकिन विभिन्न चरणों और स्वतंत्र विस्थापन दिशाओं के साथ, एक गोलाकार ध्रुवीकरण या अण्डाकार ध्रुवीकरण तरंग प्राप्त होती है। ऐसी तरंग में कण आगे और पीछे जाने के अतिरिक्त वृत्ताकार या अण्डाकार प्रक्षेपवक्र का वर्णन करते हैं।
ऊपर दी गई स्ट्रिंग से इसे फिर से देखने में मदद मिल सकती है। ध्यान दें कि आप अपने हाथ को ऊपर-नीचे करने के अतिरिक्त दाएं और बाएं की ओर ले जाते हुए स्ट्रिंग पर तरंगों को चला सकते हैं। यह एक महत्वपूर्ण विषय है। दो स्वतंत्र ऑर्थोगोनल दिशाएँ होती है, जिनमें तरंगें गति कर सकती हैं। यह दो दिशाओं के लिए सही कोण पर, ऊपर नीचे, दाएं और बाएं सही दिशा में स्पष्टता के लिए चुना जाता है। तथा अपने हाथ को एक सीधी रेखा में ले जाकर लॉन्च की गई कोई भी तरंगें रैखिक रूप से ध्रुवीकृत तरंगें होती हैं।
लेकिन अब एक सर्कल में अपने हाथ को घुमाने की कल्पना करने पर आपकी गति से स्ट्रिंग पर एक सर्पिल तरंग प्रक्षेपित होती है। आप अपने हाथ को एक साथ ऊपर और नीचे दोनों तरफ घुमा रहे हैं। भुजा की गति का मैक्सिमा, एक चौथाई तरंगदैर्ध्य या वृत्त के चारों ओर एक चौथाई होता है, जो ऊपर और नीचे की गति के मैक्सिमा से 90 डिग्री या π/2 रेडियन होता है। स्ट्रिंग के साथ किसी भी बिंदु पर, स्ट्रिंग का विस्थापन आपके हाथ के समान वृत्त का वर्णन करता है, लेकिन तरंग के प्रसार की गति से विलंबित होता है। ध्यान दें कि आप अपने हाथ को एक दक्षिणावर्त सर्कल या काउंटर-वामावर्त सर्कल में भी स्थानांतरित करने का विकल्प चुन सकते हैं। ये वैकल्पिक वृत्ताकार गतियाँ से दाएं और बाएं गोलाकार ध्रुवीकृत तरंगें उत्पन्न करती हैं।
जिस सीमा तक आपका वृत्त अपूर्ण है, एक नियमित गति में दीर्घवृत्त का वर्णन करती है और अण्डाकार रूप से ध्रुवीकृत तरंगें उत्पन्न करती है। विलक्षणता के चरम पर आपका दीर्घवृत्त एक सीधी रेखा बन जाता है, जो दीर्घवृत्त के प्रमुख अक्ष के साथ रैखिक ध्रुवीकरण का निर्माण करता है। एक अण्डाकार गति को सदैव असमान आयाम के दो ओर्थोगोनल रैखिक गतियों में विघटित किया जाता है और 90 डिग्री चरण से बाहर हो सकता है, जिसमें परिपत्र ध्रुवीकरण विशेष स्थिति के रूप में होता है, जहां दो रैखिक गतियों का एक ही आयाम होता है।
- ↑ "Fluid Mechanics II: Viscosity and Shear stresses" (PDF).
{{cite web}}: CS1 maint: url-status (link)