प्रत्यक्ष कठोरता विधि

संरचनात्मक विश्लेषण के तरीकों में से एक के रूप में, प्रत्यक्ष कठोरता विधि, जिसे मैट्रिक्स कठोरता विधि के रूप में भी जाना जाता है, विशेष रूप से सांख्यिकीय रूप से अनिश्चित प्रकार सहित जटिल संरचनाओं के कंप्यूटर-स्वचालित विश्लेषण के लिए उपयुक्त है। यह एक मैट्रिक्स पद्धति है जो सदस्य बलों और संरचनाओं में विस्थापन की गणना के लिए सदस्यों की कठोरता संबंधों का उपयोग करती है। प्रत्यक्ष कठोरता विधि परिमित तत्व विधि (एफईएम) का सबसे आम कार्यान्वयन है। विधि को लागू करने में, सिस्टम को नोड्स पर परस्पर जुड़े सरल, आदर्श तत्वों के एक सेट के रूप में तैयार किया जाना चाहिए। इन तत्वों की भौतिक कठोरता गुणों को तब मैट्रिक्स (गणित) के माध्यम से एक एकल मैट्रिक्स समीकरण में संकलित किया जाता है जो संपूर्ण आदर्श संरचना के व्यवहार को नियंत्रित करता है। इस समीकरण को हल करके संरचना के अज्ञात विस्थापन और बलों को तब निर्धारित किया जा सकता है। प्रत्यक्ष कठोरता विधि अधिकांश वाणिज्यिक और मुक्त स्रोत परिमित तत्व सॉफ़्टवेयर के लिए आधार बनाती है।

डायरेक्ट स्टिफनेस मेथड की शुरुआत एयरोस्पेस के क्षेत्र में हुई थी। शोधकर्ताओं ने जटिल हवाई जहाज के फ्रेम के विश्लेषण के लिए विभिन्न दृष्टिकोणों को देखा। इनमें लोच सिद्धांत, संरचनात्मक यांत्रिकी में ऊर्जा सिद्धांत, लचीलापन विधि और मैट्रिक्स कठोरता विधि सम्मिलित हैं। यह इन तरीकों के विश्लेषण के माध्यम से था कि प्रत्यक्ष कठोरता विधि कंप्यूटर कार्यान्वयन के लिए आदर्श रूप से उपयुक्त एक कुशल विधि के रूप में उभरी।

इतिहास

1934 और 1938 के बीच आर्थर रोडरिक कॉलर|ए. आर. कॉलर और डब्ल्यू.जे. डंकन ने आज उपयोग किए जाने वाले मैट्रिक्स सिस्टम के लिए प्रतिनिधित्व और शब्दावली के साथ पहला पेपर प्रकाशित किया। द्वितीय विश्व युद्ध के माध्यम से एरोलेस्टिक अनुसंधान जारी रहा लेकिन 1938 से 1947 तक प्रकाशन प्रतिबंधों ने इस काम को ट्रेस करना मुश्किल बना दिया। मैट्रिक्स संरचनात्मक विश्लेषण में दूसरी बड़ी सफलता 1954 और 1955 के दौरान हुई जब प्रोफेसर जॉन एच. आर्गिरिस ने समीकरणों की एक प्रणाली में एक संरचना के मौलिक घटकों को जोड़ने की अवधारणा को व्यवस्थित किया। अंत में, 6 नवंबर 1959 को, बोइंग की स्ट्रक्चरल डायनेमिक्स यूनिट के प्रमुख एमजे टर्नर ने कंप्यूटर कार्यान्वयन के लिए एक कुशल मॉडल के रूप में प्रत्यक्ष कठोरता विधि को रेखांकित करते हुए एक पेपर प्रकाशित किया। (फेलिपा 2001).

सदस्य कठोरता संबंध

एक विशिष्ट सदस्य कठोरता संबंध के निम्नलिखित सामान्य रूप हैं:

$\mathbf {Q} ^{m}=\mathbf {k} ^{m}\mathbf {q} ^{m}+\mathbf {Q} ^{om}$

(1)

जहाँ

एम = सदस्य संख्या एम।

$\mathbf {Q} ^{m}$ = सदस्य की विशिष्ट शक्तियों का सदिश, जो अज्ञात आंतरिक बल हैं।

$\mathbf {k} ^{m}$ = सदस्य कठोरता मैट्रिक्स जो विकृतियों के खिलाफ सदस्य के प्रतिरोध की विशेषता है।

$\mathbf {q} ^{m}$ = सदस्यों की विशेषता विस्थापन और विकृतियों का वेक्टर।

$\mathbf {Q} ^{om}$ = बाहरी प्रभाव (जैसे ज्ञात बल और तापमान परिवर्तन) के कारण सदस्य की विशिष्ट शक्तियों का वेक्टर सदस्य पर लागू होता है $\mathbf {q} ^{m}=0$.

अगर $\mathbf {q} ^{m}$ पूर्ण विस्थापन के बजाय सदस्य विरूपण हैं, तब $\mathbf {Q} ^{m}$ स्वतंत्र सदस्य बल हैं, और ऐसे मामले में (1) को तथाकथित सदस्य लचीलापन मैट्रिक्स उत्पन्न करने के लिए उलटा किया जा सकता है, जिसका प्रयोग लचीलापन विधि में किया जाता है।

सिस्टम कठोरता संबंध

See also: कठोरता मैट्रिक्स

एक प्रणाली के लिए जिसमें कई सदस्य नोड्स नामक बिंदुओं पर परस्पर जुड़े होते हैं, सदस्यों की कठोरता संबंध जैसे Eq। (1) को निम्नलिखित अवलोकनों का उपयोग करके एकीकृत किया जा सकता है:

• सदस्य विकृति $\mathbf {q} ^{m}$ सदस्यों के बीच अनुकूलता सुनिश्चित करने के लिए सिस्टम नोडल विस्थापन आर के संदर्भ में व्यक्त किया जा सकता है। इसका अर्थ है कि r प्राथमिक अज्ञात होगा।
• सदस्य बल $\mathbf {Q} ^{m}$ नोडल बलों आर के तहत नोड्स को संतुलन में रखने में मदद करता है। इसका तात्पर्य है कि (1) के दाहिने हाथ को पूरे सिस्टम के लिए निम्नलिखित नोडल संतुलन समीकरणों के दाहिने हाथ में एकीकृत किया जाएगा:

$\mathbf {R} =\mathbf {Kr} +\mathbf {R} ^{o}$

(2)

जहाँ

$\mathbf {R}$ = नोडल बलों का वेक्टर, सिस्टम के नोड्स पर लागू बाहरी बलों का प्रतिनिधित्व करता है।

$\mathbf {K}$ = सिस्टम कठोरता मैट्रिक्स, जो सदस्यों की कठोरता मैट्रिक्स को जोड़कर स्थापित की जाती है $\mathbf {k} ^{m}$.

$\mathbf {r}$ = सिस्टम के नोडल विस्थापन का वेक्टर जो सिस्टम के सभी संभावित विकृत विन्यासों को मनमाने ढंग से नोडल बलों आर के अधीन परिभाषित कर सकता है।

$\mathbf {R} ^{o}$ = समतुल्य नोडल बलों का वेक्टर, नोडल बलों के अलावा अन्य सभी बाहरी प्रभावों का प्रतिनिधित्व करता है जो पहले से ही पूर्ववर्ती नोडल बल वेक्टर आर में सम्मिलित हैं। यह वेक्टर सदस्यों को जोड़कर स्थापित किया गया है। $\mathbf {Q} ^{om}$.

समाधान

सिस्टम कठोरता मैट्रिक्स K वर्गाकार है क्योंकि वैक्टर R और r का आकार समान है। इसके अलावा, यह सममित है क्योंकि $\mathbf {k} ^{m}$ सममित है। एक बार समर्थन की बाधाओं (2) के लिए जिम्मेदार होने के बाद, नोडल विस्थापन रैखिक समीकरणों (2) की प्रणाली को प्रतीकात्मक रूप से हल करके पाया जाता है:

$\mathbf {r} =\mathbf {K} ^{-1}(\mathbf {R} -\mathbf {R} ^{o})\qquad \qquad \qquad \mathrm {(3)}$

बाद में, सदस्यों के विशिष्ट बलों को समीकरण (1) से पाया जा सकता है, जहां $\mathbf {q} ^{m}$ संगतता विचार द्वारा आर से पाया जा सकता है।

प्रत्यक्ष कठोरता विधि

समीकरण (1) का एक ऐसे रूप में होना सामान्य है जहाँ $\mathbf {q} ^{m}$ और $\mathbf {Q} ^{om}$ क्रमशः, सदस्य-अंत विस्थापन और बल आर और आर के साथ दिशा में मेल खाते हैं। ऐसे मामले में, $\mathbf {K}$ और $\mathbf {R} ^{o}$ सदस्यों के मैट्रिसेस के सीधे योग द्वारा प्राप्त किया जा सकता है $\mathbf {k} ^{m}$ और $\mathbf {Q} ^{om}$. विधि को तब प्रत्यक्ष कठोरता विधि के रूप में जाना जाता है।

मैट्रिक्स कठोरता विधि के फायदे और नुकसान की तुलना और लचीलेपन विधि लेख में चर्चा की गई है।

उदाहरण

टूटना

प्रत्यक्ष कठोरता विधि का उपयोग करते समय पहला कदम संरचना बनाने वाले व्यक्तिगत तत्वों की पहचान करना है।

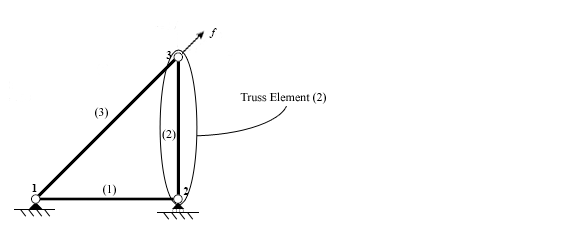तत्वों की पहचान हो जाने के बाद, संरचना नोड्स पर डिस्कनेक्ट हो जाती है, बिंदु जो विभिन्न तत्वों को एक साथ जोड़ते हैं।

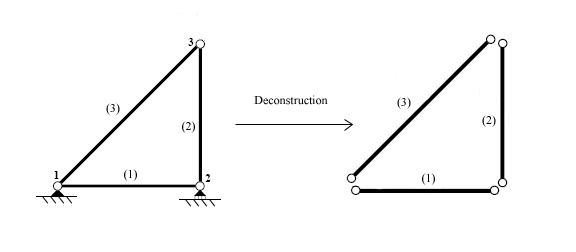सदस्य कठोरता समीकरणों को विकसित करने के लिए प्रत्येक तत्व का व्यक्तिगत रूप से विश्लेषण किया जाता है। बल और विस्थापन तत्व कठोरता मैट्रिक्स के माध्यम से संबंधित होते हैं जो तत्व की ज्यामिति और गुणों पर निर्भर करता है।

एक ट्रस तत्व केवल संपीड़न या तनाव में बल संचारित कर सकता है। इसका मतलब है कि दो आयामों में, प्रत्येक नोड में स्वतंत्रता की दो डिग्री (यांत्रिकी) (डीओएफ) होती है: क्षैतिज और ऊर्ध्वाधर विस्थापन। परिणामी समीकरण में चार गुणा चार कठोरता मैट्रिक्स होता है।

${\begin{bmatrix}f_{x1}\\f_{y1}\\f_{x2}\\f_{y2}\\\end{bmatrix}}={\begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}\\k_{21}&k_{22}&k_{23}&k_{24}\\k_{31}&k_{32}&k_{33}&k_{34}\\k_{41}&k_{42}&k_{43}&k_{44}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\u_{x2}\\u_{y2}\\\end{bmatrix}}$

एक फ्रेम तत्व संपीड़न और तनाव के अलावा झुकने वाले क्षणों का सामना करने में सक्षम है। इसके परिणामस्वरूप स्वतंत्रता की तीन डिग्री होती हैं: क्षैतिज विस्थापन, ऊर्ध्वाधर विस्थापन और इन-प्लेन रोटेशन। इस मामले में कठोरता मैट्रिक्स छह से छह है।

${\begin{bmatrix}f_{x1}\\f_{y1}\\m_{z1}\\f_{x2}\\f_{y2}\\m_{z2}\\\end{bmatrix}}={\begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}&k_{15}&k_{16}\\k_{21}&k_{22}&k_{23}&k_{24}&k_{25}&k_{26}\\k_{31}&k_{32}&k_{33}&k_{34}&k_{35}&k_{36}\\k_{41}&k_{42}&k_{43}&k_{44}&k_{45}&k_{46}\\k_{51}&k_{52}&k_{53}&k_{54}&k_{55}&k_{56}\\k_{61}&k_{62}&k_{63}&k_{64}&k_{65}&k_{66}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\\theta _{z1}\\u_{x2}\\u_{y2}\\\theta _{z2}\\\end{bmatrix}}$

अन्य तत्वों जैसे प्लेट और गोले को भी प्रत्यक्ष कठोरता विधि में सम्मिलित किया जा सकता है और इसी तरह के समीकरणों को विकसित किया जाना चाहिए।

सभा

एक बार व्यक्तिगत तत्व कठोरता संबंध विकसित हो जाने के बाद उन्हें मूल संरचना में इकट्ठा किया जाना चाहिए। इस प्रक्रिया में पहला कदम संपूर्ण संरचना के लिए अलग-अलग तत्वों के लिए कठोरता संबंधों को एक वैश्विक प्रणाली में परिवर्तित करना है। ट्रस तत्व के मामले में, कठोरता विधि का वैश्विक रूप वैश्विक समन्वय प्रणाली के संबंध में तत्व के कोण पर निर्भर करता है (यह प्रणाली आमतौर पर पारंपरिक कार्टेशियन समन्वय प्रणाली है)।

${\begin{bmatrix}f_{x1}\\f_{y1}\\f_{x2}\\f_{y2}\\\end{bmatrix}}={\frac {EA}{L}}{\begin{bmatrix}c^{2}&sc&-c^{2}&-sc\\sc&s^{2}&-sc&-s^{2}\\-c^{2}&-sc&c^{2}&sc\\-sc&-s^{2}&sc&s^{2}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\u_{x2}\\u_{y2}\\\end{bmatrix}}{\begin{array}{r }s=\sin \beta \\c=\cos \beta \\\end{array}}$

(कोण β पर एक ट्रस तत्व के लिए) समान रूप से,

${\begin{bmatrix}f_{x1}\\f_{y1}\\\hline f_{x2}\\f_{y2}\end{bmatrix}}={\frac {EA}{L}}\left[{\begin{array}{c c|c c}c_{x}c_{x}&c_{x}c_{y}&-c_{x}c_{x}&-c_{x}c_{y}\\c_{y}c_{x}&c_{y}c_{y}&-c_{y}c_{x}&-c_{y}c_{y}\\\hline -c_{x}c_{x}&-c_{x}c_{y}&c_{x}c_{x}&c_{x}c_{y}\\-c_{y}c_{x}&-c_{y}c_{y}&c_{y}c_{x}&c_{y}c_{y}\\\end{array}}\right]{\begin{bmatrix}u_{x1}\\u_{y1}\\\hline u_{x2}\\u_{y2}\end{bmatrix}}$

जहाँ $c_{x}$ और $c_{y}$ ट्रस तत्व की दिशा कोसाइन हैं (यानी, वे सदस्य के साथ संरेखित इकाई वेक्टर के घटक हैं)। इस फॉर्म से पता चलता है कि इस फॉर्मूलेशन में स्पष्ट पैटर्न को विस्तारित करके तत्व कठोरता को 3-डी स्पेस ट्रस में सामान्य कैसे किया जाए।

वैश्विक समन्वय प्रणाली में तत्व कठोरता मैट्रिक्स विकसित करने के बाद, उन्हें एक "मास्टर" या "वैश्विक" कठोरता मैट्रिक्स में विलय कर दिया जाना चाहिए। इन मेट्रिसेस को एक साथ मिलाते समय दो नियमों का पालन किया जाना चाहिए: विस्थापन की अनुकूलता और प्रत्येक नोड पर बल संतुलन। तत्व नोडल विस्थापन को वैश्विक नोडल विस्थापन से संबंधित करके इन नियमों को कायम रखा जाता है।

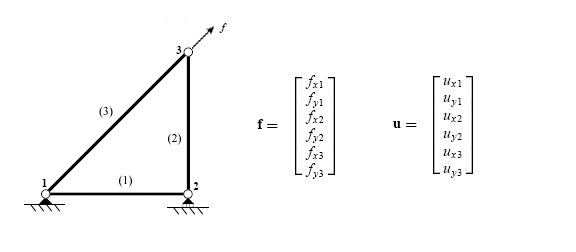वैश्विक विस्थापन और बल वैक्टर प्रत्येक में संरचना में स्वतंत्रता की प्रत्येक डिग्री के लिए एक प्रविष्टि होती है। वैश्विक विस्थापन और लोड वैक्टर के अनुरूप प्रत्येक मैट्रिक्स को बढ़ाकर या विस्तारित करके तत्व कठोरता मैट्रिसेस को मिला दिया जाता है।

$k^{(1)}={\frac {EA}{L}}{\begin{bmatrix}1&0&-1&0\\0&0&0&0\\-1&0&1&0\\0&0&0&0\\\end{bmatrix}}\rightarrow K^{(1)}={\frac {EA}{L}}{\begin{bmatrix}1&0&-1&0&0&0\\0&0&0&0&0&0\\-1&0&1&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\\end{bmatrix}}$

(उपरोक्त संरचना के तत्व (1) के लिए)

अंत में, वैश्विक कठोरता मैट्रिक्स का निर्माण व्यक्तिगत विस्तारित तत्व मैट्रिक्स को एक साथ जोड़कर किया जाता है।

समाधान

एक बार वैश्विक कठोरता मैट्रिक्स, विस्थापन वेक्टर और बल वेक्टर का निर्माण हो जाने के बाद, सिस्टम को एकल मैट्रिक्स समीकरण के रूप में व्यक्त किया जा सकता है।

संरचना में स्वतंत्रता की प्रत्येक डिग्री के लिए, या तो विस्थापन या बल ज्ञात होता है।

स्वतंत्रता की प्रत्येक डिग्री के लिए ज्ञात मूल्य डालने के बाद, मास्टर कठोरता समीकरण पूर्ण और मूल्यांकन के लिए तैयार है। मैट्रिक्स समीकरण का मूल्यांकन करने के लिए कई अलग-अलग तरीके उपलब्ध हैं, जिनमें चोल्स्की अपघटन और समीकरणों की प्रणालियों के क्रूर बल मूल्यांकन तक सीमित नहीं है। यदि किसी संरचना को ठीक से रोका नहीं गया है, तो बल के प्रयोग से यह कठोर रूप से आगे बढ़ेगा और अतिरिक्त समर्थन शर्तों को जोड़ा जाना चाहिए।

इस खंड में वर्णित विधि प्रत्यक्ष कठोरता विधि के अवलोकन के रूप में है। प्रक्रिया पर अधिक जानकारी के साथ-साथ प्रक्रिया में निहित भौतिक गुणों के बारे में धारणाओं के लिए अतिरिक्त स्रोतों से परामर्श किया जाना चाहिए।

अनुप्रयोग

बड़ी संख्या में तत्वों वाले जटिल संरचनाओं का मूल्यांकन करने के लिए कंप्यूटर सॉफ़्टवेयर में प्रभावी ढंग से और आसानी से लागू करने के लिए प्रत्यक्ष कठोरता विधि विशेष रूप से विकसित की गई थी। आज, उपलब्ध लगभग हर परिमित तत्व सॉल्वर प्रत्यक्ष कठोरता विधि पर आधारित है। जबकि प्रत्येक प्रोग्राम एक ही प्रक्रिया का उपयोग करता है, कई को संगणना समय को कम करने और आवश्यक मेमोरी को कम करने के लिए सुव्यवस्थित किया गया है। इसे प्राप्त करने के लिए, शॉर्टकट विकसित किए गए हैं।

प्रत्यक्ष कठोरता पद्धति का उपयोग करने वाले सबसे बड़े क्षेत्रों में से एक संरचनात्मक विश्लेषण का क्षेत्र है जहां इस पद्धति को मॉडलिंग सॉफ्टवेयर में सम्मिलित किया गया है। सॉफ्टवेयर उपयोगकर्ताओं को एक संरचना को मॉडल करने की अनुमति देता है और उपयोगकर्ता द्वारा तत्वों के भौतिक गुणों को परिभाषित करने के बाद, कार्यक्रम स्वचालित रूप से तत्व और वैश्विक कठोरता संबंध उत्पन्न करता है। जब विभिन्न लोडिंग शर्तों को लागू किया जाता है तो सॉफ्टवेयर संरचना का मूल्यांकन करता है और उपयोगकर्ता के लिए विक्षेप उत्पन्न करता है।

यह भी देखें

• सीमित तत्व विधि
• संरचनात्मक यांत्रिकी में परिमित तत्व विधि
• संरचनात्मक विश्लेषण
• लचीलापन विधि
• परिमित तत्व सॉफ्टवेयर पैकेजों की सूची

बाहरी संबंध

• 1-डी स्प्रिंग सिस्टम के लिए डायरेक्ट स्टिफनेस मेथड का अनुप्रयोग
• मैट्रिक्स संरचनात्मक विश्लेषण
• कठोरता विश्लेषण सिमुलेशन के एनिमेशन

संदर्भ

• Felippa, Carlos A. (2001), "A historical outline of matrix structural analysis: a play in three acts" (PDF), Computers & Structures, 79 (14): 1313–1324, doi:10.1016/S0045-7949(01)00025-6, ISSN 0045-7949, archived from the original (PDF) on 2007-06-29, retrieved 2005-10-05
• Felippa, Carlos A. Introduction to Finite Element Method. Fall 2001. University of Colorado. 18 Sept. 2005
• Robinson, John. Structural Matrix Analysis for the Engineer. New York: John Wiley & Sons, 1966
• Rubinstein, Moshe F. Matrix Computer Analysis of Structures. New Jersey: Prentice-Hall, 1966
• McGuire, W., Gallagher, R. H., and Ziemian, R. D. Matrix Structural Analysis, 2nd Ed. New York: John Wiley & Sons, 2000.