लघु-कोण सन्निकटन: Difference between revisions
(Created page with "{{Short description|Simplification of the basic trigonometric functions}} File:Kleinwinkelnaeherungen.png|thumb|upright=1.5|कुछ (त्रिकोणमितीय)...") |
No edit summary |
||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Simplification of the basic trigonometric functions}} | {{Short description|Simplification of the basic trigonometric functions}} | ||
[[File:Kleinwinkelnaeherungen.png|thumb|upright=1.5| | [[File:Kleinwinkelnaeherungen.png|thumb|upright=1.5|{{math|''x'' → 0}} के लिए कुछ (त्रिकोणमितीय) फलनों का व्यवहार लगभग बराबर है]]मुख्य [[त्रिकोणमितीय कार्य|त्रिकोणमितीय फलनोंं]] के मानों को अनुमानित करने के लिए लघु-कोण सन्निकटन का उपयोग किया जा सकता है, बशर्ते कि प्रश्न में कोण छोटा हो और [[ कांति |रेडियन]] में मापा जाता हो- | ||
:<math> | :<math> | ||
| Line 9: | Line 9: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
[[यांत्रिकी]], [[ विद्युत चुम्बकीय |विद्युत चुंबकत्व]], [[प्रकाशिकी]], [[ नक्शानवीसी |कार्टोग्राफी]], [[खगोल]] विज्ञान और [[कंप्यूटर विज्ञान]] सहित भौतिकी और [[अभियांत्रिकी]] की शाखाओं में इन अनुमानों का व्यापक उपयोग है।<ref name="Holbrow2010" /><ref name="Plesha2012"/> इसका एक कारण यह है कि वे अवकल समीकरणों को बहुत सरल बना सकते हैं जिनका उत्तर पूर्ण परिशुद्धता के साथ देने की आवश्यकता नहीं है। | |||
लघु-कोण सन्निकटनों की वैधता प्रदर्शित करने के कई तरीके हैं। सबसे प्रत्यक्ष विधि प्रत्येक त्रिकोणमितीय फलनों के लिए [[मैकलॉरिन श्रृंखला|मैक्लॉरिन श्रृंखला]] को छोटा करना है। सन्निकटन के क्रम के आधार पर <math>\textstyle \cos \theta</math> को या तो <math>1</math> या <math display="inline"> 1-\frac{\theta^2}{2}</math> के रूप में अनुमानित किया जाता है।<ref>{{Cite web|title=Small-Angle Approximation {{!}} Brilliant Math & Science Wiki|url=https://brilliant.org/wiki/small-angle-approximation/|access-date=2020-07-22|website=brilliant.org|language=en-us}}</ref> | |||
== औचित्य == | == औचित्य == | ||
=== ग्राफिक === | === ग्राफिक === | ||
सन्निकटन की सटीकता चित्र 1 और चित्र 2 में नीचे | सन्निकटन की सटीकता को चित्र 1 और चित्र 2 में नीचे देखा जा सकता है। जैसे-जैसे कोण का माप शून्य की ओर अग्रसर होता है, सन्निकटन और मूल फलन के बीच का अंतर भी 0 की ओर बढ़ता है। | ||
<gallery widths=" | <gallery widths="500" heights="400"> | ||
File:Small_angle_compair_odd.svg|चित्र 1. मूल विषम | File:Small_angle_compair_odd.svg|'''चित्र 1. मूल विषम त्रिकोणमितीय फलनों की तुलना {{mvar|θ}} से। यह देखा गया है कि जैसे-जैसे कोण 0 की ओर अग्रसर होता है, सन्निकटन बेहतर होते जाते हैं। | ||
File:Small_angle_compare_even.svg|चित्र 2. की तुलना {{math|cos ''θ''}} को {{math|1 − {{sfrac|''θ''<sup>2</sup>|2}}}}. यह देखा गया है कि जैसे-जैसे कोण 0 की ओर अग्रसर होता है सन्निकटन बेहतर होता जाता है। | File:Small_angle_compare_even.svg|'''चित्र 2. की तुलना {{math|cos ''θ''}} को {{math|1 − {{sfrac|''θ''<sup>2</sup>|2}}}}. यह देखा गया है कि जैसे-जैसे कोण 0 की ओर अग्रसर होता है सन्निकटन बेहतर होता जाता है। | ||
</gallery> | </gallery> | ||
=== ज्यामितीय === | === ज्यामितीय === | ||
[[File:Small angle triangle.svg|600px]]दाईं ओर लाल खंड, {{math|d}}, कर्ण | [[File:Small angle triangle.svg|600px]]दाईं ओर लाल खंड, {{math|d}}, कर्ण, {{mvar|H}}, और निकटवर्ती भुजा, {{mvar|A}} की लंबाई के बीच का अंतर है। जैसा कि दिखाया गया है, {{mvar|H}} और {{mvar|A}} लगभग समान लंबाई हैं, जिसका अर्थ है कि {{math|cos ''θ''}} 1 के निकट है और {{math|{{sfrac|''θ''<sup>2</sup>|2}}}} लाल को सुव्यवस्थित करने में सहायता करता है।<math display="block"> \cos{\theta} \approx 1 - \frac{\theta^2}{2}</math>विपरीत पादस्तंभ, {{mvar|O}}, नीले चाप की लंबाई {{mvar|s}} के लगभग बराबर है। ज्यामिति से तथ्यों को इकट्ठा करना, {{math|1=''s'' = ''Aθ''}}, त्रिकोणमिति से, {{math|1=sin ''θ'' = {{sfrac|''O''|''H''}}}} और {{math|1=tan ''θ'' = {{sfrac|''O''|''A''}}}}, और चित्र से, {{math|''O'' ≈ ''s''}} और {{math|''H'' ≈ ''A''}} की ओर जाता है-<math display="block">\sin \theta = \frac{O}{H}\approx\frac{O}{A} = \tan \theta = \frac{O}{A} \approx \frac{s}{A} = \frac{A\theta}{A} = \theta.</math>सरलीकरण पत्तियां,<math display="block">\sin \theta \approx \tan \theta \approx \theta.</math> | ||
<math display="block"> \cos{\theta} \approx 1 - \frac{\theta^2}{2}</math> | |||
विपरीत | |||
<math display="block">\sin \theta = \frac{O}{H}\approx\frac{O}{A} = \tan \theta = \frac{O}{A} \approx \frac{s}{A} = \frac{A\theta}{A} = \theta.</math> | |||
<math display="block">\sin \theta \approx \tan \theta \approx \theta.</math> | |||
=== गणना === | |||
[[निचोड़ प्रमेय|संकुचन (स्क्वीज) प्रमेय]] का उपयोग करके,<ref name="Larson2006" /> हम इसे सिद्ध कर सकते हैं<math display="block"> | |||
\lim_{\theta \to 0} \frac{\sin(\theta)}{\theta} = 1, | |||
</math>जो θ के लघु मानों के लिए सन्निकटन <math>\sin(\theta) \approx \theta</math> का एक औपचारिक पुनर्कथन है। | |||
स्क्वीज प्रमेय का अधिक सावधानीपूर्वक प्रयोग यह सिद्ध करता है<math display="block"> | |||
\lim_{\theta \to 0} \frac{\tan(\theta)}{\theta} = 1, | \lim_{\theta \to 0} \frac{\tan(\theta)}{\theta} = 1, | ||
</math> जिससे हम यह निष्कर्ष निकालते हैं <math>\tan(\theta) \approx \theta</math> | </math>जिससे हम यह निष्कर्ष निकालते हैं कि θ के लघु मानों के लिए <math>\tan(\theta) \approx \theta</math> है। | ||
अंत में, | |||
अंत में, एल'हॉपिटल का नियम हमें यह बताता है<math display="block"> | |||
\lim_{\theta \to 0} \frac{\cos(\theta)-1}{\theta^2} = \lim_{\theta \to 0} \frac{-\sin(\theta)}{2\theta} = -\frac{1}{2}, | \lim_{\theta \to 0} \frac{\cos(\theta)-1}{\theta^2} = \lim_{\theta \to 0} \frac{-\sin(\theta)}{2\theta} = -\frac{1}{2}, | ||
</math> जो | </math>जो θ के लघु मानों के लिए <math display="inline">\cos(\theta) \approx 1 - \frac{\theta^2}{2}</math> में पुनर्व्यवस्थित होता है। वैकल्पिक रूप से, हम द्विकोण सूत्र <math>\cos 2A \equiv 1-2\sin^2 A</math> का उपयोग कर सकते हैं। <math>\theta = 2A</math> देने पर हमें<math display="inline">\cos\theta=1-2\sin^2\frac{\theta}{2}\approx1-\frac{\theta^2}{2}</math> प्राप्त होता है। | ||
=== | === बीजगणितीय === | ||
[[File:Small-angle approximation for sine function.svg|thumb|300px|साइन | [[File:Small-angle approximation for sine function.svg|thumb|300px|साइन फलन के लिए लघु-कोण सन्निकटन।]]संबंधित त्रिकोणमितीय फलन का मैक्लॉरिन विस्तार (लगभग 0 टेलर विस्तार) है<ref>{{cite book| authorlink=Mary L. Boas|last=Boas| first=Mary L.|title=[[Mathematical Methods in the Physical Sciences]]|year=2006| publisher=Wiley|page=26| isbn=978-0-471-19826-0}}</ref><math display="block">\begin{align} | ||
<math display="block">\begin{align} | |||
\sin \theta &= \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} \theta^{2n+1} \\ | \sin \theta &= \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} \theta^{2n+1} \\ | ||
&= \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \frac{\theta^7}{7!} + \cdots | &= \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \frac{\theta^7}{7!} + \cdots | ||
\end{align}</math> | \end{align}</math>जहां {{mvar|θ}} रेडियन में कोण है। स्पष्ट शब्दों में,<math display="block">\sin \theta = \theta - \frac{\theta^3}{6} + \frac{\theta^5}{120} - \frac{\theta^7}{5040} + \cdots </math>यह आसानी से देखा जा सकता है कि दूसरा सबसे महत्वपूर्ण (तीसरा क्रम) पद प्रथम पद के घन के रूप में गिरता है इस प्रकार, 0.01 जैसे लघु तर्क के लिए भी, दूसरे सबसे महत्वपूर्ण पद का मान {{val|0.000001}}, या {{sfrac|{{val|10000}}}} प्रथम पद के क्रम पर है। इस प्रकार कोई सुरक्षित रूप से अनुमानित कर सकता है-<math display="block">\sin \theta \approx \theta</math>विस्तार से, चूंकि एक लघु कोण का कोज्या बहुत निकट 1 है, और स्पर्शरेखा कोज्या द्वारा विभाजित ज्या द्वारा दी गई है,<math display="block">\tan \theta \approx \sin \theta \approx \theta,</math> | ||
यह आसानी से देखा जा सकता है कि दूसरा सबसे महत्वपूर्ण (तीसरा क्रम) पद | |||
विस्तार से, चूंकि एक | |||
== सन्निकटन की त्रुटि == | == सन्निकटन की त्रुटि == | ||
[[File:Small angle compare error.svg|thumb|upright=2|चित्रा 3. | [[File:Small angle compare error.svg|thumb|upright=2|चित्रा 3. लघु कोण सन्निकटन के लिए सापेक्ष त्रुटियों का एक ग्राफ।]]चित्रा 3 लघु कोण सन्निकटन की सापेक्ष त्रुटियों को दर्शाता है। जिस कोण पर सापेक्ष त्रुटि 1% से अधिक होती है वह इस प्रकार है- | ||
* {{math|cos ''θ'' ≈ 1}} लगभग 0.1408 रेडियन (8.07°) पर | * {{math|cos ''θ'' ≈ 1}} लगभग 0.1408 रेडियन (8.07°) पर | ||
| Line 70: | Line 66: | ||
== कोण योग और अंतर == | == कोण योग और अंतर == | ||
जब | जब कोणों में से एक कोण छोटा (β ≈ 0) होता है तो [[कोण जोड़ और घटाव प्रमेय]] निम्नलिखित में कम हो जाते हैं- | ||
:{| | :{| | ||
|style="text-align:right;"| cos(''α'' + ''β'') ||≈ cos(''α'') − ''β'' sin(''α''), | |style="text-align:right;"| cos(''α'' + ''β'') ||≈ cos(''α'') − ''β'' sin(''α''), | ||
| Line 80: | Line 76: | ||
|style="text-align:right;"| sin(''α'' − ''β'') ||≈ sin(''α'') − ''β'' cos(''α''). | |style="text-align:right;"| sin(''α'' − ''β'') ||≈ sin(''α'') − ''β'' cos(''α''). | ||
|} | |} | ||
== विशिष्ट उपयोग == | == विशिष्ट उपयोग == | ||
=== खगोल विज्ञान === | === खगोल विज्ञान === | ||
खगोल विज्ञान में, एक दूर की वस्तु की छवि द्वारा | खगोल विज्ञान में, एक दूर की वस्तु की छवि द्वारा अंतरित [[कोणीय आकार]] या कोण प्रायः केवल कुछ [[ arcsecond |आर्कसेकंड]] होते हैं, इसलिए यह लघु कोण सन्निकटन के लिए उपयुक्त है।<ref name=Green1985/> रैखिक आकार ({{mvar|D}}) कोणीय आकार ({{mvar|X}}) और प्रेक्षक से दूरी ({{mvar|d}}) से सरल सूत्र द्वारा संबंधित है- | ||
:<math>D = X \frac{d}{206\,265}</math> | :<math>D = X \frac{d}{206\,265}</math> | ||
जहाँ {{mvar|X}} को आर्कसेकंड में मापा जाता है। | |||
संख्या {{val|206265}} लगभग एक वृत्त ({{val|1296000}}) में आर्कसेकंड की संख्या के बराबर है, जिसे {{math|2π}} से विभाजित किया गया है, या 1 रेडियन में आर्कसेकंड की संख्या है। | |||
सटीक सूत्र है | सटीक सूत्र है | ||
:<math>D = d \tan \left( X \frac{2\pi}{1\,296\,000} \right)</math> | :<math>D = d \tan \left( X \frac{2\pi}{1\,296\,000} \right)</math> | ||
और उपरोक्त सन्निकटन तब होता है जब {{math|tan ''X''}} | और उपरोक्त सन्निकटन तब होता है जब {{math|tan ''X''}} को {{mvar|X}} से प्रतिस्थापित किया जाता है। | ||
=== | === [[ लंगर |लोलक]] की गति === | ||
दूसरे क्रम का | दूसरे क्रम का कोज्या सन्निकटन विशेष रूप से एक लोलक की [[संभावित ऊर्जा]] की गणना करने में उपयोगी होता है, जिसे तब गति के अप्रत्यक्ष (ऊर्जा) समीकरण को खोजने के लिए लैग्रैन्जियन के साथ प्रयोग किया जा सकता है। | ||
एक साधारण | एक साधारण लोलक की [[आवृत्ति|अवधि]] की गणना करते समय, साइन के लिए लघु-कोण सन्निकटन का उपयोग परिणामी अवकल समीकरण को सरल आवर्ती गति का वर्णन करने वाले अवकल समीकरण के साथ तुलना करके आसानी से हल करने की अनुमति देने के लिए किया जाता है। | ||
=== प्रकाशिकी === | === प्रकाशिकी === | ||
प्रकाशिकी में, लघु-कोण सन्निकटन [[पैराएक्सियल सन्निकटन]] का आधार बनाते हैं। | प्रकाशिकी में, लघु-कोण सन्निकटन, [[पैराएक्सियल सन्निकटन|पराक्षीय सन्निकटन]] का आधार बनाते हैं। | ||
=== तरंग हस्तक्षेप === | |||
साइन और स्पर्शरेखा लघु-कोण सन्निकटन का उपयोग [[डबल-स्लिट प्रयोग]] या समीकरणों को सरल बनाने के लिए एक विवर्तन झंझरी के संबंध में किया जाता है, उदाहरण के लिए 'फ्रिंज रिक्ति' = 'तरंग दैर्ध्य' × 'स्लिट्स से स्क्रीन की दूरी' ÷ 'स्लिट पृथक्करण'।<ref>{{Cite web|url=http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/slits.html|title=Slit Interference}}</ref> | |||
=== संरचनात्मक यांत्रिकी === | === संरचनात्मक यांत्रिकी === | ||
लघु-कोण सन्निकटन संरचनात्मक यांत्रिकी में भी दिखाई देता है, विशेष रूप से स्थिरता और द्विभाजन विश्लेषण में (मुख्य रूप से अक्षीय रूप से लोड किए गए | लघु-कोण सन्निकटन संरचनात्मक यांत्रिकी में भी दिखाई देता है, विशेष रूप से स्थिरता और द्विभाजन विश्लेषण में (मुख्य रूप से अक्षीय रूप से लोड किए गए स्तंभ [[ buckling |प्रांकुचन]] से गुजरने के लिए तैयार)। यह महत्वपूर्ण सरलीकरण की ओर जाता है, हालांकि सटीकता और वास्तविक व्यवहार में अंतर्दृष्टि की कीमत पर। | ||
=== | === मार्ग दर्शन === | ||
[[हवाई नेविगेशन]] में उपयोग किए जाने वाले 60 में से 1 नियम का आधार लघु-कोण सन्निकटन है, साथ ही तथ्य | [[हवाई नेविगेशन|हवाई मार्गनिर्देशन]] में उपयोग किए जाने वाले 60 में से 1 नियम का आधार लघु-कोण सन्निकटन है, साथ ही यह तथ्य भी है कि एक रेडियन लगभग 60 डिग्री है। | ||
=== | === प्रक्षेप === | ||
[[त्रिकोणमितीय तालिका]] मानों के बीच प्रक्षेपित करने के लिए | [[त्रिकोणमितीय तालिका]] मानों के बीच प्रक्षेपित करने के लिए एक लघु कोण को सम्मिलित करने के लिए जोड़ और घटाव के सूत्र का उपयोग किया जा सकता है- | ||
उदाहरण | उदाहरण- sin(0.755)<math display="block">\begin{align} | ||
<math display="block">\begin{align} | |||
\sin(0.755) &= \sin(0.75 + 0.005) \\ | \sin(0.755) &= \sin(0.75 + 0.005) \\ | ||
& \approx \sin(0.75) + (0.005) \cos(0.75) \\ | & \approx \sin(0.75) + (0.005) \cos(0.75) \\ | ||
& \approx (0.6816) + (0.005)(0.7317) \\ | & \approx (0.6816) + (0.005)(0.7317) \\ | ||
& \approx 0.6853. | & \approx 0.6853. | ||
\end{align}</math> | \end{align}</math>जहां त्रिकोणमितीय तालिका से sin(0.75) और cos(0.75) के मान प्राप्त किए जाते हैं | ||
जहां त्रिकोणमितीय तालिका से sin(0.75) और cos(0.75) के मान प्राप्त किए जाते हैं | |||
== यह भी देखें == | == यह भी देखें == | ||
* [[पतला त्रिकोण]] | * [[पतला त्रिकोण|पतला त्रिभुज]] | ||
* | * लोलक के अति सूक्ष्म दोलन | ||
* [[वर्साइन और हावरसाइन]] | * [[वर्साइन और हावरसाइन|वरसाइन और हावरसाइन]] | ||
* [[एक्ससेकेंट और एक्सोसेकेंट]] | *[[एक्ससेकेंट और एक्सोसेकेंट]] | ||
== संदर्भ == | == संदर्भ == | ||
| Line 170: | Line 160: | ||
}} | }} | ||
{{DEFAULTSORT:Small-Angle Approximation}} | {{DEFAULTSORT:Small-Angle Approximation}} | ||
[[Category: | [[Category:CS1 English-language sources (en)]] | ||
[[Category:Created On 17/03/2023]] | [[Category:Created On 17/03/2023|Small-Angle Approximation]] | ||
[[Category:Lua-based templates|Small-Angle Approximation]] | |||
[[Category:Machine Translated Page|Small-Angle Approximation]] | |||
[[Category:Pages with broken file links|Small-Angle Approximation]] | |||
[[Category:Pages with script errors|Small-Angle Approximation]] | |||
[[Category:Short description with empty Wikidata description|Small-Angle Approximation]] | |||
[[Category:Template documentation pages|Short description/doc]] | |||
[[Category:Templates Vigyan Ready|Small-Angle Approximation]] | |||
[[Category:Templates that add a tracking category|Small-Angle Approximation]] | |||
[[Category:Templates that generate short descriptions|Small-Angle Approximation]] | |||
[[Category:Templates using TemplateData|Small-Angle Approximation]] | |||
[[Category:खगोल विज्ञान के समीकरण|Small-Angle Approximation]] | |||
[[Category:त्रिकोणमिति|Small-Angle Approximation]] | |||
Latest revision as of 09:52, 28 March 2023
मुख्य त्रिकोणमितीय फलनोंं के मानों को अनुमानित करने के लिए लघु-कोण सन्निकटन का उपयोग किया जा सकता है, बशर्ते कि प्रश्न में कोण छोटा हो और रेडियन में मापा जाता हो-
यांत्रिकी, विद्युत चुंबकत्व, प्रकाशिकी, कार्टोग्राफी, खगोल विज्ञान और कंप्यूटर विज्ञान सहित भौतिकी और अभियांत्रिकी की शाखाओं में इन अनुमानों का व्यापक उपयोग है।[1][2] इसका एक कारण यह है कि वे अवकल समीकरणों को बहुत सरल बना सकते हैं जिनका उत्तर पूर्ण परिशुद्धता के साथ देने की आवश्यकता नहीं है।
लघु-कोण सन्निकटनों की वैधता प्रदर्शित करने के कई तरीके हैं। सबसे प्रत्यक्ष विधि प्रत्येक त्रिकोणमितीय फलनों के लिए मैक्लॉरिन श्रृंखला को छोटा करना है। सन्निकटन के क्रम के आधार पर को या तो या के रूप में अनुमानित किया जाता है।[3]
औचित्य
ग्राफिक
सन्निकटन की सटीकता को चित्र 1 और चित्र 2 में नीचे देखा जा सकता है। जैसे-जैसे कोण का माप शून्य की ओर अग्रसर होता है, सन्निकटन और मूल फलन के बीच का अंतर भी 0 की ओर बढ़ता है।
ज्यामितीय
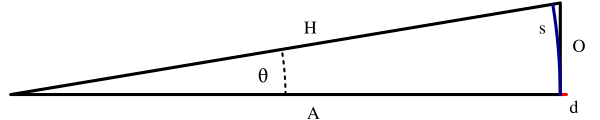 दाईं ओर लाल खंड, d, कर्ण, H, और निकटवर्ती भुजा, A की लंबाई के बीच का अंतर है। जैसा कि दिखाया गया है, H और A लगभग समान लंबाई हैं, जिसका अर्थ है कि cos θ 1 के निकट है और θ2/2 लाल को सुव्यवस्थित करने में सहायता करता है।
दाईं ओर लाल खंड, d, कर्ण, H, और निकटवर्ती भुजा, A की लंबाई के बीच का अंतर है। जैसा कि दिखाया गया है, H और A लगभग समान लंबाई हैं, जिसका अर्थ है कि cos θ 1 के निकट है और θ2/2 लाल को सुव्यवस्थित करने में सहायता करता है।
गणना
संकुचन (स्क्वीज) प्रमेय का उपयोग करके,[4] हम इसे सिद्ध कर सकते हैं
स्क्वीज प्रमेय का अधिक सावधानीपूर्वक प्रयोग यह सिद्ध करता है
अंत में, एल'हॉपिटल का नियम हमें यह बताता है
बीजगणितीय
संबंधित त्रिकोणमितीय फलन का मैक्लॉरिन विस्तार (लगभग 0 टेलर विस्तार) है[5]
सन्निकटन की त्रुटि
चित्रा 3 लघु कोण सन्निकटन की सापेक्ष त्रुटियों को दर्शाता है। जिस कोण पर सापेक्ष त्रुटि 1% से अधिक होती है वह इस प्रकार है-
- cos θ ≈ 1 लगभग 0.1408 रेडियन (8.07°) पर
- tan θ ≈ θ लगभग 0.1730 रेडियन (9.91°) पर
- sin θ ≈ θ लगभग 0.2441 रेडियन (13.99°) पर
- cos θ ≈ 1 − θ2/2 लगभग 0.6620 रेडियन (37.93°) पर
कोण योग और अंतर
जब कोणों में से एक कोण छोटा (β ≈ 0) होता है तो कोण जोड़ और घटाव प्रमेय निम्नलिखित में कम हो जाते हैं-
cos(α + β) ≈ cos(α) − β sin(α), cos(α − β) ≈ cos(α) + β sin(α), sin(α + β) ≈ sin(α) + β cos(α), sin(α − β) ≈ sin(α) − β cos(α).
विशिष्ट उपयोग
खगोल विज्ञान
खगोल विज्ञान में, एक दूर की वस्तु की छवि द्वारा अंतरित कोणीय आकार या कोण प्रायः केवल कुछ आर्कसेकंड होते हैं, इसलिए यह लघु कोण सन्निकटन के लिए उपयुक्त है।[6] रैखिक आकार (D) कोणीय आकार (X) और प्रेक्षक से दूरी (d) से सरल सूत्र द्वारा संबंधित है-
जहाँ X को आर्कसेकंड में मापा जाता है।
संख्या 206265 लगभग एक वृत्त (1296000) में आर्कसेकंड की संख्या के बराबर है, जिसे 2π से विभाजित किया गया है, या 1 रेडियन में आर्कसेकंड की संख्या है।
सटीक सूत्र है
और उपरोक्त सन्निकटन तब होता है जब tan X को X से प्रतिस्थापित किया जाता है।
लोलक की गति
दूसरे क्रम का कोज्या सन्निकटन विशेष रूप से एक लोलक की संभावित ऊर्जा की गणना करने में उपयोगी होता है, जिसे तब गति के अप्रत्यक्ष (ऊर्जा) समीकरण को खोजने के लिए लैग्रैन्जियन के साथ प्रयोग किया जा सकता है।
एक साधारण लोलक की अवधि की गणना करते समय, साइन के लिए लघु-कोण सन्निकटन का उपयोग परिणामी अवकल समीकरण को सरल आवर्ती गति का वर्णन करने वाले अवकल समीकरण के साथ तुलना करके आसानी से हल करने की अनुमति देने के लिए किया जाता है।
प्रकाशिकी
प्रकाशिकी में, लघु-कोण सन्निकटन, पराक्षीय सन्निकटन का आधार बनाते हैं।
तरंग हस्तक्षेप
साइन और स्पर्शरेखा लघु-कोण सन्निकटन का उपयोग डबल-स्लिट प्रयोग या समीकरणों को सरल बनाने के लिए एक विवर्तन झंझरी के संबंध में किया जाता है, उदाहरण के लिए 'फ्रिंज रिक्ति' = 'तरंग दैर्ध्य' × 'स्लिट्स से स्क्रीन की दूरी' ÷ 'स्लिट पृथक्करण'।[7]
संरचनात्मक यांत्रिकी
लघु-कोण सन्निकटन संरचनात्मक यांत्रिकी में भी दिखाई देता है, विशेष रूप से स्थिरता और द्विभाजन विश्लेषण में (मुख्य रूप से अक्षीय रूप से लोड किए गए स्तंभ प्रांकुचन से गुजरने के लिए तैयार)। यह महत्वपूर्ण सरलीकरण की ओर जाता है, हालांकि सटीकता और वास्तविक व्यवहार में अंतर्दृष्टि की कीमत पर।
मार्ग दर्शन
हवाई मार्गनिर्देशन में उपयोग किए जाने वाले 60 में से 1 नियम का आधार लघु-कोण सन्निकटन है, साथ ही यह तथ्य भी है कि एक रेडियन लगभग 60 डिग्री है।
प्रक्षेप
त्रिकोणमितीय तालिका मानों के बीच प्रक्षेपित करने के लिए एक लघु कोण को सम्मिलित करने के लिए जोड़ और घटाव के सूत्र का उपयोग किया जा सकता है-
उदाहरण- sin(0.755)
यह भी देखें
- पतला त्रिभुज
- लोलक के अति सूक्ष्म दोलन
- वरसाइन और हावरसाइन
- एक्ससेकेंट और एक्सोसेकेंट
संदर्भ
- ↑ Holbrow, Charles H.; et al. (2010), Modern Introductory Physics (2nd ed.), Springer Science & Business Media, pp. 30–32, ISBN 978-0387790794.
- ↑ Plesha, Michael; et al. (2012), Engineering Mechanics: Statics and Dynamics (2nd ed.), McGraw-Hill Higher Education, p. 12, ISBN 978-0077570613.
- ↑ "Small-Angle Approximation | Brilliant Math & Science Wiki". brilliant.org (in English). Retrieved 2020-07-22.
- ↑ Larson, Ron; et al. (2006), Calculus of a Single Variable: Early Transcendental Functions (4th ed.), Cengage Learning, p. 85, ISBN 0618606254.
- ↑ Boas, Mary L. (2006). Mathematical Methods in the Physical Sciences. Wiley. p. 26. ISBN 978-0-471-19826-0.
- ↑ Green, Robin M. (1985), Spherical Astronomy, Cambridge University Press, p. 19, ISBN 0521317797.
- ↑ "Slit Interference".




