केंद्रीय सीमा प्रमेय: Difference between revisions
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
प्रायिकता सिद्धांत में, केंद्रीय सीमा प्रमेय (CLT) स्थापित करता है, और कई स्थितियों में, समान रूप से वितरित स्वतंत्र प्रतिरूपो के लिए, मानकीकृत प्रतिरूप माध्य मानक सामान्य वितरण की ओर जाता है, भले ही मूल चर स्वयं सामान्य रूप से वितरित न हों। | प्रायिकता सिद्धांत में, केंद्रीय सीमा प्रमेय (CLT) स्थापित करता है, और कई स्थितियों में, समान रूप से वितरित स्वतंत्र प्रतिरूपो के लिए, मानकीकृत प्रतिरूप माध्य मानक सामान्य वितरण की ओर जाता है, भले ही मूल चर स्वयं सामान्य रूप से वितरित न हों। | ||
प्रायिकता सिद्धांत में प्रमेय एक महत्वपूर्ण अवधारणा है क्योंकि इसका तात्पर्य है कि प्रायिकता और सांख्यिकी विधियां जो सामान्य वितरण के लिए कार्य करती हैं, अन्य प्रकार के वितरणों से जुड़ी कई समस्याओं पर अनुप्रयोज्य हो सकती हैं। | प्रायिकता सिद्धांत में प्रमेय एक महत्वपूर्ण अवधारणा है क्योंकि इसका तात्पर्य है कि प्रायिकता और सांख्यिकी विधियां जो सामान्य वितरण के लिए कार्य करती हैं, और अन्य प्रकार के वितरणों से जुड़ी कई समस्याओं पर अनुप्रयोज्य हो सकती हैं। | ||
प्रायिकता सिद्धांत के औपचारिक विकास के पर्यन्त इस प्रमेय में कई परिवर्तन देखे गए हैं। प्रमेय के पूर्व संस्करण 1811 से पूर्व के हैं, परन्तु अपने आधुनिक सामान्य रूप में, प्रायिकता सिद्धांत में इस मौलिक परिणाम को 1920 के अंत तक सटीक रूप से कहा गया था,<ref>{{cite web |last1=Fischer |first1=Hans |title=केंद्रीय सीमा प्रमेय का इतिहास|url=http://www.medicine.mcgill.ca/epidemiology/hanley/bios601/GaussianModel/HistoryCentralLimitTheorem.pdf |archive-url=https://web.archive.org/web/20171031171033/http://www.medicine.mcgill.ca/epidemiology/hanley/bios601/GaussianModel/HistoryCentralLimitTheorem.pdf |archive-date=2017-10-31 |url-status=live |publisher=Springer New York Dordrecht Heidelberg London |access-date=29 April 2021}}</ref> इस प्रकार लौकिक और आधुनिक प्रायिकता सिद्धांत के मध्य एक सेतु के रूप में कार्य करना है। | प्रायिकता सिद्धांत के औपचारिक विकास के पर्यन्त इस प्रमेय में कई परिवर्तन देखे गए हैं। प्रमेय के पूर्व संस्करण 1811 से पूर्व के हैं, परन्तु अपने आधुनिक सामान्य रूप में, प्रायिकता सिद्धांत में इस मौलिक परिणाम को 1920 के अंत तक सटीक रूप से कहा गया था,<ref>{{cite web |last1=Fischer |first1=Hans |title=केंद्रीय सीमा प्रमेय का इतिहास|url=http://www.medicine.mcgill.ca/epidemiology/hanley/bios601/GaussianModel/HistoryCentralLimitTheorem.pdf |archive-url=https://web.archive.org/web/20171031171033/http://www.medicine.mcgill.ca/epidemiology/hanley/bios601/GaussianModel/HistoryCentralLimitTheorem.pdf |archive-date=2017-10-31 |url-status=live |publisher=Springer New York Dordrecht Heidelberg London |access-date=29 April 2021}}</ref> इस प्रकार लौकिक और आधुनिक प्रायिकता सिद्धांत के मध्य एक सेतु के रूप में कार्य करना है। | ||
| Line 21: | Line 21: | ||
माना <math display="inline">\{X_1, \ldots, X_n}\</math> [[ यादृच्छिक नमूना |यादृच्छिक प्रतिरूप]] का एक क्रम हो - अर्थात, आई.आई.डी. के एक क्रम द्वारा दिए गए अपेक्षित मान के वितरण से निर्मित किए गए यादृच्छिक चर <math display="inline">\mu</math> और परिमित विचरण {{nowrap|<math display="inline">\sigma^2</math>}} द्वारा दिया गया है, मान लीजिए हम प्रथम <math display="inline">n</math> प्रतिरूप माध्य में रुचि रखते हैं। | माना <math display="inline">\{X_1, \ldots, X_n}\</math> [[ यादृच्छिक नमूना |यादृच्छिक प्रतिरूप]] का एक क्रम हो - अर्थात, आई.आई.डी. के एक क्रम द्वारा दिए गए अपेक्षित मान के वितरण से निर्मित किए गए यादृच्छिक चर <math display="inline">\mu</math> और परिमित विचरण {{nowrap|<math display="inline">\sigma^2</math>}} द्वारा दिया गया है, मान लीजिए हम प्रथम <math display="inline">n</math> प्रतिरूप माध्य में रुचि रखते हैं। | ||
<math display="block">\bar{X}_n \equiv \frac{X_1 + \cdots + X_n}{n}</math> | <math display="block">\bar{X}_n \equiv \frac{X_1 + \cdots + X_n}{n}</math> | ||
बड़ी संख्या के नियम के अनुसार, प्रतिरूप औसत अनुमानित मान के [[लगभग सुनिश्चित अभिसरण|लगभग निश्चित रूप से]] (और इसलिए प्रायिकता में भी अभिसरित) अपेक्षित मान <math display="inline">\mu</math> जब {{nowrap|<math display="inline">n\to\infty</math>}} पर अभिसरित होता है। | बड़ी संख्या के नियम के अनुसार, प्रतिरूप औसत अनुमानित मान के [[लगभग सुनिश्चित अभिसरण|लगभग निश्चित रूप से]] (और इसलिए प्रायिकता में भी अभिसरित) अपेक्षित मान <math display="inline">\mu</math> जब {{nowrap|<math display="inline">n\to\infty</math>}} पर अभिसरित होता है। | ||
लौकिक केंद्रीय सीमा प्रमेय नियतात्मक संख्या <math display="inline">\mu</math> इस अभिसरण के पर्यन्त आसपास प्रसंभाव्य अस्थिरता के आकार और वितरण रूप का वर्णन करता है। अधिक सटीक रूप से, यह बताता है कि | लौकिक केंद्रीय सीमा प्रमेय नियतात्मक संख्या <math display="inline">\mu</math> इस अभिसरण के पर्यन्त आसपास प्रसंभाव्य अस्थिरता के आकार और वितरण रूप का वर्णन करता है। अधिक सटीक रूप से, यह बताता है कि जैसे <math display="inline">n</math> बड़ा हो जाता है, प्रतिरूप औसत के मध्य अंतर का वितरण <math display="inline">\bar{X}_n</math> और इसकी सीमा {{nowrap|<math display="inline">\mu</math>,}} जब कारक <math display="inline">\sqrt{n}</math> {{nowrap|<big>(</big>अर्थात <math display="inline">\sqrt{n}(\bar{X}_n - \mu)</math><big>)</big>}} द्वारा गुणा किया जाता है। माध्य 0 और विचरण के साथ सामान्य वितरण {{nowrap|<math display="inline">\sigma^2</math>}} का अनुमान लगाता है। काफी बड़े {{mvar|n}} के लिए, <math display="inline">\bar{X}_n</math> का वितरण माध्य के साथ अव्यवस्थिततः सामान्य वितरण <math display="inline">\mu</math> और विचरण {{nowrap|<math display="inline">\sigma^2/n</math>}} के अंतअ हो जाता है। | ||
प्रमेय की उपयोगिता यह है कि <math display="inline">\sqrt{n}(\bar{X}_n - \mu)</math> का वितरण विशिष्ट {{nowrap|<math display="inline">X_i</math>}} के वितरण के आकार की उपेक्षा किए बिना सामान्यता तक पहुँचता है। औपचारिक रूप से, प्रमेय को निम्नानुसार कहा जा सकता है: | प्रमेय की उपयोगिता यह है कि <math display="inline">\sqrt{n}(\bar{X}_n - \mu)</math> का वितरण विशिष्ट {{nowrap|<math display="inline">X_i</math>}} के वितरण के आकार की उपेक्षा किए बिना सामान्यता तक पहुँचता है। औपचारिक रूप से, प्रमेय को निम्नानुसार कहा जा सकता है: | ||
| Line 35: | Line 36: | ||
यदि {{nowrap|<math display="inline">\sigma > 0</math>,}} वितरण में अभिसरण का अर्थ है कि [[संचयी वितरण कार्य|संचयी वितरण]] <math display="inline">\sqrt{n}(\bar{X}_n - \mu)</math> कार्य करता है, <math display="inline">\mathcal{N}(0, \sigma^2)</math> वितरण के बिंदुवार को सीडीएफ में अभिसरण करें: प्रत्येक वास्तविक {{nowrap|संख्या <math display="inline">z</math>}} के लिए, | यदि {{nowrap|<math display="inline">\sigma > 0</math>,}} वितरण में अभिसरण का अर्थ है कि [[संचयी वितरण कार्य|संचयी वितरण]] <math display="inline">\sqrt{n}(\bar{X}_n - \mu)</math> कार्य करता है, <math display="inline">\mathcal{N}(0, \sigma^2)</math> वितरण के बिंदुवार को सीडीएफ में अभिसरण करें: प्रत्येक वास्तविक {{nowrap|संख्या <math display="inline">z</math>}} के लिए, | ||
<math display="block">\lim_{n\to\infty} \mathbb{P}\left[\sqrt{n}(\bar{X}_n-\mu) \le z\right] = \lim_{n\to\infty} \mathbb{P}\left[\frac{\sqrt{n}(\bar{X}_n-\mu)}{\sigma } \le \frac{z}{\sigma}\right]= \Phi\left(\frac{z}{\sigma}\right) ,</math> | <math display="block">\lim_{n\to\infty} \mathbb{P}\left[\sqrt{n}(\bar{X}_n-\mu) \le z\right] = \lim_{n\to\infty} \mathbb{P}\left[\frac{\sqrt{n}(\bar{X}_n-\mu)}{\sigma } \le \frac{z}{\sigma}\right]= \Phi\left(\frac{z}{\sigma}\right) ,</math> | ||
जहाँ <math display="inline">\Phi(z)</math> मानक सामान्य सीडीएफ है, जिसका <math display="inline">z</math> पर मूल्यांकन किया जाता है | जहाँ <math display="inline">\Phi(z)</math> मानक सामान्य सीडीएफ है, जिसका <math display="inline">z</math> पर मूल्यांकन किया जाता है और अभिसरण <math display="inline">z</math> एक समान है, इस अर्थ में कि | ||
<math display="block">\lim_{n\to\infty}\;\sup_{z\in\R}\;\left|\mathbb{P}\left[\sqrt{n}(\bar{X}_n-\mu) \le z\right] - \Phi\left(\frac{z}{\sigma}\right)\right| = 0~,</math> | <math display="block">\lim_{n\to\infty}\;\sup_{z\in\R}\;\left|\mathbb{P}\left[\sqrt{n}(\bar{X}_n-\mu) \le z\right] - \Phi\left(\frac{z}{\sigma}\right)\right| = 0~,</math> | ||
जहाँ <math display="inline">\sup</math> समुच्चय के न्यूनतम ऊपरी सीमा (या सर्वोच्च) को दर्शाता है।<ref>Bauer (2001, Theorem 30.13, p.199)</ref> | जहाँ <math display="inline">\sup</math> समुच्चय के न्यूनतम ऊपरी सीमा (या सर्वोच्च) को दर्शाता है।<ref>Bauer (2001, Theorem 30.13, p.199)</ref> | ||
| Line 68: | Line 69: | ||
=== बहुआयामी सीएलटी === | === बहुआयामी सीएलटी === | ||
विशिष्ट फलनों का उपयोग करने वाले प्रमाणों को उन स्थितियों तक बढ़ाया जा सकता है जहां प्रत्येक विशिष्ट <math display="inline">\mathbf{X}_i</math> में एक यादृच्छिक सदिश {{nowrap|<math display="inline">\R^k</math>}} है, <math display="inline">\boldsymbol\mu = \mathbb{E}[\mathbf{X}_i]</math> अभिप्राय सदिश के साथ और सहप्रसरण आव्यूह <math display="inline">\mathbf{\Sigma}</math> (सदिश के घटकों के मध्य), और ये यादृच्छिक सदिश स्वतंत्र और समान रूप से वितरित हैं। बहुआयामी केंद्रीय सीमा प्रमेय में | विशिष्ट फलनों का उपयोग करने वाले प्रमाणों को उन स्थितियों तक बढ़ाया जा सकता है जहां प्रत्येक विशिष्ट <math display="inline">\mathbf{X}_i</math> में एक यादृच्छिक सदिश {{nowrap|<math display="inline">\R^k</math>}} है, <math display="inline">\boldsymbol\mu = \mathbb{E}[\mathbf{X}_i]</math> अभिप्राय सदिश के साथ और सहप्रसरण आव्यूह <math display="inline">\mathbf{\Sigma}</math> (सदिश के घटकों के मध्य), और ये यादृच्छिक सदिश स्वतंत्र और समान रूप से वितरित हैं। बहुआयामी केंद्रीय सीमा प्रमेय में वर्णित है कि जब माप क्रमित किया जाता है, तो योग एक [[बहुभिन्नरूपी सामान्य वितरण]] में परिवर्तित हो जाते हैं।<ref>{{Cite book |last=van der Vaart |first=A.W. |title=स्पर्शोन्मुख आँकड़े|year=1998 |publisher=Cambridge University Press |location=New York, NY |isbn=978-0-521-49603-2 |lccn=98015176 |ref=CITEREFvan_der_Vaart1998}}</ref> | ||
माना | माना | ||
<math display="block">\mathbf{X}_i = \begin{bmatrix} X_{i(1)} \\ \vdots \\ X_{i(k)} \end{bmatrix}</math> | <math display="block">\mathbf{X}_i = \begin{bmatrix} X_{i(1)} \\ \vdots \\ X_{i(k)} \end{bmatrix}</math> | ||
{{mvar|k}}-सदिश है। माप क्रमित <math display="inline">\mathbf{X}_i</math> | {{mvar|k}}-सदिश है। माप क्रमित <math display="inline">\mathbf{X}_i</math> का अर्थ है कि यह एक यादृच्छिक सदिश है, न कि एक यादृच्छिक (अविभाजित) चर है। तब यादृच्छिक सदिशों का [[योग]] होगा; | ||
<math display="block">\begin{bmatrix} X_{1(1)} \\ \vdots \\ X_{1(k)} \end{bmatrix} + \begin{bmatrix} X_{2(1)} \\ \vdots \\ X_{2(k)} \end{bmatrix} + \cdots + \begin{bmatrix} X_{n(1)} \\ \vdots \\ X_{n(k)} \end{bmatrix} = \begin{bmatrix} \sum_{i=1}^{n} \left [ X_{i(1)} \right ] \\ \vdots \\ \sum_{i=1}^{n} \left [ X_{i(k)} \right ] \end{bmatrix} = \sum_{i=1}^{n} \mathbf{X}_i</math> | <math display="block">\begin{bmatrix} X_{1(1)} \\ \vdots \\ X_{1(k)} \end{bmatrix} + \begin{bmatrix} X_{2(1)} \\ \vdots \\ X_{2(k)} \end{bmatrix} + \cdots + \begin{bmatrix} X_{n(1)} \\ \vdots \\ X_{n(k)} \end{bmatrix} = \begin{bmatrix} \sum_{i=1}^{n} \left [ X_{i(1)} \right ] \\ \vdots \\ \sum_{i=1}^{n} \left [ X_{i(k)} \right ] \end{bmatrix} = \sum_{i=1}^{n} \mathbf{X}_i</math> | ||
और औसत है | और औसत है | ||
| Line 102: | Line 103: | ||
{{Main|स्थिर वितरण#एक सामान्यीकृत केंद्रीय सीमा प्रमेय}} | {{Main|स्थिर वितरण#एक सामान्यीकृत केंद्रीय सीमा प्रमेय}} | ||
केंद्रीय सीमा प्रमेय में | केंद्रीय सीमा प्रमेय में वर्णित है कि परिमित भिन्नताओं के साथ कई स्वतंत्र और समान रूप से वितरित यादृच्छिक चर का योग एक सामान्य वितरण की ओर अग्रसर होगा क्योंकि चर की संख्या बढ़ती है। [[बोरिस व्लादिमीरोविच गेदेंको]] और [[एंड्री निकोलाइविच कोलमोगोरोव]] के कारण एक सामान्यीकरण बताता है कि पावर-लॉ टेल (पारेतो वितरण) वितरण के साथ कई यादृच्छिक चर <math display="inline">{|x|}^{-\alpha-1}</math> का योग घटता है, जहाँ <math display="inline">0 < \alpha < 2</math> (और इसलिए अनंत विचरण) एक स्थिर वितरण <math display="inline">f(x; \alpha, 0, c, 0)</math> की ओर प्रवृत्त होगा, जैसे-जैसे योगों की संख्या बढ़ती है।<ref name=Voit2003a>{{cite book |first=Johannes |last=Voit |year=2003 |title=वित्तीय बाजारों के सांख्यिकीय यांत्रिकी|series=Texts and Monographs in Physics |publisher=Springer-Verlag |isbn=3-540-00978-7 |chapter=Section f5.4.3 |chapter-url=https://books.google.com/books?id=6zUlh_TkWSwC }}</ref><ref>{{cite book |first1=B.V. |last1=Gnedenko |first2=A.N. |last2=Kolmogorov |title=स्वतंत्र यादृच्छिक चर के योग के लिए वितरण सीमित करें|location=Cambridge |publisher=Addison-Wesley |year=1954 |url=https://archive.org/details/limitdistributio00gned_0 |url-access=registration }}</ref> यदि <math display="inline">\alpha > 2</math> तो योग 2 के समान स्थिरता मापदंड के साथ एक [[स्थिर वितरण]] में परिवर्तित हो जाता है, अर्थात गॉसियन वितरण।<ref name=Uchaikin>{{cite book |first1=Vladimir V. |last1=Uchaikin |first2=V.M. |last2=Zolotarev |year=1999 |title=Chance and Stability: Stable distributions and their applications |publisher=VSP |isbn=90-6764-301-7 |pages=61–62}}</ref> | ||
| Line 120: | Line 121: | ||
जहां श्रृंखला पूर्णतया से अभिसरण करती है। | जहां श्रृंखला पूर्णतया से अभिसरण करती है। | ||
पुर्वानुमान <math display="inline">\sigma \ne 0</math> छोड़ा नहीं जा सकता, क्योंकि स्पर्शोन्मुख सामान्यता <math display="inline">X_n = Y_n - Y_{n-1}</math> विफल हो जाता है, जहाँ <math display="inline">Y_n</math> एक अन्य स्थिर क्रम हैं। | |||
प्रमेय का एक प्रबल संस्करण है:<ref>Durrett (2004, Sect. 7.7(c), Theorem 7.8)</ref> | प्रमेय का एक प्रबल संस्करण है:<ref>Durrett (2004, Sect. 7.7(c), Theorem 7.8)</ref> पुर्वानुमान <math display="inline">\mathbb{E}\left[{X_n}^{12}\right] < \infty</math> को {{nowrap|<math display="inline">\mathbb{E}\left[{\left|X_n\right|}^{2+\delta}\right] < \infty</math>,}} से और धारणा <math display="inline">\alpha_n = O\left(n^{-5}\right) </math> से प्रतिस्थापित किया जाता है | ||
<math display="block">\sum_n \alpha_n^{\frac\delta{2(2+\delta)}} < \infty.</math> | <math display="block">\sum_n \alpha_n^{\frac\delta{2(2+\delta)}} < \infty.</math> | ||
ऐसे | ऐसे <math display="inline">\delta > 0</math> का अस्तित्व निष्कर्ष सुनिश्चित करता है। मिश्रित स्थितियों के अंतर्गत सीमा प्रमेय के विश्वकोषीय विवेचन के लिए {{harv|ब्राडली|2007}} देखें। | ||
=== मार्टिंगेल अंतर सीएलटी === | === मार्टिंगेल अंतर सीएलटी === | ||
| Line 132: | Line 133: | ||
* प्रत्येक {{math|''ε'' > 0}} के लिए, <math> \frac1n \sum_{k=1}^n{\mathbb{E}\left[\left(M_k-M_{k-1}\right)^2\mathbf{1}\left[|M_k-M_{k-1}|>\varepsilon\sqrt{n}\right]\right]} \to 0 </math> जैसे {{math|''n'' → ∞}}, | * प्रत्येक {{math|''ε'' > 0}} के लिए, <math> \frac1n \sum_{k=1}^n{\mathbb{E}\left[\left(M_k-M_{k-1}\right)^2\mathbf{1}\left[|M_k-M_{k-1}|>\varepsilon\sqrt{n}\right]\right]} \to 0 </math> जैसे {{math|''n'' → ∞}}, | ||
तब <math display="inline">\frac{M_n}{\sqrt{n}}</math> वितरण <math display="inline">\mathcal{N}(0, 1)</math> जैसे <math display="inline">n \to \infty</math> | तब <math display="inline">\frac{M_n}{\sqrt{n}}</math> वितरण <math display="inline">\mathcal{N}(0, 1)</math> जैसे <math display="inline">n \to \infty</math> <ref>Durrett (2004, Sect. 7.7, Theorem 7.4)</ref><ref>Billingsley (1995, Theorem 35.12)</ref>में परिवर्तित करता है।}} | ||
== टिप्पणी == | == टिप्पणी == | ||
| Line 141: | Line 142: | ||
मान लीजिए <math display="inline">\{X_1, \ldots, X_n, \ldots \}</math> स्वतंत्र और समान रूप से वितरित यादृच्छिक चर हैं, प्रत्येक का अर्थ <math display="inline">\mu</math>, और परिमित विचरण {{nowrap|<math display="inline">\sigma^2</math>}} है। योग <math display="inline">X_1 + \cdots + X_n</math> का अर्थ <math display="inline">n\mu</math>, और प्रसरण {{nowrap|<math display="inline">n\sigma^2</math>}} है। यादृच्छिक चर पर विचार करें, | मान लीजिए <math display="inline">\{X_1, \ldots, X_n, \ldots \}</math> स्वतंत्र और समान रूप से वितरित यादृच्छिक चर हैं, प्रत्येक का अर्थ <math display="inline">\mu</math>, और परिमित विचरण {{nowrap|<math display="inline">\sigma^2</math>}} है। योग <math display="inline">X_1 + \cdots + X_n</math> का अर्थ <math display="inline">n\mu</math>, और प्रसरण {{nowrap|<math display="inline">n\sigma^2</math>}} है। यादृच्छिक चर पर विचार करें, | ||
<math display="block">Z_n = \frac{X_1+\cdots+X_n - n \mu}{\sqrt{n \sigma^2}} = \sum_{i=1}^n \frac{X_i - \mu}{\sqrt{n \sigma^2}} = \sum_{i=1}^n \frac{1}{\sqrt{n}} Y_i,</math> | <math display="block">Z_n = \frac{X_1+\cdots+X_n - n \mu}{\sqrt{n \sigma^2}} = \sum_{i=1}^n \frac{X_i - \mu}{\sqrt{n \sigma^2}} = \sum_{i=1}^n \frac{1}{\sqrt{n}} Y_i,</math> | ||
जहां अंतिम चरण में हमने नए यादृच्छिक चर {{nowrap|<math display="inline">Y_i = \frac{X_i - \mu}{\sigma} </math> | जहां अंतिम चरण में हमने नए यादृच्छिक चर {{nowrap|<math display="inline">Y_i = \frac{X_i - \mu}{\sigma} </math>}} परिभाषित किए, प्रत्येक शून्य माध्य और इकाई विचरण के साथ {{nowrap|(<math display="inline">\operatorname{var}(Y) = 1</math>)}} का अभिलाक्षणिक फलन <math display="inline">Z_n</math> द्वारा दिया गया है। | ||
<math display="block">\varphi_{Z_n}\!(t) = \varphi_{\sum_{i=1}^n {\frac{1}{\sqrt{n}}Y_i}}\!(t) \ =\ \varphi_{Y_1}\!\!\left(\frac{t}{\sqrt{n}}\right) \varphi_{Y_2}\!\! \left(\frac{t}{\sqrt{n}}\right)\cdots \varphi_{Y_n}\!\! \left(\frac{t}{\sqrt{n}}\right) \ =\ \left[\varphi_{Y_1}\!\!\left(\frac{t}{\sqrt{n}}\right)\right]^n, | <math display="block">\varphi_{Z_n}\!(t) = \varphi_{\sum_{i=1}^n {\frac{1}{\sqrt{n}}Y_i}}\!(t) \ =\ \varphi_{Y_1}\!\!\left(\frac{t}{\sqrt{n}}\right) \varphi_{Y_2}\!\! \left(\frac{t}{\sqrt{n}}\right)\cdots \varphi_{Y_n}\!\! \left(\frac{t}{\sqrt{n}}\right) \ =\ \left[\varphi_{Y_1}\!\!\left(\frac{t}{\sqrt{n}}\right)\right]^n, | ||
</math> | </math> | ||
| Line 148: | Line 149: | ||
जहाँ <math display="inline">o(t^2 / n)</math> के कुछ फलनो के लिए "छोटा o प्रतीकांकन" <math display="inline">t</math> है, जो शून्य से अधिक तीव्रता {{nowrap|<math display="inline">t^2 / n</math>}} से जाता है। चरघातांकी फलनो की सीमा से {{nowrap|(<math display="inline">e^x = \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n</math>),}} का अभिलाक्षणिक फलन <math>Z_n</math> के समान होता है। | जहाँ <math display="inline">o(t^2 / n)</math> के कुछ फलनो के लिए "छोटा o प्रतीकांकन" <math display="inline">t</math> है, जो शून्य से अधिक तीव्रता {{nowrap|<math display="inline">t^2 / n</math>}} से जाता है। चरघातांकी फलनो की सीमा से {{nowrap|(<math display="inline">e^x = \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n</math>),}} का अभिलाक्षणिक फलन <math>Z_n</math> के समान होता है। | ||
<math display="block">\varphi_{Z_n}(t) = \left(1 - \frac{t^2}{2n} + o\left(\frac{t^2}{n}\right) \right)^n \rightarrow e^{-\frac{1}{2} t^2}, \quad n \to \infty.</math> | <math display="block">\varphi_{Z_n}(t) = \left(1 - \frac{t^2}{2n} + o\left(\frac{t^2}{n}\right) \right)^n \rightarrow e^{-\frac{1}{2} t^2}, \quad n \to \infty.</math> | ||
उच्च आदेश की सभी पद सीमा {{nowrap|<math display="inline">n\to\infty</math>}} में लुप्त हो | उच्च आदेश की सभी पद सीमा {{nowrap|<math display="inline">n\to\infty</math>}} में लुप्त हो जाती है, दाहिने हाथ की ओर एक मानक सामान्य वितरण <math display="inline">\mathcal{N}(0, 1)</math> के अभिलाक्षणिक फलन के समान है। जिसका तात्पर्य लेवी की निरंतरता प्रमेय के माध्यम से है कि वितरण <math display="inline">Z_n</math>, <math display="inline">\mathcal{N}(0,1)</math> से संपर्क करेगा, जैसा {{nowrap|<math display="inline">n\to\infty</math>.}} इसलिए, प्रतिरूप अभिप्राय | ||
<math display="block">\bar{X}_n = \frac{X_1+\cdots+X_n}{n}</math> | <math display="block">\bar{X}_n = \frac{X_1+\cdots+X_n}{n}</math> | ||
इस प्रकार कि | इस प्रकार कि | ||
| Line 155: | Line 156: | ||
=== सीमा तक अभिसरण === | === सीमा तक अभिसरण === | ||
केंद्रीय सीमा प्रमेय केवल एक [[स्पर्शोन्मुख वितरण]] प्रदान करता है। प्रेक्षणों की परिमित संख्या के लिए सन्निकटन के रूप में, यह सामान्य वितरण के शीर्ष के अंतअ होने पर ही एक उचित सन्निकटन प्रदान करता है; अवशिष्ट में विस्तार के लिए इसे बहुत बड़ी संख्या में अवलोकन की आवश्यकता होती है।{{citation needed|reason=तुरंत स्पष्ट नहीं, मुझे गूगल के माध्यम से कोई स्रोत नहीं मिला|date=जुलाई 2016}} | केंद्रीय सीमा प्रमेय केवल एक [[स्पर्शोन्मुख वितरण]] प्रदान करता है। प्रेक्षणों की परिमित संख्या के लिए सन्निकटन के रूप में, यह सामान्य वितरण के शीर्ष के अंतअ होने पर ही एक उचित सन्निकटन प्रदान करता है; अवशिष्ट में विस्तार के लिए इसे बहुत बड़ी संख्या में अवलोकन करने की आवश्यकता होती है।{{citation needed|reason=तुरंत स्पष्ट नहीं, मुझे गूगल के माध्यम से कोई स्रोत नहीं मिला|date=जुलाई 2016}} | ||
केंद्रीय सीमा प्रमेय में अभिसरण एक समान अभिसरण है क्योंकि सीमित संचयी वितरण | केंद्रीय सीमा प्रमेय में अभिसरण एक समान अभिसरण है क्योंकि सीमित संचयी वितरण फलन निरंतर है। यदि तृतीय केंद्रीय क्षण <math display="inline">\operatorname{E}\left[(X_1 - \mu)^3\right]</math> उपस्थित है और परिमित है, तो अभिसरण की गति कम से कम के क्रम <math display="inline">1 / \sqrt{n}</math> (बेरी-एसेन प्रमेय देखें) में है। स्टीन की विधि<ref name="stein1972">{{Cite journal| last = Stein |first=C. |author-link=Charles Stein (statistician)| title = आश्रित यादृच्छिक चर के योग के वितरण के लिए सामान्य सन्निकटन में त्रुटि के लिए बाध्य| journal = Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability| pages= 583–602| year = 1972|volume=6 |issue=2 | mr=402873 | zbl = 0278.60026| url=http://projecteuclid.org/euclid.bsmsp/1200514239 }}</ref>का उपयोग न केवल केंद्रीय सीमा प्रमेय को सिद्ध करने के लिए किया जा सकता है, बल्कि चयनित आव्यूह के लिए अभिसरण की दरों पर सीमा प्रदान करने के लिए भी किया जा सकता है।<ref>{{Cite book| title = Normal approximation by Stein's method| publisher = Springer| year = 2011|last1=Chen |first1=L. H. Y. |last2=Goldstein |first2=L. |last3=Shao |first3=Q. M. |isbn = 978-3-642-15006-7}}</ref> | ||
सामान्य वितरण का अभिसरण एकदिष्ट है, इस अर्थ में कि एन्ट्रापी <math display="inline">Z_n</math> सामान्य वितरण के [[मोनोटोनिक फ़ंक्शन|एकदिष्ट फलन]] को | सामान्य वितरण का अभिसरण एकदिष्ट है, इस अर्थ में कि एन्ट्रापी <math display="inline">Z_n</math> सामान्य वितरण के [[मोनोटोनिक फ़ंक्शन|एकदिष्ट फलन]] को बढ़ाती है।<ref name="ABBN" /> | ||
केंद्रीय सीमा प्रमेय विशेष रूप से स्वतंत्र और समान रूप से वितरित [[असतत यादृच्छिक चर]] के योग पर अनुप्रयोज्य होता है। असतत यादृच्छिक चर का योग अभी भी एक असतत यादृच्छिक चर है, ताकि हम असतत यादृच्छिक चर के एक अनुक्रम के साथ सामना कर सकें, जिसका संचयी प्रायिकता वितरण फलन एक सतत चर (अर्थात् सामान्य वितरण का) के अनुरूप संचयी प्रायिकता वितरण फलन की ओर अभिसरण करता है। . इसका अभिप्राय यह है कि यदि हम {{mvar|n}} स्वतंत्र समान असतत चर के योग की प्राप्ति का एक [[हिस्टोग्राम|आयतचित्र]] बनाते हैं, वह वक्र जो आयतचित्र बनाने वाले आयतों के ऊपरी फलको के केंद्रों से जुड़ता है, आयतचित्र एक गॉसियन वक्र की ओर अभिसरण करता है क्योंकि {{mvar|n}} अनंत तक पहुंचता है, इस संबंध को डी मोइवर-लाप्लास प्रमेय के रूप में जाना जाता है। द्विपद वितरण लेख केवल दो संभावित मान लेने वाले असतत चर की साधारण स्थितियों में केंद्रीय सीमा प्रमेय के ऐसे अनुप्रयोगो का विवरण देता है। | केंद्रीय सीमा प्रमेय विशेष रूप से स्वतंत्र और समान रूप से वितरित [[असतत यादृच्छिक चर]] के योग पर अनुप्रयोज्य होता है। असतत यादृच्छिक चर का योग अभी भी एक असतत यादृच्छिक चर है, ताकि हम असतत यादृच्छिक चर के एक अनुक्रम के साथ सामना कर सकें, जिसका संचयी प्रायिकता वितरण फलन एक सतत चर (अर्थात् सामान्य वितरण का) के अनुरूप संचयी प्रायिकता वितरण फलन की ओर अभिसरण करता है। . इसका अभिप्राय यह है कि यदि हम {{mvar|n}} स्वतंत्र समान असतत चर के योग की प्राप्ति का एक [[हिस्टोग्राम|आयतचित्र]] बनाते हैं, वह वक्र जो आयतचित्र बनाने वाले आयतों के ऊपरी फलको के केंद्रों से जुड़ता है, और आयतचित्र एक गॉसियन वक्र की ओर अभिसरण करता है क्योंकि {{mvar|n}} अनंत तक पहुंचता है, इस संबंध को डी मोइवर-लाप्लास प्रमेय के रूप में जाना जाता है। द्विपद वितरण लेख केवल दो संभावित मान लेने वाले असतत चर की साधारण स्थितियों में केंद्रीय सीमा प्रमेय के ऐसे अनुप्रयोगो का विवरण देता है। | ||
===बड़ी संख्या के नियम से संबंध=== | ===बड़ी संख्या के नियम से संबंध=== | ||
| Line 168: | Line 169: | ||
मान लीजिए कि हमारे पास एक स्पर्शोन्मुख विस्तार <math display="inline">f(n)</math> है: | मान लीजिए कि हमारे पास एक स्पर्शोन्मुख विस्तार <math display="inline">f(n)</math> है: | ||
<math display="block">f(n)= a_1 \varphi_{1}(n)+a_2 \varphi_{2}(n)+O\big(\varphi_{3}(n)\big) \qquad (n \to \infty).</math> | <math display="block">f(n)= a_1 \varphi_{1}(n)+a_2 \varphi_{2}(n)+O\big(\varphi_{3}(n)\big) \qquad (n \to \infty).</math> | ||
दोनों भागों को {{math|''φ''<sub>1</sub>(''n'')}} विभाजित करने और सीमा | दोनों भागों को {{math|''φ''<sub>1</sub>(''n'')}} से विभाजित करने और सीमा ग्रहण करने से {{math|''a''<sub>1</sub>}} उत्पादन होगा, विस्तार में उच्चतम-क्रम अवधि का गुणांक, जो उस दर का प्रतिनिधित्व करता है जिस पर {{math|''f''(''n'')}} इसके अग्रग पद में परिवर्तन करता है। | ||
<math display="block">\lim_{n\to\infty} \frac{f(n)}{\varphi_{1}(n)} = a_1.</math> | <math display="block">\lim_{n\to\infty} \frac{f(n)}{\varphi_{1}(n)} = a_1.</math> | ||
अनौपचारिक रूप से, कोई कह सकता है: {{math|''f''(''n'')}} लगभग | अनौपचारिक रूप से, कोई कह सकता है: {{math|''f''(''n'')}} लगभग {{math|''a''<sub>1</sub>''φ''<sub>1</sub>(''n'')}} के रूप में बढ़ता है, {{math|''f''(''n'')}} और इसके सन्निकटन के मध्य के अंतर को लेते हुए और फिर विस्तार में अगले पद से विभाजित करने पर, हम {{math|''f''(''n'')}} के विषय में अधिक परिष्कृत कथन पर पहुँचते हैंː | ||
<math display="block">\lim_{n\to\infty} \frac{f(n)-a_1 \varphi_{1}(n)}{\varphi_{2}(n)} = a_2 .</math> | <math display="block">\lim_{n\to\infty} \frac{f(n)-a_1 \varphi_{1}(n)}{\varphi_{2}(n)} = a_2 .</math> | ||
यहाँ कोई कह सकता है कि फलन और उसके सन्निकटन के मध्य का अंतर लगभग | यहाँ कोई कह सकता है कि फलन और उसके सन्निकटन के मध्य का अंतर लगभग {{math|''a''<sub>2</sub>''φ''<sub>2</sub>(''n'')}} के रूप में बढ़ता है। विचार यह है कि फलन को उपयुक्त सामान्यीकृत फलनो द्वारा विभाजित करना, और परिणाम के सीमित व्यवहार को देखते हुए, हमें मूल फलन के सीमित व्यवहार के विषय में बहुत कुछ बता सकता है। | ||
अनौपचारिक रूप से, इन पंक्तियों के साथ कुछ तब होता है जब स्वतंत्र समान रूप से वितरित यादृच्छिक चर के, {{math|''X''<sub>1</sub>, ..., ''X<sub>n</sub>''}} का योग, {{mvar|S<sub>n</sub>}}, लौकिक प्रायिकता सिद्धांत में अध्ययन किया जाता है।{{Citation needed|date=अप्रैल 2012}} यदि प्रत्येक {{mvar|X<sub>i</sub>}} का परिमित माध्य {{mvar|μ}} हो, तो बड़ी संख्या के नियम द्वारा, {{math|{{sfrac|''S<sub>n</sub>''|''n''}} → ''μ''}} होगा।<ref>{{cite book|last=Rosenthal |first=Jeffrey Seth |date=2000 |title=कठोर संभाव्यता सिद्धांत पर पहली नज़र|publisher=World Scientific |isbn=981-02-4322-7 |at=Theorem 5.3.4, p. 47}}</ref> यदि इसके अतिरिक्त प्रत्येक {{mvar|X<sub>i</sub>}} परिमित विचरण {{math|''σ''<sup>2</sup>}} है, तो केंद्रीय सीमा प्रमेय द्वारा, | अनौपचारिक रूप से, इन पंक्तियों के साथ कुछ तब होता है जब स्वतंत्र समान रूप से वितरित यादृच्छिक चर के, {{math|''X''<sub>1</sub>, ..., ''X<sub>n</sub>''}} का योग, {{mvar|S<sub>n</sub>}}, लौकिक प्रायिकता सिद्धांत में अध्ययन किया जाता है।{{Citation needed|date=अप्रैल 2012}} यदि प्रत्येक {{mvar|X<sub>i</sub>}} का परिमित माध्य {{mvar|μ}} हो, तो बड़ी संख्या के नियम द्वारा, {{math|{{sfrac|''S<sub>n</sub>''|''n''}} → ''μ''}} होगा।<ref>{{cite book|last=Rosenthal |first=Jeffrey Seth |date=2000 |title=कठोर संभाव्यता सिद्धांत पर पहली नज़र|publisher=World Scientific |isbn=981-02-4322-7 |at=Theorem 5.3.4, p. 47}}</ref> यदि इसके अतिरिक्त प्रत्येक {{mvar|X<sub>i</sub>}} परिमित विचरण {{math|''σ''<sup>2</sup>}} है, तो केंद्रीय सीमा प्रमेय द्वारा, | ||
<math display="block"> \frac{S_n-n\mu}{\sqrt{n}} \to \xi ,</math> | <math display="block"> \frac{S_n-n\mu}{\sqrt{n}} \to \xi ,</math> | ||
जहाँ {{mvar|ξ}} को {{math|''N''(0,''σ''<sup>2</sup>)}} के रूप में वितरित किया जाता है। यह अनौपचारिक विस्तार में प्रथम दो स्थिरांकों | जहाँ {{mvar|ξ}} को {{math|''N''(0,''σ''<sup>2</sup>)}} के रूप में वितरित किया जाता है। यह अनौपचारिक विस्तार में प्रथम दो स्थिरांकों का मान प्रदान करता है। | ||
<math display="block">S_n \approx \mu n+\xi \sqrt{n}. </math> | <math display="block">S_n \approx \mu n+\xi \sqrt{n}. </math> | ||
ऐसी स्थितियों में जहां {{mvar|X<sub>i</sub>}} के पास परिमित माध्य या प्रसरण नहीं है, स्थानांतरित और पुनः पैमाने योग का अभिसरण भी विभिन्न केंद्रित और माप क्रम गणक कारकों के साथ हो सकता है: | ऐसी स्थितियों में जहां {{mvar|X<sub>i</sub>}} के पास परिमित माध्य या प्रसरण नहीं है, स्थानांतरित और पुनः पैमाने योग का अभिसरण भी विभिन्न केंद्रित और माप क्रम गणक कारकों के साथ हो सकता है: | ||
| Line 189: | Line 190: | ||
==== घनत्व फलन ==== | ==== घनत्व फलन ==== | ||
दो या दो से अधिक स्वतंत्र चरों के योग का प्रायिकता घनत्व फलन उनके घनत्वों का [[कनवल्शन|संवलन]] है (यदि ये घनत्व उपस्थित हैं)। इस प्रकार केंद्रीय सीमा प्रमेय को संवलन के अंतर्गत घनत्व | दो या दो से अधिक स्वतंत्र चरों के योग का प्रायिकता घनत्व फलन उनके घनत्वों का [[कनवल्शन|संवलन]] है (यदि ये घनत्व उपस्थित हैं)। इस प्रकार केंद्रीय सीमा प्रमेय को संवलन के अंतर्गत घनत्व फलनों के गुणों के विषय में एक विवरण के रूप में व्याख्या की जा सकती है: कई घनत्व फलनों का संवलन सामान्य घनत्व की ओर जाता है क्योंकि घनत्व फलनों की संख्या बिना बाध्यता के बढ़ जाती है। इन प्रमेयों को ऊपर दिए गए केंद्रीय सीमा प्रमेय के रूपों की तुलना में प्रबल परिपुर्वानुमानओं की आवश्यकता होती है। इस प्रकार के प्रमेयों को प्रायः स्थानीय सीमा प्रमेय कहा जाता है। पेट्रोव<ref>{{Cite book|last=Petrov|first=V. V. |title=स्वतंत्र यादृच्छिक चर का योग|year=1976|publisher=Springer-Verlag|location=New York-Heidelberg | isbn=9783642658099 | at=ch. 7|url=https://books.google.com/books?id=zSDqCAAAQBAJ}}</ref> [[स्वतंत्र और समान रूप से वितरित यादृच्छिक चर]] के योग के लिए एक विशेष स्थानीय सीमा प्रमेय के लिए देखें। | ||
==== विशेषता फलन ==== | ==== विशेषता फलन ==== | ||
चूंकि संवलन का अभिलाक्षणिक फलन (प्रायिकता सिद्धांत) सम्मिलित घनत्वों के अभिलाक्षणिक फलनों का गुणनफल होता है, केंद्रीय सीमा प्रमेय का एक और पुनर्कथन होता है: कई घनत्व फलनों के अभिलाक्षणिक फलनों का गुणनफल अभिलक्षणिक फलन के अंतअ हो जाता है। जैसा कि ऊपर | चूंकि संवलन का अभिलाक्षणिक फलन (प्रायिकता सिद्धांत) सम्मिलित घनत्वों के अभिलाक्षणिक फलनों का गुणनफल होता है, केंद्रीय सीमा प्रमेय का एक और पुनर्कथन होता है: कई घनत्व फलनों के अभिलाक्षणिक फलनों का गुणनफल अभिलक्षणिक फलन के अंतअ हो जाता है। जैसा कि ऊपर बताये गए प्रतिबंधों के अंतर्गत घनत्व फलनों की संख्या बिना बाध्यता के बढ़ जाती है। विशेष रूप से, विशेषता फलन के तर्क पर उचित माप क्रम गणक कारक को अनुप्रयोज्य करने की आवश्यकता है। | ||
[[फूरियर रूपांतरण]] के विषय में एक समान विवरण दिया जा सकता है, क्योंकि विशिष्ट फलन अनिवार्य रूप से फूरियर रूपांतरण है। | [[फूरियर रूपांतरण]] के विषय में एक समान विवरण दिया जा सकता है, क्योंकि विशिष्ट फलन अनिवार्य रूप से फूरियर रूपांतरण है। | ||
| Line 211: | Line 212: | ||
किसी उत्पाद का लघुगणक केवल कारकों के लघुगणक का योग है। इसलिए, जब यादृच्छिक चर के एक उत्पाद का लघुगणक जो केवल धनात्मक मान लेता है, और सामान्य वितरण तक पहुंचता है, उत्पाद स्वयं [[लॉग-सामान्य वितरण|अभिलेख-सामान्य वितरण]] तक पहुंचता है। कई भौतिक मात्राएं (विशेष रूप से द्रव्यमान या लंबाई, जो मापक्रम का विषय हैं और ऋणात्मक नहीं हो सकती हैं) विभिन्न यादृच्छिक कारकों के उत्पाद हैं, इसलिए वे अभिलेख-सामान्य वितरण का पालन करते हैं। केंद्रीय सीमा प्रमेय के इस गुणात्मक संस्करण को कभी-कभी जिब्रत का नियम कहा जाता है। | किसी उत्पाद का लघुगणक केवल कारकों के लघुगणक का योग है। इसलिए, जब यादृच्छिक चर के एक उत्पाद का लघुगणक जो केवल धनात्मक मान लेता है, और सामान्य वितरण तक पहुंचता है, उत्पाद स्वयं [[लॉग-सामान्य वितरण|अभिलेख-सामान्य वितरण]] तक पहुंचता है। कई भौतिक मात्राएं (विशेष रूप से द्रव्यमान या लंबाई, जो मापक्रम का विषय हैं और ऋणात्मक नहीं हो सकती हैं) विभिन्न यादृच्छिक कारकों के उत्पाद हैं, इसलिए वे अभिलेख-सामान्य वितरण का पालन करते हैं। केंद्रीय सीमा प्रमेय के इस गुणात्मक संस्करण को कभी-कभी जिब्रत का नियम कहा जाता है। | ||
जबकि यादृच्छिक चर के योग के लिए केंद्रीय सीमा प्रमेय को परिमित विचरण की स्थिति की आवश्यकता होती है, उत्पादों के लिए संबंधित प्रमेय को इसी स्थिति की आवश्यकता होती है कि घनत्व फलन वर्ग-पूर्णांक हो।<ref name=Rempala/> | जबकि यादृच्छिक चर के योग के लिए केंद्रीय सीमा प्रमेय को परिमित विचरण की स्थिति की आवश्यकता होती है, और उत्पादों के लिए संबंधित प्रमेय को इसी स्थिति की आवश्यकता होती है कि घनत्व फलन वर्ग-पूर्णांक हो।<ref name=Rempala/> | ||
| Line 218: | Line 219: | ||
=== अवमुख निकाय === | === अवमुख निकाय === | ||
{{math theorem | math_statement = एक अनुक्रम {{math|''ε<sub>n</sub>'' ↓ 0}} उपस्थित | {{math theorem | math_statement = एक अनुक्रम {{math|''ε<sub>n</sub>'' ↓ 0}} उपस्थित है, जिसके लिए निम्नलिखित धारण करता है। माना {{math|''n'' ≥ 1}}, और माना यादृच्छिक चर {{math|''X''<sub>1</sub>, ..., ''X<sub>n</sub>''}} [[लघुगणकीय रूप से अवतल कार्य|में अभिलेख-उन्मुख]] [[संयुक्त घनत्व कार्य|संयुक्त घनत्व]] {{mvar|f }} है, जैसे {{math|1=''f''(''x''<sub>1</sub>, ..., ''x<sub>n</sub>'') = ''f''({{abs|''x''<sub>1</sub>}}, ..., {{abs|''x<sub>n</sub>''}})}} सभी {{math|''x''<sub>1</sub>, ..., ''x<sub>n</sub>''}} के लिए, और {{math|1=E(''X''{{su|b=''k''|p=2}}) = 1}} सभी {{math|1=''k'' = 1, ..., ''n''}} के लिए, तब | ||
<math display="block"> \frac{X_1+\cdots+X_n}{\sqrt n} </math> | <math display="block"> \frac{X_1+\cdots+X_n}{\sqrt n} </math> | ||
{{mvar|ε<sub>n</sub>}}-के अंतअ <math display="inline"> \mathcal{N}(0, 1)</math> में [[संभाव्यता उपायों की कुल भिन्नता दूरी|कुल भिन्नता दूरी का वितरण है।]]<ref>Klartag (2007, Theorem 1.2)</ref>}} | |||
इन दो {{mvar|ε<sub>n</sub>}}-अंतअ वितरणों में घनत्व होते है (वास्तव में, अभिलेख-उन्मुख घनत्व), इस प्रकार, उनके मध्य की कुल विचरण दूरी घनत्वों के मध्य के अंतर के निरपेक्ष मान का अभिन्न अंग है। कुल विचरण में अभिसरण दुर्बल अभिसरण से अधिक प्रबल होता है। | |||
अभिलेख-उन्मुख घनत्व का एक महत्वपूर्ण उदाहरण एक दिए गए अवमुख निकाय के भीतर स्थिर और बाहर लुप्त होने वाला कार्य है; यह अवमुख पिंड पर समान वितरण के अनुरुप है, जो अवमुख पिंडों के लिए पद केंद्रीय सीमा प्रमेय की व्याख्या करता है। | अभिलेख-उन्मुख घनत्व का एक महत्वपूर्ण उदाहरण एक दिए गए अवमुख निकाय के भीतर स्थिर और बाहर लुप्त होने वाला कार्य है; यह अवमुख पिंड पर समान वितरण के अनुरुप है, जो अवमुख पिंडों के लिए पद केंद्रीय सीमा प्रमेय की व्याख्या करता है। | ||
| Line 234: | Line 235: | ||
{{math theorem | math_statement = माना {{math|''X''<sub>1</sub>, ..., ''X<sub>n</sub>''}} पूर्व प्रमेय की मान्यताओं को संतुष्ट करें, तब<ref>Klartag (2008, Theorem 1)</ref> | {{math theorem | math_statement = माना {{math|''X''<sub>1</sub>, ..., ''X<sub>n</sub>''}} पूर्व प्रमेय की मान्यताओं को संतुष्ट करें, तब<ref>Klartag (2008, Theorem 1)</ref> | ||
<math display="block"> \left| \mathbb{P} \left( a \le \frac{ X_1+\cdots+X_n }{ \sqrt n } \le b \right) - \frac1{\sqrt{2\pi}} \int_a^b e^{-\frac{1}{2} t^2} \, dt \right| \le \frac{C}{n} </math> | <math display="block"> \left| \mathbb{P} \left( a \le \frac{ X_1+\cdots+X_n }{ \sqrt n } \le b \right) - \frac1{\sqrt{2\pi}} \int_a^b e^{-\frac{1}{2} t^2} \, dt \right| \le \frac{C}{n} </math> | ||
सभी | सभी {{math|''a'' < ''b''}} के लिए; यहाँ {{mvar|C}} एक [[गणितीय स्थिरांक|सार्वभौमिक (पूर्ण) स्थिरांक]] है। इसके अतिरिक्त, प्रत्येक {{math|''c''<sub>1</sub>, ..., ''c<sub>n</sub>'' ∈ '''R'''}} के लिए ऐसा है कि {{math|1=''c''{{su|b=1|p=2}} + ⋯ + ''c''{{su|b=''n''|p=2}} = 1}}, | ||
<math display="block"> \left| \mathbb{P} \left( a \le c_1 X_1+\cdots+c_n X_n \le b \right) - \frac{1}{\sqrt{2\pi}} \int_a^b e^{-\frac{1}{2} t^2} \, dt \right| \le C \left( c_1^4+\dots+c_n^4 \right). </math>}} | <math display="block"> \left| \mathbb{P} \left( a \le c_1 X_1+\cdots+c_n X_n \le b \right) - \frac{1}{\sqrt{2\pi}} \int_a^b e^{-\frac{1}{2} t^2} \, dt \right| \le C \left( c_1^4+\dots+c_n^4 \right). </math>}} | ||
{{math|{{sfrac|''X''<sub>1</sub> + ⋯ + ''X<sub>n</sub>''|{{sqrt|''n''}}}}}} के वितरण को लगभग सामान्य होने की आवश्यकता नहीं है (वास्तव में, यह एक समान हो सकता है)।<ref>Klartag (2007, Theorem 1.1)</ref> हालांकि, {{math|''c''<sub>1</sub>''X''<sub>1</sub> + ⋯ + ''c<sub>n</sub>X<sub>n</sub>''}} का वितरण | {{math|{{sfrac|''X''<sub>1</sub> + ⋯ + ''X<sub>n</sub>''|{{sqrt|''n''}}}}}} के वितरण को लगभग सामान्य होने की आवश्यकता नहीं है (वास्तव में, यह एक समान हो सकता है)।<ref>Klartag (2007, Theorem 1.1)</ref> हालांकि, {{math|''c''<sub>1</sub>''X''<sub>1</sub> + ⋯ + ''c<sub>n</sub>X<sub>n</sub>''}} का वितरण <math display="inline"> \mathcal{N}(0, 1)</math> के अंतअ है, (कुल भिन्नता दूरी में) अधिकांश सदिशों {{math|(''c''<sub>1</sub>, ..., ''c<sub>n</sub>'')}} के लिए गोले {{math|1=''c''{{su|b=1|p=2}} + ⋯ + ''c''{{su|b=''n''|p=2}} = 1}} पर समान वितरण के अनुसार है। | ||
=== लैक्यूनरी त्रिकोणमितीय श्रृंखला === | === लैक्यूनरी त्रिकोणमितीय श्रृंखला === | ||
{{math theorem | name = प्रमेय ([[राफेल सलेम|सलेम]]–[[एंटोनी ज़िगमंड|ज़िगमंड]]) | math_statement = | {{math theorem | name = प्रमेय ([[राफेल सलेम|सलेम]]–[[एंटोनी ज़िगमंड|ज़िगमंड]]) | math_statement = | ||
माना {{mvar|U}} समान रूप से वितरित एक यादृच्छिक चर | माना {{mvar|U}} समान रूप से वितरित एक यादृच्छिक चर {{math|(0,2π)}}, और {{math|1=''X<sub>k</sub>'' = ''r<sub>k</sub>'' cos(''n<sub>k</sub> U'' + ''a<sub>k</sub>'')}} हो, जहां | ||
* {{mvar|n<sub>k</sub>}} अभाव की स्थिति को संतुष्ट करें: | * {{mvar|n<sub>k</sub>}} अभाव की स्थिति को संतुष्ट करें: वहाँ {{math|''q'' > 1}} उपस्थित है ऐसा है कि {{math|''n''<sub>''k'' + 1</sub> ≥ ''qn''<sub>''k''</sub>}} सभी {{mvar|k}} के लिए, | ||
* {{mvar|r<sub>k</sub>}} | * {{mvar|r<sub>k</sub>}} ऐसा है कि <math display="block"> r_1^2 + r_2^2 + \cdots = \infty \quad\text{ और }\quad \frac{ r_k^2 }{ r_1^2+\cdots+r_k^2 } \to 0, </math> | ||
* {{math|0 ≤ ''a''<sub>''k''</sub> < 2π}}. | * {{math|0 ≤ ''a''<sub>''k''</sub> < 2π}}. | ||
तब <ref name=Zygmund/><ref>Gaposhkin (1966, Theorem 2.1.13)</ref> | तब <ref name=Zygmund/><ref>Gaposhkin (1966, Theorem 2.1.13)</ref> | ||
<math display="block"> \frac{ X_1+\cdots+X_k }{ \sqrt{r_1^2+\cdots+r_k^2} } </math> | <math display="block"> \frac{ X_1+\cdots+X_k }{ \sqrt{r_1^2+\cdots+r_k^2} } </math> | ||
वितरण | वितरण <math display="inline"> \mathcal{N}\big(0, \frac{1}{2}\big)</math> में अभिसरण करता है।}} | ||
=== गाऊसी बहुतलीय === | === गाऊसी बहुतलीय === | ||
{{math theorem | math_statement = | {{math theorem | math_statement = | ||
माना {{math|''A''<sub>1</sub>, ..., ''A''<sub>''n''</sub>}} समतलीय | माना {{math|''A''<sub>1</sub>, ..., ''A''<sub>''n''</sub>}} में द्वि-आयामी मानक सामान्य वितरण वाले प्रत्येक समतलीय {{math|'''R'''<sup>2</sup>}} पर स्वतंत्र यादृच्छिक बिंदु हैं। माना {{mvar|K<sub>n</sub>}} इन बिंदुओं का [[अवमुख समावरक]] है, और {{mvar|X<sub>n</sub>}} , {{mvar|K<sub>n</sub>}} का क्षेत्रफल है, तब <ref>Bárány & Vu (2007, Theorem 1.1)</ref> | ||
<math display="block"> \frac{ X_n - \mathbb{E} (X_n) }{ \sqrt{\operatorname{Var} (X_n)} } </math> | <math display="block"> \frac{ X_n - \mathbb{E} (X_n) }{ \sqrt{\operatorname{Var} (X_n)} } </math> | ||
वितरण | वितरण <math display="inline"> \mathcal{N}(0, 1)</math> में अभिसरण करता है, जैसे {{mvar|n}} अनंत की ओर जाता है।}} | ||
यही 2 से बड़े सभी आयामों में भी अनुप्रयोज्य होता है। | यही 2 से बड़े सभी आयामों में भी अनुप्रयोज्य होता है। | ||
| Line 259: | Line 260: | ||
[[उत्तल पॉलीटॉप|बहुतलीय]] {{mvar|K<sub>n</sub>}} को गॉसियन यादृच्छिक बहुतलीय कहा जाता है। | [[उत्तल पॉलीटॉप|बहुतलीय]] {{mvar|K<sub>n</sub>}} को गॉसियन यादृच्छिक बहुतलीय कहा जाता है। | ||
एक समान परिणाम शीर्षों की संख्या (गाऊसी बहुतलीय के), किनारों की संख्या और वास्तव में, सभी आयामों के फलको के लिए | एक समान परिणाम शीर्षों की संख्या (गाऊसी बहुतलीय के), किनारों की संख्या और वास्तव में, सभी आयामों के फलको के लिए होती है।<ref>Bárány & Vu (2007, Theorem 1.2)</ref> | ||
===लांबिक आव्यूह के रैखिक | ===लांबिक आव्यूह के रैखिक फलन === | ||
एक आव्यूह {{math|'''M'''}} का रैखिक | एक आव्यूह {{math|'''M'''}} का रैखिक फलन इसके तत्वों का एक रैखिक संयोजन है (दिए गए गुणांकों के साथ), {{math|'''M''' ↦ tr('''AM''')}} जहाँ {{math|'''A'''}} गुणांकों का आव्यूह है; अनुरेख (रैखिक बीजगणित)#आंतरिक उत्पाद देखें। | ||
एक यादृच्छिक [[ऑर्थोगोनल मैट्रिक्स|लांबिक आव्यूह]] को समान रूप से वितरित किया जाता है, यदि इसका वितरण [[ऑर्थोगोनल समूह|लांबिक समूह]] | एक यादृच्छिक [[ऑर्थोगोनल मैट्रिक्स|लांबिक आव्यूह]] को समान रूप से वितरित किया जाता है, यदि इसका वितरण [[ऑर्थोगोनल समूह|लांबिक समूह]] {{math|O(''n'','''R''')}} पर सामान्यीकृत हार माप है; चक्रानुक्रम आव्यूह#एकरूप यादृच्छिक चक्रानुक्रम आव्यूह देखें। | ||
{{math theorem | math_statement = माना {{math|'''M'''}} एक यादृच्छिक लांबिक {{math|''n'' × ''n''}} | {{math theorem | math_statement = माना {{math|'''M'''}} एक यादृच्छिक लांबिक {{math|''n'' × ''n''}} | ||
आव्यूह समान रूप से वितरित, और {{math|'''A'''}} निश्चित {{math|''n'' × ''n''}} आव्यूह ऐसा है {{math|1=tr('''AA'''*) = ''n''}}, और | आव्यूह समान रूप से वितरित किया जाता है, और {{math|'''A'''}} एक निश्चित {{math|''n'' × ''n''}} आव्यूह ऐसा है कि {{math|1=tr('''AA'''*) = ''n''}}, और {{math|1=''X'' = tr('''AM''')}} प्रदान करता है। तब <ref name=Meckes/> {{mvar|X }} का वितरण <math display="inline"> \mathcal{N}(0, 1)</math> के अंतअ कुल भिन्नता मापीय में{{स्पष्टीकरण|कारण=यहाँ अप का क्या अर्थ है|तिथि=जून 2012}} {{math|{{sfrac|2{{sqrt|3}}|''n'' − 1}}}} तक है।}} | ||
=== अनुवर्ती === | === अनुवर्ती === | ||
Revision as of 12:12, 27 March 2023
प्रायिकता सिद्धांत में, केंद्रीय सीमा प्रमेय (CLT) स्थापित करता है, और कई स्थितियों में, समान रूप से वितरित स्वतंत्र प्रतिरूपो के लिए, मानकीकृत प्रतिरूप माध्य मानक सामान्य वितरण की ओर जाता है, भले ही मूल चर स्वयं सामान्य रूप से वितरित न हों।
प्रायिकता सिद्धांत में प्रमेय एक महत्वपूर्ण अवधारणा है क्योंकि इसका तात्पर्य है कि प्रायिकता और सांख्यिकी विधियां जो सामान्य वितरण के लिए कार्य करती हैं, और अन्य प्रकार के वितरणों से जुड़ी कई समस्याओं पर अनुप्रयोज्य हो सकती हैं।
प्रायिकता सिद्धांत के औपचारिक विकास के पर्यन्त इस प्रमेय में कई परिवर्तन देखे गए हैं। प्रमेय के पूर्व संस्करण 1811 से पूर्व के हैं, परन्तु अपने आधुनिक सामान्य रूप में, प्रायिकता सिद्धांत में इस मौलिक परिणाम को 1920 के अंत तक सटीक रूप से कहा गया था,[1] इस प्रकार लौकिक और आधुनिक प्रायिकता सिद्धांत के मध्य एक सेतु के रूप में कार्य करना है।
यदि समग्र अपेक्षित मान वाली समष्टि से लिए गए यादृच्छिक प्रतिरूप है, परिमित विचरण , यदि प्रथम का प्रतिरूप माध्य है, और फिर वितरण का सीमित रूप, , के साथ , एक मानक सामान्य वितरण है।[2]
उदाहरण के लिए, मान लीजिए कि एक प्रतिरूप प्राप्त किया जाता है जिसमें कई यादृच्छिक चर होते हैं, प्रत्येक अवलोकन यादृच्छिक रूप से इस तरह से उत्पन्न होता है जो अन्य अवलोकनों के मानों पर निर्भर नहीं होता है, और अवलोकन किए गए मानों के अंकगणितीय माध्य की गणना की जाती है। यदि यह प्रक्रिया कई बार की जाती है, तो केंद्रीय सीमा प्रमेय का तात्पर्य है कि औसत की प्रायिकता वितरण एक सामान्य वितरण के अंतअ होगा।
केंद्रीय सीमा प्रमेय के कई रूप हैं। अपने सामान्य रूप में, यादृच्छिक चर स्वतंत्र और समान रूप से वितरित (i.i.d.) होना चाहिए। भिन्नताओं में, सामान्य वितरण के माध्य का अभिसरण गैर-समान वितरणों के लिए या गैर-स्वतंत्र प्रेक्षणों के लिए भी होता है, यदि वे कुछ प्रतिबंधों का अनुपालन करते हैं।
इस प्रमेय का प्रारंभिक संस्करण, कि सामान्य वितरण को द्विपद वितरण के सन्निकटन के रूप में उपयोग किया जा सकता है, तथा द्विपद वितरण, डी मोइवर-लाप्लास प्रमेय है।
स्वतंत्र क्रम

लौकिक सीएलटी
माना यादृच्छिक प्रतिरूप का एक क्रम हो - अर्थात, आई.आई.डी. के एक क्रम द्वारा दिए गए अपेक्षित मान के वितरण से निर्मित किए गए यादृच्छिक चर और परिमित विचरण द्वारा दिया गया है, मान लीजिए हम प्रथम प्रतिरूप माध्य में रुचि रखते हैं।
बड़ी संख्या के नियम के अनुसार, प्रतिरूप औसत अनुमानित मान के लगभग निश्चित रूप से (और इसलिए प्रायिकता में भी अभिसरित) अपेक्षित मान जब पर अभिसरित होता है।
लौकिक केंद्रीय सीमा प्रमेय नियतात्मक संख्या इस अभिसरण के पर्यन्त आसपास प्रसंभाव्य अस्थिरता के आकार और वितरण रूप का वर्णन करता है। अधिक सटीक रूप से, यह बताता है कि जैसे बड़ा हो जाता है, प्रतिरूप औसत के मध्य अंतर का वितरण और इसकी सीमा , जब कारक (अर्थात ) द्वारा गुणा किया जाता है। माध्य 0 और विचरण के साथ सामान्य वितरण का अनुमान लगाता है। काफी बड़े n के लिए, का वितरण माध्य के साथ अव्यवस्थिततः सामान्य वितरण और विचरण के अंतअ हो जाता है।
प्रमेय की उपयोगिता यह है कि का वितरण विशिष्ट के वितरण के आकार की उपेक्षा किए बिना सामान्यता तक पहुँचता है। औपचारिक रूप से, प्रमेय को निम्नानुसार कहा जा सकता है:
Lindeberg–Lévy CLT — मान लीजिए i.i.d. का क्रम है, यादृच्छिक चर और के साथ, तब ऐसे अनंत तक पहुंचता है, यादृच्छिक चर वितरण में अभिसरण एक के लिए सामान्य है:[4]
यदि , वितरण में अभिसरण का अर्थ है कि संचयी वितरण कार्य करता है, वितरण के बिंदुवार को सीडीएफ में अभिसरण करें: प्रत्येक वास्तविक संख्या के लिए,
लायपुनोव सीएलटी
प्रमेय का नाम रूसी गणितज्ञ अलेक्जेंडर लायपुनोव के नाम पर रखा गया है। केंद्रीय सीमा प्रमेय के इस संस्करण में यादृच्छिक चर स्वतंत्र होना चाहिए, परन्तु आवश्यक नहीं कि समान रूप से वितरित किया जाए। प्रमेय को भी यादृच्छिक चर की आवश्यकता होती है, कुछ क्रम के क्षण है और यह कि इन क्षणो के वृद्धि की दर नीचे दी गई लायपुनोव स्थिति द्वारा सीमित है।
Lyapunov CLT[6] — मान लीजिए कि स्वतंत्र यादृच्छिक चर का एक क्रम है, प्रत्येक परिमित अपेक्षित मान और विचरण के साथ परिभाषित
यदि कुछ के लिए , लायपुनोव स्थिति
व्यवहार में सामान्यतः लायपुनोव की स्थिति की जांच करना सबसे सरल होता है।
यदि यादृच्छिक चर का एक क्रम लायपुनोव की स्थिति को संतुष्ट करता है, तो यह लिंडबर्ग की स्थिति को भी संतुष्ट करता है। हालांकि, विपरीत निहितार्थ पकड़ में नहीं आता है।
लिंडबर्ग सीएलटी
उसी समुच्चयन में और उपरोक्त के समान संकेतन के साथ, लायपुनोव की स्थिति को निम्नलिखित दुर्बल (1920 में जारल वाल्डेमर लिंडेबर्ग से) के साथ परिवर्तित किया जा सकता है।
मान लीजिए कि प्रत्येक के लिए
बहुआयामी सीएलटी
विशिष्ट फलनों का उपयोग करने वाले प्रमाणों को उन स्थितियों तक बढ़ाया जा सकता है जहां प्रत्येक विशिष्ट में एक यादृच्छिक सदिश है, अभिप्राय सदिश के साथ और सहप्रसरण आव्यूह (सदिश के घटकों के मध्य), और ये यादृच्छिक सदिश स्वतंत्र और समान रूप से वितरित हैं। बहुआयामी केंद्रीय सीमा प्रमेय में वर्णित है कि जब माप क्रमित किया जाता है, तो योग एक बहुभिन्नरूपी सामान्य वितरण में परिवर्तित हो जाते हैं।[7]
माना
Theorem[8] — माना स्वतंत्र है, -मूल्यवान यादृच्छिक सदिश के प्रत्येक का औसत शून्य है। लेखन और मान लो प्रतीप्य है। माना एक -समान माध्य और समान सहप्रसरण आव्यूह के साथ आयामी गॉसियन है। फिर सभी अवमुख समुच्चयों के लिए है,
यह अज्ञात है कि क्या कारक आवश्यक है।[9]
सामान्यीकृत प्रमेय
केंद्रीय सीमा प्रमेय में वर्णित है कि परिमित भिन्नताओं के साथ कई स्वतंत्र और समान रूप से वितरित यादृच्छिक चर का योग एक सामान्य वितरण की ओर अग्रसर होगा क्योंकि चर की संख्या बढ़ती है। बोरिस व्लादिमीरोविच गेदेंको और एंड्री निकोलाइविच कोलमोगोरोव के कारण एक सामान्यीकरण बताता है कि पावर-लॉ टेल (पारेतो वितरण) वितरण के साथ कई यादृच्छिक चर का योग घटता है, जहाँ (और इसलिए अनंत विचरण) एक स्थिर वितरण की ओर प्रवृत्त होगा, जैसे-जैसे योगों की संख्या बढ़ती है।[10][11] यदि तो योग 2 के समान स्थिरता मापदंड के साथ एक स्थिर वितरण में परिवर्तित हो जाता है, अर्थात गॉसियन वितरण।[12]
आश्रित प्रक्रियाएं
दुर्बल आश्रितता के अंतर्गत सीएलटी
स्वतंत्र, समान रूप से वितरित यादृच्छिक चर के अनुक्रम का एक उपयोगी सामान्यीकरण असतत समय में एक मिश्रित यादृच्छिक प्रक्रिया है; जहां मिश्रित का अर्थ है, स्थूलतः, यादृच्छिक चर अस्थायी रूप से एक दूसरे से दूर लगभग स्वतंत्र हैं। एर्गोडिक सिद्धांत और प्रायिकता सिद्धांत में कई प्रकार के मिश्रित का उपयोग किया जाता है। इनके द्वारा परिभाषित जहाँ विशेष रूप से मिश्रित (जिसे α-मिश्रित भी कहा जाता है) देखें, तथाकथित मिश्रित गुणांक है।
प्रबल मिश्रण के अंतर्गत केंद्रीय सीमा प्रमेय का एक सरल सूत्रीकरण है:[13]
Theorem — मान लीजिए कि स्थिर है और -के साथ और जो और के साथ मिश्रित है। निरूपित , फिर सीमा
वास्तव में,
पुर्वानुमान छोड़ा नहीं जा सकता, क्योंकि स्पर्शोन्मुख सामान्यता विफल हो जाता है, जहाँ एक अन्य स्थिर क्रम हैं।
प्रमेय का एक प्रबल संस्करण है:[14] पुर्वानुमान को , से और धारणा से प्रतिस्थापित किया जाता है
मार्टिंगेल अंतर सीएलटी
Theorem — माना मार्टिंगेल संतुष्ट करता हैː
- संभाव्यता के रूप में n → ∞,
- प्रत्येक ε > 0 के लिए, जैसे n → ∞,
टिप्पणी
लौकिक सीएलटी का प्रमाण
केंद्रीय सीमा प्रमेय में अभिलाक्षणिक फलनो का उपयोग करते हुए एक प्रमाण है।[17] यह बड़ी संख्या के (दुर्बल) नियम के प्रमाण के प्रमाण के समान है।
मान लीजिए स्वतंत्र और समान रूप से वितरित यादृच्छिक चर हैं, प्रत्येक का अर्थ , और परिमित विचरण है। योग का अर्थ , और प्रसरण है। यादृच्छिक चर पर विचार करें,
सामान्य वितरण में परिवर्तित हो जाता है, जिससे केंद्रीय सीमा प्रमेय अनुसरण करता है।
सीमा तक अभिसरण
केंद्रीय सीमा प्रमेय केवल एक स्पर्शोन्मुख वितरण प्रदान करता है। प्रेक्षणों की परिमित संख्या के लिए सन्निकटन के रूप में, यह सामान्य वितरण के शीर्ष के अंतअ होने पर ही एक उचित सन्निकटन प्रदान करता है; अवशिष्ट में विस्तार के लिए इसे बहुत बड़ी संख्या में अवलोकन करने की आवश्यकता होती है।[citation needed]
केंद्रीय सीमा प्रमेय में अभिसरण एक समान अभिसरण है क्योंकि सीमित संचयी वितरण फलन निरंतर है। यदि तृतीय केंद्रीय क्षण उपस्थित है और परिमित है, तो अभिसरण की गति कम से कम के क्रम (बेरी-एसेन प्रमेय देखें) में है। स्टीन की विधि[18]का उपयोग न केवल केंद्रीय सीमा प्रमेय को सिद्ध करने के लिए किया जा सकता है, बल्कि चयनित आव्यूह के लिए अभिसरण की दरों पर सीमा प्रदान करने के लिए भी किया जा सकता है।[19]
सामान्य वितरण का अभिसरण एकदिष्ट है, इस अर्थ में कि एन्ट्रापी सामान्य वितरण के एकदिष्ट फलन को बढ़ाती है।[20]
केंद्रीय सीमा प्रमेय विशेष रूप से स्वतंत्र और समान रूप से वितरित असतत यादृच्छिक चर के योग पर अनुप्रयोज्य होता है। असतत यादृच्छिक चर का योग अभी भी एक असतत यादृच्छिक चर है, ताकि हम असतत यादृच्छिक चर के एक अनुक्रम के साथ सामना कर सकें, जिसका संचयी प्रायिकता वितरण फलन एक सतत चर (अर्थात् सामान्य वितरण का) के अनुरूप संचयी प्रायिकता वितरण फलन की ओर अभिसरण करता है। . इसका अभिप्राय यह है कि यदि हम n स्वतंत्र समान असतत चर के योग की प्राप्ति का एक आयतचित्र बनाते हैं, वह वक्र जो आयतचित्र बनाने वाले आयतों के ऊपरी फलको के केंद्रों से जुड़ता है, और आयतचित्र एक गॉसियन वक्र की ओर अभिसरण करता है क्योंकि n अनंत तक पहुंचता है, इस संबंध को डी मोइवर-लाप्लास प्रमेय के रूप में जाना जाता है। द्विपद वितरण लेख केवल दो संभावित मान लेने वाले असतत चर की साधारण स्थितियों में केंद्रीय सीमा प्रमेय के ऐसे अनुप्रयोगो का विवरण देता है।
बड़ी संख्या के नियम से संबंध
बड़ी संख्या के नियम के साथ-साथ केंद्रीय सीमा प्रमेय एक सामान्य समस्या का आंशिक उपाय है: n के अनंत तक पहुंचने पर Sn का सीमित व्यवहार क्या है? गणितीय विश्लेषण में, स्पर्शोन्मुख श्रृंखला ऐसे प्रश्नों को हल करने के लिए नियोजित सबसे लोकप्रिय साधनो में से एक है।
मान लीजिए कि हमारे पास एक स्पर्शोन्मुख विस्तार है:
अनौपचारिक रूप से, इन पंक्तियों के साथ कुछ तब होता है जब स्वतंत्र समान रूप से वितरित यादृच्छिक चर के, X1, ..., Xn का योग, Sn, लौकिक प्रायिकता सिद्धांत में अध्ययन किया जाता है।[citation needed] यदि प्रत्येक Xi का परिमित माध्य μ हो, तो बड़ी संख्या के नियम द्वारा, Sn/n → μ होगा।[21] यदि इसके अतिरिक्त प्रत्येक Xi परिमित विचरण σ2 है, तो केंद्रीय सीमा प्रमेय द्वारा,
पुनरावृत्त लघुगणक का नियम निर्दिष्ट करता है कि बड़ी संख्या के नियम और केंद्रीय सीमा प्रमेय के "मध्य" क्या हो रहा है। विशेष रूप से यह कहता है कि सामान्यीकृत फलन √n log log n, बड़ी संख्या के नियम के n और केंद्रीय सीमा प्रमेय के √n के मध्य आकार में मध्यवर्ती, एक गैर-तुच्छ सीमित व्यवहार प्रदान करता है।
प्रमेय के वैकल्पिक कथन
घनत्व फलन
दो या दो से अधिक स्वतंत्र चरों के योग का प्रायिकता घनत्व फलन उनके घनत्वों का संवलन है (यदि ये घनत्व उपस्थित हैं)। इस प्रकार केंद्रीय सीमा प्रमेय को संवलन के अंतर्गत घनत्व फलनों के गुणों के विषय में एक विवरण के रूप में व्याख्या की जा सकती है: कई घनत्व फलनों का संवलन सामान्य घनत्व की ओर जाता है क्योंकि घनत्व फलनों की संख्या बिना बाध्यता के बढ़ जाती है। इन प्रमेयों को ऊपर दिए गए केंद्रीय सीमा प्रमेय के रूपों की तुलना में प्रबल परिपुर्वानुमानओं की आवश्यकता होती है। इस प्रकार के प्रमेयों को प्रायः स्थानीय सीमा प्रमेय कहा जाता है। पेट्रोव[24] स्वतंत्र और समान रूप से वितरित यादृच्छिक चर के योग के लिए एक विशेष स्थानीय सीमा प्रमेय के लिए देखें।
विशेषता फलन
चूंकि संवलन का अभिलाक्षणिक फलन (प्रायिकता सिद्धांत) सम्मिलित घनत्वों के अभिलाक्षणिक फलनों का गुणनफल होता है, केंद्रीय सीमा प्रमेय का एक और पुनर्कथन होता है: कई घनत्व फलनों के अभिलाक्षणिक फलनों का गुणनफल अभिलक्षणिक फलन के अंतअ हो जाता है। जैसा कि ऊपर बताये गए प्रतिबंधों के अंतर्गत घनत्व फलनों की संख्या बिना बाध्यता के बढ़ जाती है। विशेष रूप से, विशेषता फलन के तर्क पर उचित माप क्रम गणक कारक को अनुप्रयोज्य करने की आवश्यकता है।
फूरियर रूपांतरण के विषय में एक समान विवरण दिया जा सकता है, क्योंकि विशिष्ट फलन अनिवार्य रूप से फूरियर रूपांतरण है।
विचरण की गणना
माना कि Sn यादृच्छिक चर n का योग है। कई केंद्रीय सीमा प्रमेय ऐसी स्थितियाँ प्रदान करते हैं, जैसे कि Sn/√Var(Sn) वितरण में N(0,1) (अभिप्राय 0, विचरण 1 के साथ सामान्य वितरण) को n → ∞ के रूप में परिवर्तित करता है। कुछ स्थितियों में, एक स्थिरांक σ2 और फलन f(n) को खोजना संभव है जैसे कि Sn/(σ√n⋅f(n)), N(0,1) के वितरण में n→ ∞ के रूप में परिवर्तित हो जाता है।
Lemma[25] — मान लीजिए के साथ वास्तविक-मूल्यांकन और दृढता से स्थिर यादृच्छिक चर का एक क्रम है, सभी , के लिए, और . रचना
- यदि पूर्णतः अभिसारी है, , और तब जैसे जहां है,
- यदि इसके अतिरिक्त और वितरण जैसे में अभिसरण करता है, तब वितरण जैसे में भी अभिसरित होता है।
विस्तारण
धनात्मक यादृच्छिक चर के उत्पाद
किसी उत्पाद का लघुगणक केवल कारकों के लघुगणक का योग है। इसलिए, जब यादृच्छिक चर के एक उत्पाद का लघुगणक जो केवल धनात्मक मान लेता है, और सामान्य वितरण तक पहुंचता है, उत्पाद स्वयं अभिलेख-सामान्य वितरण तक पहुंचता है। कई भौतिक मात्राएं (विशेष रूप से द्रव्यमान या लंबाई, जो मापक्रम का विषय हैं और ऋणात्मक नहीं हो सकती हैं) विभिन्न यादृच्छिक कारकों के उत्पाद हैं, इसलिए वे अभिलेख-सामान्य वितरण का पालन करते हैं। केंद्रीय सीमा प्रमेय के इस गुणात्मक संस्करण को कभी-कभी जिब्रत का नियम कहा जाता है।
जबकि यादृच्छिक चर के योग के लिए केंद्रीय सीमा प्रमेय को परिमित विचरण की स्थिति की आवश्यकता होती है, और उत्पादों के लिए संबंधित प्रमेय को इसी स्थिति की आवश्यकता होती है कि घनत्व फलन वर्ग-पूर्णांक हो।[26]
लौकिक प्राधार के अतिरिक्त
स्पर्शोन्मुख सामान्यता, अर्थात्, उचित परिवर्तन और पुनर्विक्रय के पश्चात सामान्य वितरण में अभिसरण, एक ऐसी घटना है, अर्थात् स्वतंत्र यादृच्छिक चर (या सदिश) का योग जो ऊपर वर्णित लौकिक प्राधारो की तुलना में कहीं अधिक सामान्य है। समय-समय पर नए प्राधार सामने आते हैं; और अभी के लिए कोई एकल एकीकृत प्राधार उपलब्ध नहीं है।
अवमुख निकाय
Theorem — एक अनुक्रम εn ↓ 0 उपस्थित है, जिसके लिए निम्नलिखित धारण करता है। माना n ≥ 1, और माना यादृच्छिक चर X1, ..., Xn में अभिलेख-उन्मुख संयुक्त घनत्व f है, जैसे f(x1, ..., xn) = f(|x1|, ..., |xn|) सभी x1, ..., xn के लिए, और E(X2
k) = 1 सभी k = 1, ..., n के लिए, तब
इन दो εn-अंतअ वितरणों में घनत्व होते है (वास्तव में, अभिलेख-उन्मुख घनत्व), इस प्रकार, उनके मध्य की कुल विचरण दूरी घनत्वों के मध्य के अंतर के निरपेक्ष मान का अभिन्न अंग है। कुल विचरण में अभिसरण दुर्बल अभिसरण से अधिक प्रबल होता है।
अभिलेख-उन्मुख घनत्व का एक महत्वपूर्ण उदाहरण एक दिए गए अवमुख निकाय के भीतर स्थिर और बाहर लुप्त होने वाला कार्य है; यह अवमुख पिंड पर समान वितरण के अनुरुप है, जो अवमुख पिंडों के लिए पद केंद्रीय सीमा प्रमेय की व्याख्या करता है।
अन्य उदाहरण: f(x1, ..., xn) = const · exp(−(|x1|α + ⋯ + |xn|α)β) जहाँ α > 1 और αβ > 1. यदि β = 1 तब f(x1, ..., xn) में गुणनखंड const · exp (−|x1|α) … exp(−|xn|α) करता है, जिसका अर्थ X1, ..., Xn स्वतंत्र हैं। हालांकि, सामान्यतः, वे निर्भर हैं।
स्थिति f(x1, ..., xn) = f(|x1|, ..., |xn|) निश्चित करता है कि X1, ..., Xn शून्य माध्य और असंबद्ध हैं;[citation needed] फिर भी, उन्हें स्वतंत्र होने की आवश्यकता नहीं है, और न ही युग्मानूसार स्वतंत्रता होने की आवश्यकता है।[citation needed] वैसे, युग्मानूसार स्वतंत्रता लौकिक केंद्रीय सीमा प्रमेय में स्वतंत्रता को प्रतिस्थापित नहीं कर सकती है।[28]
यहाँ एक बेरी-एस्सेन प्रकार का परिणाम है।
Theorem — माना X1, ..., Xn पूर्व प्रमेय की मान्यताओं को संतुष्ट करें, तब[29]
1 + ⋯ + c2
n = 1,
X1 + ⋯ + Xn/√n के वितरण को लगभग सामान्य होने की आवश्यकता नहीं है (वास्तव में, यह एक समान हो सकता है)।[30] हालांकि, c1X1 + ⋯ + cnXn का वितरण के अंतअ है, (कुल भिन्नता दूरी में) अधिकांश सदिशों (c1, ..., cn) के लिए गोले c2
1 + ⋯ + c2
n = 1 पर समान वितरण के अनुसार है।
लैक्यूनरी त्रिकोणमितीय श्रृंखला
प्रमेय (सलेम–ज़िगमंड) — माना U समान रूप से वितरित एक यादृच्छिक चर (0,2π), और Xk = rk cos(nk U + ak) हो, जहां
- nk अभाव की स्थिति को संतुष्ट करें: वहाँ q > 1 उपस्थित है ऐसा है कि nk + 1 ≥ qnk सभी k के लिए,
- rk ऐसा है कि
- 0 ≤ ak < 2π.
गाऊसी बहुतलीय
Theorem — माना A1, ..., An में द्वि-आयामी मानक सामान्य वितरण वाले प्रत्येक समतलीय R2 पर स्वतंत्र यादृच्छिक बिंदु हैं। माना Kn इन बिंदुओं का अवमुख समावरक है, और Xn , Kn का क्षेत्रफल है, तब [33]
यही 2 से बड़े सभी आयामों में भी अनुप्रयोज्य होता है।
बहुतलीय Kn को गॉसियन यादृच्छिक बहुतलीय कहा जाता है।
एक समान परिणाम शीर्षों की संख्या (गाऊसी बहुतलीय के), किनारों की संख्या और वास्तव में, सभी आयामों के फलको के लिए होती है।[34]
लांबिक आव्यूह के रैखिक फलन
एक आव्यूह M का रैखिक फलन इसके तत्वों का एक रैखिक संयोजन है (दिए गए गुणांकों के साथ), M ↦ tr(AM) जहाँ A गुणांकों का आव्यूह है; अनुरेख (रैखिक बीजगणित)#आंतरिक उत्पाद देखें।
एक यादृच्छिक लांबिक आव्यूह को समान रूप से वितरित किया जाता है, यदि इसका वितरण लांबिक समूह O(n,R) पर सामान्यीकृत हार माप है; चक्रानुक्रम आव्यूह#एकरूप यादृच्छिक चक्रानुक्रम आव्यूह देखें।
Theorem — माना M एक यादृच्छिक लांबिक n × n आव्यूह समान रूप से वितरित किया जाता है, और A एक निश्चित n × n आव्यूह ऐसा है कि tr(AA*) = n, और X = tr(AM) प्रदान करता है। तब [35] X का वितरण के अंतअ कुल भिन्नता मापीय मेंTemplate:स्पष्टीकरण 2√3/n − 1 तक है।
अनुवर्ती
Theorem — माना यादृच्छिक चर X1, X2, ... ∈ L2(Ω) ऐसा हो कि Xn → 0 अशक्त में L2(Ω) और X
n → 1 अशक्त रूप से L1(Ω) हो। तब पूर्णांक में n1 < n2 < ⋯ उपस्थित हैं, ऐसा है कि
एक क्रिस्टल जालक पर यादृच्छिक चलना
केंद्रीय सीमा प्रमेय को एक क्रिस्टल जालक (एक परिमित आलेख पर आलेख को समाविष्ट करने वाला एक अनंत-गुना एबेलियन) पर सरल यादृच्छिक चलने के लिए स्थापित किया जा सकता है, और क्रिस्टल संरचनाओं के
के लिए उपयोग किया जाता है।[37][38]
अनुप्रयोग और उदाहरण
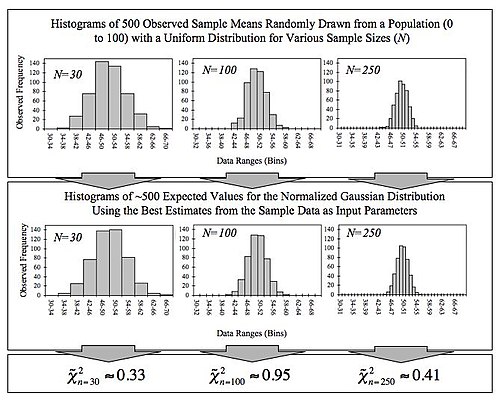
केंद्रीय सीमा प्रमेय का एक सरल उदाहरण कई समान, निष्पक्ष पासा फेंकना है। वेल्लित नंबरों के योग (या औसत) का वितरण सामान्य वितरण द्वारा अच्छी तरह अनुमानित होगा। चूँकि वास्तविक दुनिया की मात्राएँ प्रायः कई अलक्षित यादृच्छिक घटनाओं का संतुलित योग होती हैं, केंद्रीय सीमा प्रमेय भी सामान्य प्रायिकता वितरण की व्यापकता के लिए आंशिक स्पष्टीकरण प्रदान करता है। यह नियंत्रित प्रयोगों में सामान्य वितरण के लिए बड़े-प्रतिरूप आँकड़ों के सन्निकटन को भी सही ठहराता है।

प्रतिगमन
प्रतिगमन विश्लेषण और विशेष रूप से सामान्य न्यूनतम वर्ग निर्दिष्ट करते हैं कि एक आश्रित चर एक योगात्मक त्रुटि पद के साथ एक या अधिक स्वतंत्र चर पर कुछ फलनों के अनुसार निर्भर करता है। प्रतिगमन पर विभिन्न प्रकार के सांख्यिकीय निष्कर्ष मानते हैं कि त्रुटि पद सामान्य रूप से वितरित किया जाता है। इस धारणा को यह मानकर उचित अभिगृहीत किया जा सकता है कि त्रुटि पद वास्तव में कई स्वतंत्र त्रुटि पदों का योग है; भले ही व्यक्तिगत त्रुटि पदों को सामान्य रूप से वितरित नहीं किया जाता है, केंद्रीय सीमा प्रमेय द्वारा उनके योग को सामान्य वितरण द्वारा अच्छी तरह से अनुमानित किया जा सकता है।
अन्य उदाहरण
सांख्यिकी के महत्व को देखते हुए, कई लेख और परिकलक संपुष्टि उपलब्ध हैं जो केंद्रीय सीमा प्रमेय में सम्मिलित अभिसरण को प्रदर्शित करते हैं।[39]
इतिहास
डच गणितज्ञ हेंक टिम्स लिखते हैं:[40]
केंद्रीय सीमा प्रमेय का एक रोचक इतिहास है। इस प्रमेय का प्रथम संस्करण फ्रांस में जन्मे गणितज्ञ अब्राहम डी मोइवर द्वारा प्रतिपादित किया गया था, जिन्होंने 1733 में प्रकाशित एक उल्लेखनीय लेख में, सामान्य वितरण का उपयोग एक सिक्के के कई उछालों के परिणामस्वरूप शीर्षों की संख्या के वितरण का अनुमान लगाने के लिए किया था। यह खोज अपने समय से बहुत आगे थी, और लगभग तब तक विस्मृत हो गई थी। जब तक कि प्रसिद्ध फ्रांसीसी गणितज्ञ पियरे-साइमन लाप्लास ने इसे अपने स्मारकीय कार्य 'प्रायिकता के विश्लेषण' में अस्पष्टता से नहीं बचाया था, जो 1812 में प्रकाशित हुआ था। लाप्लास सामान्य वितरण के साथ द्विपद वितरण का अनुमान लगाकर डी मोइवर की खोज का विस्तार किया। परन्तु डी मोइवर की भाति, लाप्लास की खोज ने अपने समय में बहुत कम ध्यान दिया। उन्नीसवीं शताब्दी के अंत तक केंद्रीय सीमा प्रमेय के महत्व को समझा नहीं गया था, जब 1901 में, रूसी गणितज्ञ अलेक्जेंडर लायपुनोव ने इसे सामान्य शब्दों में परिभाषित किया और यह सिद्ध किया कि यह गणितीय रूप से कैसे कार्य करता है। आजकल, केंद्रीय सीमा प्रमेय को प्रायिकता सिद्धांत का अनौपचारिक प्रभुत्व माना जाता है।
सरफ्रांसिस गैल्टन ने केंद्रीय सीमा प्रमेय का इस प्रकार वर्णन किया:[41]
मैं कल्पना को प्रभावित करने के लिए सम्भवतः ही कुछ जानता हूं जो "त्रुटि के आवृत्ति के नियम" द्वारा व्यक्त किए गए लौकिक आदेश के अद्भुत रूप में कल्पना को प्रभावित करता है। यूनानियों द्वारा नियम को मूर्त रूप दिया गया होता और अगर वे इसके विषय में ज्ञात होता तो देवीकृत बन जाते। यह सबसे बड़े भ्रम के मध्य, शांति और पूर्ण आत्म-विस्मृति के साथ शासन करता है। भीड़ जितनी बड़ी होती है, और जितनी बड़ी स्पष्ट अराजकता होती है, उसका प्रभूत्व उतना ही उचित होता है। यह अकारण का सर्वोच्च नियम है। जब भी अराजक तत्वों का एक बड़ा प्रतिरूप हाथ में लिया जाता है और उनके परिमाण के क्रम में व्यवस्थित किया जाता है, तो नियमितता का एक असंभावित और सबसे सुंदर रूप सदैव के लिए अव्यक्त सिद्ध होता है।
वास्तविक पद केंद्रीय सीमा प्रमेय (जर्मन में: जेंट्रालर ग्रेनज़वर्ट्सत्ज़) का प्रथम बार उपयोग जॉर्ज पोल्या ने 1920 में एक लेख के शीर्षक में किया था।[42][43]प्रायिकता सिद्धांत में इसके महत्व के कारण पोल्या ने प्रमेय को "केंद्रीय" कहा। ले कैम के अनुसार, प्रायिकता का फ्रांसीसी विद्यालय ने केंद्रीय पद की व्याख्या इस अर्थ में करता है कि यह वितरण के केंद्र के व्यवहार को उसके पृष्ठभाग के विपरीत बताता है।[43]1920 में पोल्या[42]द्वारा प्रायिकता की गणना और क्षणों की समस्या की केंद्रीय सीमा प्रमेय पर लेख का सार इस प्रकार है।
गाऊसी संभाव्यता घनत्व की घटना 1 = e−x2 दोहराए गए प्रयोगों में, माप की त्रुटियों में, जिसके परिणामस्वरूप बहुत अधिक और बहुत छोटी प्राथमिक त्रुटियों का संयोजन होता है, प्रसार प्रक्रियाओं आदि में समझाया जा सकता है, जैसा कि सर्वविदित है , उसी सीमा प्रमेय द्वारा, जो प्रायिकता की गणना में केंद्रीय भूमिका निभाता है। इस सीमा प्रमेय के वास्तविक खोजकर्ता का नाम लाप्लास है; यह संभावना है कि इसका कठोर प्रमाण सर्वप्रथम चेबीशेफ द्वारा दिया गया था और जहां तक मुझे ज्ञात है, लियापौनॉफ़ के एक लेख में इसका सबसे तीक्ष्ण सूत्रीकरण पाया जा सकता है। ...
हैल्ड द्वारा प्रमेय के इतिहास का एक विस्तृत विवरण, लाप्लास के मूलभूत कार्य के साथ-साथ ऑगस्टिन-लुई कॉची, फ्रेडरिक बेसेल और सिमोन डेनिस पॉइसन के योगदान का विवरण प्रदान किया गया है।[44]दो ऐतिहासिक वृत्तांत, एक लैपलेस से कॉची तक के विकास को आवरक करता है, दूसरा 1920 के दशक के पर्यन्त रिचर्ड वॉन मिसेस, जॉर्ज पोल्या, जारल वाल्डेमर लिंडेबर्ग, पॉल लेवी, और क्रैमर द्वारा योगदान, हंस फिशर द्वारा दिया गया है। ।[45]ले कैम 1935 के आसपास की अवधि का वर्णन करता है।[43]बर्नस्टीन[46]पफन्युटी चेबीशेव और उनके छात्रों एंड्री मार्कोव और अलेक्सांद्र लायपुनोव के कार्य पर ध्यान केंद्रित करते हुए एक ऐतिहासिक आलोचना प्रस्तुत करता है जिसके कारण एक सामान्य समुच्चयन में सीएलटी का प्रथम प्रमाण प्राप्त हुआ।
केंद्रीय सीमा प्रमेय के इतिहास के लिए एक असामान्य पाद टिप्पणी यह है कि 1922 के लिंडबर्ग सीएलटी के समान परिणाम का प्रमाण कैम्ब्रिज विश्वविद्यालय में किंग्स विश्वविद्यालयों के लिए एलन ट्यूरिंग के 1934 अधिसदस्यता शोध प्रबंध का विषय था। कार्य जमा करने के पश्चात ही ट्यूरिंग को पता चला कि यह पूर्व में सिद्ध हो चुका है। परिणामस्वरूप, ट्यूरिंग का शोध प्रबंध प्रकाशित नहीं हुआ था।[47]
यह भी देखें
- स्पर्शोन्मुख समविभाजन गुणधर्म
- स्पर्शोन्मुख वितरण
- बेट्स वितरण
- बेनफोर्ड का नियम - यादृच्छिक चर के उत्पाद के लिए सीएलटी के विस्तार का परिणाम है।
- बेरी-एसेन प्रमेय
- दिशात्मक सांख्यिकी के लिए केंद्रीय सीमा प्रमेय - केंद्रीय सीमा प्रमेय दिशात्मक सांख्यिकी की स्थितियों में अनुप्रयोज्य होता है।
- डेल्टा पद्धति - एक यादृच्छिक चर के एक फलन के सीमा वितरण की गणना करने के लिए।
- एर्डोस-केएसी प्रमेय - किसी पूर्णांक के अभाज्य गुणनखण्डों की संख्या को सामान्य प्रायिकता वितरण से जोड़ता है।
- फिशर-टिपेट-गनेडेन्को प्रमेय - चरम मानों के लिए सीमा प्रमेय (जैसे max{Xn})
- इरविन-हॉल वितरण
- मार्कोव श्रृंखला केंद्रीय सीमा प्रमेय
- सामान्य वितरण
- ट्वीडी वितरण - एक प्रमेय जिसे केंद्रीय सीमा प्रमेय और प्वासों अभिसरण प्रमेय के मध्य पाटने के लिए माना जा सकता है[48]
टिप्पणियाँ
- ↑ Fischer, Hans. "केंद्रीय सीमा प्रमेय का इतिहास" (PDF). Springer New York Dordrecht Heidelberg London. Archived (PDF) from the original on 2017-10-31. Retrieved 29 April 2021.
- ↑ Montgomery, Douglas C.; Runger, George C. (2014). एप्लाइड सांख्यिकी और इंजीनियरों के लिए संभावना (6th ed.). Wiley. p. 241. ISBN 9781118539712.
- ↑ Rouaud, Mathieu (2013). संभाव्यता, सांख्यिकी और अनुमान (PDF). p. 10. Archived (PDF) from the original on 2022-10-09.
- ↑ Billingsley (1995, p. 357)
- ↑ Bauer (2001, Theorem 30.13, p.199)
- ↑ Billingsley (1995, p.362)
- ↑ van der Vaart, A.W. (1998). स्पर्शोन्मुख आँकड़े. New York, NY: Cambridge University Press. ISBN 978-0-521-49603-2. LCCN 98015176.
{{cite book}}: CS1 maint: ref duplicates default (link) - ↑ O’Donnell, Ryan (2014). "Theorem 5.38". Archived from the original on 2019-04-08. Retrieved 2017-10-18.
- ↑ Bentkus, V. (2005). "A Lyapunov-type bound in ". Theory Probab. Appl. 49 (2): 311–323. doi:10.1137/S0040585X97981123.
- ↑ Voit, Johannes (2003). "Section f5.4.3". वित्तीय बाजारों के सांख्यिकीय यांत्रिकी. Texts and Monographs in Physics. Springer-Verlag. ISBN 3-540-00978-7.
- ↑ Gnedenko, B.V.; Kolmogorov, A.N. (1954). स्वतंत्र यादृच्छिक चर के योग के लिए वितरण सीमित करें. Cambridge: Addison-Wesley.
- ↑ 12.0 12.1 Uchaikin, Vladimir V.; Zolotarev, V.M. (1999). Chance and Stability: Stable distributions and their applications. VSP. pp. 61–62. ISBN 90-6764-301-7.
- ↑ Billingsley (1995, Theorem 27.4)
- ↑ Durrett (2004, Sect. 7.7(c), Theorem 7.8)
- ↑ Durrett (2004, Sect. 7.7, Theorem 7.4)
- ↑ Billingsley (1995, Theorem 35.12)
- ↑ "भौतिकी में स्टोकेस्टिक प्रक्रियाओं का परिचय". jhupbooks.press.jhu.edu. Retrieved 2016-08-11.
- ↑ Stein, C. (1972). "आश्रित यादृच्छिक चर के योग के वितरण के लिए सामान्य सन्निकटन में त्रुटि के लिए बाध्य". Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability. 6 (2): 583–602. MR 0402873. Zbl 0278.60026.
- ↑ Chen, L. H. Y.; Goldstein, L.; Shao, Q. M. (2011). Normal approximation by Stein's method. Springer. ISBN 978-3-642-15006-7.
- ↑ Artstein, S.; Ball, K.; Barthe, F.; Naor, A. (2004), "Solution of Shannon's Problem on the Monotonicity of Entropy", Journal of the American Mathematical Society, 17 (4): 975–982, doi:10.1090/S0894-0347-04-00459-X
- ↑ Rosenthal, Jeffrey Seth (2000). कठोर संभाव्यता सिद्धांत पर पहली नज़र. World Scientific. Theorem 5.3.4, p. 47. ISBN 981-02-4322-7.
- ↑ Johnson, Oliver Thomas (2004). सूचना सिद्धांत और केंद्रीय सीमा प्रमेय. Imperial College Press. p. 88. ISBN 1-86094-473-6.
- ↑ Borodin, A. N.; Ibragimov, I. A.; Sudakov, V. N. (1995). रैंडम वॉक के कार्यात्मकताओं के लिए सीमा प्रमेय. AMS Bookstore. Theorem 1.1, p. 8. ISBN 0-8218-0438-3.
- ↑ Petrov, V. V. (1976). स्वतंत्र यादृच्छिक चर का योग. New York-Heidelberg: Springer-Verlag. ch. 7. ISBN 9783642658099.
- ↑ Hew, Patrick Chisan (2017). "Asymptotic distribution of rewards accumulated by alternating renewal processes". Statistics and Probability Letters. 129: 355–359. doi:10.1016/j.spl.2017.06.027.
- ↑ Rempala, G.; Wesolowski, J. (2002). "Asymptotics of products of sums and U-statistics" (PDF). Electronic Communications in Probability. 7: 47–54. doi:10.1214/ecp.v7-1046.
- ↑ Klartag (2007, Theorem 1.2)
- ↑ Durrett (2004, Section 2.4, Example 4.5)
- ↑ Klartag (2008, Theorem 1)
- ↑ Klartag (2007, Theorem 1.1)
- ↑ Zygmund, Antoni (2003) [1959]. Trigonometric Series. Cambridge University Press. vol. II, sect. XVI.5, Theorem 5-5. ISBN 0-521-89053-5.
- ↑ Gaposhkin (1966, Theorem 2.1.13)
- ↑ Bárány & Vu (2007, Theorem 1.1)
- ↑ Bárány & Vu (2007, Theorem 1.2)
- ↑ Meckes, Elizabeth (2008). "Linear functions on the classical matrix groups". Transactions of the American Mathematical Society. 360 (10): 5355–5366. arXiv:math/0509441. doi:10.1090/S0002-9947-08-04444-9. S2CID 11981408.
- ↑ Gaposhkin (1966, Sect. 1.5)
- ↑ Kotani, M.; Sunada, Toshikazu (2003). क्रिस्टल लैटिस की स्पेक्ट्रल ज्यामिति. Vol. 338. Contemporary Math. pp. 271–305. ISBN 978-0-8218-4269-0.
- ↑ Sunada, Toshikazu (2012). Topological Crystallography – With a View Towards Discrete Geometric Analysis. Surveys and Tutorials in the Applied Mathematical Sciences. Vol. 6. Springer. ISBN 978-4-431-54177-6.
- ↑ Marasinghe, M.; Meeker, W.; Cook, D.; Shin, T. S. (Aug 1994). "सांख्यिकीय अवधारणाओं को पढ़ाने के लिए ग्राफिक्स और सिमुलेशन का उपयोग करना". Paper presented at the Annual meeting of the American Statistician Association, Toronto, Canada.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Henk, Tijms (2004). Understanding Probability: Chance Rules in Everyday Life. Cambridge: Cambridge University Press. p. 169. ISBN 0-521-54036-4.
- ↑ Galton, F. (1889). प्राकृतिक विरासत. p. 66.
- ↑ 42.0 42.1 Pólya, George (1920). "Über den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung und das Momentenproblem" [On the central limit theorem of probability calculation and the problem of moments]. Mathematische Zeitschrift (in Deutsch). 8 (3–4): 171–181. doi:10.1007/BF01206525. S2CID 123063388.
- ↑ 43.0 43.1 43.2 Le Cam, Lucien (1986). "The central limit theorem around 1935". Statistical Science. 1 (1): 78–91. doi:10.1214/ss/1177013818.
- ↑ Hald, Andreas (22 April 1998). A History of Mathematical Statistics from 1750 to 1930 (PDF). chapter 17. ISBN 978-0471179122. Archived (PDF) from the original on 2022-10-09.
{{cite book}}:|website=ignored (help) - ↑ Fischer, Hans (2011). A History of the Central Limit Theorem: From Classical to Modern Probability Theory. Sources and Studies in the History of Mathematics and Physical Sciences. New York: Springer. doi:10.1007/978-0-387-87857-7. ISBN 978-0-387-87856-0. MR 2743162. Zbl 1226.60004. (Chapter 2: The Central Limit Theorem from Laplace to Cauchy: Changes in Stochastic Objectives and in Analytical Methods, Chapter 5.2: The Central Limit Theorem in the Twenties)
- ↑ Bernstein, S. N. (1945). "On the work of P. L. Chebyshev in Probability Theory". In Bernstein., S. N. (ed.). Nauchnoe Nasledie P. L. Chebysheva. Vypusk Pervyi: Matematika [The Scientific Legacy of P. L. Chebyshev. Part I: Mathematics] (in русский). Moscow & Leningrad: Academiya Nauk SSSR. p. 174.
- ↑ Zabell, S. L. (1995). "एलन ट्यूरिंग और केंद्रीय सीमा प्रमेय". American Mathematical Monthly. 102 (6): 483–494. doi:10.1080/00029890.1995.12004608.
- ↑ Jørgensen, Bent (1997). फैलाव मॉडल का सिद्धांत. Chapman & Hall. ISBN 978-0412997112.
संदर्भ
- Bárány, Imre; Vu, Van (2007). "Central limit theorems for Gaussian polytopes". Annals of Probability. Institute of Mathematical Statistics. 35 (4): 1593–1621. arXiv:math/0610192. doi:10.1214/009117906000000791. S2CID 9128253.
- Bauer, Heinz (2001). Measure and Integration Theory. Berlin: de Gruyter. ISBN 3110167190.
- Billingsley, Patrick (1995). Probability and Measure (3rd ed.). John Wiley & Sons. ISBN 0-471-00710-2.
- Bradley, Richard (2007). Introduction to Strong Mixing Conditions (1st ed.). Heber City, UT: Kendrick Press. ISBN 978-0-9740427-9-4.
- Bradley, Richard (2005). "Basic Properties of Strong Mixing Conditions. A Survey and Some Open Questions". Probability Surveys. 2: 107–144. arXiv:math/0511078. Bibcode:2005math.....11078B. doi:10.1214/154957805100000104. S2CID 8395267.
- Dinov, Ivo; Christou, Nicolas; Sanchez, Juana (2008). "Central Limit Theorem: New SOCR Applet and Demonstration Activity". Journal of Statistics Education. ASA. 16 (2): 1–15. doi:10.1080/10691898.2008.11889560. PMC 3152447. PMID 21833159.
- Durrett, Richard (2004). Probability: theory and examples (3rd ed.). Cambridge University Press. ISBN 0521765390.
- Gaposhkin, V. F. (1966). "Lacunary series and independent functions". Russian Mathematical Surveys. 21 (6): 1–82. Bibcode:1966RuMaS..21....1G. doi:10.1070/RM1966v021n06ABEH001196. S2CID 250833638..
- Klartag, Bo'az (2007). "A central limit theorem for convex sets". Inventiones Mathematicae. 168 (1): 91–131. arXiv:math/0605014. Bibcode:2007InMat.168...91K. doi:10.1007/s00222-006-0028-8. S2CID 119169773.
- Klartag, Bo'az (2008). "A Berry–Esseen type inequality for convex bodies with an unconditional basis". Probability Theory and Related Fields. 145 (1–2): 1–33. arXiv:0705.0832. doi:10.1007/s00440-008-0158-6. S2CID 10163322.
बाहरी संबंध
- Central Limit Theorem at Khan Academy
- "Central limit theorem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Central Limit Theorem". MathWorld.
- A music video demonstrating the central limit theorem with a Galton board by Carl McTague
