परम शून्य: Difference between revisions

Revision as of 15:53, 22 March 2023

शून्य केल्विन (−273.15 डिग्री सेल्सियस) को पूर्ण शून्य के रूप में परिभाषित किया गया है।

निरपेक्ष शून्य उष्मगतिशील तापमान पैमाने की सबसे निचली सीमा है, एक ऐसी अवस्था जिस पर ठंडी आदर्श गैस की तापीय धारिता और एन्ट्रापी अपने न्यूनतम मान तक पहुँच जाती है, जिसे शून्य केल्विन के रूप में लिया जाता है। प्रकृति के मौलिक कणों में न्यूनतम कंपन गति होती है, जो केवल क्वांटम यांत्रिक, शून्य-बिंदु ऊर्जा-प्रेरित कण गति को बनाए रखती है। सैद्धांतिक तापमान आदर्श गैस नियम को बहिर्गमन करके निर्धारित किया जाता है; अंतरराष्ट्रीय समझौते के अनुसार, पूर्ण शून्य को सेल्सीयस पैमाने (इकाइयों की अंतर्राष्ट्रीय प्रणाली) पर -273.15 डिग्री के रूप में लिया जाता है,^[1]^[2]^[3] जो फ़ारेनहाइट पैमाने पर -459.67 डिग्री के बराबर है (संयुक्त राज्य प्रथागत इकाइयाँ या शाही इकाइयाँ)।^[4] संबंधित केल्विन और रैंकिन स्केल तापमान स्केल परिभाषा के अनुसार अपने शून्य बिंदु को पूर्ण शून्य पर उपयुक्त करते हैं

इसे सामान्यतः सबसे कम संभव तापमान के रूप में माना जाता है, किन्तु यह सबसे कम संभव एन्थैल्पी अवस्था नहीं है, क्योंकि ठंडा होने पर सभी वास्तविक पदार्थ आदर्श गैस से प्रस्थान करना शुरू कर देते हैं क्योंकि वे अवस्था परिवर्तन से पहले तरल और फिर ठोस में बदल जाते हैं; और वाष्पीकरण की तापीय धारिता (गैस से तरल) और संलयन की तापीय धारिता (तरल से ठोस) का योग, आदर्श गैस के तापीय धारिता में परम शून्य परिवर्तन से अधिक है। क्वांटम यांत्रिकी विवरण में, पूर्ण शून्य पर पदार्थ (ठोस) इसकी जमीनी अवस्था में है, जो सबसे कम आंतरिक ऊर्जा का बिंदु है।

ऊष्मप्रवैगिकी के नियमों से संकेत मिलता है कि पूर्ण शून्य को केवल ऊष्मप्रवैगिक साधनों का उपयोग करके नहीं पहुंचा जा सकता है, क्योंकि ठंडा होने वाले पदार्थ का तापमान शीतलन एजेंट के तापमान के समान रूप से पहुंचता है।^[5] यहां तक कि पूर्ण शून्य पर एक प्रणाली यदि इसे किसी तरह प्राप्त किया जा सकता है, तब भी क्वांटम यांत्रिक शून्य-बिंदु ऊर्जा, इसकी जमीनी स्थिति की ऊर्जा पूर्ण शून्य पर होगी; जमीनी अवस्था की गतिज ऊर्जा को हटाया नहीं जा सकता।

वैज्ञानिक और प्रौद्योगिकीविद् नियमित रूप से पूर्ण शून्य के करीब तापमान प्राप्त करते हैं, जहां पदार्थ बोस-आइंस्टीन संघनन, अतिचालकता और अति तरल जैसे क्वांटम प्रभाव प्रदर्शित करता है।

उष्मगतिशील्स पूर्ण शून्य के पास

0 K (−273.15 °C; −459.67 °F) के पास तापमान पर लगभग सभी आणविक गति समाप्त हो जाती है और किसी भी रूद्धोष्म प्रक्रिया के लिए ΔS = 0, जहां S एंट्रॉपी है। ऐसी परिस्थिति में, शुद्ध पदार्थ (आदर्श रूप से) T → 0 के रूप में बिना किसी संरचनात्मक खामियों के सही क्रिस्टल बना सकते हैं। उष्मगतिशील्स के तीसरे नियम का मैक्स प्लैंक का शक्तिशाली रूप बताता है कि एक पूर्ण क्रिस्टल की एन्ट्रापी पूर्ण शून्य पर गायब हो जाती है। मूल वाल्थर नर्नस्ट नर्नस्ट ताप प्रमेय अशक्त और कम विवादास्पद प्रमाणित करता है कि किसी भी इज़ोटेर्माल प्रक्रिया के लिए एन्ट्रॉपी परिवर्तन शून्य तक पहुंच जाता है क्योंकि T → 0:

\lim _{T\to 0}\Delta S=0

निहितार्थ यह है कि एक आदर्श क्रिस्टल की एन्ट्रापी एक स्थिर मान तक पहुँचती है। रुद्धोष्म निरंतर एन्ट्रॉपी वाली एक स्थिति है, जिसे सामान्यतः एक वक्र के रूप में एक वक्र के रूप में प्रतिनिधित्व किया जाता है जो समताप रेखा और आइसोबार के समान होता है।

ऊष्मप्रवैगिकी का तीसरा नियम समतापीय प्रक्रिया T = 0 की पहचान रुद्धोष्म S = 0 के साथ संयोग के रूप में करता है, चूंकि अन्य समतापी और रुद्धोष्म भिन्न हैं। चूँकि कोई भी दो रुद्धोष्म प्रतिच्छेद नहीं करते हैं, कोई भी अन्य रुद्धोष्म टी = 0 समताप रेखा को रेखा–रेखा प्रतिच्छेद नहीं कर सकता है। परिणाम स्वरुप गैर-शून्य तापमान पर प्रारंभिकू की गई कोई एडियाबेटिक प्रक्रिया शून्य तापमान तक नहीं पहुंच सकती है। (≈ कालेन, पीपी. 189–190)

एक आदर्श क्रिस्टल वह है जिसमें आंतरिक जाली (समूह) संरचना सभी दिशाओं में निर्बाध रूप से फैली हुई है। पूर्ण क्रम को तीन (सामान्यतः ओर्थोगोनालिटी नहीं) कार्टेशियन समन्वय प्रणाली के साथ ट्रांसलेशनल समरूपता द्वारा दर्शाया जा सकता है। संरचना का प्रत्येक जाली तत्व अपने उचित स्थान पर है, चाहे वह एक परमाणु हो या आणविक समूह। ऐसे रासायनिक पदार्थों के लिए जो दो (या अधिक) स्थिर क्रिस्टलीय रूपों में उपस्थित होते हैं, जैसे कि कार्बन के लिए हीरा और ग्रेफाइट, एक प्रकार की रासायनिक विकृति होती है। यह प्रश्न बना रहता है कि क्या दोनों के पास T = 0 पर शून्य एंट्रोपी हो सकती है, तथापि प्रत्येक पूरी तरह से आदेशित हो।

अभ्यास में बिल्कुल सही क्रिस्टल कभी नहीं होते हैं; खामियां, और यहां तक कि संपूर्ण अनाकार सामग्री समावेशन, कम तापमान पर "जमे हुए" हो सकते हैं इसलिए अधिक स्थिर अवस्थाओं में संक्रमण नहीं होता है।

डेबी मॉडल का उपयोग करते हुए, एक शुद्ध क्रिस्टल की विशिष्ट ऊष्मा और एन्ट्रापी T ³ के समानुपाती होते हैं, जबकि थैलेपी और रासायनिक क्षमता T ⁴ के समानुपाती होते हैं । (गगेनहाइम, पृ. 111) ये मात्राएँ अपने टी = 0 सीमित मूल्यों की ओर गिरती हैं और शून्य ढलान के साथ पहुँचती हैं। कम से कम विशिष्ट तापों के लिए, सीमित मान स्वयं निश्चित रूप से शून्य है, जैसा कि 10 K से नीचे के प्रयोगों से पता चलता है। यहां तक कि कम विस्तृत आइंस्टीन ठोस भी विशिष्ट तापों में इस अजीब गिरावट को दर्शाता है। वास्तव में, केवल क्रिस्टल के ही नहीं, किंतु सभी विशिष्ट ऊष्माएं पूर्ण शून्य पर गायब हो जाती हैं। इसी तरह थर्मल विस्तार के गुणांक के लिए। मैक्सवेल संबंध|मैक्सवेल के संबंध बताते हैं कि कई अन्य राशियां भी लुप्त हो जाती हैं। ये घटनाएं अप्रत्याशित थीं।

चूँकि गिब्स मुक्त ऊर्जा (G), एन्थैल्पी (H) और एन्ट्रॉपी में परिवर्तन के बीच संबंध है

\Delta G=\Delta H-T\Delta S\,

इस प्रकार, जैसे-जैसे T घटता है, ΔG और ΔH एक-दूसरे की ओर बढ़ते हैं (जब तक ΔS परिबद्ध है)। प्रायोगिक रूप से यह पाया गया है कि सभी सहज प्रक्रियाओं (रासायनिक प्रतिक्रियाओं सहित) के परिणामस्वरूप जी में कमी आती है क्योंकि वे उष्मगतिशील संतुलन की ओर बढ़ते हैं। यदि ΔS और/या T छोटे हैं, तो स्थिति ΔG < 0 का अर्थ ΔH < 0 हो सकता है, जो एक उष्माक्षेपी प्रतिक्रिया का संकेत देगा। चूंकि, यह आवश्यक नहीं है; यदि TΔS शब्द अधिक बड़ा है तो ऊष्माशोषी प्रतिक्रियाएं सहज रूप से आगे बढ़ सकती हैं।

इसके अलावा, ΔG और ΔH के डेरिवेटिव के ढलान T = 0 पर अभिसरण करते हैं और शून्य के बराबर होते हैं। यह सुनिश्चित करता है कि ΔG और ΔH तापमान की काफी सीमा पर लगभग समान हैं और थॉमसन और बर्थेलॉट के अनुमानित अनुभवजन्य सिद्धांत को सही ठहराते हैं जो बताता है वह संतुलन अवस्था जिसके लिए एक प्रणाली आगे बढ़ती है वह सबसे बड़ी मात्रा में गर्मी विकसित करती है, अर्थात, एक वास्तविक प्रक्रिया सबसे अधिक उष्माक्षेपी है। (कालेन, पीपी. 186-187)

एक मॉडल जो धातुओं में पूर्ण शून्य पर एक इलेक्ट्रॉन गैस के गुणों का अनुमान लगाता है, वह फर्मी गैस है। इलेक्ट्रॉन, फर्मियन होने के नाते, अलग-अलग क्वांटम अवस्थाओं में होने चाहिए, जो इलेक्ट्रॉनों को पूर्ण शून्य पर भी बहुत उच्च विशिष्ट वेग प्राप्त करने की ओर ले जाता है। अधिकतम ऊर्जा जो इलेक्ट्रॉनों में पूर्ण शून्य पर हो सकती है, फर्मी ऊर्जा कहलाती है। फर्मी तापमान को बोल्ट्जमैन स्थिरांक द्वारा विभाजित इस अधिकतम ऊर्जा के रूप में परिभाषित किया गया है, और धातुओं में पाए जाने वाले विशिष्ट इलेक्ट्रॉन घनत्वों के लिए 80,000 K के क्रम में है। फर्मी तापमान से अधिक नीचे के तापमान के लिए, इलेक्ट्रॉन लगभग उसी तरह व्यवहार करते हैं जैसे पूर्ण शून्य पर। यह धातुओं के मौलिक समविभाजन प्रमेय की विफलता की व्याख्या करता है जो 19वीं शताब्दी के अंत में मौलिक भौतिकविदों से दूर हो गया था।

बोस-आइंस्टीन घनीभूत के साथ संबंध

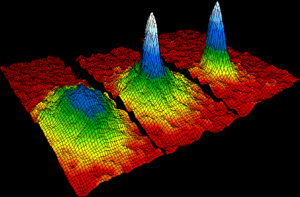
पूर्ण शून्य से ऊपर डिग्री के कुछ अरबवें हिस्से के तापमान पर रूबिडीयाम परमाणुओं की गैस का वेग-वितरण डेटा। बायां: बोस-आइंस्टीन कंडेनसेट के प्रकट होने से ठीक पहले। केंद्र: घनीभूत होने के तुरंत बाद। दाएं: आगे के वाष्पीकरण के बाद, लगभग शुद्ध घनीभूत का एक नमूना छोड़कर।

बोस-आइंस्टीन कंडेनसेट (बीईसी) एक बाहरी क्षमता में सीमित रूप से परस्पर क्रिया करने वाले बोसॉन की तनु गैस की स्थिति है और तापमान को पूर्ण शून्य के करीब ठंडा किया जाता है। ऐसी परिस्थितियों में, बोसोन का एक बड़ा अंश बाहरी क्षमता की निम्नतम कितना स्थिति पर कब्जा कर लेता है, जिस बिंदु पर स्थूल स्केल पर क्वांटम प्रभाव स्पष्ट हो जाते हैं।^[6]

पदार्थ की इस अवस्था की भविष्यवाणी सबसे पहले 1924-25 में सत्येन्द्र नाथ बोस और अल्बर्ट आइंस्टीन ने की थी। बोस ने सबसे पहले आइंस्टीन को प्रकाश क्वांटा (अब फोटॉन कहा जाता है) के क्वांटम सांख्यिकी पर एक पेपर भेजा था। आइंस्टीन प्रभावित हुए, कागज का अंग्रेजी से जर्मन में अनुवाद किया और इसे बोस के लिए जेट्सच्रिफ्त फर फिजिक को सौंप दिया, जिसने इसे प्रकाशित किया। आइंस्टीन ने तब बोस के विचारों को भौतिक कणों (या पदार्थ) तक दो अन्य पत्रों में विस्तारित किया।^[7]

सत्तर साल बाद, 1995 में, बोल्डर निस्ट-जिला लैब में कोलोराडो विश्वविद्यालय में एरिक एलिन कॉर्नेल और कार्ल वाईमन द्वारा पहला गैसीय बोस-आइंस्टीन कंडेनसेट बनाया गया था, जिसमें 170 केल्विन (इकाइयां) (एनके) (1.7×10⁻⁷ K) तक ठंडा रूबिडियम परमाणुओं की गैस का उपयोग किया गया था। ^[8] ^[9]

मैसाचुसेट्स की विधि संस्था (एमआईटी) के शोधकर्ताओं द्वारा 2003 में सोडियम परमाणुओं के बीईसी 450 ± 80 पिकोकेल्विन (पीके) का रिकॉर्ड ठंडा तापमान में प्राप्त किया गया था।^[10] संबंधित काले पदार्थ (शिखर उत्सर्जन) 6,400 किलोमीटर की तरंग दैर्ध्य लगभग पृथ्वी की त्रिज्या है।

निरपेक्ष तापमान पैमाने

निरपेक्ष, या उष्मगतिशील तापमान, तापमान पारंपरिक रूप से केल्विन (सेल्सियस-स्केल्ड वृद्धि ) और रैंकिन स्केल (फारेनहाइट-स्केल्ड वृद्धि) में बढ़ती दुर्लभता के साथ मापा जाता है। पूर्ण तापमान माप विशिष्ट रूप से गुणक स्थिरांक द्वारा निर्धारित किया जाता है जो डिग्री के आकार को निर्दिष्ट करता है, इसलिए दो पूर्ण तापमानों ,T₂/T₁, का अनुपात सभी पैमानों में समान हैं। इस मानक की सबसे पारदर्शी परिभाषा मैक्सवेल-बोल्ट्ज़मान वितरण से आती है। यह फर्मी-डिराक सांख्यिकी (अर्ध-पूर्णांक स्पिन (भौतिकी) के कणों के लिए) और बोस-आइंस्टीन सांख्यिकी (पूर्णांक स्पिन के कणों के लिए) में भी पाया जा सकता है। ये सभी एक प्रणाली में कणों की सापेक्ष संख्या को kT से अधिक ऊर्जा (कण स्तर पर) के घटते हुए घातीय कार्यों के रूप में परिभाषित करते हैं, जिसमें k बोल्ट्ज़मान स्थिरांक का प्रतिनिधित्व करता है और T स्थूल स्तर पर देखे गए तापमान का प्रतिनिधित्व करता है।^[1]

नकारात्मक तापमान

परिचित सेल्सियस या फ़ारेनहाइट स्केल पर ऋणात्मक संख्याओं के रूप में व्यक्त किए जाने वाले तापमान उन पैमानों के शून्य बिंदुओं की तुलना में अधिक ठंडे होते हैं। कुछ उष्मगतिशील प्रणाली वास्तव में नकारात्मक तापमान प्राप्त कर सकते हैं; अर्थात्, उनका उष्मगतिशील तापमान (केल्विन में व्यक्त) एक ऋणात्मक संख्या मात्रा का हो सकता है। वास्तव में नकारात्मक तापमान वाली प्रणाली पूर्ण शून्य से अधिक ठंडी नहीं होती है। किंतु, एक नकारात्मक तापमान वाली प्रणाली सकारात्मक तापमान वाली किसी भी प्रणाली की तुलना में अधिक गर्म होती है, इस अर्थ में कि यदि एक नकारात्मक-तापमान प्रणाली और एक सकारात्मक-तापमान प्रणाली संपर्क में आती है, तो गर्मी नकारात्मक से सकारात्मक-तापमान प्रणाली में प्रवाहित होती है।^[11]

अधिकांश परिचित प्रणालियां नकारात्मक तापमान प्राप्त नहीं कर सकती हैं क्योंकि ऊर्जा जोड़ने से उनकी एन्ट्रापी सदैव बढ़ जाती है। चूंकि, कुछ प्रणालियों में ऊर्जा की अधिकतम मात्रा होती है जिसे वे धारण कर सकते हैं, और जैसे-जैसे वे उस अधिकतम ऊर्जा तक पहुँचते हैं, उनकी एन्ट्रापी वास्तव में कम होने लगती है। क्योंकि तापमान को ऊर्जा और एन्ट्रापी के बीच के संबंध से परिभाषित किया जाता है, इस तरह की प्रणाली का तापमान नकारात्मक हो जाता है, तथापि ऊर्जा को जोड़ा जा रहा हो।^[11]परिणाम स्वरुप , बढ़ती राज्य ऊर्जा के साथ घटने के अतिरिक्त नकारात्मक तापमान पर प्रणाली के राज्यों के लिए बोल्टज़मान कारक बढ़ता है। इसलिए, कोई पूर्ण प्रणाली, यानी विद्युत चुम्बकीय मोड सहित, नकारात्मक तापमान नहीं हो सकता है, क्योंकि कोई उच्चतम ऊर्जा स्थिति नहीं है,^{[citation needed]} जिससे नकारात्मक तापमान के लिए राज्यों की संभावनाओं का योग अलग हो जाए। चूंकि, अर्ध-संतुलन प्रणालियों के लिए (उदाहरण के लिए विद्युत चुम्बकीय क्षेत्र के साथ संतुलन से बाहर स्पिन) यह तर्क प्रयुक्त नहीं होता है, और नकारात्मक प्रभावी तापमान प्राप्य हैं।

3 जनवरी 2013 को, भौतिकविदों ने घोषणा की कि पहली बार उन्होंने पोटेशियम परमाणुओं से बनी एक क्वांटम गैस का निर्माण किया है, जो स्वतंत्रता की गतिमान डिग्री में एक नकारात्मक तापमान के साथ है।^[12]

इतिहास

रॉबर्ट बॉयल ने पूर्ण शून्य के विचार का बीड़ा उठाया

पूर्ण न्यूनतम तापमान की संभावना पर चर्चा करने वालों में सबसे पहले रॉबर्ट बॉयल थे। शीत को छूने वाले उनके 1665 के नए प्रयोगों और टिप्पणियों ने विवाद को व्यक्त किया जिसे प्राइमम फ्रिगिडम के रूप में जाना जाता है।^[13] यह अवधारणा उस समय के प्रकृतिवादियों के बीच अच्छी तरह से जानी जाती थी। कुछ ने पृथ्वी के अंदर (चार मौलिक तत्वों में से एक के रूप में) एक पूर्ण न्यूनतम तापमान का विरोध किया, अन्य पानी के अंदर , अन्य हवा में, और कुछ हाल ही में नाइट्र के अंदर । किन्तु वे सभी इस बात से सहमत थे कि, कोई न कोई ऐसा शरीर है जो अपने स्वभाव से अत्यंत ठंडा है और जिसकी भागीदारी से अन्य सभी शरीर वह गुण प्राप्त करते हैं।^[14]

ठंड की डिग्री तक सीमित करें

सवाल यह है कि क्या शीतलता की डिग्री की एक सीमा संभव है, और यदि ऐसा है, जहां शून्य को रखा जाना चाहिए, पहली बार 1702 में गैस थर्मामीटर में उनके सुधार के संबंध में फ्रांसीसी भौतिक विज्ञानी गिलियूम अमोन्टन द्वारा संबोधित किया गया था। उनके उपकरण ने ऊंचाई से तापमान का संकेत दिया जिस पर हवा का एक निश्चित द्रव्यमान पारे के एक स्तंभ को बनाए रखता है - हवा का आयतन, या वसंत तापमान के साथ बदलता रहता है। एमोंटोंस ने इसलिए तर्क दिया कि उनके थर्मामीटर का शून्य वह तापमान होगा जिस पर हवा का वसंत शून्य हो गया था। उन्होंने एक पैमाने का उपयोग किया जिसने पानी के क्वथनांक को +73 पर और बर्फ के पिघलने बिंदु को + पर चिह्नित किया51+1⁄2, जिससे शून्य सेल्सियस पैमाने पर लगभग -240 के बराबर हो।^[15] एमोंटोंस का मानना था कि पूर्ण शून्य तक नहीं पहुंचा जा सकता है, इसलिए कभी भी स्पष्ट रूप से इसकी गणना करने का प्रयास नहीं किया।^[16]

-240 °C का मान, या 431 डिवीज़न [फारेनहाइट के थर्मामीटर में] ठंडे पानी के नीचे^[17] 1740 में जॉर्ज मार्टीन (चिकित्सक) द्वारा प्रकाशित किया गया था।

यह -273.15 डिग्री सेल्सियस के आधुनिक मान के करीब है^[1]वायु थर्मामीटर के शून्य के लिए 1779 में जोहान हेनरिक लैम्बर्ट द्वारा और सुधार किया गया, जिन्होंने देखा कि −270 °C (−454.00 °F; 3.15 K) को पूरी तरह से ठंडा माना जा सकता है।^[18] चूंकि, पूर्ण शून्य के लिए इस क्रम के मान इस अवधि के बारे में सार्वभौमिक रूप से स्वीकार नहीं किए गए थे। पियरे-साइमन लाप्लास और एंटोनी लेवोइसियर, गर्मी पर अपने 1780 के ग्रंथ में, पानी के ठंडक बिंदु से 1,500 से 3,000 नीचे के मूल्यों पर पहुंचे, और सोचा कि किसी भी स्थितियोंमें यह कम से कम 600 नीचे होना चाहिए। जॉन डाल्टन ने अपने रासायनिक दर्शन में इस मान की दस गणनाएँ कीं, और अंत में तापमान के प्राकृतिक शून्य के रूप में -3,000 °C को अपनाया।

चार्ल्स का नियम

1787 से 1802 तक, यह जैक्स-चार्ल्स (अप्रकाशित), जॉन डाल्टन, द्वारा निर्धारित किया गया था।^[19] और जोसेफ लुइस गे-लुसाक^[20] कि, स्थिर दबाव पर, आदर्श गैसों ने अपने आयतन को रैखिक रूप से (चार्ल्स का नियम) विस्तारित या अनुबंधित किया, तापमान के प्रति डिग्री सेल्सियस के लगभग 1/273 भागों में 0° और 100°C के बीच ऊपर या नीचे परिवर्तन होता है। इससे पता चलता है कि गैस का आयतन लगभग -273 डिग्री सेल्सियस पर ठंडा होने पर शून्य हो जाएगा।

भगवान केल्विन का काम

जेम्स प्रेस्कॉट जौल द्वारा ऊष्मा के यांत्रिक समतुल्य का निर्धारण करने के बाद, विलियम थॉमसन, प्रथम बैरन केल्विन ने पूरी तरह से अलग दृष्टिकोण से इस प्रश्न पर विचार किया, और 1848 में पूर्ण तापमान का एक मापदंड तैयार किया जो किसी विशेष पदार्थ के गुणों से स्वतंत्र था और था निकोलस लियोनार्ड साडी कार्नाट के ताप की प्रेरक शक्ति के सिद्धांत और हेनरी विक्टर रेग्नॉल्ट द्वारा प्रकाशित डेटा पर आधारित।^[21] यह उन सिद्धांतों का अनुसरण करता है जिनके आधार पर इस पैमाने का निर्माण किया गया था कि इसका शून्य -273 °C पर रखा गया था, लगभग ठीक उसी बिंदु पर जिस पर वायु थर्मामीटर का शून्य था,^[15]जहां हवा की मात्रा कुछ भी नहीं पहुंचेगी। यह मान तुरंत स्वीकार नहीं किया गया था; से लेकर मूल्य −271.1 °C (−455.98 °F) को −274.5 °C (−462.10 °F), वायुमंडलीय अपवर्तन #खगोलीय अपवर्तन के प्रयोगशाला मापन और प्रेक्षणों से प्राप्त, 20वीं शताब्दी के प्रारंभ में उपयोग में रहा।^[22]

पूर्ण शून्य की दौड़

लीडेन में स्मारक पट्टिका

पूर्ण शून्य की उत्तम सैद्धांतिक समझ के साथ, वैज्ञानिक प्रयोगशाला में इस तापमान तक पहुँचने के लिए उत्सुक थे।^[23] 1845 तक, माइकल फैराडे उस समय उपस्थित अधिकांश गैसों को द्रवित करने में कामयाब हो गए थे, और सबसे कम तापमान के लिए एक नए रिकॉर्ड तक पहुंच गए थे −130 °C (−202 °F; 143 K). फैराडे का मानना था कि ऑक्सीजन, नाइट्रोजन और हाइड्रोजन जैसी कुछ गैसें स्थायी गैसें थीं और उन्हें द्रवित नहीं किया जा सकता था।^[24] दशकों बाद, 1873 में डच सैद्धांतिक वैज्ञानिक जोहान्स डिडेरिक वैन डेर वाल्स ने प्रदर्शित किया कि इन गैसों को द्रवीभूत किया जा सकता है, किन्तु केवल बहुत उच्च दबाव और बहुत कम तापमान की स्थितियों में। 1877 में, फ्रांस में लुई पॉल कैलेटेट और स्विट्जरलैंड में राउल पिक्टेट ने तरल हवा की पहली बूंदों का उत्पादन करने में सफलता प्राप्त की। −195 °C (−319.0 °F; 78.1 K). इसके बाद 1883 में तरल ऑक्सीजन का उत्पादन हुआ −218 °C (−360.4 °F; 55.1 K) पोलिश प्रोफेसर ज़िग्मंट व्रॉब्लेव्स्की और करोल ओल्ज़वेस्की द्वारा।

स्कॉटिश रसायनज्ञ और भौतिक विज्ञानी जेम्स देवर और डच भौतिक विज्ञानी हेइके कामेरलिंग ओन्स ने शेष गैसों, हाइड्रोजन और हीलियम को द्रवीभूत करने की चुनौती ली। 1898 में, 20 वर्षों के प्रयास के बाद, देवर ने सबसे पहले हाइड्रोजन का द्रवीकरण किया, जो कम तापमान के एक नए रिकॉर्ड तक पहुंच गया। −252 °C (−421.6 °F; 21.1 K). चूंकि, उनके प्रतिद्वंद्वी, कामेरलिंग ओन्स, 1908 में कई प्रीकूलिंग चरणों और हैम्पसन-लिंडे चक्र का उपयोग करके हीलियम को द्रवीभूत करने वाले पहले व्यक्ति थे। उसने तापमान को हीलियम के क्वथनांक तक कम कर दिया −269 °C (−452.20 °F; 4.15 K). तरल हीलियम के दबाव को कम करके उन्होंने 1.5 K के करीब और भी कम तापमान प्राप्त किया। ये उस समय पृथ्वी पर अंकित किए गए सबसे कम तापमान थे और उनकी उपलब्धि ने उन्हें 1913 में नोबेल पुरस्कार दिलाया।^[25] कामेरलिंग ओन्स पहली बार सुपरकंडक्टिविटी और superfluid का वर्णन करते हुए पूर्ण शून्य के करीब तापमान पर सामग्री के गुणों का अध्ययन करना जारी रखेंगे।

बहुत कम तापमान

सेंटोरस में बुमेरांग नेबुला, एक द्वि-ध्रुवीय, फिलामेंटरी, संभावित प्रोटो-ग्रहीय नेबुला छोड़ने वाली गैसों के तेजी से विस्तार का तापमान 1 K है, जो किसी प्रयोगशाला के बाहर सबसे कम देखा गया है।

आज ब्रह्मांड का औसत तापमान लगभग है 2.73 kelvins (−454.76 °F), या लगभग -270.42 ºC, ब्रह्मांडीय माइक्रोवेव पृष्ठभूमि विकिरण के मापन के आधार पर।^[26]^[27] एक विस्तारित ब्रह्मांड के भविष्य के मानक मॉडल भविष्यवाणी करते हैं कि ब्रह्मांड का औसत तापमान समय के साथ घट रहा है।^[28] इस तापमान की गणना अंतरिक्ष में ऊर्जा के औसत घनत्व के रूप में की जाती है; इसे औसत इलेक्ट्रॉन तापमान (कणों की संख्या से विभाजित कुल ऊर्जा) के साथ भ्रमित नहीं होना चाहिए जो समय के साथ बढ़ा है।^[29]

पूर्ण शून्य प्राप्त नहीं किया जा सकता है, चूंकि बाष्पीकरणीय शीतलन (परमाणु भौतिकी), क्राईकूलर , अशक्त पड़ने अशक्त पड़ने रेफ्रिजरेटर के उपयोग के माध्यम से इसके करीब तापमान तक पहुंचना संभव है।^[30] और चुंबकीय प्रशीतन#परमाणु विचुंबकत्व। लेजर शीतलन के उपयोग से केल्विन के एक अरबवें हिस्से से भी कम तापमान उत्पन्न हुआ है।^[31] पूर्ण शून्य के आसपास बहुत कम तापमान पर, पदार्थ सुपरकंडक्टिविटी, सुपरफ्लूडिटी और बोस-आइंस्टीन कंडेनसेट | बोस-आइंस्टीन संक्षेपण सहित कई असामान्य गुणों को प्रदर्शित करता है। ऐसी घटनाओं का अध्ययन करने के लिए, वैज्ञानिकों ने और भी कम तापमान प्राप्त करने के लिए काम किया है।

नवंबर 2000 में, फिनलैंड के एस्पो में प्रौद्योगिकी के हेलसिंकी विश्वविद्यालय की निम्न तापमान प्रयोगशाला में एक प्रयोग के लिए 100 pK से कम परमाणु स्पिन तापमान की सूची की गई थी। चूंकि, यह स्वतंत्रता की एक विशेष डिग्री (भौतिकी और रसायन विज्ञान) का तापमान था - एक मात्रा संपत्ति जिसे परमाणु स्पिन कहा जाता है - स्वतंत्रता में सभी संभावित डिग्री के लिए समग्र औसत उष्मगतिशील तापमान नहीं।^[32]^[33]
फरवरी 2003 में, बुमेरांग नेबुला की गति से गैसों को छोड़ते हुए देखा गया था 500,000 km/h (310,000 mph) पिछले 1,500 वर्षों से। इसने इसे लगभग 1 K तक ठंडा कर दिया है, जैसा कि खगोलीय अवलोकन से पता चला है, जो अब तक अंकित किया गया सबसे कम प्राकृतिक तापमान है।^[34]
नवंबर 2003 में, 90377 सदना की खोज की गई थी और यह सौर मंडल की सबसे ठंडी ज्ञात वस्तुओं में से एक है। -400°F (-240°C) के औसत सतही तापमान के साथ,^[35] 903 खगोलीय इकाइयों की इसकी अत्यंत दूर की कक्षा के कारण।
मई 2005 में, यूरोपीय अंतरिक्ष एजेंसी ने स्त्री-तापमान प्राप्त करने के लिए अंतरिक्ष में अनुसंधान का प्रस्ताव रखा।^[36]
मई 2006 में, हनोवर विश्वविद्यालय में क्वांटम ऑप्टिक्स संस्थान ने अंतरिक्ष में फेम्टोकेल्विन अनुसंधान की विधि ों और लाभों का विवरण दिया।^[37]
जनवरी 2013 में, जर्मनी में म्यूनिख विश्वविद्यालय के भौतिक विज्ञानी उलरिच श्नाइडर ने गैसों में औपचारिक रूप से पूर्ण शून्य (नकारात्मक तापमान) से नीचे तापमान प्राप्त करने की सूचना दी। गैस को कृत्रिम रूप से संतुलन से बाहर एक उच्च क्षमता वाली ऊर्जा अवस्था में लाया जाता है, जो कि, चूंकि, ठंडी होती है। जब यह तब विकिरण का उत्सर्जन करता है तो यह संतुलन की ओर पहुंचता है, और औपचारिक पूर्ण शून्य तक पहुंचने के अतिरिक्त उत्सर्जन जारी रख सकता है; इस प्रकार, तापमान औपचारिक रूप से नकारात्मक है।^[38]
सितंबर 2014 में, इटली में ग्रैन सासो नेशनल लेबोरेटरीज में दिल सहयोग में वैज्ञानिकों ने एक घन मीटर की मात्रा के साथ एक तांबे के बर्तन को ठंडा किया 0.006 kelvins (−273.144 °C; −459.659 °F) 15 दिनों के लिए, इतनी बड़ी सन्निहित मात्रा में ज्ञात ब्रह्मांड में सबसे कम तापमान के लिए एक रिकॉर्ड स्थापित करना।^[39]
जून 2015 में, एमआईटी के प्रायोगिक भौतिकविदों ने सोडियम पोटेशियम की गैस में अणुओं को 500 नैनोकेल्विन के तापमान पर ठंडा किया, और इन अणुओं को कुछ और ठंडा करके पदार्थ की एक विदेशी स्थिति प्रदर्शित करने की उम्मीद है।^[40]
2017 में, शीत परमाणु प्रयोगशाला (CAL), एक प्रायोगिक उपकरण को 2018 में अंतर्राष्ट्रीय अंतरिक्ष स्टेशन (ISS) में लॉन्च करने के लिए विकसित किया गया था।^[41] उपकरण ने आईएसएस के सूक्ष्म गुरुत्वाकर्षण वातावरण में अत्यधिक ठंड की स्थिति उत्पन्न की है जिससे बोस-आइंस्टीन कंडेनसेट का निर्माण हुआ है। इस अंतरिक्ष-आधारित प्रयोगशाला में, तापमान 1 पिकोकेल्विन (10^-12 के) तापमान प्राप्त करने योग्य होने का अनुमान है, और यह अज्ञात क्वांटम यांत्रिकी घटना की खोज को आगे बढ़ा सकता है और भौतिकी के कुछ सबसे मौलिक नियमों का परीक्षण कर सकता है।^[42]^[43]
प्रभावी तापमान का वर्तमान विश्व रिकॉर्ड 2021 में 38 पिकोकेल्विन (pK), या 0.000000000038 केल्विन पर, रूबिडियम बोस-आइंस्टीन कंडेनसेट के मैटर-वेव लेंसिंग के माध्यम से स्थापित किया गया था।^[44]

यह भी देखें

केल्विन (तापमान की इकाई)
चार्ल्स का नियम
गर्मी
1990 का अंतर्राष्ट्रीय तापमान पैमाना
परिमाण के आदेश (तापमान)
थर्मोडायनामिक तापमान
तीन बिंदु
अल्ट्राकोल्ड परमाणु
गतिज ऊर्जा
एंट्रॉपी
प्लैंक तापमान और हैडोर्न तापमान, थर्मोडायनामिक तापमान पैमाने पर काल्पनिक ऊपरी सीमाएँ

संदर्भ

↑ ^1.0 ^1.1 ^1.2 "थर्मोडायनामिक तापमान की इकाई (केल्विन)". SI Brochure, 8th edition. Bureau International des Poids et Mesures. 13 March 2010 [1967]. Section 2.1.1.5. Archived from the original on 7 October 2014. Retrieved 20 June 2017. Note: The triple point of water is 0.01 °C, not 0 °C; thus 0 K is −2890.15 °C, not −273.16 °C.
↑ Arora, C. P. (2001). ऊष्मप्रवैगिकी. Tata McGraw-Hill. Table 2.4 page 43. ISBN 978-0-07-462014-4.
↑ "SI Brochure: The International System of Units (SI)". Bureau international des poids et mesures. Retrieved 2022-02-08.
↑ Zielinski, Sarah (1 January 2008). "परम शून्य". Smithsonian Institution. Archived from the original on 1 April 2013. Retrieved 26 January 2012.
↑ Masanes, Lluís; Oppenheim, Jonathan (14 March 2017), "A general derivation and quantification of the third law of thermodynamics", Nature Communications, 8 (14538): 14538, arXiv:1412.3828, Bibcode:2017NatCo...814538M, doi:10.1038/ncomms14538, PMC 5355879, PMID 28290452
↑ Donley, Elizabeth A.; Claussen, Neil R.; Cornish, Simon L.; Roberts, Jacob L.; Cornell, Eric A.; Wieman, Carl E. (2001). "Dynamics of collapsing and exploding Bose–Einstein condensates". Nature. 412 (6844): 295–299. arXiv:cond-mat/0105019. Bibcode:2001Natur.412..295D. doi:10.1038/35085500. PMID 11460153. S2CID 969048.
↑ Clark, Ronald W. "Einstein: The Life and Times" (Avon Books, 1971) pp. 408–9 ISBN 0-380-01159-X
↑ "निरपेक्ष शून्य के पास पदार्थ की नई अवस्था देखी गई". NIST. Archived from the original on 1 June 2010.
↑ Levi, Barbara Goss (2001). "Cornell, Ketterle, and Wieman Share Nobel Prize for Bose–Einstein Condensates". Search & Discovery. Physics Today online. Archived from the original on 24 October 2007. Retrieved 26 January 2008.
↑ Leanhardt, A. E.; Pasquini, TA; Saba, M; Schirotzek, A; Shin, Y; Kielpinski, D; Pritchard, DE; Ketterle, W (2003). "Cooling Bose–Einstein Condensates Below 500 Picokelvin" (PDF). Science. 301 (5639): 1513–1515. Bibcode:2003Sci...301.1513L. doi:10.1126/science.1088827. PMID 12970559. S2CID 30259606. Archived (PDF) from the original on 2022-10-09.
↑ ^11.0 ^11.1 Chase, Scott. "Below Absolute Zero -What Does Negative Temperature Mean?". The Physics and Relativity FAQ. Archived from the original on 15 August 2011. Retrieved 2 July 2010.
↑ Merali, Zeeya (2013). "क्वांटम गैस परम शून्य से नीचे चली जाती है". Nature. doi:10.1038/nature.2013.12146. S2CID 124101032.
↑ Stanford, John Frederick (1892). अंग्रेजी शब्दों और वाक्यांशों का स्टैनफोर्ड डिक्शनरी.
↑ Boyle, Robert (1665). ठंड को छूने वाले नए प्रयोग और अवलोकन.
↑ ^15.0 ^15.1 Chisholm, Hugh, ed. (1911). "Cold" . Encyclopædia Britannica (in English) (11th ed.). Cambridge University Press.
↑ Talbot, G.R.; Pacey, A.C. (1972). "गुइलौमे एमोंटोंस के कार्य में ऊष्मप्रवैगिकी के पूर्ववर्ती". Centaurus. 16 (1): 20–40. Bibcode:1972Cent...16...20T. doi:10.1111/j.1600-0498.1972.tb00163.x.
↑ Essays Medical and Philosophical, p. PA291, at Google Books
↑ Lambert, Johann Heinrich (1779). पायरोमेट्री. Berlin. OCLC 165756016.
↑ J. Dalton (1802), "Essay II. On the force of steam or vapour from water and various other liquids, both in vacuum and in air" and Essay IV. "On the expansion of elastic fluids by heat," Memoirs of the Literary and Philosophical Society of Manchester, vol. 8, pt. 2, pp. 550–74, 595–602.
↑ Gay-Lussac, J. L. (1802), "Recherches sur la dilatation des gaz et des vapeurs", Annales de Chimie, XLIII: 137. English translation (extract).
↑ Thomson, William (1848). "ऊष्मा की प्रेरक शक्ति के कार्नाट के सिद्धांत पर स्थापित एक निरपेक्ष थर्मोमेट्रिक स्केल पर, और रेग्नॉल्ट के प्रेक्षणों से गणना की गई।". Proceedings of the Cambridge Philosophical Society. 1: 66–71.
↑ Newcomb, Simon (1906), A Compendium of Spherical Astronomy, New York: The Macmillan Company, p. 175, OCLC 64423127
↑ {{cite web |url=https://www.youtube.com/watch?v=mTFRgosx4aQ&t=894s | archive-url=https://web.archive.org/web/20170406015107/https://www.youtube.com/watch?v=mTFRgosx4aQ%7C archive-date=2017-04-06 | url-status=dead|title=पूर्ण शून्य - पीबीएस नोवा वृत्तचित्र (पूरी लंबाई)|newspaper=YouTube |access-date= 23 November 2016}
↑ Cryogenics. Scienceclarified.com. Retrieved on 22 July 2012.
↑ "The Nobel Prize in Physics 1913: Heike Kamerlingh Onnes". Nobel Media AB. Retrieved 24 April 2012.
↑ Kruszelnicki, Karl S. (25 September 2003). "ब्रह्मांड का सबसे ठंडा स्थान 1". Australian Broadcasting Corporation. Retrieved 24 September 2012.
↑ "What's the temperature of space?". The Straight Dope. 3 August 2004. Retrieved 24 September 2012.
↑ John, Anslyn J. (25 August 2021). "ब्रह्मांड के निर्माण खंड". HTS Teologiese Studies/Theological Studies. 77 (3). doi:10.4102/hts.v77i3.6831. S2CID 238730757.
↑ "History of temperature changes in the Universe revealed—First measurement using the Sunyaev-Zeldovich effect" (in English). Kavli Institute for the Physics and Mathematics of the Universe. 10 November 2020.
↑ Zu, H.; Dai, W.; de Waele, A.T.A.M. (2022). "Development of Dilution refrigerators – A review". Cryogenics. 121. Bibcode:2022Cryo..121....1Z. doi:10.1016/j.cryogenics.2021.103390. ISSN 0011-2275. S2CID 244005391.
↑ Catchpole, Heather (4 September 2008). "Cosmos Online – Verging on absolute zero". Archived from the original on 22 November 2008.
↑ Knuuttila, Tauno (2000). रोडियाम में परमाणु चुंबकत्व और अतिचालकता. Espoo, Finland: Helsinki University of Technology. ISBN 978-951-22-5208-4. Archived from the original on 28 April 2001. Retrieved 11 February 2008.
↑ "कम तापमान का विश्व रिकॉर्ड" (Press release). Low Temperature Laboratory, Teknillinen Korkeakoulu. 8 December 2000. Archived from the original on 18 February 2008. Retrieved 11 February 2008.
↑ Sahai, Raghvendra; Nyman, Lars-Åke (1997). "The Boomerang Nebula: The Coldest Region of the Universe?". The Astrophysical Journal. 487 (2): L155–L159. Bibcode:1997ApJ...487L.155S. doi:10.1086/310897. hdl:2014/22450. S2CID 121465475.
↑ "Mysterious Sedna | Science Mission Directorate". science.nasa.gov. Retrieved 2022-11-25.
↑ "अंतरिक्ष में जीवन और भौतिक विज्ञान में ईएसए के भविष्य के कार्यक्रम के लिए वैज्ञानिक परिप्रेक्ष्य" (PDF). esf.org. Archived from the original (PDF) on 6 October 2014. Retrieved 28 March 2014.
↑ "अंतरिक्ष में परमाणु क्वांटम सेंसर" (PDF). University of California, Los Angeles. Archived (PDF) from the original on 2022-10-09.
↑ "परमाणु रिकॉर्ड तापमान तक पहुँचते हैं, पूर्ण शून्य से अधिक ठंडा". livescience.com. 3 January 2013.
↑ "CUORE: The Coldest Heart in the Known Universe". INFN Press Release. Retrieved 21 October 2014.
↑ "एमआईटी की टीम ने बनाया अल्ट्राकोल्ड अणु". Massachusetts Institute of Technology, Massachusetts, Cambridge. Archived from the original on 18 August 2015. Retrieved 10 June 2015.
↑ "अब तक का सबसे ठंडा विज्ञान अंतरिक्ष स्टेशन पहुंचा". Science | AAAS (in English). 5 September 2017. Retrieved 24 September 2017.
↑ "शीत परमाणु प्रयोगशाला मिशन". Jet Propulsion Laboratory. NASA. 2017. Archived from the original on 2013-03-29. Retrieved 22 December 2016.
↑ "कोल्ड एटम लेबोरेटरी एटॉमिक डांस बनाती है". NASA News. 26 September 2014. Retrieved 21 May 2015.
↑ Deppner, Christian; Herr, Waldemar; Cornelius, Merle; Stromberger, Peter; Sternke, Tammo; Grzeschik, Christoph; Grote, Alexander; Rudolph, Jan; Herrmann, Sven; Krutzik, Markus; Wenzlawski, André (2021-08-30). "कलेक्टिव-मोड एन्हांस्ड मैटर-वेव ऑप्टिक्स". Physical Review Letters (in English). 127 (10): 100401. Bibcode:2021PhRvL.127j0401D. doi:10.1103/PhysRevLett.127.100401. ISSN 0031-9007. PMID 34533345. S2CID 237396804.

अग्रिम पठन

Herbert B. Callen (1960). "Chapter 10". Thermodynamics. New York: John Wiley & Sons. ISBN 978-0-471-13035-2. OCLC 535083.
Herbert B. Callen (1985). Thermodynamics and an Introduction to Thermostatistics (Second ed.). New York: John Wiley & Sons. ISBN 978-0-471-86256-7.
E.A. Guggenheim (1967). Thermodynamics: An Advanced Treatment for Chemists and Physicists (Fifth ed.). Amsterdam: North Holland Publishing. ISBN 978-0-444-86951-7. OCLC 324553.
George Stanley Rushbrooke (1949). Introduction to Statistical Mechanics. Oxford: Clarendon Press. OCLC 531928.
BIPM Mise en pratique - Kelvin - Appendix 2 - SI Brochure

बाहरी संबंध

"Absolute zero": a two part NOVA episode originally aired January 2008
"What is absolute zero?" Lansing State Journal

[sib2115-1] 1.0 ^1.1 ^1.2 "थर्मोडायनामिक तापमान की इकाई (केल्विन)". SI Brochure, 8th edition. Bureau International des Poids et Mesures. 13 March 2010 [1967]. Section 2.1.1.5. Archived from the original on 7 October 2014. Retrieved 20 June 2017. Note: The triple point of water is 0.01 °C, not 0 °C; thus 0 K is −2890.15 °C, not −273.16 °C.

[arora-2] Arora, C. P. (2001). ऊष्मप्रवैगिकी. Tata McGraw-Hill. Table 2.4 page 43. ISBN 978-0-07-462014-4.

[3] "SI Brochure: The International System of Units (SI)". Bureau international des poids et mesures. Retrieved 2022-02-08.

[4] Zielinski, Sarah (1 January 2008). "परम शून्य". Smithsonian Institution. Archived from the original on 1 April 2013. Retrieved 26 January 2012.

[5] Masanes, Lluís; Oppenheim, Jonathan (14 March 2017), "A general derivation and quantification of the third law of thermodynamics", Nature Communications, 8 (14538): 14538, arXiv:1412.3828, Bibcode:2017NatCo...814538M, doi:10.1038/ncomms14538, PMC 5355879, PMID 28290452

[6] Donley, Elizabeth A.; Claussen, Neil R.; Cornish, Simon L.; Roberts, Jacob L.; Cornell, Eric A.; Wieman, Carl E. (2001). "Dynamics of collapsing and exploding Bose–Einstein condensates". Nature. 412 (6844): 295–299. arXiv:cond-mat/0105019. Bibcode:2001Natur.412..295D. doi:10.1038/35085500. PMID 11460153. S2CID 969048.

[7] Clark, Ronald W. "Einstein: The Life and Times" (Avon Books, 1971) pp. 408–9 ISBN 0-380-01159-X

[8] "निरपेक्ष शून्य के पास पदार्थ की नई अवस्था देखी गई". NIST. Archived from the original on 1 June 2010.

[9] Levi, Barbara Goss (2001). "Cornell, Ketterle, and Wieman Share Nobel Prize for Bose–Einstein Condensates". Search & Discovery. Physics Today online. Archived from the original on 24 October 2007. Retrieved 26 January 2008.

[10] Leanhardt, A. E.; Pasquini, TA; Saba, M; Schirotzek, A; Shin, Y; Kielpinski, D; Pritchard, DE; Ketterle, W (2003). "Cooling Bose–Einstein Condensates Below 500 Picokelvin" (PDF). Science. 301 (5639): 1513–1515. Bibcode:2003Sci...301.1513L. doi:10.1126/science.1088827. PMID 12970559. S2CID 30259606. Archived (PDF) from the original on 2022-10-09.

[Chase-11] 11.0 ^11.1 Chase, Scott. "Below Absolute Zero -What Does Negative Temperature Mean?". The Physics and Relativity FAQ. Archived from the original on 15 August 2011. Retrieved 2 July 2010.

[12] Merali, Zeeya (2013). "क्वांटम गैस परम शून्य से नीचे चली जाती है". Nature. doi:10.1038/nature.2013.12146. S2CID 124101032.

[13] Stanford, John Frederick (1892). अंग्रेजी शब्दों और वाक्यांशों का स्टैनफोर्ड डिक्शनरी.

[14] Boyle, Robert (1665). ठंड को छूने वाले नए प्रयोग और अवलोकन.

[AS2016-15] 15.0 ^15.1 Chisholm, Hugh, ed. (1911). "Cold" . Encyclopædia Britannica (in English) (11th ed.). Cambridge University Press.

[16] Talbot, G.R.; Pacey, A.C. (1972). "गुइलौमे एमोंटोंस के कार्य में ऊष्मप्रवैगिकी के पूर्ववर्ती". Centaurus. 16 (1): 20–40. Bibcode:1972Cent...16...20T. doi:10.1111/j.1600-0498.1972.tb00163.x.

[17] Essays Medical and Philosophical, p. PA291, at Google Books

[18] Lambert, Johann Heinrich (1779). पायरोमेट्री. Berlin. OCLC 165756016.

[19] J. Dalton (1802), "Essay II. On the force of steam or vapour from water and various other liquids, both in vacuum and in air" and Essay IV. "On the expansion of elastic fluids by heat," Memoirs of the Literary and Philosophical Society of Manchester, vol. 8, pt. 2, pp. 550–74, 595–602.

[20] Gay-Lussac, J. L. (1802), "Recherches sur la dilatation des gaz et des vapeurs", Annales de Chimie, XLIII: 137. English translation (extract).

[21] Thomson, William (1848). "ऊष्मा की प्रेरक शक्ति के कार्नाट के सिद्धांत पर स्थापित एक निरपेक्ष थर्मोमेट्रिक स्केल पर, और रेग्नॉल्ट के प्रेक्षणों से गणना की गई।". Proceedings of the Cambridge Philosophical Society. 1: 66–71.

[22] Newcomb, Simon (1906), A Compendium of Spherical Astronomy, New York: The Macmillan Company, p. 175, OCLC 64423127

[MyUser_YouTube_November_23_2016c-23] {{cite web |url=https://www.youtube.com/watch?v=mTFRgosx4aQ&t=894s | archive-url=https://web.archive.org/web/20170406015107/https://www.youtube.com/watch?v=mTFRgosx4aQ%7C archive-date=2017-04-06 | url-status=dead|title=पूर्ण शून्य - पीबीएस नोवा वृत्तचित्र (पूरी लंबाई)|newspaper=YouTube |access-date= 23 November 2016}

[24] Cryogenics. Scienceclarified.com. Retrieved on 22 July 2012.

[nobel-25] "The Nobel Prize in Physics 1913: Heike Kamerlingh Onnes". Nobel Media AB. Retrieved 24 April 2012.

[26] Kruszelnicki, Karl S. (25 September 2003). "ब्रह्मांड का सबसे ठंडा स्थान 1". Australian Broadcasting Corporation. Retrieved 24 September 2012.

[27] "What's the temperature of space?". The Straight Dope. 3 August 2004. Retrieved 24 September 2012.

[28] John, Anslyn J. (25 August 2021). "ब्रह्मांड के निर्माण खंड". HTS Teologiese Studies/Theological Studies. 77 (3). doi:10.4102/hts.v77i3.6831. S2CID 238730757.

[29] "History of temperature changes in the Universe revealed—First measurement using the Sunyaev-Zeldovich effect" (in English). Kavli Institute for the Physics and Mathematics of the Universe. 10 November 2020.

[30] Zu, H.; Dai, W.; de Waele, A.T.A.M. (2022). "Development of Dilution refrigerators – A review". Cryogenics. 121. Bibcode:2022Cryo..121....1Z. doi:10.1016/j.cryogenics.2021.103390. ISSN 0011-2275. S2CID 244005391.

[31] Catchpole, Heather (4 September 2008). "Cosmos Online – Verging on absolute zero". Archived from the original on 22 November 2008.

[32] Knuuttila, Tauno (2000). रोडियाम में परमाणु चुंबकत्व और अतिचालकता. Espoo, Finland: Helsinki University of Technology. ISBN 978-951-22-5208-4. Archived from the original on 28 April 2001. Retrieved 11 February 2008.

[33] "कम तापमान का विश्व रिकॉर्ड" (Press release). Low Temperature Laboratory, Teknillinen Korkeakoulu. 8 December 2000. Archived from the original on 18 February 2008. Retrieved 11 February 2008.

[34] Sahai, Raghvendra; Nyman, Lars-Åke (1997). "The Boomerang Nebula: The Coldest Region of the Universe?". The Astrophysical Journal. 487 (2): L155–L159. Bibcode:1997ApJ...487L.155S. doi:10.1086/310897. hdl:2014/22450. S2CID 121465475.

[35] "Mysterious Sedna | Science Mission Directorate". science.nasa.gov. Retrieved 2022-11-25.

[36] "अंतरिक्ष में जीवन और भौतिक विज्ञान में ईएसए के भविष्य के कार्यक्रम के लिए वैज्ञानिक परिप्रेक्ष्य" (PDF). esf.org. Archived from the original (PDF) on 6 October 2014. Retrieved 28 March 2014.

[37] "अंतरिक्ष में परमाणु क्वांटम सेंसर" (PDF). University of California, Los Angeles. Archived (PDF) from the original on 2022-10-09.

[38] "परमाणु रिकॉर्ड तापमान तक पहुँचते हैं, पूर्ण शून्य से अधिक ठंडा". livescience.com. 3 January 2013.

[39] "CUORE: The Coldest Heart in the Known Universe". INFN Press Release. Retrieved 21 October 2014.

[40] "एमआईटी की टीम ने बनाया अल्ट्राकोल्ड अणु". Massachusetts Institute of Technology, Massachusetts, Cambridge. Archived from the original on 18 August 2015. Retrieved 10 June 2015.

[41] "अब तक का सबसे ठंडा विज्ञान अंतरिक्ष स्टेशन पहुंचा". Science | AAAS (in English). 5 September 2017. Retrieved 24 September 2017.

[NASA_Cold_Atom_Laboratory_Mission-42] "शीत परमाणु प्रयोगशाला मिशन". Jet Propulsion Laboratory. NASA. 2017. Archived from the original on 2013-03-29. Retrieved 22 December 2016.

[CALnasa-43] "कोल्ड एटम लेबोरेटरी एटॉमिक डांस बनाती है". NASA News. 26 September 2014. Retrieved 21 May 2015.

[44] Deppner, Christian; Herr, Waldemar; Cornelius, Merle; Stromberger, Peter; Sternke, Tammo; Grzeschik, Christoph; Grote, Alexander; Rudolph, Jan; Herrmann, Sven; Krutzik, Markus; Wenzlawski, André (2021-08-30). "कलेक्टिव-मोड एन्हांस्ड मैटर-वेव ऑप्टिक्स". Physical Review Letters (in English). 127 (10): 100401. Bibcode:2021PhRvL.127j0401D. doi:10.1103/PhysRevLett.127.100401. ISSN 0031-9007. PMID 34533345. S2CID 237396804.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

@@ Line 4: / Line 4: @@
 [[File:CelsiusKelvin.svg|thumb|right|150px|शून्य केल्विन (−273.15 डिग्री सेल्सियस) को पूर्ण शून्य के रूप में परिभाषित किया गया है।]]निरपेक्ष शून्य [[थर्मोडायनामिक तापमान|उष्मगतिशील तापमान]] पैमाने की सबसे निचली सीमा है, एक ऐसी अवस्था जिस पर ठंडी [[आदर्श गैस]] की [[तापीय धारिता]] और [[एन्ट्रापी]] अपने न्यूनतम मान तक पहुँच जाती है, जिसे शून्य [[केल्विन]] के रूप में लिया जाता है। प्रकृति के मौलिक कणों में न्यूनतम कंपन गति होती है, जो केवल क्वांटम यांत्रिक, [[शून्य-बिंदु ऊर्जा]]-प्रेरित कण गति को बनाए रखती है। सैद्धांतिक तापमान [[आदर्श गैस कानून|आदर्श गैस नियम]]  को बहिर्गमन करके निर्धारित किया जाता है; अंतरराष्ट्रीय समझौते के अनुसार, पूर्ण शून्य को [[ सेल्सीयस ]] पैमाने ([[इकाइयों की अंतर्राष्ट्रीय प्रणाली]]) पर -273.15 डिग्री के रूप में लिया जाता है,<ref name=sib2115>{{cite web|title=थर्मोडायनामिक तापमान की इकाई (केल्विन)|work=SI Brochure, 8th edition |at=Section 2.1.1.5 |url=http://www.bipm.org/en/publications/si-brochure/kelvin.html |publisher=Bureau International des Poids et Mesures |date=13 March 2010 |orig-year=1967 |access-date=20 June 2017 |url-status=dead |archive-url=https://web.archive.org/web/20141007053944/http://www.bipm.org/en/publications/si-brochure/kelvin.html |archive-date=7 October 2014 }} '''Note''': The triple point of water is 0.01&nbsp;°C, not 0&nbsp;°C; thus 0&nbsp;K is −2890.15&nbsp;°C, not −273.16&nbsp;°C.</ref><ref name="arora">{{cite book|title=ऊष्मप्रवैगिकी|first1=C. P.|last1=Arora|publisher=Tata McGraw-Hill |year=2001|isbn=978-0-07-462014-4|at=Table 2.4 page 43|url=https://books.google.com/books?id=w8GhW3J8RHIC&pg=PA43}}</ref><ref>{{Cite web |title=SI Brochure: The International System of Units (SI) |url=https://www.bipm.org/en/publications/si-brochure |access-date=2022-02-08 |website=Bureau international des poids et mesures}}</ref> जो [[फ़ारेनहाइट]] पैमाने पर -459.67 डिग्री के बराबर है (संयुक्त राज्य प्रथागत इकाइयाँ या शाही इकाइयाँ)।<ref>{{Cite web|url=http://www.smithsonianmag.com/science-nature/absolute-zero-200801.html|last1=Zielinski|first1=Sarah|date=1 January 2008|title=परम शून्य|publisher=Smithsonian Institution|access-date=26 January 2012|archive-url=https://web.archive.org/web/20130401180715/http://www.smithsonianmag.com/science-nature/absolute-zero-200801.html|archive-date=1 April 2013|url-status=dead}}</ref> संबंधित केल्विन और [[रैंकिन स्केल]] तापमान स्केल परिभाषा के अनुसार अपने शून्य बिंदु को पूर्ण शून्य पर उपयुक्त करते हैं
-इसे सामान्यतः सबसे कम संभव तापमान के रूप में माना जाता है, किन्तु  यह सबसे कम संभव एन्थैल्पी अवस्था नहीं है, क्योंकि ठंडा होने पर सभी वास्तविक पदार्थ आदर्श गैस से निकलने लगते हैं, क्योंकि वे अवस्था परिवर्तन से पहले तरल और फिर ठोस में बदल जाते हैं; और [[वाष्पीकरण की तापीय धारिता]] (गैस से तरल) और [[संलयन की तापीय धारिता]] (तरल से ठोस) का योग, आदर्श गैस के तापीय धारिता में परम शून्य परिवर्तन से अधिक है। [[क्वांटम यांत्रिकी]] | क्वांटम-मैकेनिकल विवरण में, पूर्ण शून्य पर पदार्थ (ठोस) इसकी जमीनी अवस्था में है, जो सबसे कम [[आंतरिक ऊर्जा]] का बिंदु है।
+इसे सामान्यतः सबसे कम संभव तापमान के रूप में माना जाता है, किन्तु  यह सबसे कम संभव एन्थैल्पी अवस्था नहीं है, क्योंकि ठंडा होने पर सभी वास्तविक पदार्थ आदर्श गैस  से प्रस्थान करना शुरू कर देते हैं क्योंकि वे अवस्था परिवर्तन से पहले तरल और फिर ठोस में बदल जाते हैं; और [[वाष्पीकरण की तापीय धारिता]] (गैस से तरल) और [[संलयन की तापीय धारिता]] (तरल से ठोस) का योग, आदर्श गैस के तापीय धारिता में परम शून्य परिवर्तन से अधिक है। [[क्वांटम यांत्रिकी]] विवरण में, पूर्ण शून्य पर पदार्थ (ठोस) इसकी जमीनी अवस्था में है, जो सबसे कम [[आंतरिक ऊर्जा]] का बिंदु है।
-[[ऊष्मप्रवैगिकी के नियम]]ों से संकेत मिलता है कि पूर्ण शून्य को केवल ऊष्मप्रवैगिक साधनों का उपयोग करके नहीं पहुंचा जा सकता है, क्योंकि ठंडा होने वाले पदार्थ का तापमान शीतलन एजेंट के तापमान के समान रूप से पहुंचता है।<ref>{{ Citation | last1 = Masanes | first1 = Lluís | last2 = Oppenheim | first2 = Jonathan | author2-link = Jonathan Oppenheim | date = 14 March 2017 | title = A general derivation and quantification of the third law of thermodynamics | journal = Nature Communications | volume = 8 | pages = 14538 | number = 14538 | doi = 10.1038/ncomms14538 | pmid = 28290452 | pmc = 5355879 | arxiv = 1412.3828 | bibcode = 2017NatCo...814538M }}</ref> यहां तक कि पूर्ण शून्य पर एक प्रणाली, यदि इसे किसी तरह प्राप्त किया जा सकता है, तब भी क्वांटम मैकेनिकल शून्य-बिंदु ऊर्जा, इसकी जमीनी स्थिति की ऊर्जा पूर्ण शून्य पर होगी; जमीनी अवस्था की [[गतिज ऊर्जा]] को हटाया नहीं जा सकता।
+[[ऊष्मप्रवैगिकी के नियम|ऊष्मप्रवैगिकी के नियमों]] से संकेत मिलता है कि पूर्ण शून्य को केवल ऊष्मप्रवैगिक साधनों का उपयोग करके नहीं पहुंचा जा सकता है, क्योंकि ठंडा होने वाले पदार्थ का तापमान शीतलन एजेंट के तापमान के समान रूप से पहुंचता है।<ref>{{ Citation | last1 = Masanes | first1 = Lluís | last2 = Oppenheim | first2 = Jonathan | author2-link = Jonathan Oppenheim | date = 14 March 2017 | title = A general derivation and quantification of the third law of thermodynamics | journal = Nature Communications | volume = 8 | pages = 14538 | number = 14538 | doi = 10.1038/ncomms14538 | pmid = 28290452 | pmc = 5355879 | arxiv = 1412.3828 | bibcode = 2017NatCo...814538M }}</ref> यहां तक कि पूर्ण शून्य पर एक प्रणाली यदि इसे किसी तरह प्राप्त किया जा सकता है, तब भी क्वांटम यांत्रिक शून्य-बिंदु ऊर्जा, इसकी जमीनी स्थिति की ऊर्जा पूर्ण शून्य पर होगी; जमीनी अवस्था की [[गतिज ऊर्जा]] को हटाया नहीं जा सकता।
-वैज्ञानिक और प्रौद्योगिकीविद् नियमित रूप से पूर्ण शून्य के करीब तापमान प्राप्त करते हैं, जहां पदार्थ बोस-आइंस्टीन कंडेनसेट, [[ अतिचालकता ]] और [[ अति तरल ]] जैसे क्वांटम प्रभाव प्रदर्शित करता है।
+वैज्ञानिक और प्रौद्योगिकीविद् नियमित रूप से पूर्ण शून्य के करीब तापमान प्राप्त करते हैं, जहां पदार्थ बोस-आइंस्टीन संघनन, [[ अतिचालकता ]] और [[ अति तरल ]] जैसे क्वांटम प्रभाव प्रदर्शित करता है।
 ===== उष्मगतिशील्स पूर्ण शून्य के पास =====
-तापमान के पास {{convert|0|K|C F}}, लगभग सभी आणविक गति बंद हो जाती है और ΔS = 0 किसी भी रूद्धोष्म प्रक्रिया के लिए, जहां S एंट्रॉपी है। ऐसी परिस्थिति में, शुद्ध पदार्थ (आदर्श रूप से) टी → 0 के रूप में बिना किसी संरचनात्मक खामियों के [[सही क्रिस्टल]] बना सकते हैं। उष्मगतिशील्स के तीसरे नियम का [[मैक्स प्लैंक]] का शक्तिशाली  रूप बताता है कि एक पूर्ण क्रिस्टल की एन्ट्रापी पूर्ण शून्य पर गायब हो जाती है। मूल [[वाल्थर नर्नस्ट]] [[नर्नस्ट ताप प्रमेय]] अशक्त  और कम विवादास्पद प्रमाणित  करता है कि किसी भी इज़ोटेर्माल प्रक्रिया के लिए एन्ट्रॉपी परिवर्तन शून्य तक पहुंच जाता है क्योंकि टी → 0:
+{{convert|0|K|C F}} के पास तापमान पर लगभग सभी आणविक गति समाप्त हो जाती है और किसी भी रूद्धोष्म प्रक्रिया के लिए ΔS = 0, जहां S एंट्रॉपी है। ऐसी परिस्थिति में, शुद्ध पदार्थ (आदर्श रूप से) ''T'' → 0 के रूप में बिना किसी संरचनात्मक खामियों के [[सही क्रिस्टल]] बना सकते हैं। उष्मगतिशील्स के तीसरे नियम का [[मैक्स प्लैंक]] का शक्तिशाली  रूप बताता है कि एक पूर्ण क्रिस्टल की एन्ट्रापी पूर्ण शून्य पर गायब हो जाती है। मूल [[वाल्थर नर्नस्ट]] [[नर्नस्ट ताप प्रमेय]] अशक्त  और कम विवादास्पद प्रमाणित  करता है कि किसी भी इज़ोटेर्माल प्रक्रिया के लिए एन्ट्रॉपी परिवर्तन शून्य तक पहुंच जाता है क्योंकि ''T'' → 0:
 :<math> \lim_{T \to 0} \Delta S = 0 </math>
-निहितार्थ यह है कि एक आदर्श क्रिस्टल की एन्ट्रापी एक स्थिर मान तक पहुँचती है। एडियाबैट निरंतर एन्ट्रॉपी वाला एक राज्य है, जिसे सामान्यतः एक वक्र के रूप में एक वक्र के रूप में प्रतिनिधित्व किया जाता है जो इज़ोटेर्म और आइसोबार के समान होता है।
+निहितार्थ यह है कि एक आदर्श क्रिस्टल की एन्ट्रापी एक स्थिर मान तक पहुँचती है। रुद्धोष्म निरंतर एन्ट्रॉपी वाली एक स्थिति है, जिसे सामान्यतः एक वक्र के रूप में एक वक्र के रूप में प्रतिनिधित्व किया जाता है जो समताप रेखा और आइसोबार के समान होता है।
 <blockquote>ऊष्मप्रवैगिकी का तीसरा नियम समतापीय प्रक्रिया T = 0 की पहचान रुद्धोष्म S = 0 के साथ संयोग के रूप में करता है, चूंकि अन्य समतापी और रुद्धोष्म भिन्न हैं। चूँकि कोई भी दो रुद्धोष्म प्रतिच्छेद नहीं करते हैं, कोई भी अन्य रुद्धोष्म टी = 0 समताप रेखा को रेखा–रेखा प्रतिच्छेद नहीं कर सकता है। परिणाम स्वरुप  गैर-शून्य तापमान पर प्रारंभिकू की गई कोई एडियाबेटिक प्रक्रिया शून्य तापमान तक नहीं पहुंच सकती है। (≈ कालेन, पीपी. 189–190)</blockquote>
-एक आदर्श क्रिस्टल वह है जिसमें आंतरिक [[जाली (समूह)]] संरचना सभी दिशाओं में निर्बाध रूप से फैली हुई है। पूर्ण क्रम को तीन (सामान्यतः [[ओर्थोगोनालिटी]] नहीं) कार्टेशियन समन्वय प्रणाली के साथ ट्रांसलेशनल [[समरूपता]] द्वारा दर्शाया जा सकता है। संरचना का प्रत्येक जाली तत्व अपने उचित स्थान पर है, चाहे वह एक परमाणु हो या आणविक समूह। [[रासायनिक पदार्थ]]ों के लिए जो दो (या अधिक) स्थिर क्रिस्टलीय रूपों में उपस्थित होते हैं, जैसे कि [[कार्बन]] के लिए हीरा और [[ग्रेफाइट]], एक प्रकार की रासायनिक विकृति होती है। यह प्रश्न बना रहता है कि क्या दोनों के पास T = 0 पर शून्य एंट्रोपी हो सकती है, तथापि  प्रत्येक पूरी तरह से आदेशित हो।
+एक आदर्श क्रिस्टल वह है जिसमें आंतरिक [[जाली (समूह)]] संरचना सभी दिशाओं में निर्बाध रूप से फैली हुई है। पूर्ण क्रम को तीन (सामान्यतः [[ओर्थोगोनालिटी]] नहीं) कार्टेशियन समन्वय प्रणाली के साथ ट्रांसलेशनल [[समरूपता]] द्वारा दर्शाया जा सकता है। संरचना का प्रत्येक जाली तत्व अपने उचित स्थान पर है, चाहे वह एक परमाणु हो या आणविक समूह। ऐसे [[रासायनिक पदार्थ|रासायनिक पदार्थों]] के लिए जो दो (या अधिक) स्थिर क्रिस्टलीय रूपों में उपस्थित होते हैं, जैसे कि [[कार्बन]] के लिए हीरा और [[ग्रेफाइट]], एक प्रकार की रासायनिक विकृति होती है। यह प्रश्न बना रहता है कि क्या दोनों के पास T = 0 पर शून्य एंट्रोपी हो सकती है, तथापि  प्रत्येक पूरी तरह से आदेशित हो।
-अभ्यास में बिल्कुल सही क्रिस्टल कभी नहीं होते हैं; खामियां, और यहां तक कि संपूर्ण अनाकार सामग्री समावेशन, कम तापमान पर जम सकते हैं और जम जाते हैं, इसलिए अधिक स्थिर अवस्थाओं में संक्रमण नहीं होता है।
+अभ्यास में बिल्कुल सही क्रिस्टल कभी नहीं होते हैं; खामियां, और यहां तक कि संपूर्ण अनाकार सामग्री समावेशन, कम तापमान पर "जमे हुए" हो सकते हैं इसलिए अधिक स्थिर अवस्थाओं में संक्रमण नहीं होता है।
-[[डेबी मॉडल]] का उपयोग करते हुए, शुद्ध क्रिस्टल की विशिष्ट ताप क्षमता और एन्ट्रापी टी के समानुपाती होते हैं<sup>3</sup>, जबकि थैलेपी और [[रासायनिक क्षमता]] T के समानुपाती होते हैं<sup>4</उप>। (गगेनहाइम, पृ. 111) ये मात्राएँ अपने टी = 0 सीमित मूल्यों की ओर गिरती हैं और शून्य ढलान के साथ पहुँचती हैं। कम से कम विशिष्ट तापों के लिए, सीमित मान स्वयं निश्चित रूप से शून्य है, जैसा कि 10 K से नीचे के प्रयोगों से पता चलता है। यहां तक कि कम विस्तृत [[आइंस्टीन ठोस]] भी विशिष्ट तापों में इस अजीब गिरावट को दर्शाता है। वास्तव में, केवल क्रिस्टल के ही नहीं, किंतु सभी विशिष्ट ऊष्माएं पूर्ण शून्य पर गायब हो जाती हैं। इसी तरह [[थर्मल विस्तार]] के गुणांक के लिए। मैक्सवेल संबंध|मैक्सवेल के संबंध बताते हैं कि कई अन्य राशियां भी लुप्त हो जाती हैं। ये घटनाएं अप्रत्याशित थीं।
+[[डेबी मॉडल]] का उपयोग करते हुए, एक शुद्ध क्रिस्टल की विशिष्ट ऊष्मा और एन्ट्रापी ''T'' <sup>3</sup> के समानुपाती होते हैं, जबकि थैलेपी और [[रासायनिक क्षमता]] ''T'' <sup>4</sup> के समानुपाती होते हैं । (गगेनहाइम, पृ. 111) ये मात्राएँ अपने टी = 0 सीमित मूल्यों की ओर गिरती हैं और शून्य ढलान के साथ पहुँचती हैं। कम से कम विशिष्ट तापों के लिए, सीमित मान स्वयं निश्चित रूप से शून्य है, जैसा कि 10 K से नीचे के प्रयोगों से पता चलता है। यहां तक कि कम विस्तृत [[आइंस्टीन ठोस]] भी विशिष्ट तापों में इस अजीब गिरावट को दर्शाता है। वास्तव में, केवल क्रिस्टल के ही नहीं, किंतु सभी विशिष्ट ऊष्माएं पूर्ण शून्य पर गायब हो जाती हैं। इसी तरह [[थर्मल विस्तार]] के गुणांक के लिए। मैक्सवेल संबंध|मैक्सवेल के संबंध बताते हैं कि कई अन्य राशियां भी लुप्त हो जाती हैं। ये घटनाएं अप्रत्याशित थीं।
 चूँकि [[गिब्स मुक्त ऊर्जा]] (G), एन्थैल्पी (H) और एन्ट्रॉपी में परिवर्तन के बीच संबंध है
 :<math> \Delta G = \Delta H - T \Delta S \,</math>
-इस प्रकार, जैसे-जैसे T घटता है, ΔG और ΔH एक-दूसरे की ओर बढ़ते हैं (जब तक ΔS परिबद्ध है)। प्रायोगिक रूप से, यह पाया गया है कि सभी सहज प्रक्रियाओं ([[रासायनिक प्रतिक्रिया]]ओं सहित) के परिणामस्वरूप जी में कमी आती है क्योंकि वे [[थर्मोडायनामिक संतुलन|उष्मगतिशील संतुलन]] की ओर बढ़ते हैं। यदि ΔS और/या T छोटे हैं, तो स्थिति ΔG < 0 का अर्थ हो सकता है कि ΔH < 0, जो एक उष्माक्षेपी प्रतिक्रिया का संकेत देगा। चूंकि, यह आवश्यक नहीं है; यदि TΔS शब्द अधिक  बड़ा है तो [[ एन्दोठेर्मिक ]] प्रतिक्रियाएं सहज रूप से आगे बढ़ सकती हैं।
+इस प्रकार, जैसे-जैसे T घटता है, ΔG और ΔH एक-दूसरे की ओर बढ़ते हैं (जब तक ΔS परिबद्ध है)। प्रायोगिक रूप से यह पाया गया है कि सभी सहज प्रक्रियाओं ([[रासायनिक प्रतिक्रिया]]ओं सहित) के परिणामस्वरूप जी में कमी आती है क्योंकि वे [[थर्मोडायनामिक संतुलन|उष्मगतिशील संतुलन]] की ओर बढ़ते हैं। यदि ΔS और/या T छोटे हैं, तो स्थिति ΔG < 0 का अर्थ  ΔH < 0 हो सकता है, जो एक उष्माक्षेपी प्रतिक्रिया का संकेत देगा। चूंकि, यह आवश्यक नहीं है; यदि TΔS शब्द अधिक  बड़ा है तो [[ एन्दोठेर्मिक | ऊष्माशोषी]] प्रतिक्रियाएं सहज रूप से आगे बढ़ सकती हैं।
-इसके अतिरिक्त, ΔG और ΔH के [[ यौगिक ]] के ढलान T = 0 पर अभिसरण करते हैं और शून्य के बराबर होते हैं। यह सुनिश्चित करता है कि ΔG और ΔH तापमान की अधिक  सीमा पर लगभग समान हैं और थॉमसन और बर्थेलॉट के अनुमानित [[अनुभववाद]] सिद्धांत को सही ठहराते हैं, जो बताता है कि एक प्रणाली जिस संतुलन की ओर बढ़ती है, वह वह है जो ऊष्मा की सबसे बड़ी मात्रा को विकसित करता है, अर्थात, एक वास्तविक प्रक्रिया सबसे अधिक [[एक्ज़ोथिर्मिक]] है। (कालेन, पीपी. 186-187)
+इसके अलावा, ΔG और ΔH के डेरिवेटिव के ढलान T = 0 पर अभिसरण करते हैं और शून्य के बराबर होते हैं। यह सुनिश्चित करता है कि ΔG और ΔH तापमान की काफी सीमा पर लगभग समान हैं और थॉमसन और बर्थेलॉट के अनुमानित अनुभवजन्य सिद्धांत को सही ठहराते हैं जो बताता है वह संतुलन अवस्था जिसके लिए एक प्रणाली आगे बढ़ती है वह सबसे बड़ी मात्रा में गर्मी विकसित करती है, अर्थात, एक वास्तविक प्रक्रिया सबसे अधिक उष्माक्षेपी है। (कालेन, पीपी. 186-187)
 एक मॉडल जो धातुओं में पूर्ण शून्य पर एक [[इलेक्ट्रॉन]] गैस के गुणों का अनुमान लगाता है, वह [[फर्मी गैस]] है। इलेक्ट्रॉन, [[फर्मियन]] होने के नाते, अलग-अलग क्वांटम अवस्थाओं में होने चाहिए, जो इलेक्ट्रॉनों को पूर्ण शून्य पर भी बहुत उच्च विशिष्ट [[वेग]] प्राप्त करने की ओर ले जाता है। अधिकतम ऊर्जा जो इलेक्ट्रॉनों में पूर्ण शून्य पर हो सकती है, [[फर्मी ऊर्जा]] कहलाती है। फर्मी तापमान को बोल्ट्जमैन स्थिरांक द्वारा विभाजित इस अधिकतम ऊर्जा के रूप में परिभाषित किया गया है, और धातुओं में पाए जाने वाले विशिष्ट इलेक्ट्रॉन घनत्वों के लिए 80,000 K के क्रम में है। फर्मी तापमान से अधिक  नीचे के तापमान के लिए, इलेक्ट्रॉन लगभग उसी तरह व्यवहार करते हैं जैसे पूर्ण शून्य पर। यह धातुओं के मौलिक [[समविभाजन प्रमेय]] की विफलता की व्याख्या करता है जो 19वीं शताब्दी के अंत में मौलिक भौतिकविदों से दूर हो गया था।
 == बोस-आइंस्टीन घनीभूत के साथ संबंध ==
-{{Main|Bose–Einstein condensate}}
+{{Main|बोस-आइंस्टीन घनीभूत}}
-[[File:Bose Einstein condensate.png|left|thumb|पूर्ण शून्य से ऊपर डिग्री के कुछ अरबवें हिस्से के तापमान पर [[ रूबिडीयाम ]] परमाणुओं की गैस का वेग-वितरण डेटा। बायां: बोस-आइंस्टीन कंडेनसेट के प्रकट होने से ठीक पहले। केंद्र: घनीभूत होने के तुरंत बाद। दाएं: आगे के वाष्पीकरण के बाद, लगभग शुद्ध घनीभूत का एक नमूना छोड़कर।]]बोस-आइंस्टीन कंडेनसेट (बीईसी) एक बाहरी क्षमता में सीमित रूप से परस्पर क्रिया करने वाले [[बोसॉन]] की तनु गैस की स्थिति है और तापमान को पूर्ण शून्य के करीब ठंडा किया जाता है। ऐसी परिस्थितियों में, बोसोन का एक बड़ा अंश बाहरी क्षमता की निम्नतम [[कितना राज्य]] पर कब्जा कर लेता है, जिस बिंदु पर [[मैक्रोस्कोपिक स्केल]] पर क्वांटम प्रभाव स्पष्ट हो जाते हैं।<ref>{{cite journal|journal=Nature|volume=412|pages=295–299|year=2001|title=Dynamics of collapsing and exploding Bose–Einstein condensates|pmid=11460153|issue=6844|doi=10.1038/35085500|arxiv = cond-mat/0105019 |bibcode = 2001Natur.412..295D|last1=Donley|first1=Elizabeth A.|last2=Claussen|first2=Neil R.|last3=Cornish|first3=Simon L.|last4=Roberts|first4=Jacob L.|last5=Cornell|first5=Eric A.|last6=Wieman|first6=Carl E.|s2cid=969048}}</ref>
+[[File:Bose Einstein condensate.png|left|thumb|पूर्ण शून्य से ऊपर डिग्री के कुछ अरबवें हिस्से के तापमान पर [[ रूबिडीयाम ]] परमाणुओं की गैस का वेग-वितरण डेटा। बायां: बोस-आइंस्टीन कंडेनसेट के प्रकट होने से ठीक पहले। केंद्र: घनीभूत होने के तुरंत बाद। दाएं: आगे के वाष्पीकरण के बाद, लगभग शुद्ध घनीभूत का एक नमूना छोड़कर।]]बोस-आइंस्टीन कंडेनसेट (बीईसी) एक बाहरी क्षमता में सीमित रूप से परस्पर क्रिया करने वाले [[बोसॉन]] की तनु गैस की स्थिति है और तापमान को पूर्ण शून्य के करीब ठंडा किया जाता है। ऐसी परिस्थितियों में, बोसोन का एक बड़ा अंश बाहरी क्षमता की निम्नतम [[कितना राज्य|कितना स्थिति]]  पर कब्जा कर लेता है, जिस बिंदु पर [[मैक्रोस्कोपिक स्केल|स्थूल स्केल]] पर क्वांटम प्रभाव स्पष्ट हो जाते हैं।<ref>{{cite journal|journal=Nature|volume=412|pages=295–299|year=2001|title=Dynamics of collapsing and exploding Bose–Einstein condensates|pmid=11460153|issue=6844|doi=10.1038/35085500|arxiv = cond-mat/0105019 |bibcode = 2001Natur.412..295D|last1=Donley|first1=Elizabeth A.|last2=Claussen|first2=Neil R.|last3=Cornish|first3=Simon L.|last4=Roberts|first4=Jacob L.|last5=Cornell|first5=Eric A.|last6=Wieman|first6=Carl E.|s2cid=969048}}</ref>
-पदार्थ की इस अवस्था की भविष्यवाणी सबसे पहले 1924-25 में [[सत्येन्द्र नाथ बोस]] और [[अल्बर्ट आइंस्टीन]] ने की थी। बोस ने सबसे पहले आइंस्टीन को प्रकाश क्वांटा (अब फोटॉन कहा जाता है) के [[क्वांटम सांख्यिकी]] पर एक पेपर भेजा था। आइंस्टीन प्रभावित हुए, कागज का अंग्रेजी से जर्मन में अनुवाद किया और इसे बोस के लिए Zeitschrift für Physik को सौंप दिया, जिसने इसे प्रकाशित किया। आइंस्टीन ने तब बोस के विचारों को भौतिक कणों (या पदार्थ) तक दो अन्य पत्रों में विस्तारित किया।<ref>Clark, Ronald W. "Einstein: The Life and Times" (Avon Books, 1971) pp. 408–9 {{ISBN|0-380-01159-X}}</ref>
+पदार्थ की इस अवस्था की भविष्यवाणी सबसे पहले 1924-25 में [[सत्येन्द्र नाथ बोस]] और [[अल्बर्ट आइंस्टीन]] ने की थी। बोस ने सबसे पहले आइंस्टीन को प्रकाश क्वांटा (अब फोटॉन कहा जाता है) के [[क्वांटम सांख्यिकी]] पर एक पेपर भेजा था। आइंस्टीन प्रभावित हुए, कागज का अंग्रेजी से जर्मन में अनुवाद किया और इसे बोस के लिए जेट्सच्रिफ्त फर फिजिक को सौंप दिया, जिसने इसे प्रकाशित किया। आइंस्टीन ने तब बोस के विचारों को भौतिक कणों (या पदार्थ) तक दो अन्य पत्रों में विस्तारित किया।<ref>Clark, Ronald W. "Einstein: The Life and Times" (Avon Books, 1971) pp. 408–9 {{ISBN|0-380-01159-X}}</ref>
-सत्तर साल बाद, 1995 में, बोल्डर [[NIST]]-[[JILA]] लैब में कोलोराडो विश्वविद्यालय में [[एरिक एलिन कॉर्नेल]] और [[कार्ल वाईमन]] द्वारा पहला गैसीय बोस-आइंस्टीन कंडेनसेट बनाया गया था, जिसमें 170 [[ केल्विन (इकाइयां) ]] (nK) तक ठंडा रूबिडियम परमाणुओं की गैस का उपयोग किया गया था। )<ref>{{cite web|title=निरपेक्ष शून्य के पास पदार्थ की नई अवस्था देखी गई|url=http://physics.nist.gov/News/Update/950724.html |publisher=NIST |url-status=dead |archive-url=https://web.archive.org/web/20100601175245/http://physics.nist.gov/News/Update/950724.html |archive-date=1 June 2010  }}</ref> ({{val|1.7|e=-7|u=K}}).<ref>{{cite web|last = Levi|first = Barbara Goss|author-link=Barbara Goss Levi|title = Cornell, Ketterle, and Wieman Share Nobel Prize for Bose–Einstein Condensates|work = Search & Discovery|publisher = Physics Today online| year = 2001|url = http://www.physicstoday.org/pt/vol-54/iss-12/p14.html|access-date =26 January 2008 |archive-url = https://web.archive.org/web/20071024134547/http://www.physicstoday.org/pt/vol-54/iss-12/p14.html |archive-date =24 October 2007}}</ref>
- ± 80 पिकोकेल्विन (pK) का रिकॉर्ड ठंडा तापमान ({{val|4.5|e=-10|u=K}}) [[मैसाचुसेट्स की तकनीकी संस्था|मैसाचुसेट्स की विधि  ी संस्था]] (एमआईटी) के शोधकर्ताओं द्वारा 2003 में सोडियम परमाणुओं के BEC में प्राप्त किया गया था।<ref>{{cite journal|url=http://www.dsf.unica.it/~michele/michele/picokelvin.pdf |archive-url=https://ghostarchive.org/archive/20221009/http://www.dsf.unica.it/~michele/michele/picokelvin.pdf |archive-date=2022-10-09 |url-status=live|title=Cooling Bose–Einstein Condensates Below 500 Picokelvin|doi=10.1126/science.1088827|volume=301|issue=5639|pages=1513–1515 |journal=Science|year=2003|last1=Leanhardt|first1=A. E.|pmid=12970559|last2=Pasquini|first2=TA|last3=Saba|first3=M|last4=Schirotzek|first4=A|last5=Shin|first5=Y|last6=Kielpinski|first6=D|last7=Pritchard|first7=DE|last8=Ketterle|first8=W|bibcode = 2003Sci...301.1513L |s2cid=30259606}}</ref> संबंधित [[ काले पदार्थ ]] (शिखर उत्सर्जन) 6,400 किलोमीटर की तरंग दैर्ध्य लगभग पृथ्वी की त्रिज्या है।
+सत्तर साल बाद, 1995 में, बोल्डर निस्ट-जिला लैब में कोलोराडो विश्वविद्यालय में [[एरिक एलिन कॉर्नेल]] और [[कार्ल वाईमन]] द्वारा पहला गैसीय बोस-आइंस्टीन कंडेनसेट बनाया गया था, जिसमें 170 [[ केल्विन (इकाइयां) | केल्विन (इकाइयां)]] (एनके) ({{val|1.7|e=-7|u=K}}) तक ठंडा रूबिडियम परमाणुओं की गैस का उपयोग किया गया था। <ref>{{cite web|title=निरपेक्ष शून्य के पास पदार्थ की नई अवस्था देखी गई|url=http://physics.nist.gov/News/Update/950724.html |publisher=NIST |url-status=dead |archive-url=https://web.archive.org/web/20100601175245/http://physics.nist.gov/News/Update/950724.html |archive-date=1 June 2010  }}</ref> <ref>{{cite web|last = Levi|first = Barbara Goss|author-link=Barbara Goss Levi|title = Cornell, Ketterle, and Wieman Share Nobel Prize for Bose–Einstein Condensates|work = Search & Discovery|publisher = Physics Today online| year = 2001|url = http://www.physicstoday.org/pt/vol-54/iss-12/p14.html|access-date =26 January 2008 |archive-url = https://web.archive.org/web/20071024134547/http://www.physicstoday.org/pt/vol-54/iss-12/p14.html |archive-date =24 October 2007}}</ref>
+[[मैसाचुसेट्स की तकनीकी संस्था|मैसाचुसेट्स की विधि संस्था]] (एमआईटी) के शोधकर्ताओं द्वारा 2003 में सोडियम परमाणुओं के बीईसी 450 ± 80  पिकोकेल्विन (पीके) का रिकॉर्ड ठंडा तापमान में प्राप्त किया गया था।<ref>{{cite journal|url=http://www.dsf.unica.it/~michele/michele/picokelvin.pdf |archive-url=https://ghostarchive.org/archive/20221009/http://www.dsf.unica.it/~michele/michele/picokelvin.pdf |archive-date=2022-10-09 |url-status=live|title=Cooling Bose–Einstein Condensates Below 500 Picokelvin|doi=10.1126/science.1088827|volume=301|issue=5639|pages=1513–1515 |journal=Science|year=2003|last1=Leanhardt|first1=A. E.|pmid=12970559|last2=Pasquini|first2=TA|last3=Saba|first3=M|last4=Schirotzek|first4=A|last5=Shin|first5=Y|last6=Kielpinski|first6=D|last7=Pritchard|first7=DE|last8=Ketterle|first8=W|bibcode = 2003Sci...301.1513L |s2cid=30259606}}</ref> संबंधित [[ काले पदार्थ | काले पदार्थ]] (शिखर उत्सर्जन) 6,400 किलोमीटर की तरंग दैर्ध्य लगभग पृथ्वी की त्रिज्या है।
 == निरपेक्ष तापमान पैमाने ==
-निरपेक्ष, या उष्मगतिशील तापमान, तापमान पारंपरिक रूप से केल्विन (सेल्सियस-स्केल्ड इंक्रीमेंट) और रैंकिन स्केल (फारेनहाइट-स्केल्ड इंक्रीमेंट) में बढ़ती दुर्लभता के साथ मापा जाता है। पूर्ण तापमान माप विशिष्ट रूप से गुणक स्थिरांक द्वारा निर्धारित किया जाता है जो डिग्री के आकार को निर्दिष्ट करता है, इसलिए दो पूर्ण तापमानों का अनुपात, टी<sub>2</sub>/टी<sub>1</sub>, सभी पैमानों में समान हैं। इस मानक की सबसे पारदर्शी परिभाषा मैक्सवेल-बोल्ट्ज़मान वितरण से आती है। यह फर्मी-डिराक सांख्यिकी (अर्ध-पूर्णांक [[स्पिन (भौतिकी)]] के कणों के लिए) और बोस-आइंस्टीन सांख्यिकी (पूर्णांक स्पिन के कणों के लिए) में भी पाया जा सकता है। ये सभी एक प्रणाली में कणों की सापेक्ष संख्या को kT से अधिक ऊर्जा (कण स्तर पर) के घटते हुए घातीय कार्यों के रूप में परिभाषित करते हैं, जिसमें k बोल्ट्ज़मान स्थिरांक का प्रतिनिधित्व करता है और T [[ स्थूल ]] स्तर पर देखे गए तापमान का प्रतिनिधित्व करता है।<ref name="sib2115"/>
+निरपेक्ष, या उष्मगतिशील तापमान, तापमान पारंपरिक रूप से केल्विन (सेल्सियस-स्केल्ड वृद्धि ) और रैंकिन स्केल (फारेनहाइट-स्केल्ड वृद्धि) में बढ़ती दुर्लभता के साथ मापा जाता है। पूर्ण तापमान माप विशिष्ट रूप से गुणक स्थिरांक द्वारा निर्धारित किया जाता है जो डिग्री के आकार को निर्दिष्ट करता है, इसलिए दो पूर्ण तापमानों ,''T''<sub>2</sub>/''T''<sub>1</sub>, का अनुपात सभी पैमानों में समान हैं। इस मानक की सबसे पारदर्शी परिभाषा मैक्सवेल-बोल्ट्ज़मान वितरण से आती है। यह फर्मी-डिराक सांख्यिकी (अर्ध-पूर्णांक [[स्पिन (भौतिकी)]] के कणों के लिए) और बोस-आइंस्टीन सांख्यिकी (पूर्णांक स्पिन के कणों के लिए) में भी पाया जा सकता है। ये सभी एक प्रणाली में कणों की सापेक्ष संख्या को kT से अधिक ऊर्जा (कण स्तर पर) के घटते हुए घातीय कार्यों के रूप में परिभाषित करते हैं, जिसमें k बोल्ट्ज़मान स्थिरांक का प्रतिनिधित्व करता है और T [[ स्थूल ]] स्तर पर देखे गए तापमान का प्रतिनिधित्व करता है।<ref name="sib2115"/>
 == नकारात्मक तापमान ==
-{{Main|Negative temperature}}
+{{Main|ऋणात्मक तापमान}}
 परिचित सेल्सियस या फ़ारेनहाइट स्केल पर [[ऋणात्मक संख्या]]ओं के रूप में व्यक्त किए जाने वाले तापमान उन पैमानों के शून्य बिंदुओं की तुलना में अधिक ठंडे होते हैं। कुछ [[थर्मोडायनामिक सिस्टम|उष्मगतिशील]] प्रणाली वास्तव में नकारात्मक तापमान प्राप्त कर सकते हैं; अर्थात्, उनका उष्मगतिशील तापमान (केल्विन में व्यक्त) एक ऋणात्मक संख्या मात्रा का हो सकता है। वास्तव में नकारात्मक तापमान वाली प्रणाली पूर्ण शून्य से अधिक ठंडी नहीं होती है। किंतु, एक नकारात्मक तापमान वाली प्रणाली सकारात्मक तापमान वाली किसी भी प्रणाली की तुलना में अधिक गर्म होती है, इस अर्थ में कि यदि एक नकारात्मक-तापमान प्रणाली और एक सकारात्मक-तापमान प्रणाली संपर्क में आती है, तो गर्मी नकारात्मक से सकारात्मक-तापमान प्रणाली में प्रवाहित होती है।<ref name="Chase">{{cite web|last=Chase|first=Scott|title=Below Absolute Zero -What Does Negative Temperature Mean?|url=http://www.phys.ncku.edu.tw/mirrors/physicsfaq/ParticleAndNuclear/neg_temperature.html|work=The Physics and Relativity FAQ|access-date=2 July 2010|archive-url=https://web.archive.org/web/20110815144418/http://www.phys.ncku.edu.tw/mirrors/physicsfaq/ParticleAndNuclear/neg_temperature.html|archive-date=15 August 2011|url-status=dead}}</ref>
-अधिकांश परिचित प्रणालियां नकारात्मक तापमान प्राप्त नहीं कर सकती हैं क्योंकि ऊर्जा जोड़ने से उनकी एन्ट्रापी सदैव  बढ़ जाती है। चूंकि, कुछ प्रणालियों में ऊर्जा की अधिकतम मात्रा होती है जिसे वे धारण कर सकते हैं, और जैसे-जैसे वे उस अधिकतम ऊर्जा तक पहुँचते हैं, उनकी एन्ट्रापी वास्तव में कम होने लगती है। क्योंकि तापमान को ऊर्जा और एन्ट्रापी के बीच के संबंध से परिभाषित किया जाता है, इस तरह की प्रणाली का तापमान नकारात्मक हो जाता है, तथापि  ऊर्जा को जोड़ा जा रहा हो।<ref name="Chase"/>परिणाम स्वरुप , बढ़ती राज्य ऊर्जा के साथ घटने के अतिरिक्त नकारात्मक तापमान पर प्रणाली के राज्यों के लिए बोल्टज़मान कारक बढ़ता है। इसलिए, कोई पूर्ण प्रणाली, यानी  विद्युत चुम्बकीय मोड सहित, नकारात्मक तापमान नहीं हो सकता है, क्योंकि कोई उच्चतम ऊर्जा स्थिति नहीं है,{{citation needed|date=October 2016}} जिससे नकारात्मक तापमान के लिए राज्यों की संभावनाओं का योग अलग हो जाए। चूंकि, अर्ध-संतुलन प्रणालियों के लिए (उदाहरण के लिए विद्युत चुम्बकीय क्षेत्र के साथ संतुलन से बाहर स्पिन) यह तर्क प्रयुक्त  नहीं होता है, और नकारात्मक प्रभावी तापमान प्राप्य हैं।
+अधिकांश परिचित प्रणालियां नकारात्मक तापमान प्राप्त नहीं कर सकती हैं क्योंकि ऊर्जा जोड़ने से उनकी एन्ट्रापी सदैव  बढ़ जाती है। चूंकि, कुछ प्रणालियों में ऊर्जा की अधिकतम मात्रा होती है जिसे वे धारण कर सकते हैं, और जैसे-जैसे वे उस अधिकतम ऊर्जा तक पहुँचते हैं, उनकी एन्ट्रापी वास्तव में कम होने लगती है। क्योंकि तापमान को ऊर्जा और एन्ट्रापी के बीच के संबंध से परिभाषित किया जाता है, इस तरह की प्रणाली का तापमान नकारात्मक हो जाता है, तथापि  ऊर्जा को जोड़ा जा रहा हो।<ref name="Chase" />परिणाम स्वरुप , बढ़ती राज्य ऊर्जा के साथ घटने के अतिरिक्त नकारात्मक तापमान पर प्रणाली के राज्यों के लिए बोल्टज़मान कारक बढ़ता है। इसलिए, कोई पूर्ण प्रणाली, यानी  विद्युत चुम्बकीय मोड सहित, नकारात्मक तापमान नहीं हो सकता है, क्योंकि कोई उच्चतम ऊर्जा स्थिति नहीं है,{{citation needed|date=October 2016}} जिससे नकारात्मक तापमान के लिए राज्यों की संभावनाओं का योग अलग हो जाए। चूंकि, अर्ध-संतुलन प्रणालियों के लिए (उदाहरण के लिए विद्युत चुम्बकीय क्षेत्र के साथ संतुलन से बाहर स्पिन) यह तर्क प्रयुक्त  नहीं होता है, और नकारात्मक प्रभावी तापमान प्राप्य हैं।
 जनवरी 2013 को, भौतिकविदों ने घोषणा की कि पहली बार उन्होंने पोटेशियम परमाणुओं से बनी एक क्वांटम गैस का निर्माण किया है, जो स्वतंत्रता की गतिमान डिग्री में एक नकारात्मक तापमान के साथ है।<ref>{{cite journal|doi=10.1038/nature.2013.12146|title=क्वांटम गैस परम शून्य से नीचे चली जाती है|journal=Nature|year=2013|last1=Merali|first1=Zeeya|s2cid=124101032|doi-access=free}}</ref>

Anonymous

Search

परम शून्य: Difference between revisions

Namespaces

More

Page actions

Revision as of 15:53, 22 March 2023

Contents

उष्मगतिशील्स पूर्ण शून्य के पास

बोस-आइंस्टीन घनीभूत के साथ संबंध

निरपेक्ष तापमान पैमाने

नकारात्मक तापमान

इतिहास

ठंड की डिग्री तक सीमित करें

चार्ल्स का नियम

भगवान केल्विन का काम

पूर्ण शून्य की दौड़

बहुत कम तापमान

यह भी देखें

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

परम शून्य: Difference between revisions

Revision as of 15:53, 22 March 2023

उष्मगतिशील्स पूर्ण शून्य के पास

बोस-आइंस्टीन घनीभूत के साथ संबंध

निरपेक्ष तापमान पैमाने

नकारात्मक तापमान

इतिहास

ठंड की डिग्री तक सीमित करें

चार्ल्स का नियम

भगवान केल्विन का काम

पूर्ण शून्य की दौड़

बहुत कम तापमान

यह भी देखें

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories