प्रत्यक्ष और अप्रत्यक्ष बैंड अंतराल: Difference between revisions

Latest revision as of 13:50, 6 September 2022

अर्धचालक भौतिकी semiconductor physics) में, एक अर्धचालक का बैंड अंतराल (band gap) मूल रुप से दो प्रकार का होता है, प्रत्यक्ष बैंड अंतराल(direct band gap) और अप्रत्यक्ष बैंड अंतराल (indirect band gap)। चालन बैंड (conduction band) में न्यूनतम-ऊर्जा की स्थिति और वैलेंस बैंड (valence band) में अधिकतम-ऊर्जा अवस्था प्रत्येक को ब्रिलौइन ज़ोन (Brillouin zone) में एक निश्चित क्रिस्टल गति (के-वेक्टर) (crystal momentum (k-vector)) की विशेषता है। यदि के-वेक्टर अलग हैं, तो सामग्री में एक अप्रत्यक्ष अंतराल ("indirect gap") है। बैंड अंतराल को प्रत्यक्ष ("direct") कहा जाता है यदि इलेक्ट्रॉनों और होल्स (holes) का क्रिस्टल गति चालन बैंड (conduction band) और वैलेंस बैंड (valence band) दोनों में समान है; एक इलेक्ट्रॉन ,सीधे एक फोटॉन का उत्सर्जन कर सकता है। एक अप्रत्यक्ष अंतराल में ("indirect" gap"), एक फोटॉन को उत्सर्जित नहीं किया जा सकता है क्योंकि इलेक्ट्रॉन को एक मध्यवर्ती स्थिति से गुजरना होता है और क्रिस्टल जाली (crystal lattice) में गति को स्थानांतरित करना होता है।

प्रत्यक्ष बैंडअंतराल सामग्रियों के उदाहरणों में अनाकार सिलिकॉन (amorphous silicon) और कुछ (III-V) सामग्री जैसे आईएनएस (INAS) और गास (GAAS) शामिल हैं। अप्रत्यक्ष बैंड अंतराल सामग्री में क्रिस्टलीय सिलिकॉन (amorphous silicon) और जीई (Ge) शामिल हैं। कुछ (III-V) सामग्री अप्रत्यक्ष बैंडअंतराल के रूप में अच्छी तरह से हैं, उदाहरण के लिए (ALSB)।

एक अप्रत्यक्ष बैंड अंतराल के साथ अर्धचालक के लिए ऊर्जा बनाम क्रिस्टल गति, यह दर्शाता है कि एक इलेक्ट्रॉन वैलेंस बैंड (लाल) में उच्चतम-ऊर्जा राज्य से चालन बैंड (हरा) में निम्नतम-ऊर्जा राज्य में बिना किसी बदलाव के स्थानांतरित नहीं हो सकता है गति। यहां, लगभग सभी ऊर्जा एक फोटॉन (ऊर्ध्वाधर तीर) से आती है, जबकि लगभग सभी गति फोनन (क्षैतिज तीर) से आती है।

एक प्रत्यक्ष बैंड अंतराल के साथ एक अर्धचालक के लिए ऊर्जा बनाम क्रिस्टल गति, यह दर्शाता है कि एक इलेक्ट्रॉन वैलेंस बैंड (लाल) में उच्चतम-ऊर्जा राज्य से चालन बैंड (ग्रीन) में सबसे कम ऊर्जा राज्य में बदलाव के बिना बदलाव कर सकता है।क्रिस्टल गति।चित्रित एक संक्रमण है जिसमें एक फोटॉन वैलेंस बैंड से चालन बैंड तक एक इलेक्ट्रॉन को उत्तेजित करता है।

एसआई, जीई, जीएएएस और इनस के लिए थोक बैंड संरचना तंग बाध्यकारी मॉडल के साथ उत्पन्न हुई।ध्यान दें कि एसआई और जीई एक्स और एल में मिनीमा के साथ अप्रत्यक्ष बैंड अंतराल हैं, जबकि गाआ और इनस प्रत्यक्ष बैंड अंतराल सामग्री हैं।

विकिरण पुनर्संयोजन के लिए निहितार्थ (Implications for radiative recombination)

इलेक्ट्रॉनों, होल्स (holes), फोनन (phonons), फोटॉन (photons) और अन्य कणों के बीच परस्पर क्रिया को ऊर्जा और क्रिस्टल गति( crystal momentum) (यानी, कुल के-वेक्टर का संरक्षण) के संरक्षण को संतुष्ट करने के लिए आवश्यकता होती है। अर्धचालक बैंड अंतराल के पास ऊर्जा वाले एक फोटॉन लगभग शून्य गति होती है। एक महत्वपूर्ण प्रक्रिया को विकिरण पुनर्संयोजन (radiative recombination) कहा जाता है, जहां चालन बैंड में एक इलेक्ट्रॉन वैलेंस बैंड में एक छेद को नष्ट करता है, जो एक फोटॉन के रूप में अतिरिक्त ऊर्जा को जारी करता है। यह एक प्रत्यक्ष बैंड अंतराल सेमीकंडक्टर में संभव है यदि इलेक्ट्रॉन में चालन बैंड न्यूनतम के पास एक के-वेक्टर (k-vector) है (छेद एक ही K-Vector साझा करेगा), लेकिन अप्रत्यक्ष बैंड अंतराल सेमीकंडक्टर (indirect band gap semiconductor) में संभव नहीं है, क्योंकि फोटॉन क्रिस्टल गति नहीं ले सकते हैं, और इस प्रकार से क्रिस्टल गति के संरक्षण का उल्लंघन किया जाएगा। अप्रत्यक्ष बैंड अंतराल (indirect band gap) सामग्री में होने वाले विकिरण पुनर्संयोजन (radiative recombination) के लिए, प्रक्रिया को एक फोनन (phonons) के अवशोषण या उत्सर्जन को भी शामिल करना चाहिए, जहां फोनन गति इलेक्ट्रॉन और फोनन गति (phonon momentum) के बीच अंतर के बराबर होता है। इसके बजाय, एक क्रिस्टलोग्राफिक दोष (crystallographic defect) शामिल हो सकता है, जो अनिवार्य रूप से एक ही भूमिका निभाता है। फोनन (phonons) की भागीदारी की इस प्रक्रिया को दिए गए निश्चित समय में होने की संभावना को बहुत कम करती है, यही वजह है कि विकिरण पुनर्संयोजन (radiative recombination), प्रत्यक्ष बैंड अंतराल (direct band gap) की तुलना में अप्रत्यक्ष बैंड अंतराल (indirect band gap) सामग्री में बहुत धीमा है। यही कारण है कि लाइट-एमिटिंग डायोड और लेजर डायोड लगभग हमेशा प्रत्यक्ष बैंड अंतराल(direct band gap) सामग्री से बने होते हैं, न कि सिलिकॉन जैसे अप्रत्यक्ष बैंड अंतराल वाले (indirect band gap)।

तथ्य यह है कि अप्रत्यक्ष बैंड अंतराल (indirect band gap) सामग्री में विकिरण पुनर्संयोजन (radiative recombination) धीमा है, इससे तात्पर्य यह भी है कि, ज्यादातर परिस्थितियों में, विकिरण पुनर्संयोजन (radiative recombination) कुल पुनर्संयोजन (recombinations) का एक छोटा अनुपात होता है, जिसमें अधिकांश पुनर्संयोजन (recombinations) गैर-विकिरणक (non-radiative) होते हैं, जो बिंदु दोषों (point defects) पर या ग्रेन बाउंड्रीज (grain boundaries) पर होते हैं। हालांकि, यदि उत्साहित इलेक्ट्रॉनों (excited electrons) को इन पुनर्संयोजन स्थानों तक पहुंचने से रोका जाता है, तो उनके पास कोई विकल्प नहीं है, लेकिन अंततः विकिरण पुनर्संयोजन (radiative recombination) द्वारा वैलेंस बैंड (valence band) में वापस आने के लिए, यह सामग्री में एक डिसलोकेशन लूप (dislocation loop) बनाकर किया जा सकता है।^{[clarification needed]} लूप के किनारे पर, डिसलोकेशन डिस्क ("dislocation disk") के ऊपर और नीचे के तलों को अलग कर दिया जाता है, जिससे एक नकारात्मक दबाव होता है, जो चालन बैंड की ऊर्जा को काफी हद तक बढ़ाता है, जिसके परिणामस्वरूप इलेक्ट्रॉन इस किनारे को पास नहीं कर सकते हैं। बशर्ते कि डिसलोकेशन लूप (dislocation loop) के ऊपर का क्षेत्र डिफेक्ट फ्री (defect-free) है (कोई गैर-विकिरणकारी पुनर्संयोजन संभव नहीं है), इलेक्ट्रॉन विकिरण पुनर्संयोजन (radiative recombination) द्वारा वैलेंस शेल (valence shell) में वापस गिर जाएगा, इस प्रकार प्रकाश का उत्सर्जन होगा।यह वह सिद्धांत है जिस पर डेलेड्स ("DELEDs") (डिसलोकेशन इंजीनियर्ड एलईडी) आधारित हैं।^{[citation needed]}

प्रकाश अवशोषण के लिए निहितार्थ (Implications for light absorption)

विकिरण पुनर्संयोजन (radiative recombination) का सटीक उल्टा प्रकाश अवशोषण (light absorption) है। ऊपर के समान कारण के लिए, बैंड अंतराल (band gap) के करीब एक फोटॉन (photon) ऊर्जा के साथ प्रकाश एक प्रत्यक्ष बैंड अंतराल (direct band gap) एक की तुलना में एक अप्रत्यक्ष बैंड अंतराल (indirect band gap) सामग्री में अवशोषित होने से पहले बहुत दूर प्रवेश कर सकता है (कम से कम इंसोफ़र (insofar) के रूप में प्रकाश अवशोषण (light absorption) एक्ससिस्टिंग इलेक्ट्रॉनों (exciting electrons) के कारण है बैंड अंतराल)।

यह तथ्य फोटोवोल्टिक (सौर कोशिकाओं) के लिए बहुत महत्वपूर्ण है। क्रिस्टलीय सिलिकॉन (Crystalline silicon) सबसे आम सोलर-सेल सब्सट्रेट (solar-cell substrate material) सामग्री है, इस तथ्य के बावजूद कि यह अप्रत्यक्ष-अंतराल (indirect-gap) है और इसलिए प्रकाश को बहुत अच्छी तरह से अवशोषित नहीं करता है। जैसे, आम तौर पर सैकड़ों माइक्रोन (microns) घने होते हैं; थिनर वेफर्स (thinner wafers) बहुत अधिक प्रकाश (विशेष रूप से लंबे समय तक तरंग दैर्ध्य में) को गुजरने की अनुमति देगा। तुलनात्मक रूप से, पतली-फिल्म सौर कोशिकाएं (thin-film solar cells) प्रत्यक्ष बैंड अंतराल सामग्री (जैसे कि अनाकार सिलिकॉन (amorphous silicon), सीडीटीई (CdTe), सीआईजीएस (CIGS) या सीजेडटी (CZTS)) से बनी होती हैं, जो बहुत पतले क्षेत्र में प्रकाश को अवशोषित करती हैं, और परिणामस्वरूप बहुत पतली सक्रिय परत के साथ बनाया जा सकता है ( अक्सर 1 माइक्रोन थिक(micron thick) से कम)।

एक अप्रत्यक्ष बैंड अंतराल (indirect band gap) सामग्री का अवशोषण स्पेक्ट्रम (absorption spectrum) सामान्यतः एक प्रत्यक्ष सामग्री की तुलना में तापमान पर अधिक निर्भर करता है, क्योंकि कम तापमान पर कम फोनन (phonons) होते हैं, और इसलिए यह कम संभावना है कि एक फोटॉन (photons) और फोनन (phonons) को एक साथ एक अप्रत्यक्ष संक्रमण (indirect transition) बनाने के लिए अवशोषित किया जा सकता है । उदाहरण के लिए, सिलिकॉन कमरे के तापमान पर प्रकाश को देखने के लिए अपारदर्शी है, लेकिन तरल हीलियमl (iquid helium) तापमान पर लाल प्रकाश (red light) के लिए पारदर्शी है, क्योंकि लाल फोटॉन (red photons) केवल एक अप्रत्यक्ष संक्रमण (indirect transition) में अवशोषित हो सकते हैं।^{[clarification needed]}

अवशोषण के लिए सूत्र (Formula for absorption)

यह निर्धारित करने के लिए एक सामान्य और सरल विधि है कि क्या एक बैंड अंतराल प्रत्यक्ष या अप्रत्यक्ष अवशोषण स्पेक्ट्रोस्कोपी (absorption spectroscopy) का उपयोग करता है। फोटॉन ऊर्जा के खिलाफ अवशोषण गुणांक (absorption coefficient) की कुछ शक्तियों प्लॉट (plotting certain powers) करके, कोई भी सामान्य रूप से बता सकता है कि बैंड अंतराल का क्या वैल्यू (Value) है, और यह प्रत्यक्ष है या नहीं।

एक प्रत्यक्ष बैंड अंतराल (direct band gap) के लिए, अवशोषण गुणांक $\alpha$ (absorption coefficient) निम्न सूत्र के अनुसार प्रकाश आवृत्ति (light frequency) से संबंधित है:^[1]^[2]

\alpha \approx A^{*}{\sqrt {h\nu -E_{\text{g}}}}

, विथ(with)

A^{*}={\frac {q^{2}x_{vc}^{2}(2m_{\text{r}})^{3/2}}{\lambda _{0}\epsilon _{0}\hbar ^{3}n}}

जहां पर:

$\alpha$ अवशोषण गुणांक (absorption coefficient) है, जोकि प्रकाश आवृत्ति का एक फंक्शन है
$\nu$ प्रकाश आवृत्ति (light frequency) है
h प्लैंक स्थिरांक है
$\hbar$ रेड्यूसड प्लैंक स्थिरांक है ( $\hbar =h/2\pi$ )
$E_{\text{g}}$ बैंड अंतराल ऊर्जा है
$A^{*}$ एक निश्चित आवृत्ति-स्वतंत्र स्थिरांक (certain frequency-independent constant है), ऊपर सूत्र के साथ
$m_{\text{r}}={\frac {m_{\text{h}}^{*}m_{\text{e}}^{*}}{m_{\text{h}}^{*}+m_{\text{e}}^{*}}}$ , जहां पर $m_{\text{e}}^{*}$ तथा $m_{\text{h}}^{*}$ प्रभावी द्रव्यमान (effective masses) हैं | क्रमशः इलेक्ट्रॉन और होल (hole) के प्रभावी द्रव्यमान ( $m_{\text{r}}$ को रेड्यूसड मॉस कहा जाता है)
$q$ प्राथमिक चार्ज (elementary charge) है
$n$ अपवर्तन का (वास्तविक) सूचकांक (index of refraction) है
$\epsilon _{0}$ वैक्यूम पारगम्यता (vacuum permittivity) है
$x_{vc}$ एक मैट्रिक्स तत्व ("matrix element") है, लंबाई और विशिष्ट मूल्य की इकाइयों के साथ लैत्तीस कांस्टेंट (lattice constant) के रूप में स्थिर है।

यह सूत्र केवल फोटॉन ऊर्जा के साथ प्रकाश के लिए मान्य है, लेकिन बैंड अंतराल की तुलना में (अधिक विशेष रूप से, यह सूत्र मानता है कि बैंड लगभग परवलयिक हैं) बहुत अधिक बड़ा नहीं है, और बैंड-टू-बैंड के अलावा अन्य सभी अन्य स्रोतों को अनदेखा करता है-प्रश्न में बैंड अवशोषण, साथ ही नए बनाए गए इलेक्ट्रॉन औरहोल (hole) के बीच विद्युत आकर्षण (एक्सिटॉन देखें) (see exciton)। इस मामले में यह भी अमान्य है कि प्रत्यक्ष संक्रमण (direct transition) निषिद्ध है, या इस मामले में कि कई वैलेंस बैंड स्टेट्स (valence band states) खाली हैं या चालन बैंड स्टेट्स (conduction band states) भरे हुए हैं।^[3]

दूसरी ओर, एक अप्रत्यक्ष बैंड अंतराल (indirect band gap) के लिए,

सूत्र है:^[3]: $\alpha \propto {\frac {(h\nu -E_{\text{g}}+E_{\text{p}})^{2}}{\exp({\frac {E_{\text{p}}}{kT}})-1}}+{\frac {(h\nu -E_{\text{g}}-E_{\text{p}})^{2}}{1-\exp(-{\frac {E_{\text{p}}}{kT}})}}$

जहां पर:

$E_{\text{p}}$ फोनन (phonon) की ऊर्जा है जो संक्रमण में सहायता करती है
$k$ बोल्ट्जमैन स्थिरांक है
$T$ थर्मोडायनामिक तापमान है

इस सूत्र में ऊपर वर्णित समान अनुमान शामिल हैं।

इसलिए, अगर एक प्लाट $h\nu$ बनाम $\alpha ^{2}$ एक सीधी रेखा बनाता है, यह सामान्य रूप से अनुमान लगाया जा सकता है कि एक सीधा बैंड अंतराल है, सीधी रेखा, को एक्सट्रपलेशन (extrapolating) करके औसत दर्जे का $\alpha =0$ एक्सिस। दूसरी ओर, अगर एक प्लाट $h\nu$ बनाम $\alpha ^{1/2}$ एक सीधी रेखा बनाता है, यह सामान्य रूप से अनुमान लगाया जा सकता है कि एक अप्रत्यक्ष बैंड अंतराल है, सीधी रेखा को एक्सट्रपलेशन (extrapolating) करके औसत दर्जे का ( $\alpha =0$ अक्ष) $E_{\text{p}}\approx 0$ )।

अन्य पहलू

अप्रत्यक्ष अंतर के साथ कुछ सामग्रियों में, अंतर (gap) का मूल्य नकारात्मक है। वैलेंस बैंड (valence band) का शीर्ष ऊर्जा में चालन बैंड (conduction band) के बॉटम (bottom) से अधिक है। इस तरह की सामग्रियों को सेमीमेटल (semimetals) के रूप में जाना जाता है।

यह भी देखें

मॉस -बर्स्टीन प्रभाव (Moss–Burstein effect)

ताउक प्लॉट (Tauc plot)

संदर्भ

↑ Optoelectronics, by E. Rosencher, 2002, equation (7.25).
↑ Pankove has the same equation, but with an apparently different prefactor $A^{*}$ . However, in the Pankove version, the units / dimensional analysis appears not to work out.
↑ ^3.0 ^3.1 J.I. Pankove, Optical Processes in Semiconductors. Dover, 1971.

बाहरी संबंध

B. Van Zeghbroeck's Principles of Semiconductor Devices Archived 2009-01-22 at the Wayback Machine at Electrical and Computer Engineering Department of University of Colorado at Boulder

]

[1] Optoelectronics, by E. Rosencher, 2002, equation (7.25).

[2] Pankove has the same equation, but with an apparently different prefactor $A^{*}$ . However, in the Pankove version, the units / dimensional analysis appears not to work out.

[Pankove-3] 3.0 ^3.1 J.I. Pankove, Optical Processes in Semiconductors. Dover, 1971.

[1]

[2]

[3]

@@ Line 1: / Line 1: @@
 {{Short description|Types of energy range in a solid where no electron states can exist}}
-अर्धचालक भौतिकी में (In semiconductor physics), एक अर्धचालक का बैंड गैप (band gap) मूल रुप से दो प्रकार का होता है, '''''प्रत्यक्ष बैंड गैप''''' ('''direct band gap) और''' '''''अप्रत्यक्ष बैंड गैप''''' ('''indirect band gap)'''। चालन बैंड (conduction band) में न्यूनतम-ऊर्जा की स्थिति और वैलेंस बैंड (valence band) में अधिकतम-ऊर्जा अवस्था प्रत्येक को ब्रिलौइन ज़ोन (Brillouin zone) में एक निश्चित क्रिस्टल गति (के-वेक्टर) (crystal momentum (k-vector)) की विशेषता है। यदि के-वैक्टर अलग हैं, तो सामग्री में एक अप्रत्यक्ष अंतराल ("indirect gap") है। बैंड गैप को प्रत्यक्ष ("direct") कहा जाता है यदि इलेक्ट्रॉनों और होल्स (holes) का क्रिस्टल गति चालन बैंड (conduction band) और वैलेंस बैंड (valence band) दोनों में समान है; एक इलेक्ट्रॉन सीधे एक फोटॉन का उत्सर्जन कर सकता है। एक अप्रत्यक्ष अंतराल में ("indirect" gap"), एक फोटॉन को उत्सर्जित नहीं किया जा सकता है क्योंकि इलेक्ट्रॉन को एक मध्यवर्ती स्थिति से गुजरना होता है और क्रिस्टल जाली (crystal lattice) में गति को स्थानांतरित करना होता है।
+अर्धचालक भौतिकी semiconductor physics) में, एक अर्धचालक का बैंड अंतराल (band gap) मूल रुप से दो प्रकार का होता है, '''''प्रत्यक्ष बैंड''''' '''अंतराल(direct band gap) और''' '''''अप्रत्यक्ष बैंड अंतराल''''' ('''indirect band gap)'''। चालन बैंड (conduction band) में न्यूनतम-ऊर्जा की स्थिति और वैलेंस बैंड (valence band) में अधिकतम-ऊर्जा अवस्था प्रत्येक को ब्रिलौइन ज़ोन (Brillouin zone) में एक निश्चित क्रिस्टल गति (के-वेक्टर) (crystal momentum (k-vector)) की विशेषता है। यदि के-वेक्टर अलग हैं, तो सामग्री में एक अप्रत्यक्ष अंतराल ("indirect gap") है। बैंड अंतराल को प्रत्यक्ष ("direct") कहा जाता है यदि इलेक्ट्रॉनों और होल्स (holes) का क्रिस्टल गति चालन बैंड (conduction band) और वैलेंस बैंड (valence band) दोनों में समान है; एक इलेक्ट्रॉन ,सीधे एक फोटॉन का उत्सर्जन कर सकता है। एक अप्रत्यक्ष अंतराल में ("indirect" gap"), एक फोटॉन को उत्सर्जित नहीं किया जा सकता है क्योंकि इलेक्ट्रॉन को एक मध्यवर्ती स्थिति से गुजरना होता है और क्रिस्टल जाली (crystal lattice) में गति को स्थानांतरित करना होता है।
-प्रत्यक्ष बैंडगैप सामग्रियों के उदाहरणों में अनाकार सिलिकॉन (amorphous silicon) और कुछ (III-V) सामग्री जैसे आईएनएस (INAS) और गास (GAAS) शामिल हैं। अप्रत्यक्ष बैंडगैप सामग्री में क्रिस्टलीय सिलिकॉन (amorphous silicon) और जीई (Ge) शामिल हैं। कुछ (III-V) सामग्री अप्रत्यक्ष बैंडगैप के रूप में अच्छी तरह से हैं, उदाहरण के लिए (ALSB)।
+प्रत्यक्ष बैंडअंतराल सामग्रियों के उदाहरणों में अनाकार सिलिकॉन (amorphous silicon) और कुछ (III-V) सामग्री जैसे आईएनएस (INAS) और गास (GAAS) शामिल हैं। अप्रत्यक्ष बैंड अंतराल सामग्री में क्रिस्टलीय सिलिकॉन (amorphous silicon) और जीई (Ge) शामिल हैं। कुछ (III-V) सामग्री अप्रत्यक्ष बैंडअंतराल के रूप में अच्छी तरह से हैं, उदाहरण के लिए (ALSB)।
+[[File:Indirect Bandgap (fr).svg|thumb|287x287px|एक अप्रत्यक्ष बैंड अंतराल के साथ अर्धचालक के लिए ऊर्जा बनाम [[:hi:क्रिस्टल गति|क्रिस्टल गति]], यह दर्शाता है कि एक इलेक्ट्रॉन वैलेंस बैंड (लाल) में उच्चतम-ऊर्जा राज्य से चालन बैंड (हरा) में निम्नतम-ऊर्जा राज्य में बिना किसी बदलाव के स्थानांतरित नहीं हो सकता है गति। यहां, लगभग सभी ऊर्जा एक [[:hi:फोटॉन|फोटॉन]] (ऊर्ध्वाधर तीर) से आती है, जबकि लगभग सभी गति [[:hi:फोनोन|फोनन]] (क्षैतिज तीर) से आती है।]]
+[[Image:Direct.svg|thumb|287x287px|एक प्रत्यक्ष बैंड अंतराल के साथ एक अर्धचालक के लिए ऊर्जा बनाम क्रिस्टल गति, यह दर्शाता है कि एक इलेक्ट्रॉन वैलेंस बैंड (लाल) में उच्चतम-ऊर्जा राज्य से चालन बैंड (ग्रीन) में सबसे कम ऊर्जा राज्य में बदलाव के बिना बदलाव कर सकता है।क्रिस्टल गति।चित्रित एक संक्रमण है जिसमें एक फोटॉन वैलेंस बैंड से चालन बैंड तक एक इलेक्ट्रॉन को उत्तेजित करता है।]]
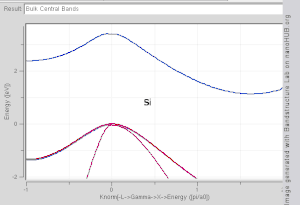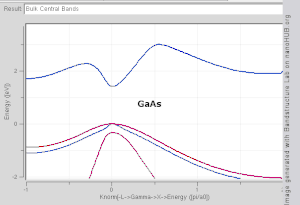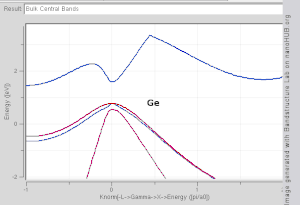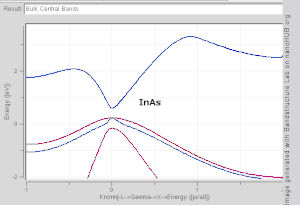
-[[Image:Indirect Bandgap.svg|thumb|350px|एक अप्रत्यक्ष बैंड गैप के साथ एक अर्धचालक के लिए ऊर्जा बनाम क्रिस्टल गति, यह दर्शाता है कि एक इलेक्ट्रॉन वैलेंस बैंड (लाल) में उच्चतम-ऊर्जा राज्य से चालन बैंड (ग्रीन) में सबसे कम ऊर्जा की स्थिति में बदलाव के बिना बदलाव नहीं कर सकता है।गति।यहाँ, लगभग सभी ऊर्जा एक फोटॉन (ऊर्ध्वाधर तीर) से आती है, जबकि लगभग सभी गति एक फोनन (क्षैतिज तीर) से आती है।]]
+[[Image:Bulkbandstructure.gif|thumb|right|300px|एसआई, जीई, जीएएएस और इनस के लिए थोक बैंड संरचना तंग बाध्यकारी मॉडल के साथ उत्पन्न हुई।ध्यान दें कि एसआई और जीई एक्स और एल में मिनीमा के साथ अप्रत्यक्ष बैंड अंतराल हैं, जबकि गाआ और इनस प्रत्यक्ष बैंड अंतराल सामग्री हैं।]]
-[[Image:Direct.svg|thumb|350px|एक प्रत्यक्ष बैंड गैप के साथ एक अर्धचालक के लिए ऊर्जा बनाम क्रिस्टल गति, यह दर्शाता है कि एक इलेक्ट्रॉन वैलेंस बैंड (लाल) में उच्चतम-ऊर्जा राज्य से चालन बैंड (ग्रीन) में सबसे कम ऊर्जा राज्य में बदलाव के बिना बदलाव कर सकता है।क्रिस्टल गति।चित्रित एक संक्रमण है जिसमें एक फोटॉन वैलेंस बैंड से चालन बैंड तक एक इलेक्ट्रॉन को उत्तेजित करता है।]]
-[[Image:Bulkbandstructure.gif|thumb|right|300px|एसआई, जीई, जीएएएस और इनस के लिए थोक बैंड संरचना तंग बाध्यकारी मॉडल के साथ उत्पन्न हुई।ध्यान दें कि एसआई और जीई एक्स और एल में मिनीमा के साथ अप्रत्यक्ष बैंड गैप हैं, जबकि गाआ और इनस प्रत्यक्ष बैंड गैप सामग्री हैं।]]
 == विकिरण पुनर्संयोजन के लिए निहितार्थ   (Implications for radiative recombination) ==
 {{see also|Radiative recombination}}
-इलेक्ट्रॉनों, होल्स (holes), फोनन (phonons), फोटॉन (photons) और अन्य कणों के बीच परस्पर क्रिया को ऊर्जा और क्रिस्टल गति( crystal momentum) (यानी, कुल के-वेक्टर का संरक्षण) के संरक्षण को संतुष्ट करने के लिए आवश्यकता होती है। अर्धचालक बैंड गैप के पास ऊर्जा वाले एक फोटॉन लगभग शून्य गति होती है। एक महत्वपूर्ण प्रक्रिया को विकिरण पुनर्संयोजन (radiative recombination) कहा जाता है, जहां चालन बैंड में एक इलेक्ट्रॉन वैलेंस बैंड में एक छेदएक छेद को नष्ट करता है, जो एक फोटॉन के रूप में अतिरिक्त ऊर्जा को जारी करता है। यह एक प्रत्यक्ष बैंड गैप सेमीकंडक्टर में संभव है यदि इलेक्ट्रॉन में चालन बैंड न्यूनतम के पास एक के वेक्टर (k-vector) है (छेद एक ही K-Vector साझा करेगा), लेकिन अप्रत्यक्ष बैंड गैप सेमीकंडक्टर (indirect band gap semiconductor) में संभव नहीं है, क्योंकि फोटॉन क्रिस्टल गति नहीं ले सकते हैं,  और इस प्रकार से क्रिस्टल गति के संरक्षण का उल्लंघन किया जाएगा। अप्रत्यक्ष बैंड गैप (indirect band gap) सामग्री में होने वाले विकिरण पुनर्संयोजन (radiative recombination) के लिए, प्रक्रिया को एक फोनन (phonons) के अवशोषण या उत्सर्जन को भी शामिल करना चाहिए, जहां फोनन गति इलेक्ट्रॉन और फोनन गति (phonon momentum) के बीच अंतर के बराबर होता है। इसके बजाय, एक क्रिस्टलोग्राफिक दोष (crystallographic defect) शामिल हो सकता है, जो अनिवार्य रूप से एक ही भूमिका निभाता है। फोनन (phonons) की भागीदारी की इस प्रक्रिया को दिए गए निश्चित समय में होने की संभावना को बहुत कम करती है, यही वजह है कि विकिरण पुनर्संयोजन (radiative recombination), प्रत्यक्ष बैंड गैप (direct band gap) की तुलना में अप्रत्यक्ष बैंड गैप (indirect band gap) सामग्री में बहुत धीमा है। यही कारण है कि लाइट-एमिटिंग डायोड और लेजर डायोड लगभग हमेशा प्रत्यक्ष बैंड गैप(direct band gap) सामग्री से बने होते हैं, न कि सिलिकॉन जैसे अप्रत्यक्ष बैंड गैप वाले (indirect band gap)।
+इलेक्ट्रॉनों, होल्स (holes), फोनन (phonons), फोटॉन (photons) और अन्य कणों के बीच परस्पर क्रिया को ऊर्जा और क्रिस्टल गति( crystal momentum) (यानी, कुल के-वेक्टर का संरक्षण) के संरक्षण को संतुष्ट करने के लिए आवश्यकता होती है। अर्धचालक बैंड अंतराल के पास ऊर्जा वाले एक फोटॉन लगभग शून्य गति होती है। एक महत्वपूर्ण प्रक्रिया को विकिरण पुनर्संयोजन (radiative recombination) कहा जाता है, जहां चालन बैंड में एक इलेक्ट्रॉन वैलेंस बैंड में एक छेद को नष्ट करता है, जो एक फोटॉन के रूप में अतिरिक्त ऊर्जा को जारी करता है। यह एक प्रत्यक्ष बैंड अंतराल सेमीकंडक्टर में संभव है यदि इलेक्ट्रॉन में चालन बैंड न्यूनतम के पास एक के-वेक्टर (k-vector) है (छेद एक ही K-Vector साझा करेगा), लेकिन अप्रत्यक्ष बैंड अंतराल सेमीकंडक्टर (indirect band gap semiconductor) में संभव नहीं है, क्योंकि फोटॉन क्रिस्टल गति नहीं ले सकते हैं,  और इस प्रकार से क्रिस्टल गति के संरक्षण का उल्लंघन किया जाएगा। अप्रत्यक्ष बैंड अंतराल (indirect band gap) सामग्री में होने वाले विकिरण पुनर्संयोजन (radiative recombination) के लिए, प्रक्रिया को एक फोनन (phonons) के अवशोषण या उत्सर्जन को भी शामिल करना चाहिए, जहां फोनन गति इलेक्ट्रॉन और फोनन गति (phonon momentum) के बीच अंतर के बराबर होता है। इसके बजाय, एक क्रिस्टलोग्राफिक दोष (crystallographic defect) शामिल हो सकता है, जो अनिवार्य रूप से एक ही भूमिका निभाता है। फोनन (phonons) की भागीदारी की इस प्रक्रिया को दिए गए निश्चित समय में होने की संभावना को बहुत कम करती है, यही वजह है कि विकिरण पुनर्संयोजन (radiative recombination), प्रत्यक्ष बैंड अंतराल (direct band gap) की तुलना में अप्रत्यक्ष बैंड अंतराल (indirect band gap) सामग्री में बहुत धीमा है। यही कारण है कि लाइट-एमिटिंग डायोड और लेजर डायोड लगभग हमेशा प्रत्यक्ष बैंड अंतराल(direct band gap) सामग्री से बने होते हैं, न कि सिलिकॉन जैसे अप्रत्यक्ष बैंड अंतराल वाले (indirect band gap)।
-तथ्य यह है कि अप्रत्यक्ष बैंड गैप (indirect band gap) सामग्री में विकिरण पुनर्संयोजन (radiative recombination) धीमा है, इससे तात्पर्य यह भी है कि, ज्यादातर परिस्थितियों में, विकिरण पुनर्संयोजन (radiative recombination) कुल पुनर्संयोजन (recombinations) का एक छोटा अनुपात होता है, जिसमें अधिकांश पुनर्संयोजन (recombinations) गैर-विकिरणक (non-radiative) होते हैं, जो बिंदु दोषों (point defects) पर या ग्रेन बाउंड्रीज (grain boundaries) पर होते हैं। हालांकि, यदि उत्साहित इलेक्ट्रॉनों (excited electrons) को इन पुनर्संयोजन स्थानों तक पहुंचने से रोका जाता है, तो उनके पास कोई विकल्प नहीं है, लेकिन अंततः विकिरण पुनर्संयोजन (radiative recombination) द्वारा वैलेंस बैंड (valence band) में वापस आने के लिए, यह सामग्री में एक डिसलोकेशन लूप (dislocation loop) बनाकर किया जा सकता है।{{clarify|date=June 2019}} लूप के किनारे पर, डिसलोकेशन डिस्क ("dislocation disk") के ऊपर और नीचे के तलों को अलग कर दिया जाता है, जिससे एक नकारात्मक दबाव होता है, जो चालन बैंड की ऊर्जा को काफी हद तक बढ़ाता है, जिसके परिणामस्वरूप इलेक्ट्रॉन इस किनारे को पास नहीं कर सकते हैं। बशर्ते कि डिसलोकेशन लूप (dislocation loop) के ऊपर का क्षेत्र डिफेक्ट फ्री (defect-free) है (कोई गैर-विकिरणकारी पुनर्संयोजन संभव नहीं है), इलेक्ट्रॉन विकिरण पुनर्संयोजन (radiative recombination) द्वारा वैलेंस शेल (valence shell) में वापस गिर जाएगा, इस प्रकार प्रकाश का उत्सर्जन होगा।यह वह सिद्धांत है जिस पर डेलेड्स  ("DELEDs") (डिसलोकेशन इंजीनियर्ड एलईडी) आधारित हैं।{{cn|date=June 2019}}
+तथ्य यह है कि अप्रत्यक्ष बैंड अंतराल (indirect band gap) सामग्री में विकिरण पुनर्संयोजन (radiative recombination) धीमा है, इससे तात्पर्य यह भी है कि, ज्यादातर परिस्थितियों में, विकिरण पुनर्संयोजन (radiative recombination) कुल पुनर्संयोजन (recombinations) का एक छोटा अनुपात होता है, जिसमें अधिकांश पुनर्संयोजन (recombinations) गैर-विकिरणक (non-radiative) होते हैं, जो बिंदु दोषों (point defects) पर या ग्रेन बाउंड्रीज (grain boundaries) पर होते हैं। हालांकि, यदि उत्साहित इलेक्ट्रॉनों (excited electrons) को इन पुनर्संयोजन स्थानों तक पहुंचने से रोका जाता है, तो उनके पास कोई विकल्प नहीं है, लेकिन अंततः विकिरण पुनर्संयोजन (radiative recombination) द्वारा वैलेंस बैंड (valence band) में वापस आने के लिए, यह सामग्री में एक डिसलोकेशन लूप (dislocation loop) बनाकर किया जा सकता है।{{clarify|date=June 2019}} लूप के किनारे पर, डिसलोकेशन डिस्क ("dislocation disk") के ऊपर और नीचे के तलों को अलग कर दिया जाता है, जिससे एक नकारात्मक दबाव होता है, जो चालन बैंड की ऊर्जा को काफी हद तक बढ़ाता है, जिसके परिणामस्वरूप इलेक्ट्रॉन इस किनारे को पास नहीं कर सकते हैं। बशर्ते कि डिसलोकेशन लूप (dislocation loop) के ऊपर का क्षेत्र डिफेक्ट फ्री (defect-free) है (कोई गैर-विकिरणकारी पुनर्संयोजन संभव नहीं है), इलेक्ट्रॉन विकिरण पुनर्संयोजन (radiative recombination) द्वारा वैलेंस शेल (valence shell) में वापस गिर जाएगा, इस प्रकार प्रकाश का उत्सर्जन होगा।यह वह सिद्धांत है जिस पर डेलेड्स  ("DELEDs") (डिसलोकेशन इंजीनियर्ड एलईडी) आधारित हैं।{{cn|date=June 2019}}
-== '''प्रकाश अवशोषण के लिए निहितार्थ  (Implications for light absorption)''' ==
+== प्रकाश अवशोषण के लिए निहितार्थ  (Implications for light absorption) ==
-विकिरण पुनर्संयोजन (radiative recombination) का सटीक उल्टा प्रकाश अवशोषण (light absorption) है। ऊपर के समान कारण के लिए, बैंड गैप  (band gap) के करीब एक फोटॉन (photon) ऊर्जा के साथ प्रकाश एक प्रत्यक्ष बैंड गैप (direct band gap) एक की तुलना में एक अप्रत्यक्ष बैंड गैप (indirect band gap) सामग्री में अवशोषित होने से पहले बहुत दूर प्रवेश कर सकता है (कम से कम इंसोफ़र (insofar) के रूप में प्रकाश अवशोषण (light absorption) एक्ससिस्टिंग इलेक्ट्रॉनों (exciting electrons) के कारण है बैंड गैप)।
+विकिरण पुनर्संयोजन (radiative recombination) का सटीक उल्टा प्रकाश अवशोषण (light absorption) है। ऊपर के समान कारण के लिए, बैंड अंतराल  (band gap) के करीब एक फोटॉन (photon) ऊर्जा के साथ प्रकाश एक प्रत्यक्ष बैंड अंतराल (direct band gap) एक की तुलना में एक अप्रत्यक्ष बैंड अंतराल (indirect band gap) सामग्री में अवशोषित होने से पहले बहुत दूर प्रवेश कर सकता है (कम से कम इंसोफ़र (insofar) के रूप में प्रकाश अवशोषण (light absorption) एक्ससिस्टिंग इलेक्ट्रॉनों (exciting electrons) के कारण है बैंड अंतराल)।
-यह तथ्य फोटोवोल्टिक (सौर कोशिकाओं) के लिए बहुत महत्वपूर्ण है। क्रिस्टलीय सिलिकॉन (Crystalline silicon) सबसे आम सोलर-सेल सब्सट्रेट (solar-cell substrate material) सामग्री है, इस तथ्य के बावजूद कि यह अप्रत्यक्ष-अंतराल (indirect-gap) है और इसलिए प्रकाश को बहुत अच्छी तरह से अवशोषित नहीं करता है। जैसे, आम तौर पर सैकड़ों माइक्रोन (microns) घने होते हैं; थिनर वेफर्स (thinner wafers) बहुत अधिक प्रकाश (विशेष रूप से लंबे समय तक तरंग दैर्ध्य में) को गुजरने की अनुमति देगा। तुलनात्मक रूप से, पतली-फिल्म सौर कोशिकाएं  (thin-film solar cells) प्रत्यक्ष बैंड गैप सामग्री (जैसे कि अनाकार सिलिकॉन (amorphous silicon), सीडीटीई (CdTe), सीआईजीएस (CIGS) या सीजेडटी (CZTS)) से बनी होती हैं, जो बहुत पतले क्षेत्र में प्रकाश को अवशोषित करती हैं, और परिणामस्वरूप बहुत पतली सक्रिय परत के साथ बनाया जा सकता है ( अक्सर 1 माइक्रोन थिक(micron thick) से कम)।
+यह तथ्य फोटोवोल्टिक (सौर कोशिकाओं) के लिए बहुत महत्वपूर्ण है। क्रिस्टलीय सिलिकॉन (Crystalline silicon) सबसे आम सोलर-सेल सब्सट्रेट (solar-cell substrate material) सामग्री है, इस तथ्य के बावजूद कि यह अप्रत्यक्ष-अंतराल (indirect-gap) है और इसलिए प्रकाश को बहुत अच्छी तरह से अवशोषित नहीं करता है। जैसे, आम तौर पर सैकड़ों माइक्रोन (microns) घने होते हैं; थिनर वेफर्स (thinner wafers) बहुत अधिक प्रकाश (विशेष रूप से लंबे समय तक तरंग दैर्ध्य में) को गुजरने की अनुमति देगा। तुलनात्मक रूप से, पतली-फिल्म सौर कोशिकाएं  (thin-film solar cells) प्रत्यक्ष बैंड अंतराल सामग्री (जैसे कि अनाकार सिलिकॉन (amorphous silicon), सीडीटीई (CdTe), सीआईजीएस (CIGS) या सीजेडटी (CZTS)) से बनी होती हैं, जो बहुत पतले क्षेत्र में प्रकाश को अवशोषित करती हैं, और परिणामस्वरूप बहुत पतली सक्रिय परत के साथ बनाया जा सकता है ( अक्सर 1 माइक्रोन थिक(micron thick) से कम)।
-एक अप्रत्यक्ष बैंड गैप (indirect band gap) सामग्री का अवशोषण स्पेक्ट्रम (absorption spectrum) सामान्यतः एक प्रत्यक्ष सामग्री की तुलना में तापमान पर अधिक निर्भर करता है, क्योंकि कम तापमान पर कम फोनन (phonons) होते हैं, और इसलिए यह कम संभावना है कि एक फोटॉन (photons) और फोनन (phonons) को एक साथ एक अप्रत्यक्ष संक्रमण (indirect transition) बनाने के लिए अवशोषित किया जा सकता है । उदाहरण के लिए, सिलिकॉन कमरे के तापमान पर प्रकाश को देखने के लिए अपारदर्शी है, लेकिन तरल हीलियमl (iquid helium) तापमान पर लाल प्रकाश (red light) के लिए पारदर्शी है, क्योंकि लाल फोटॉन (red photons) केवल एक अप्रत्यक्ष संक्रमण (indirect transition) में अवशोषित हो सकते हैं।{{clarify|date=June 2019}}
+एक अप्रत्यक्ष बैंड अंतराल (indirect band gap) सामग्री का अवशोषण स्पेक्ट्रम (absorption spectrum) सामान्यतः एक प्रत्यक्ष सामग्री की तुलना में तापमान पर अधिक निर्भर करता है, क्योंकि कम तापमान पर कम फोनन (phonons) होते हैं, और इसलिए यह कम संभावना है कि एक फोटॉन (photons) और फोनन (phonons) को एक साथ एक अप्रत्यक्ष संक्रमण (indirect transition) बनाने के लिए अवशोषित किया जा सकता है । उदाहरण के लिए, सिलिकॉन कमरे के तापमान पर प्रकाश को देखने के लिए अपारदर्शी है, लेकिन तरल हीलियमl (iquid helium) तापमान पर लाल प्रकाश (red light) के लिए पारदर्शी है, क्योंकि लाल फोटॉन (red photons) केवल एक अप्रत्यक्ष संक्रमण (indirect transition) में अवशोषित हो सकते हैं।{{clarify|date=June 2019}}
 === अवशोषण के लिए सूत्र  (Formula for absorption) ===
-यह निर्धारित करने के लिए एक सामान्य और सरल विधि है कि क्या एक बैंड गैप प्रत्यक्ष या अप्रत्यक्ष अवशोषण स्पेक्ट्रोस्कोपी (absorption spectroscopy) का उपयोग करता है। फोटॉन ऊर्जा के खिलाफ अवशोषण गुणांक (absorption coefficient) की कुछ शक्तियों प्लॉट (plotting certain powers) करके, कोई भी सामान्य रूप से बता सकता है कि बैंड गैप का क्या वैल्यू (Value) है, और यह प्रत्यक्ष है या नहीं।
+यह निर्धारित करने के लिए एक सामान्य और सरल विधि है कि क्या एक बैंड अंतराल प्रत्यक्ष या अप्रत्यक्ष अवशोषण स्पेक्ट्रोस्कोपी (absorption spectroscopy) का उपयोग करता है। फोटॉन ऊर्जा के खिलाफ अवशोषण गुणांक (absorption coefficient) की कुछ शक्तियों प्लॉट (plotting certain powers) करके, कोई भी सामान्य रूप से बता सकता है कि बैंड अंतराल का क्या वैल्यू (Value) है, और यह प्रत्यक्ष है या नहीं।
-एक प्रत्यक्ष बैंड गैप (direct band gap) के लिए, अवशोषण गुणांक <math>\alpha</math>  (absorption coefficient) निम्न सूत्र के अनुसार प्रकाश आवृत्ति (light frequency) से संबंधित है:<ref>''Optoelectronics'', by E. Rosencher, 2002, equation (7.25).</ref><ref>Pankove has the same equation, but with an apparently different prefactor <math>A^*</math>. However, in the Pankove version, the units / dimensional analysis appears not to work out.</ref>
+एक प्रत्यक्ष बैंड अंतराल (direct band gap) के लिए, अवशोषण गुणांक <math>\alpha</math>  (absorption coefficient) निम्न सूत्र के अनुसार प्रकाश आवृत्ति (light frequency) से संबंधित है:<ref>''Optoelectronics'', by E. Rosencher, 2002, equation (7.25).</ref><ref>Pankove has the same equation, but with an apparently different prefactor <math>A^*</math>. However, in the Pankove version, the units / dimensional analysis appears not to work out.</ref>
 :<math>\alpha \approx A^*\sqrt{h\nu - E_{\text{g}}}</math>, विथ(with)  <math>A^*=\frac{q^2 x_{vc}^2 (2m_{\text{r}})^{3/2}}{\lambda_0 \epsilon_0 \hbar^3 n}</math>
 जहां पर:
 * <math>\alpha</math> अवशोषण गुणांक (absorption coefficient) है, जोकि प्रकाश आवृत्ति का एक फंक्शन है
 *<math>\nu</math> प्रकाश आवृत्ति (light frequency) है
-*h प्लैंक स्थिरांक है (
+*h प्लैंक स्थिरांक है
-*<math>\hbar</math> कम हो गया है प्लैंक का स्थिरांक (<math>\hbar=h/2\pi</math>)
+*<math>\hbar</math> रेड्यूसड प्लैंक स्थिरांक है (<math>\hbar=h/2\pi</math>)
-*<math>E_{\text{g}}</math> बैंड गैप ऊर्जा है
+*<math>E_{\text{g}}</math> बैंड अंतराल ऊर्जा है
-*<math>A^*</math> एक निश्चित आवृत्ति-स्वतंत्र स्थिरांक है, ऊपर सूत्र के साथ
+*<math>A^*</math> एक निश्चित आवृत्ति-स्वतंत्र स्थिरांक (certain frequency-independent constant है), ऊपर सूत्र के साथ
-*<math>m_{\text{r}}=\frac{m_{\text{h}}^* m_{\text{e}}^*}{m_{\text{h}}^* + m_{\text{e}}^*}</math>, कहाँ पे <math>m_{\text{e}}^*</math> तथा <math>m_{\text{h}}^*</math> प्रभावी द्रव्यमान (ठोस-राज्य भौतिकी) हैं | क्रमशः इलेक्ट्रॉन और छेद के प्रभावी द्रव्यमान<math>m_{\text{r}}</math> एक कम द्रव्यमान कहा जाता है)
+*<math>m_{\text{r}}=\frac{m_{\text{h}}^* m_{\text{e}}^*}{m_{\text{h}}^* + m_{\text{e}}^*}</math>, जहां पर  <math>m_{\text{e}}^*</math> तथा <math>m_{\text{h}}^*</math> प्रभावी द्रव्यमान (effective masses) हैं | क्रमशः इलेक्ट्रॉन और होल (hole) के प्रभावी द्रव्यमान  (<math>m_{\text{r}}</math> को रेड्यूसड मॉस कहा जाता है)
-*<math>q</math> प्राथमिक चार्ज है
+*<math>q</math> प्राथमिक चार्ज (elementary charge) है
-*<math>n</math> अपवर्तन का (वास्तविक) सूचकांक है
+*<math>n</math> अपवर्तन का (वास्तविक) सूचकांक (index of refraction) है
-*<math>\epsilon_0</math> वैक्यूम पारगम्यता है
+*<math>\epsilon_0</math> वैक्यूम पारगम्यता (vacuum permittivity) है
-*<math>x_{vc}</math> एक मैट्रिक्स तत्व है, लंबाई और विशिष्ट मूल्य की इकाइयों के साथ परिमाण का एक ही क्रम जाली के रूप में स्थिर है।
+*<math>x_{vc}</math> एक मैट्रिक्स तत्व ("matrix element") है, लंबाई और विशिष्ट मूल्य की इकाइयों के साथ लैत्तीस कांस्टेंट (lattice constant) के रूप में स्थिर है।
+यह सूत्र केवल फोटॉन ऊर्जा के साथ प्रकाश के लिए मान्य है, लेकिन बैंड अंतराल की तुलना में (अधिक विशेष रूप से, यह सूत्र मानता है कि बैंड लगभग परवलयिक हैं) बहुत अधिक बड़ा नहीं है, और बैंड-टू-बैंड के अलावा अन्य सभी अन्य स्रोतों को अनदेखा करता है-प्रश्न में बैंड अवशोषण, साथ ही नए बनाए गए इलेक्ट्रॉन औरहोल (hole) के बीच विद्युत आकर्षण (एक्सिटॉन देखें) (see exciton)। इस मामले में यह भी अमान्य है कि प्रत्यक्ष संक्रमण (direct transition) निषिद्ध है, या इस मामले में कि कई वैलेंस बैंड स्टेट्स (valence band states) खाली हैं या चालन बैंड स्टेट्स (conduction band states) भरे हुए हैं।<ref name=Pankove>J.I. Pankove, ''Optical Processes in Semiconductors''. Dover, 1971.</ref>
+दूसरी ओर, एक अप्रत्यक्ष बैंड अंतराल  (indirect band gap) के लिए,
+सूत्र है:<ref name="Pankove" />:<math>\alpha \propto \frac{(h\nu-E_{\text{g}}+E_{\text{p}})^2}{\exp(\frac{E_{\text{p}}}{kT})-1} + \frac{(h\nu-E_{\text{g}}-E_{\text{p}})^2}{1-\exp(-\frac{E_{\text{p}}}{kT})}</math>
-यह सूत्र केवल फोटॉन ऊर्जा के साथ प्रकाश के लिए मान्य है, लेकिन बहुत अधिक बड़ा नहीं है, बैंड गैप की तुलना में (अधिक विशेष रूप से, यह सूत्र मानता है कि बैंड लगभग परवलयिक हैं), और बैंड-टू के अलावा अन्य सभी अन्य स्रोतों को अनदेखा करता है-प्रश्न में बैंड अवशोषण, साथ ही नए बनाए गए इलेक्ट्रॉन और छेद के बीच विद्युत आकर्षण (एक्सिटॉन देखें)।यह भी इस मामले में अमान्य है कि प्रत्यक्ष संक्रमण निषिद्ध है, या इस मामले में कि कई वैलेंस बैंड राज्य खाली हैं या चालन बैंड राज्य भरे हुए हैं।<ref name=Pankove>J.I. Pankove, ''Optical Processes in Semiconductors''. Dover, 1971.</ref>
+जहां पर:
-दूसरी ओर, एक अप्रत्यक्ष बैंड गैप के लिए, सूत्र है:<ref name=Pankove/>:<math>\alpha \propto \frac{(h\nu-E_{\text{g}}+E_{\text{p}})^2}{\exp(\frac{E_{\text{p}}}{kT})-1} + \frac{(h\nu-E_{\text{g}}-E_{\text{p}})^2}{1-\exp(-\frac{E_{\text{p}}}{kT})}</math>
+*<math>E_{\text{p}}</math> फोनन (phonon) की ऊर्जा है जो संक्रमण में सहायता करती है
-कहाँ पे:
+*<math>k</math> बोल्ट्जमैन स्थिरांक है
-*<math>E_{\text{p}}</math> फोनन की ऊर्जा है जो संक्रमण में सहायता करती है
-*<math>k</math> बोल्ट्जमैन का स्थिरांक है
 *<math>T</math> थर्मोडायनामिक तापमान है
 इस सूत्र में ऊपर वर्णित समान अनुमान शामिल हैं।
-इसलिए, अगर एक साजिश <math>h\nu</math> बनाम <math>\alpha^2</math> एक सीधी रेखा बनाता है, यह सामान्य रूप से अनुमान लगाया जा सकता है कि एक सीधा बैंड गैप है, सीधी रेखा को एक्सट्रपलेशन करके औसत दर्जे का <math>\alpha=0</math> एक्सिस।दूसरी ओर, अगर एक भूखंड <math>h\nu</math> बनाम <math>\alpha^{1/2}</math> एक सीधी रेखा बनाता है, यह सामान्य रूप से अनुमान लगाया जा सकता है कि एक अप्रत्यक्ष बैंड गैप है, सीधी रेखा को एक्सट्रपलेशन करके औसत दर्जे का <math>\alpha=0</math> अक्ष) <math>E_{\text{p}}\approx 0</math>)।
+इसलिए, अगर एक प्लाट  <math>h\nu</math> बनाम <math>\alpha^2</math> एक सीधी रेखा बनाता है, यह सामान्य रूप से अनुमान लगाया जा सकता है कि एक सीधा बैंड अंतराल है, सीधी रेखा, को एक्सट्रपलेशन (extrapolating) करके औसत दर्जे का <math>\alpha=0</math> एक्सिस। दूसरी ओर, अगर एक प्लाट <math>h\nu</math> बनाम <math>\alpha^{1/2}</math> एक सीधी रेखा बनाता है, यह सामान्य रूप से अनुमान लगाया जा सकता है कि एक अप्रत्यक्ष बैंड अंतराल है, सीधी रेखा को एक्सट्रपलेशन (extrapolating) करके औसत दर्जे का (<math>\alpha=0</math> अक्ष) <math>E_{\text{p}}\approx 0</math>)।
+== अन्य पहलू  ==
-== अन्य पहलू ==
+अप्रत्यक्ष अंतर के साथ कुछ सामग्रियों में, अंतर (gap) का मूल्य नकारात्मक है। वैलेंस बैंड (valence band) का शीर्ष ऊर्जा में चालन बैंड (conduction band) के बॉटम (bottom) से अधिक है। इस तरह की सामग्रियों को सेमीमेटल (semimetals) के रूप में जाना जाता है।
-अप्रत्यक्ष अंतर के साथ कुछ सामग्रियों में, अंतर का मूल्य नकारात्मक है।वैलेंस बैंड का शीर्ष ऊर्जा में चालन बैंड के नीचे से अधिक है।इस तरह की सामग्रियों को सेमीमेटल के रूप में जाना जाता है।
+== यह भी देखें  ==
+* मॉस -बर्स्टीन प्रभाव (Moss–Burstein effect)
-== यह भी देखें ==
+* ताउक प्लॉट (Tauc plot)
-* मॉस -बर्स्टीन प्रभाव
-* ताउक प्लॉट
 ==संदर्भ==
@@ Line 70: / Line 74: @@
 ==बाहरी संबंध==
 * [http://ece-www.colorado.edu/~bart/book/book/chapter4/ch4_6.htm B. Van Zeghbroeck's Principles of Semiconductor Devices] {{Webarchive|url=https://web.archive.org/web/20090122123744/http://ece-www.colorado.edu/~bart/book/book/chapter4/ch4_6.htm |date=2009-01-22 }} at Electrical and Computer Engineering Department of University of Colorado at Boulder
-[[Category: इलेक्ट्रॉनिक बैंड संरचनाएं]]
-[[Category: ऑप्टोइलेक्ट्रॉनिक्स]]]
+]
-[[Category: Machine Translated Page]]
+[[Category:All articles with unsourced statements]]
+[[Category:Articles with hatnote templates targeting a nonexistent page]]
+[[Category:Articles with invalid date parameter in template]]
+[[Category:Articles with short description]]
+[[Category:Articles with unsourced statements from June 2019]]
+[[Category:Machine Translated Page]]
+[[Category:Short description with empty Wikidata description]]
+[[Category:Webarchive template wayback links]]
+[[Category:Wikipedia articles needing clarification from June 2019]]
+[[Category:इलेक्ट्रॉनिक बैंड संरचनाएं]]
+[[Category:ऑप्टोइलेक्ट्रॉनिक्स]]

Anonymous

Search

प्रत्यक्ष और अप्रत्यक्ष बैंड अंतराल: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 13:50, 6 September 2022

Contents

विकिरण पुनर्संयोजन के लिए निहितार्थ (Implications for radiative recombination)

प्रकाश अवशोषण के लिए निहितार्थ (Implications for light absorption)

अवशोषण के लिए सूत्र (Formula for absorption)

अन्य पहलू

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

प्रत्यक्ष और अप्रत्यक्ष बैंड अंतराल: Difference between revisions

Latest revision as of 13:50, 6 September 2022

विकिरण पुनर्संयोजन के लिए निहितार्थ (Implications for radiative recombination)

प्रकाश अवशोषण के लिए निहितार्थ (Implications for light absorption)

अवशोषण के लिए सूत्र (Formula for absorption)

अन्य पहलू

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories