दूरसंचार में सिग्नल की ताकत: Difference between revisions

Revision as of 22:41, 5 April 2023

"सिग्नल सामर्थ्य" यहां पुनर्निर्देश करती है। संकेत सामर्थ्य (भौतिकी) के साथ भ्रमित न हों।

दूरसंचार में, विशेष रूप से रेडियो-आवृत्ति अभियांत्रिकी में, सिग्नल सामर्थ्य प्रेषक बिजली उत्पादन को संदर्भित करता है जैसा कि प्रसारण एंटीना से दूरी पर संदर्भ एंटीना द्वारा प्राप्त किया जाता है। उच्च-शक्ति वाले प्रसारण, जैसे प्रसारण में उपयोग किए जाने वाले, डेसीबल-मिलीवोल्ट प्रति मीटर (dBmV/m) में व्यक्त किए जाते हैं। मोबाइल फोन जैसे बहुत कम बिजली व्यवस्था के लिए, सिग्नल सामर्थ्य सामान्य रूप से डेसीबल-मिलीवोल्ट प्रति मीटर (dBμV/m) या एक मिलीवाट (dBm) के संदर्भ स्तर से ऊपर डेसिबल में व्यक्त की जाती है। प्रसारण शब्दावली में, 1 mV/m 1000 μV/m या 60 dBμ (जिसे प्रायः dBu लिखा जाता है) होता है।

उदाहरण

100 dBμ या 100 mV/m: कुछ अभिग्राही पर आवृत व्यवधान उत्पन्न हो सकता है।
60 dBμ या 1.0 mV/m: प्रायः उत्तरी अमेरिका में एक प्रसारण केंद्र के संरक्षित क्षेत्र का कोर माना जाता है
40 dBμ या 0.1 mV/m: न्यूनतम सामर्थ्य जिस पर एक केंद्र को अधिकांश अभिग्राही पर स्वीकार्य गुणवत्ता के साथ प्राप्त किया जा सकता है

औसत विकीर्ण शक्ति से संबंध

विशिष्ट बिंदु पर विद्युत क्षेत्र की सामर्थ्य को प्रसारण एंटीना, इसकी ज्यामिति और विकिरण प्रतिरोध को दी गई शक्ति से निर्धारित किया जा सकता है। मुक्त आकाशीय में केंद्र-सिंचित अर्ध तरंग द्विध्रुवीय एंटीना की स्थिति पर विचार करें, जहां कुल लंबाई L अर्ध तरंग-दैर्ध्य (λ/2) के समतुल्य है। यदि पतले संवाहकों से निर्मित किया जाता है, तो धारा वितरण अनिवार्य रूप से ज्यावक्रीय होता है और विकिरण विद्युत क्षेत्र द्वारा दिया जाता है

लंबाई के एंटीना पर धारा वितरण

\scriptstyle {L}

अर्ध- तरंग दैर्ध्य के समतुल्य (

\scriptstyle {\lambda /2}

) है।

: $E_{\theta }(r)={-jI_{\circ } \over 2\pi \varepsilon _{0}c\,r}{\cos \left(\scriptstyle {\pi \over 2}\cos \theta \right) \over \sin \theta }e^{j\left(\omega t-kr\right)}$

जहाँ $\scriptstyle {\theta }$ ऐन्टेना अक्ष और वेक्टर के बीच अवलोकन बिंदु के बीच का कोण है, और प्रभरण बिंदु पर $\scriptstyle {I_{\circ }}$ श्रंग धारा है, मुक्त आकाशीय $\scriptstyle {\varepsilon _{0}\,=\,8.85\times 10^{-12}\,F/m}$ की पारगम्यता है, निर्वात में $\scriptstyle {c\,=\,3\times 10^{8}\,m/S}$ प्रकाश की गति है, और $\scriptstyle {r}$ मीटर में एंटीना की दूरी है। जब एंटीना को व्यापक रूप से ( $\scriptstyle {\theta \,=\,\pi /2}$ ) देखा जाता है, विद्युत क्षेत्र अधिकतम होता है और इसके द्वारा दिया जाता है

\vert E_{\pi /2}(r)\vert ={I_{\circ } \over 2\pi \varepsilon _{0}c\,r}\,.

श्रंग धारा उत्पादन के लिए इस सूत्र को हल करना

I_{\circ }=2\pi \varepsilon _{0}c\,r\vert E_{\pi /2}(r)\vert \,.

एंटीना की औसत शक्ति है

{P_{avg}={1 \over 2}R_{a}\,I_{\circ }^{2}}

जहाँ $\scriptstyle {R_{a}=73.13\,\Omega }$ केंद्र-सिंचित अर्ध तरंग एंटीना का विकिरण प्रतिरोध है। और $\scriptstyle {I_{\circ }}$ के लिए सूत्र को $\scriptstyle {P_{avg}}$ मे प्रतिस्थापित करना और अधिकतम विद्युत क्षेत्र उत्पादन के लिए हल करना

\vert E_{\pi /2}(r)\vert \,=\,{1 \over \pi \varepsilon _{0}c\,r}{\sqrt {P_{avg} \over 2R_{a}}}\,=\,{9.91 \over r}{\sqrt {P_{avg}}}\quad (L=\lambda /2)\,.

इसलिए, यदि अर्ध-तरंग द्विध्रुव एंटेना की औसत शक्ति 1 मेगावाट है, तो 313 मीटर (1027 फीट) पर अधिकतम विद्युत क्षेत्र 1 मिलिवोल्ट/मीटर (60 dBμ) है।

लघु द्विध्रुव के लिए ( $\scriptstyle {L\ll \lambda /2}$ ) धारा वितरण लगभग त्रिकोणीय है। इस स्थिति में, विद्युत क्षेत्र और विकिरण प्रतिरोध हैं

E_{\theta }(r)={-jI_{\circ }\sin(\theta ) \over 4\varepsilon _{0}c\,r}\left({L \over \lambda }\right)e^{j\left(\omega t-kr\right)}\,,\quad R_{a}=20\pi ^{2}\left({L \over \lambda }\right)^{2}.

उपरोक्त के समान एक प्रक्रिया का उपयोग करते हुए, केंद्र-सिंचित लघु द्विध्रुव के लिए अधिकतम विद्युत क्षेत्र है

\vert E_{\pi /2}(r)\vert \,=\,{1 \over \pi \varepsilon _{0}c\,r}{\sqrt {P_{avg} \over 160}}\,=\,{9.48 \over r}{\sqrt {P_{avg}}}\quad (L\ll \lambda /2)\,.

रेडियो-आवृति सिग्नल

यद्यपि वैश्विक स्तर पर कई देशों में सेल फोन आधार केंद्र टॉवर नेटवर्क हैं, फिर भी उन देशों के अंदर कई क्षेत्र ऐसे हैं जिनका अच्छा अभिग्रहण नहीं है। कुछ ग्रामीण क्षेत्रों को कभी भी प्रभावी रूप से आवृत करने की संभावना नहीं है क्योंकि केवल कुछ ग्राहकों के लिए सेल टावर लगाने की कीमत बहुत अधिक है। उच्च सिग्नल सामर्थ्य वाले क्षेत्रों में भी, आधारक और बड़े भवनों के आंतरिक भागों में प्रायः विकृत अभिग्रहण होता है।

दुर्बल सिग्नल की सामर्थ्य शहरी क्षेत्रों में स्थानीय टावरों से सिग्नल के विनाशी व्यतिकरण या कुछ भवनों में उपयोग की जाने वाली निर्माण सामग्री के कारण सिग्नल सामर्थ्य के महत्वपूर्ण क्षीणन के कारण भी हो सकती है। प्रायः गोदामों, अस्पतालों और कारखानों जैसी बड़ी इमारतों में बाहरी दीवारों से कुछ मीटर की दूरी पर कोई उपयोगी सिग्नल नहीं होता है।

यह उन नेटवर्कों के लिए विशेष रूप से सत्य है जो उच्च आवृत्ति पर काम करते हैं क्योंकि इन्हें अन्तः क्षेप करने वाले अवरोध से अधिक क्षीण किया जाता है, हालांकि वे प्रतिबिंब (भौतिकी) का उपयोग करने में सक्षम होते हैं और अवरोध को दूर करने के लिए विवर्तन करते हैं।

अनुमानित प्राप्त सिग्नल सामर्थ्य

सक्रिय रेडियो आवृति पहचान टैग में अनुमानित प्राप्त सिग्नल शक्ति का अनुमान निम्नानुसार लगाया जा सकता है:

\mathrm {dBm_{e}} =-43.0-40.0\ \log _{10}\left({\frac {r}{R}}\right)

सामान्य रूप से, आप पथ हानि घातांक को ध्यान में रख सकते हैं:^[1]

\mathrm {dBm_{e}} =-43.0-10.0\ \gamma \ \log _{10}\left({\frac {r}{R}}\right)

पैरामीटर	विवरण
dBm_e	सक्रिय डियो आवृति पहचान टैग में अनुमानित शक्ति प्राप्त हुई
−43	न्यूनतम प्राप्त शक्ति
40	मोबाइल नेटवर्क के लिए प्रति दशक औसत पथ हानि
$r$	दूरी मोबाइल उपकरण - सेल टावर
$R$	सेल टॉवर की औसत त्रिज्या
$γ$	पथ हानि घातांक

प्रभावी पथ हानि रेडियो आवृत्ति, स्थलाकृति और पर्यावरणीय परिस्थितियों पर निर्भर करती है।

वास्तव में, कोई भी ज्ञात सिग्नल शक्ति dBm₀ का उपयोग कर सकता है किसी भी दूरी पर r₀ संदर्भ मे:

\mathrm {dBm_{e}} =\mathrm {dBm} _{0}-10.0\ \gamma \ \log _{10}\left({\frac {r}{r_{0}}}\right)

दशकों की संख्या

\log _{10}(R/r)

दशकों की संख्या का अनुमान देगा, जो 40 डेसीबल/दशक की औसत पथ हानि के साथ समान है।

सेल त्रिज्या का अनुमान लगाएं

जब हम सेल की दूरी r और प्राप्त शक्ति dBm_m जोड़े को मापते हैं, तो हम माध्य सेल त्रिज्या का अनुमान निम्नानुसार लगा सकते हैं:

R_{e}=\operatorname {avg} [\ r\ 10^{(\mathrm {dBm_{m}} +43.0)/40.0}\ ]

विशिष्ट गणना मॉडल एक नए सेल टॉवर के स्थान की योजना बनाने के लिए सम्मिलित हैं, स्थानीय परिस्थितियों और रेडियो उपकरण मापदंडों को ध्यान में रखते हुए, साथ ही साथ मोबाइल रेडियो सिग्नलों में दृष्टिरेखीय संचरण होता है, जब तक कि प्रतिबिंब न हो।

यह भी देखें

संदर्भ

↑ Figueiras, João; Frattasi, Simone (2010). Mobile Positioning and Tracking: From Conventional to Cooperative Techniques. John Wiley & Sons. ISBN 978-1119957560.

बाहरी संबंध

[1] Figueiras, João; Frattasi, Simone (2010). Mobile Positioning and Tracking: From Conventional to Cooperative Techniques. John Wiley & Sons. ISBN 978-1119957560.

[1]

@@ Line 1: / Line 1: @@
-{{distinguish-redirect|Signal strength|Signal strength (physics)}}
+"सिग्नल सामर्थ्य" यहां पुनर्निर्देश करती है। संकेत सामर्थ्य (भौतिकी) के साथ भ्रमित न हों।
-[[दूरसंचार]] में, विशेष रूप से [[रेडियो फ्रीक्वेंसी इंजीनियरिंग]] में, सिग्नल स्ट्रेंथ [[ट्रांसमीटर बिजली उत्पादन]] को संदर्भित करता है जैसा कि ट्रांसमिटिंग एंटीना से दूरी पर संदर्भ एंटीना द्वारा प्राप्त किया जाता है। [[नाममात्र शक्ति]] | उच्च-शक्ति वाले [[प्रसारण]], जैसे प्रसारण में उपयोग किए जाने वाले, [[डेसिबल]]-मिलीवोल्ट प्रति मीटर ([[dBm]]V/m) में व्यक्त किए जाते हैं। बहुत कम बिजली वाले सिस्टम, जैसे कि [[ चल दूरभाष ]] के लिए, सिग्नल की शक्ति आमतौर पर डेसिबल-[[ microvolt ]]्स प्रति मीटर (dBμV/m) या एक वाट (यूनिट) (dBm) के संदर्भ स्तर से ऊपर डेसिबल में व्यक्त की जाती है। प्रसारण शब्दावली में, 1 mV/m 1000 μV/m या 60 डेसीबल#रेडियो शक्ति, ऊर्जा और क्षेत्र शक्ति|dBμ (अक्सर dBu लिखा जाता है) है।
+दूरसंचार में, विशेष रूप से रेडियो-आवृत्ति अभियांत्रिकी में, '''सिग्नल सामर्थ्य''' प्रेषक बिजली उत्पादन को संदर्भित करता है जैसा कि प्रसारण एंटीना से दूरी पर संदर्भ एंटीना द्वारा प्राप्त किया जाता है। उच्च-शक्ति वाले प्रसारण, जैसे प्रसारण में उपयोग किए जाने वाले, डेसीबल-मिलीवोल्ट प्रति मीटर (dBmV/m) में व्यक्त किए जाते हैं। मोबाइल फोन जैसे बहुत कम बिजली व्यवस्था के लिए, सिग्नल सामर्थ्य सामान्य रूप से डेसीबल-मिलीवोल्ट प्रति मीटर (dBμV/m) या एक मिलीवाट (dBm) के संदर्भ स्तर से ऊपर डेसिबल में व्यक्त की जाती है। प्रसारण शब्दावली में, 1 mV/m 1000 μV/m या 60 dBμ (जिसे प्रायः dBu लिखा जाता है) होता है।
 ;उदाहरण:
-*100 dBμ या 100 mV/m: कुछ रिसीवर्स पर [[ कंबल ]] इंटरफेरेंस हो सकता है
+*100 dBμ या 100 mV/m: कुछ अभिग्राही पर आवृत व्यवधान उत्पन्न हो सकता है।
-*60 dBμ या 1.0 mV/m: अक्सर उत्तरी अमेरिका में एक [[रेडियो स्टेशन]] के संरक्षित क्षेत्र का किनारा माना जाता है
+*60 dBμ या 1.0 mV/m: प्रायः उत्तरी अमेरिका में एक [[रेडियो स्टेशन|प्रसारण केंद्र]] के संरक्षित क्षेत्र का कोर माना जाता है
-*40 dBμ या 0.1 mV/m: न्यूनतम शक्ति जिस पर एक स्टेशन को अधिकांश रिसीवरों पर स्वीकार्य गुणवत्ता के साथ प्राप्त किया जा सकता है
+*40 dBμ या 0.1 mV/m: न्यूनतम सामर्थ्य जिस पर एक केंद्र को अधिकांश अभिग्राही पर स्वीकार्य गुणवत्ता के साथ प्राप्त किया जा सकता है
 == औसत विकीर्ण शक्ति से संबंध ==
-एक विशिष्ट बिंदु पर विद्युत क्षेत्र की ताकत को ट्रांसमिटिंग एंटीना, इसकी ज्यामिति और विकिरण प्रतिरोध को दी गई शक्ति से निर्धारित किया जा सकता है। [[फ्री-स्पेस ऑप्टिकल संचार]] में सेंटर-फेड हाफ-वेव [[द्विध्रुवीय एंटीना]] के मामले पर विचार करें, जहां कुल लंबाई एल एक आधे वेवलेंथ (λ/2) के बराबर है। यदि पतले कंडक्टरों से निर्मित किया जाता है, तो वर्तमान वितरण अनिवार्य रूप से साइनसोइडल होता है और विकिरण विद्युत क्षेत्र द्वारा दिया जाता है
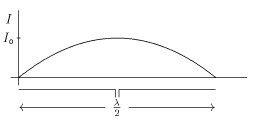
+विशिष्ट बिंदु पर विद्युत क्षेत्र की सामर्थ्य को प्रसारण एंटीना, इसकी ज्यामिति और विकिरण प्रतिरोध को दी गई शक्ति से निर्धारित किया जा सकता है। [[फ्री-स्पेस ऑप्टिकल संचार|मुक्त आकाशीय]] में केंद्र-सिंचित अर्ध तरंग [[द्विध्रुवीय एंटीना]] की स्थिति पर विचार करें, जहां कुल लंबाई L अर्ध तरंग-दैर्ध्य (λ/2) के समतुल्य है। यदि पतले संवाहकों से निर्मित किया जाता है, तो धारा वितरण अनिवार्य रूप से ज्यावक्रीय होता है और विकिरण विद्युत क्षेत्र द्वारा दिया जाता है
-[[Image:lambdaover2-antenna.jpg|frame|लंबाई के एंटीना पर वर्तमान वितरण <math> \scriptstyle{L} </math> एक आधा तरंग दैर्ध्य के बराबर (<math>\scriptstyle{\lambda /2}</math>).]]:<math>
+[[Image:lambdaover2-antenna.jpg|frame|लंबाई के एंटीना पर धारा वितरण <math> \scriptstyle{L} </math> अर्ध- तरंग दैर्ध्य के समतुल्य (<math>\scriptstyle{\lambda /2}</math>) है।]]:<math>
 E_\theta (r) =
 {-jI_\circ\over 2\pi\varepsilon_0 c\, r}
@@ Line 17: / Line 18: @@
 e^{j\left(\omega t-kr\right)}
 </math>
-कहाँ <math>\scriptstyle{\theta}</math> ऐन्टेना अक्ष और वेक्टर के बीच अवलोकन बिंदु के बीच का कोण है, <math>\scriptstyle{I_\circ}</math> फीड-पॉइंट पर पीक करंट है, <math>\scriptstyle{\varepsilon_0 \, = \, 8.85\times 10^{-12} \, F/m }</math> मुक्त स्थान की पारगम्यता है, <math>\scriptstyle{c \, = \, 3\times 10^8 \, m/S}</math> निर्वात में प्रकाश की गति है, और <math>\scriptstyle{r}</math> मीटर में एंटीना की दूरी है। जब एंटीना को व्यापक रूप से देखा जाता है (<math>\scriptstyle{\theta \, = \, \pi/2}</math>) विद्युत क्षेत्र अधिकतम होता है और इसके द्वारा दिया जाता है
+जहाँ <math>\scriptstyle{\theta}</math> ऐन्टेना अक्ष और वेक्टर के बीच अवलोकन बिंदु के बीच का कोण है, और प्रभरण बिंदु पर <math>\scriptstyle{I_\circ}</math> श्रंग धारा है, मुक्त आकाशीय <math>\scriptstyle{\varepsilon_0 \, = \, 8.85\times 10^{-12} \, F/m }</math> की पारगम्यता है, निर्वात में <math>\scriptstyle{c \, = \, 3\times 10^8 \, m/S}</math> प्रकाश की गति है, और <math>\scriptstyle{r}</math> मीटर में एंटीना की दूरी है। जब एंटीना को व्यापक रूप से (<math>\scriptstyle{\theta \, = \, \pi/2}</math>) देखा जाता है, विद्युत क्षेत्र अधिकतम होता है और इसके द्वारा दिया जाता है
 :<math>
 \vert E_{\pi/2}(r) \vert = { I_\circ \over 2\pi\varepsilon_0 c\, r }\, .
 </math>
-पीक करंट यील्ड के लिए इस फॉर्मूले को हल करना
+श्रंग धारा उत्पादन के लिए इस सूत्र को हल करना
 :<math>
@@ Line 29: / Line 30: @@
 :<math> {P_{avg} = {1 \over 2} R_a \, I_\circ^2 } </math>
-कहाँ <math> \scriptstyle{R_a = 73.13\,\Omega} </math> केंद्र-पोषित हाफ-वेव एंटीना का विकिरण प्रतिरोध है। के लिए सूत्र को प्रतिस्थापित करना <math> \scriptstyle{I_\circ} </math> के लिए एक में <math> \scriptstyle{P_{avg}} </math> और अधिकतम विद्युत क्षेत्र पैदावार के लिए हल करना
+जहाँ <math> \scriptstyle{R_a = 73.13\,\Omega} </math> केंद्र-सिंचित अर्ध तरंग एंटीना का विकिरण प्रतिरोध है। और <math> \scriptstyle{I_\circ} </math> के लिए सूत्र को <math> \scriptstyle{P_{avg}} </math> मे प्रतिस्थापित करना और अधिकतम विद्युत क्षेत्र उत्पादन के लिए हल करना
 :<math>
@@ Line 36: / Line 37: @@
 {9.91 \over r} \sqrt{ P_{avg} } \quad (L = \lambda /2) \, .
 </math>
-इसलिए, यदि अर्ध-तरंग द्विध्रुव एंटेना की औसत शक्ति 1 mW है, तो 313 m (1027 ft) पर अधिकतम विद्युत क्षेत्र 1 mV/m (60 dBμ) है।
+इसलिए, यदि अर्ध-तरंग द्विध्रुव एंटेना की औसत शक्ति 1 मेगावाट है, तो 313 मीटर (1027 फीट) पर अधिकतम विद्युत क्षेत्र 1 मिलिवोल्ट/मीटर (60 dBμ) है।
-लघु द्विध्रुव के लिए (<math>\scriptstyle{L \ll \lambda /2}</math>) वर्तमान वितरण लगभग त्रिकोणीय है। इस मामले में, विद्युत क्षेत्र और विकिरण प्रतिरोध हैं
+लघु द्विध्रुव के लिए (<math>\scriptstyle{L \ll \lambda /2}</math>) धारा वितरण लगभग त्रिकोणीय है। इस स्थिति में, विद्युत क्षेत्र और विकिरण प्रतिरोध हैं
 :<math>
@@ Line 46: / Line 47: @@
 R_a = 20\pi^2 \left ( {L \over \lambda} \right )^2 .
 </math>
-उपरोक्त के समान एक प्रक्रिया का उपयोग करते हुए, केंद्र-पोषित लघु द्विध्रुव के लिए अधिकतम विद्युत क्षेत्र है
+उपरोक्त के समान एक प्रक्रिया का उपयोग करते हुए, केंद्र-सिंचित लघु द्विध्रुव के लिए अधिकतम विद्युत क्षेत्र है
 :<math>
@@ Line 55: / Line 56: @@
-== आरएफ सिग्नल ==
+== रेडियो-आवृति सिग्नल ==
-यद्यपि वैश्विक स्तर पर कई देशों में सेल फोन बेस स्टेशन टॉवर नेटवर्क हैं, फिर भी उन देशों के भीतर कई क्षेत्र ऐसे हैं जिनका अच्छा स्वागत नहीं है। कुछ ग्रामीण क्षेत्रों को कभी भी प्रभावी ढंग से कवर करने की संभावना नहीं है क्योंकि केवल कुछ ग्राहकों के लिए सेल टावर लगाने की लागत बहुत अधिक है। उच्च सिग्नल शक्ति वाले क्षेत्रों में भी, बेसमेंट और बड़ी इमारतों के अंदरूनी हिस्सों में अक्सर खराब स्वागत होता है।
+यद्यपि वैश्विक स्तर पर कई देशों में सेल फोन आधार केंद्र टॉवर नेटवर्क हैं, फिर भी उन देशों के अंदर कई क्षेत्र ऐसे हैं जिनका अच्छा अभिग्रहण नहीं है। कुछ ग्रामीण क्षेत्रों को कभी भी प्रभावी रूप से आवृत करने की संभावना नहीं है क्योंकि केवल कुछ ग्राहकों के लिए सेल टावर लगाने की कीमत बहुत अधिक है। उच्च सिग्नल सामर्थ्य वाले क्षेत्रों में भी, आधारक और बड़े भवनों के आंतरिक भागों में प्रायः विकृत अभिग्रहण होता है।
-कमजोर सिग्नल की शक्ति शहरी क्षेत्रों में स्थानीय टावरों से सिग्नल के विनाशकारी हस्तक्षेप या कुछ इमारतों में उपयोग की जाने वाली निर्माण सामग्री के कारण सिग्नल की शक्ति के महत्वपूर्ण क्षीणन के कारण भी हो सकती है। गोदामों, अस्पतालों और कारखानों जैसी बड़ी इमारतों में अक्सर बाहरी दीवारों से कुछ मीटर की दूरी पर कोई उपयोगी संकेत नहीं होता है।
+दुर्बल सिग्नल की सामर्थ्य शहरी क्षेत्रों में स्थानीय टावरों से सिग्नल के विनाशी व्यतिकरण या कुछ भवनों में उपयोग की जाने वाली निर्माण सामग्री के कारण सिग्नल सामर्थ्य के महत्वपूर्ण क्षीणन के कारण भी हो सकती है। प्रायः गोदामों, अस्पतालों और कारखानों जैसी बड़ी इमारतों में बाहरी दीवारों से कुछ मीटर की दूरी पर कोई उपयोगी सिग्नल नहीं होता है।
-यह उन नेटवर्कों के लिए विशेष रूप से सच है जो उच्च [[आवृत्ति]] पर काम करते हैं क्योंकि इन्हें हस्तक्षेप करने वाली बाधाओं से अधिक क्षीण किया जाता है, हालांकि वे [[प्रतिबिंब (भौतिकी)]] का उपयोग करने में सक्षम होते हैं और बाधाओं को दूर करने के लिए [[विवर्तन]] करते हैं।
+यह उन नेटवर्कों के लिए विशेष रूप से सत्य है जो उच्च [[आवृत्ति]] पर काम करते हैं क्योंकि इन्हें अन्तः क्षेप करने वाले अवरोध से अधिक क्षीण किया जाता है, हालांकि वे [[प्रतिबिंब (भौतिकी)]] का उपयोग करने में सक्षम होते हैं और अवरोध को दूर करने के लिए [[विवर्तन]] करते हैं।
-===अनुमानित प्राप्त सिग्नल शक्ति===
+===अनुमानित प्राप्त सिग्नल सामर्थ्य===
-एक सक्रिय [[आरएफआईडी टैग]] में अनुमानित प्राप्त सिग्नल शक्ति का अनुमान निम्नानुसार लगाया जा सकता है:
+सक्रिय रेडियो आवृति पहचान [[आरएफआईडी टैग|टैग]] में अनुमानित प्राप्त सिग्नल शक्ति का अनुमान निम्नानुसार लगाया जा सकता है:
 :<math>\mathrm{dBm_e} = -43.0 - 40.0\ \log_{10}\left( \frac{r}{R}\right)</math>
-सामान्य तौर पर, आप पथ हानि को ध्यान में रख सकते हैं:<ref>{{Cite book|title = Mobile Positioning and Tracking: From Conventional to Cooperative Techniques|last1 = Figueiras|first1 = João|publisher = John Wiley & Sons|year = 2010|isbn = 978-1119957560|last2 = Frattasi|first2 = Simone}}</ref>
+सामान्य रूप से, आप पथ हानि घातांक को ध्यान में रख सकते हैं:<ref>{{Cite book|title = Mobile Positioning and Tracking: From Conventional to Cooperative Techniques|last1 = Figueiras|first1 = João|publisher = John Wiley & Sons|year = 2010|isbn = 978-1119957560|last2 = Frattasi|first2 = Simone}}</ref>
 :<math>\mathrm{dBm_e} = -43.0 - 10.0 \ \gamma \ \log_{10}\left( \frac{r}{R}\right)</math>
 {|class="wikitable"
-!Parameter||Description
+!पैरामीटर||विवरण
 |-
-|dBm<sub>e</sub>||Estimated received power in active RFID tag
+|dBm<sub>e</sub>||सक्रिय डियो आवृति पहचान टैग में अनुमानित शक्ति प्राप्त हुई
 |-
-| &minus;43||Minimum received power
+| &minus;43||न्यूनतम प्राप्त शक्ति
 |-
-| 40||Average path loss per decade for mobile networks
+| 40||मोबाइल नेटवर्क के लिए प्रति दशक औसत पथ हानि
 |-
-|{{mvar|r}}||Distance mobile device - cell tower
+|{{mvar|r}}||दूरी मोबाइल उपकरण - सेल टावर
 |-
-|{{mvar|R}}||Mean radius of the cell tower
+|{{mvar|R}}||सेल टॉवर की औसत त्रिज्या
 |-
-|{{mvar|&gamma;}}||Path loss exponent
+|{{mvar|&gamma;}}||पथ हानि घातांक
 |}
 प्रभावी पथ हानि रेडियो आवृत्ति, स्थलाकृति और पर्यावरणीय परिस्थितियों पर निर्भर करती है।
-दरअसल, कोई भी ज्ञात सिग्नल पावर dBm का उपयोग कर सकता है<sub>0</sub> किसी भी दूरी पर आर<sub>0</sub> संदर्भ मे:
+वास्तव में, कोई भी ज्ञात सिग्नल शक्ति dBm<sub>0</sub> का उपयोग कर सकता है किसी भी दूरी पर r<sub>0</sub> संदर्भ मे:
 :<math>\mathrm{dBm_e} = \mathrm{dBm}_0 - 10.0 \ \gamma \ \log_{10}\left( \frac{r}{r_0} \right)</math>
 ===दशकों की संख्या===
-:<math>\log_{10} ( R / r )</math> दशकों की संख्या का अनुमान देगा, जो 40 dB/दशक की औसत पथ हानि के साथ मेल खाता है।
+:<math>\log_{10} ( R / r )</math> दशकों की संख्या का अनुमान देगा, जो 40 डेसीबल/दशक की औसत पथ हानि के साथ समान है।
 === सेल त्रिज्या का अनुमान लगाएं ===
-जब हम सेल की दूरी r मापते हैं और शक्ति प्राप्त करते हैं {{math|dBm<sub>m</sub>}} जोड़े,
+जब हम सेल की दूरी r और प्राप्त शक्ति dBm<sub>m</sub> जोड़े को मापते हैं, तो हम माध्य सेल त्रिज्या का अनुमान निम्नानुसार लगा सकते हैं:
-हम माध्य सेल त्रिज्या का अनुमान निम्नानुसार लगा सकते हैं:
 :<math>R_e = \operatorname{avg}[ \ r \ 10 ^ { ( \mathrm{dBm_m} + 43.0 ) / 40.0 } \ ]</math>
-विशिष्ट गणना मॉडल एक नए सेल टॉवर के स्थान की योजना बनाने के लिए मौजूद हैं, स्थानीय परिस्थितियों और [[रेडियो उपकरण]] मापदंडों को ध्यान में रखते हुए, साथ ही साथ यह विचार करते हुए कि [[ बेतार तंत्र ]] में [[लाइन-ऑफ़-विज़न प्रचार]] है, जब तक कि प्रतिबिंब न हो।
+विशिष्ट गणना मॉडल एक नए सेल टॉवर के स्थान की योजना बनाने के लिए सम्मिलित हैं, स्थानीय परिस्थितियों और [[रेडियो उपकरण]] मापदंडों को ध्यान में रखते हुए, साथ ही साथ मोबाइल रेडियो सिग्नलों में [[लाइन-ऑफ़-विज़न प्रचार|दृष्टिरेखीय संचरण]] होता है, जब तक कि प्रतिबिंब न हो।
 == यह भी देखें ==
@@ Line 104: / Line 104: @@
 * [[सेल नेटवर्क]]
 * [[सेलफोन]]
-* [[सेलुलर पुनरावर्तक]]
+* [[सेलुलर पुनरावर्तक|कोशिकीय पुनरावर्तक]]
-* [[ड्रॉप्ड कॉल]]
+* [[ड्रॉप्ड कॉल|अस्वीकृत कॉल]]
-* [[मृत क्षेत्र (सेल फोन)]]
+*[[मृत क्षेत्र (सेल फोन)|अक्रिय क्षेत्र (सेल फोन)]]
-* फ्री स्पेस में फील्ड स्ट्रेंथ
+* मुक्त आकाश में क्षेत्र सामर्थ्य
-* [[फील्ड स्ट्रेंथ मीटर]]
+* [[फील्ड स्ट्रेंथ मीटर|क्षेत्र सामर्थ्य मीटर]]
 * प्राप्त संकेत शक्ति संकेत
 * [[एस मीटर]]
-* [[सिग्नल (इलेक्ट्रिकल इंजीनियरिंग)]]
+* [[सिग्नल (इलेक्ट्रिकल इंजीनियरिंग)|सिग्नल (विद्युत अभियांत्रिकी)]]
 * [[मोबाइल फोन सिग्नल]]
-* [[कवरेज (दूरसंचार)]]
+* [[कवरेज (दूरसंचार)|मोबाइल कवरेज (दूरसंचार)]]
 ==संदर्भ==
-{{Refimprove|date=January 2017}}
 {{reflist}}

Anonymous

Search

दूरसंचार में सिग्नल की ताकत: Difference between revisions

Namespaces

More

Page actions

Revision as of 22:41, 5 April 2023

Contents

औसत विकीर्ण शक्ति से संबंध