अस्थायी क्षेत्र: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Type of field where the net flow of electromagnetic energy is zero}}{{redirect|अदृश्य|एक प्रतिच्छाया की एनाटॉमी द्वारा चित्र संग्रह के लिए देखें|अदृश्य (चित्र संग्रह)}} | {{Short description|Type of field where the net flow of electromagnetic energy is zero}}{{redirect|अदृश्य|एक प्रतिच्छाया की एनाटॉमी द्वारा चित्र संग्रह के लिए देखें|अदृश्य (चित्र संग्रह)}} | ||
{{Use dmy dates|date=जुलाई 2013}} | {{Use dmy dates|date=जुलाई 2013}} | ||
[[File:Electron density wave - plasmon excitations.png|thumb|325px|धातु परावैद्युत अंतरापृष्ठ के साथ संचरण करने वाली सतह तरंग ([[सतह प्लास्मोन पोलरिटोन|सतह प्रद्रव्येक पोलरिटोन]]) का योजनाबद्ध प्रतिनिधित्व है। सतह से दूर के क्षेत्र तेजी से नष्ट हो जाते हैं (दाहिने हस्त का आलेख) और उन क्षेत्रों को z दिशा में क्षणभंगुर के रूप में वर्णित किया जाता है।]]विद्युतचुंबकीय में, एक क्षणभंगुर क्षेत्र | [[File:Electron density wave - plasmon excitations.png|thumb|325px|धातु परावैद्युत अंतरापृष्ठ के साथ संचरण करने वाली सतह तरंग ([[सतह प्लास्मोन पोलरिटोन|सतह प्रद्रव्येक पोलरिटोन]]) का योजनाबद्ध प्रतिनिधित्व है। सतह से दूर के क्षेत्र तेजी से नष्ट हो जाते हैं (दाहिने हस्त का आलेख) और उन क्षेत्रों को z दिशा में क्षणभंगुर के रूप में वर्णित किया जाता है।]]विद्युतचुंबकीय में, एक क्षणभंगुर क्षेत्र या क्षणभंगुर तरंग, एक दोलनशील विद्युत और/या चुंबकीय क्षेत्र है, जो एक [[विद्युत चुम्बकीय]] तरंग के रूप में संचरण नहीं करते है, परन्तु जिसकी ऊर्जा स्थानिक रूप से स्रोत के आसपास केंद्रित (दोलन आवेश और धाराएं) होती है। यहां तक कि जब एक संचरण विद्युत चुम्बकीय तरंग उत्पन्न होती है (उदाहरण के लिए, एक प्रेषी [[एंटीना (रेडियो)|ऐन्टेना]] द्वारा), तब भी कोई विद्युत या चुंबकीय क्षेत्र के घटक को एक क्षणिक क्षेत्र के रूप में स्पष्ट किया सकता है जिसे कई तरंग दैर्ध्य की दूरी पर देखे गए संचरण तरंग (जैसे एक प्रेषी एंटीना का दूर क्षेत्र) के लिए दोषी नहीं ठहराया जा सकता है। | ||
क्षणभंगुर क्षेत्र की एक | क्षणभंगुर क्षेत्र की एक विशेषता यह है कि उस क्षेत्र में कोई शुद्ध ऊर्जा प्रवाह नहीं होती है। चूंकि विद्युत चुम्बकीय ऊर्जा का शुद्ध प्रवाह औसत प्वाइन्टिंग सदिश द्वारा दिया जाता है, इसका तात्पर्य है कि इन क्षेत्रों में [[पॉयंटिंग वेक्टर|पॉयंटिंग सदिश]], जैसे कि एक पूर्ण दोलन चक्र पर औसत शून्य है।{{efn|Or, expressing the fields '''E''' and '''H''' as [[phasor]]s, the complex Poynting vector <math>\mathbf{S} = \mathbf{E} \times \mathbf{H}^*</math> has a zero real part.}} | ||
== | == पदों का प्रयोग == | ||
कई स्थितियों में कोई केवल यह नहीं | कई स्थितियों में कोई केवल यह नहीं कहा जा सकता है कि एक क्षेत्र "क्षणभंगुर" है या नहीं है: पॉयंटिंग सदिश का औसत किसी दिशा में (या सभी दिशाओं में) शून्य होता है। अधिकतम स्थितियों में जहां वे उपस्थित होते हैं, क्षणिक क्षेत्रों को केवल अन्य विद्युतीय या चुंबकीय क्षेत्रों के रूप में संदर्भित किया जाता है और उन क्षेत्रों की विशेष पहचान के बिना सम्मिलित किया जाता है। पद का उपयोग अधिकतम उन स्थितियों में एक क्षेत्र या समाधान के एक भाग को पृथक करने तक सीमित होता है जहां कोई केवल संचरण तरंग के क्षेत्रों की अपेक्षा कर सकता है। | ||
उदाहरण के लिए, लेख के शीर्ष पर दिए गए चित्रण में, ऊर्जा वास्तव में क्षैतिज दिशा में ले जाई जाती है। हालांकि, ऊर्ध्वाधर दिशा में, सतह के ऊपर बढ़ती दूरी के साथ क्षेत्र की प्रबलता तीव्रता से गिरती है। यह अंतरापृष्ठ के | उदाहरण के लिए, लेख के शीर्ष पर दिए गए चित्रण में, ऊर्जा वास्तव में क्षैतिज दिशा में ले जाई जाती है। हालांकि, ऊर्ध्वाधर दिशा में, सतह के ऊपर बढ़ती दूरी के साथ क्षेत्र की प्रबलता तीव्रता से गिरती है। यह अंतरापृष्ठ के निकट एक पतली सीमा परत में केंद्रित अधिकांश क्षेत्र को छोड़ देता है; इसी कारण से, इसे पृष्ठीय तरंग कहा जाता है।<ref>{{cite journal |author1=Takayama, O. |author2=Bogdanov, A.A. |author3=Lavrinenko, A.V. |year=2017 |title=मेटामेट्री इंटरफेस पर फोटोनिक सतह तरंगें|journal=Journal of Physics: Condensed Matter |volume=29 |issue=46 |page=463001 |doi=10.1088/1361-648X/aa8bdd |pmid=29053474 |bibcode=2017JPCM...29T3001T}}</ref> हालांकि, ऊर्जा क्षैतिज रूप से प्रवाहित होने पर भी, ऊर्ध्वाधर के साथ सतह से दूर (या ओर) ऊर्जा का कोई शुद्ध संचरण नहीं होता है, ताकि कोई भी क्षेत्र को ऊर्ध्वाधर दिशा में क्षणभंगुर होने के रूप में ठीक से वर्णित कर सके। यह पद की संदर्भ निर्भरता का एक उदाहरण है। | ||
प्रतिदिन | प्रतिदिन विद्युत् युक्तियाँ और विद्युत् उपकरण बड़े क्षेत्रों से घिरे होते हैं जो क्षणभंगुर होते हैं; उनके संचालन में वैकल्पिक वोल्टता (उनके मध्य एक विद्युत क्षेत्र का निर्माण) और वैकल्पिक धाराएं (उनके चारों ओर एक चुंबकीय क्षेत्र का निर्माण) सम्मिलित हैं, जिनसे केवल आंतरिक तारों के साथ ऊर्जा ले जाने की आशा की जाती है, न कि उपकरणों के बाहरी भाग में। हालांकि, इस सामान्य संदर्भ में क्षणभंगुर पद का उल्लेख नहीं किया गया है, फिर भी उपकरणों के अभिकल्पक अभी भी फैलने वाली विद्युत चुम्बकीय तरंग के उत्पादन को रोकने या सीमित करने के लिए क्षणभंगुरता बनाए रखने से संबंधित हो सकते हैं, विकिरण हानि का कारण बन सकता है क्योंकि एक संचरण तरंग परिपथिकी से अपनी ऊर्जा चुरा लेती है या अवांछित [[रेडियो हस्तक्षेप|वैद्युतचुंबकीय व्यतिकरण]] दान करती है। | ||
पद "क्षणभंगुर क्षेत्र" विभिन्न संदर्भों में उत्पन्न होता है जहां एक संचरण विद्युत चुम्बकीय तरंग सम्मिलित | पद "क्षणभंगुर क्षेत्र" विभिन्न संदर्भों में उत्पन्न होता है जहां एक संचरण विद्युत चुम्बकीय तरंग सम्मिलित होता है। पद तब विद्युत चुम्बकीय क्षेत्र घटकों को पृथक करता है जो संचरण तरंग के साथ होते हैं, परन्तु जो स्वयं संचरण नहीं करते हैं। अन्य, इसी प्रकार की स्थितियों में, जहां एक संचरण विद्युत चुम्बकीय तरंग की सामान्य रूप से अपेक्षा की जाती है (जैसे कि कांच और वायु के मध्य के अंतरापृष्ठ पर [[अपवर्तित]] प्रकाश), इस पद का प्रयोग उस क्षेत्र के उस भाग का वर्णन करने के लिए किया जाता है, जहां तरंग को (जैसे प्रकाश संचारण कांच के माध्यम से, कांच से वायु अंतरापृष्ठ पर प्रभाव पड़ता है, परन्तु क्रांतिक कोण से परे) दबा दिया जाता है। | ||
हालांकि मैक्सवेल के समीकरणों के अनुसार सभी विद्युत चुम्बकीय क्षेत्रों को लौकिक रूप से नियंत्रित किया जाता है, विभिन्न प्रविधियो या समस्याओं के कुछ प्रकार के अपेक्षित | हालांकि मैक्सवेल के समीकरणों के अनुसार सभी विद्युत चुम्बकीय क्षेत्रों को लौकिक रूप से नियंत्रित किया जाता है, विभिन्न प्रविधियो या समस्याओं के कुछ प्रकार के अपेक्षित समाधान होते हैं, और जब प्राथमिक समाधानों में तरंग संचरण सम्मिलित होता है, तो पद क्षणभंगुर प्रायः उन क्षेत्रों के घटकों या समाधानों पर अनुप्रयुक्त होता है जो उस गुणधर्म को साझा नहीं करते हैं। | ||
उदाहरण के लिए, एक खोखले धातु [[वेवगाइड|तरंग पथक]] का [[प्रसार स्थिरांक|संचरण स्थिरांक]] आवृत्ति का एक प्रबल अभिलक्षक (तथाकथित [[फैलाव संबंध|परिक्षेपण संबंध]]) है। एक निश्चित आवृत्ति ([[आपूर्ती बंद करने की आवृत्ति|अंतक आवृत्ति]]) के नीचे | उदाहरण के लिए, एक खोखले धातु [[वेवगाइड|तरंग पथक]] का [[प्रसार स्थिरांक|संचरण स्थिरांक]] आवृत्ति का एक प्रबल अभिलक्षक (तथाकथित [[फैलाव संबंध|परिक्षेपण संबंध]]) है। एक निश्चित आवृत्ति ([[आपूर्ती बंद करने की आवृत्ति|अंतक आवृत्ति]]) के नीचे संचरण स्थिरांक एक काल्पनिक संख्या बन जाता है। एक काल्पनिक तरंग संख्या वाले [[तरंग समीकरण]] का समाधान तरंग के रूप में संचरणित नहीं होता है, परन्तु चरघातांकी रूप से गिर जाता है, इसलिए उस कम आवृत्ति पर उत्तेजित क्षेत्र को क्षणभंगुर माना जाता है। इसे सरलता से यह भी कहा जा सकता है कि उस आवृत्ति के लिए संचरण "अस्वीकृत" होता है। | ||
तरंग समीकरण का औपचारिक | तरंग समीकरण का औपचारिक समाधान एक समान रूप वाली विधा का वर्णन कर सकते है, परन्तु वास्तविक से काल्पनिक तक संचरण स्थिरांक का परिवर्तन अंतक आवृत्ति के नीचे आवृत्ति के रूप में पूर्णतया से परिणाम की भौतिक प्रकृति को परिवर्तित कर देता है। समाधानों को अंतक विधा या क्षणभंगुर विधा के रूप में वर्णित किया जा सकता है;<ref name="IEEEDict_1992">{{cite book |title=इलेक्ट्रिकल और इलेक्ट्रॉनिक्स शर्तों का IEEE मानक शब्दकोश|year=1992 |publisher=[[The Institute of Electrical and Electronics Engineers]] |location=New York, NY |isbn=978-1-55937-240-4 |page=458 |id=IEEE STD 100-1992}}</ref><ref name="Jackson_3rd">{{cite book |last=Jackson |first=John David |year=1999 |title=शास्त्रीय इलेक्ट्रोडायनामिक्स|edition=3rd |publisher=John-Wiley |isbn=047130932X }}</ref>{{rp|360}} जबकि एक अलग लेखक केवल यह वर्णन करेगा कि ऐसी कोई विधा उपस्थित नहीं है। चूंकि विधा के अनुरूप क्षणभंगुर क्षेत्र की गणना तरंग समीकरण के समाधानों के रूप में की गई थी, इसलिए इसकी चर्चा प्रायः एक क्षणभंगुर तरंग के रूप में की जाती है, हालांकि इसके गुण (जैसे कोई ऊर्जा नहीं) [[लहर|तरंग]] की परिभाषा के साथ असंगत हैं। | ||
यद्यपि यह लेख वैद्युतचुंबकिकी पर ध्यान केंद्रित | यद्यपि यह लेख वैद्युतचुंबकिकी पर ध्यान केंद्रित करते है, पद क्षणभंगुर का उपयोग इसी प्रकार ध्वनिकी और [[क्वांटम यांत्रिकी]] जैसे क्षेत्रों में किया जाता है, जहां सम्मिलित भौतिकी से तरंग समीकरण उत्पन्न होता है। इन स्थितियों में, तरंग समीकरण के समाधान जिसके परिणामस्वरूप काल्पनिक संचरण स्थिरांक को इसी प्रकार क्षणभंगुर कहा जाता है और इसमें एक आवश्यक विशेषता यह होती है कि इसमें कोई शुद्ध ऊर्जा स्थानांतरित नहीं होती है, यद्यपि एक गैर-शून्य क्षेत्र हो। | ||
== क्षणिक तरंग अनुप्रयोग == | == क्षणिक तरंग अनुप्रयोग == | ||
[[प्रकाशिकी]] और ध्वनिकी में, क्षणभंगुर तरंगें तब बनती हैं जब एक माध्यम में संचारण करने वाली तरंगें अपनी सीमा पर [[कुल आंतरिक प्रतिबिंब|पूर्ण आंतरिक परावर्तन]] से गुजरती हैं क्योंकि वे इसे तथाकथित क्रांतिक कोण से बड़े कोण पर टकराती हैं।<ref name=Tineke>{{Cite journal|title=सबवेवलेंथ प्रकाश स्रोतों के लिए एक उज्ज्वल भविष्य|author=Tineke Thio|volume=94|issue=1|pages=40–47|year=2006|doi=10.1511/2006.1.40|journal=American Scientist}}</ref><ref name=Marstin-acoustic>{{Cite journal | last = Marston | first =Philip L. |author2=Matula, T.J. | title =ध्वनिक वाष्पशील तरंगों का बिखराव| journal = [[Journal of the Acoustical Society of America]] | volume =111 | issue =5 | page =2378 | date =May 2002 | bibcode =2002ASAJ..111.2378M | doi=10.1121/1.4778056 }}</ref> क्षणभंगुर तरंगो के अस्तित्व के लिए भौतिक व्याख्या यह है कि विद्युत और चुंबकीय क्षेत्र (या ध्वनिक तरंगों के स्थितियों में [[दबाव प्रवणता|दाब प्रवणता]]) एक सीमा पर बंद नहीं हो सकते | [[प्रकाशिकी]] और ध्वनिकी में, क्षणभंगुर तरंगें तब बनती हैं जब एक माध्यम में संचारण करने वाली तरंगें अपनी सीमा पर [[कुल आंतरिक प्रतिबिंब|पूर्ण आंतरिक परावर्तन]] से गुजरती हैं क्योंकि वे इसे तथाकथित क्रांतिक कोण से बड़े कोण पर टकराती हैं।<ref name=Tineke>{{Cite journal|title=सबवेवलेंथ प्रकाश स्रोतों के लिए एक उज्ज्वल भविष्य|author=Tineke Thio|volume=94|issue=1|pages=40–47|year=2006|doi=10.1511/2006.1.40|journal=American Scientist}}</ref><ref name=Marstin-acoustic>{{Cite journal | last = Marston | first =Philip L. |author2=Matula, T.J. | title =ध्वनिक वाष्पशील तरंगों का बिखराव| journal = [[Journal of the Acoustical Society of America]] | volume =111 | issue =5 | page =2378 | date =May 2002 | bibcode =2002ASAJ..111.2378M | doi=10.1121/1.4778056 }}</ref> क्षणभंगुर तरंगो के अस्तित्व के लिए भौतिक व्याख्या यह है कि विद्युत और चुंबकीय क्षेत्र (या ध्वनिक तरंगों के स्थितियों में [[दबाव प्रवणता|दाब प्रवणता]]) एक सीमा पर बंद नहीं हो सकते हैं। क्वांटम यांत्रिकी में, भौतिक व्याख्या पूर्णतया समान है- श्रोडिंगर तरंग-फलन सीमा के लिए सामान्य कण गति का प्रतिनिधित्व करता है और सीमा पर असतत नहीं हो सकता है। | ||
विद्युतचुंबकीय क्षणभंगुर तरंगों का उपयोग छोटे कणों पर प्रकाशीय [[विकिरण दबाव|विकिरण दाब]] डालने के लिए किया जाता है ताकि उन्हें प्रयोग के लिए फंसाया जा सके या उन्हें बहुत कम तापमान पर प्रशीतित किया जा सके और [[माइक्रोस्कोपी|सूक्ष्मदर्शिकी]] [[कुल आंतरिक प्रतिबिंब प्रतिदीप्ति माइक्रोस्कोप|(कुल आंतरिक परावर्तन प्रतिदीप्ति सूक्ष्मदर्शी)]]के लिए [[जैविक कोशिका|जैविक कोशिकाओं]] या [[एकल-अणु प्रयोग]] जैसी बहुत छोटी वस्तुओं को प्रकाशित किया जा सके। एक [[प्रकाशित तंतु]] से क्षणभंगुर तरंग का उपयोग गैस संवेदक में किया जा सकता है और [[ अवरक्त स्पेक्ट्रोस्कोपी |अवरक्त स्पेक्ट्रमिकी]] प्रविधि में क्षणभंगुर तरंगों को क्षीणित कुल परावर्तन के रूप में जाना जाता है। | विद्युतचुंबकीय क्षणभंगुर तरंगों का उपयोग छोटे कणों पर प्रकाशीय [[विकिरण दबाव|विकिरण दाब]] डालने के लिए किया जाता है ताकि उन्हें प्रयोग के लिए फंसाया जा सके या उन्हें बहुत कम तापमान पर प्रशीतित किया जा सके और [[माइक्रोस्कोपी|सूक्ष्मदर्शिकी]] [[कुल आंतरिक प्रतिबिंब प्रतिदीप्ति माइक्रोस्कोप|(कुल आंतरिक परावर्तन प्रतिदीप्ति सूक्ष्मदर्शी)]]के लिए [[जैविक कोशिका|जैविक कोशिकाओं]] या [[एकल-अणु प्रयोग]] जैसी बहुत छोटी वस्तुओं को प्रकाशित किया जा सके। एक [[प्रकाशित तंतु]] से क्षणभंगुर तरंग का उपयोग गैस संवेदक में किया जा सकता है और [[ अवरक्त स्पेक्ट्रोस्कोपी |अवरक्त स्पेक्ट्रमिकी]] प्रविधि में क्षणभंगुर तरंगों को क्षीणित कुल परावर्तन के रूप में जाना जाता है। | ||
| Line 31: | Line 31: | ||
हाल ही में, एक ग्राफीन-आधारित ब्रैग ग्रेटिंग (एक आयामी [[फोटोनिक क्रिस्टल|फोटोनिक मणिभ]]) का निर्माण किया गया है और [[प्रिज्म युग्मक|वर्णक्रम युग्मक]] प्रविधि का उपयोग करके आवधिक संरचना में सतह विद्युत चुम्बकीय तरंगों के उत्तेजना के लिए अपनी क्षमता का प्रदर्शन किया है।<ref>{{cite journal |title=ग्राफीन-आधारित ब्रैग झंझरी में सतह विद्युत चुम्बकीय तरंगों का उत्तेजना|journal=Scientific Reports |year=2012 |doi=10.1038/srep00737 |volume=2 |pages=737 |last1=Sreekanth |first1=Kandammathe Valiyaveedu |last2=Zeng |first2=Shuwen |last3=Shang |first3=Jingzhi |last4=Yong |first4=Ken-Tye |last5=Yu |first5=Ting |bibcode = 2012NatSR...2E.737S |pmid=23071901 |pmc=3471096}}</ref> | हाल ही में, एक ग्राफीन-आधारित ब्रैग ग्रेटिंग (एक आयामी [[फोटोनिक क्रिस्टल|फोटोनिक मणिभ]]) का निर्माण किया गया है और [[प्रिज्म युग्मक|वर्णक्रम युग्मक]] प्रविधि का उपयोग करके आवधिक संरचना में सतह विद्युत चुम्बकीय तरंगों के उत्तेजना के लिए अपनी क्षमता का प्रदर्शन किया है।<ref>{{cite journal |title=ग्राफीन-आधारित ब्रैग झंझरी में सतह विद्युत चुम्बकीय तरंगों का उत्तेजना|journal=Scientific Reports |year=2012 |doi=10.1038/srep00737 |volume=2 |pages=737 |last1=Sreekanth |first1=Kandammathe Valiyaveedu |last2=Zeng |first2=Shuwen |last3=Shang |first3=Jingzhi |last4=Yong |first4=Ken-Tye |last5=Yu |first5=Ting |bibcode = 2012NatSR...2E.737S |pmid=23071901 |pmc=3471096}}</ref> | ||
क्वांटम यांत्रिकी में, श्रोडिंगर समीकरण के क्षणभंगुर-तरंग | क्वांटम यांत्रिकी में, श्रोडिंगर समीकरण के क्षणभंगुर-तरंग समाधानों तरंग-यांत्रिक सुरंगन की घटना को उत्थान देते हैं। | ||
सूक्ष्मदर्शिकी में, ऐसी प्रणाली जो क्षणभंगुर तरंगों में निहित सूचना को अधिकृत करती है, जिसका उपयोग [[सुपर-रिज़ॉल्यूशन माइक्रोस्कोपी|उत्कृष्ट-वियोजन सूक्ष्मदर्शिकी]] बनाने के लिए किया जा सकता है। पदार्थ संचरण और क्षणभंगुर विद्युत चुम्बकीय तरंगों दोनों को विकीर्ण करता है। पारंपरिक प्रकाशीय प्रणालियाँ केवल संचरण तरंगों में सूचना को ग्रहण करती हैं और इसलिए [[विवर्तन-सीमित प्रणाली|विवर्तन सीमा]] के अधीन होती हैं। ऐसी प्रणालियाँ जो क्षणभंगुर तरंगों में निहित सूचनाओं को अधिकृत करती हैं, जैसे कि [[ app |सुपर लेंस]] और [[फील्ड स्कैनिंग ऑप्टिकल माइक्रोस्कोपी के पास|क्षेत्र क्रमवीक्षण प्रकाशीय सूक्ष्मदर्शिकी के निकट]], विवर्तन सीमा को पार कर सकती हैं; हालाँकि ये पद्धतियाँ तब प्रणाली की क्षणभंगुर तरंगों को सटीक रूप से पकड़ने की क्षमता से सीमित होती हैं।<ref>Neice, A., "Methods and Limitations of Subwavelength Imaging", Advances in Imaging and Electron Physics, Vol. 163, July 2010.</ref> उनके संकल्प पर सीमा द्वारा दिया गया है | सूक्ष्मदर्शिकी में, ऐसी प्रणाली जो क्षणभंगुर तरंगों में निहित सूचना को अधिकृत करती है, जिसका उपयोग [[सुपर-रिज़ॉल्यूशन माइक्रोस्कोपी|उत्कृष्ट-वियोजन सूक्ष्मदर्शिकी]] बनाने के लिए किया जा सकता है। पदार्थ संचरण और क्षणभंगुर विद्युत चुम्बकीय तरंगों दोनों को विकीर्ण करता है। पारंपरिक प्रकाशीय प्रणालियाँ केवल संचरण तरंगों में सूचना को ग्रहण करती हैं और इसलिए [[विवर्तन-सीमित प्रणाली|विवर्तन सीमा]] के अधीन होती हैं। ऐसी प्रणालियाँ जो क्षणभंगुर तरंगों में निहित सूचनाओं को अधिकृत करती हैं, जैसे कि [[ app |सुपर लेंस]] और [[फील्ड स्कैनिंग ऑप्टिकल माइक्रोस्कोपी के पास|क्षेत्र क्रमवीक्षण प्रकाशीय सूक्ष्मदर्शिकी के निकट]], विवर्तन सीमा को पार कर सकती हैं; हालाँकि ये पद्धतियाँ तब प्रणाली की क्षणभंगुर तरंगों को सटीक रूप से पकड़ने की क्षमता से सीमित होती हैं।<ref>Neice, A., "Methods and Limitations of Subwavelength Imaging", Advances in Imaging and Electron Physics, Vol. 163, July 2010.</ref> उनके संकल्प पर सीमा द्वारा दिया गया है; | ||
: <math> k \propto \frac{1}{d} \ln \frac{1}{\delta}</math> | : <math> k \propto \frac{1}{d} \ln \frac{1}{\delta}</math> | ||
जहां <math>k</math> अधिकतम तरंग सदिश है जिसे हल किया जा सकता है, <math>d</math> वस्तु और संवेदक के मध्य की दूरी है और <math>\delta</math> संवेदक की [[क्यू कारक|गुणवत्ता]] का एक मापक है। | जहां <math>k</math> अधिकतम तरंग सदिश है जिसे हल किया जा सकता है, <math>d</math> वस्तु और संवेदक के मध्य की दूरी है और <math>\delta</math> संवेदक की [[क्यू कारक|गुणवत्ता]] का एक मापक है। | ||
सामान्यतः, क्षणभंगुर तरंगों के व्यावहारिक अनुप्रयोगों को (1) के रूप में वर्गीकृत किया जा सकता है, जिसमें तरंग से जुड़ी ऊर्जा का उपयोग अंतरिक्ष के क्षेत्र के भीतर किसी अन्य घटना को उत्तेजित करने के लिए किया जाता है, जहां मूल संचारण तरंग क्षणभंगुर हो जाती है (उदाहरण के लिए, जैसा कि कुल आंतरिक परावर्तन प्रतिदीप्ति सूक्ष्मदर्शी) या (2) वे जिनमें क्षणभंगुर तरंगें दो माध्यमों को जोड़ती है जिसमें संचारण तरंगों की अनुमति होती है और इसलिए संचारो के मध्य ऊर्जा या एक कण के | सामान्यतः, क्षणभंगुर तरंगों के व्यावहारिक अनुप्रयोगों को (1) के रूप में वर्गीकृत किया जा सकता है, जिसमें तरंग से जुड़ी ऊर्जा का उपयोग अंतरिक्ष के क्षेत्र के भीतर किसी अन्य घटना को उत्तेजित करने के लिए किया जाता है, जहां मूल संचारण तरंग क्षणभंगुर हो जाती है (उदाहरण के लिए, जैसा कि कुल आंतरिक परावर्तन प्रतिदीप्ति सूक्ष्मदर्शी) या (2) वे जिनमें क्षणभंगुर तरंगें दो माध्यमों को जोड़ती है जिसमें संचारण तरंगों की अनुमति होती है और इसलिए संचारो के मध्य ऊर्जा या एक कण के स्थानान्तरण की अनुमति देता है (उपयोग में तरंग समीकरण के आधार पर), यहां तक कि हालांकि दो माध्यमों के मध्य अंतरिक्ष के क्षेत्र में किसी संचारण-तरंग समाधानों की अनुमति नहीं है। इसका एक उदाहरण तथाकथित तरंग-यांत्रिक सुरंगन है और इसे सामान्यतः क्षणिक तरंग युग्मन के रूप में जाना जाता है। | ||
== प्रकाश का पूर्ण आंतरिक परावर्तन == | == प्रकाश का पूर्ण आंतरिक परावर्तन == | ||
| Line 43: | Line 43: | ||
[[File:Total internal reflection.jpg|thumb|200px|कुल आंतरिक परावर्तन]] | [[File:Total internal reflection.jpg|thumb|200px|कुल आंतरिक परावर्तन]] | ||
[[File:Evanescent wave.jpg|thumb|200px |एक (शीर्ष) [[अपवर्तन]] का प्रतिनिधित्व और (नीचे) लाल रंग में अंतरापृष्ठ पर वाष्पशील तरंगों (परावर्तित तरंगों को छोड़ दिया गया) है।]]उदाहरण के लिए, दो आयामों में कुल आंतरिक परावर्तन पर विचार करें, x अक्ष पर स्थित माध्यम के मध्य | [[File:Evanescent wave.jpg|thumb|200px |एक (शीर्ष) [[अपवर्तन]] का प्रतिनिधित्व और (नीचे) लाल रंग में अंतरापृष्ठ पर वाष्पशील तरंगों (परावर्तित तरंगों को छोड़ दिया गया) है।]]उदाहरण के लिए, दो आयामों में कुल आंतरिक परावर्तन पर विचार करें, x-अक्ष पर स्थित माध्यम के मध्य, y के साथ सामान्य और z के साथ ध्रुवीकरण (तरंगें) अंतरापृष्ठ के साथ हैं। कोई आशा कर सकता है कि पूर्ण आंतरिक परावर्तन की ओर ले जाने वाले कोणों के लिए, समाधानों में एक घटना तरंग और एक परावर्तित तरंग सम्मिलित होगी, जिसमें कोई संचरित तरंग पूर्णतया भी नहीं होगी, परन्तु ऐसा कोई समाधान नहीं है जो मैक्सवेल के समीकरणों का पालन करता हो। एक परावैद्युत माध्यम में मैक्सवेल के समीकरण क्षेत्रो ''E<sub>||</sub>, H<sub>||</sub>, D<sub>y</sub>'' और ''B<sub>y</sub>'' के घटकों के लिए निरंतरता की सीमा की स्थिति पर आरोपण करते हैं। इस उदाहरण में विचार किए गए ध्रुवीकरण के लिए, ''E<sub>||</sub>'' और ''B<sub>y</sub>'' पर स्थितियां संतुष्ट हैं और यदि परावर्तित तरंग का आयाम घटना के समान ही है क्योंकि घटना के ये घटक और परावर्तित तरंगें विनाशकारी रूप से आरोपित होती हैं। हालांकि, उनके ''H<sub>x</sub>'' घटक रचनात्मक रूप से अध्यारोपित होते हैं, इसलिए बिना लुप्त होने वाली संचरित तरंग के बिना कोई समाधान नहीं हो सकता है। संचरित तरंग, हालांकि, ज्यावक्रीय तरंग नहीं हो सकती है क्योंकि यह तब ऊर्जा को सीमा से दूर ऊर्जा का परिवहन करेगी, परन्तु चूंकि घटना और परावर्तित तरंगों में समान ऊर्जा होती है, यह ऊर्जा के संरक्षण का उल्लंघन करेगी। इसलिए हम निष्कर्ष निकालते हैं कि प्रेषित तरंग मैक्सवेल के समीकरणों के लिए एक गैर-लुप्त होने वाला समाधान होना चाहिए जो कि एक संचारण तरंग नहीं है और एक परावैद्युत में केवल ऐसे समाधान हैं, जो चरघातांकी रूप से क्षय होते हैं: जैसे क्षणभंगुर तरंगें हैं। | ||
गणितीय रूप से, क्षणभंगुर तरंगों को एक तरंग सदिश द्वारा चित्रित किया जा सकता है, जहां सदिश के एक या अधिक घटकों में एक [[काल्पनिक संख्या]] मान होता है क्योंकि सदिश में काल्पनिक घटक होते हैं, इसका परिमाण इसके वास्तविक घटकों से कम हो सकता है। | गणितीय रूप से, क्षणभंगुर तरंगों को एक तरंग सदिश द्वारा चित्रित किया जा सकता है, जहां सदिश के एक या अधिक घटकों में एक [[काल्पनिक संख्या]] मान होता है क्योंकि सदिश में काल्पनिक घटक होते हैं, इसका परिमाण इसके वास्तविक घटकों से कम हो सकता है। | ||
| Line 69: | Line 69: | ||
== क्षणभंगुर-तरंग युग्मन == | == क्षणभंगुर-तरंग युग्मन == | ||
[[File:FITR penetration depth.svg|thumb|विभिन्न अपवर्तन सूचकांकों के लिए तरंगदैर्घ्य की इकाइयों में आपतन कोण के विरुद्ध क्षणभंगुर तरंग की 1/e-प्रवेश गहराई का आलेख।]]विशेष रूप से प्रकाशिकी में, क्षणभंगुर-तरंग युग्मन भौतिक अतिव्यापन के कारण दो तरंगों के मध्य युग्मन को संदर्भित करता है जिसे अन्यथा संचरण तरंगों के अनुरूप अपवर्तक क्षेत्रों के रूप में वर्णित किया जाएगा।<ref>{{cite journal|title=अंतर चरण माप के आधार पर एयू एनपी-संवर्धित सतह समतल अनुनाद की आकार निर्भरता|journal=Sensors and Actuators B: Chemical |year=2013|doi=10.1016/j.snb.2012.09.073|volume=176|pages=1128–1133|last1=Zeng|first1=Shuwen|last2=Yu|first2=Xia|last3=Law|first3=Wing-Cheung|last4=Zhang|first4=Yating|last5=Hu|first5=Rui|last6=Dinh|first6=Xuan-Quyen|last7=Ho|first7=Ho-Pui|last8=Yong|first8=Ken-Tye |url=https://www.researchgate.net/publication/268225952 }}</ref> | [[File:FITR penetration depth.svg|thumb|विभिन्न अपवर्तन सूचकांकों के लिए तरंगदैर्घ्य की इकाइयों में आपतन कोण के विरुद्ध क्षणभंगुर तरंग की 1/e-प्रवेश गहराई का आलेख।]]विशेष रूप से प्रकाशिकी में, क्षणभंगुर-तरंग युग्मन भौतिक अतिव्यापन के कारण दो तरंगों के मध्य युग्मन को संदर्भित करता है जिसे अन्यथा संचरण तरंगों के अनुरूप अपवर्तक क्षेत्रों के रूप में वर्णित किया जाएगा।<ref>{{cite journal|title=अंतर चरण माप के आधार पर एयू एनपी-संवर्धित सतह समतल अनुनाद की आकार निर्भरता|journal=Sensors and Actuators B: Chemical |year=2013|doi=10.1016/j.snb.2012.09.073|volume=176|pages=1128–1133|last1=Zeng|first1=Shuwen|last2=Yu|first2=Xia|last3=Law|first3=Wing-Cheung|last4=Zhang|first4=Yating|last5=Hu|first5=Rui|last6=Dinh|first6=Xuan-Quyen|last7=Ho|first7=Ho-Pui|last8=Yong|first8=Ken-Tye |url=https://www.researchgate.net/publication/268225952 }}</ref> | ||
एक लौकिक उदाहरण एफटीआईआर (असंतुष्ट कुल आंतरिक परावर्तन) है। जिसमें एक सघन माध्यम की सतह पर क्षणभंगुर क्षेत्र | एक लौकिक उदाहरण एफटीआईआर (असंतुष्ट कुल आंतरिक परावर्तन) है। जिसमें एक सघन माध्यम की सतह पर क्षणभंगुर क्षेत्र अत्यन्त निकट (आलेख देखें) जिस पर एक तरंग सामान्यतः कुल आंतरिक परावर्तन से गुजरती है, आसपास के क्षेत्र में एक और सघन माध्यम को अतिव्यापन करता है। यह परावर्तन की समग्रता को बाधित करता है और कुछ ऊर्जा को दूसरे माध्यम में परिवर्तित कर देता है। | ||
तंतु अंतर्भाग को एक साथ बंद करके दो [[ऑप्टिकल वेवगाइड|प्रकाशीय तरंग पथक]] के मध्य युग्मन को प्रभावित किया जा सकता है ताकि एक तत्व द्वारा उत्पन्न क्षणिक क्षेत्र दूसरे तंतु में एक तरंग को उत्तेजित कर सके। इसका उपयोग [[फाइबर ऑप्टिक फाड़नेवाला|तंतु प्रकाशीय विखंडक]] और [[फाइबर टैपिंग|तंतु निकासन]] में किया जाता है। रेडियो (और यहां तक कि प्रकाशीय) आवृत्तियों पर, ऐसे उपकरण को दिशात्मक युग्मक कहा जाता है। उपकरणों को सामान्यतः सूक्ष्म तरंग संचरण और प्रतिरुपण की स्थितियों में ऊर्जा विभाजक कहा जाता है। क्षणभंगुर-तरंग युग्मन विद्युत चुम्बकीय क्षेत्र सिद्धांत में निकट और दूर क्षेत्र की अन्तःक्रिया का पर्याय है। स्रोत तत्व की प्रकृति के आधार पर, सम्मिलित क्षणभंगुर क्षेत्र या तो मुख्य रूप से विद्युत (संधारित्र) या चुंबकीय (आगमनात्मक) होता है, दूर के क्षेत्र में तरंगों के विपरीत (संचरण) जहां ये घटक जुड़े होते हैं। क्षणभंगुर तरंग युग्मन प्रत्येक माध्यम के पास गैर-विकिरण क्षेत्र में होता है और इस प्रकार सदैव पदार्थ, अर्थात, आंशिक रूप से परावर्तक सतह के भीतर प्रेरित धाराओं और आवेशों के साथ जुड़ा होता है। क्वांटम यांत्रिकी में कणों के संदर्भ में तरंग | तंतु अंतर्भाग को एक साथ बंद करके दो [[ऑप्टिकल वेवगाइड|प्रकाशीय तरंग पथक]] के मध्य युग्मन को प्रभावित किया जा सकता है ताकि एक तत्व द्वारा उत्पन्न क्षणिक क्षेत्र दूसरे तंतु में एक तरंग को उत्तेजित कर सके। इसका उपयोग [[फाइबर ऑप्टिक फाड़नेवाला|तंतु प्रकाशीय विखंडक]] और [[फाइबर टैपिंग|तंतु निकासन]] में किया जाता है। रेडियो (और यहां तक कि प्रकाशीय) आवृत्तियों पर, ऐसे उपकरण को दिशात्मक युग्मक कहा जाता है। उपकरणों को सामान्यतः सूक्ष्म तरंग संचरण और प्रतिरुपण की स्थितियों में ऊर्जा विभाजक कहा जाता है। क्षणभंगुर-तरंग युग्मन विद्युत चुम्बकीय क्षेत्र सिद्धांत में निकट और दूर क्षेत्र की अन्तःक्रिया का पर्याय है। स्रोत तत्व की प्रकृति के आधार पर, सम्मिलित क्षणभंगुर क्षेत्र या तो मुख्य रूप से विद्युत (संधारित्र) या चुंबकीय (आगमनात्मक) होता है, दूर के क्षेत्र में तरंगों के विपरीत (संचरण) जहां ये घटक जुड़े होते हैं। क्षणभंगुर तरंग युग्मन प्रत्येक माध्यम के पास गैर-विकिरण क्षेत्र में होता है और इस प्रकार सदैव पदार्थ, अर्थात, आंशिक रूप से परावर्तक सतह के भीतर प्रेरित धाराओं और आवेशों के साथ जुड़ा होता है। क्वांटम यांत्रिकी में कणों के संदर्भ में तरंग फलन की अन्तःक्रिया पर चर्चा की जा सकती है और इसे [[क्वांटम टनलिंग|क्वांटम सुरंगन]] के रूप में वर्णित किया जा सकता है। | ||
=== अनुप्रयोग === | === अनुप्रयोग === | ||
क्षणभंगुर तरंग युग्मन का उपयोग उत्तेजित करने के लिए किया जाता है, उदाहरण के लिए, परावैद्युत सूक्ष्मगोलक अनुनादक। | * क्षणभंगुर तरंग युग्मन सामान्यतः फोटोनिक और नैनोफोटोनिक उपकरणों में तरंग पथक संवेदक या समायोजक के रूप में उपयोग किया जाता है (उदाहरण के लिए, वर्णक्रम युग्मक देखें)।<ref>{{cite journal |last1=Lova |first1=Paola |last2=Manfredi |first2=Giovanni |last3=Comoretto |first3=Davide |title=कार्यात्मक समाधान संसाधित प्लानर 1डी फोटोनिक क्रिस्टल में अग्रिम|journal=Advanced Optical Materials |date=2018 |volume=6 |issue=24 |pages=1800730 |doi=10.1002/adom.201800730 |language=en |issn=2195-1071|doi-access=free }}</ref> | ||
* क्षणभंगुर तरंग युग्मन का उपयोग उत्तेजित करने के लिए किया जाता है, उदाहरण के लिए, परावैद्युत सूक्ष्मगोलक अनुनादक। | |||
क्षणभंगुर युग्मन, निकट क्षेत्र की अन्तःक्रिया के रूप में, [[विद्युत चुम्बकीय संगतता|वैद्युतचुंबकीय सुंसंगति]] की स्थितियों में से एक है। | * क्षणभंगुर युग्मन, निकट क्षेत्र की अन्तःक्रिया के रूप में, [[विद्युत चुम्बकीय संगतता|वैद्युतचुंबकीय सुंसंगति]] की स्थितियों में से एक है। | ||
* तंतु निकासन की हानि के बिना प्रकाशीय तंतु का युग्मन। | |||
तंतु निकासन की हानि के बिना प्रकाशीय तंतु का युग्मन। | * असाधारण प्रकाशीय संचरण की सैद्धांतिक व्याख्या में क्षणभंगुर तरंग युग्मन एक प्रमुख भूमिका निभाते है।<ref>{{cite journal|doi=10.1016/j.optcom.2008.07.077|title=Critical process of extraordinary optical transmission through periodic subwavelength hole array: Hole-assisted evanescent-field coupling|year=2008|last1=Fan|first1=Zhiyuan|last2=Zhan|first2=Li|last3=Hu|first3=Xiao|last4=Xia|first4=Yuxing|journal=Optics Communications|volume=281|issue=21|pages=5467|bibcode = 2008OptCo.281.5467F }}</ref> | ||
* क्षणभंगुर तरंग युग्मन का उपयोग उपकरणों को वायरलेस तरीके से चलाने में किया जाता है।<ref>{{cite journal | last = Karalis | first = Aristeidis |author2=J.D. Joannopoulos |author3=Marin Soljačić |date=February 2007 | title = कुशल वायरलेस गैर-विकिरणकारी मध्य-श्रेणी ऊर्जा हस्तांतरण| arxiv = physics/0611063 |bibcode = 2008AnPhy.323...34K |doi = 10.1016/j.aop.2007.04.017 | journal = Annals of Physics | volume = 323 | issue = 1 | page = 34 | s2cid = 1887505 }}</ref><ref>[https://www.newscientist.com/article/dn10575-evanescent-coupling-could-power-gadgets-wirelessly.html "'Evanescent coupling' could power gadgets wirelessly", Celeste Biever, ''NewScientist.com'', 15 November 2006]</ref><ref>[http://web.mit.edu/newsoffice/2006/wireless.html Wireless energy could power consumer, industrial electronics] – [[MIT]] press release</ref> | |||
असाधारण प्रकाशीय संचरण की सैद्धांतिक व्याख्या में क्षणभंगुर तरंग युग्मन एक प्रमुख भूमिका निभाते है।<ref>{{cite journal|doi=10.1016/j.optcom.2008.07.077|title=Critical process of extraordinary optical transmission through periodic subwavelength hole array: Hole-assisted evanescent-field coupling|year=2008|last1=Fan|first1=Zhiyuan|last2=Zhan|first2=Li|last3=Hu|first3=Xiao|last4=Xia|first4=Yuxing|journal=Optics Communications|volume=281|issue=21|pages=5467|bibcode = 2008OptCo.281.5467F }}</ref> | * कुल आंतरिक परावर्तन प्रतिदीप्ति सूक्ष्मदर्शी सतह के निकट प्रतिदीप्तिधर को उत्तेजित करने के लिए कुल आंतरिक परावर्तन द्वारा उत्पादित क्षणभंगुर तरंग का उपयोग करता है। यह तब उपयोगी होता है जब जैविक प्रारूपों की सतह के गुणों का अध्ययन करने की आवश्यकता होती है।<ref>{{cite journal|last=Axelrod|first=D.|title=कुल आंतरिक प्रतिबिंब प्रतिदीप्ति द्वारा प्रकाशित सेल-सब्सट्रेट संपर्क|journal=The Journal of Cell Biology|date=1 April 1981|volume=89|issue=1|pages=141–145|doi=10.1083/jcb.89.1.141|pmid=7014571|pmc=2111781}}</ref> | ||
क्षणभंगुर तरंग युग्मन का उपयोग उपकरणों को वायरलेस तरीके से चलाने में किया जाता है।<ref>{{cite journal | last = Karalis | first = Aristeidis |author2=J.D. Joannopoulos |author3=Marin Soljačić |date=February 2007 | title = कुशल वायरलेस गैर-विकिरणकारी मध्य-श्रेणी ऊर्जा हस्तांतरण| arxiv = physics/0611063 |bibcode = 2008AnPhy.323...34K |doi = 10.1016/j.aop.2007.04.017 | journal = Annals of Physics | volume = 323 | issue = 1 | page = 34 | s2cid = 1887505 }}</ref><ref>[https://www.newscientist.com/article/dn10575-evanescent-coupling-could-power-gadgets-wirelessly.html "'Evanescent coupling' could power gadgets wirelessly", Celeste Biever, ''NewScientist.com'', 15 November 2006]</ref><ref>[http://web.mit.edu/newsoffice/2006/wireless.html Wireless energy could power consumer, industrial electronics] – [[MIT]] press release</ref> | |||
कुल आंतरिक परावर्तन प्रतिदीप्ति सूक्ष्मदर्शी सतह के | |||
Revision as of 17:15, 4 April 2023
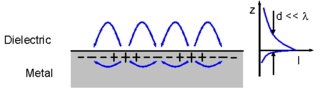
विद्युतचुंबकीय में, एक क्षणभंगुर क्षेत्र या क्षणभंगुर तरंग, एक दोलनशील विद्युत और/या चुंबकीय क्षेत्र है, जो एक विद्युत चुम्बकीय तरंग के रूप में संचरण नहीं करते है, परन्तु जिसकी ऊर्जा स्थानिक रूप से स्रोत के आसपास केंद्रित (दोलन आवेश और धाराएं) होती है। यहां तक कि जब एक संचरण विद्युत चुम्बकीय तरंग उत्पन्न होती है (उदाहरण के लिए, एक प्रेषी ऐन्टेना द्वारा), तब भी कोई विद्युत या चुंबकीय क्षेत्र के घटक को एक क्षणिक क्षेत्र के रूप में स्पष्ट किया सकता है जिसे कई तरंग दैर्ध्य की दूरी पर देखे गए संचरण तरंग (जैसे एक प्रेषी एंटीना का दूर क्षेत्र) के लिए दोषी नहीं ठहराया जा सकता है।
क्षणभंगुर क्षेत्र की एक विशेषता यह है कि उस क्षेत्र में कोई शुद्ध ऊर्जा प्रवाह नहीं होती है। चूंकि विद्युत चुम्बकीय ऊर्जा का शुद्ध प्रवाह औसत प्वाइन्टिंग सदिश द्वारा दिया जाता है, इसका तात्पर्य है कि इन क्षेत्रों में पॉयंटिंग सदिश, जैसे कि एक पूर्ण दोलन चक्र पर औसत शून्य है।[lower-alpha 1]
पदों का प्रयोग
कई स्थितियों में कोई केवल यह नहीं कहा जा सकता है कि एक क्षेत्र "क्षणभंगुर" है या नहीं है: पॉयंटिंग सदिश का औसत किसी दिशा में (या सभी दिशाओं में) शून्य होता है। अधिकतम स्थितियों में जहां वे उपस्थित होते हैं, क्षणिक क्षेत्रों को केवल अन्य विद्युतीय या चुंबकीय क्षेत्रों के रूप में संदर्भित किया जाता है और उन क्षेत्रों की विशेष पहचान के बिना सम्मिलित किया जाता है। पद का उपयोग अधिकतम उन स्थितियों में एक क्षेत्र या समाधान के एक भाग को पृथक करने तक सीमित होता है जहां कोई केवल संचरण तरंग के क्षेत्रों की अपेक्षा कर सकता है।
उदाहरण के लिए, लेख के शीर्ष पर दिए गए चित्रण में, ऊर्जा वास्तव में क्षैतिज दिशा में ले जाई जाती है। हालांकि, ऊर्ध्वाधर दिशा में, सतह के ऊपर बढ़ती दूरी के साथ क्षेत्र की प्रबलता तीव्रता से गिरती है। यह अंतरापृष्ठ के निकट एक पतली सीमा परत में केंद्रित अधिकांश क्षेत्र को छोड़ देता है; इसी कारण से, इसे पृष्ठीय तरंग कहा जाता है।[1] हालांकि, ऊर्जा क्षैतिज रूप से प्रवाहित होने पर भी, ऊर्ध्वाधर के साथ सतह से दूर (या ओर) ऊर्जा का कोई शुद्ध संचरण नहीं होता है, ताकि कोई भी क्षेत्र को ऊर्ध्वाधर दिशा में क्षणभंगुर होने के रूप में ठीक से वर्णित कर सके। यह पद की संदर्भ निर्भरता का एक उदाहरण है।
प्रतिदिन विद्युत् युक्तियाँ और विद्युत् उपकरण बड़े क्षेत्रों से घिरे होते हैं जो क्षणभंगुर होते हैं; उनके संचालन में वैकल्पिक वोल्टता (उनके मध्य एक विद्युत क्षेत्र का निर्माण) और वैकल्पिक धाराएं (उनके चारों ओर एक चुंबकीय क्षेत्र का निर्माण) सम्मिलित हैं, जिनसे केवल आंतरिक तारों के साथ ऊर्जा ले जाने की आशा की जाती है, न कि उपकरणों के बाहरी भाग में। हालांकि, इस सामान्य संदर्भ में क्षणभंगुर पद का उल्लेख नहीं किया गया है, फिर भी उपकरणों के अभिकल्पक अभी भी फैलने वाली विद्युत चुम्बकीय तरंग के उत्पादन को रोकने या सीमित करने के लिए क्षणभंगुरता बनाए रखने से संबंधित हो सकते हैं, विकिरण हानि का कारण बन सकता है क्योंकि एक संचरण तरंग परिपथिकी से अपनी ऊर्जा चुरा लेती है या अवांछित वैद्युतचुंबकीय व्यतिकरण दान करती है।
पद "क्षणभंगुर क्षेत्र" विभिन्न संदर्भों में उत्पन्न होता है जहां एक संचरण विद्युत चुम्बकीय तरंग सम्मिलित होता है। पद तब विद्युत चुम्बकीय क्षेत्र घटकों को पृथक करता है जो संचरण तरंग के साथ होते हैं, परन्तु जो स्वयं संचरण नहीं करते हैं। अन्य, इसी प्रकार की स्थितियों में, जहां एक संचरण विद्युत चुम्बकीय तरंग की सामान्य रूप से अपेक्षा की जाती है (जैसे कि कांच और वायु के मध्य के अंतरापृष्ठ पर अपवर्तित प्रकाश), इस पद का प्रयोग उस क्षेत्र के उस भाग का वर्णन करने के लिए किया जाता है, जहां तरंग को (जैसे प्रकाश संचारण कांच के माध्यम से, कांच से वायु अंतरापृष्ठ पर प्रभाव पड़ता है, परन्तु क्रांतिक कोण से परे) दबा दिया जाता है।
हालांकि मैक्सवेल के समीकरणों के अनुसार सभी विद्युत चुम्बकीय क्षेत्रों को लौकिक रूप से नियंत्रित किया जाता है, विभिन्न प्रविधियो या समस्याओं के कुछ प्रकार के अपेक्षित समाधान होते हैं, और जब प्राथमिक समाधानों में तरंग संचरण सम्मिलित होता है, तो पद क्षणभंगुर प्रायः उन क्षेत्रों के घटकों या समाधानों पर अनुप्रयुक्त होता है जो उस गुणधर्म को साझा नहीं करते हैं।
उदाहरण के लिए, एक खोखले धातु तरंग पथक का संचरण स्थिरांक आवृत्ति का एक प्रबल अभिलक्षक (तथाकथित परिक्षेपण संबंध) है। एक निश्चित आवृत्ति (अंतक आवृत्ति) के नीचे संचरण स्थिरांक एक काल्पनिक संख्या बन जाता है। एक काल्पनिक तरंग संख्या वाले तरंग समीकरण का समाधान तरंग के रूप में संचरणित नहीं होता है, परन्तु चरघातांकी रूप से गिर जाता है, इसलिए उस कम आवृत्ति पर उत्तेजित क्षेत्र को क्षणभंगुर माना जाता है। इसे सरलता से यह भी कहा जा सकता है कि उस आवृत्ति के लिए संचरण "अस्वीकृत" होता है।
तरंग समीकरण का औपचारिक समाधान एक समान रूप वाली विधा का वर्णन कर सकते है, परन्तु वास्तविक से काल्पनिक तक संचरण स्थिरांक का परिवर्तन अंतक आवृत्ति के नीचे आवृत्ति के रूप में पूर्णतया से परिणाम की भौतिक प्रकृति को परिवर्तित कर देता है। समाधानों को अंतक विधा या क्षणभंगुर विधा के रूप में वर्णित किया जा सकता है;[2][3]: 360 जबकि एक अलग लेखक केवल यह वर्णन करेगा कि ऐसी कोई विधा उपस्थित नहीं है। चूंकि विधा के अनुरूप क्षणभंगुर क्षेत्र की गणना तरंग समीकरण के समाधानों के रूप में की गई थी, इसलिए इसकी चर्चा प्रायः एक क्षणभंगुर तरंग के रूप में की जाती है, हालांकि इसके गुण (जैसे कोई ऊर्जा नहीं) तरंग की परिभाषा के साथ असंगत हैं।
यद्यपि यह लेख वैद्युतचुंबकिकी पर ध्यान केंद्रित करते है, पद क्षणभंगुर का उपयोग इसी प्रकार ध्वनिकी और क्वांटम यांत्रिकी जैसे क्षेत्रों में किया जाता है, जहां सम्मिलित भौतिकी से तरंग समीकरण उत्पन्न होता है। इन स्थितियों में, तरंग समीकरण के समाधान जिसके परिणामस्वरूप काल्पनिक संचरण स्थिरांक को इसी प्रकार क्षणभंगुर कहा जाता है और इसमें एक आवश्यक विशेषता यह होती है कि इसमें कोई शुद्ध ऊर्जा स्थानांतरित नहीं होती है, यद्यपि एक गैर-शून्य क्षेत्र हो।
क्षणिक तरंग अनुप्रयोग
प्रकाशिकी और ध्वनिकी में, क्षणभंगुर तरंगें तब बनती हैं जब एक माध्यम में संचारण करने वाली तरंगें अपनी सीमा पर पूर्ण आंतरिक परावर्तन से गुजरती हैं क्योंकि वे इसे तथाकथित क्रांतिक कोण से बड़े कोण पर टकराती हैं।[4][5] क्षणभंगुर तरंगो के अस्तित्व के लिए भौतिक व्याख्या यह है कि विद्युत और चुंबकीय क्षेत्र (या ध्वनिक तरंगों के स्थितियों में दाब प्रवणता) एक सीमा पर बंद नहीं हो सकते हैं। क्वांटम यांत्रिकी में, भौतिक व्याख्या पूर्णतया समान है- श्रोडिंगर तरंग-फलन सीमा के लिए सामान्य कण गति का प्रतिनिधित्व करता है और सीमा पर असतत नहीं हो सकता है।
विद्युतचुंबकीय क्षणभंगुर तरंगों का उपयोग छोटे कणों पर प्रकाशीय विकिरण दाब डालने के लिए किया जाता है ताकि उन्हें प्रयोग के लिए फंसाया जा सके या उन्हें बहुत कम तापमान पर प्रशीतित किया जा सके और सूक्ष्मदर्शिकी (कुल आंतरिक परावर्तन प्रतिदीप्ति सूक्ष्मदर्शी)के लिए जैविक कोशिकाओं या एकल-अणु प्रयोग जैसी बहुत छोटी वस्तुओं को प्रकाशित किया जा सके। एक प्रकाशित तंतु से क्षणभंगुर तरंग का उपयोग गैस संवेदक में किया जा सकता है और अवरक्त स्पेक्ट्रमिकी प्रविधि में क्षणभंगुर तरंगों को क्षीणित कुल परावर्तन के रूप में जाना जाता है।
विद्युत अभियान्त्रिकी में, किसी भी रेडियो ऐन्टेना के तरंग दैर्ध्य के एक तिहाई के भीतर विद्युत चुम्बकीय विकिरण क्षेत्र में क्षणभंगुर तरंगें पाई जाती हैं। सामान्य संचालन के पर्यन्त, एक ऐन्टेना आसपास के क्षेत्रो में विद्युत चुम्बकीय क्षेत्र का उत्सर्जन करता है और क्षेत्र ऊर्जा का एक भाग पुन: अवशोषित हो जाता है, जबकि शेष ईएम तरंगों के रूप में विकीर्ण होती है।
हाल ही में, एक ग्राफीन-आधारित ब्रैग ग्रेटिंग (एक आयामी फोटोनिक मणिभ) का निर्माण किया गया है और वर्णक्रम युग्मक प्रविधि का उपयोग करके आवधिक संरचना में सतह विद्युत चुम्बकीय तरंगों के उत्तेजना के लिए अपनी क्षमता का प्रदर्शन किया है।[6]
क्वांटम यांत्रिकी में, श्रोडिंगर समीकरण के क्षणभंगुर-तरंग समाधानों तरंग-यांत्रिक सुरंगन की घटना को उत्थान देते हैं।
सूक्ष्मदर्शिकी में, ऐसी प्रणाली जो क्षणभंगुर तरंगों में निहित सूचना को अधिकृत करती है, जिसका उपयोग उत्कृष्ट-वियोजन सूक्ष्मदर्शिकी बनाने के लिए किया जा सकता है। पदार्थ संचरण और क्षणभंगुर विद्युत चुम्बकीय तरंगों दोनों को विकीर्ण करता है। पारंपरिक प्रकाशीय प्रणालियाँ केवल संचरण तरंगों में सूचना को ग्रहण करती हैं और इसलिए विवर्तन सीमा के अधीन होती हैं। ऐसी प्रणालियाँ जो क्षणभंगुर तरंगों में निहित सूचनाओं को अधिकृत करती हैं, जैसे कि सुपर लेंस और क्षेत्र क्रमवीक्षण प्रकाशीय सूक्ष्मदर्शिकी के निकट, विवर्तन सीमा को पार कर सकती हैं; हालाँकि ये पद्धतियाँ तब प्रणाली की क्षणभंगुर तरंगों को सटीक रूप से पकड़ने की क्षमता से सीमित होती हैं।[7] उनके संकल्प पर सीमा द्वारा दिया गया है;
जहां अधिकतम तरंग सदिश है जिसे हल किया जा सकता है, वस्तु और संवेदक के मध्य की दूरी है और संवेदक की गुणवत्ता का एक मापक है।
सामान्यतः, क्षणभंगुर तरंगों के व्यावहारिक अनुप्रयोगों को (1) के रूप में वर्गीकृत किया जा सकता है, जिसमें तरंग से जुड़ी ऊर्जा का उपयोग अंतरिक्ष के क्षेत्र के भीतर किसी अन्य घटना को उत्तेजित करने के लिए किया जाता है, जहां मूल संचारण तरंग क्षणभंगुर हो जाती है (उदाहरण के लिए, जैसा कि कुल आंतरिक परावर्तन प्रतिदीप्ति सूक्ष्मदर्शी) या (2) वे जिनमें क्षणभंगुर तरंगें दो माध्यमों को जोड़ती है जिसमें संचारण तरंगों की अनुमति होती है और इसलिए संचारो के मध्य ऊर्जा या एक कण के स्थानान्तरण की अनुमति देता है (उपयोग में तरंग समीकरण के आधार पर), यहां तक कि हालांकि दो माध्यमों के मध्य अंतरिक्ष के क्षेत्र में किसी संचारण-तरंग समाधानों की अनुमति नहीं है। इसका एक उदाहरण तथाकथित तरंग-यांत्रिक सुरंगन है और इसे सामान्यतः क्षणिक तरंग युग्मन के रूप में जाना जाता है।
प्रकाश का पूर्ण आंतरिक परावर्तन

उदाहरण के लिए, दो आयामों में कुल आंतरिक परावर्तन पर विचार करें, x-अक्ष पर स्थित माध्यम के मध्य, y के साथ सामान्य और z के साथ ध्रुवीकरण (तरंगें) अंतरापृष्ठ के साथ हैं। कोई आशा कर सकता है कि पूर्ण आंतरिक परावर्तन की ओर ले जाने वाले कोणों के लिए, समाधानों में एक घटना तरंग और एक परावर्तित तरंग सम्मिलित होगी, जिसमें कोई संचरित तरंग पूर्णतया भी नहीं होगी, परन्तु ऐसा कोई समाधान नहीं है जो मैक्सवेल के समीकरणों का पालन करता हो। एक परावैद्युत माध्यम में मैक्सवेल के समीकरण क्षेत्रो E||, H||, Dy और By के घटकों के लिए निरंतरता की सीमा की स्थिति पर आरोपण करते हैं। इस उदाहरण में विचार किए गए ध्रुवीकरण के लिए, E|| और By पर स्थितियां संतुष्ट हैं और यदि परावर्तित तरंग का आयाम घटना के समान ही है क्योंकि घटना के ये घटक और परावर्तित तरंगें विनाशकारी रूप से आरोपित होती हैं। हालांकि, उनके Hx घटक रचनात्मक रूप से अध्यारोपित होते हैं, इसलिए बिना लुप्त होने वाली संचरित तरंग के बिना कोई समाधान नहीं हो सकता है। संचरित तरंग, हालांकि, ज्यावक्रीय तरंग नहीं हो सकती है क्योंकि यह तब ऊर्जा को सीमा से दूर ऊर्जा का परिवहन करेगी, परन्तु चूंकि घटना और परावर्तित तरंगों में समान ऊर्जा होती है, यह ऊर्जा के संरक्षण का उल्लंघन करेगी। इसलिए हम निष्कर्ष निकालते हैं कि प्रेषित तरंग मैक्सवेल के समीकरणों के लिए एक गैर-लुप्त होने वाला समाधान होना चाहिए जो कि एक संचारण तरंग नहीं है और एक परावैद्युत में केवल ऐसे समाधान हैं, जो चरघातांकी रूप से क्षय होते हैं: जैसे क्षणभंगुर तरंगें हैं।
गणितीय रूप से, क्षणभंगुर तरंगों को एक तरंग सदिश द्वारा चित्रित किया जा सकता है, जहां सदिश के एक या अधिक घटकों में एक काल्पनिक संख्या मान होता है क्योंकि सदिश में काल्पनिक घटक होते हैं, इसका परिमाण इसके वास्तविक घटकों से कम हो सकता है।
आपतन तल के लिए के रूप में तल पर और दो माध्यमों के अंतरापृष्ठ के रूप में तल पर , प्रेषित तरंग के तरंग सदिश का रूप होता है[8]
के साथ और , जहां प्रेषित तरंग के तरंग सदिश का परिमाण है (इसलिए तरंग संख्या), अपवर्तन का कोण है और और के साथ इकाई सदिश अक्ष दिशा और अक्ष दिशा क्रमशः होते हैं।
स्नेल के नियम का उपयोग करके जहां , और उस माध्यम का अपवर्तनांक है, जहाँ आपतित तरंग और परावर्तित तरंग उपस्थित होते हैं, उस माध्यम का अपवर्तक सूचकांक जहाँ संचरित तरंग उपस्थित होते है और आपतन कोण क्रमशः होता हैं,
के साथ
यदि पूर्ण आंतरिक परावर्तन की स्थिति के एक भाग के रूप में संतुष्ट है, तो
यदि ध्रुवीकरण (तरंगें) घटना के तल के लंबवत है (साथ में दिशा), तो किसी भी तरंग (घटना, परावर्तित, या संचरित) के विद्युत क्षेत्र को व्यक्त किया जा सकता है,
जहां में इकाई सदिश अक्ष दिशा है।
समतल तरंगों को मानकर और संचरित तरंग सदिश में को प्रतिस्थापित करना, हम संचरित तरंग के लिए पाते हैं:
जहां संचरण स्थिरांक है और चरण स्थिर है और को उपेक्षित कर दिया जाता है क्योंकि यह शारीरिक रूप से समझ में नहीं आता हैं।
क्षणभंगुर-तरंग युग्मन
विशेष रूप से प्रकाशिकी में, क्षणभंगुर-तरंग युग्मन भौतिक अतिव्यापन के कारण दो तरंगों के मध्य युग्मन को संदर्भित करता है जिसे अन्यथा संचरण तरंगों के अनुरूप अपवर्तक क्षेत्रों के रूप में वर्णित किया जाएगा।[9]
एक लौकिक उदाहरण एफटीआईआर (असंतुष्ट कुल आंतरिक परावर्तन) है। जिसमें एक सघन माध्यम की सतह पर क्षणभंगुर क्षेत्र अत्यन्त निकट (आलेख देखें) जिस पर एक तरंग सामान्यतः कुल आंतरिक परावर्तन से गुजरती है, आसपास के क्षेत्र में एक और सघन माध्यम को अतिव्यापन करता है। यह परावर्तन की समग्रता को बाधित करता है और कुछ ऊर्जा को दूसरे माध्यम में परिवर्तित कर देता है।
तंतु अंतर्भाग को एक साथ बंद करके दो प्रकाशीय तरंग पथक के मध्य युग्मन को प्रभावित किया जा सकता है ताकि एक तत्व द्वारा उत्पन्न क्षणिक क्षेत्र दूसरे तंतु में एक तरंग को उत्तेजित कर सके। इसका उपयोग तंतु प्रकाशीय विखंडक और तंतु निकासन में किया जाता है। रेडियो (और यहां तक कि प्रकाशीय) आवृत्तियों पर, ऐसे उपकरण को दिशात्मक युग्मक कहा जाता है। उपकरणों को सामान्यतः सूक्ष्म तरंग संचरण और प्रतिरुपण की स्थितियों में ऊर्जा विभाजक कहा जाता है। क्षणभंगुर-तरंग युग्मन विद्युत चुम्बकीय क्षेत्र सिद्धांत में निकट और दूर क्षेत्र की अन्तःक्रिया का पर्याय है। स्रोत तत्व की प्रकृति के आधार पर, सम्मिलित क्षणभंगुर क्षेत्र या तो मुख्य रूप से विद्युत (संधारित्र) या चुंबकीय (आगमनात्मक) होता है, दूर के क्षेत्र में तरंगों के विपरीत (संचरण) जहां ये घटक जुड़े होते हैं। क्षणभंगुर तरंग युग्मन प्रत्येक माध्यम के पास गैर-विकिरण क्षेत्र में होता है और इस प्रकार सदैव पदार्थ, अर्थात, आंशिक रूप से परावर्तक सतह के भीतर प्रेरित धाराओं और आवेशों के साथ जुड़ा होता है। क्वांटम यांत्रिकी में कणों के संदर्भ में तरंग फलन की अन्तःक्रिया पर चर्चा की जा सकती है और इसे क्वांटम सुरंगन के रूप में वर्णित किया जा सकता है।
अनुप्रयोग
- क्षणभंगुर तरंग युग्मन सामान्यतः फोटोनिक और नैनोफोटोनिक उपकरणों में तरंग पथक संवेदक या समायोजक के रूप में उपयोग किया जाता है (उदाहरण के लिए, वर्णक्रम युग्मक देखें)।[10]
- क्षणभंगुर तरंग युग्मन का उपयोग उत्तेजित करने के लिए किया जाता है, उदाहरण के लिए, परावैद्युत सूक्ष्मगोलक अनुनादक।
- क्षणभंगुर युग्मन, निकट क्षेत्र की अन्तःक्रिया के रूप में, वैद्युतचुंबकीय सुंसंगति की स्थितियों में से एक है।
- तंतु निकासन की हानि के बिना प्रकाशीय तंतु का युग्मन।
- असाधारण प्रकाशीय संचरण की सैद्धांतिक व्याख्या में क्षणभंगुर तरंग युग्मन एक प्रमुख भूमिका निभाते है।[11]
- क्षणभंगुर तरंग युग्मन का उपयोग उपकरणों को वायरलेस तरीके से चलाने में किया जाता है।[12][13][14]
- कुल आंतरिक परावर्तन प्रतिदीप्ति सूक्ष्मदर्शी सतह के निकट प्रतिदीप्तिधर को उत्तेजित करने के लिए कुल आंतरिक परावर्तन द्वारा उत्पादित क्षणभंगुर तरंग का उपयोग करता है। यह तब उपयोगी होता है जब जैविक प्रारूपों की सतह के गुणों का अध्ययन करने की आवश्यकता होती है।[15]
यह भी देखें
टिप्पणियाँ
संदर्भ
- ↑ Takayama, O.; Bogdanov, A.A.; Lavrinenko, A.V. (2017). "मेटामेट्री इंटरफेस पर फोटोनिक सतह तरंगें". Journal of Physics: Condensed Matter. 29 (46): 463001. Bibcode:2017JPCM...29T3001T. doi:10.1088/1361-648X/aa8bdd. PMID 29053474.
- ↑ इलेक्ट्रिकल और इलेक्ट्रॉनिक्स शर्तों का IEEE मानक शब्दकोश. New York, NY: The Institute of Electrical and Electronics Engineers. 1992. p. 458. ISBN 978-1-55937-240-4. IEEE STD 100-1992.
- ↑ Jackson, John David (1999). शास्त्रीय इलेक्ट्रोडायनामिक्स (3rd ed.). John-Wiley. ISBN 047130932X.
- ↑ Tineke Thio (2006). "सबवेवलेंथ प्रकाश स्रोतों के लिए एक उज्ज्वल भविष्य". American Scientist. 94 (1): 40–47. doi:10.1511/2006.1.40.
- ↑ Marston, Philip L.; Matula, T.J. (May 2002). "ध्वनिक वाष्पशील तरंगों का बिखराव". Journal of the Acoustical Society of America. 111 (5): 2378. Bibcode:2002ASAJ..111.2378M. doi:10.1121/1.4778056.
- ↑ Sreekanth, Kandammathe Valiyaveedu; Zeng, Shuwen; Shang, Jingzhi; Yong, Ken-Tye; Yu, Ting (2012). "ग्राफीन-आधारित ब्रैग झंझरी में सतह विद्युत चुम्बकीय तरंगों का उत्तेजना". Scientific Reports. 2: 737. Bibcode:2012NatSR...2E.737S. doi:10.1038/srep00737. PMC 3471096. PMID 23071901.
- ↑ Neice, A., "Methods and Limitations of Subwavelength Imaging", Advances in Imaging and Electron Physics, Vol. 163, July 2010.
- ↑ Hecht, Eugene (2017). प्रकाशिकी (5th Global ed.). Pearson. pp. 135–137. ISBN 978-1-292-09693-3.
- ↑ Zeng, Shuwen; Yu, Xia; Law, Wing-Cheung; Zhang, Yating; Hu, Rui; Dinh, Xuan-Quyen; Ho, Ho-Pui; Yong, Ken-Tye (2013). "अंतर चरण माप के आधार पर एयू एनपी-संवर्धित सतह समतल अनुनाद की आकार निर्भरता". Sensors and Actuators B: Chemical. 176: 1128–1133. doi:10.1016/j.snb.2012.09.073.
- ↑ Lova, Paola; Manfredi, Giovanni; Comoretto, Davide (2018). "कार्यात्मक समाधान संसाधित प्लानर 1डी फोटोनिक क्रिस्टल में अग्रिम". Advanced Optical Materials (in English). 6 (24): 1800730. doi:10.1002/adom.201800730. ISSN 2195-1071.
- ↑ Fan, Zhiyuan; Zhan, Li; Hu, Xiao; Xia, Yuxing (2008). "Critical process of extraordinary optical transmission through periodic subwavelength hole array: Hole-assisted evanescent-field coupling". Optics Communications. 281 (21): 5467. Bibcode:2008OptCo.281.5467F. doi:10.1016/j.optcom.2008.07.077.
- ↑ Karalis, Aristeidis; J.D. Joannopoulos; Marin Soljačić (February 2007). "कुशल वायरलेस गैर-विकिरणकारी मध्य-श्रेणी ऊर्जा हस्तांतरण". Annals of Physics. 323 (1): 34. arXiv:physics/0611063. Bibcode:2008AnPhy.323...34K. doi:10.1016/j.aop.2007.04.017. S2CID 1887505.
- ↑ "'Evanescent coupling' could power gadgets wirelessly", Celeste Biever, NewScientist.com, 15 November 2006
- ↑ Wireless energy could power consumer, industrial electronics – MIT press release
- ↑ Axelrod, D. (1 April 1981). "कुल आंतरिक प्रतिबिंब प्रतिदीप्ति द्वारा प्रकाशित सेल-सब्सट्रेट संपर्क". The Journal of Cell Biology. 89 (1): 141–145. doi:10.1083/jcb.89.1.141. PMC 2111781. PMID 7014571.

