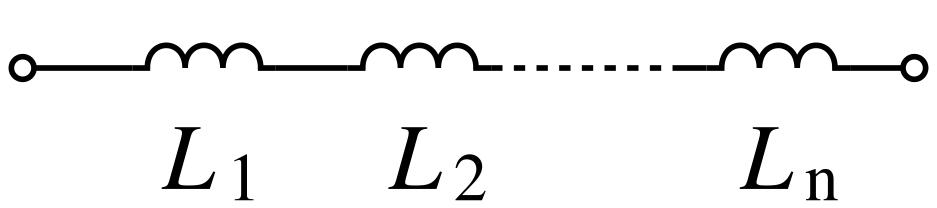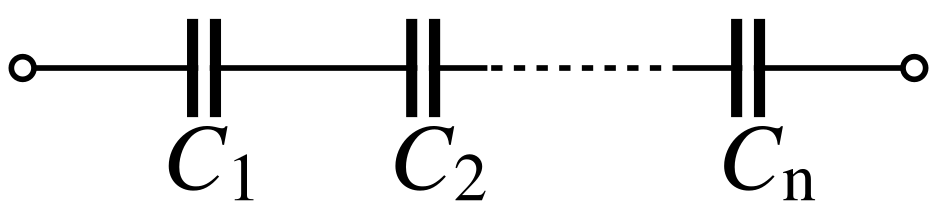श्रृंखला और समानांतर सर्किट: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Types of electrical circuits}} | {{Short description|Types of electrical circuits}} | ||
[[Image:Series circuit.svg|right|thumb|[[ वोल्टेज स्रोत | विद्युत दाब स्रोत]] (जैसे बैटरी, या इस | [[Image:Series circuit.svg|right|thumb|[[ वोल्टेज स्रोत | विद्युत दाब स्रोत]] (जैसे बैटरी, या इस स्थिति में सेल) और 3 प्रतिरोध इकाइयों के साथ श्रेणी परिपथ]] | ||
[[ टर्मिनल (इलेक्ट्रॉनिक्स) | [[ टर्मिनल (इलेक्ट्रॉनिक्स) | दो-टर्मिनल (इलेक्ट्रॉनिक्स)]] घटकों और [[ विद्युत नेटवर्क |वैद्युत जालक्रम]] को '''श्रेणी''' या '''समानांतर''' में जोड़ा जा सकता है। परिणामी वैद्युत जालक्रम में दो टर्मिनल होंगे, और स्वयं श्रेणी या समानांतर [[ टोपोलॉजी (विद्युत सर्किट) |सांस्थिति (विद्युत परिपथ)]] में भाग ले सकते हैं। फिर दो-टर्मिनल वस्तु विद्युत घटक (जैसे प्रतिरोधक) हो या वैद्युत जालक्रम (जैसे श्रेणी में प्रतिरोधक) परिप्रेक्ष्य का विषय है। यह आलेख श्रेणी/समानांतर जालक्रम में भाग लेने वाले दो-टर्मिनल वस्तु को संदर्भित करने के लिए घटक का उपयोग करेगा। | ||
श्रेणी में जुड़े घटक | श्रेणी में जुड़े घटक समान विद्युत पथ के साथ जुड़े हुए हैं, और प्रत्येक घटक में समान [[ विद्युत प्रवाह |विद्युत प्रवाह]] होता है, जो जालक्रम के माध्यम से धारा के समतुल्य होता है। पूरे जालक्रम में विद्युत दाब प्रत्येक घटक में विद्युत दाब के योग के समान होता है।<ref name="Resnick_1966"/><ref name="Smith_1966"/> | ||
समानांतर में जुड़े घटक कई | समानांतर में जुड़े घटक कई पथों से जुड़े होते हैं, और प्रत्येक घटक में समान [[ वोल्टेज |विद्युत दाब]] होता है, जो पूरे जालक्रम में विद्युत दाब के समान होता है। जालक्रम के माध्यम से धारा प्रत्येक घटक के माध्यम से धाराओं के योग के समान होता है। | ||
वोल्टेज और धारा की भूमिका के विनिमय को छोड़कर, पूर्ववर्ती दो कथन समतुल्य हैं। | |||
केवल श्रेणी में जुड़े घटकों से बना | केवल श्रेणी में जुड़े घटकों से बना परिपथ श्रेणी परिपथ के रूप में जाना जाता है; इसी तरह, समानांतर में पूरी तरह से जुड़ा हुआ समानांतर परिपथ के रूप में जाना जाता है। कई परिपथों का विश्लेषण सांस्थिति (विद्युत परिपथ) के साथ-साथ श्रेणी और समानांतर परिपथ के संयोजन के रूप में किया जा सकता है। | ||
श्रेणी परिपथ में, प्रत्येक घटक के माध्यम से प्रवाहित होने वाली धारा समान होती है, और परिपथ में विद्युत दाब प्रत्येक घटक में अलग-अलग विद्युत दाब पात का योग होता है।<ref name="Resnick_1966"/> समानांतर परिपथ में, प्रत्येक घटक में विद्युत दाब समान होता है, और कुल धारा प्रत्येक घटक के माध्यम से प्रवाहित होने वाली धाराओं का योग होता है।<ref name="Resnick_1966"/> | |||
बहुत ही सरल परिपथ पर विचार करें जिसमें चार प्रकाश बल्ब और 12-वोल्ट [[ ऑटोमोटिव बैटरी |यांत्रिक बैटरी]] सम्मिलित है। यदि तार बैटरी को बल्ब से, अगले बल्ब से, अगले बल्ब से, अगले बल्ब से जोड़ता है, तो निरंतर कुंडली में बैटरी से वापस जुड़ता है, बल्ब को श्रेणी में होते है। यदि प्रत्येक बल्ब को अलग कुंडली में बैटरी से जोड़ा जाता है, तो बल्ब को समानांतर में होते है। यदि चार प्रकाश बल्ब श्रेणी में जुड़े हुए हैं, तो उन सभी में समान धारा प्रवाहित होती है और प्रत्येक बल्ब में विद्युत दाब पात 3-वोल्ट होता है, जो उन्हें उद्दीप्ति करने के लिए पर्याप्त नहीं हो सकता है। यदि प्रकाश बल्ब समानांतर में जुड़े होते हैं, तो प्रकाश बल्ब के माध्यम से धाराएं बैटरी में धारा बनाने के लिए संयोजित होती हैं, जबकि विद्युत दाब पात प्रत्येक बल्ब में 12-वोल्ट होता है और वे सभी उद्दीप्ति हैं। | |||
श्रेणी परिपथ में, परिपथ को पूरा करने के लिए प्रत्येक उपकरण को कार्य करना चाहिए। यदि श्रेणी परिपथ में बल्ब जलता है, तो पूरा परिपथ अवरूद्ध हो जाता है। समानांतर परिपथ में, प्रत्येक प्रकाश बल्ब का अपना परिपथ होता है, इसलिए प्रकाश को छोड़कर सभी को जला दिया जा सकता है, और अंतिम अभी भी कार्य करेगा। | |||
==श्रेणी परिपथ == | ==श्रेणी परिपथ == | ||
{{Electromagnetism|Network}} | {{Electromagnetism|Network}} | ||
श्रेणी परिपथ को कभी-कभी | श्रेणी परिपथ को कभी-कभी धारा-युग्मित या डेज़ी शृंखला (विद्युत अभियांत्रिकी)-युग्मित के रूप में संदर्भित किया जाता है। श्रेणी परिपथ में विद्युत धारा परिपथ के प्रत्येक घटक से होकर गुजरती है। इसलिए, श्रेणी संयोजन के सभी घटकों में समान धारा प्रवाहित होती है। | ||
श्रेणी परिपथ में केवल समान पथ होता है जिसके माध्यम से इसकी धारा प्रवाहित हो सकती है। विफलता के किसी एकल बिंदु पर श्रेणी परिपथ को प्रस्फुटन या विभंजन पूरे परिपथ को सक्रिय करने या संचालन बंद करने का कारण बनता है। उदाहरण के लिए, यदि क्रिसमस ट्री प्रकाश की पुरानी शैली की शृंखला में से एक भी प्रकाश बल्ब जल जाता है या हटा दिया जाता है, तो दोषपूर्ण बल्ब को बदलने तक पूरी शृंखला निष्क्रिय हो जाती है। | |||
=== | ===धारा === | ||
<math display="block">I = I_1 = I_2 = \cdots = I_n</math> | <math display="block">I = I_1 = I_2 = \cdots = I_n</math> | ||
श्रेणी परिपथ में, सभी तत्वों के लिए धारा समान होता है। | |||
=== विद्युत दाब === | === विद्युत दाब === | ||
श्रेणी परिपथ में, विद्युत दाब व्यक्तिगत घटकों (प्रतिरोध इकाइयों) की विद्युत दाब पात का योग होता है। | |||
<math display="block">V = V_1 + V_2 + \dots + V_n = I \left( R_1 + R_2 + \dots + R_n \right)</math> | <math display="block">V = V_1 + V_2 + \dots + V_n = I \left( R_1 + R_2 + \dots + R_n \right)</math> | ||
===प्रतिरोध इकाइयाँ === | ===प्रतिरोध इकाइयाँ === | ||
श्रेणी में जुड़े दो या दो से अधिक प्रतिरोधों का कुल प्रतिरोध उनके व्यक्तिगत प्रतिरोधों के योग के | श्रेणी में जुड़े दो या दो से अधिक प्रतिरोधों का कुल प्रतिरोध उनके व्यक्तिगत प्रतिरोधों के योग के समान होता है: | ||
[[Image:Resistors in series.svg|यह कई प्रतिरोधों का एक आरेख है, जो अंत से अंत तक जुड़ा हुआ है, प्रत्येक के माध्यम से समान मात्रा में धारा के साथ।]] | [[Image:Resistors in series.svg|यह कई प्रतिरोधों का एक आरेख है, जो अंत से अंत तक जुड़ा हुआ है, प्रत्येक के माध्यम से समान मात्रा में धारा के साथ।]] | ||
<math display="block">R_\text{total} = R_\text{s} = R_1 + R_2 + \cdots + R_n.</math> | <math display="block">R_\text{total} = R_\text{s} = R_1 + R_2 + \cdots + R_n.</math> | ||
यहाँ, | यहाँ, {{math|''R''<sub>s</sub>}} मे पादाक्षर s श्रेणी को दर्शाता है, और {{math|''R''<sub>s</sub>}} श्रेणी में प्रतिरोध को दर्शाता है। | ||
विद्युत चालन प्रतिरोध के लिए | विद्युत चालन प्रतिरोध के लिए पारस्परिक मात्रा प्रस्तुत करता है। इसलिए, शुद्ध प्रतिरोधों के श्रेणी परिपथ के कुल संचालन की गणना निम्नलिखित अभिव्यक्ति से की जा सकती है: | ||
<math display="block">\frac{1}{G_\text{total}} = \frac{1}{G_1} + \frac{1}{G_2} + \cdots + \frac{1}{G_n}.</math> | <math display="block">\frac{1}{G_\text{total}} = \frac{1}{G_1} + \frac{1}{G_2} + \cdots + \frac{1}{G_n}.</math> | ||
श्रेणी में दो चालन के | श्रेणी में दो चालन के विशेष स्थिति के लिए, कुल चालन के समान है: | ||
<math display="block">G_\text{total} = \frac{G_1 G_2}{G_1 + G_2}.</math> | <math display="block">G_\text{total} = \frac{G_1 G_2}{G_1 + G_2}.</math> | ||
=== [[ प्रारंभ करनेवाला ]] | === [[ प्रारंभ करनेवाला | प्रेरित्र]] === | ||
प्रेरित्र समान नियम का अनुसरण करते हैं, जिसमें श्रेणी में गैर-युग्मित प्रेरकों का कुल [[ अधिष्ठापन |प्रेरकत्व]] उनके व्यक्तिगत प्रेरकत्व के योग के समान होता है: | |||
[[Image:Inductors in series.svg|कई इंडक्टर्स का एक आरेख, अंत से अंत तक जुड़ा हुआ है, जिसमें समान मात्रा में करंट प्रवाहित होता है।]] | [[Image:Inductors in series.svg|कई इंडक्टर्स का एक आरेख, अंत से अंत तक जुड़ा हुआ है, जिसमें समान मात्रा में करंट प्रवाहित होता है।]] | ||
<math display="block">L_\mathrm{total} = L_1 + L_2 + \cdots + L_n</math> | <math display="block">L_\mathrm{total} = L_1 + L_2 + \cdots + L_n</math> | ||
हालांकि, कुछ स्थितियों में, आसन्न प्रेरकों को | हालांकि, कुछ स्थितियों में, आसन्न प्रेरकों को दूसरे को प्रभावित करने से रोकना कठिन होता है क्योंकि उपकरण के चुंबकीय क्षेत्र अपने परिवेशों की कुंडलन के साथ जोड़े होते हैं। यह प्रभाव पारस्परिक प्रेरकत्व M द्वारा परिभाषित किया गया है। उदाहरण के लिए, यदि दो प्रेरक श्रेणी में हैं, तो दोनों प्रेरकों के चुंबकीय क्षेत्र दूसरे को कैसे प्रभावित करते हैं, इस पर निर्भर करते हुए दो संभावित समकक्ष प्रेरकत्व होते हैं। | ||
जब दो से अधिक प्रेरक होते हैं, तो उनमें से प्रत्येक के बीच पारस्परिक | जब दो से अधिक प्रेरक होते हैं, तो उनमें से प्रत्येक के बीच पारस्परिक प्रेरकत्व और जिस तरह से कुण्डली दूसरे को प्रभावित करते हैं, और गणना को जटिल बनाते हैं। बड़ी संख्या में कुण्डली के लिए कुल संयुक्त प्रेरकत्व विभिन्न कुण्डली के बीच सभी आपसी प्रेरकत्व के योग से दिया जाता है, जिसमें प्रत्येक दिए गए कुण्डली का स्वयं के साथ आपसी प्रेरकत्व भी सम्मिलित है, जिसे हम स्व -प्रेरकत्व या सामान्य प्रेरकत्व कहते हैं। तीन कुंडलियों के लिए, छह पारस्परिक प्रेरकत्व <math>M_{12}</math>, <math>M_{13}</math>, <math>M_{23}</math> तथा <math>M_{21}</math>, <math>M_{31}</math> तथा <math>M_{32}</math> हैं। तीन कुंडलियों के तीन स्व-प्रेरकत्व भी <math>M_{11}</math>, <math>M_{22}</math> तथा <math>M_{33}</math> हैं। | ||
इसलिए | इसलिए | ||
<math display="block">L_\text{total} = \left(M_{11} + M_{22} + M_{33}\right) + \left(M_{12} + M_{13} + M_{23}\right) + \left(M_{21} + M_{31} + M_{32}\right)</math> | <math display="block">L_\text{total} = \left(M_{11} + M_{22} + M_{33}\right) + \left(M_{12} + M_{13} + M_{23}\right) + \left(M_{21} + M_{31} + M_{32}\right)</math> | ||
पारस्परिकता से, <math>M_{ij}</math> = <math>M_{ji}</math> ताकि अंतिम दो समूहों को जोड़ा जा सके। पहले तीन पद विभिन्न कुंडलियों के स्व-प्रेरकत्वों के योग का प्रतिनिधित्व करते हैं। आपसी युग्मन के साथ सूत्र को आसानी से किसी भी श्रेणी के | पारस्परिकता से, <math>M_{ij}</math> = <math>M_{ji}</math> ताकि अंतिम दो समूहों को जोड़ा जा सके। पहले तीन पद विभिन्न कुंडलियों के स्व-प्रेरकत्वों के योग का प्रतिनिधित्व करते हैं। आपसी युग्मन के साथ सूत्र को आसानी से किसी भी श्रेणी के कुण्डली तक बढ़ाया जाता है। इस विधि का उपयोग किसी भी प्रतिनिध्यात्मक आकार के तार के बड़े कुण्डली के स्व-प्रेरण को खोजने के लिए किया जा सकता है, जो कुण्डली में तार के प्रत्येक मोड़ के प्रत्येक दूसरे मोड़ के साथ पारस्परिक प्रेरकत्व के योग की गणना करता है क्योंकि इस तरह के कुण्डली में सभी घुमाव श्रृंखला में होते हैं। | ||
=== | ===संधारित्र === | ||
{{see also| | {{see also|संधारित्र और जालक्रम}} | ||
[[ समाई ]] पारस्परिक का उपयोग करके | [[ समाई |धारिता]] पारस्परिक का उपयोग करके समान नियम का अनुसरण करते हैं। श्रेणी में [[ संधारित्र |संधारित्र]] की कुल धारिता उनकी व्यक्तिगत धारिता के गुणनात्मक प्रतिलोम के योग के व्युत्क्रम के समान होती है: | ||
[[Image:Capacitors in series.svg|कई कैपेसिटर का एक आरेख, अंत से अंत तक जुड़ा हुआ है, जिसमें समान मात्रा में करंट प्रवाहित होता है।]] | [[Image:Capacitors in series.svg|कई कैपेसिटर का एक आरेख, अंत से अंत तक जुड़ा हुआ है, जिसमें समान मात्रा में करंट प्रवाहित होता है।]] | ||
| Line 68: | Line 68: | ||
=== [[ बदलना ]] === | === [[ बदलना |स्विच]] === | ||
श्रेणी में दो या दो से अधिक स्विच | श्रेणी में दो या दो से अधिक स्विच [[ तार्किक संयोजन |तार्किक संयोजन]] बनाते हैं; यदि सभी स्विच बंद हैं तो परिपथ में केवल धारा प्रवाहित होता है। [[ और गेट |एएनडी गेट देखें]]। | ||
=== सेल [[ कार बैटरी ]] === | === सेल [[ कार बैटरी |कार बैटरी]] === | ||
[[ बैटरी (बिजली) |बैटरी (बिजली)]] विद्युत रासायनिक कोशिकाओं का संग्रह है। यदि सेल श्रेणी में जुड़े हुए हैं, तो बैटरी का विद्युत दाब सेल विद्युत दाब का योग होगा। उदाहरण के लिए, 12 वोल्ट की कार की बैटरी में श्रेणी में जुड़े छह 2-वोल्ट सेल होते हैं। कुछ वाहनों, जैसे ट्रक, में 24-वोल्ट प्रणाली को निर्धारित करने के लिए श्रेणी में दो 12 वोल्ट की बैटरी होती है। | |||
==<span class= एंकर id= Bparallel > </span>समानांतर परिपथ== | ==<span class= एंकर id= Bparallel > </span>समानांतर परिपथ== | ||
[[File:Resistors inductors capacitors in series and parallel.svg|alt=श्रृंखला और समानांतर में दो प्रतिरोधों, प्रेरकों और कैपेसिटर के प्रभावी प्रतिरोध, अधिष्ठापन और समाई की तुलना|thumb|श्रृंखला और समानांतर में दो प्रतिरोधों, प्रेरकों और संधारित्र के प्रभावी प्रतिरोध, प्रेरकत्व और धारिता की तुलना]] | |||
यदि दो या दो से अधिक घटकों को समानांतर में जोड़ा जाता है, तो उनके सिरों में क्षमता (विद्युत दाब) का समान अंतर होता है। घटकों में संभावित अंतर परिमाण में समान हैं, और उनमें समान ध्रुवताएं भी हैं। समान विद्युत दाब समानांतर में जुड़े सभी परिपथ घटकों पर प्रयुक्त होता है। किरचॉफ के धारा नियम के अनुसार, कुल धारा व्यक्तिगत घटकों के माध्यम से धाराओं का योग है। | |||
यदि दो या दो से अधिक घटकों को समानांतर में जोड़ा जाता है, तो उनके सिरों में क्षमता (विद्युत दाब) का समान अंतर होता है। घटकों में संभावित अंतर परिमाण में समान हैं, और उनमें समान ध्रुवताएं भी हैं। समान विद्युत दाब समानांतर में जुड़े सभी परिपथ घटकों पर | |||
=== | ===विद्युत दाब=== | ||
समानांतर परिपथ में, सभी तत्वों के लिए विद्युत दाब समान होता है। | समानांतर परिपथ में, सभी तत्वों के लिए विद्युत दाब समान होता है। | ||
<math display="block">V = V_1 = V_2 = \dots = V_n</math> | <math display="block">V = V_1 = V_2 = \dots = V_n</math> | ||
=== | === धारा === | ||
प्रत्येक व्यक्तिगत प्रतिरोधक में धारा ओम के नियम द्वारा पाई जाती है। विद्युत दाब बाहर | प्रत्येक व्यक्तिगत प्रतिरोधक में धारा ओम के नियम द्वारा पाई जाती है। विद्युत दाब बाहर कारक देता है | ||
<math display="block">I_\text{total} = I_1 + I_2 + \cdots + I_n = V\left(\frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n}\right).</math> | <math display="block">I_\text{total} = I_1 + I_2 + \cdots + I_n = V\left(\frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n}\right).</math> | ||
=== | ===प्रतिरोध इकाइयाँ === | ||
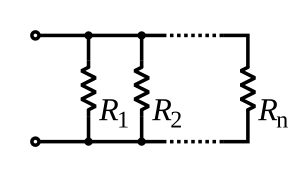
सभी घटकों के कुल विद्युत प्रतिरोध को खोजने के लिए, प्रतिरोधों | सभी घटकों के कुल विद्युत प्रतिरोध को खोजने के लिए, प्रतिरोधों <math>R_i</math> के गुणक प्रतिलोम को जोड़ें और प्रत्येक घटक का और योग का व्युत्क्रम लें। कुल प्रतिरोध सदैव सबसे छोटे प्रतिरोध के मान से कम होगा: | ||
[[Image:Resistors in parallel.svg|कई प्रतिरोधों का आरेख, अगल-बगल, दोनों एक ही तार से जुड़े हुए हैं।]] | [[Image:Resistors in parallel.svg|कई प्रतिरोधों का आरेख, अगल-बगल, दोनों एक ही तार से जुड़े हुए हैं।]] | ||
<math display="block">\frac{1}{R_\text{total}} = \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n}.</math> | <math display="block">\frac{1}{R_\text{total}} = \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n}.</math> | ||
केवल दो प्रतिरोधों के लिए, पारस्परिक | केवल दो प्रतिरोधों के लिए, पारस्परिक पद अपेक्षाकृत अधिक सरल है: | ||
<math display="block">R_\text{total} = \frac{R_1 R_2}{R_1 + R_2} .</math> | <math display="block">R_\text{total} = \frac{R_1 R_2}{R_1 + R_2} .</math> | ||
यह कभी-कभी योग पर स्मरक | यह कभी-कभी योग पर स्मरक गुणनफल द्वारा दिया जाता है। | ||
समानांतर में | समानांतर में N समान प्रतिरोधों के लिए, पारस्परिक योग पद को सरल करता है: | ||
<math display="block">\frac{1}{R_\text{total}} = N \frac{1}{R}.</math> | <math display="block">\frac{1}{R_\text{total}} = N \frac{1}{R}.</math> | ||
और इसलिए करने के लिए: | और इसलिए करने के लिए: | ||
| Line 105: | Line 103: | ||
प्रतिरोध वाले किसी घटक में धारा (विद्युत) ज्ञात करने के लिए <math>R_i</math>, ओम के नियम का पुन: उपयोग करें: | प्रतिरोध वाले किसी घटक में धारा (विद्युत) ज्ञात करने के लिए <math>R_i</math>, ओम के नियम का पुन: उपयोग करें: | ||
<math display="block">I_i = \frac{V}{R_i}\,.</math> | <math display="block">I_i = \frac{V}{R_i}\,.</math> | ||
घटक विद्युत धारा को उनके पारस्परिक प्रतिरोधों के अनुसार विभाजित करते हैं, इसलिए, दो प्रतिरोधों के | घटक विद्युत धारा को उनके पारस्परिक प्रतिरोधों के अनुसार विभाजित करते हैं, इसलिए, दो प्रतिरोधों के स्थिति में, | ||
<math display="block">\frac{I_1}{I_2} = \frac{R_2}{R_1}.</math> | <math display="block">\frac{I_1}{I_2} = \frac{R_2}{R_1}.</math> | ||
समानांतर में जुड़े उपकरणों के लिए | समानांतर में जुड़े उपकरणों के लिए पूर्व पद एकाधिक है, जैसे आर्क लैंप के लिए एकाधिक संयोजन होते है। | ||
विद्युत चालकता के बाद से <math>G</math> प्रतिरोध के लिए पारस्परिक है, प्रतिरोधों के समानांतर परिपथ के कुल चालकता के लिए | विद्युत चालकता के बाद से <math>G</math> प्रतिरोध के लिए पारस्परिक है, प्रतिरोधों के समानांतर परिपथ के कुल चालकता के लिए पद निर्धारित करते है: | ||
<math display="block">G_\text{total} = G_1 + G_2 + \cdots + G_n.</math> | <math display="block">G_\text{total} = G_1 + G_2 + \cdots + G_n.</math> | ||
कुल चालन और प्रतिरोध के संबंध | कुल चालन और प्रतिरोध के संबंध पूरक संबंध में स्थापित होते हैं: प्रतिरोधों के श्रेणी संयोजन के लिए पद चालन के समानांतर संयोजन के समान होती है, और इसके विपरीत होते है। | ||
=== | ===प्रेरित्र=== | ||
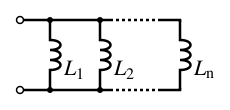
प्रेरित्र समान नियम का अनुसरण करते हैं, जिसमें समानांतर में गैर-युग्मित प्रेरकों का कुल प्रेरकत्व उनके व्यक्तिगत प्रेरकत्व के पारस्परिक योग के पारस्परिक के समान होता है: | |||
[[Image:Inductors in parallel.svg|कई प्रेरकों का एक आरेख, साथ-साथ, दोनों एक ही तार से जुड़े हुए हैं।]] | [[Image:Inductors in parallel.svg|कई प्रेरकों का एक आरेख, साथ-साथ, दोनों एक ही तार से जुड़े हुए हैं।]] | ||
<math display="block">\frac{1}{L_\text{total}} = \frac{1}{L_1} + \frac{1}{L_2} + \cdots + \frac{1}{L_n}.</math> | <math display="block">\frac{1}{L_\text{total}} = \frac{1}{L_1} + \frac{1}{L_2} + \cdots + \frac{1}{L_n}.</math> | ||
यदि | यदि प्रेरित्र -दूसरे के चुंबकीय क्षेत्र में स्थित हैं, तो पारस्परिक प्रेरण के कारण यह दृष्टिकोण अमान्य है। यदि समानांतर में दो कुंडलियों के बीच पारस्परिक प्रेरकत्व {{mvar|M}} है, और समतुल्य प्रेरित्र है: | ||
<math display="block">\frac{1}{L_\text{total}} = \frac{L_1 + L_2 - 2M}{L_1L_2 - M^2}</math> | <math display="block">\frac{1}{L_\text{total}} = \frac{L_1 + L_2 - 2M}{L_1L_2 - M^2}</math> | ||
यदि <math>L_1 = L_2</math> | यदि <math>L_1 = L_2</math> | ||
<math display="block"> L_\text{total} = \frac{L + M}{2}</math> | <math display="block"> L_\text{total} = \frac{L + M}{2}</math> | ||
<math>M</math> का चिन्ह यह निर्भर करता है कि चुंबकीय क्षेत्र दूसरे को कैसे प्रभावित करते हैं। दो समान कसकर युग्मित कुण्डली के लिए कुल प्रेरकत्व प्रत्येक कुण्डली के समीप होता है। यदि कुण्डली की ध्रुवता को इस प्रकार प्रतिवर्त कर दिया जाए कि {{mvar|M}} ऋणात्मक है, तो समानांतर प्रेरकत्व लगभग शून्य है या संयोजन लगभग गैर-प्रेरक है। यह दृढता युग्मित स्थिति में माना जाता है कि {{mvar|M}} लगभग {{mvar|L}} के समान है। हालाँकि, यदि प्रेरकत्व समान नहीं हैं और कुण्डली दृढ़ता युग्मित हैं, तो लघु परिपथ की स्थिति और धनात्मक और ऋणात्मक दोनों मानो के लिए उच्च परिसंचारी धाराएं {{mvar|M}} हो सकती हैं, जो समस्या उत्पन्न कर सकती है। | |||
तीन से अधिक प्रेरक अधिक जटिल हो जाते हैं और | तीन से अधिक प्रेरक अधिक जटिल हो जाते हैं और दूसरे पर प्रत्येक प्रेरित्र के पारस्परिक प्रेरकत्व और दूसरे पर उनके प्रभाव पर विचार किया जाना चाहिए। तीन कुंडलियों के लिए, तीन परस्पर प्रेरकत्व <math>M_{12}</math>, <math>M_{13}</math> तथा <math>M_{23}</math> होते हैं। यह आधात्री विधियों द्वारा सबसे अच्छा नियंत्रित किया जाता है और <math>L</math> आधात्री (इस स्थिति में 3×3) इसके व्युत्क्रम की शर्तों को संक्षेप में प्रस्तुत करता है। | ||
प्रासंगिक समीकरण इस प्रकार हैं: | प्रासंगिक समीकरण इस प्रकार हैं: | ||
| Line 130: | Line 128: | ||
=== | ===[[ संधारित्र ]]=== | ||
समानांतर में | समानांतर में संधारित्र की कुल धारिता उनके व्यक्तिगत धारिता के योग के समान है: | ||
[[Image:Capacitors in parallel.svg|कई कैपेसिटर का एक आरेख, साथ-साथ, एक ही तार से जुड़े प्रत्येक के दोनों लीड।]] | [[Image:Capacitors in parallel.svg|कई कैपेसिटर का एक आरेख, साथ-साथ, एक ही तार से जुड़े प्रत्येक के दोनों लीड।]] | ||
<math display="block">C_\text{total} = C_1 + C_2 + \cdots + C_n.</math> | <math display="block">C_\text{total} = C_1 + C_2 + \cdots + C_n.</math> | ||
संधारित्र के समानांतर संयोजन का कार्यशील विद्युत दाब सदैव व्यक्तिगत संधारित्र के सबसे छोटे कार्यशील विद्युत दाब द्वारा सीमित होता है। | |||
=== स्विच === | === स्विच === | ||
समानांतर में दो या दो से अधिक स्विच | समानांतर में दो या दो से अधिक स्विच तार्किक संयोजन बनाते हैं; यदि कम से कम स्विच बंद है तो परिपथ में करंट प्रवाहित होता है। [[ या गेट |या गेट]] देखें। | ||
=== सेल और बैटरी === | === सेल और बैटरी === | ||
यदि बैटरी की कोशिकाओं को समानांतर में जोड़ा जाता है, तो बैटरी विद्युत दाब सेल विद्युत दाब के समान होगा, लेकिन प्रत्येक सेल द्वारा आपूर्ति की जाने वाली धारा कुल धारा का | यदि बैटरी की कोशिकाओं को समानांतर में जोड़ा जाता है, तो बैटरी विद्युत दाब सेल विद्युत दाब के समान होगा, लेकिन प्रत्येक सेल द्वारा आपूर्ति की जाने वाली धारा कुल धारा का अंश होगी। उदाहरण के लिए, यदि बैटरी में समानांतर में जुड़े चार समान सेल होते हैं और 1 [[ एम्पेयर |एम्पेयर]] की धारा देता है, तो प्रत्येक सेल द्वारा आपूर्ति की जाने वाली धारा 0.25 एम्पीयर होगी। यदि कोशिकाएं समान नहीं हैं, तो उच्च विद्युत दाब वाले सेल कम विद्युत दाब वाले को चार्ज करने का प्रयास करेंगे, और संभावित रूप से उन्हें हानी पहुंचाएंगे। | ||
[[ वहनीय रेडियो ]] में [[ वेक्यूम - ट्यूब ]] | [[ वहनीय रेडियो | संवहन रेडियो]] में [[ वेक्यूम - ट्यूब |निर्वात-नलिका]] संवहन तार को शक्ति देने के लिए समानांतर-संयोजित बैटरियों का व्यापक रूप से उपयोग किया जाता था। लिथियम-आयन पुनःआवेशनीय बैटरी (विशेष रूप से लैपटॉप बैटरी) प्रायः एम्पीयर-घंटे दर बढ़ाने के लिए समानांतर में जुड़ी होती हैं। कुछ सौर विद्युत प्रणालियों में भंडारण क्षमता बढ़ाने के लिए समानांतर में बैटरी होती है; कुल एम्पीयर-घंटे का निकट सन्निकटन समानांतर बैटरी के सभी एम्पीयर-घंटे का योग है। | ||
==चालन का संयोजन == | ==चालन का संयोजन == | ||
किरचॉफ के परिपथ नियमों से हम चालन के संयोजन के नियमों को घटा सकते हैं। दो चालन के लिए <math>G_1</math> तथा <math>G_2</math> समानांतर में, उनके पार विद्युत दाब समान है और किरचॉफ के | किरचॉफ के परिपथ नियमों से हम चालन के संयोजन के नियमों को घटा सकते हैं। दो चालन के लिए <math>G_1</math> तथा <math>G_2</math> समानांतर में, उनके पार विद्युत दाब समान है और किरचॉफ के धारा नियम (केसीएल) से कुल धारा है | ||
<math display="block">I_\text{eq} = I_1 + I_2.</math> | <math display="block">I_\text{eq} = I_1 + I_2.</math> | ||
ओम के नियम को चालन के स्थान पर रखने पर प्राप्त होता है | ओम के नियम को चालन के स्थान पर रखने पर प्राप्त होता है | ||
| Line 158: | Line 156: | ||
जो बदले में तुल्य चालकता का सूत्र देता है, | जो बदले में तुल्य चालकता का सूत्र देता है, | ||
<math display="block">\frac{1}{G_\text{eq}} = \frac{1}{G_1} + \frac{1}{G_2}.</math> | <math display="block">\frac{1}{G_\text{eq}} = \frac{1}{G_1} + \frac{1}{G_2}.</math> | ||
इस समीकरण को | इस समीकरण को आंशिक पुनर्व्यवस्थित किया जा सकता है, हालांकि यह विशेष स्थिति है जो केवल दो घटकों के लिए इस तरह पुनर्व्यवस्थित करेगा। | ||
<math display="block">G_\text{eq} = \frac{G_1 G_2}{G_1 + G_2}.</math> | <math display="block">G_\text{eq} = \frac{G_1 G_2}{G_1 + G_2}.</math> | ||
| Line 166: | Line 164: | ||
== संकेतन == | == संकेतन == | ||
समानांतर में दो घटकों का मान प्रायः [[ समानांतर ऑपरेटर ]] द्वारा समीकरणों में दर्शाया जाता है, | समानांतर में दो घटकों का मान प्रायः [[ समानांतर ऑपरेटर |समानांतर परिचालक]] दो लंबवत रेखाओं (∥) द्वारा समीकरणों में दर्शाया जाता है, ज्यामिति से समांतर रेखाओं के संकेतन को अभिग्रहण कर लेते हैं। | ||
<math display="block">R_\mathrm{eq} \equiv R_1 \parallel R_2 \equiv \left(R_1^{-1} + R_2^{-1}\right)^{-1} \equiv \frac{R_1 R_2}{R_1 + R_2}</math> | <math display="block">R_\mathrm{eq} \equiv R_1 \parallel R_2 \equiv \left(R_1^{-1} + R_2^{-1}\right)^{-1} \equiv \frac{R_1 R_2}{R_1 + R_2}</math> | ||
यह उन | यह उन पदों को सरल करता है जो अन्यथा शर्तों के विस्तार से जटिल हो जाते है। उदाहरण के लिए: | ||
<math display="block">R_1 \parallel R_2 \parallel R_3 \equiv \frac{R_1 R_2 R_3}{R_1 R_2 + R_1 R_3 + R_2 R_3} . </math> | <math display="block">R_1 \parallel R_2 \parallel R_3 \equiv \frac{R_1 R_2 R_3}{R_1 R_2 + R_1 R_3 + R_2 R_3} . </math> | ||
यदि {{math|''n''}} घटक समानांतर में हैं, तो | यदि {{math|''n''}} घटक समानांतर में हैं, तो | ||
| Line 174: | Line 172: | ||
== | == अनुप्रयोग == | ||
उपभोक्ता इलेक्ट्रॉनिक्स में श्रेणी परिपथ का | उपभोक्ता इलेक्ट्रॉनिक्स में श्रेणी परिपथ का सामान्य अनुप्रयोग बैटरी में होता है, जहां श्रेणी में जुड़े कई कोशिकाओं का उपयोग सुविधाजनक परिचालन विद्युत दाब प्राप्त करने के लिए किया जाता है। श्रेणी में दो प्रयोज्य जिंक सेल 3 वोल्ट पर फ्लैशलाइट या दूरस्थ नियंत्रण को शक्ति दे सकते हैं; हस्त बिजली उपकरण के बैटरी पैक में 48 वोल्ट प्रदान करने के लिए श्रेणी में तार बारह लिथियम-आयन सेल हो सकते हैं। | ||
श्रेणी परिपथ का उपयोग पहले [[ इलेक्ट्रिक मल्टीपल यूनिट्स |विद्युत बहु एकक गाडी]] में प्रदीपन के लिए किया जाता था। उदाहरण के लिए, यदि आपूर्ति विद्युत दाब 600 वोल्ट था, तो श्रेणी में आठ 70-वोल्ट बल्ब (कुल 560 वोल्ट) और शेष 40 वोल्ट को छोड़ने के लिए प्रतिरोधक हो सकता है। पहले [[ मोटर जनरेटर |मोटर जनित्र]] द्वारा, फिर ठोस अवस्था (इलेक्ट्रॉनिक्स) उपकरणों द्वारा, ट्रेन की रोशनी के लिए श्रेणी परिपथ को हटा दिया गया था। | |||
किसी दिए गए | किसी दिए गए उपकरण के अंदर रक्त वाहिकाओं की व्यवस्था के लिए श्रेणी प्रतिरोध भी प्रयुक्त किया जा सकता है। प्रत्येक अंग को श्रेणी में व्यवस्थित बड़ी धमनी, छोटी धमनियों, धमनियों, केशिकाओं और नसों द्वारा आपूर्ति की जाती है। कुल प्रतिरोध व्यक्तिगत प्रतिरोधों का योग है, जैसा कि निम्नलिखित समीकरण {{math|1=''R''<sub>total</sub> = ''R''<sub>artery</sub> + ''R''<sub>arterioles</sub> + ''R''<sub>capillaries</sub>}} द्वारा व्यक्त किया गया है। इस श्रेणी में प्रतिरोध का सबसे बड़ा अनुपात धमनी द्वारा योगदान दिया जाता है।<ref name="BRS"/> | ||
समानांतर प्रतिरोध [[ संचार प्रणाली ]] द्वारा सचित्र है। प्रत्येक | समानांतर प्रतिरोध [[ संचार प्रणाली |संचार प्रणाली]] द्वारा सचित्र है। प्रत्येक उपकरण को धमनी द्वारा आपूर्ति की जाती है जो [[ महाधमनी |महाधमनी]] से निकलती है। इस समांतर व्यवस्था का कुल प्रतिरोध निम्नलिखित समीकरण {{math|1=1/''R''<sub>total</sub> = 1/''R''<sub>a</sub> + 1/''R''<sub>b</sub> + ... + 1/''R''<sub>n</sub>}}. {{math|''R''<sub>a</sub>}}, {{math|''R''<sub>b</sub>}}, तथा {{math|''R''<sub>n</sub>}} द्वारा व्यक्त किया जाता है। क्रमशः वृक्क, यकृत और अन्य धमनियों के प्रतिरोध हैं। कुल प्रतिरोध किसी भी व्यक्तिगत धमनियों के प्रतिरोध से कम है।<ref name="BRS"/> | ||
==यह भी देखें== | ==यह भी देखें== | ||
* [[ नेटवर्क विश्लेषण (विद्युत सर्किट) | | * [[ नेटवर्क विश्लेषण (विद्युत सर्किट) |विरोधी समानांतर (इलेक्ट्रॉनिक्स)]] | ||
* | * प्रतिबाधाओं का संयोजन | ||
* [[ व्हीटस्टोन पुल ]] | * [[ व्हीटस्टोन पुल |धारा विभाजक]] | ||
* | * समतुल्य प्रतिबाधा रूपांतरित होती है | ||
* [[ वोल्टेज विभक्त | | * [[ वोल्टेज विभक्त | द्रवगैसप्रवाह सादृश्य]] | ||
*[[ वर्तमान विभक्त | *[[ वर्तमान विभक्त | नेटवर्क विश्लेषण (विद्युत परिपथ )]] | ||
*[[ प्रतिरोध दूरी ]] | *[[ प्रतिरोध दूरी ]] | ||
*[[ श्रृंखला-समानांतर द्वैत | श्रेणी-समानांतर द्वैत]] <ref name="Ellerman_1995"/><ref name="Ellerman_2004"/> | *[[ श्रृंखला-समानांतर द्वैत | श्रेणी-समानांतर द्वैत]] <ref name="Ellerman_1995"/><ref name="Ellerman_2004"/> | ||
*[[ श्रृंखला-समानांतर आंशिक क्रम | श्रेणी-समानांतर आंशिक क्रम]] | *[[ श्रृंखला-समानांतर आंशिक क्रम | श्रेणी-समानांतर आंशिक क्रम]] | ||
*[[ श्रृंखला और समानांतर स्प्रिंग्स | श्रेणी और समानांतर | *[[ श्रृंखला और समानांतर स्प्रिंग्स | श्रेणी और समानांतर शृंखला]] | ||
* [[ हाइड्रोलिक सादृश्य ]] | * [[ हाइड्रोलिक सादृश्य | सांस्थिति (विद्युत परिपथ)]] | ||
* [[ विरोधी समानांतर (इलेक्ट्रॉनिक्स) ]] | * [[ विरोधी समानांतर (इलेक्ट्रॉनिक्स) | वोल्टेज विभक्त]] | ||
*व्हीटस्टोन ब्रिज | |||
*Y-Δ रूपांतरण | |||
==संदर्भ== | ==संदर्भ== | ||
| Line 220: | Line 218: | ||
*अवरोध | *अवरोध | ||
*विद्युत दाब | *विद्युत दाब पात | ||
*द्वैत (विद्युत परिपथ) | *द्वैत (विद्युत परिपथ) | ||
*डेज़ी चेन ( | *डेज़ी चेन (विद्युत अभियांत्रिकी) | ||
*क्रिसमस ट्री रोशनी | *क्रिसमस ट्री रोशनी | ||
*असफलता की | *असफलता की भी वजह | ||
*विद्युत चालकता | *विद्युत चालकता | ||
*गुणात्मक प्रतिलोम | *गुणात्मक प्रतिलोम | ||
Revision as of 10:11, 10 April 2023

दो-टर्मिनल (इलेक्ट्रॉनिक्स) घटकों और वैद्युत जालक्रम को श्रेणी या समानांतर में जोड़ा जा सकता है। परिणामी वैद्युत जालक्रम में दो टर्मिनल होंगे, और स्वयं श्रेणी या समानांतर सांस्थिति (विद्युत परिपथ) में भाग ले सकते हैं। फिर दो-टर्मिनल वस्तु विद्युत घटक (जैसे प्रतिरोधक) हो या वैद्युत जालक्रम (जैसे श्रेणी में प्रतिरोधक) परिप्रेक्ष्य का विषय है। यह आलेख श्रेणी/समानांतर जालक्रम में भाग लेने वाले दो-टर्मिनल वस्तु को संदर्भित करने के लिए घटक का उपयोग करेगा।
श्रेणी में जुड़े घटक समान विद्युत पथ के साथ जुड़े हुए हैं, और प्रत्येक घटक में समान विद्युत प्रवाह होता है, जो जालक्रम के माध्यम से धारा के समतुल्य होता है। पूरे जालक्रम में विद्युत दाब प्रत्येक घटक में विद्युत दाब के योग के समान होता है।[1][2]
समानांतर में जुड़े घटक कई पथों से जुड़े होते हैं, और प्रत्येक घटक में समान विद्युत दाब होता है, जो पूरे जालक्रम में विद्युत दाब के समान होता है। जालक्रम के माध्यम से धारा प्रत्येक घटक के माध्यम से धाराओं के योग के समान होता है।
वोल्टेज और धारा की भूमिका के विनिमय को छोड़कर, पूर्ववर्ती दो कथन समतुल्य हैं।
केवल श्रेणी में जुड़े घटकों से बना परिपथ श्रेणी परिपथ के रूप में जाना जाता है; इसी तरह, समानांतर में पूरी तरह से जुड़ा हुआ समानांतर परिपथ के रूप में जाना जाता है। कई परिपथों का विश्लेषण सांस्थिति (विद्युत परिपथ) के साथ-साथ श्रेणी और समानांतर परिपथ के संयोजन के रूप में किया जा सकता है।
श्रेणी परिपथ में, प्रत्येक घटक के माध्यम से प्रवाहित होने वाली धारा समान होती है, और परिपथ में विद्युत दाब प्रत्येक घटक में अलग-अलग विद्युत दाब पात का योग होता है।[1] समानांतर परिपथ में, प्रत्येक घटक में विद्युत दाब समान होता है, और कुल धारा प्रत्येक घटक के माध्यम से प्रवाहित होने वाली धाराओं का योग होता है।[1]
बहुत ही सरल परिपथ पर विचार करें जिसमें चार प्रकाश बल्ब और 12-वोल्ट यांत्रिक बैटरी सम्मिलित है। यदि तार बैटरी को बल्ब से, अगले बल्ब से, अगले बल्ब से, अगले बल्ब से जोड़ता है, तो निरंतर कुंडली में बैटरी से वापस जुड़ता है, बल्ब को श्रेणी में होते है। यदि प्रत्येक बल्ब को अलग कुंडली में बैटरी से जोड़ा जाता है, तो बल्ब को समानांतर में होते है। यदि चार प्रकाश बल्ब श्रेणी में जुड़े हुए हैं, तो उन सभी में समान धारा प्रवाहित होती है और प्रत्येक बल्ब में विद्युत दाब पात 3-वोल्ट होता है, जो उन्हें उद्दीप्ति करने के लिए पर्याप्त नहीं हो सकता है। यदि प्रकाश बल्ब समानांतर में जुड़े होते हैं, तो प्रकाश बल्ब के माध्यम से धाराएं बैटरी में धारा बनाने के लिए संयोजित होती हैं, जबकि विद्युत दाब पात प्रत्येक बल्ब में 12-वोल्ट होता है और वे सभी उद्दीप्ति हैं।
श्रेणी परिपथ में, परिपथ को पूरा करने के लिए प्रत्येक उपकरण को कार्य करना चाहिए। यदि श्रेणी परिपथ में बल्ब जलता है, तो पूरा परिपथ अवरूद्ध हो जाता है। समानांतर परिपथ में, प्रत्येक प्रकाश बल्ब का अपना परिपथ होता है, इसलिए प्रकाश को छोड़कर सभी को जला दिया जा सकता है, और अंतिम अभी भी कार्य करेगा।
श्रेणी परिपथ
| Articles about |
| Electromagnetism |
|---|
 |
श्रेणी परिपथ को कभी-कभी धारा-युग्मित या डेज़ी शृंखला (विद्युत अभियांत्रिकी)-युग्मित के रूप में संदर्भित किया जाता है। श्रेणी परिपथ में विद्युत धारा परिपथ के प्रत्येक घटक से होकर गुजरती है। इसलिए, श्रेणी संयोजन के सभी घटकों में समान धारा प्रवाहित होती है।
श्रेणी परिपथ में केवल समान पथ होता है जिसके माध्यम से इसकी धारा प्रवाहित हो सकती है। विफलता के किसी एकल बिंदु पर श्रेणी परिपथ को प्रस्फुटन या विभंजन पूरे परिपथ को सक्रिय करने या संचालन बंद करने का कारण बनता है। उदाहरण के लिए, यदि क्रिसमस ट्री प्रकाश की पुरानी शैली की शृंखला में से एक भी प्रकाश बल्ब जल जाता है या हटा दिया जाता है, तो दोषपूर्ण बल्ब को बदलने तक पूरी शृंखला निष्क्रिय हो जाती है।
धारा
विद्युत दाब
श्रेणी परिपथ में, विद्युत दाब व्यक्तिगत घटकों (प्रतिरोध इकाइयों) की विद्युत दाब पात का योग होता है।
प्रतिरोध इकाइयाँ
श्रेणी में जुड़े दो या दो से अधिक प्रतिरोधों का कुल प्रतिरोध उनके व्यक्तिगत प्रतिरोधों के योग के समान होता है:
विद्युत चालन प्रतिरोध के लिए पारस्परिक मात्रा प्रस्तुत करता है। इसलिए, शुद्ध प्रतिरोधों के श्रेणी परिपथ के कुल संचालन की गणना निम्नलिखित अभिव्यक्ति से की जा सकती है:
प्रेरित्र
प्रेरित्र समान नियम का अनुसरण करते हैं, जिसमें श्रेणी में गैर-युग्मित प्रेरकों का कुल प्रेरकत्व उनके व्यक्तिगत प्रेरकत्व के योग के समान होता है:
जब दो से अधिक प्रेरक होते हैं, तो उनमें से प्रत्येक के बीच पारस्परिक प्रेरकत्व और जिस तरह से कुण्डली दूसरे को प्रभावित करते हैं, और गणना को जटिल बनाते हैं। बड़ी संख्या में कुण्डली के लिए कुल संयुक्त प्रेरकत्व विभिन्न कुण्डली के बीच सभी आपसी प्रेरकत्व के योग से दिया जाता है, जिसमें प्रत्येक दिए गए कुण्डली का स्वयं के साथ आपसी प्रेरकत्व भी सम्मिलित है, जिसे हम स्व -प्रेरकत्व या सामान्य प्रेरकत्व कहते हैं। तीन कुंडलियों के लिए, छह पारस्परिक प्रेरकत्व , , तथा , तथा हैं। तीन कुंडलियों के तीन स्व-प्रेरकत्व भी , तथा हैं।
इसलिए
संधारित्र
धारिता पारस्परिक का उपयोग करके समान नियम का अनुसरण करते हैं। श्रेणी में संधारित्र की कुल धारिता उनकी व्यक्तिगत धारिता के गुणनात्मक प्रतिलोम के योग के व्युत्क्रम के समान होती है:
स्विच
श्रेणी में दो या दो से अधिक स्विच तार्किक संयोजन बनाते हैं; यदि सभी स्विच बंद हैं तो परिपथ में केवल धारा प्रवाहित होता है। एएनडी गेट देखें।
सेल कार बैटरी
बैटरी (बिजली) विद्युत रासायनिक कोशिकाओं का संग्रह है। यदि सेल श्रेणी में जुड़े हुए हैं, तो बैटरी का विद्युत दाब सेल विद्युत दाब का योग होगा। उदाहरण के लिए, 12 वोल्ट की कार की बैटरी में श्रेणी में जुड़े छह 2-वोल्ट सेल होते हैं। कुछ वाहनों, जैसे ट्रक, में 24-वोल्ट प्रणाली को निर्धारित करने के लिए श्रेणी में दो 12 वोल्ट की बैटरी होती है।
समानांतर परिपथ
यदि दो या दो से अधिक घटकों को समानांतर में जोड़ा जाता है, तो उनके सिरों में क्षमता (विद्युत दाब) का समान अंतर होता है। घटकों में संभावित अंतर परिमाण में समान हैं, और उनमें समान ध्रुवताएं भी हैं। समान विद्युत दाब समानांतर में जुड़े सभी परिपथ घटकों पर प्रयुक्त होता है। किरचॉफ के धारा नियम के अनुसार, कुल धारा व्यक्तिगत घटकों के माध्यम से धाराओं का योग है।
विद्युत दाब
समानांतर परिपथ में, सभी तत्वों के लिए विद्युत दाब समान होता है।
धारा
प्रत्येक व्यक्तिगत प्रतिरोधक में धारा ओम के नियम द्वारा पाई जाती है। विद्युत दाब बाहर कारक देता है
प्रतिरोध इकाइयाँ
सभी घटकों के कुल विद्युत प्रतिरोध को खोजने के लिए, प्रतिरोधों के गुणक प्रतिलोम को जोड़ें और प्रत्येक घटक का और योग का व्युत्क्रम लें। कुल प्रतिरोध सदैव सबसे छोटे प्रतिरोध के मान से कम होगा:
समानांतर में N समान प्रतिरोधों के लिए, पारस्परिक योग पद को सरल करता है:
विद्युत चालकता के बाद से प्रतिरोध के लिए पारस्परिक है, प्रतिरोधों के समानांतर परिपथ के कुल चालकता के लिए पद निर्धारित करते है:
प्रेरित्र
प्रेरित्र समान नियम का अनुसरण करते हैं, जिसमें समानांतर में गैर-युग्मित प्रेरकों का कुल प्रेरकत्व उनके व्यक्तिगत प्रेरकत्व के पारस्परिक योग के पारस्परिक के समान होता है:
तीन से अधिक प्रेरक अधिक जटिल हो जाते हैं और दूसरे पर प्रत्येक प्रेरित्र के पारस्परिक प्रेरकत्व और दूसरे पर उनके प्रभाव पर विचार किया जाना चाहिए। तीन कुंडलियों के लिए, तीन परस्पर प्रेरकत्व , तथा होते हैं। यह आधात्री विधियों द्वारा सबसे अच्छा नियंत्रित किया जाता है और आधात्री (इस स्थिति में 3×3) इसके व्युत्क्रम की शर्तों को संक्षेप में प्रस्तुत करता है।
प्रासंगिक समीकरण इस प्रकार हैं:
संधारित्र
समानांतर में संधारित्र की कुल धारिता उनके व्यक्तिगत धारिता के योग के समान है:
स्विच
समानांतर में दो या दो से अधिक स्विच तार्किक संयोजन बनाते हैं; यदि कम से कम स्विच बंद है तो परिपथ में करंट प्रवाहित होता है। या गेट देखें।
सेल और बैटरी
यदि बैटरी की कोशिकाओं को समानांतर में जोड़ा जाता है, तो बैटरी विद्युत दाब सेल विद्युत दाब के समान होगा, लेकिन प्रत्येक सेल द्वारा आपूर्ति की जाने वाली धारा कुल धारा का अंश होगी। उदाहरण के लिए, यदि बैटरी में समानांतर में जुड़े चार समान सेल होते हैं और 1 एम्पेयर की धारा देता है, तो प्रत्येक सेल द्वारा आपूर्ति की जाने वाली धारा 0.25 एम्पीयर होगी। यदि कोशिकाएं समान नहीं हैं, तो उच्च विद्युत दाब वाले सेल कम विद्युत दाब वाले को चार्ज करने का प्रयास करेंगे, और संभावित रूप से उन्हें हानी पहुंचाएंगे।
संवहन रेडियो में निर्वात-नलिका संवहन तार को शक्ति देने के लिए समानांतर-संयोजित बैटरियों का व्यापक रूप से उपयोग किया जाता था। लिथियम-आयन पुनःआवेशनीय बैटरी (विशेष रूप से लैपटॉप बैटरी) प्रायः एम्पीयर-घंटे दर बढ़ाने के लिए समानांतर में जुड़ी होती हैं। कुछ सौर विद्युत प्रणालियों में भंडारण क्षमता बढ़ाने के लिए समानांतर में बैटरी होती है; कुल एम्पीयर-घंटे का निकट सन्निकटन समानांतर बैटरी के सभी एम्पीयर-घंटे का योग है।
चालन का संयोजन
किरचॉफ के परिपथ नियमों से हम चालन के संयोजन के नियमों को घटा सकते हैं। दो चालन के लिए तथा समानांतर में, उनके पार विद्युत दाब समान है और किरचॉफ के धारा नियम (केसीएल) से कुल धारा है
संकेतन
समानांतर में दो घटकों का मान प्रायः समानांतर परिचालक दो लंबवत रेखाओं (∥) द्वारा समीकरणों में दर्शाया जाता है, ज्यामिति से समांतर रेखाओं के संकेतन को अभिग्रहण कर लेते हैं।
अनुप्रयोग
उपभोक्ता इलेक्ट्रॉनिक्स में श्रेणी परिपथ का सामान्य अनुप्रयोग बैटरी में होता है, जहां श्रेणी में जुड़े कई कोशिकाओं का उपयोग सुविधाजनक परिचालन विद्युत दाब प्राप्त करने के लिए किया जाता है। श्रेणी में दो प्रयोज्य जिंक सेल 3 वोल्ट पर फ्लैशलाइट या दूरस्थ नियंत्रण को शक्ति दे सकते हैं; हस्त बिजली उपकरण के बैटरी पैक में 48 वोल्ट प्रदान करने के लिए श्रेणी में तार बारह लिथियम-आयन सेल हो सकते हैं।
श्रेणी परिपथ का उपयोग पहले विद्युत बहु एकक गाडी में प्रदीपन के लिए किया जाता था। उदाहरण के लिए, यदि आपूर्ति विद्युत दाब 600 वोल्ट था, तो श्रेणी में आठ 70-वोल्ट बल्ब (कुल 560 वोल्ट) और शेष 40 वोल्ट को छोड़ने के लिए प्रतिरोधक हो सकता है। पहले मोटर जनित्र द्वारा, फिर ठोस अवस्था (इलेक्ट्रॉनिक्स) उपकरणों द्वारा, ट्रेन की रोशनी के लिए श्रेणी परिपथ को हटा दिया गया था।
किसी दिए गए उपकरण के अंदर रक्त वाहिकाओं की व्यवस्था के लिए श्रेणी प्रतिरोध भी प्रयुक्त किया जा सकता है। प्रत्येक अंग को श्रेणी में व्यवस्थित बड़ी धमनी, छोटी धमनियों, धमनियों, केशिकाओं और नसों द्वारा आपूर्ति की जाती है। कुल प्रतिरोध व्यक्तिगत प्रतिरोधों का योग है, जैसा कि निम्नलिखित समीकरण Rtotal = Rartery + Rarterioles + Rcapillaries द्वारा व्यक्त किया गया है। इस श्रेणी में प्रतिरोध का सबसे बड़ा अनुपात धमनी द्वारा योगदान दिया जाता है।[3]
समानांतर प्रतिरोध संचार प्रणाली द्वारा सचित्र है। प्रत्येक उपकरण को धमनी द्वारा आपूर्ति की जाती है जो महाधमनी से निकलती है। इस समांतर व्यवस्था का कुल प्रतिरोध निम्नलिखित समीकरण 1/Rtotal = 1/Ra + 1/Rb + ... + 1/Rn. Ra, Rb, तथा Rn द्वारा व्यक्त किया जाता है। क्रमशः वृक्क, यकृत और अन्य धमनियों के प्रतिरोध हैं। कुल प्रतिरोध किसी भी व्यक्तिगत धमनियों के प्रतिरोध से कम है।[3]
यह भी देखें
- विरोधी समानांतर (इलेक्ट्रॉनिक्स)
- प्रतिबाधाओं का संयोजन
- धारा विभाजक
- समतुल्य प्रतिबाधा रूपांतरित होती है
- द्रवगैसप्रवाह सादृश्य
- नेटवर्क विश्लेषण (विद्युत परिपथ )
- प्रतिरोध दूरी
- श्रेणी-समानांतर द्वैत [4][5]
- श्रेणी-समानांतर आंशिक क्रम
- श्रेणी और समानांतर शृंखला
- सांस्थिति (विद्युत परिपथ)
- वोल्टेज विभक्त
- व्हीटस्टोन ब्रिज
- Y-Δ रूपांतरण
संदर्भ
- ↑ 1.0 1.1 1.2 Resnick, Robert; Halliday, David (1966). "Chapter 32". Physics. Vol. I and II (Combined international ed.). Wiley. LCCN 66-11527. Example 1.
- ↑ Smith, R. J. (1966). Circuits, Devices and Systems (International ed.). New York: Wiley. p. 21. LCCN 66-17612.
- ↑ 3.0 3.1 Costanzo, Linda S. Physiology. Board Review Series. p. 74.
- ↑ Ellerman, David Patterson (1995-03-21). "Chapter 12: Parallel Addition, Series-Parallel Duality, and Financial Mathematics". Intellectual Trespassing as a Way of Life: Essays in Philosophy, Economics, and Mathematics (PDF). pp. 237–268. ISBN 0-8476-7932-2. Archived (PDF) from the original on 2016-03-05. Retrieved 2019-08-09.
[…] When resistors with resistance a and b are placed in series, their compound resistance is the usual sum (hereafter the series sum) of the resistances a + b. If the resistances are placed in parallel, their compound resistance is the parallel sum of the resistances, which is denoted by the full colon […]
{{cite book}}:|work=ignored (help) [1] (271 pages) - ↑ Ellerman, David Patterson (May 2004) [1995-03-21]. "Introduction to Series-Parallel Duality" (PDF). University of California at Riverside. CiteSeerX 10.1.1.90.3666. Archived from the original on 2019-08-10. Retrieved 2019-08-09.
The parallel sum of two positive real numbers x:y = [(1/x) + (1/y)]−1 arises in electrical circuit theory as the resistance resulting from hooking two resistances x and y in parallel. There is a duality between the usual (series) sum and the parallel sum. […]
[2] (24 pages)
अग्रिम पठन
- Williams, Tim (2005). The Circuit Designer's Companion. Butterworth-Heinemann. ISBN 0-7506-6370-7.
- "Resistor combinations: How many values using 1K ohm resistors?". EDN magazine.
- Grotz, Bernhard (2018-01-04), "Strömungswiderstand", Mechanik der Flüssigkeiten (in Deutsch)
इस पृष्ठ में अनुपलब्ध आंतरिक कड़ियों की सूची
- अवरोध
- विद्युत दाब पात
- द्वैत (विद्युत परिपथ)
- डेज़ी चेन (विद्युत अभियांत्रिकी)
- क्रिसमस ट्री रोशनी
- असफलता की भी वजह
- विद्युत चालकता
- गुणात्मक प्रतिलोम
- विद्युत रासायनिक सेल
- विद्युतीय प्रतिरोध
- चालू बिजली)
- चाप दीपक
- तार्किक वियोजन
- ठोस अवस्था (इलेक्ट्रॉनिक्स)
बाहरी संबंध
- Series circuit, Parallel circuit
- Series and Parallel Circuits chapter from Lessons In Electric Circuits Vol 1 DC free ebook and Lessons In Electric Circuits series.
- Series-Parallel Combination Circuits chapter from Lessons In Electric Circuits Vol 1 DC free ebook and Lessons In Electric Circuits series.
- Video “What's a Circuit, Series and Parallel (ElectroBOOM101–005)” by ElectroBOOM.