वर्णनात्मक ज्यामिति: Difference between revisions
No edit summary |
No edit summary |
||
| (10 intermediate revisions by 4 users not shown) | |||
| Line 15: | Line 15: | ||
|url=https://www.ams.org/featurecolumn/archive/art1.html | |url=https://www.ams.org/featurecolumn/archive/art1.html | ||
}} | }} | ||
</ref> वर्णनात्मक ज्यामिति के लिए सैद्धांतिक आधार [[चित्रमय प्रक्षेपण]] द्वारा प्रदान किया जाता है। तकनीक पर सबसे पहले ज्ञात प्रकाशन "अंडरवेसुंग डेर मेसंग मिट डेम ज़िर्केल एंड रिचचेयट" था, जो "अल्ब्रेक्ट ड्यूरर" द्वारा लिनियन, नूर्नबर्ग: 1525 में प्रकाशित हुआ था। इतालवी वास्तुकार "[[ग्वारिनो ग्वारिनी]]" भी प्रक्षेप्य और वर्णनात्मक ज्यामिति के अग्रणी थे, जैसा कि उनके "प्लासिटा फिलोसोफिका" (1665), "यूक्लिड्स एडौक्टस" (1671) और "आर्किटेटुरा सिविले" (1686-1737 तक प्रकाशित नहीं) से स्पष्ट है, "[[गैसपार्ड मोंगे|गैसपार्ड मोंगे"]] (1746 -1818), जिन्हें | </ref> वर्णनात्मक ज्यामिति के लिए सैद्धांतिक आधार [[चित्रमय प्रक्षेपण]] द्वारा प्रदान किया जाता है। तकनीक पर सबसे पहले ज्ञात प्रकाशन "अंडरवेसुंग डेर मेसंग मिट डेम ज़िर्केल एंड रिचचेयट" था, जो "अल्ब्रेक्ट ड्यूरर" द्वारा लिनियन, नूर्नबर्ग: 1525 में प्रकाशित हुआ था। इतालवी वास्तुकार "[[ग्वारिनो ग्वारिनी]]" भी प्रक्षेप्य और वर्णनात्मक ज्यामिति के अग्रणी थे, जैसा कि उनके "प्लासिटा फिलोसोफिका" (1665), "यूक्लिड्स एडौक्टस" (1671) और "आर्किटेटुरा सिविले" (1686-1737 तक प्रकाशित नहीं) से स्पष्ट है, "[[गैसपार्ड मोंगे|गैसपार्ड मोंगे"]] (1746 -1818), जिन्हें सामान्यत: वर्णनात्मक ज्यामिति के आविष्कार का श्रेय दिया जाता है।<ref>{{cite encyclopedia|title=ग्वारिनी, ग्वारिनो|encyclopedia=A Dictionary of Architecture|year=2015|publisher=[[Oxford University Press]]|editor=[[James Stevens Curl]]|isbn=9780198606789|url=https://books.google.com/books?id=jIWr0IO9dYIC&pg=PA337|page=337}}</ref><ref>{{cite journal|title=ग्वारिनो गुआरिनी के अंतरिक्ष अनुसंधान में स्टीरियोटॉमी की भूमिका|last=Bianchini|first=Carlo|year=2012|journal=Nuts and Bolts of Construction History|volume=1|pages=257–263|isbn=978-2-7084-0929-3}}</ref> गैसपार्ड मोंगे को सामान्यत: ज्यामितीय समस्या हल में उनके विकास के कारण वर्णनात्मक ज्यामिति का जनक माना जाता है। उनकी पहली खोज 1765 में हुई थी जब वह सैन्य किलेबंदी के लिए एक प्रारूपकार के रूप में काम कर रहे थे, चूंकि उनके निष्कर्ष बाद में प्रकाशित हुए थे।<ref>{{Citation | ||
|author=Ingrid Carlbom, Joseph Paciorek | |author=Ingrid Carlbom, Joseph Paciorek | ||
|title=Planar Geometric Projections and Viewing Transformations | |title=Planar Geometric Projections and Viewing Transformations | ||
| Line 31: | Line 31: | ||
वर्णनात्मक ज्यामिति एक काल्पनिक वस्तु से निकलने वाली काल्पनिक, समानांतर प्रक्षेपित्र की छवि बनाने की तकनीक का उपयोग करती है और समकोण पर प्रक्षेपण के एक काल्पनिक समतल को काटती है। प्रतिच्छेद के संचयी बिंदु वांछित छवि बनाते हैं | वर्णनात्मक ज्यामिति एक काल्पनिक वस्तु से निकलने वाली काल्पनिक, समानांतर प्रक्षेपित्र की छवि बनाने की तकनीक का उपयोग करती है और समकोण पर प्रक्षेपण के एक काल्पनिक समतल को काटती है। प्रतिच्छेद के संचयी बिंदु वांछित छवि बनाते हैं | ||
== | == संलेख == | ||
* | * एक वस्तु की दो छवियों को परस्पर लंबवत में बहिर्विष्ट करें। प्रत्येक छवि दृश्य में स्थान के तीन आयाम समायोजित है, दो आयाम पूर्ण पैमाने पर प्रदर्शित होते हैं, परस्पर-लंबवत अक्ष और एक अदृश्य (बिंदु दृश्य) अक्ष के रूप में छवि स्थान (गहराई) में घटता है। दो आसन्न छवि दृश्यों में से प्रत्येक तीन आयामों में से एक का पूर्ण-स्तरीय दृश्य साझा करता है। | ||
* इनमें से कोई भी छवि तीसरे अनुमानित दृश्य के लिए | * इनमें से कोई भी छवि तीसरे अनुमानित दृश्य के लिए आरंभिक बिंदु के रूप में काम कर सकती है। तीसरा दृश्य चौथा प्रक्षेपण आरंभ कर सकता है, अनंत तक। ये अनुक्रमिक प्रक्षेपण प्रत्येक वस्तु को एक अलग दिशा से देखने के लिए अंतरिक्ष में एक घुमावदार, 90 डिग्री मोड़ का प्रतिनिधित्व करते हैं। | ||
* प्रत्येक नया प्रक्षेपण पूर्ण पैमाने में एक आयाम का उपयोग करता है जो पिछले दृश्य में बिंदु-दृश्य आयाम के रूप में प्रकट होता है। इस आयाम के पूर्ण पैमाने के दृश्य को प्राप्त करने और इसे नए दृश्य में समायोजित करने के लिए पिछले दृश्य को अनदेखा करने और दूसरे पिछले दृश्य पर आगे बढ़ने की आवश्यकता होती है जहां यह आयाम पूर्ण पैमाने पर दिखाई देता है। | * प्रत्येक नया प्रक्षेपण पूर्ण पैमाने में एक आयाम का उपयोग करता है जो पिछले दृश्य में बिंदु-दृश्य आयाम के रूप में प्रकट होता है। इस आयाम के पूर्ण पैमाने के दृश्य को प्राप्त करने और इसे नए दृश्य में समायोजित करने के लिए पिछले दृश्य को अनदेखा करने और दूसरे पिछले दृश्य पर आगे बढ़ने की आवश्यकता होती है जहां यह आयाम पूर्ण पैमाने पर दिखाई देता है। | ||
* प्रत्येक नया दृश्य प्रक्षेपण की पिछली दिशा के लंबवत किसी भी अनंत दिशाओं में प्रक्षेपित करके बनाया जा सकता है। (वैगन व्हील के स्पोक्स की कई दिशाओं की कल्पना करें, जिनमें से प्रत्येक एक्सल की दिशा के लंबवत हो।) परिणाम 90° घुमावों में किसी वस्तु के चारों ओर चक्कर लगाने और प्रत्येक चरण से | * प्रत्येक नया दृश्य प्रक्षेपण की पिछली दिशा के लंबवत किसी भी अनंत दिशाओं में प्रक्षेपित करके बनाया जा सकता है। (वैगन व्हील के स्पोक्स की कई दिशाओं की कल्पना करें, जिनमें से प्रत्येक एक्सल की दिशा के लंबवत हो।) परिणाम 90° घुमावों में किसी वस्तु के चारों ओर चक्कर लगाने और प्रत्येक चरण से वस्तु को देखने का एक परिणाम है। प्रत्येक नया दृश्य एक खाका प्रदर्शक के लिए एक अतिरिक्त दृश्य के रूप में जोड़ा जाता है और ग्लास बॉक्स मॉडल के प्रकटीकरण में दिखाई देता है। | ||
लिखने के अतिरिक्त, छह मानक प्रमुख दृश्य (फ्रंट; राइट साइड; लेफ्ट साइड; टॉप; बॉटम; रियर), वर्णनात्मक ज्यामिति चार बुनियादी हल दृश्य प्राप्त करने का प्रयास करती है: एक रेखा की [[सही लंबाई]] (अर्थात, पूर्ण आकार, पूर्वाभास नहीं) , एक रेखा का बिंदु दृश्य (अंतिम दृश्य), एक तल का वास्तविक आकार (अर्थात, पैमाने के लिए पूर्ण आकार, या पूर्वसंकेत नहीं), और एक तल का किनारा दृश्य (अर्थात, दृष्टि रेखा के साथ एक तल का दृश्य एक समतल के वास्तविक आकार का उत्पादन करने के लिए दृष्टि की रेखा से जुड़ी दृष्टि रेखा के लंबवत)। ये अधिकांशत: बाद के दृश्य के लिए प्रक्षेपण की दिशा निर्धारित करने का काम करते हैं। 90° घुमावदार कदम प्रक्रिया द्वारा, किसी रेखा के बिंदु दृश्य से किसी भी दिशा में प्रक्षेपित करने से इसकी वास्तविक लंबाई का दृश्य प्राप्त होता है; वास्तविक लंबाई रेखा दृश्य के समानांतर एक दिशा में प्रक्षेपित करने से इसका बिंदु दृश्य प्राप्त होता है, किसी तल पर किसी भी रेखा के बिंदु दृश्य को प्रक्षेपित करने से समतल का किनारा दृश्य प्राप्त होता है; एक समतल के किनारे के दृश्य के लंबवत दिशा में प्रक्षेपित करने से वास्तविक आकार (पैमाने पर) दृश्य प्राप्त होगा। ठोस-ज्यामिति सिद्धांतों द्वारा उत्पन्न अभियान्त्रिकी समस्याओं को हल करने में मदद करने के लिए इन विभिन्न विचारों का आह्वान किया जा सकता है | |||
== ह्यूरिस्टिक्स == | == ह्यूरिस्टिक्स == | ||
वर्णनात्मक ज्यामिति का अध्ययन करने के लिए अनुमानी | वर्णनात्मक ज्यामिति का अध्ययन करने के लिए अनुमानी मान है। यह मानस प्रत्यक्षीकरण और स्थानिक विश्लेषणात्मक क्षमताओं के साथ-साथ हल के लिए ज्यामितीय समस्या को सर्वोत्तम रूप से प्रस्तुत करने के लिए देखने की दिशा को पहचानने की सहज क्षमता को बढ़ावा देता है। प्रतिनिधि उदाहरण: | ||
=== देखने के लिए सबसे अच्छी दिशा === | === देखने के लिए सबसे अच्छी दिशा === | ||
* उनके सबसे छोटे | * उनके सबसे छोटे संयोजक (सामान्य लंबवत) के स्थान को निर्धारित करने के लिए सामान्य स्थिति में दो [[तिरछी रेखाएँ]] | ||
* सामान्य स्थिति में दो तिरछी रेखाएँ (पाइप) इस तरह कि उनका सबसे छोटा | * सामान्य स्थिति में दो तिरछी रेखाएँ (पाइप) इस तरह कि उनका सबसे छोटा संयोजक पूर्ण पैमाने पर देखा जाता है | ||
* सामान्य स्थिति में दो तिरछी रेखाएँ किसी दिए गए | * सामान्य स्थिति में दो तिरछी रेखाएँ किसी दिए गए समतल के समानांतर सबसे छोटा संयोजक पूर्ण पैमाने पर देखा जाता है (कहते हैं, एक विकिरण सतह से निरंतर दूरी पर सबसे छोटे संयोजक की स्थिति और आयाम निर्धारित करने के लिए) | ||
* एक समतल सतह जैसे कि ड्रिल किया हुआ छेद पूर्ण पैमाने पर देखा जाता है, जैसे कि छेद के माध्यम से देख रहे हों (कहते हैं, अन्य ड्रिल किए गए छेदों के साथ निकासी के लिए परीक्षण करने के लिए) | * एक समतल सतह जैसे कि ड्रिल किया हुआ छेद पूर्ण पैमाने पर देखा जाता है, जैसे कि छेद के माध्यम से देख रहे हों (कहते हैं, अन्य ड्रिल किए गए छेदों के साथ निकासी के लिए परीक्षण करने के लिए) | ||
* सामान्य स्थिति में दो तिरछी रेखाओं से समदूरस्थ एक समतल (कहते हैं, सुरक्षित विकिरण दूरी की पुष्टि करने के लिए?) | * सामान्य स्थिति में दो तिरछी रेखाओं से समदूरस्थ एक समतल (कहते हैं, सुरक्षित विकिरण दूरी की पुष्टि करने के लिए?) | ||
* एक बिंदु से एक | * एक बिंदु से एक समतल तक की सबसे छोटी दूरी (जैसे, ब्रेसिंग के लिए सबसे किफायती स्थिति का पता लगाने के लिए) | ||
* घुमावदार सतहों सहित दो सतहों के बीच | * घुमावदार सतहों सहित दो सतहों के बीच प्रतिच्छेदन की रेखा (कहते हैं, वर्गों के सबसे किफायती आकार के लिए?) | ||
* दो तलों के बीच के कोण का सही आकार | * दो तलों के बीच के कोण का सही आकार | ||
अनुक्रमिक अनुमानों के अनुरूप संगणक-मॉडलिंग दृश्य प्रस्तुत करने के लिए एक मानक अभी तक अपनाया नहीं गया है। इस तरह के एक उम्मीदवार को नीचे दिए गए चित्रों में प्रस्तुत किया गया है। चित्रों में छवियां त्रि-आयामी, अभियान्त्रिकी संगणक आलेखिकी का उपयोग करके बनाई गई थीं। | |||
त्रि-आयामी, | त्रि-आयामी, संगणक मॉडलिंग ट्यूब के पीछे आभासी स्थान उत्पन्न करता है, और इस आभासी स्थान के भीतर किसी भी दिशा से किसी मॉडल के किसी भी दृश्य का उत्पादन कर सकता है। यह आसन्न लिखने के विचारों की आवश्यकता के बिना ऐसा करता है और इसलिए वर्णनात्मक ज्यामिति के अप्रचलित, स्टेपिंग संलेख को अप्रचलित करने के लिए प्रतीत हो सकता है। चूंकि वर्णनात्मक ज्यामिति एक सपाट तल पर तीन या अधिक आयामी अंतरिक्ष के वैध या स्वीकार्य इमेजिंग का विज्ञान है, यह संगणक मॉडलिंग संभावनाओं को बढ़ाने के लिए एक अनिवार्य अध्ययन है। | ||
=== उदाहरण === | === उदाहरण === | ||
'''दो तिरछी रेखाओं PR और SU के बीच सबसे छोटा संबंधक ज्ञात करना''' | |||
[[File:Descriptive geometry lines.svg|thumb|350px|दो तिरछी रेखाओं के बीच सबसे छोटा संबंधक खोजने के लिए वर्णनात्मक ज्यामिति के उपयोग का उदाहरण। लाल, पीले और हरे रंग की हाइलाइट दूरियां दिखाती हैं जो बिंदु P के अनुमानों के लिए समान होती हैं।]]P, R, S और U के X, Y और Z निर्देशांक दिए गए हैं, अनुमान 1 और 2 क्रमशः XY और XZ | [[File:Descriptive geometry lines.svg|thumb|350px|दो तिरछी रेखाओं के बीच सबसे छोटा संबंधक खोजने के लिए वर्णनात्मक ज्यामिति के उपयोग का उदाहरण। लाल, पीले और हरे रंग की हाइलाइट दूरियां दिखाती हैं जो बिंदु P के अनुमानों के लिए समान होती हैं।]]P, R, S और U के X, Y और Z निर्देशांक दिए गए हैं, अनुमान 1 और 2 क्रमशः XY और XZ समतलों पर स्केल करने के लिए तैयार किए गए हैं। | ||
किसी एक रेखा का सही दृश्य (प्रक्षेपण में लंबाई 3डी अंतरिक्ष में लंबाई के बराबर है) प्राप्त करने के लिए: इस उदाहरण में SU, प्रक्षेपण 3 को हिंज रेखा H | किसी एक रेखा का सही दृश्य (प्रक्षेपण में लंबाई 3डी अंतरिक्ष में लंबाई के बराबर है) प्राप्त करने के लिए: इस उदाहरण में SU, प्रक्षेपण 3 को हिंज रेखा H<sub>2,3</sub> के समानांतर S<sub>2</sub>U<sub>2</sub> साथ खींचा गया है। SU का अंतिम दृश्य प्राप्त करने के लिए, प्रोजेक्शन 4 को हिंज लाइन H<sub>3,4</sub> को S<sub>3</sub>U<sub>3</sub>. के लिए लंबवत खींचा गया है। लम्बवत दूरी d, PR और SU के बीच न्यूनतम दूरी दर्शाती है। | ||
इस न्यूनतम दूरी को देने वाली इन रेखाओं पर बिंदु Q और T प्राप्त करने के लिए, प्रोजेक्शन 5 को हिंग लाइन H | इस न्यूनतम दूरी को देने वाली इन रेखाओं पर बिंदु Q और T प्राप्त करने के लिए, प्रोजेक्शन 5 को हिंग लाइन H<sub>4,5</sub> के समानांतर P<sub>4</sub> R<sub>4</sub>,के साथ खींचा गया है दोनों P<sub>5</sub> R<sub>5</sub> और S<sub>5</sub>U<sub>5</sub> यथार्थ मत बना रहा है(अंतिम दृश्य का कोई भी प्रक्षेपण एक सच्चा दृश्य है)। इन रेखाओं के प्रतिच्छेदन को प्रक्षेपित करते हुए, Q<sub>5</sub> और T<sub>5</sub> प्रोजेक्शन 1 पर वापस (मैजेंटा लाइन और लेबल) उनके निर्देशांक को X, Y और Z अक्षों से पढ़ने की अनुमति देता है। | ||
== | == व्यापकहल == | ||
व्यापकहल वर्णनात्मक ज्यामिति के भीतर हलों का एक वर्ग है जिसमें किसी समस्या के सभी संभावित हल होते हैं। व्यापकहल को एक एकल, त्रि-आयामी वस्तु, सामान्यत: एक शंकु द्वारा दर्शाया जाता है, जिसके तत्वों की दिशा किसी भी अनंत संख्या के हल विचारों के लिए देखने (प्रक्षेपण) की वांछित दिशा है। | |||
उदाहरण के लिए: | उदाहरण के लिए: व्यापकहल खोजने के लिए जैसे कि दो, असमान लंबाई, तिरछी रेखाएं सामान्य स्थिति में दिखाई देती हैं (कहते हैं, उड़ान में रॉकेट?) | ||
* समान लंबाई | * समान लंबाई | ||
| Line 78: | Line 78: | ||
* अन्य। | * अन्य। | ||
उदाहरणों में, प्रत्येक वांछित | उदाहरणों में, प्रत्येक वांछित विशिष्ट हल के लिए व्यापकहल एक शंकु है, जिनमें से प्रत्येक तत्व एक अनंत संख्या में हल दृश्य उत्पन्न करता है। जब दो या दो से अधिक विशेषताओं, के ऊपर सूचीबद्ध हैं, वांछित हैं (और जिसके लिए एक हल मौजूद है) हल दृश्य दो शंकुओं के बीच प्रतिच्छेदन के दो तत्वों (एक तत्व, यदि शंकु स्पर्शरेखा हैं) की दिशा में बहिर्विष्ट करना वांछित उत्पन्न करता है । यदि शंकु प्रतिच्छेद नहीं करते हैं तो हल मौजूद नहीं है। हलों में प्रयुक्त वर्णनात्मक ज्यामितीय सिद्धांतों को दिखाने के लिए नीचे दिए गए उदाहरणों की व्याख्या की गई है। TL = True-Length; EV = Edge View. | ||
नीचे चित्र 1-3 प्रदर्शित करता है (1) वर्णनात्मक ज्यामिति, व्यापकहल (2) एक साथ, लंबकोणिक, मल्टीव्यू, अभिविनयास स्वरूपों में ऐसे हल प्रस्तुत करने के लिए एक संभावित मानक। | |||
संभावित मानक के बीच एक मानक | संभावित मानक के बीच एक मानक तय रेखा के साथ दो आसन्न, मानक, लंबकोणिक दृश्य (यहाँ, सामने और ऊपर) कार्यरत हैं। चूंकि हल दृश्य पर पहुंचने के लिए मानक, दो-चरण अनुक्रमों में वस्तु के चारों ओर 90° चक्कर लगाने की कोई आवश्यकता नहीं है (यह सीधे हल दृश्य पर जाना संभव है), इस छोटे संलेख को ध्यान में रखा गया है अभिविनयास के लिए। जहां पहला चरण संलेख दो-चरणीय संलेख को प्रतिस्थापित करता है, द्वि वलन पंक्ति का उपयोग किया जाता है। दूसरे शब्दों में, जब कोई दोहरी रेखाओं को पार करता है तो वह 90° का घुमावदार घुमाव नहीं बना रहा होता है बल्कि सीधे हल दृश्य की ओर एक गैर-ऑर्थोडायरेक्शनल मोड़ बना रहा होता है। जैसा कि अधिकांश अभियान्त्रिकी संगणक आलेखिकी पैकेज स्वचालित रूप से ग्लास बॉक्स मॉडल के छह प्रमुख दृश्य, साथ ही एक सममितीय दृश्य उत्पन्न करते हैं, इन विचारों को कभी-कभी अनुमानी जिज्ञासा से जोड़ा जाता है। | ||
[[File:Descriptive geometry - skew lines appearing perpendicular.png|बॉर्डर | चित्र 1 वर्णनात्मक ज्यामिति - तिरछी रेखाएँ लंबवत दिखाई देती हैं]]<br>चित्र 1: वर्णनात्मक ज्यामिति - लंबवत दिखाई देने वाली तिरछी रेखाएं | |||
[[File:Descriptive geometry - skew lines appear equal length.png|बॉर्डर | चित्र 2 वर्णनात्मक ज्यामिति - तिरछी रेखाएँ समान लंबाई की दिखाई देती हैं]]<br>चित्र 2: वर्णनात्मक ज्यामिति - तिरछी रेखाएँ समान लंबाई की दिखाई देती हैं | |||
[[File:Descriptive geometry - skew lines appear in specified length ratio.png|बॉर्डर | चित्र 3 वर्णनात्मक ज्यामिति - तिरछी रेखाएँ निर्दिष्ट लंबाई अनुपात में दिखाई देती हैं]]<br>चित्र 3: वर्णनात्मक ज्यामिति - तिरछी रेखाएँ निर्दिष्ट लंबाई अनुपात में दिखाई देती हैं | |||
== यह भी देखें == | == यह भी देखें == | ||
| Line 113: | Line 113: | ||
{{visualization}} | {{visualization}} | ||
{{Authority control}} | {{Authority control}} | ||
[[Category:Collapse templates]] | |||
[[Category:Commons category link is locally defined]] | |||
[[Category: | |||
[[Category:Created On 23/03/2023]] | [[Category:Created On 23/03/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages using multiple image with manual scaled images]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:वर्णनात्मक ज्यामिति| वर्णनात्मक ज्यामिति ]] | |||
Latest revision as of 19:03, 19 April 2023
वर्णनात्मक ज्यामिति ज्यामिति की शाखा है जो प्रक्रियाओं के एक विशिष्ट सेट का उपयोग करके त्रि-आयामी वस्तुओं को दो आयामों में प्रस्तुत करने की अनुमति देती है। परिणामी तकनीकें अभियांत्रिकी, वास्तुकला, अभिकल्पना और कला के लिए महत्वपूर्ण हैं।[1] वर्णनात्मक ज्यामिति के लिए सैद्धांतिक आधार चित्रमय प्रक्षेपण द्वारा प्रदान किया जाता है। तकनीक पर सबसे पहले ज्ञात प्रकाशन "अंडरवेसुंग डेर मेसंग मिट डेम ज़िर्केल एंड रिचचेयट" था, जो "अल्ब्रेक्ट ड्यूरर" द्वारा लिनियन, नूर्नबर्ग: 1525 में प्रकाशित हुआ था। इतालवी वास्तुकार "ग्वारिनो ग्वारिनी" भी प्रक्षेप्य और वर्णनात्मक ज्यामिति के अग्रणी थे, जैसा कि उनके "प्लासिटा फिलोसोफिका" (1665), "यूक्लिड्स एडौक्टस" (1671) और "आर्किटेटुरा सिविले" (1686-1737 तक प्रकाशित नहीं) से स्पष्ट है, "गैसपार्ड मोंगे" (1746 -1818), जिन्हें सामान्यत: वर्णनात्मक ज्यामिति के आविष्कार का श्रेय दिया जाता है।[2][3] गैसपार्ड मोंगे को सामान्यत: ज्यामितीय समस्या हल में उनके विकास के कारण वर्णनात्मक ज्यामिति का जनक माना जाता है। उनकी पहली खोज 1765 में हुई थी जब वह सैन्य किलेबंदी के लिए एक प्रारूपकार के रूप में काम कर रहे थे, चूंकि उनके निष्कर्ष बाद में प्रकाशित हुए थे।[4] मोंगे के आदिलेख एक काल्पनिक वस्तु को इस तरह से खींचने की अनुमति देते हैं कि इसे तीन आयामों में तैयार किया जा सके। काल्पनिक वस्तु के सभी ज्यामितीय पहलुओं को सही आकार/टू-स्केल और आकार में हिसाब में लिया जाता है, और अंतरिक्ष से किसी भी स्थिति से देखा जा सकता है। सभी छवियों को द्वि-आयामी सतह पर दर्शाया गया है।
वर्णनात्मक ज्यामिति एक काल्पनिक वस्तु से निकलने वाली काल्पनिक, समानांतर प्रक्षेपित्र की छवि बनाने की तकनीक का उपयोग करती है और समकोण पर प्रक्षेपण के एक काल्पनिक समतल को काटती है। प्रतिच्छेद के संचयी बिंदु वांछित छवि बनाते हैं
संलेख
- एक वस्तु की दो छवियों को परस्पर लंबवत में बहिर्विष्ट करें। प्रत्येक छवि दृश्य में स्थान के तीन आयाम समायोजित है, दो आयाम पूर्ण पैमाने पर प्रदर्शित होते हैं, परस्पर-लंबवत अक्ष और एक अदृश्य (बिंदु दृश्य) अक्ष के रूप में छवि स्थान (गहराई) में घटता है। दो आसन्न छवि दृश्यों में से प्रत्येक तीन आयामों में से एक का पूर्ण-स्तरीय दृश्य साझा करता है।
- इनमें से कोई भी छवि तीसरे अनुमानित दृश्य के लिए आरंभिक बिंदु के रूप में काम कर सकती है। तीसरा दृश्य चौथा प्रक्षेपण आरंभ कर सकता है, अनंत तक। ये अनुक्रमिक प्रक्षेपण प्रत्येक वस्तु को एक अलग दिशा से देखने के लिए अंतरिक्ष में एक घुमावदार, 90 डिग्री मोड़ का प्रतिनिधित्व करते हैं।
- प्रत्येक नया प्रक्षेपण पूर्ण पैमाने में एक आयाम का उपयोग करता है जो पिछले दृश्य में बिंदु-दृश्य आयाम के रूप में प्रकट होता है। इस आयाम के पूर्ण पैमाने के दृश्य को प्राप्त करने और इसे नए दृश्य में समायोजित करने के लिए पिछले दृश्य को अनदेखा करने और दूसरे पिछले दृश्य पर आगे बढ़ने की आवश्यकता होती है जहां यह आयाम पूर्ण पैमाने पर दिखाई देता है।
- प्रत्येक नया दृश्य प्रक्षेपण की पिछली दिशा के लंबवत किसी भी अनंत दिशाओं में प्रक्षेपित करके बनाया जा सकता है। (वैगन व्हील के स्पोक्स की कई दिशाओं की कल्पना करें, जिनमें से प्रत्येक एक्सल की दिशा के लंबवत हो।) परिणाम 90° घुमावों में किसी वस्तु के चारों ओर चक्कर लगाने और प्रत्येक चरण से वस्तु को देखने का एक परिणाम है। प्रत्येक नया दृश्य एक खाका प्रदर्शक के लिए एक अतिरिक्त दृश्य के रूप में जोड़ा जाता है और ग्लास बॉक्स मॉडल के प्रकटीकरण में दिखाई देता है।
लिखने के अतिरिक्त, छह मानक प्रमुख दृश्य (फ्रंट; राइट साइड; लेफ्ट साइड; टॉप; बॉटम; रियर), वर्णनात्मक ज्यामिति चार बुनियादी हल दृश्य प्राप्त करने का प्रयास करती है: एक रेखा की सही लंबाई (अर्थात, पूर्ण आकार, पूर्वाभास नहीं) , एक रेखा का बिंदु दृश्य (अंतिम दृश्य), एक तल का वास्तविक आकार (अर्थात, पैमाने के लिए पूर्ण आकार, या पूर्वसंकेत नहीं), और एक तल का किनारा दृश्य (अर्थात, दृष्टि रेखा के साथ एक तल का दृश्य एक समतल के वास्तविक आकार का उत्पादन करने के लिए दृष्टि की रेखा से जुड़ी दृष्टि रेखा के लंबवत)। ये अधिकांशत: बाद के दृश्य के लिए प्रक्षेपण की दिशा निर्धारित करने का काम करते हैं। 90° घुमावदार कदम प्रक्रिया द्वारा, किसी रेखा के बिंदु दृश्य से किसी भी दिशा में प्रक्षेपित करने से इसकी वास्तविक लंबाई का दृश्य प्राप्त होता है; वास्तविक लंबाई रेखा दृश्य के समानांतर एक दिशा में प्रक्षेपित करने से इसका बिंदु दृश्य प्राप्त होता है, किसी तल पर किसी भी रेखा के बिंदु दृश्य को प्रक्षेपित करने से समतल का किनारा दृश्य प्राप्त होता है; एक समतल के किनारे के दृश्य के लंबवत दिशा में प्रक्षेपित करने से वास्तविक आकार (पैमाने पर) दृश्य प्राप्त होगा। ठोस-ज्यामिति सिद्धांतों द्वारा उत्पन्न अभियान्त्रिकी समस्याओं को हल करने में मदद करने के लिए इन विभिन्न विचारों का आह्वान किया जा सकता है
ह्यूरिस्टिक्स
वर्णनात्मक ज्यामिति का अध्ययन करने के लिए अनुमानी मान है। यह मानस प्रत्यक्षीकरण और स्थानिक विश्लेषणात्मक क्षमताओं के साथ-साथ हल के लिए ज्यामितीय समस्या को सर्वोत्तम रूप से प्रस्तुत करने के लिए देखने की दिशा को पहचानने की सहज क्षमता को बढ़ावा देता है। प्रतिनिधि उदाहरण:
देखने के लिए सबसे अच्छी दिशा
- उनके सबसे छोटे संयोजक (सामान्य लंबवत) के स्थान को निर्धारित करने के लिए सामान्य स्थिति में दो तिरछी रेखाएँ
- सामान्य स्थिति में दो तिरछी रेखाएँ (पाइप) इस तरह कि उनका सबसे छोटा संयोजक पूर्ण पैमाने पर देखा जाता है
- सामान्य स्थिति में दो तिरछी रेखाएँ किसी दिए गए समतल के समानांतर सबसे छोटा संयोजक पूर्ण पैमाने पर देखा जाता है (कहते हैं, एक विकिरण सतह से निरंतर दूरी पर सबसे छोटे संयोजक की स्थिति और आयाम निर्धारित करने के लिए)
- एक समतल सतह जैसे कि ड्रिल किया हुआ छेद पूर्ण पैमाने पर देखा जाता है, जैसे कि छेद के माध्यम से देख रहे हों (कहते हैं, अन्य ड्रिल किए गए छेदों के साथ निकासी के लिए परीक्षण करने के लिए)
- सामान्य स्थिति में दो तिरछी रेखाओं से समदूरस्थ एक समतल (कहते हैं, सुरक्षित विकिरण दूरी की पुष्टि करने के लिए?)
- एक बिंदु से एक समतल तक की सबसे छोटी दूरी (जैसे, ब्रेसिंग के लिए सबसे किफायती स्थिति का पता लगाने के लिए)
- घुमावदार सतहों सहित दो सतहों के बीच प्रतिच्छेदन की रेखा (कहते हैं, वर्गों के सबसे किफायती आकार के लिए?)
- दो तलों के बीच के कोण का सही आकार
अनुक्रमिक अनुमानों के अनुरूप संगणक-मॉडलिंग दृश्य प्रस्तुत करने के लिए एक मानक अभी तक अपनाया नहीं गया है। इस तरह के एक उम्मीदवार को नीचे दिए गए चित्रों में प्रस्तुत किया गया है। चित्रों में छवियां त्रि-आयामी, अभियान्त्रिकी संगणक आलेखिकी का उपयोग करके बनाई गई थीं।
त्रि-आयामी, संगणक मॉडलिंग ट्यूब के पीछे आभासी स्थान उत्पन्न करता है, और इस आभासी स्थान के भीतर किसी भी दिशा से किसी मॉडल के किसी भी दृश्य का उत्पादन कर सकता है। यह आसन्न लिखने के विचारों की आवश्यकता के बिना ऐसा करता है और इसलिए वर्णनात्मक ज्यामिति के अप्रचलित, स्टेपिंग संलेख को अप्रचलित करने के लिए प्रतीत हो सकता है। चूंकि वर्णनात्मक ज्यामिति एक सपाट तल पर तीन या अधिक आयामी अंतरिक्ष के वैध या स्वीकार्य इमेजिंग का विज्ञान है, यह संगणक मॉडलिंग संभावनाओं को बढ़ाने के लिए एक अनिवार्य अध्ययन है।
उदाहरण
दो तिरछी रेखाओं PR और SU के बीच सबसे छोटा संबंधक ज्ञात करना
P, R, S और U के X, Y और Z निर्देशांक दिए गए हैं, अनुमान 1 और 2 क्रमशः XY और XZ समतलों पर स्केल करने के लिए तैयार किए गए हैं।
किसी एक रेखा का सही दृश्य (प्रक्षेपण में लंबाई 3डी अंतरिक्ष में लंबाई के बराबर है) प्राप्त करने के लिए: इस उदाहरण में SU, प्रक्षेपण 3 को हिंज रेखा H2,3 के समानांतर S2U2 साथ खींचा गया है। SU का अंतिम दृश्य प्राप्त करने के लिए, प्रोजेक्शन 4 को हिंज लाइन H3,4 को S3U3. के लिए लंबवत खींचा गया है। लम्बवत दूरी d, PR और SU के बीच न्यूनतम दूरी दर्शाती है।
इस न्यूनतम दूरी को देने वाली इन रेखाओं पर बिंदु Q और T प्राप्त करने के लिए, प्रोजेक्शन 5 को हिंग लाइन H4,5 के समानांतर P4 R4,के साथ खींचा गया है दोनों P5 R5 और S5U5 यथार्थ मत बना रहा है(अंतिम दृश्य का कोई भी प्रक्षेपण एक सच्चा दृश्य है)। इन रेखाओं के प्रतिच्छेदन को प्रक्षेपित करते हुए, Q5 और T5 प्रोजेक्शन 1 पर वापस (मैजेंटा लाइन और लेबल) उनके निर्देशांक को X, Y और Z अक्षों से पढ़ने की अनुमति देता है।
व्यापकहल
व्यापकहल वर्णनात्मक ज्यामिति के भीतर हलों का एक वर्ग है जिसमें किसी समस्या के सभी संभावित हल होते हैं। व्यापकहल को एक एकल, त्रि-आयामी वस्तु, सामान्यत: एक शंकु द्वारा दर्शाया जाता है, जिसके तत्वों की दिशा किसी भी अनंत संख्या के हल विचारों के लिए देखने (प्रक्षेपण) की वांछित दिशा है।
उदाहरण के लिए: व्यापकहल खोजने के लिए जैसे कि दो, असमान लंबाई, तिरछी रेखाएं सामान्य स्थिति में दिखाई देती हैं (कहते हैं, उड़ान में रॉकेट?)
- समान लंबाई
- समान लंबाई और समानांतर
- समान लंबाई और लम्बवत (जैसे, कम से कम एक के आदर्श लक्ष्यीकरण के लिए)
- एक निर्दिष्ट अनुपात की लंबाई के बराबर
- अन्य।
उदाहरणों में, प्रत्येक वांछित विशिष्ट हल के लिए व्यापकहल एक शंकु है, जिनमें से प्रत्येक तत्व एक अनंत संख्या में हल दृश्य उत्पन्न करता है। जब दो या दो से अधिक विशेषताओं, के ऊपर सूचीबद्ध हैं, वांछित हैं (और जिसके लिए एक हल मौजूद है) हल दृश्य दो शंकुओं के बीच प्रतिच्छेदन के दो तत्वों (एक तत्व, यदि शंकु स्पर्शरेखा हैं) की दिशा में बहिर्विष्ट करना वांछित उत्पन्न करता है । यदि शंकु प्रतिच्छेद नहीं करते हैं तो हल मौजूद नहीं है। हलों में प्रयुक्त वर्णनात्मक ज्यामितीय सिद्धांतों को दिखाने के लिए नीचे दिए गए उदाहरणों की व्याख्या की गई है। TL = True-Length; EV = Edge View.
नीचे चित्र 1-3 प्रदर्शित करता है (1) वर्णनात्मक ज्यामिति, व्यापकहल (2) एक साथ, लंबकोणिक, मल्टीव्यू, अभिविनयास स्वरूपों में ऐसे हल प्रस्तुत करने के लिए एक संभावित मानक।
संभावित मानक के बीच एक मानक तय रेखा के साथ दो आसन्न, मानक, लंबकोणिक दृश्य (यहाँ, सामने और ऊपर) कार्यरत हैं। चूंकि हल दृश्य पर पहुंचने के लिए मानक, दो-चरण अनुक्रमों में वस्तु के चारों ओर 90° चक्कर लगाने की कोई आवश्यकता नहीं है (यह सीधे हल दृश्य पर जाना संभव है), इस छोटे संलेख को ध्यान में रखा गया है अभिविनयास के लिए। जहां पहला चरण संलेख दो-चरणीय संलेख को प्रतिस्थापित करता है, द्वि वलन पंक्ति का उपयोग किया जाता है। दूसरे शब्दों में, जब कोई दोहरी रेखाओं को पार करता है तो वह 90° का घुमावदार घुमाव नहीं बना रहा होता है बल्कि सीधे हल दृश्य की ओर एक गैर-ऑर्थोडायरेक्शनल मोड़ बना रहा होता है। जैसा कि अधिकांश अभियान्त्रिकी संगणक आलेखिकी पैकेज स्वचालित रूप से ग्लास बॉक्स मॉडल के छह प्रमुख दृश्य, साथ ही एक सममितीय दृश्य उत्पन्न करते हैं, इन विचारों को कभी-कभी अनुमानी जिज्ञासा से जोड़ा जाता है।

चित्र 1: वर्णनात्मक ज्यामिति - लंबवत दिखाई देने वाली तिरछी रेखाएं

चित्र 2: वर्णनात्मक ज्यामिति - तिरछी रेखाएँ समान लंबाई की दिखाई देती हैं
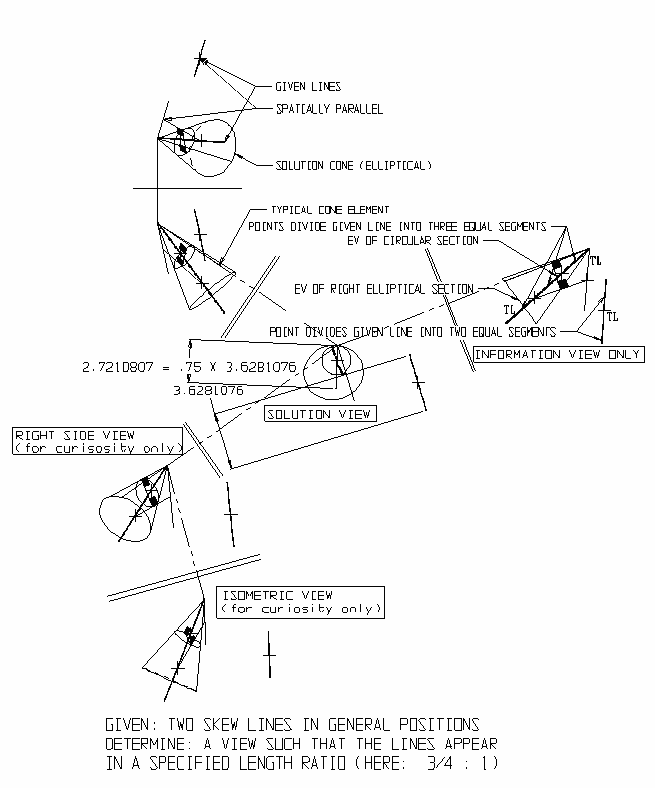
चित्र 3: वर्णनात्मक ज्यामिति - तिरछी रेखाएँ निर्दिष्ट लंबाई अनुपात में दिखाई देती हैं
यह भी देखें
- प्रक्षेपी ज्यामिति
- ग्राफिकल प्रक्षेपण
- लिखने का प्रक्षेपण
- एक्सोनोमेट्रिक प्रक्षेपण
- सममितीय प्रक्षेपण
- आइसोमेट्रिक प्रक्षेपण
- त्रिमितीय प्रक्षेपण
- ऑर्थोगोनल प्रोजेक्शन
- तिरछा प्रक्षेपण
- परिप्रेक्ष्य प्रक्षेपण, परिप्रेक्ष्य (चित्रमय)
- स्टीरियोटॉमी (वर्णनात्मक ज्यामिति)
- टेक्निकल ड्राइंग
- इंजीनियरिंग ड्राइंग
संदर्भ
- ↑ Joseph Malkevitch (April 2003), "Mathematics and Art", Feature Column Archive, American Mathematical Society
- ↑ James Stevens Curl, ed. (2015). "ग्वारिनी, ग्वारिनो". A Dictionary of Architecture. Oxford University Press. p. 337. ISBN 9780198606789.
- ↑ Bianchini, Carlo (2012). "ग्वारिनो गुआरिनी के अंतरिक्ष अनुसंधान में स्टीरियोटॉमी की भूमिका". Nuts and Bolts of Construction History. 1: 257–263. ISBN 978-2-7084-0929-3.
- ↑ Ingrid Carlbom, Joseph Paciorek (December 1978), "Planar Geometric Projections and Viewing Transformations", ACM Computing Surveys, 10 (4): 465–502, CiteSeerX 10.1.1.532.4774, doi:10.1145/356744.356750, S2CID 708008