दुरभिविन्यास: Difference between revisions
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
सामग्री विज्ञान में, दुरभिविन्यास एक पॉलीक्रिस्टलाइन सामग्री में दो क्रिस्टलीय के बीच [[क्रिस्टलोग्राफी|क्रिस्टलोग्राफिक]] अभिविन्यास में अंतर है। | सामग्री विज्ञान में, दुरभिविन्यास एक पॉलीक्रिस्टलाइन सामग्री में दो क्रिस्टलीय के बीच [[क्रिस्टलोग्राफी|क्रिस्टलोग्राफिक]] अभिविन्यास में अंतर है। | ||
क्रिस्टलीय सामग्रियों में, एक क्रिस्टलीय का अभिविन्यास एक नमूना [[संदर्भ फ्रेम]] (अर्थात एक रोलिंग (मेटल वर्किंग) या [[ बाहर निकालना |बाहर निकालना]] प्रक्रिया और दो [[ ओर्थोगोनल ]] दिशाओं की दिशा द्वारा परिभाषित) से [[क्रिस्टलीय जाली]] के स्थानीय संदर्भ फ्रेम में परिवर्तन द्वारा परिभाषित किया जाता है। [[यूनिट सेल|इकाई कोशिका]] के आधार पर परिभाषित किया गया है। इसी तरह, एक स्थानीय क्रिस्टल फ्रेम से दूसरे क्रिस्टल फ्रेम में जाने के लिए आवश्यक परिवर्तन को गलत विधि से बदलना है। यही है, यह दो अलग-अलग अभिविन्यासों के बीच अभिविन्यास स्थान में दूरी है। यदि अभिविन्यास दिशा कोसाइन {{mvar|g{{sub|A}}}} और {{mvar|g{{sub|B}}}}, के [[रोटेशन मैट्रिक्स|आव्यूह]] के संदर्भ में निर्दिष्ट हैं | क्रिस्टलीय सामग्रियों में, एक क्रिस्टलीय का अभिविन्यास एक नमूना [[संदर्भ फ्रेम]] (अर्थात एक रोलिंग (मेटल वर्किंग) या [[ बाहर निकालना |बाहर निकालना]] प्रक्रिया और दो [[ ओर्थोगोनल ]] दिशाओं की दिशा द्वारा परिभाषित) से [[क्रिस्टलीय जाली]] के स्थानीय संदर्भ फ्रेम में परिवर्तन द्वारा परिभाषित किया जाता है। [[यूनिट सेल|इकाई कोशिका]] के आधार पर परिभाषित किया गया है। इसी तरह, एक स्थानीय क्रिस्टल फ्रेम से दूसरे क्रिस्टल फ्रेम में जाने के लिए आवश्यक परिवर्तन को गलत विधि से बदलना है। यही है, यह दो अलग-अलग अभिविन्यासों के बीच अभिविन्यास स्थान में दूरी है। यदि अभिविन्यास दिशा कोसाइन {{mvar|g{{sub|A}}}} और {{mvar|g{{sub|B}}}}, के [[रोटेशन मैट्रिक्स|आव्यूह]] के संदर्भ में निर्दिष्ट हैं तो A से B तक जाने वाले दुरभिविन्यास ऑपरेटर {{math|∆''g{{sub|AB}}''}} को निम्नानुसार परिभाषित किया जा सकता है: '''से जा रहे हैं {{mvar|A}} को {{mvar|B}} को इस प्रकार परिभाषित किया जा सकता है:''' | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 11: | Line 11: | ||
जहां शब्द {{tmath|g_A^{-1} }} {{mvar|g{{sub|A}}}} का उत्क्रम ऑपरेशन है, अर्थात क्रिस्टल फ्रेम {{mvar|A}} से वापस नमूना फ्रेम में परिवर्तन है। यह पहले क्रिस्टल फ्रेम ({{mvar|A}}) वापस नमूना फ्रेम में और बाद में नए क्रिस्टल फ्रेम में ({{mvar|B}}).में बदलने के क्रमिक संचालन के रूप में गलत धारणा का एक वैकल्पिक विवरण प्रदान करता है | जहां शब्द {{tmath|g_A^{-1} }} {{mvar|g{{sub|A}}}} का उत्क्रम ऑपरेशन है, अर्थात क्रिस्टल फ्रेम {{mvar|A}} से वापस नमूना फ्रेम में परिवर्तन है। यह पहले क्रिस्टल फ्रेम ({{mvar|A}}) वापस नमूना फ्रेम में और बाद में नए क्रिस्टल फ्रेम में ({{mvar|B}}).में बदलने के क्रमिक संचालन के रूप में गलत धारणा का एक वैकल्पिक विवरण प्रदान करता है | ||
इस रूपांतरण प्रक्रिया को प्रदर्शित करने के लिए विभिन्न विधियों का उपयोग किया जा सकता है, जैसे: [[यूलर कोण]], रोड्रिग्स वैक्टर, अक्ष कोण | इस रूपांतरण प्रक्रिया को प्रदर्शित करने के लिए विभिन्न विधियों का उपयोग किया जा सकता है, जैसे: [[यूलर कोण]], रोड्रिग्स वैक्टर, अक्ष कोण(जहां अक्ष को क्रिस्टलोग्राफिक दिशा के रूप में निर्दिष्ट किया गया है), या इकाई चतुष्कोण है। | ||
== समरूपता और गलत धारणा == | == समरूपता और गलत धारणा == | ||
दुरभिविन्यास पर [[क्रिस्टल समरूपता]] का प्रभाव पूर्ण अभिविन्यास स्थान के अंश को कम करना है जो सभी संभावित गलत संबंधों को विशिष्ट रूप से प्रदर्शित करने के लिए आवश्यक है। उदाहरण के लिए, | दुरभिविन्यास पर [[क्रिस्टल समरूपता]] का प्रभाव पूर्ण अभिविन्यास स्थान के अंश को कम करना है जो सभी संभावित गलत संबंधों को विशिष्ट रूप से प्रदर्शित करने के लिए आवश्यक है। उदाहरण के लिए, घन क्रिस्टल (अर्थात एफसीसी) में 24 सममित रूप से संबंधित अभिविन्यास हैं। इनमें से प्रत्येक अभिविन्यास शारीरिक रूप से अप्रभेद्य है, किंतु गणितीय रूप से भिन्न है। इसलिए, अभिविन्यास स्थान का आकार 24 के एक कारक से कम हो जाता है। यह घन समरूपता के लिए मूलभूत क्षेत्र (FZ) को परिभाषित करता है। दो घनीय स्फटिकों के बीच दुर्विन्यास के लिए, प्रत्येक में 24 '''के पास अपनी 24''' अंतर्निहित समरूपताएँ होती हैं। इसके अतिरिक्त , एक स्विचिंग समरूपता उपस्थित है, जिसे परिभाषित किया गया है: | ||
:<math>\Delta g_{AB}=\Delta g_{BA}</math> | :<math>\Delta g_{AB}=\Delta g_{BA}</math> | ||
जो दिशा के प्रति दुर्भिमुखता की निश्चरता को पहचानता है; | जो दिशा के प्रति दुर्भिमुखता की निश्चरता को पहचानता है; A→B or B→A। दुरभिविन्यास के लिए घन -घन मौलिक क्षेत्र में कुल अभिविन्यास स्थान का अंश इसके द्वारा दिया गया है: | ||
:<math>\frac{1}{24\cdot24\cdot2}=\frac{1}{1152}</math> | :<math>\frac{1}{24\cdot24\cdot2}=\frac{1}{1152}</math> | ||
या 1/48 घन मौलिक क्षेत्र का आयतन। यह अधिकतम अद्वितीय दुरभिविन्यास कोण को 62. | या 1/48 घन मौलिक क्षेत्र का आयतन। यह अधिकतम अद्वितीय दुरभिविन्यास कोण को 62.8°तक सीमित करने का प्रभाव भी रखता है | ||
<br /> | |||
<br />विचलन FZ के अंदर आने वाले सभी सममित रूप से समतुल्य दुरभिविन्यास में से सबसे छोटे संभावित घुमाव कोण के साथ दुरभिविन्यास का वर्णन करता है (सामान्यतः घन के लिए मानक त्रिविम त्रिकोण में एक अक्ष होने के रूप में निर्दिष्ट)। इन प्रकारों की गणना में दुरभिविन्यास की गणना के समय प्रत्येक अभिविन्यास के लिए क्रिस्टल समरूपता ऑपरेटरों का अनुप्रयोग सम्मिलित है। | |||
<math>\Delta g_{AB}=O_{B}^{crys}g_{B}(O_{A}^{crys}g_{A})^{-1}</math><br /> | |||
जहां | <br /><math>\Delta g_{AB}=O_{B}^{crys}g_{B}(O_{A}^{crys}g_{A})^{-1}</math><br /> | ||
जहां O<sup>crys</sup> सामग्री के लिए सममिति संचालकों में से एक को दर्शाता है। | |||
== | == दुरभिविन्यास वितरण == | ||
[[Image:MDF rodrigues AA5083.jpg|thumb|alt=alt text|AA5083 प्लेट के नमूने के लिए रोड्रिग्स स्पेस में दिखाया गया उदाहरण MDF]] | [[Image:MDF rodrigues AA5083.jpg|thumb|alt=alt text|AA5083 प्लेट के नमूने के लिए रोड्रिग्स स्पेस में दिखाया गया उदाहरण MDF]]दुरभिविन्यास वितरण (एमडी) [[ अभिविन्यास वितरण समारोह | '''अभिविन्यास वितरण समारोह''']] के अनुरूप है जिसका उपयोग बनावट को चित्रित करने में किया जाता है। एमडी दिए गए गलत वर्गीकरण <math>d \Delta g</math> के आस-पास <math>\Delta g</math> श्रेणी में आने वाले किन्हीं भी दो अनाजों के बीच गलत वर्गीकरण की संभावना का वर्णन करता है।,जबकि प्रायिकता घनत्व के समान '''सामान्यीकरण के कारण''' एमडी गणितीय रूप से समान नहीं है। एक एमडी में तीव्रता समान रूप से वितरित दुरभिविन्यास वाली सामग्री में अपेक्षित वितरण के संबंध में यादृच्छिक घनत्व (एमआरडी) के गुणकों के रूप में दी जाती है। एमडी की गणना या तो श्रृंखला विस्तार द्वारा की जा सकती है, सामान्यतः सामान्यीकृत [[गोलाकार हार्मोनिक्स]] का उपयोग करके, या असतत बिनिंग योजना द्वारा, जहां प्रत्येक डेटा बिंदु को एक बिन को सौंपा जाता है और संचित किया जाता है। | ||
== ग्राफिकल प्रतिनिधित्व == | == ग्राफिकल प्रतिनिधित्व == | ||
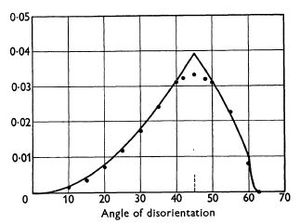
[[Image:Mackenzie plot.jpg|thumb|alt=alt text|मैकेंज़ी (1958) से एक बेतरतीब ढंग से बनावट वाले पॉलीक्रिस्टल के लिए मिसऑरिएंटेशन एंगल्स का वितरण]]असतत दुरभिविन्यास या दुरभिविन्यास वितरण को यूलर कोण, अक्ष/कोण, या रोड्रिग्स वेक्टर अंतरिक्ष में भूखंडों के रूप में पूरी तरह से वर्णित किया जा सकता है। यूनिट चतुष्कोण, कम्प्यूटेशनल रूप से सुविधाजनक होते हुए, अपने चार-आयामी प्रकृति के कारण ग्राफिकल प्रतिनिधित्व के लिए खुद को उधार नहीं देते हैं। किसी भी अभ्यावेदन के लिए, भूखंडों को | [[Image:Mackenzie plot.jpg|thumb|alt=alt text|मैकेंज़ी (1958) से एक बेतरतीब ढंग से बनावट वाले पॉलीक्रिस्टल के लिए मिसऑरिएंटेशन एंगल्स का वितरण]]असतत दुरभिविन्यास या दुरभिविन्यास वितरण को यूलर कोण, अक्ष/कोण, या रोड्रिग्स वेक्टर अंतरिक्ष में भूखंडों के रूप में पूरी तरह से वर्णित किया जा सकता है। यूनिट चतुष्कोण, कम्प्यूटेशनल रूप से सुविधाजनक होते हुए, अपने चार-आयामी प्रकृति के कारण ग्राफिकल प्रतिनिधित्व के लिए खुद को उधार नहीं देते हैं। किसी भी अभ्यावेदन के लिए, भूखंडों को सामान्यतः मौलिक क्षेत्र के माध्यम से वर्गों के रूप में बनाया जाता है; φ के साथ<sub>2</sub> यूलर कोणों में, अक्ष/कोण के लिए घूर्णन कोण की वृद्धि पर, और स्थिर ρ पर<sub>3</sub> (<001> के समानांतर) रोड्रिग्स के लिए। घन-घन FZ के अनियमित आकार के कारण, भूखंडों को आम तौर पर घन FZ के माध्यम से अधिक प्रतिबंधात्मक सीमाओं के साथ वर्गों के रूप में दिया जाता है।<br /> | ||
<br /> | <br /> | ||
मैकेंज़ी भूखंड एमडी के एक आयामी प्रतिनिधित्व हैं, जो अक्ष के बावजूद, दुर्बलता कोण की सापेक्ष आवृत्ति की साजिश रचते हैं। मैकेंज़ी ने एक यादृच्छिक बनावट के साथ | मैकेंज़ी भूखंड एमडी के एक आयामी प्रतिनिधित्व हैं, जो अक्ष के बावजूद, दुर्बलता कोण की सापेक्ष आवृत्ति की साजिश रचते हैं। मैकेंज़ी ने एक यादृच्छिक बनावट के साथ घन नमूने के लिए गलत वर्गीकरण वितरण निर्धारित किया। | ||
== दुर्बलता की गणना का उदाहरण == | == दुर्बलता की गणना का उदाहरण == | ||
Revision as of 10:50, 13 April 2023
सामग्री विज्ञान में, दुरभिविन्यास एक पॉलीक्रिस्टलाइन सामग्री में दो क्रिस्टलीय के बीच क्रिस्टलोग्राफिक अभिविन्यास में अंतर है।
क्रिस्टलीय सामग्रियों में, एक क्रिस्टलीय का अभिविन्यास एक नमूना संदर्भ फ्रेम (अर्थात एक रोलिंग (मेटल वर्किंग) या बाहर निकालना प्रक्रिया और दो ओर्थोगोनल दिशाओं की दिशा द्वारा परिभाषित) से क्रिस्टलीय जाली के स्थानीय संदर्भ फ्रेम में परिवर्तन द्वारा परिभाषित किया जाता है। इकाई कोशिका के आधार पर परिभाषित किया गया है। इसी तरह, एक स्थानीय क्रिस्टल फ्रेम से दूसरे क्रिस्टल फ्रेम में जाने के लिए आवश्यक परिवर्तन को गलत विधि से बदलना है। यही है, यह दो अलग-अलग अभिविन्यासों के बीच अभिविन्यास स्थान में दूरी है। यदि अभिविन्यास दिशा कोसाइन gA और gB, के आव्यूह के संदर्भ में निर्दिष्ट हैं तो A से B तक जाने वाले दुरभिविन्यास ऑपरेटर ∆gAB को निम्नानुसार परिभाषित किया जा सकता है: से जा रहे हैं A को B को इस प्रकार परिभाषित किया जा सकता है:
जहां शब्द gA का उत्क्रम ऑपरेशन है, अर्थात क्रिस्टल फ्रेम A से वापस नमूना फ्रेम में परिवर्तन है। यह पहले क्रिस्टल फ्रेम (A) वापस नमूना फ्रेम में और बाद में नए क्रिस्टल फ्रेम में (B).में बदलने के क्रमिक संचालन के रूप में गलत धारणा का एक वैकल्पिक विवरण प्रदान करता है
इस रूपांतरण प्रक्रिया को प्रदर्शित करने के लिए विभिन्न विधियों का उपयोग किया जा सकता है, जैसे: यूलर कोण, रोड्रिग्स वैक्टर, अक्ष कोण(जहां अक्ष को क्रिस्टलोग्राफिक दिशा के रूप में निर्दिष्ट किया गया है), या इकाई चतुष्कोण है।
समरूपता और गलत धारणा
दुरभिविन्यास पर क्रिस्टल समरूपता का प्रभाव पूर्ण अभिविन्यास स्थान के अंश को कम करना है जो सभी संभावित गलत संबंधों को विशिष्ट रूप से प्रदर्शित करने के लिए आवश्यक है। उदाहरण के लिए, घन क्रिस्टल (अर्थात एफसीसी) में 24 सममित रूप से संबंधित अभिविन्यास हैं। इनमें से प्रत्येक अभिविन्यास शारीरिक रूप से अप्रभेद्य है, किंतु गणितीय रूप से भिन्न है। इसलिए, अभिविन्यास स्थान का आकार 24 के एक कारक से कम हो जाता है। यह घन समरूपता के लिए मूलभूत क्षेत्र (FZ) को परिभाषित करता है। दो घनीय स्फटिकों के बीच दुर्विन्यास के लिए, प्रत्येक में 24 के पास अपनी 24 अंतर्निहित समरूपताएँ होती हैं। इसके अतिरिक्त , एक स्विचिंग समरूपता उपस्थित है, जिसे परिभाषित किया गया है:
जो दिशा के प्रति दुर्भिमुखता की निश्चरता को पहचानता है; A→B or B→A। दुरभिविन्यास के लिए घन -घन मौलिक क्षेत्र में कुल अभिविन्यास स्थान का अंश इसके द्वारा दिया गया है:
या 1/48 घन मौलिक क्षेत्र का आयतन। यह अधिकतम अद्वितीय दुरभिविन्यास कोण को 62.8°तक सीमित करने का प्रभाव भी रखता है
विचलन FZ के अंदर आने वाले सभी सममित रूप से समतुल्य दुरभिविन्यास में से सबसे छोटे संभावित घुमाव कोण के साथ दुरभिविन्यास का वर्णन करता है (सामान्यतः घन के लिए मानक त्रिविम त्रिकोण में एक अक्ष होने के रूप में निर्दिष्ट)। इन प्रकारों की गणना में दुरभिविन्यास की गणना के समय प्रत्येक अभिविन्यास के लिए क्रिस्टल समरूपता ऑपरेटरों का अनुप्रयोग सम्मिलित है।
जहां Ocrys सामग्री के लिए सममिति संचालकों में से एक को दर्शाता है।
दुरभिविन्यास वितरण
दुरभिविन्यास वितरण (एमडी) अभिविन्यास वितरण समारोह के अनुरूप है जिसका उपयोग बनावट को चित्रित करने में किया जाता है। एमडी दिए गए गलत वर्गीकरण के आस-पास श्रेणी में आने वाले किन्हीं भी दो अनाजों के बीच गलत वर्गीकरण की संभावना का वर्णन करता है।,जबकि प्रायिकता घनत्व के समान सामान्यीकरण के कारण एमडी गणितीय रूप से समान नहीं है। एक एमडी में तीव्रता समान रूप से वितरित दुरभिविन्यास वाली सामग्री में अपेक्षित वितरण के संबंध में यादृच्छिक घनत्व (एमआरडी) के गुणकों के रूप में दी जाती है। एमडी की गणना या तो श्रृंखला विस्तार द्वारा की जा सकती है, सामान्यतः सामान्यीकृत गोलाकार हार्मोनिक्स का उपयोग करके, या असतत बिनिंग योजना द्वारा, जहां प्रत्येक डेटा बिंदु को एक बिन को सौंपा जाता है और संचित किया जाता है।
ग्राफिकल प्रतिनिधित्व
असतत दुरभिविन्यास या दुरभिविन्यास वितरण को यूलर कोण, अक्ष/कोण, या रोड्रिग्स वेक्टर अंतरिक्ष में भूखंडों के रूप में पूरी तरह से वर्णित किया जा सकता है। यूनिट चतुष्कोण, कम्प्यूटेशनल रूप से सुविधाजनक होते हुए, अपने चार-आयामी प्रकृति के कारण ग्राफिकल प्रतिनिधित्व के लिए खुद को उधार नहीं देते हैं। किसी भी अभ्यावेदन के लिए, भूखंडों को सामान्यतः मौलिक क्षेत्र के माध्यम से वर्गों के रूप में बनाया जाता है; φ के साथ2 यूलर कोणों में, अक्ष/कोण के लिए घूर्णन कोण की वृद्धि पर, और स्थिर ρ पर3 (<001> के समानांतर) रोड्रिग्स के लिए। घन-घन FZ के अनियमित आकार के कारण, भूखंडों को आम तौर पर घन FZ के माध्यम से अधिक प्रतिबंधात्मक सीमाओं के साथ वर्गों के रूप में दिया जाता है।
मैकेंज़ी भूखंड एमडी के एक आयामी प्रतिनिधित्व हैं, जो अक्ष के बावजूद, दुर्बलता कोण की सापेक्ष आवृत्ति की साजिश रचते हैं। मैकेंज़ी ने एक यादृच्छिक बनावट के साथ घन नमूने के लिए गलत वर्गीकरण वितरण निर्धारित किया।
दुर्बलता की गणना का उदाहरण
यूलर कोणों के रूप में दिए गए दो बनावट घटकों के बीच गलतफहमी के धुरी/कोण प्रतिनिधित्व को निर्धारित करने के लिए निम्नलिखित एल्गोरिदम का एक उदाहरण है:
- कॉपर [90,35,45]
- S3 [59,37,63]
पहला चरण यूलर कोण प्रतिनिधित्व को परिवर्तित कर रहा है, अभिविन्यास मैट्रिक्स के लिए g द्वारा:
कहाँ और प्रतिनिधित्व करना और क्रमश। यह निम्नलिखित ओरिएंटेशन मैट्रिक्स उत्पन्न करता है:
दुस्साहस तब होता है:
अक्ष/कोण विवरण (एक इकाई सदिश के रूप में अक्ष के साथ) दुरभिविन्यास मैट्रिक्स से संबंधित है:
(रैंडल और एंग्लर द्वारा पुस्तक में दिए गए 'आर' के घटकों के समान सूत्रों में त्रुटियां हैं (संदर्भ देखें), जिन्हें उनकी पुस्तक के अगले संस्करण में ठीक किया जाएगा। उपरोक्त सही संस्करण हैं, ध्यान दें यदि Θ = 180 डिग्री है तो इन समीकरणों के लिए भिन्न रूप का उपयोग करना होगा।)
तांबे के लिए- एस3 द्वारा दिया गया दुराग्रह ΔgAB, अक्ष/कोण विवरण 19.5° लगभग [0.689,0.623,0.369] है, जो कि <221> से केवल 2.3° है। यह परिणाम केवल 1152 सममित रूप से संबंधित संभावनाओं में से एक है, लेकिन गलत दिशा को निर्दिष्ट करता है। अभिविन्यास समरूपता (स्विचिंग समरूपता सहित) के सभी संभावित संयोजनों पर विचार करके इसे सत्यापित किया जा सकता है।
संदर्भ
- Kocks, U.F., C.N. Tomé, and H.-R. Wenk (1998). Texture and Anisotropy: Preferred Orientations in Polycrystals and their Effect on Materials Properties, Cambridge University Press.
- Mackenzie, J.K. (1958). Second Paper on the Statistics Associated with the Random Disorientation of Cubes, Biometrika 45,229.
- Randle, Valerie and Olaf Engler (2000). Introduction to Texture Analysis: Macrotexture, Microtexture & Orientation Mapping, CRC Press.
- Reed-Hill, Robert E. and Reza Abbaschian (1994). Physical Metallurgy Principles (Third Edition), PWS.
- Sutton, A.P. and R.W. Balluffi (1995). Interfaces in Crystalline Materials, Clarendon Press.
- G. Zhu, W. Mao and Y. Yu (1997). "Calculation of misorientation distribution between recrystallized grains and deformed matrix", Scripta mater. 42(2000) 37-41.