जोड़ी उत्पादन: Difference between revisions
(Created page with "{{Short description|Interaction of a photon with matter resulting into creation of electron-positron pair}} {{more citations needed|date=May 2013}} {{Light–matter interactio...") |
No edit summary |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Interaction of a photon with matter resulting into creation of electron-positron pair}} | {{Short description|Interaction of a photon with matter resulting into creation of electron-positron pair}} | ||
{{Light–matter interaction}} | {{Light–matter interaction}} | ||
'''''युग्म उत्पादन''''' एक विद्युत आवेश [[बोसॉन]] से अपरमाणविक कण और उसके प्रतिकण का निर्माण है। उदाहरणों में एक [[इलेक्ट्रॉन]] और पॉज़िट्रॉन, एक म्यूऑन और एक प्रतिम्यूऑन, या एक [[प्रोटॉन]] और एक [[उपाध्यक्ष|प्रतिप्रोटन]] बनाना सम्मिलित है। युग्म उत्पादन प्रायः विशेष रूप से एक नाभिक के पास इलेक्ट्रॉन-पॉजिट्रॉन युग्म बनाने वाले फोटॉन को संदर्भित करता है। जैसा कि [[ऊर्जा]] को संरक्षित किया जाना चाहिए, युग्म उत्पादन होने के लिए, फोटॉन की आने वाली ऊर्जा कम से कम दो कणों की कुल शेष द्रव्यमान ऊर्जा की सीमा से ऊपर होनी चाहिए। (चूंकि इलेक्ट्रॉन सबसे हल्का है, इसलिए, सबसे कम द्रव्यमान/ऊर्जा, प्राथमिक कण, इसके लिए सभी संभव युग्म-उत्पादन प्रक्रियाओं के कम से कम ऊर्जावान फोटॉन की आवश्यकता होती है।) ऊर्जा और संवेग का संरक्षण प्रक्रिया पर प्रमुख बाधाएँ हैं।<ref>{{Cite book|url=https://archive.org/details/introductiontonu0000dasa_a6y8|url-access=registration|title=परमाणु और कण भौतिकी का परिचय|last=Das|first=A.|last2=Ferbel|first2=T.|date=2003-12-23|publisher=World Scientific|isbn=9789814483339|language=en}}</ref> उत्पादित कणों की अन्य सभी संरक्षित क्वांटम संख्याएं (कोणीय गति, विद्युत आवेश, लिप्टन संख्या) का योग शून्य होना चाहिए{{spaced ndash}} इस प्रकार निर्मित कणों में एक दूसरे के विपरीत मान होंगे। उदाहरण के लिए, यदि एक कण का विद्युत आवेश +1 है, तो दूसरे का विद्युत आवेश -1 होना चाहिए, या यदि एक कण में +1 का [[विचित्रता (कण भौतिकी)|विलक्षणता (कण भौतिकी)]] है तो दूसरे में -1 की विलक्षणता होनी चाहिए। | |||
फोटॉन- | फोटॉन-पदार्थ अंतःक्रिया में युग्म उत्पादन की संभावना [[फोटॉन ऊर्जा]] के साथ बढ़ जाती है और पास के परमाणु की [[परमाणु संख्या]] (इसलिए, प्रोटॉन की संख्या) के वर्ग के रूप में भी बढ़ जाती है।<ref>{{Cite web|url=http://meroli.web.cern.ch/meroli/Lecture_photon_interaction.html|title=फोटॉन पदार्थ के साथ कैसे इंटरैक्ट करते हैं|last=Stefano|first=Meroli|website=Meroli Stefano Webpage|access-date=2016-08-28}}</ref> | ||
== फोटॉन से इलेक्ट्रॉन और पॉज़िट्रॉन == | == फोटॉन से इलेक्ट्रॉन और पॉज़िट्रॉन == | ||
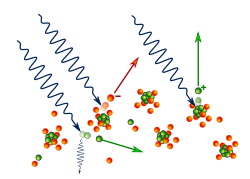
[[File:Pair production Cartoon.gif|thumb|आरेख इलेक्ट्रॉन-पॉज़िट्रॉन | [[File:Pair production Cartoon.gif|thumb|आरेख इलेक्ट्रॉन-पॉज़िट्रॉन युग्म उत्पादन की प्रक्रिया दिखा रहा है। वास्तव में उत्पादित युग्म लगभग संरेखी हैं। काले बिन्दु चिह्नित 'Z' परमाणु संख्या {{mvar|Z}} के साथ एक आसन्न परमाणु का प्रतिनिधित्व करता है।]]उच्च फोटॉन ऊर्जा ([[MeV|मेगाइलेक्ट्रॉन वोल्ट]] माप और उच्चतम) वाले फोटॉनों के लिए, युग्म उत्पादन पदार्थ के साथ फोटॉन अंतःक्रिया का प्रमुख तरीका है। इन अंतःक्रियाओं को पहली बार [[पैट्रिक मेनार्ड स्टुअर्ट ब्लैकेट]] के प्रति-नियंत्रित अभ्रकोष्ठ में देखा गया, जिसके कारण 1948 में भौतिकी का नोबेल पुरस्कार मिला।<ref> | ||
{{cite web | {{cite web | ||
|last=Bywater |first=Jenn | |last=Bywater |first=Jenn | ||
| Line 18: | Line 17: | ||
|access-date=29 August 2016 | |access-date=29 August 2016 | ||
}} | }} | ||
</ref> | </ref> यदि फोटॉन परमाणु नाभिक के पास है, तो फोटॉन की ऊर्जा को इलेक्ट्रॉन-पॉजिट्रॉन युग्म में परिवर्तित किया जा सकता है: | ||
( | (Z+)γ → {{SubatomicParticle|Electron|link=yes}} + {{SubatomicParticle|Positron|link=yes}} | ||
फोटॉन की ऊर्जा आइंस्टीन के समीकरण, E = m ⋅ c2 के अनुसार कण द्रव्यमान में परिवर्तित हो जाती है; जहाँ E ऊर्जा है, m द्रव्यमान है और c प्रकाश की गति है। उत्पादन होने के लिए फोटॉन में एक इलेक्ट्रॉन और पॉज़िट्रॉन (2 ⋅ 511 keV = 1.022 मेगाइलेक्ट्रॉन वोल्ट, जिसके परिणामस्वरूप 1.2132 पिकोमीटर का फोटॉन-तरंग दैर्ध्य होता है) की शेष द्रव्यमान ऊर्जाओं के योग से अधिक ऊर्जा होनी चाहिए। (इस प्रकार, मेडिकल एक्स-रे प्रतिबिंबन में युग्म उत्पादन नहीं होता है क्योंकि इन एक्स-रे में केवल ~150 किलो-इलेक्ट्रॉन-वोल्ट होता है।) संवेग के संरक्षण को संतुष्ट करने के लिए फोटॉन को एक नाभिक के पास होना चाहिए, संवेग के संरक्षण को संतुष्ट करने के लिए फोटॉन को एक नाभिक के पास होना चाहिए क्योंकि मुक्त आकाश में उत्पादित एक इलेक्ट्रॉन-पॉज़िट्रॉन युग्म ऊर्जा और संवेग दोनों के संरक्षण को संतुष्ट नहीं कर सकती है।<ref> | |||
संवेग के संरक्षण को संतुष्ट करने के लिए फोटॉन को एक नाभिक के पास होना चाहिए, क्योंकि मुक्त | |||
{{cite journal | {{cite journal | ||
| last=Hubbell | first=J.H. | | last=Hubbell | first=J.H. | ||
| Line 33: | Line 31: | ||
| url=https://zenodo.org/record/1259327 | | url=https://zenodo.org/record/1259327 | ||
}} | }} | ||
</ref> इस | </ref> इस कारण से, जब युग्म उत्पादन होता है, परमाणु नाभिक को [[परमाणु हटना|कुछ प्रतिक्षेप]] प्राप्त करता है। इस प्रक्रिया का प्रतिवर्त इलेक्ट्रॉन-पॉज़िट्रॉन विलोपन है। | ||
=== | === मौलिक शुद्ध गतिकी === | ||
इन गुणों को | इन गुणों को अंतःक्रिया के शुद्ध गतिकी के माध्यम से प्राप्त किया जा सकता है। [[चार वेक्टर|चतुर्विम वेक्टर]] संकेतन का उपयोग करते हुए, अंतःक्रिया से पहले और बाद में ऊर्जा-संवेग का संरक्षण देता है:<ref> | ||
{{cite web | {{cite web | ||
|last=Kuncic |first=Zdenka, Dr. | |last=Kuncic |first=Zdenka, Dr. | ||
| Line 52: | Line 50: | ||
</ref> | </ref> | ||
:<math>p_\gamma = p_{\text{e}^-} + p_{\text{e}^+} + p_{\text{ʀ}}</math> | :<math>p_\gamma = p_{\text{e}^-} + p_{\text{e}^+} + p_{\text{ʀ}}</math> | ||
जहां <math>p_\text{ʀ}</math> नाभिक का प्रतिक्षेप है। चतुर्विम वेक्टर के मापांक पर ध्यान दें | |||
:<math>A \equiv (A^0,\mathbf{A}) </math> | :<math>A \equiv (A^0,\mathbf{A}) </math> | ||
है: | है: | ||
:<math>A^2 = A^{\mu} A_{\mu} = - (A^0)^2 + \mathbf{A} \cdot \mathbf{A} </math> | :<math>A^2 = A^{\mu} A_{\mu} = - (A^0)^2 + \mathbf{A} \cdot \mathbf{A} </math> | ||
जिसका तात्पर्य है <math>(p_\gamma)^2 = 0 </math> सभी | जिसका तात्पर्य है कि <math>(p_\gamma)^2 = 0 </math> सभी स्थितियो <math>(p_{\text{e}^-})^2 = -m_\text{e}^2 c^2 </math> के लिए है। हम संरक्षण समीकरण को वर्ग कर सकते हैं: | ||
:<math>(p_\gamma)^2 = (p_{\text{e}^-} + p_{\text{e}^+} + p_\text{ʀ})^2 </math> | :<math>(p_\gamma)^2 = (p_{\text{e}^-} + p_{\text{e}^+} + p_\text{ʀ})^2 </math> | ||
हालांकि, | हालांकि, अधिकतम स्थितियों में नाभिक का प्रतिक्षेप फोटॉन की ऊर्जा की तुलना में बहुत छोटा होता है और इसे उपेक्षित किया जा सकता है। इस अनुमान <math>p_{R} \approx 0</math> को लेते हुए शेष संबंध को सरल और विस्तारित करने के लिए: | ||
:<math>(p_\gamma)^2 \approx (p_{\text{e}^-})^2 + 2 p_{\text{e}^-} p_{\text{e}^+} + (p_{\text{e}^+})^2 </math> | :<math>(p_\gamma)^2 \approx (p_{\text{e}^-})^2 + 2 p_{\text{e}^-} p_{\text{e}^+} + (p_{\text{e}^+})^2 </math> | ||
:<math>-2\, m_\text{e}^2 c^2 + 2 \left( -\frac{E^2}{c^2} + \mathbf{p}_{\text{e}^-} \cdot \mathbf{p}_{\text{e}^+} \right) \approx 0 </math> | :<math>-2\, m_\text{e}^2 c^2 + 2 \left( -\frac{E^2}{c^2} + \mathbf{p}_{\text{e}^-} \cdot \mathbf{p}_{\text{e}^+} \right) \approx 0 </math> | ||
:<math>2\,(\gamma^2 - 1)\,m_\text{e}^2\,c^2\,(\cos \theta_\text{e} - 1) \approx 0 </math> | :<math>2\,(\gamma^2 - 1)\,m_\text{e}^2\,c^2\,(\cos \theta_\text{e} - 1) \approx 0 </math> | ||
इसलिए, यह सन्निकटन तभी संतुष्ट हो सकता है जब इलेक्ट्रॉन और पॉज़िट्रॉन लगभग | इसलिए, यह सन्निकटन तभी संतुष्ट हो सकता है जब इलेक्ट्रॉन और पॉज़िट्रॉन लगभग समान दिशा में उत्सर्जित हों, अर्थात, <math>\theta_\text{e} \approx 0 </math> है। | ||
यह व्युत्पत्ति एक अर्ध- | यह व्युत्पत्ति एक अर्ध-उत्कृष्ट सन्निकटन है। फोटॉन और नाभिक के पूर्ण क्वांटम यांत्रिक प्रकीर्णन को ध्यान में रखते हुए शुद्ध गतिक का एक परिशुद्ध निस्त्रावण किया जा सकता है। | ||
=== ऊर्जा हस्तांतरण === | === ऊर्जा हस्तांतरण === | ||
| Line 72: | Line 70: | ||
:<math>(E_k^{pp})_\text{tr} = h \nu - 2\, m_\text{e} c^2</math> | :<math>(E_k^{pp})_\text{tr} = h \nu - 2\, m_\text{e} c^2</math> | ||
जहां <math>h</math> प्लैंक स्थिरांक है, <math>\nu </math> फोटॉन की आवृत्ति है और <math>2\, m_\text{e} c^2</math> इलेक्ट्रॉन-पॉज़िट्रॉन का संयुक्त विराम द्रव्यमान है। सामान्य रूप से, नाभिक के प्रतिक्षेप को उपेक्षा करते हुए, इलेक्ट्रॉन और पॉज़िट्रॉन को विभिन्न गतिज ऊर्जाओं के साथ उत्सर्जित किया जा सकता है, लेकिन प्रत्येक को हस्तांतरित औसत है: | |||
:<math>(\bar E_k^{pp})_\text{tr} = \frac{1}{2} (h \nu - 2\, m_\text{e} c^2)</math> | :<math>(\bar E_k^{pp})_\text{tr} = \frac{1}{2} (h \nu - 2\, m_\text{e} c^2)</math> | ||
=== | === अनुप्रस्थ परिच्छेद === | ||
{{See also| | {{See also|गामा किरणों का अनुप्रस्थ परिच्छेद}} | ||
[[File:Electron-Positron nuclear Pair production Feynman Diagram.svg|thumb|इलेक्ट्रॉन-पॉज़िट्रॉन | [[File:Electron-Positron nuclear Pair production Feynman Diagram.svg|thumb|इलेक्ट्रॉन-पॉज़िट्रॉन युग्म उत्पादन का [[फेनमैन आरेख]]। शुद्ध परिच्छेद प्राप्त करने के लिए किसी को कई आरेखों की गणना करनी चाहिए]]युग्म उत्पादन के अनुप्रस्थ परिच्छेद के लिए परिशुद्ध विश्लेषणात्मक रूप की गणना फेनमैन आरेखों के रूप में [[क्वांटम इलेक्ट्रोडायनामिक्स|क्वांटम विद्युतगतिकी]] के माध्यम से की जानी चाहिए और इसके परिणामस्वरूप एक जटिल फलन होता है। सरल करने के लिए, अनुप्रस्थ परिच्छेद को इस प्रकार लिखा जा सकता है: | ||
:<math>\sigma = \alpha \, r_\text{e}^2 \, Z^2 \, P(E,Z)</math> | :<math>\sigma = \alpha \, r_\text{e}^2 \, Z^2 \, P(E,Z)</math> | ||
जहां <math>\alpha</math> सूक्ष्म-संरचना स्थिरांक है, <math>r_\text{e}</math> [[शास्त्रीय इलेक्ट्रॉन त्रिज्या|उत्कृष्ट इलेक्ट्रॉन त्रिज्या]] है, <math>Z</math> वस्तु की परमाणु संख्या है, और <math>P(E,Z)</math> कुछ जटिल-मान फलन है जो ऊर्जा और परमाणु संख्या पर निर्भर करता है। अनुप्रस्थ परिच्छेद विभिन्न सामग्रियों और ऊर्जाओं के लिए सारणीबद्ध हैं। | |||
2008 में 1 मिलीमीटर- | 2008 में 1 मिलीमीटर-स्थूल स्वर्ण के प्रयोजन के लिए [[टाइटन लेजर]] का उपयोग बड़ी संख्या में पॉज़िट्रॉन-इलेक्ट्रॉन युग्म उत्पन्न करने के लिए किया गया था।<ref> | ||
{{cite news | {{cite news | ||
|title=Laser technique produces bevy of antimatter | |title=Laser technique produces bevy of antimatter | ||
| Line 97: | Line 95: | ||
== खगोल विज्ञान == | == खगोल विज्ञान == | ||
परिकल्पनात्मक [[हॉकिंग विकिरण]] की अनुमानी व्याख्या में युग्म उत्पादन को प्रयुक्त किया जाता है। [[क्वांटम यांत्रिकी]] के अनुसार, कण युग्म क्वांटम फोम के रूप में निरंतर दिखाई और विलोप हो रहे हैं। प्रबल गुरुत्वाकर्षण ज्वारीय बलों के एक क्षेत्र में, एक युग्म में दो कण कभी-कभी अलग हो सकते हैं इससे पहले कि उन्हें परस्पर [[विनाश|विलोपन]] का अवसर मिले। जब यह एक [[ब्लैक होल]] (''कृष्ण विवर)'' के आसपास के क्षेत्र में होता है, तो एक कण संरक्षित हो सकता है जबकि उसका प्रति कण सहभागी ब्लैक होल द्वारा प्रग्रहण कर लिया जाता है। | |||
युग्म उत्पादन परिकल्पित युग्म-अस्थिरता [[सुपरनोवा|अधिनव तारा]] प्रकार के तारकीय विस्फोट के पीछे का तंत्र भी है, जहां युग्म उत्पादन अचानक एक अति विशाल तारे के अंदर दबाव कम करता है, जिससे आंशिक अंतःस्फोट होता है, और फिर विस्फोटक ताप-नाभिकीय जलता है। अधिनव तारा [[SN 2006gy|एसएन 2006जीवाई]] की परिकल्पना एक युग्म उत्पादन प्रकार के अधिनव तारा के रूप में की गई है। | |||
== यह भी देखें == | == यह भी देखें == | ||
*ब्रेट- | *ब्रेट-चक्र प्रक्रिया | ||
* [[डायराक समीकरण]] | * [[डायराक समीकरण]] | ||
* [[पदार्थ निर्माण]] | * [[पदार्थ निर्माण]] | ||
* मीटनर-हपफेल्ड प्रभाव | * मीटनर-हपफेल्ड प्रभाव | ||
* लैंडौ-पोमेरानचुक-मिग्डल प्रभाव | * लैंडौ-पोमेरानचुक-मिग्डल प्रभाव | ||
* | * दो-फोटोन भौतिकी | ||
{{Reflist}} | {{Reflist}} | ||
| Line 118: | Line 115: | ||
{{Authority control}} | {{Authority control}} | ||
{{DEFAULTSORT:Pair Production}} | {{DEFAULTSORT:Pair Production}} | ||
[[Category:Antimatter|Pair Production]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page|Pair Production]] | |||
[[Category: | [[Category:CS1 English-language sources (en)]] | ||
[[Category:Created On 29/03/2023]] | [[Category:Created On 29/03/2023|Pair Production]] | ||
[[Category:Lua-based templates|Pair Production]] | |||
[[Category:Machine Translated Page|Pair Production]] | |||
[[Category:Pages with script errors|Pair Production]] | |||
[[Category:Templates Vigyan Ready|Pair Production]] | |||
[[Category:Templates that add a tracking category|Pair Production]] | |||
[[Category:Templates that generate short descriptions|Pair Production]] | |||
[[Category:Templates using TemplateData|Pair Production]] | |||
[[Category:कण भौतिकी|Pair Production]] | |||
[[Category:परमाणु भौतिकी|Pair Production]] | |||
Latest revision as of 11:33, 24 April 2023
| Light–matter interaction |
|---|
 |
| Low-energy phenomena: |
| Photoelectric effect |
| Mid-energy phenomena: |
| Thomson scattering |
| Compton scattering |
| High-energy phenomena: |
| Pair production |
| Photodisintegration |
| Photofission |
युग्म उत्पादन एक विद्युत आवेश बोसॉन से अपरमाणविक कण और उसके प्रतिकण का निर्माण है। उदाहरणों में एक इलेक्ट्रॉन और पॉज़िट्रॉन, एक म्यूऑन और एक प्रतिम्यूऑन, या एक प्रोटॉन और एक प्रतिप्रोटन बनाना सम्मिलित है। युग्म उत्पादन प्रायः विशेष रूप से एक नाभिक के पास इलेक्ट्रॉन-पॉजिट्रॉन युग्म बनाने वाले फोटॉन को संदर्भित करता है। जैसा कि ऊर्जा को संरक्षित किया जाना चाहिए, युग्म उत्पादन होने के लिए, फोटॉन की आने वाली ऊर्जा कम से कम दो कणों की कुल शेष द्रव्यमान ऊर्जा की सीमा से ऊपर होनी चाहिए। (चूंकि इलेक्ट्रॉन सबसे हल्का है, इसलिए, सबसे कम द्रव्यमान/ऊर्जा, प्राथमिक कण, इसके लिए सभी संभव युग्म-उत्पादन प्रक्रियाओं के कम से कम ऊर्जावान फोटॉन की आवश्यकता होती है।) ऊर्जा और संवेग का संरक्षण प्रक्रिया पर प्रमुख बाधाएँ हैं।[1] उत्पादित कणों की अन्य सभी संरक्षित क्वांटम संख्याएं (कोणीय गति, विद्युत आवेश, लिप्टन संख्या) का योग शून्य होना चाहिए – इस प्रकार निर्मित कणों में एक दूसरे के विपरीत मान होंगे। उदाहरण के लिए, यदि एक कण का विद्युत आवेश +1 है, तो दूसरे का विद्युत आवेश -1 होना चाहिए, या यदि एक कण में +1 का विलक्षणता (कण भौतिकी) है तो दूसरे में -1 की विलक्षणता होनी चाहिए।
फोटॉन-पदार्थ अंतःक्रिया में युग्म उत्पादन की संभावना फोटॉन ऊर्जा के साथ बढ़ जाती है और पास के परमाणु की परमाणु संख्या (इसलिए, प्रोटॉन की संख्या) के वर्ग के रूप में भी बढ़ जाती है।[2]
फोटॉन से इलेक्ट्रॉन और पॉज़िट्रॉन
उच्च फोटॉन ऊर्जा (मेगाइलेक्ट्रॉन वोल्ट माप और उच्चतम) वाले फोटॉनों के लिए, युग्म उत्पादन पदार्थ के साथ फोटॉन अंतःक्रिया का प्रमुख तरीका है। इन अंतःक्रियाओं को पहली बार पैट्रिक मेनार्ड स्टुअर्ट ब्लैकेट के प्रति-नियंत्रित अभ्रकोष्ठ में देखा गया, जिसके कारण 1948 में भौतिकी का नोबेल पुरस्कार मिला।[3] यदि फोटॉन परमाणु नाभिक के पास है, तो फोटॉन की ऊर्जा को इलेक्ट्रॉन-पॉजिट्रॉन युग्म में परिवर्तित किया जा सकता है:
फोटॉन की ऊर्जा आइंस्टीन के समीकरण, E = m ⋅ c2 के अनुसार कण द्रव्यमान में परिवर्तित हो जाती है; जहाँ E ऊर्जा है, m द्रव्यमान है और c प्रकाश की गति है। उत्पादन होने के लिए फोटॉन में एक इलेक्ट्रॉन और पॉज़िट्रॉन (2 ⋅ 511 keV = 1.022 मेगाइलेक्ट्रॉन वोल्ट, जिसके परिणामस्वरूप 1.2132 पिकोमीटर का फोटॉन-तरंग दैर्ध्य होता है) की शेष द्रव्यमान ऊर्जाओं के योग से अधिक ऊर्जा होनी चाहिए। (इस प्रकार, मेडिकल एक्स-रे प्रतिबिंबन में युग्म उत्पादन नहीं होता है क्योंकि इन एक्स-रे में केवल ~150 किलो-इलेक्ट्रॉन-वोल्ट होता है।) संवेग के संरक्षण को संतुष्ट करने के लिए फोटॉन को एक नाभिक के पास होना चाहिए, संवेग के संरक्षण को संतुष्ट करने के लिए फोटॉन को एक नाभिक के पास होना चाहिए क्योंकि मुक्त आकाश में उत्पादित एक इलेक्ट्रॉन-पॉज़िट्रॉन युग्म ऊर्जा और संवेग दोनों के संरक्षण को संतुष्ट नहीं कर सकती है।[4] इस कारण से, जब युग्म उत्पादन होता है, परमाणु नाभिक को कुछ प्रतिक्षेप प्राप्त करता है। इस प्रक्रिया का प्रतिवर्त इलेक्ट्रॉन-पॉज़िट्रॉन विलोपन है।
मौलिक शुद्ध गतिकी
इन गुणों को अंतःक्रिया के शुद्ध गतिकी के माध्यम से प्राप्त किया जा सकता है। चतुर्विम वेक्टर संकेतन का उपयोग करते हुए, अंतःक्रिया से पहले और बाद में ऊर्जा-संवेग का संरक्षण देता है:[5]
जहां नाभिक का प्रतिक्षेप है। चतुर्विम वेक्टर के मापांक पर ध्यान दें
है:
जिसका तात्पर्य है कि सभी स्थितियो के लिए है। हम संरक्षण समीकरण को वर्ग कर सकते हैं:
हालांकि, अधिकतम स्थितियों में नाभिक का प्रतिक्षेप फोटॉन की ऊर्जा की तुलना में बहुत छोटा होता है और इसे उपेक्षित किया जा सकता है। इस अनुमान को लेते हुए शेष संबंध को सरल और विस्तारित करने के लिए:
इसलिए, यह सन्निकटन तभी संतुष्ट हो सकता है जब इलेक्ट्रॉन और पॉज़िट्रॉन लगभग समान दिशा में उत्सर्जित हों, अर्थात, है।
यह व्युत्पत्ति एक अर्ध-उत्कृष्ट सन्निकटन है। फोटॉन और नाभिक के पूर्ण क्वांटम यांत्रिक प्रकीर्णन को ध्यान में रखते हुए शुद्ध गतिक का एक परिशुद्ध निस्त्रावण किया जा सकता है।
ऊर्जा हस्तांतरण
युग्म उत्पादन अंतःक्रियाओं में इलेक्ट्रॉन और पॉज़िट्रॉन को ऊर्जा हस्तांतरण द्वारा दिया जाता है:
जहां प्लैंक स्थिरांक है, फोटॉन की आवृत्ति है और इलेक्ट्रॉन-पॉज़िट्रॉन का संयुक्त विराम द्रव्यमान है। सामान्य रूप से, नाभिक के प्रतिक्षेप को उपेक्षा करते हुए, इलेक्ट्रॉन और पॉज़िट्रॉन को विभिन्न गतिज ऊर्जाओं के साथ उत्सर्जित किया जा सकता है, लेकिन प्रत्येक को हस्तांतरित औसत है:
अनुप्रस्थ परिच्छेद

युग्म उत्पादन के अनुप्रस्थ परिच्छेद के लिए परिशुद्ध विश्लेषणात्मक रूप की गणना फेनमैन आरेखों के रूप में क्वांटम विद्युतगतिकी के माध्यम से की जानी चाहिए और इसके परिणामस्वरूप एक जटिल फलन होता है। सरल करने के लिए, अनुप्रस्थ परिच्छेद को इस प्रकार लिखा जा सकता है:
जहां सूक्ष्म-संरचना स्थिरांक है, उत्कृष्ट इलेक्ट्रॉन त्रिज्या है, वस्तु की परमाणु संख्या है, और कुछ जटिल-मान फलन है जो ऊर्जा और परमाणु संख्या पर निर्भर करता है। अनुप्रस्थ परिच्छेद विभिन्न सामग्रियों और ऊर्जाओं के लिए सारणीबद्ध हैं।
2008 में 1 मिलीमीटर-स्थूल स्वर्ण के प्रयोजन के लिए टाइटन लेजर का उपयोग बड़ी संख्या में पॉज़िट्रॉन-इलेक्ट्रॉन युग्म उत्पन्न करने के लिए किया गया था।[6]
खगोल विज्ञान
परिकल्पनात्मक हॉकिंग विकिरण की अनुमानी व्याख्या में युग्म उत्पादन को प्रयुक्त किया जाता है। क्वांटम यांत्रिकी के अनुसार, कण युग्म क्वांटम फोम के रूप में निरंतर दिखाई और विलोप हो रहे हैं। प्रबल गुरुत्वाकर्षण ज्वारीय बलों के एक क्षेत्र में, एक युग्म में दो कण कभी-कभी अलग हो सकते हैं इससे पहले कि उन्हें परस्पर विलोपन का अवसर मिले। जब यह एक ब्लैक होल (कृष्ण विवर) के आसपास के क्षेत्र में होता है, तो एक कण संरक्षित हो सकता है जबकि उसका प्रति कण सहभागी ब्लैक होल द्वारा प्रग्रहण कर लिया जाता है।
युग्म उत्पादन परिकल्पित युग्म-अस्थिरता अधिनव तारा प्रकार के तारकीय विस्फोट के पीछे का तंत्र भी है, जहां युग्म उत्पादन अचानक एक अति विशाल तारे के अंदर दबाव कम करता है, जिससे आंशिक अंतःस्फोट होता है, और फिर विस्फोटक ताप-नाभिकीय जलता है। अधिनव तारा एसएन 2006जीवाई की परिकल्पना एक युग्म उत्पादन प्रकार के अधिनव तारा के रूप में की गई है।
यह भी देखें
- ब्रेट-चक्र प्रक्रिया
- डायराक समीकरण
- पदार्थ निर्माण
- मीटनर-हपफेल्ड प्रभाव
- लैंडौ-पोमेरानचुक-मिग्डल प्रभाव
- दो-फोटोन भौतिकी
- ↑ Das, A.; Ferbel, T. (2003-12-23). परमाणु और कण भौतिकी का परिचय (in English). World Scientific. ISBN 9789814483339.
- ↑ Stefano, Meroli. "फोटॉन पदार्थ के साथ कैसे इंटरैक्ट करते हैं". Meroli Stefano Webpage. Retrieved 2016-08-28.
- ↑ Bywater, Jenn (29 October 2015). "Exploring dark matter in the inaugural Blackett Colloquium". Imperial College London. Retrieved 29 August 2016.
- ↑ Hubbell, J.H. (June 2006). "Electron positron pair production by photons: A historical overview". Radiation Physics and Chemistry. 75 (6): 614–623. Bibcode:2006RaPC...75..614H. doi:10.1016/j.radphyschem.2005.10.008.
- ↑
Kuncic, Zdenka, Dr. (12 March 2013). "PRadiation Physics and Dosimetry" (PDF). Index of Dr. Kuncic's Lectures. PHYS 5012. Sydney, Australia: The University of Sydney. Archived from the original (PDF) on 11 March 2016. Retrieved 2015-04-14.
{{cite web}}: CS1 maint: multiple names: authors list (link) - ↑
"Laser technique produces bevy of antimatter". MSNBC. 2008. Retrieved 2019-05-27.
The LLNL scientists created the positrons by shooting the lab's high-powered Titan laser onto a one-millimeter-thick piece of gold.
