लेंस (ज्यामिति): Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{short description|Convex plane region bounded by two circular arcs}} | {{short description|Convex plane region bounded by two circular arcs}} | ||
{{Other uses|लेंस (प्रकाशिकी)}} | {{Other uses|लेंस (प्रकाशिकी)}} | ||
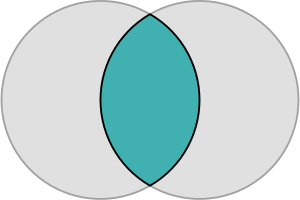
[[Image:Geometric lens.gif|thumb|त्रिज्या के दो वृत्ताकार चापों के मध्य समाहित लेंस {{mvar|R}}, और केंद्र पर {{math|''O''{{sub|1}}}} और {{math|''O''{{sub|2}}}}]]2-आयामी [[ज्यामिति]] में, लेंस [[उत्तल सेट|उत्तल]] क्षेत्र होता है जो दो [[गोलाकार चाप|वृताकार चापों]] से घिरा होता है जो उनके अंत बिंदुओं पर परस्पर जुड़े | [[Image:Geometric lens.gif|thumb|त्रिज्या के दो वृत्ताकार चापों के मध्य समाहित लेंस {{mvar|R}}, और केंद्र पर {{math|''O''{{sub|1}}}} और {{math|''O''{{sub|2}}}}]]2-आयामी [[ज्यामिति]] में, लेंस का [[उत्तल सेट|उत्तल]] क्षेत्र होता है जो दो [[गोलाकार चाप|वृताकार चापों]] से घिरा होता है जो उनके अंत बिंदुओं पर परस्पर जुड़े होते हैं। इस आकृति को उत्तल होने के लिए, दोनों चापों को बाहर की ओर झुकना चाहिए (उत्तल-उत्तल)। यह आकृति दो वृताकार [[डिस्क (गणित)]] के प्रतिच्छेदन के रूप में बन सकती है। इसे दो वृत्ताकार खंडों (वृत्त की जीवा (ज्यामिति) और स्वयं वृत्त के मध्य का क्षेत्र) के युग्मन के रूप में भी बनाया जा सकता है, जो सामान्य जीवा के साथ जुड़ा हुआ है। | ||
== प्रकार == | == प्रकार == | ||
[[File:geometric_lens_examples.png|thumb|दो असममित लेंस (बाएं और दाएं) और सममित लेंस (मध्य में) का उदाहरण]] | [[File:geometric_lens_examples.png|thumb|दो असममित लेंस (बाएं और दाएं) और सममित लेंस (मध्य में) का उदाहरण]] | ||
[[File:Vesica_piscis_circles.svg|thumb|right|upright=1|[[मूत्राशय मछली]] दो [[डिस्क (ज्यामिति)]] की त्रिज्या, R, और केंद्रों के मध्य की दूरी भी R के समान है।]]यदि लेंस के दो चापों की त्रिज्या समान है, तो इसे सममित लेंस कहा जाता है, अन्यथा असममित लेंस होता है। | [[File:Vesica_piscis_circles.svg|thumb|right|upright=1|[[मूत्राशय मछली|वेसिका पिसिस]] दो [[डिस्क (ज्यामिति)]] की त्रिज्या, R, और केंद्रों के मध्य की दूरी भी R के समान है।]]यदि लेंस के दो चापों की त्रिज्या समान है, तो इसे सममित लेंस कहा जाता है, अन्यथा असममित लेंस होता है। | ||
वेसिका पिसिस सममित लेंस का रूप है, जो दो वृत्तों के चापों द्वारा निर्मित होता है, जिनके केंद्र विपरीत चाप पर स्थित होते हैं। चाप अपने अंतिम बिंदुओं पर 120° के कोण पर मिलते हैं। | वेसिका पिसिस सममित लेंस का रूप है, जो दो वृत्तों के चापों द्वारा निर्मित होता है, जिनके केंद्र विपरीत चाप पर स्थित होते हैं। चाप अपने अंतिम बिंदुओं पर 120° के कोण पर मिलते हैं। | ||
| Line 25: | Line 25: | ||
यदि दो वृत्त ओवरलैप करते हैं <math>d<r+R</math>. अधिक बड़े के लिए <math>d</math>, लेंस केंद्र का समन्वय <math>x</math> दो वृत्त केंद्रों के निर्देशांक के मध्य स्थित है- | यदि दो वृत्त ओवरलैप करते हैं <math>d<r+R</math>. अधिक बड़े के लिए <math>d</math>, लेंस केंद्र का समन्वय <math>x</math> दो वृत्त केंद्रों के निर्देशांक के मध्य स्थित है- | ||
[[Image:Two overlapping circles with large distance.svg|300px|d की दूरी पर त्रिज्या R और r के दो गोलाकार चापों के बीच एक लेंस समाहित है]]छोटे के लिए <math>d</math>, लेंस केंद्र का समन्वय <math>x</math> उस रेखा के बाहर स्थित होता है जो वृत्त केंद्रों को जोड़ती है- | [[Image:Two overlapping circles with large distance.svg|300px|d की दूरी पर त्रिज्या R और r के दो गोलाकार चापों के बीच एक लेंस समाहित है]] छोटे के लिए <math>d</math>, लेंस केंद्र का समन्वय <math>x</math> उस रेखा के बाहर स्थित होता है जो वृत्त केंद्रों को जोड़ती है- | ||
[[Image:Two overlapping circles with small distance.svg|300px|d की दूरी पर त्रिज्या R और r के दो गोलाकार चापों के बीच एक लेंस समाहित है]]वृत्त समीकरणों से y को विस्थापित करने पर <math>x^2+y^2=r^2</math> और <math>(x-d)^2+y^2=R^2</math> प्रतिच्छेदी रिम्स | [[Image:Two overlapping circles with small distance.svg|300px|d की दूरी पर त्रिज्या R और r के दो गोलाकार चापों के बीच एक लेंस समाहित है]] वृत्त समीकरणों से y को विस्थापित करने पर <math>x^2+y^2=r^2</math> और <math>(x-d)^2+y^2=R^2</math> प्रतिच्छेदी रिम्स की भुज और कोटि है- | ||
:<math>x=(d^2+r^2-R^2)/(2d)</math>. | :<math>x=(d^2+r^2-R^2)/(2d)</math>. | ||
| Line 39: | Line 39: | ||
वर्गमूल के अंतर्गत ऋणात्मक मान संकेत करते हैं कि दो वृत्तों के घेरे स्पर्श नहीं करते हैं, | वर्गमूल के अंतर्गत ऋणात्मक मान संकेत करते हैं कि दो वृत्तों के घेरे स्पर्श नहीं करते हैं, | ||
क्योंकि वृत्त अधिक दूर हैं या वृत्त दूसरे के भीतर पूर्ण रूप से स्थित है। | क्योंकि वृत्त अधिक दूर हैं या वृत्त दूसरे के भीतर पूर्ण रूप से स्थित होती है। | ||
वर्गमूल के अंतर्गत मान d का द्विवर्गीय बहुपद है। इस बहुपद की चार जड़ें y = 0 और d के चार मानों के साथ जुड़ी हुई हैं, जहाँ दो वृत्तों में बिंदु उभयनिष्ठ है। | वर्गमूल के अंतर्गत मान d का द्विवर्गीय बहुपद है। इस बहुपद की चार जड़ें y = 0 और d के चार मानों के साथ जुड़ी हुई हैं, जहाँ दो वृत्तों में बिंदु उभयनिष्ठ होता है। | ||
भुजाओं d, r और R वाले नीले त्रिभुज में कोण हैं | भुजाओं d, r और R वाले नीले त्रिभुज में कोण हैं | ||
| Line 47: | Line 47: | ||
जहाँ y प्रतिच्छेदन की कोटि है। यदि <math>d^2<R^2-r^2</math> आर्क्सिन की शाखा <math>a_r>\pi/2</math> के साथ लिया जाता है| | जहाँ y प्रतिच्छेदन की कोटि है। यदि <math>d^2<R^2-r^2</math> आर्क्सिन की शाखा <math>a_r>\pi/2</math> के साथ लिया जाता है| | ||
त्रिभुज का क्षेत्रफल | त्रिभुज का क्षेत्रफल <math>\Delta = \frac12 yd</math> है| | ||
असममित लेंस का क्षेत्रफल | असममित लेंस का क्षेत्रफल <math>A=a_r r^2+a_R R^2-yd</math> है, जहाँ दो कोणों को रेडियन में मापा जाता है। | ||
[यह [[समावेशन-बहिष्करण सिद्धांत]] का अनुप्रयोग है: केंद्रीय के साथ (0,0) और (d, 0) पर केंद्रित दो परिपत्र क्षेत्र | [यह [[समावेशन-बहिष्करण सिद्धांत]] का अनुप्रयोग है: केंद्रीय के साथ (0,0) और (d, 0) पर केंद्रित दो परिपत्र क्षेत्र | ||
<math>2a_r</math> और <math>2a_R</math> | <math>2a_r</math> और <math>2a_R</math> जिनके <math>2a_r r^2</math> और <math>2a_R R^2</math> क्षेत्रफल हैं, उनका संघ त्रिकोण को कवर करता है, (x, -y) सिरे पर त्रिकोण लेंस क्षेत्र से दोगुना होता है।] | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
श्रीमती मिनिवर की समस्या का उत्तर भिन्न आकार वाला लेंस दो वृत्तों के | श्रीमती मिनिवर की समस्या का उत्तर भिन्न आकार वाला लेंस दो वृत्तों के युग्मन के अर्द्ध क्षेत्रफल वाले लेंस का उपयोग करता है। | ||
लेंस का उपयोग [[बीटा कंकाल]] | लेंस का उपयोग [[बीटा कंकाल|बीटा स्केलेटन्स]] को परिभाषित करने के लिए किया जाता है, जब भी दो बिंदुओं द्वारा निर्धारित लेंस रिक्त होता है, तो बिंदुओं के जोड़े को शीर्षों से जोड़कर बिंदुओं के सेट पर परिभाषित ज्यामितीय का रेखांकन किया जाता है। | ||
== यह भी देखें == | == यह भी देखें == | ||
* | * वृत-वृत अन्तःखण्ड | ||
*लून (ज्यामिति), संबंधित गैर-उत्तल आकार जो दो गोलाकार चापों से बनता है, बाहर की ओर झुकता है और दूसरा अंदर की ओर झुकता है | *लून (ज्यामिति), संबंधित गैर-उत्तल आकार जो दो गोलाकार चापों से बनता है, बाहर की ओर झुकता है और दूसरा अंदर की ओर झुकता है | ||
*[[नींबू (ज्यामिति)]], लेंस द्वारा बनाया गया है जो अपनी युक्तियों के माध्यम से अक्ष के चारों ओर घूमता है।<ref name=mathworld>{{cite web|url=http://mathworld.wolfram.com/नींबू.html|title=नींबू|website=Wolfram [[:en:MathWorld|MathWorld]]|author=Weisstein, Eric W.|access-date=2019-11-04}}</ref> | *[[नींबू (ज्यामिति)|लेमन (ज्यामिति)]], लेंस द्वारा बनाया गया है जो अपनी युक्तियों के माध्यम से अक्ष के चारों ओर घूमता है।<ref name=mathworld>{{cite web|url=http://mathworld.wolfram.com/नींबू.html|title=नींबू|website=Wolfram [[:en:MathWorld|MathWorld]]|author=Weisstein, Eric W.|access-date=2019-11-04}}</ref> | ||
[[File:Lemon (geometry).png|thumb| | [[File:Lemon (geometry).png|thumb|लेमन (ज्यामिति)।]] | ||
==संदर्भ== | ==संदर्भ== | ||
Revision as of 22:59, 19 April 2023
2-आयामी ज्यामिति में, लेंस का उत्तल क्षेत्र होता है जो दो वृताकार चापों से घिरा होता है जो उनके अंत बिंदुओं पर परस्पर जुड़े होते हैं। इस आकृति को उत्तल होने के लिए, दोनों चापों को बाहर की ओर झुकना चाहिए (उत्तल-उत्तल)। यह आकृति दो वृताकार डिस्क (गणित) के प्रतिच्छेदन के रूप में बन सकती है। इसे दो वृत्ताकार खंडों (वृत्त की जीवा (ज्यामिति) और स्वयं वृत्त के मध्य का क्षेत्र) के युग्मन के रूप में भी बनाया जा सकता है, जो सामान्य जीवा के साथ जुड़ा हुआ है।
प्रकार
यदि लेंस के दो चापों की त्रिज्या समान है, तो इसे सममित लेंस कहा जाता है, अन्यथा असममित लेंस होता है।
वेसिका पिसिस सममित लेंस का रूप है, जो दो वृत्तों के चापों द्वारा निर्मित होता है, जिनके केंद्र विपरीत चाप पर स्थित होते हैं। चाप अपने अंतिम बिंदुओं पर 120° के कोण पर मिलते हैं।
क्षेत्र
सममित
सममित लेंस के क्षेत्र को रेडियन में त्रिज्या R और चाप की लंबाई θ के संदर्भ में व्यक्त किया जा सकता है-
असममित
उनके केंद्रों के मध्य की दूरी d के साथ त्रिज्या R और r के वृत्तों से बने असममित लेंस का क्षेत्रफल है[1]
जहाँ
भुजाओं d, r, और R वाले त्रिभुज का क्षेत्रफल है।
यदि दो वृत्त ओवरलैप करते हैं . अधिक बड़े के लिए , लेंस केंद्र का समन्वय दो वृत्त केंद्रों के निर्देशांक के मध्य स्थित है-
 छोटे के लिए , लेंस केंद्र का समन्वय उस रेखा के बाहर स्थित होता है जो वृत्त केंद्रों को जोड़ती है-
छोटे के लिए , लेंस केंद्र का समन्वय उस रेखा के बाहर स्थित होता है जो वृत्त केंद्रों को जोड़ती है-
 वृत्त समीकरणों से y को विस्थापित करने पर और प्रतिच्छेदी रिम्स की भुज और कोटि है-
वृत्त समीकरणों से y को विस्थापित करने पर और प्रतिच्छेदी रिम्स की भुज और कोटि है-
- .
x का चिह्न, अर्थात, से बड़ा या छोटा होना , छवियों में प्रदर्शित की गयी दो स्तिथियों को भिन्न करता है।
प्रतिच्छेदन का भुज और कोटि है-
- .
वर्गमूल के अंतर्गत ऋणात्मक मान संकेत करते हैं कि दो वृत्तों के घेरे स्पर्श नहीं करते हैं,
क्योंकि वृत्त अधिक दूर हैं या वृत्त दूसरे के भीतर पूर्ण रूप से स्थित होती है।
वर्गमूल के अंतर्गत मान d का द्विवर्गीय बहुपद है। इस बहुपद की चार जड़ें y = 0 और d के चार मानों के साथ जुड़ी हुई हैं, जहाँ दो वृत्तों में बिंदु उभयनिष्ठ होता है।
भुजाओं d, r और R वाले नीले त्रिभुज में कोण हैं
जहाँ y प्रतिच्छेदन की कोटि है। यदि आर्क्सिन की शाखा के साथ लिया जाता है|
त्रिभुज का क्षेत्रफल है|
असममित लेंस का क्षेत्रफल है, जहाँ दो कोणों को रेडियन में मापा जाता है।
[यह समावेशन-बहिष्करण सिद्धांत का अनुप्रयोग है: केंद्रीय के साथ (0,0) और (d, 0) पर केंद्रित दो परिपत्र क्षेत्र
और जिनके और क्षेत्रफल हैं, उनका संघ त्रिकोण को कवर करता है, (x, -y) सिरे पर त्रिकोण लेंस क्षेत्र से दोगुना होता है।]
अनुप्रयोग
श्रीमती मिनिवर की समस्या का उत्तर भिन्न आकार वाला लेंस दो वृत्तों के युग्मन के अर्द्ध क्षेत्रफल वाले लेंस का उपयोग करता है।
लेंस का उपयोग बीटा स्केलेटन्स को परिभाषित करने के लिए किया जाता है, जब भी दो बिंदुओं द्वारा निर्धारित लेंस रिक्त होता है, तो बिंदुओं के जोड़े को शीर्षों से जोड़कर बिंदुओं के सेट पर परिभाषित ज्यामितीय का रेखांकन किया जाता है।
यह भी देखें
- वृत-वृत अन्तःखण्ड
- लून (ज्यामिति), संबंधित गैर-उत्तल आकार जो दो गोलाकार चापों से बनता है, बाहर की ओर झुकता है और दूसरा अंदर की ओर झुकता है
- लेमन (ज्यामिति), लेंस द्वारा बनाया गया है जो अपनी युक्तियों के माध्यम से अक्ष के चारों ओर घूमता है।[2]
संदर्भ
- Pedoe, D. (1995). "Circles: A Mathematical View, rev. ed". Washington, DC: Math. Assoc. Amer. MR 1349339.
- Plummer, H. (1960). An Introductory Treatise of Dynamical Astronomy. York: Dover. Bibcode:1960aitd.book.....P.
- Watson, G. N. (1966). A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press. MR 1349110.
- Fewell, M. P. (2006). "Area of common overlap of three circles". Defence Science and Technology Organisation. Archived from the original on March 3, 2022.
- Librion, Federico; Levorato, Marco; Zorzi, Michele (2012). "An algorithmic solution for computing circle intersection areas and its application to wireless communications". Wirel. Commun. Mobile Comput. 14 (18): 1672–1690. doi:10.1002/wcm.2305. S2CID 2828261.