समान अंतःवृत्त प्रमेय: Difference between revisions
(Created page with "{{short description|On rays from a point to a line, with equal inscribed circles between adjacent rays}} Image:Incircles.JPG|thumb|360px|यदि नीले वृत्...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{short description|On rays from a point to a line, with equal inscribed circles between adjacent rays}} | {{short description|On rays from a point to a line, with equal inscribed circles between adjacent rays}} | ||
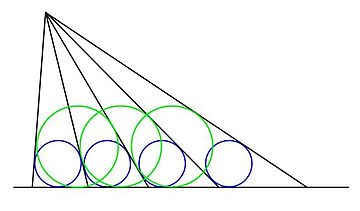
[[Image:Incircles.JPG|thumb|360px|यदि नीले वृत्त समान हैं, तो हरे वृत्त भी समान हैं।]][[ज्यामिति]] में, समान अंतर्वृत्त प्रमेय | [[Image:Incircles.JPG|thumb|360px|यदि नीले वृत्त समान हैं, तो हरे वृत्त भी समान हैं।]][[ज्यामिति]] में, समान अंतर्वृत्त प्रमेय जापानी [[पहाड़ों]] से निकला है, और निम्नलिखित निर्माण से संबंधित है: किरणों की श्रृंखला दिए गए बिंदु से दी गई रेखा तक खींची जाती है, जैसे कि आसन्न किरणों और आधार रेखा द्वारा गठित त्रिभुजों के खुदे हुए घेरे बराबर हैं। चित्रण में समान नीले वृत्त किरणों के बीच की दूरी को परिभाषित करते हैं, जैसा कि वर्णित है। | ||
प्रमेय में कहा गया है कि हर दूसरी किरण, हर तीसरी किरण आदि से बनने वाले त्रिकोण (किसी भी किरण से शुरू) के अंतःवृत्त और आधार रेखा भी बराबर होती है। हर दूसरी किरण की स्थिति हरे वृत्तों द्वारा ऊपर चित्रित की गई है, जो सभी समान हैं। | प्रमेय में कहा गया है कि हर दूसरी किरण, हर तीसरी किरण आदि से बनने वाले त्रिकोण (किसी भी किरण से शुरू) के अंतःवृत्त और आधार रेखा भी बराबर होती है। हर दूसरी किरण की स्थिति हरे वृत्तों द्वारा ऊपर चित्रित की गई है, जो सभी समान हैं। | ||
| Line 8: | Line 8: | ||
प्रमेय निम्नलिखित लेम्मा का प्रत्यक्ष परिणाम है: | प्रमेय निम्नलिखित लेम्मा का प्रत्यक्ष परिणाम है: | ||
मान लीजिए कि ''n'' किरण | मान लीजिए कि ''n'' किरण कोण बनाती है <math>\gamma_n</math> बेसलाइन के सामान्य के साथ। अगर <math>\gamma_n</math> समीकरण के अनुसार पैरामिट्रीकृत है, <math>\tan \gamma_n = \sinh\theta_n</math>, फिर के मान <math>\theta_n = a + nb</math>, कहाँ <math>a</math> और <math>b</math> वास्तविक स्थिरांक हैं, किरणों के क्रम को परिभाषित करते हैं जो समान अंतःवृत्तों की स्थिति को संतुष्ट करते हैं, और इसके अलावा किरणों के किसी भी क्रम को स्थिरांक के उपयुक्त विकल्प द्वारा उत्पादित किया जा सकता है <math>a</math> और <math>b</math>. | ||
== लेम्मा का प्रमाण == | == लेम्मा का प्रमाण == | ||
[[Image:equal incircles theorem.svg|600px|center]]रेखाचित्र में, रेखाएँ PS और PT आसन्न किरणें हैं जो कोण बनाती हैं <math>\gamma_n</math> और <math>\gamma_{n+1}</math> लाइन पीआर के साथ, जो बेसलाइन, आरएसटी के लंबवत है। | [[Image:equal incircles theorem.svg|600px|center]]रेखाचित्र में, रेखाएँ PS और PT आसन्न किरणें हैं जो कोण बनाती हैं <math>\gamma_n</math> और <math>\gamma_{n+1}</math> लाइन पीआर के साथ, जो बेसलाइन, आरएसटी के लंबवत है। | ||
| Line 17: | Line 16: | ||
तब <math>\triangle</math> ओडब्ल्यूएक्स के समान है <math>\triangle</math> पीक्यूएक्स और <math>\triangle</math> ओजीवाई के समान है <math>\triangle</math> PAY, और XY = X + Y से हमें मिलता है | तब <math>\triangle</math> ओडब्ल्यूएक्स के समान है <math>\triangle</math> पीक्यूएक्स और <math>\triangle</math> ओजीवाई के समान है <math>\triangle</math> PAY, और XY = X + Y से हमें मिलता है | ||
: <math>(h-r) ( \tan \gamma_{n+1} - \tan \gamma_n ) = r ( \sec \gamma_n + \sec \gamma_{n+1} ).</math> | : <math>(h-r) ( \tan \gamma_{n+1} - \tan \gamma_n ) = r ( \sec \gamma_n + \sec \gamma_{n+1} ).</math> | ||
कोणों के | कोणों के सेट पर यह संबंध, <math>\{ \gamma_m \}</math>, समान अंतःवृत्तों की स्थिति को व्यक्त करता है। | ||
लेम्मा को साबित करने के लिए, हम सेट करते हैं <math> \tan \gamma_n = \sinh (a+nb)</math>, जो देता है <math> \sec \gamma_n = \cosh(a+nb)</math>. | लेम्मा को साबित करने के लिए, हम सेट करते हैं <math> \tan \gamma_n = \sinh (a+nb)</math>, जो देता है <math> \sec \gamma_n = \cosh(a+nb)</math>. | ||
| Line 24: | Line 23: | ||
: <math>\frac {r}{h-r} = \tanh\frac{b}{2}.</math> | : <math>\frac {r}{h-r} = \tanh\frac{b}{2}.</math> | ||
यह पैरामीटर के लिए | यह पैरामीटर के लिए अभिव्यक्ति देता है <math>b</math> ज्यामितीय उपायों के संदर्भ में, <math>h</math> और <math>r</math>. इस परिभाषा के साथ <math>b</math> फिर हम त्रिज्या के लिए व्यंजक प्राप्त करते हैं, <math>r_N</math>, प्रत्येक Nth किरण को त्रिभुजों की भुजाओं के रूप में लेने से बनने वाले वृत्तों का | ||
: <math>\frac {r_N}{h-r_N} = \tanh\frac{Nb}{2}.</math> | : <math>\frac {r_N}{h-r_N} = \tanh\frac{Nb}{2}.</math> | ||
Revision as of 17:56, 23 April 2023
ज्यामिति में, समान अंतर्वृत्त प्रमेय जापानी पहाड़ों से निकला है, और निम्नलिखित निर्माण से संबंधित है: किरणों की श्रृंखला दिए गए बिंदु से दी गई रेखा तक खींची जाती है, जैसे कि आसन्न किरणों और आधार रेखा द्वारा गठित त्रिभुजों के खुदे हुए घेरे बराबर हैं। चित्रण में समान नीले वृत्त किरणों के बीच की दूरी को परिभाषित करते हैं, जैसा कि वर्णित है।
प्रमेय में कहा गया है कि हर दूसरी किरण, हर तीसरी किरण आदि से बनने वाले त्रिकोण (किसी भी किरण से शुरू) के अंतःवृत्त और आधार रेखा भी बराबर होती है। हर दूसरी किरण की स्थिति हरे वृत्तों द्वारा ऊपर चित्रित की गई है, जो सभी समान हैं।
इस तथ्य से कि प्रमेय प्रारंभिक किरण के कोण पर निर्भर नहीं करता है, यह देखा जा सकता है कि प्रमेय ज्यामिति के बजाय गणितीय विश्लेषण से ठीक से संबंधित है, और निरंतर स्केलिंग फ़ंक्शन से संबंधित होना चाहिए जो किरणों के अंतर को परिभाषित करता है। वास्तव में, यह कार्य अतिशयोक्तिपूर्ण कार्य है।
प्रमेय निम्नलिखित लेम्मा का प्रत्यक्ष परिणाम है:
मान लीजिए कि n किरण कोण बनाती है बेसलाइन के सामान्य के साथ। अगर समीकरण के अनुसार पैरामिट्रीकृत है, , फिर के मान , कहाँ और वास्तविक स्थिरांक हैं, किरणों के क्रम को परिभाषित करते हैं जो समान अंतःवृत्तों की स्थिति को संतुष्ट करते हैं, और इसके अलावा किरणों के किसी भी क्रम को स्थिरांक के उपयुक्त विकल्प द्वारा उत्पादित किया जा सकता है और .
लेम्मा का प्रमाण
रेखाचित्र में, रेखाएँ PS और PT आसन्न किरणें हैं जो कोण बनाती हैं और लाइन पीआर के साथ, जो बेसलाइन, आरएसटी के लंबवत है।
लाइन QXOY बेसलाइन के समानांतर है और ओ के माध्यम से गुजरती है, के बीच का केंद्र PST, जो W और Z पर किरणों की स्पर्शरेखा है। साथ ही, रेखा PQ की लंबाई है , और रेखा QR की लंबाई है , अंतःवृत्त की त्रिज्या।
तब ओडब्ल्यूएक्स के समान है पीक्यूएक्स और ओजीवाई के समान है PAY, और XY = X + Y से हमें मिलता है
कोणों के सेट पर यह संबंध, , समान अंतःवृत्तों की स्थिति को व्यक्त करता है।
लेम्मा को साबित करने के लिए, हम सेट करते हैं , जो देता है .
का उपयोग करते हुए , हम इसके लिए अतिरिक्त नियम लागू करते हैं और , और सत्यापित करें कि समान अंतःवृत्त संबंध सेटिंग द्वारा संतुष्ट है
यह पैरामीटर के लिए अभिव्यक्ति देता है ज्यामितीय उपायों के संदर्भ में, और . इस परिभाषा के साथ फिर हम त्रिज्या के लिए व्यंजक प्राप्त करते हैं, , प्रत्येक Nth किरण को त्रिभुजों की भुजाओं के रूप में लेने से बनने वाले वृत्तों का
यह भी देखें
- अतिशयोक्तिपूर्ण समारोह
- चक्रीय बहुभुजों के लिए जापानी प्रमेय
- चक्रीय चतुर्भुजों के लिए जापानी प्रमेय
- वृत्तों की स्पर्श रेखाएँ
संदर्भ
- Equal Incircles Theorem at cut-the-knot
- J. Tabov. A note on the five-circle theorem. Mathematics Magazine 63 (1989), 2, 92–94.