सामान्यीकृत त्रिकोणमिति: Difference between revisions

From Vigyanwiki
No edit summary
No edit summary
 
(24 intermediate revisions by 3 users not shown)
Line 2: Line 2:
{{Trigonometry}}
{{Trigonometry}}


सामान्य [[त्रिकोणमिति]] [[यूक्लिडियन अंतरिक्ष|यूक्लिडियन तल]] {{tmath|\mathbb{R}^2}} में [[त्रिभुजों]] का अध्ययन करती है। वास्तविक संख्याओं पर सामान्य [[यूक्लिडियन ज्यामिति|यूक्लिडियन ज्यामितीय]] त्रिकोणमितीय फलन को परिभाषित करने के कई तरीके हैं, उदाहरण के लिए त्रिकोणमितीय कार्य #Right-angle_triangle_definitions|समकोण त्रिकोण परिभाषाएँ, त्रिकोणमितीय कार्य#इकाई-सर्कल_परिभाषाएँ, त्रिकोणमितीय कार्य#श्रृंखला_परिभाषाएँ, त्रिकोणमितीय कार्य#परिभाषाएँ_के माध्यम से_अंतर समीकरण , और त्रिकोणमितीय फ़ंक्शन # परिभाषाएं_उपयोग_कार्यात्मक_समीकरण। त्रिकोणमितीय कार्यों के सामान्यीकरण को अक्सर उपरोक्त विधियों में से एक के साथ शुरू करके और इसे यूक्लिडियन ज्यामिति की वास्तविक संख्या के अलावा किसी अन्य स्थिति में अनुकूलित करके विकसित किया जाता है। आम तौर पर, त्रिकोणमिति ज्यामिति या [[अंतरिक्ष (गणित)]] के किसी भी प्रकार के ज्यामिति विषयों की सूची # प्रकार, कार्यप्रणाली और शब्दावली में बिंदुओं के त्रिगुणों का अध्ययन हो सकता है। त्रिभुज वह [[बहुभुज]] होता है जिसके शीर्षों की संख्या सबसे कम होती है, इसलिए सामान्यीकृत करने की एक दिशा कोणों और बहुभुजों के उच्च-आयामी अनुरूपों का अध्ययन करना है: [[ठोस कोण]] और बहुशीर्ष जैसे [[ चतुर्पाश्वीय ]] और एन-सिम्प्लेक्स|{{mvar|n}}-सरल।
सामान्य [[त्रिकोणमिति]] [[यूक्लिडियन अंतरिक्ष|यूक्लिडियन तल]] {{tmath|\mathbb{R}^2}} में [[त्रिभुजों]] का अध्ययन करती है। [[वास्तविक संख्याओं]] पर सामान्य [[यूक्लिडियन ज्यामिति|यूक्लिडियन ज्यामितीय]] [[त्रिकोणमितीय]] [[फलन]] को परिभाषित करने के कई तरीके हैं, उदाहरण के लिए [[समकोण त्रिभुज परिभाषाएँ]], [[एकक  वृत्त परिभाषाएँ]], [[श्रेणी परिभाषाएँ]], [[अवकल समीकरणों के माध्यम से परिभाषाएँ]] और [[फलनिक समीकरणों]] [[का उपयोग करके परिभाषाएँ]]। '''त्रिकोणमितीय फलन के सामान्यीकरण''' को अक्सर उपरोक्त विधियों में से एक के साथ शुरू करके और इसे यूक्लिडियन ज्यामिति की वास्तविक संख्या के अलावा किसी अन्य स्थिति में रूपान्तरित करके विकसित किया जाता है। आम तौर पर, त्रिकोणमिति किसी भी प्रकार की [[ज्यामिति]] या [[समष्टि]] में बिंदुओं के त्रिगुणों का अध्ययन हो सकता है। त्रिभुज वह [[बहुभुज]] होता है जिसके शीर्षों की संख्या सबसे कम होती है, इसलिए सामान्यीकृत करने की एक दिशा कोणों और बहुभुजों के उच्च-विमीय अनुरूपों का अध्ययन करना है: [[घन कोण]] और [[बहुतलीय]] जैसे[[ चतुर्पाश्वीय | चतुष्फलक]] और [[एन-सिंप्लिस]]।


==त्रिकोणमिति==
==त्रिकोणमिति==
* गोलीय त्रिकोणमिति में गोले की सतह पर स्थित त्रिभुजों का अध्ययन किया जाता है। गोलीय त्रिभुज सर्वसमिकाएँ सामान्य त्रिकोणमितीय फलनों के रूप में लिखी जाती हैं, लेकिन समतल त्रिभुज सर्वसमिकाओं से भिन्न होती हैं।
* [[गोलाकार त्रिकोणमिति]] में [[गोले]] की सतह पर स्थित त्रिभुजों का अध्ययन किया जाता है। गोलीय [[त्रिभुज सर्वसमिकाएँ]] सामान्य त्रिकोणमितीय फलनों के रूप में लिखी जाती हैं, लेकिन समतल त्रिभुज सर्वसमिकाओं से भिन्न होते हैं।
* [[अतिशयोक्ति]]पूर्ण त्रिकोणमिति:
* अतिपरवलीय त्रिकोणमिति:
*# [[अतिशयोक्तिपूर्ण कार्य]]ों के साथ अतिपरवलयिक ज्यामिति में अतिशयोक्तिपूर्ण त्रिभुजों का अध्ययन।
*# [[अतिशयोक्तिपूर्ण कार्य|अतिपरवलयिक]] [[फलनों]] के साथ [[अतिपरवलयिक ज्यामिति]] में [[अतिपरवलीय त्रिभुजों]] का अध्ययन।
*# यूक्लिडियन ज्यामिति में अतिपरवलयिक कार्य: इकाई [[वृत्त]] को (cos t, sin t) द्वारा परिचालित किया जाता है जबकि समबाहु अतिपरवलय को (cosh t, sinh t) द्वारा परिचालित किया जाता है।
*# यूक्लिडियन ज्यामिति में [[अतिपरवलयिक फलन]]: [[एकक]] [[वृत्त]] को (cos t, sin t) द्वारा प्राचलिकृत किया जाता है जबकि समबाहु [[अतिपरवलय]] को (cosh t, sinh t) द्वारा प्राचलिकृत किया जाता है।
*#जायरोवेक्टर_स्पेस#ग्योरोट्रिगोनोमेट्री: [[विशेष सापेक्षता]] और क्वांटम संगणना के अनुप्रयोगों के साथ, हाइपरबोलिक ज्यामिति के लिए [[जायरोवेक्टर स्पेस]] दृष्टिकोण में प्रयुक्त त्रिकोणमिति का एक रूप।
*#[[जाइरोत्रिकोणमिति]]: [[विशेष सापेक्षता|विशिष्ट आपेक्षिकता]] और [[परिमाण अभिकलन]] के अनुप्रयोगों के साथ, [[अतिपरवलयिक ज्यामिति]] के लिए [[जायरोवेक्टर स्पेस|जायरोवेक्टर समष्टि]] दृष्टिकोण में प्रयुक्त त्रिकोणमिति का एक रूप।
*[[तर्कसंगत त्रिकोणमिति]] - कोण और लंबाई के बजाय प्रसार और चतुर्भुज के संदर्भ में त्रिकोणमिति का एक सुधार।{{dubious|reason=This is a fringe theory; if it is to be mentioned here, that should be made clear.|date=February 2020}}
*[[तर्कसंगत त्रिकोणमिति|परिमेय त्रिकोणमिति]] - कोण और लंबाई के बजाय चौड़ाई और चतुष्कोण के संबंध में त्रिकोणमिति का पुनर्निमाण।{{dubious|reason=This is a fringe theory; if it is to be mentioned here, that should be made clear.|date=February 2020}}
* टेक्सीकैब ज्यामिति के लिए त्रिकोणमिति<ref>{{citation|url=http://www.physics.orst.edu/~tevian/taxicab/taxicab.pdf|title=Taxicab angles and trigonometry|first1=K.|last1=Thompson|first2=T.|last2=Dray|journal=Pi Mu Epsilon Journal|year=2000|volume=11|issue=2|pages=87–96|arxiv=1101.2917|bibcode=2011arXiv1101.2917T}}</ref>
* [[टेक्सीकैब]] ज्यामिति के लिए त्रिकोणमिति<ref>{{citation|url=http://www.physics.orst.edu/~tevian/taxicab/taxicab.pdf|title=Taxicab angles and trigonometry|first1=K.|last1=Thompson|first2=T.|last2=Dray|journal=Pi Mu Epsilon Journal|year=2000|volume=11|issue=2|pages=87–96|arxiv=1101.2917|bibcode=2011arXiv1101.2917T}}</ref>
* स्पेसटाइम त्रिकोणमिति<ref>{{citation
* दिक्काल त्रिकोणमिति<ref>{{citation
  | last1 = Herranz | first1 = Francisco J.
  | last1 = Herranz | first1 = Francisco J.
  | last2 = Ortega | first2 = Ramón
  | last2 = Ortega | first2 = Ramón
Line 26: Line 26:
  | year = 2000| bibcode = 2000JPhA...33.4525H| s2cid = 15313035
  | year = 2000| bibcode = 2000JPhA...33.4525H| s2cid = 15313035
  }}</ref>
  }}</ref>
* फजी गुणात्मक त्रिकोणमिति<ref>{{citation|url=http://userweb.port.ac.uk/~liuh/Papers/LiuCoghill05c_SMC.pdf |contribution=Fuzzy Qualitative Trigonometry |first1=Honghai |last1=Liu |first2=George M. |last2=Coghill |title=2005 IEEE International Conference on Systems, Man and Cybernetics |year=2005 |volume=2 |pages=1291–1296 |url-status=dead |archiveurl=https://web.archive.org/web/20110725170037/http://userweb.port.ac.uk/~liuh/Papers/LiuCoghill05c_SMC.pdf |archivedate=2011-07-25 }}</ref>
* अस्पष्ट गुणात्मक त्रिकोणमिति<ref>{{citation|url=http://userweb.port.ac.uk/~liuh/Papers/LiuCoghill05c_SMC.pdf |contribution=Fuzzy Qualitative Trigonometry |first1=Honghai |last1=Liu |first2=George M. |last2=Coghill |title=2005 IEEE International Conference on Systems, Man and Cybernetics |year=2005 |volume=2 |pages=1291–1296 |url-status=dead |archiveurl=https://web.archive.org/web/20110725170037/http://userweb.port.ac.uk/~liuh/Papers/LiuCoghill05c_SMC.pdf |archivedate=2011-07-25 }}</ref>
*संचालक त्रिकोणमिति<ref>{{citation|url=http://www.ict.nsc.ru/jct/getfile.php?id=159|title=A computational trigonometry, and related contributions by Russians Kantorovich, Krein, Kaporin|first=K. E.|last=Gustafson|journal=Вычислительные технологии|volume=4|issue=3|pages=73–83|year=1999}}</ref>
*प्रचालक त्रिकोणमिति<ref>{{citation|url=http://www.ict.nsc.ru/jct/getfile.php?id=159|title=A computational trigonometry, and related contributions by Russians Kantorovich, Krein, Kaporin|first=K. E.|last=Gustafson|journal=Вычислительные технологии|volume=4|issue=3|pages=73–83|year=1999}}</ref>
* जाली त्रिकोणमिति<ref>{{citation
* जालक त्रिकोणमिति<ref>{{citation
  | last = Karpenkov | first = Oleg
  | last = Karpenkov | first = Oleg
  | arxiv = math/0604129
  | arxiv = math/0604129
Line 40: Line 40:
  | doi=10.7146/math.scand.a-15058| s2cid = 49911437
  | doi=10.7146/math.scand.a-15058| s2cid = 49911437
  }}</ref>
  }}</ref>
* सममित रिक्त स्थान पर त्रिकोणमिति<ref>{{citation
* सममितसमष्‍टि पर त्रिकोणमिति<ref>{{citation
  | last1 = Aslaksen | first1 = Helmer
  | last1 = Aslaksen | first1 = Helmer
  | last2 = Huynh | first2 = Hsueh-Ling
  | last2 = Huynh | first2 = Hsueh-Ling
Line 73: Line 73:
== उच्च आयाम ==
== उच्च आयाम ==


* श्लाफली ऑर्थोस्केम्स - राइट सिंप्लेक्स (n आयामों के लिए सामान्यीकृत सही त्रिकोण) - [[पीटर हेंड्रिक स्काउट]] द्वारा अध्ययन किया गया, जिन्होंने n यूक्लिडियन आयामों के सामान्यीकृत त्रिकोणमिति को '[[बहुभुजमिति]]' कहा।
* [[श्लाफली ऑर्थोस्केम्स]] - सम सिंप्लेक्स (n आयामों के लिए सामान्यीकृत सम त्रिकोण) -का अध्ययन [[शाउट]] द्वारा किया गया, जिन्होंने n यूक्लिडियन आयाम [[बहुभुजमिति]] के सामान्यीकृत त्रिकोणमिति को कहा।
** एन-सिम्प्लेक्स के लिए पाइथागोरस प्रमेय#ऑर्थोगोनल कॉर्नर के साथ सिम्प्लिसेस |ऑर्थोगोनल कॉर्नर के साथ एन-सिम्पलिस
** एक "[[लंबकोणीय कोना" के साथ n-सिंप्लिस]] के लिए पायथागॉरियन प्रमेय
* चतुष्फलक का त्रिकोणमिति<ref>{{Cite journal|title = टेट्राहेड्रॉन का त्रिकोणमिति|jstor = 3603090|journal = The Mathematical Gazette|date = 1902-03-01|pages = 149–158|volume = 2|issue = 32|doi = 10.2307/3603090|first = G.|last = Richardson|url = https://zenodo.org/record/1449743}}</ref>
* [[चतुष्फलक का त्रिकोणमिति]]<ref>{{Cite journal|title = टेट्राहेड्रॉन का त्रिकोणमिति|jstor = 3603090|journal = The Mathematical Gazette|date = 1902-03-01|pages = 149–158|volume = 2|issue = 32|doi = 10.2307/3603090|first = G.|last = Richardson|url = https://zenodo.org/record/1449743}}</ref>
** डी गुआ की प्रमेय - एक क्यूब कोने के साथ टेट्राहेड्रॉन के लिए पायथागॉरियन प्रमेय
** [[डी गुआ की प्रमेय]] - एक घन कोण के साथ चतुष्फलक के लिए पायथागॉरियन प्रमेय
** चतुष्फलक # चतुष्फलक के लिए ज्या का नियम और चतुष्फलक के सभी आकारों का स्थान
** [[चतुष्फलक के लिए ज्या का नियम]]
* ध्रुवीय साइन
* [[ध्रुवीय ज्या]]


== त्रिकोणमितीय कार्य ==
== त्रिकोणमितीय फलन ==


*त्रिकोणमितीय कार्यों को [[आंशिक अंतर समीकरण]]ों के लिए परिभाषित किया जा सकता है।<ref>{{citation
*त्रिकोणमितीय फलनो को [[आंशिक अंतर समीकरण|भिन्नात्मक अवकल]] [[समीकरणों]] के लिए परिभाषित किया जा सकता है।<ref>{{citation
  | last1 = West | first1 = Bruce J.
  | last1 = West | first1 = Bruce J.
  | last2 = Bologna | first2 = Mauro
  | last2 = Bologna | first2 = Mauro
Line 94: Line 94:
  | title = Physics of fractal operators
  | title = Physics of fractal operators
  | year = 2003 | doi=10.1007/978-0-387-21746-8}}</ref>
  | year = 2003 | doi=10.1007/978-0-387-21746-8}}</ref>
*[[समय पैमाने की गणना]] में, डिफरेंशियल इक्वेशन और डिफरेंशियल इक्वेशन को टाइम स्केल पर डायनेमिक इक्वेशन में एकीकृत किया जाता है जिसमें q-[[ [[अंतर समीकरण]] ]] भी शामिल होता है। त्रिकोणमितीय कार्यों को मनमाने ढंग से समय के पैमाने (वास्तविक संख्याओं का एक सबसेट) पर परिभाषित किया जा सकता है।
*[[समय पैमाने की गणना|समय मापक्रम के कलन]] में, अवकल समीकरणों और [[अवकल समीकरण]] को समय मापक्रम पर गतिक समीकरण में एकीकृत किया जाता है जिसमें q-[[अंतर समीकरण]] भी सम्मिलित होती है। त्रिकोणमितीय फलनों को स्वेच्छ [[समय पैमाने की गणना|समय मापक्रम]] (वास्तविक संख्याओं का एक उपसमुच्चय) पर परिभाषित किया जा सकता है।
*त्रिकोणमितीय फलन#sin और cos की शृंखला परिभाषाएँ इन फलनों को किसी भी बीजगणित पर एक ऐसे क्षेत्र पर परिभाषित करती हैं जहाँ [[श्रृंखला (गणित)]] अभिसरण श्रंखला जैसे त्रिकोणमितीय फलन #घातांकीय फलन से संबंध (यूलर का सूत्र), p-adic विश्लेषण|p-adic संख्याएँ, आव्यूहों के त्रिकोणमितीय फलन, और विभिन्न बानाच बीजगणित।
*sin और cos की [[श्रेणी परिभाषाएँ]] इन फलनों को किसी भी [[बीजगणित]] पर एक ऐसे क्षेत्र पर परिभाषित करती हैं जहाँ [[श्रृंखला (गणित)|श्रेणी]] अभिसरित होती है जैसे [[सम्मिश्र संख्याएं]], [[पी-एडिक संख्याएं]], मैट्रिक्स और विभिन्न [[बानाच बीजगणित]]।


== अन्य ==
== अन्य ==
*[[हाइपरकॉम्प्लेक्स संख्या]]ओं के ध्रुवीय/त्रिकोणमितीय रूप<ref>{{citation
*[[हाइपरकॉम्प्लेक्स संख्या|अतिमिश्र संख्या]][[ओं]] के ध्रुवीय/त्रिकोणमितीय रूप<ref>{{citation
  | last1 = Harkin | first1 = Anthony A.
  | last1 = Harkin | first1 = Anthony A.
  | last2 = Harkin | first2 = Joseph B.
  | last2 = Harkin | first2 = Joseph B.
Line 127: Line 127:
  |archivedate=2011-07-22  
  |archivedate=2011-07-22  
}}</ref>
}}</ref>
*बहुभुजमिति - कई अलग-अलग कोणों के लिए त्रिकोणमितीय पहचान<ref>{{citation
*[[बहुभुजमिति]] - कई अलग-अलग कोणों के लिए त्रिकोणमितीय सर्वसमिका<ref>{{citation
  | last = Antippa | first = Adel F.
  | last = Antippa | first = Adel F.
  | doi = 10.1155/S0161171203106230
  | doi = 10.1155/S0161171203106230
Line 139: Line 139:
  | year = 2003| doi-access = free
  | year = 2003| doi-access = free
  }}</ref>
  }}</ref>
* [[लेम्निस्केट अण्डाकार कार्य]], सिनलेम और कोस्लेम
* [[लेम्निस्केट अण्डाकार कार्य|द्विपाशी दीर्घवृत्तीय फलन]], सिनलेम और कोस्लेम


== यह भी देखें ==
== यह भी देखें ==
*पाइथागोरस प्रमेय#गैर-यूक्लिडियन ज्यामिति|गैर-यूक्लिडियन ज्यामिति में पाइथागोरस प्रमेय
*[[गैर-यूक्लिडियन ज्यामिति में पाइथागोरस प्रमेय]]


==संदर्भ==
==संदर्भ==
{{reflist}}
{{reflist}}


{{DEFAULTSORT:Generalized Trigonometry}}[[Category: त्रिकोणमिति]]
{{DEFAULTSORT:Generalized Trigonometry}}


 
[[Category:All accuracy disputes|Generalized Trigonometry]]
 
[[Category:Articles with disputed statements from February 2020|Generalized Trigonometry]]
[[Category: Machine Translated Page]]
[[Category:Articles with invalid date parameter in template|Generalized Trigonometry]]
[[Category:Created On 10/04/2023]]
[[Category:CS1]]
[[Category:CS1 errors]]
[[Category:Created On 10/04/2023|Generalized Trigonometry]]
[[Category:Lua-based templates|Generalized Trigonometry]]
[[Category:Machine Translated Page|Generalized Trigonometry]]
[[Category:Mathematics sidebar templates|Generalized Trigonometry]]
[[Category:Pages with script errors|Generalized Trigonometry]]
[[Category:Sidebars with styles needing conversion|Generalized Trigonometry]]
[[Category:Templates Vigyan Ready|Generalized Trigonometry]]
[[Category:Templates that add a tracking category|Generalized Trigonometry]]
[[Category:Templates that generate short descriptions|Generalized Trigonometry]]
[[Category:Templates using TemplateData|Generalized Trigonometry]]
[[Category:त्रिकोणमिति|Generalized Trigonometry]]

Latest revision as of 16:48, 26 April 2023

त्रिकोणमिति
Sinus und Kosinus am Einheitskreis 1.svg
संदर्भ
कानून और सिद्धांत
पथरी

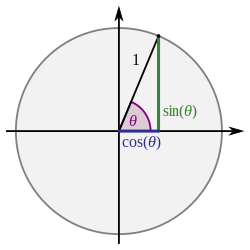
सामान्य त्रिकोणमिति यूक्लिडियन तल में त्रिभुजों का अध्ययन करती है। वास्तविक संख्याओं पर सामान्य यूक्लिडियन ज्यामितीय त्रिकोणमितीय फलन को परिभाषित करने के कई तरीके हैं, उदाहरण के लिए समकोण त्रिभुज परिभाषाएँ, एकक वृत्त परिभाषाएँ, श्रेणी परिभाषाएँ, अवकल समीकरणों के माध्यम से परिभाषाएँ और फलनिक समीकरणों का उपयोग करके परिभाषाएँ। त्रिकोणमितीय फलन के सामान्यीकरण को अक्सर उपरोक्त विधियों में से एक के साथ शुरू करके और इसे यूक्लिडियन ज्यामिति की वास्तविक संख्या के अलावा किसी अन्य स्थिति में रूपान्तरित करके विकसित किया जाता है। आम तौर पर, त्रिकोणमिति किसी भी प्रकार की ज्यामिति या समष्टि में बिंदुओं के त्रिगुणों का अध्ययन हो सकता है। त्रिभुज वह बहुभुज होता है जिसके शीर्षों की संख्या सबसे कम होती है, इसलिए सामान्यीकृत करने की एक दिशा कोणों और बहुभुजों के उच्च-विमीय अनुरूपों का अध्ययन करना है: घन कोण और बहुतलीय जैसे चतुष्फलक और एन-सिंप्लिस।

त्रिकोणमिति


उच्च आयाम

त्रिकोणमितीय फलन

अन्य

यह भी देखें

संदर्भ

  1. ↑ Thompson, K.; Dray, T. (2000), "Taxicab angles and trigonometry" (PDF), Pi Mu Epsilon Journal, 11 (2): 87–96, arXiv:1101.2917, Bibcode:2011arXiv1101.2917T
  2. ↑ Herranz, Francisco J.; Ortega, Ramón; Santander, Mariano (2000), "Trigonometry of spacetimes: a new self-dual approach to a curvature/signature (in)dependent trigonometry", Journal of Physics A, 33 (24): 4525–4551, arXiv:math-ph/9910041, Bibcode:2000JPhA...33.4525H, doi:10.1088/0305-4470/33/24/309, MR 1768742, S2CID 15313035
  3. ↑ Liu, Honghai; Coghill, George M. (2005), "Fuzzy Qualitative Trigonometry", 2005 IEEE International Conference on Systems, Man and Cybernetics (PDF), vol. 2, pp. 1291–1296, archived from the original (PDF) on 2011-07-25
  4. ↑ Gustafson, K. E. (1999), "A computational trigonometry, and related contributions by Russians Kantorovich, Krein, Kaporin", Вычислительные технологии, 4 (3): 73–83
  5. ↑ Karpenkov, Oleg (2008), "Elementary notions of lattice trigonometry", Mathematica Scandinavica, 102 (2): 161–205, arXiv:math/0604129, doi:10.7146/math.scand.a-15058, MR 2437186, S2CID 49911437
  6. ↑ Aslaksen, Helmer; Huynh, Hsueh-Ling (1997), "Laws of trigonometry in symmetric spaces", Geometry from the Pacific Rim (Singapore, 1994), Berlin: de Gruyter, pp. 23–36, CiteSeerX 10.1.1.160.1580, MR 1468236
  7. ↑ Leuzinger, Enrico (1992), "On the trigonometry of symmetric spaces", Commentarii Mathematici Helvetici, 67 (2): 252–286, doi:10.1007/BF02566499, MR 1161284, S2CID 123684622
  8. ↑ Masala, G. (1999), "Regular triangles and isoclinic triangles in the Grassmann manifolds G2(RN)", Rendiconti del Seminario Matematico Università e Politecnico di Torino., 57 (2): 91–104, MR 1974445
  9. ↑ Richardson, G. (1902-03-01). "टेट्राहेड्रॉन का त्रिकोणमिति". The Mathematical Gazette. 2 (32): 149–158. doi:10.2307/3603090. JSTOR 3603090.
  10. ↑ West, Bruce J.; Bologna, Mauro; Grigolini, Paolo (2003), Physics of fractal operators, Institute for Nonlinear Science, New York: Springer-Verlag, p. 101, doi:10.1007/978-0-387-21746-8, ISBN 0-387-95554-2, MR 1988873
  11. ↑ Harkin, Anthony A.; Harkin, Joseph B. (2004), "Geometry of generalized complex numbers", Mathematics Magazine, 77 (2): 118–129, doi:10.1080/0025570X.2004.11953236, JSTOR 3219099, MR 1573734, S2CID 7837108
  12. ↑ Yamaleev, Robert M. (2005), "Complex algebras on n[[Category: Templates Vigyan Ready]]-order polynomials and generalizations of trigonometry, oscillator model and Hamilton dynamics" (PDF), Advances in Applied Clifford Algebras, 15 (1): 123–150, doi:10.1007/s00006-005-0007-y, MR 2236628, S2CID 121144869, archived from the original (PDF) on 2011-07-22 {{citation}}: URL–wikilink conflict (help)
  13. ↑ Antippa, Adel F. (2003), "The combinatorial structure of trigonometry" (PDF), International Journal of Mathematics and Mathematical Sciences, 2003 (8): 475–500, doi:10.1155/S0161171203106230, MR 1967890
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=सामान्यीकृत_त्रिकोणमिति&oldid=143442’