स्क्वेर वेव

स्क्वेर वेव
साइन, स्क्वायर, ट्राएंगल, और सॉटूथ वेवफॉर्म
General information
सामान्य परिभाषा	$x(t)=4\left\lfloor t\right\rfloor -2\left\lfloor 2t\right\rfloor +1,2t\notin \mathbb {Z}$
आवेदन के क्षेत्र	इलेक्ट्रॉनिक्स, सिंथेसाइज़र
Domain, Codomain and Image
डोमेन	$\mathbb {R} \setminus \left\{{\tfrac {n}{2}}\right\},n\in \mathbb {Z}$
कोडोमेन	$\left\{-1,1\right\}$
Basic features
समता	Odd
अवधि	1
एंटीडेरिवेटिव	त्रिकोण तरंग
फोरियर श्रेणी	$x(t)={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\frac {1}{2k-1}}\sin \left(2\pi \left(2k-1\right)t\right)$

एक स्क्वायर वेव एक गैर-साइनसॉइडल आवधिक तरंग है जिसमें न्यूनतम और अधिकतम समान अवधि के साथ निश्चित न्यूनतम और अधिकतम मानों के बीच एक स्थिर आवृत्ति पर आयाम वैकल्पिक होता है। एक आदर्श स्क्वायर वेव में, न्यूनतम और अधिकतम के बीच संक्रमण तात्कालिक होते हैं।

स्क्वायर वेव पल्स वेव का एक विशेष मामला है जो न्यूनतम और अधिकतम आयामों पर मनमाने ढंग से अवधि की अनुमति देता है। पल्स वेव की कुल अवधि के उच्च अवधि के अनुपात को कर्तव्य चक्र कहा जाता है। एक सच्चे स्क्वायर वेव में 50% कर्तव्य चक्र (समान उच्च और निम्न अवधि) होता है।

इलेक्ट्रॉनिक और सिग्नल प्रोसेसिंग, विशेष रूप से डिजिटल इलेक्ट्रॉनिक्स और डिजिटल सिग्नल प्रोसेसिंग में स्क्वायर तरंगों का प्रायः सामना किया जाता है। इसका स्टोकेस्टिक समकक्ष दो-राज्य प्रक्षेपवक्र है।

उत्पत्ति और उपयोग

स्क्वायर वेव्स को डिजिटल स्विचिंग सर्किट में सार्वभौमिक रूप से सामना किया जाता है और स्वाभाविक रूप से बाइनरी (दो-स्तरीय) तर्क उपकरणों द्वारा उत्पन्न होता है। द्विध्रुवीय जंक्शन ट्रांजिस्टर (BJTs) के विपरीत, स्क्वायर वेव्स प्रायः मेटल-ऑक्साइड-सेमीकंडक्टर फील्ड-इफेक्ट ट्रांजिस्टर (MOSFET) उपकरणों द्वारा उत्पन्न होती हैं, जो इलेक्ट्रॉनिक स्विचिंग व्यवहार के तेजी से चालू-बंद व्यवहार के कारण होती हैं, जो धीरे-धीरे स्क्वायर वेव्स के बजाय साइन वेव्स के समान अधिक बारीकी से संकेत उत्पन्न करते हैं।

स्क्वायर वेव्स का उपयोग समय संदर्भ या "क्लॉक सिग्नल" के रूप में किया जाता है, क्योंकि उनके तेज़ संक्रमण सटीक निर्धारित अंतराल पर सिंक्रोनस लॉजिक सर्किट को ट्रिगर करने के लिए उपयुक्त होते हैं। हालाँकि, जैसा कि फ़्रीक्वेंसी-डोमेन ग्राफ़ दिखाता है, स्क्वायर वेव्स में हार्मोनिक्स की एक विस्तृत श्रृंखला होती है; ये विद्युत चुम्बकीय विकिरण या धारा के स्पंदन उत्पन्न कर सकते हैं जो आसपास के अन्य सर्किटों में हस्तक्षेप करते हैं, जिससे शोर या त्रुटियां होती हैं। सटीक एनालॉग-टू-डिजिटल कन्वर्टर्स जैसे बहुत संवेदनशील सर्किट में इस समस्या से बचने के लिए, साइन वेव्स का उपयोग स्क्वायर वेव्स के बजाय समय संदर्भ के रूप में किया जाता है।

संगीत के संदर्भ में, उन्हें प्रायः खोखली ध्वनि के रूप में वर्णित किया जाता है, और इसलिए उन्हें घटाव संश्लेषण का उपयोग करके बनाए गए वायु वाद्य यंत्रों के आधार के रूप में उपयोग किया जाता है। इसके अतिरिक्त, इलेक्ट्रिक गिटार पर उपयोग किया जाने वाला विरूपण प्रभाव वेवफ़ॉर्म के सबसे बाहरी क्षेत्रों को क्लिप करता है, जिससे अधिक विरूपण लागू होने पर यह स्क्वायर वेव जैसा दिखता है।

साधारण दो-स्तरीय राडेमचेर फंक्शन्स स्क्वायर वेव्स हैं।

परिभाषाएँ

गणित में स्क्वायर वेव की कई परिभाषाएँ हैं, जो विच्छिन्नताओं को छोड़कर समतुल्य हैं:

इसे केवल सिनुसाइड के साइन फंक्शन के रूप में परिभाषित किया जा सकता है:

$${\begin{aligned}x(t)&=\operatorname {sgn} \left(\sin {\frac {2\pi t}{T}}\right)=\operatorname {sgn}(\sin 2\pi ft)\\v(t)&=\operatorname {sgn} \left(\cos {\frac {2\pi t}{T}}\right)=\operatorname {sgn}(\cos 2\pi ft),\end{aligned}}$$

जो 1 होगा जब सिनुसाइड धनात्मक होगा, -1 जब सिनुसाइड ऋणात्मक होगा, और 0 विच्छेदन पर होगा। यहाँ, T स्क्वायर वेव की अवधि (भौतिकी) है और f इसकी आवृत्ति है, जो समीकरण f = 1/T से संबंधित हैं।

एक स्क्वायर वेव को हैवीसाइड स्टेप फंक्शन u(t) या आयताकार फंक्शन Π(t) के संबंध में भी परिभाषित किया जा सकता है:

$${\begin{aligned}x(t)&=2\left[\sum _{n=-\infty }^{\infty }\Pi \left({\frac {2(t-nT)}{T}}-{\frac {1}{2}}\right)\right]-1\\&=2\sum _{n=-\infty }^{\infty }\left[u\left({\frac {t}{T}}-n\right)-u\left({\frac {t}{T}}-n-{\frac {1}{2}}\right)\right]-1.\end{aligned}}$$

सीधे फ्लोर फंक्शन का उपयोग करके एक स्क्वायर वेव भी उत्पन्न की जा सकती है:

$$x(t)=2\left(2\lfloor ft\rfloor -\lfloor 2ft\rfloor \right)+1$$

और परोक्ष रूप से:

$$x(t)=\left(-1\right)^{\lfloor 2ft\rfloor }.$$

फूरियर श्रृंखला (नीचे) का उपयोग करके कोई दिखा सकता है कि फ्लोर फंक्शन को त्रिकोणमितीय रूप में लिखा जा सकता है

$${\frac {2}{\pi }}\arctan \left(\tan \left({\frac {\pi ft}{2}}\right)\right)+{\frac {2}{\pi }}\arctan \left(\cot \left({\frac {\pi ft}{2}}\right)\right)$$

फूरियर विश्लेषण

छह तीर स्क्वायर वेव की फूरियर श्रृंखला के पहले छह शब्दों का प्रतिनिधित्व करते हैं। नीचे के दो वृत्त सटीक स्क्वायर वेव (नीला) और इसके फूरियर-श्रृंखला सन्निकटन (बैंगनी) का प्रतिनिधित्व करते हैं।

(विषम) एक 1000 हर्ट्ज स्क्वायर वेव के हार्मोनिक्स

स्क्वायर वेव की फूरियर श्रृंखला के पहले 3 पदों को दर्शाने वाला ग्राफ

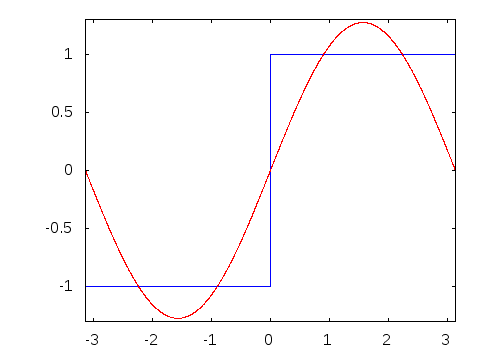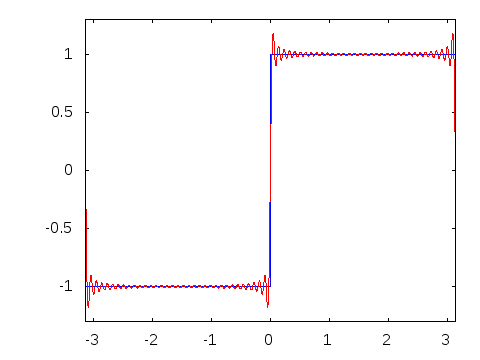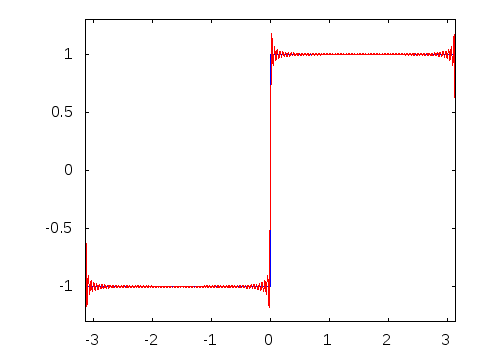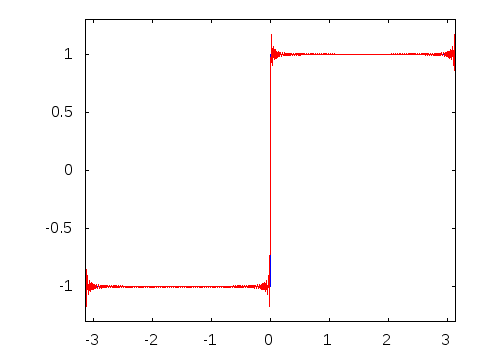
समय t के साथ चक्र आवृत्ति f के साथ फूरियर एक्सपेंशन का उपयोग करते हुए, 1 के आयाम के साथ एक आदर्श स्क्वायर वेव को सिनुसाइड तरंगों के अनंत योग के रूप में दर्शाया जा सकता है:

$${\begin{aligned}x(t)&={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin \left(2\pi (2k-1)ft\right)}{2k-1}}\\&={\frac {4}{\pi }}\left(\sin(\omega t)+{\frac {1}{3}}\sin(3\omega t)+{\frac {1}{5}}\sin(5\omega t)+\ldots \right),&{\text{where }}\omega =2\pi f.\end{aligned}}$$

आदर्श स्क्वायर वेव में केवल विषम-पूर्णांक हार्मोनिक आवृत्तियों के घटक होते हैं (रूप का 2π(2k − 1)f). आरादन्त तरंगों और वास्तविक दुनिया के संकेतों में सभी पूर्णांक हार्मोनिक्स होते हैं।

गिब्स घटना स्क्वायर वेव के फूरियर श्रृंखला प्रतिनिधित्व के अभिसरण की एक जिज्ञासा है। गैर-आदर्श स्क्वायर वेव्स में बजने वाली कलाकृतियों को इस घटना से संबंधित दिखाया जा सकता है। गिब्स की घटना को σ-सन्निकटन का उपयोग करके रोका जा सकता है, जो अनुक्रम को अधिक सुचारू रूप से परिवर्तित करने में मदद करने के लिए लैंक्ज़ोस सिग्मा कारकों का उपयोग करता है।

एक आदर्श गणितीय वर्ग तरंग उच्च और निम्न अवस्था के बीच तुरंत और बिना अंडर-या ओवर-शूटिंग के बदल जाती है। यह भौतिक प्रणालियों में प्राप्त करना असंभव है, क्योंकि इसके लिए अनंत बैंडविड्थ की आवश्यकता होगी।

हार्मोनिक्स की बढ़ती संख्या के साथ स्क्वायर वेव के योजक संश्लेषण का एनीमेशन

भौतिक प्रणालियों में स्क्वायर वेव्स में केवल परिमित बैंडविड्थ होती है और प्रायः गिब्स घटना या तरंग प्रभाव के समान रिंगिंग प्रभाव प्रदर्शित करते हैं जो σ-सन्निकटन के समान होते हैं।

स्क्वायर-वेव आकार के उचित अनुमान के लिए, कम से कम मौलिक और तीसरे हार्मोनिक को उपस्थित होने की आवश्यकता है, पांचवें हार्मोनिक वांछनीय होने के साथ। ये बैंडविड्थ आवश्यकताएं डिजिटल इलेक्ट्रॉनिक्स में महत्वपूर्ण हैं, जहां स्क्वायर-वेव-जैसे वेवफॉर्म के लिए परिमित-बैंडविड्थ एनालॉग सन्निकटन का उपयोग किया जाता है। (रिंगिंग ट्रांजिस्टर यहां एक महत्वपूर्ण इलेक्ट्रॉनिक विचार हैं, क्योंकि वे एक सर्किट की विद्युत रेटिंग सीमा से परे जा सकते हैं या कई बार खराब स्थिति वाली सीमा को पार कर सकते हैं।)

अपूर्ण स्क्वायर वेव्स के लक्षण

जैसा कि पहले ही उल्लेख किया गया है, एक आदर्श स्क्वायर वेव में उच्च और निम्न स्तरों के बीच तात्कालिक संक्रमण होता है। व्यवहार में, तरंग उत्पन्न करने वाली प्रणाली की भौतिक सीमाओं के कारण इसे कभी प्राप्त नहीं किया जाता है। सिग्नल के निम्न स्तर से उच्च स्तर तक उठने और फिर से वापस आने में लगने वाले समय को क्रमशः उठने का समय और गिरने का समय कहा जाता है।

यदि प्रणाली अत्यधिक नम है, तो तरंग वास्तव में कभी भी सैद्धांतिक उच्च और निम्न स्तर तक नहीं पहुंच सकती है, और यदि प्रणाली कम नम है, तो यह स्थिर होने से पहले उच्च और निम्न स्तरों के बारे में दोलन करेगी। इन मामलों में, वृद्धि और गिरावट के समय को निर्दिष्ट मध्यवर्ती स्तरों के बीच मापा जाता है, जैसे कि 5% और 95%, या 10% और 90% किसी सिस्टम की बैंडविड्थ (सिग्नल प्रोसेसिंग) तरंग के संक्रमण समय से संबंधित है; ऐसे सूत्र हैं जो एक को दूसरे से लगभग निर्धारित करने की अनुमति देते हैं।

यह भी देखें

• आवधिक कार्यों की सूची
• आयताकार फंक्शन
• पल्स वेव
• साइन वेव
• त्रिभुज तरंग
• आरादन्त तरंग
• तरंग
• ध्वनि
• बहुकंपित्र (multivibrator)
• रोंची शासन , इमेजिंग में उपयोग किया जाने वाला स्क्वायर-वेव स्ट्राइप टारगेट।
• रोंची रूलिंग (Ronchi ruling), एक स्क्वायर-वेव स्ट्राइप टारगेट का उपयोग इमेजिंग में किया जाता है।
• क्रॉस सी
• शहनाई, एक संगीत वाद्ययंत्र जो वर्ग तरंग का अनुमान लगाते हुए विचित्र ओवरटोन पैदा करता है।

बाहरी संबंध

• Fourier decomposition of a square wave Interactive demo of square wave synthesis using sine waves, from GeoGebra site.
• Square Wave Approximated by Sines Interactive demo of square wave synthesis using sine waves.
• Flash applets Square wave.