प्राथमिक प्रवाह: Difference between revisions
No edit summary |
No edit summary |
||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
[[नेवियर-स्टोक्स समीकरण|नेवियर-स्टोक्स समीकरणों]] के बड़े संदर्भ में परन्तु विशेष रूप से [[संभावित सिद्धांत]] के संदर्भ में प्राथमिक प्रवाह मूलभूत प्रवाह का एक संग्रह है जिससे विभिन्न तकनीकों के साथ अधिक जटिल प्रवाह का निर्माण संभव है। इस लेख में ऐतिहासिक कारणों से | [[नेवियर-स्टोक्स समीकरण|नेवियर-स्टोक्स समीकरणों]] के बड़े संदर्भ में परन्तु विशेष रूप से [[संभावित सिद्धांत|विभव सिद्धांत]] के संदर्भ में प्राथमिक प्रवाह मूलभूत प्रवाह का एक संग्रह है जिससे विभिन्न तकनीकों के साथ अधिक जटिल प्रवाह का निर्माण संभव है। इस लेख में ऐतिहासिक कारणों से पदीय प्रवाह का उपयोग पदीय हल के लिए एक दूसरे के स्थान पर किया जाता है। | ||
अधिक जटिल हल बनाने के लिए सम्मिलित तकनीकें हो सकती हैं उदाहरण के लिए [[सुपरपोज़िशन सिद्धांत|अधिस्थापन सिद्धांत]] द्वारा, | अधिक जटिल हल बनाने के लिए सम्मिलित तकनीकें हो सकती हैं उदाहरण के लिए [[सुपरपोज़िशन सिद्धांत|अधिस्थापन सिद्धांत]] द्वारा, सांस्थिति जैसी तकनीकों द्वारा या उन्हें एक निश्चित निकटवर्ती, उपप्रांत या [[सीमा परत]] पर स्थानीय हल के रूप में माना जाता है और एक साथ समझौता किया जाता है। प्राथमिक प्रवाह को नेवियर-स्टोक्स से प्राप्त विभिन्न प्रकार के समीकरणों के मूलभूत निर्माण खंड ([[मौलिक समाधान|मौलिक हल]], स्थानीय हल और [[solitons|सॉलिटन]]) माना जा सकता है। कुछ प्रवाह विशिष्ट स्थितियों के व्यवरोध को दर्शाते हैं जैसे कि असंगत प्रवाह या अघूर्णी प्रवाह, या दोनों, जैसा कि [[संभावित प्रवाह|विभव प्रवाह]] की स्थिति में होता है, और कुछ प्रवाह प्रायः 2 आयामों की स्थिति में सीमित होते हैं।<ref>{{Cite book|last=Oliver|first=David|url=https://books.google.com/books?id=0szeBwAAQBAJ&q=Elementary+flow&pg=PA55|title=The Shaggy Steed of Physics: Mathematical Beauty in the Physical World|date=2013-03-14|publisher=Springer Science & Business Media|isbn=978-1-4757-4347-0|language=en}}</ref> | ||
द्रव गतिकी से सभी [[क्षेत्र सिद्धांत (भौतिकी)]] के संबंध के कारण यह समझना महत्वपूर्ण है कि कैसे ये सभी प्रवाह न | द्रव गतिकी से सभी [[क्षेत्र सिद्धांत (भौतिकी)|क्षेत्र सिद्धांत (भौतिकी]]) के संबंध के कारण यह समझना महत्वपूर्ण है कि कैसे ये सभी प्रवाह न मात्र [[वायुगतिकी]] बल्कि सामान्य रूप से सभी क्षेत्र सिद्धांत (भौतिकी) के लिए प्रासंगिक हैं। इसे परिप्रेक्ष्य में रखने के लिए सीमा परतों को प्रजातिगत [[ कई गुना |कई गुना]] पर [[टोपोलॉजिकल दोष|सांस्थितिक दोषों]] के रूप में व्याख्या किया जा सकता है, और द्रव गतिकी उपमाओं और [[विद्युत]] चुंबकत्व, [[क्वांटम यांत्रिकी]] और [[सामान्य सापेक्षता]] में सीमित स्थितियों पर विचार कर सकते हैं कि ये सभी हल सैद्धांतिक भौतिकी में वर्तमान विकास के मूल में कैसे हैं। जैसे कि विज्ञापन/सीएफटी द्वैत, एसवाईके मॉडल, निमैटिक तरल पदार्थों की भौतिकी, दृढ़ता से सहसंबद्ध प्रणालियाँ और यहाँ तक कि क्वार्क ग्लूऑन प्लाज़्मा। | ||
== द्वि-आयामी समान प्रवाह == | == द्वि-आयामी समान प्रवाह == | ||
[[File:Flow-uniform-2D.svg|thumb|300px|right|alt=Uniform|एक आदर्श समान प्रवाह के लिए | [[File:Flow-uniform-2D.svg|thumb|300px|right|alt=Uniform|एक आदर्श समान प्रवाह के लिए विभव प्रवाह धारारेखा]]समष्टि में किसी भी स्थिति में द्रव के एकसमान वेग दिया गया है: | ||
:<math>\mathbf{V_0} = v_0 \cos(\theta_0) \mathbf{e}_x +v_0 \sin(\theta_0) \mathbf{e}_y </math> | :<math>\mathbf{V_0} = v_0 \cos(\theta_0) \mathbf{e}_x +v_0 \sin(\theta_0) \mathbf{e}_y </math> | ||
यह प्रवाह असम्पीडित है क्योंकि वेग स्थिर है, वेग घटकों का पहला | यह प्रवाह असम्पीडित है क्योंकि वेग स्थिर है, वेग घटकों का पहला व्युत्पन्न शून्य है, और कुल विचलन शून्य है: <math>\nabla \cdot \mathbf{v} = 0</math> | ||
परिचारण (द्रव गतिकी) को देखते हुए सदैव शून्य होता है, प्रवाह भी अघूर्णी होता है, हम इसे केल्विन के परिचारण प्रमेय और [[vorticity|भ्रमिलता]] की स्पष्ट गणना से प्राप्त कर सकते हैं: | |||
:<math>\omega_z = \frac {\partial v_x} {\partial y} - \frac {\partial v_y} {\partial x} = 0</math> | :<math>\omega_z = \frac {\partial v_x} {\partial y} - \frac {\partial v_y} {\partial x} = 0</math> | ||
असम्पीडित और द्वि-आयामी होने के कारण, यह प्रवाह एक [[धारा समारोह]] से निर्मित होता है: | असम्पीडित और द्वि-आयामी होने के कारण, यह प्रवाह एक [[धारा समारोह|धारा फलन]] से निर्मित होता है: | ||
:<math>v_x = \frac {\partial \psi} {\partial y}</math> | :<math>v_x = \frac {\partial \psi} {\partial y}</math> | ||
:<math>v_y = - \frac {\partial \psi} {\partial x}</math> | :<math>v_y = - \frac {\partial \psi} {\partial x}</math> | ||
जिसमें से | |||
:<math>\psi = - v_0 \sin (\theta_0) x + v_0 \cos (\theta_0) y</math> | :<math>\psi = - v_0 \sin (\theta_0) x + v_0 \cos (\theta_0) y</math> | ||
और बेलनाकार निर्देशांक में: | और बेलनाकार निर्देशांक में: | ||
:<math>v_r = - \frac 1 r \frac{\partial \psi} {\partial \theta}</math> | :<math>v_r = - \frac 1 r \frac{\partial \psi} {\partial \theta}</math> | ||
:<math>v_\theta = \frac{\partial \psi} {\partial r}</math> | :<math>v_\theta = \frac{\partial \psi} {\partial r}</math> | ||
जिससे | |||
:<math>\psi = - v_0 r \sin (\theta - \theta_0)</math> | :<math>\psi = - v_0 r \sin (\theta - \theta_0)</math> | ||
सदैव के जैसे धारा फलन को स्थिर मान तक परिभाषित किया जाता है जिसे हम यहाँ शून्य के रूप में लेते हैं। हम यह भी पुष्टि कर सकते हैं कि प्रवाह अघूर्णी है: | |||
:<math>\nabla^2 \psi = 0</math> | :<math>\nabla^2 \psi = 0</math> | ||
अपरिमेय होने के कारण, इसके | अपरिमेय होने के कारण, विभव फलन इसके अतिरिक्त है: | ||
:<math>v_x = - \frac{\partial \phi} {\partial x}</math> | :<math>v_x = - \frac{\partial \phi} {\partial x}</math> | ||
:<math>v_y = - \frac {\partial \phi} {\partial y}</math> | :<math>v_y = - \frac {\partial \phi} {\partial y}</math> | ||
और इसलिए | और इसलिए | ||
:<math>\phi = - v_0 \cos (\theta_0) x - v_0 \sin (\theta_0) y</math> | :<math>\phi = - v_0 \cos (\theta_0) x - v_0 \sin (\theta_0) y</math> | ||
और [[बेलनाकार निर्देशांक]] | और [[बेलनाकार निर्देशांक]] | ||
:<math>v_r = \frac {\partial \phi} {\partial r}</math> | :<math>v_r = \frac {\partial \phi} {\partial r}</math> | ||
:<math>v_\theta = \frac {1}{r} \frac {\partial \phi} {\partial \theta}</math> | :<math>v_\theta = \frac {1}{r} \frac {\partial \phi} {\partial \theta}</math> | ||
:<math>\phi = - v_0 r \cos(\theta - \theta_0) </math> | :<math>\phi = - v_0 r \cos(\theta - \theta_0) </math> | ||
में | |||
== द्वि-आयामी रेखा स्रोत == | == द्वि-आयामी रेखा स्रोत == | ||
[[File:Flow-source-2D.svg|thumb|300px|right|alt=Point-source| | [[File:Flow-source-2D.svg|thumb|300px|right|alt=Point-source|एक आदर्श रेखा स्रोत के लिए धारारेखा]]निश्चित दर पर उत्सर्जक लंबवत रेखा की स्थिति द्रव Q प्रति इकाई लंबाई की निरंतर मात्रा रेखा स्रोत है। समस्या में बेलनाकार समरूपता है और लंबकोणीय तल पर दो आयामों में इसका अभिक्रियित किया जा सकता है। | ||
रेखा स्रोत और रेखा निमज्जन (नीचे) महत्वपूर्ण प्रारंभिक प्रवाह हैं क्योंकि वे असम्पीडित तरल पदार्थों के लिए एकध्रुवीय (ओं) की भूमिका निभाते हैं (जिन्हें [[सोलेनोइडल क्षेत्र|परिनालिकीय क्षेत्र]] अर्थात विचलन मुक्त क्षेत्र का उदाहरण भी माना जा सकता है)। [[मल्टीपोल विस्तार|बहुध्रुव प्रसार]] के संदर्भ में सामान्य प्रवाह प्रतिरूप को भी विघटित किया जा सकता है, उसी प्रकार जैसे [[विद्युत क्षेत्र]] और [[चुंबकीय क्षेत्र]] क्षेत्रों के लिए जहां एकध्रुवीय अनिवार्य रूप से प्रसार का पहला असतहीय (जैसे स्थिर) पद है। | |||
यह प्रवाह | यह प्रवाह प्रतिरूप अघूर्णी और असम्पीडित दोनों है। | ||
यह | यह बेलनाकार समरूपता की विशेषता है: | ||
:<math>\mathbf{v} = v_r(r) \mathbf{e}_r</math> | :<math>\mathbf{v} = v_r(r) \mathbf{e}_r</math> | ||
जहां कुल | जहां कुल निर्गामी प्रवाह स्थिर | ||
: <math>\int_S \mathbf{v} \cdot d \mathbf{S} = \int_{0}^{2 \pi} ( v_r(r) \, \mathbf{e}_r ) \cdot ( \mathbf{e}_r \, r \, d \theta ) = \! 2 \pi \, r \, v_r(r) = Q</math> | : <math>\int_S \mathbf{v} \cdot d \mathbf{S} = \int_{0}^{2 \pi} ( v_r(r) \, \mathbf{e}_r ) \cdot ( \mathbf{e}_r \, r \, d \theta ) = \! 2 \pi \, r \, v_r(r) = Q</math> है | ||
इसलिए, | इसलिए, | ||
:<math>v_r = \frac {Q}{2 \pi r}</math> | :<math>v_r = \frac {Q}{2 \pi r}</math> | ||
यह एक | यह एक धारा फलन | ||
:<math>\psi(r,\theta) = -\frac{Q}{2 \pi } \theta</math> | :<math>\psi(r,\theta) = -\frac{Q}{2 \pi } \theta</math> | ||
या | या विभव फलन से | ||
:<math>\phi(r,\theta) = -\frac{Q}{2 \pi } \ln r</math> | :<math>\phi(r,\theta) = -\frac{Q}{2 \pi } \ln r</math> से लिया गया है | ||
== द्वि-आयामी रेखा | == द्वि-आयामी रेखा निमज्जन == | ||
निश्चित दर पर निश्चित मात्रा में द्रव Q प्रति इकाई लंबाई को अवशोषित करने वाली ऊर्ध्वाधर रेखा की स्थिति एक रेखा निमज्जन है। सब कुछ वैसा ही है जैसा ऋणात्मक चिन्ह से एक भाग के स्रोत की रेखा की स्थिति में होता है। | |||
:<math>v_r = - \frac {Q}{2 \pi r}</math> | :<math>v_r = - \frac {Q}{2 \pi r}</math> | ||
यह | यह धारा फलन | ||
:<math>\psi(r,\theta) = \frac{Q}{2 \pi } \theta</math> | :<math>\psi(r,\theta) = \frac{Q}{2 \pi } \theta</math> | ||
या | या विभव फलन | ||
:<math>\phi(r,\theta) = \frac{Q}{2 \pi } \ln r</math> | :<math>\phi(r,\theta) = \frac{Q}{2 \pi } \ln r</math> से लिया गया है। | ||
यह देखते हुए कि दो परिणाम | यह देखते हुए कि दो परिणाम ऋण चिह्न से एक ही भाग हैं, हम पारदर्शी रूप से रेखा स्रोतों और रेखा निमज्जन दोनों को एक ही धारा और विभव फलनों के साथ अभिक्रियित कर सकते हैं जिससे Q को धनात्मक और ऋणात्मक दोनों मानों को ग्रहण करने और Q की परिभाषा में ऋण चिह्न को अवशोषित करने की अनुमति मिलती है। | ||
== द्वि-आयामी द्विध्रुव या द्विध्रुवीय रेखा स्रोत == | == द्वि-आयामी द्विध्रुव या द्विध्रुवीय रेखा स्रोत == | ||
[[File:Flow-doublet-2D.svg|thumb|270px|right|एक आदर्श द्विध्रुव, या द्विध्रुवीय, रेखा के लिए | [[File:Flow-doublet-2D.svg|thumb|270px|right|एक आदर्श द्विध्रुव, या द्विध्रुवीय, रेखा के लिए विभव प्रवाह धारारेखा]]यदि हम d दूरी पर रेखा स्रोत और रेखा निमज्जन पर विचार करते हैं, तो हम उपरोक्त परिणामों का पुन: उपयोग कर सकते हैं और धारा फलन | ||
:<math>\psi(\mathbf{r}) = \psi_Q(\mathbf{r} - \mathbf{d}/2) - \psi_Q(\mathbf{r} + \mathbf{d}/2) \ \simeq \mathbf{d} \cdot \nabla \psi_Q(\mathbf{r}) | :<math>\psi(\mathbf{r}) = \psi_Q(\mathbf{r} - \mathbf{d}/2) - \psi_Q(\mathbf{r} + \mathbf{d}/2) \ \simeq \mathbf{d} \cdot \nabla \psi_Q(\mathbf{r}) | ||
</math> | </math> होगा | ||
अंतिम सन्निकटन d में पहले क्रम | अंतिम सन्निकटन d में पहले क्रम के लिए है। | ||
दिया गया | दिया गया | ||
| Line 82: | Line 83: | ||
v_\theta(r,\theta) = \frac{Q d}{2 \pi} \frac{\sin(\theta-\theta_0)}{r^2} | v_\theta(r,\theta) = \frac{Q d}{2 \pi} \frac{\sin(\theta-\theta_0)}{r^2} | ||
</math> | </math> | ||
और इसके | और इसके अतिरिक्त विभव | ||
:<math> | :<math> | ||
\phi(r,\theta) = \frac{Q d}{2 \pi} \frac{\cos(\theta-\theta_0)}{r} | \phi(r,\theta) = \frac{Q d}{2 \pi} \frac{\cos(\theta-\theta_0)}{r} | ||
| Line 88: | Line 89: | ||
== द्वि-आयामी | == द्वि-आयामी भ्रमिल रेखा == | ||
[[File:Flow-vortex-2D.svg|thumb|300px|right|एक आदर्श | [[File:Flow-vortex-2D.svg|thumb|300px|right|एक आदर्श भ्रमिल रेखा के लिए विभव प्रवाह धारारेखा]]यह एक भ्रमिल तंतु की स्थिति है जो निरंतर गति से घूमते है, एक बेलनाकार समरूपता होती है और लंबकोणीय तल में समस्या को हल किया जा सकता है। | ||
रेखा स्रोतों के ऊपर | रेखा स्रोतों के ऊपर की स्थिति में दोहरी, भ्रमिल रेखाएं अघूर्णी प्रवाह के लिए एकध्रुवीय की भूमिका निभाती हैं। | ||
इसके | इसके अतिरिक्त इस स्थिति में प्रवाह भी अघूर्णी प्रवाह और असंपीड्य प्रवाह दोनों है और इसलिए विभव प्रवाह की स्थिति है। | ||
यह | यह बेलनाकार समरूपता की विशेषता है: | ||
:<math>\mathbf{v} = v_\theta(r) \, \mathbf{e}_\theta</math> | :<math>\mathbf{v} = v_\theta(r) \, \mathbf{e}_\theta</math> | ||
जहां केंद्रीय | जहां केंद्रीय भ्रमिल | ||
:<math>\oint \mathbf{v} \cdot d \mathbf{s} = \int_{0}^{2 \pi} (v_\theta(r) \, \mathbf{e}_\theta) \cdot (\mathbf{e}_\theta \, r \, d\theta) = \! 2 \pi \, r\, v_\theta(r) = \Gamma</math> | :<math>\oint \mathbf{v} \cdot d \mathbf{s} = \int_{0}^{2 \pi} (v_\theta(r) \, \mathbf{e}_\theta) \cdot (\mathbf{e}_\theta \, r \, d\theta) = \! 2 \pi \, r\, v_\theta(r) = \Gamma</math> | ||
और | के चारों ओर प्रत्येक बंद रेखा के लिए कुल संचलन स्थिर है और भ्रमिल सहित किसी भी रेखा के लिए शून्य है। | ||
इसलिए, | इसलिए, | ||
:<math>v_\theta = \frac {\Gamma}{2 \pi r}</math> | :<math>v_\theta = \frac {\Gamma}{2 \pi r}</math> | ||
यह | यह धारा फलन | ||
:<math>\psi(r,\theta) = \frac{\Gamma}{2 \pi } \ln r</math> | :<math>\psi(r,\theta) = \frac{\Gamma}{2 \pi } \ln r</math> | ||
या | या विभव फलन | ||
:<math>\phi(r,\theta) = - \frac{\Gamma}{2 \pi } \theta</math> | :<math>\phi(r,\theta) = - \frac{\Gamma}{2 \pi } \theta</math> | ||
जो | से प्राप्त होते है जो रेखा स्रोत के पूर्व स्थिति से दोहरी है। | ||
== सामान्य द्वि-आयामी | == सामान्य द्वि-आयामी विभव प्रवाह == | ||
एक असंपीड़ित द्वि-आयामी प्रवाह | एक असंपीड़ित द्वि-आयामी प्रवाह दिया गया है जो हमारे निकट अघूर्णी भी है: | ||
:<math>\nabla^2 \psi = 0</math> | :<math>\nabla^2 \psi = 0</math> | ||
जो बेलनाकार निर्देशांक | जो बेलनाकार निर्देशांक<ref>[[Laplace operator]]</ref> | ||
:<math>\frac{1}{r} \frac{\partial}{\partial r} \left(r \frac{\partial \psi}{\partial r}\right) + \frac{1}{r^2} \frac{\partial^2 \psi}{\partial \theta^2}= 0</math> | :<math>\frac{1}{r} \frac{\partial}{\partial r} \left(r \frac{\partial \psi}{\partial r}\right) + \frac{1}{r^2} \frac{\partial^2 \psi}{\partial \theta^2}= 0</math> में है | ||
हम अलग-अलग चर | हम अलग-अलग चर के साथ एक हल की खोज करते हैं: | ||
:<math>\psi(r,\theta) = R(r) \Theta(\theta)</math> | :<math>\psi(r,\theta) = R(r) \Theta(\theta)</math> | ||
जो | जो | ||
:<math>\frac{r}{R(r)} \frac{d}{dr} \left(r \frac{d R(r)}{dr}\right) = -\frac{1}{\Theta(\theta)} \frac{d^2 \Theta(\theta)}{d\theta^2}</math> | :<math>\frac{r}{R(r)} \frac{d}{dr} \left(r \frac{d R(r)}{dr}\right) = -\frac{1}{\Theta(\theta)} \frac{d^2 \Theta(\theta)}{d\theta^2}</math> देते है | ||
दिया गया बायाँ भाग | दिया गया बायाँ भाग मात्र r पर निर्भर करते है और दायाँ भाग मात्र <math>\theta</math> पर निर्भर करते है, दो भागों को r और <math>\theta</math> से स्वतंत्र एक स्थिरांक के बराबर होना चाहिए। स्थिरांक धनात्मक होगा{{clarify|date=February 2018}}। इसलिए, | ||
इसलिए, | |||
:<math>r \frac{d}{dr} \left(r \frac{d}{dr} R(r)\right) = m^2 R(r) </math> | :<math>r \frac{d}{dr} \left(r \frac{d}{dr} R(r)\right) = m^2 R(r) </math> | ||
:<math>\frac{d^2 \Theta(\theta)}{d\theta^2} = - m^2 \Theta(\theta)</math> | :<math>\frac{d^2 \Theta(\theta)}{d\theta^2} = - m^2 \Theta(\theta)</math> | ||
दूसरे समीकरण का हल | दूसरे समीकरण का हल <math>e^{i m \theta}</math> और <math>e^{-i m \theta}</math> का एक रैखिक संयोजन है ताकि एकल-मानित वेग (और एकल-मानित धारा फलन भी हो) के लिए m एक धनात्मक पूर्णांक होगा। | ||
एकल- | |||
इसलिए सबसे सामान्य हल | इसलिए सबसे सामान्य हल | ||
:<math>\psi = \alpha_0 + \beta_0 \ln r + \sum_{m > 0}{\left(\alpha_m r^m + \beta_m r^{-m}\right)\sin {[m(\theta - | :<math>\psi = \alpha_0 + \beta_0 \ln r + \sum_{m > 0}{\left(\alpha_m r^m + \beta_m r^{-m}\right)\sin {[m(\theta - | ||
\theta_m)]}}</math> | \theta_m)]}}</math> द्वारा दिया गया है | ||
इसके अतिरिक | |||
:<math>\phi = \alpha_0 - \beta_0 \theta + \sum_{m \mathop > 0}{(\alpha_m r^m - \beta_m r^{-m})\cos {[m(\theta - | :<math>\phi = \alpha_0 - \beta_0 \theta + \sum_{m \mathop > 0}{(\alpha_m r^m - \beta_m r^{-m})\cos {[m(\theta - | ||
\theta_m)]}}</math> | \theta_m)]}}</math> द्वारा विभव दिया गया है | ||
| Line 200: | Line 199: | ||
}} | }} | ||
{{DEFAULTSORT:Elementary Flow}} | {{DEFAULTSORT:Elementary Flow}} | ||
[[Category: | [[Category:Articles with invalid date parameter in template|Elementary Flow]] | ||
[[Category:Created On 18/04/2023]] | [[Category:CS1 English-language sources (en)]] | ||
[[Category:Created On 18/04/2023|Elementary Flow]] | |||
[[Category:Machine Translated Page|Elementary Flow]] | |||
[[Category:Pages with maths render errors|Elementary Flow]] | |||
[[Category:Templates Vigyan Ready|Elementary Flow]] | |||
[[Category:Wikipedia articles needing clarification from February 2018|Elementary Flow]] | |||
[[Category:द्रव गतिविज्ञान|Elementary Flow]] | |||
Latest revision as of 13:24, 1 May 2023
नेवियर-स्टोक्स समीकरणों के बड़े संदर्भ में परन्तु विशेष रूप से विभव सिद्धांत के संदर्भ में प्राथमिक प्रवाह मूलभूत प्रवाह का एक संग्रह है जिससे विभिन्न तकनीकों के साथ अधिक जटिल प्रवाह का निर्माण संभव है। इस लेख में ऐतिहासिक कारणों से पदीय प्रवाह का उपयोग पदीय हल के लिए एक दूसरे के स्थान पर किया जाता है।
अधिक जटिल हल बनाने के लिए सम्मिलित तकनीकें हो सकती हैं उदाहरण के लिए अधिस्थापन सिद्धांत द्वारा, सांस्थिति जैसी तकनीकों द्वारा या उन्हें एक निश्चित निकटवर्ती, उपप्रांत या सीमा परत पर स्थानीय हल के रूप में माना जाता है और एक साथ समझौता किया जाता है। प्राथमिक प्रवाह को नेवियर-स्टोक्स से प्राप्त विभिन्न प्रकार के समीकरणों के मूलभूत निर्माण खंड (मौलिक हल, स्थानीय हल और सॉलिटन) माना जा सकता है। कुछ प्रवाह विशिष्ट स्थितियों के व्यवरोध को दर्शाते हैं जैसे कि असंगत प्रवाह या अघूर्णी प्रवाह, या दोनों, जैसा कि विभव प्रवाह की स्थिति में होता है, और कुछ प्रवाह प्रायः 2 आयामों की स्थिति में सीमित होते हैं।[1]
द्रव गतिकी से सभी क्षेत्र सिद्धांत (भौतिकी) के संबंध के कारण यह समझना महत्वपूर्ण है कि कैसे ये सभी प्रवाह न मात्र वायुगतिकी बल्कि सामान्य रूप से सभी क्षेत्र सिद्धांत (भौतिकी) के लिए प्रासंगिक हैं। इसे परिप्रेक्ष्य में रखने के लिए सीमा परतों को प्रजातिगत कई गुना पर सांस्थितिक दोषों के रूप में व्याख्या किया जा सकता है, और द्रव गतिकी उपमाओं और विद्युत चुंबकत्व, क्वांटम यांत्रिकी और सामान्य सापेक्षता में सीमित स्थितियों पर विचार कर सकते हैं कि ये सभी हल सैद्धांतिक भौतिकी में वर्तमान विकास के मूल में कैसे हैं। जैसे कि विज्ञापन/सीएफटी द्वैत, एसवाईके मॉडल, निमैटिक तरल पदार्थों की भौतिकी, दृढ़ता से सहसंबद्ध प्रणालियाँ और यहाँ तक कि क्वार्क ग्लूऑन प्लाज़्मा।
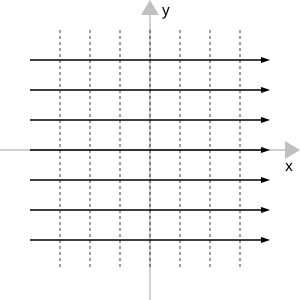
द्वि-आयामी समान प्रवाह
समष्टि में किसी भी स्थिति में द्रव के एकसमान वेग दिया गया है:
यह प्रवाह असम्पीडित है क्योंकि वेग स्थिर है, वेग घटकों का पहला व्युत्पन्न शून्य है, और कुल विचलन शून्य है:
परिचारण (द्रव गतिकी) को देखते हुए सदैव शून्य होता है, प्रवाह भी अघूर्णी होता है, हम इसे केल्विन के परिचारण प्रमेय और भ्रमिलता की स्पष्ट गणना से प्राप्त कर सकते हैं:
असम्पीडित और द्वि-आयामी होने के कारण, यह प्रवाह एक धारा फलन से निर्मित होता है:
जिसमें से
और बेलनाकार निर्देशांक में:
जिससे
सदैव के जैसे धारा फलन को स्थिर मान तक परिभाषित किया जाता है जिसे हम यहाँ शून्य के रूप में लेते हैं। हम यह भी पुष्टि कर सकते हैं कि प्रवाह अघूर्णी है:
अपरिमेय होने के कारण, विभव फलन इसके अतिरिक्त है:
और इसलिए
में
द्वि-आयामी रेखा स्रोत
निश्चित दर पर उत्सर्जक लंबवत रेखा की स्थिति द्रव Q प्रति इकाई लंबाई की निरंतर मात्रा रेखा स्रोत है। समस्या में बेलनाकार समरूपता है और लंबकोणीय तल पर दो आयामों में इसका अभिक्रियित किया जा सकता है।
रेखा स्रोत और रेखा निमज्जन (नीचे) महत्वपूर्ण प्रारंभिक प्रवाह हैं क्योंकि वे असम्पीडित तरल पदार्थों के लिए एकध्रुवीय (ओं) की भूमिका निभाते हैं (जिन्हें परिनालिकीय क्षेत्र अर्थात विचलन मुक्त क्षेत्र का उदाहरण भी माना जा सकता है)। बहुध्रुव प्रसार के संदर्भ में सामान्य प्रवाह प्रतिरूप को भी विघटित किया जा सकता है, उसी प्रकार जैसे विद्युत क्षेत्र और चुंबकीय क्षेत्र क्षेत्रों के लिए जहां एकध्रुवीय अनिवार्य रूप से प्रसार का पहला असतहीय (जैसे स्थिर) पद है।
यह प्रवाह प्रतिरूप अघूर्णी और असम्पीडित दोनों है।
यह बेलनाकार समरूपता की विशेषता है:
जहां कुल निर्गामी प्रवाह स्थिर
- है
इसलिए,
यह एक धारा फलन
या विभव फलन से
- से लिया गया है
द्वि-आयामी रेखा निमज्जन
निश्चित दर पर निश्चित मात्रा में द्रव Q प्रति इकाई लंबाई को अवशोषित करने वाली ऊर्ध्वाधर रेखा की स्थिति एक रेखा निमज्जन है। सब कुछ वैसा ही है जैसा ऋणात्मक चिन्ह से एक भाग के स्रोत की रेखा की स्थिति में होता है।
यह धारा फलन
या विभव फलन
- से लिया गया है।
यह देखते हुए कि दो परिणाम ऋण चिह्न से एक ही भाग हैं, हम पारदर्शी रूप से रेखा स्रोतों और रेखा निमज्जन दोनों को एक ही धारा और विभव फलनों के साथ अभिक्रियित कर सकते हैं जिससे Q को धनात्मक और ऋणात्मक दोनों मानों को ग्रहण करने और Q की परिभाषा में ऋण चिह्न को अवशोषित करने की अनुमति मिलती है।
द्वि-आयामी द्विध्रुव या द्विध्रुवीय रेखा स्रोत
यदि हम d दूरी पर रेखा स्रोत और रेखा निमज्जन पर विचार करते हैं, तो हम उपरोक्त परिणामों का पुन: उपयोग कर सकते हैं और धारा फलन
- होगा
अंतिम सन्निकटन d में पहले क्रम के लिए है।
दिया गया
यह बनी हुई है
वेग तो है
और इसके अतिरिक्त विभव
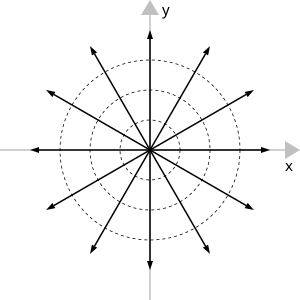
द्वि-आयामी भ्रमिल रेखा
यह एक भ्रमिल तंतु की स्थिति है जो निरंतर गति से घूमते है, एक बेलनाकार समरूपता होती है और लंबकोणीय तल में समस्या को हल किया जा सकता है।
रेखा स्रोतों के ऊपर की स्थिति में दोहरी, भ्रमिल रेखाएं अघूर्णी प्रवाह के लिए एकध्रुवीय की भूमिका निभाती हैं।
इसके अतिरिक्त इस स्थिति में प्रवाह भी अघूर्णी प्रवाह और असंपीड्य प्रवाह दोनों है और इसलिए विभव प्रवाह की स्थिति है।
यह बेलनाकार समरूपता की विशेषता है:
जहां केंद्रीय भ्रमिल
के चारों ओर प्रत्येक बंद रेखा के लिए कुल संचलन स्थिर है और भ्रमिल सहित किसी भी रेखा के लिए शून्य है।
इसलिए,
यह धारा फलन
या विभव फलन
से प्राप्त होते है जो रेखा स्रोत के पूर्व स्थिति से दोहरी है।
सामान्य द्वि-आयामी विभव प्रवाह
एक असंपीड़ित द्वि-आयामी प्रवाह दिया गया है जो हमारे निकट अघूर्णी भी है:
जो बेलनाकार निर्देशांक[2]
- में है
हम अलग-अलग चर के साथ एक हल की खोज करते हैं:
जो
- देते है
दिया गया बायाँ भाग मात्र r पर निर्भर करते है और दायाँ भाग मात्र पर निर्भर करते है, दो भागों को r और से स्वतंत्र एक स्थिरांक के बराबर होना चाहिए। स्थिरांक धनात्मक होगा[clarification needed]। इसलिए,
दूसरे समीकरण का हल और का एक रैखिक संयोजन है ताकि एकल-मानित वेग (और एकल-मानित धारा फलन भी हो) के लिए m एक धनात्मक पूर्णांक होगा।
इसलिए सबसे सामान्य हल
- द्वारा दिया गया है
इसके अतिरिक
- द्वारा विभव दिया गया है
संदर्भ
- Fitzpatrick, Richard (2017), Theoretical fluid dynamics, IOP science, ISBN 978-0-7503-1554-8
- Faber, T.E. (1995), Fluid Dynamics for Physicists, Cambridge university press, ISBN 9780511806735
- Specific
- ↑ Oliver, David (2013-03-14). The Shaggy Steed of Physics: Mathematical Beauty in the Physical World (in English). Springer Science & Business Media. ISBN 978-1-4757-4347-0.
- ↑ Laplace operator
अग्रिम पठन
- Batchelor, G.K. (1973), An introduction to fluid dynamics, Cambridge University Press, ISBN 978-0-521-09817-5
- Chanson, H. (2009), Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows, CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 478 pages, ISBN 978-0-415-49271-3
- Lamb, H. (1994) [1932], Hydrodynamics (6th ed.), Cambridge University Press, ISBN 978-0-521-45868-9
- Milne-Thomson, L.M. (1996) [1968], Theoretical hydrodynamics (5th ed.), Dover, ISBN 978-0-486-68970-8
बाहरी संबंध
- Richard Fitzpatrick University of Texas, Austin (2017). "Fluid Mechanics". University of Texas, Austin. Retrieved 2018-02-07.
- (c) Aerospace, Mechanical & Mechatronic Engg. 2005 University of Sydney (2005). "Elements of Potential Flow". University of Sydney. Retrieved 2019-04-19.