इकोसिडोडेकाहेड्रॉन

Icosidodecahedron
(Click here for rotating model)
Type	Archimedean solid Uniform polyhedron
Elements	F = 32, E = 60, V = 30 (χ = 2)
Faces by sides	20{3}+12{5}
Conway notation	aD
Schläfli symbols	r{5,3}
	t1{5,3}
Wythoff symbol	2 | 3 5
Coxeter diagram
Symmetry group	Ih, H3, [5,3], (*532), order 120
Rotation group	I, [5,3]+, (532), order 60
Dihedral angle	142.62° $\cos ^{-1}\left(-{\sqrt {{\frac {1}{15}}\left(5+2{\sqrt {5}}\right)}}\right)$
References	U24, C28, W12
Properties	Semiregular convex quasiregular
Colored faces	3.5.3.5 (Vertex figure)
Rhombic triacontahedron (dual polyhedron)	Net

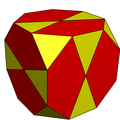
File:Icosidodecahedron.stlज्यामिति में, इकोसिडोडेकाहेड्रॉन बीस (इकोसि) त्रिकोणीय फलकों और बारह (डोडेका) पंचभुजीय फलकों वाला एक बहुफलक है। एक इकोसिडोडेकेड्रॉन में 30 समान शीर्ष (ज्यामिति) होते हैं, जिनमें दो त्रिकोण और दो पंचकोण प्रत्येक पर मिलते हैं, और 60 समान कोर होते हैं, प्रत्येक एक त्रिकोण को एक पंचभुज से अलग करते हैं। जैसे कि यह आर्किमिडीयन ठोस में से एक है और अधिक विशेष रूप से, एक अर्ध-समभुजकोणीय बहुतल है।

ज्यामिति

एक इकोसिडोडेकाहेड्रॉन में आईकोसाहेड्रल समरूपता है, और इसका पहला तारकीय द्वादशफलक और इसके दोहरे विंशफलक का सम्मिश्र है, जिसमें शीर्षों के मध्य बिंदुओं पर स्थित इकोसिडोडेकाहेड्रॉन के कोर होते हैं।

इसका दोहरा बहुफलक समचतुर्भुज त्रिकोणाफलक है। इकोसिडोडेकाहेड्रॉन को पंचभुजीय गोलाकार कक्ष का एक युग्म बनाने के लिए छह तलों में से किसी के साथ विभाजित किया जा सकता है, जो जॉनसन ठोस पदार्थों में से हैं।

इकोसिडोडेकेड्रोन को एक पंचकोणीय जाइरोबिरोटुंडा माना जा सकता है, क्योंकि दो गोलाकार कक्ष के सम्मिश्र के रूप में पंचकोणीय ऑर्थोबिरोटुंडा की तुलना की जाती है, जो जॉनसन ठोस में से एक है। इस रूप में इसकी समरूपता D_5d, [10,2⁺], (2*5), क्रम 20 है।

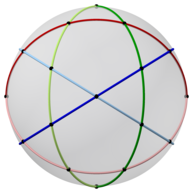
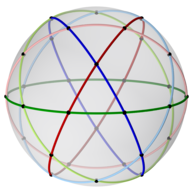
इकोसिडोडेकेड्रोन के तार-संरचना आकृति में छह सम दशभुज होते हैं, जो प्रत्येक 30 शीर्षों में से प्रत्येक में युग्म में मिलते हैं।

इकोसिडोडेकेड्रॉन में 6 केंद्रीय दशभुज होते हैं। एक गोले में प्रक्षेपित, वे 6 बड़े वृत्तों को परिभाषित करते हैं। बकमिंस्टर फुलर ने गोलाकार विंशफलक के अपने 31 बड़े वृत्तों को परिभाषित करने के लिए दो अन्य बहुकोणीय में 15 और 10 अन्य के साथ इन 6 बृहत वृत्तों का उपयोग किया है।

कार्तीय निर्देशांक

इकाई कोर के साथ एक इकोसिडोडेकेड्रॉन के शीर्ष के लिए उपयुक्त कार्तीय निर्देशांक भी क्रमपरिवर्तन द्वारा दिए गए हैं:

• (0, 0, ±φ)
• (±1/2, ±φ/2, ±φ²/2)

जहां φ स्वर्णिम अनुपात 1 + √5/2 है।

इकोसिडोडेकाहेड्रॉन का लंबा त्रिज्या (केंद्र से शीर्ष तक) इसके कोर की लंबाई के स्वर्णिम अनुपात में है; इस प्रकार इसकी त्रिज्या φ है यदि इसके शीर्ष की लंबाई 1 है, और इसके कोर की लंबाई 1/φ है यदि इसकी त्रिज्या 1 है। केवल कुछ समान बहुशीर्षों में यह गुण होता है, जिसमें चार-आयामी 600-कक्ष, त्रि-आयामी इकोसिडोडेकेड्रॉन, और द्वि-आयामी दशकोण में स्वर्णिम अनुपात सम्मिलित है। इकोसिडोडेकाहेड्रॉन 600-कक्ष का मध्यवर्ती अनुप्रस्थ परिच्छेद है, और दशभुज इकोसिडोडेकहेड्रोन का मध्यवर्ती अनुप्रस्थ परिच्छेद है। इन त्रिज्यत: स्वर्णिम बहुतल को उनके त्रिज्या के साथ स्वर्णिम त्रिकोण (गणित) से बनाया जा सकता है जो केंद्र में मिलते हैं और प्रत्येक में दो त्रिज्या और एक कोर का योगदान होता है।

लंबकोणीय प्रक्षेपण

इकोसिडोडेकहेड्रोन में चार विशेष लंबकोणीय प्रक्षेपण हैं, जो एक शीर्ष, एक कोर, एक त्रिकोणीय फलक और एक पंचकोणीय फलक पर केंद्रित हैं। पिछले दो A₂ और H₂ कॉक्सेटर तलों के अनुरूप हैं।

लंबकोणीय प्रक्षेपण

द्वारा केन्द्रित	शीर्ष	कोर	फलक त्रिकोण	फलक पंचकोण
ठोस
तार संरचना
प्रक्षेपीय समरूपता	[2]	[2]	[6]	[10]
द्विक

सतह क्षेत्र और आयतन

सतह क्षेत्र A और कोर की लंबाई के इकोसिडोडेकहेड्रोन का आयतन V हैं:

${\begin{aligned}A&=\left(5{\sqrt {3}}+3{\sqrt {5}}{\sqrt {3+4\varphi }}\right)a^{2}&&=\left(5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}&&\approx 29.3059828a^{2}\\V&={\frac {14+17\varphi }{3}}a^{3}&&={\frac {45+17{\sqrt {5}}}{6}}a^{3}&&\approx 13.8355259a^{3}.\end{aligned}}$

गोलीय टाइल

गोलाकार टाइल में बड़े वृत्तों के अनुरूप 60 कोर 6 दशभुज बनाते हैं।

आईकोसिडोडेकेड्रोन को एक गोलाकार टाइल के रूप में भी प्रदर्शित किया जा सकता है, और एक त्रिविम प्रक्षेपण के माध्यम से तल पर प्रक्षेपित किया जा सकता है। यह प्रक्षेपण अनुरूप रेखाचित्र है, और कोणों को संरक्षित करता है लेकिन क्षेत्र या लंबाई नहीं है। गोले पर सीधी रेखाएँ समतल पर वृत्ताकार चापों के रूप में प्रक्षेपित की जाती हैं।

	Pentagon-centered	Triangle-centered
लंबकोणिक प्रक्षेपण	त्रिविम प्रेक्षपण

लंबकोणीय प्रक्षेपण
2-fold, 3-fold and 5-fold symmetry axes

संबंधित बहुतलीय

इकोसिडोडेकेड्रॉन एक परिशोधित (ज्यामिति) डोडेकाहेड्रॉन है और एक परिशोधित विंशफलक भी है, जो इन समफलकी ठोस पदार्थों के बीच पूर्ण कोर विखंडन के रूप में विद्यमान है।

इकोसिडोडेकेड्रॉन में द्वादशफलक के 12 पंचभुज और समद्धिबाहु चतुष्फ़लक के 20 त्रिकोण होते हैं:

Family of uniform icosahedral polyhedra
Symmetry: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

इकोसिडोडेकेड्रॉन शीर्ष विन्यास (3.n)² के साथ अर्ध-समभुजकोणीय बहुभुजों से परिबद्ध एक ठोस और टाइल के समरूपता के अनुक्रम में सम्मिलित है, गोले के टाइल से यूक्लिडियन तल तक और अतिपरवलयिक तल में विकास करता है। और n32 की कक्षीय संकेत समरूपता के साथ, ये सभी टाइल प्रक्षेप के समकोण कोर पर उत्पादक बिंदुओं के साथ समरूपता के एक मौलिक प्रक्षेत्र के अंदर निर्माण के साथ हैं।

*n32 orbifold symmetries of quasiregular tilings: (3.n)2
Construction	Spherical			Euclidean	Hyperbolic
	*332	*432	*532	*632	*732	*832...	*∞32
Quasiregular figures
Vertex	(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.∞)2

*5n2 symmetry mutations of quasiregular tilings: (5.n)2
Symmetry *5n2 [n,5]	Spherical	Hyperbolic					Paracompact	Noncompact
	*352 [3,5]	*452 [4,5]	*552 [5,5]	*652 [6,5]	*752 [7,5]	*852 [8,5]...	*∞52 [∞,5]	[ni,5]
Figures
Config.	(5.3)2	(5.4)2	(5.5)2	(5.6)2	(5.7)2	(5.8)2	(5.∞)2	(5.ni)2
Rhombic figures
Config.	V(5.3)2	V(5.4)2	V(5.5)2	V(5.6)2	V(5.7)2	V(5.8)2	V(5.∞)2	V(5.∞)2

विच्छेदन

इकोसिडोडेकेड्रॉनजॉनसन ठोस से संबंधित है जिसे एक पंचभुजीय ऑर्थोबिरोटुंडा कहा जाता है जिसे दर्पण प्रतिबिंब के रूप में जुड़े दो पंचभुजीय गोलाकार कक्ष द्वारा बनाया गया है। इसलिए इकोसिडोडेकेड्रॉनको शीर्ष और निचले भागों के बीच घूर्णन के साथ एक पंचभुजीय जाइरोबिरोटुंडा कहा जा सकता है।

(विच्छेदन)

इकोसिडोडेकाहेड्रॉन (पंचभुज जाइरोबिरोटुंडा) पंचकोणीय ऑर्थोबिरोटुंडा पंचकोणीय गोलीय कक्ष

बहुकोणीय आकृति संबंधित

खंडित घन में एक सांस्थितिक इकोसिडोडेकेड्रॉन, अष्टफलकीय के केंद्र में 6 शीर्ष डालकर, और उन्हें 2 पंचभुज और 2 त्रिकोण में विभाजित करना।

प्रतिच्छेदित घन को अष्टकोणों को दो पंचकोणों और दो त्रिभुजों में विभाजित करके लघु इकोसीहेमिडोडेकाहेड्रॉन में बदला जा सकता है। इसमें पाइराइटफलकी समरूपता है।

आठ समान तारकीय बहुकोणीय समान शीर्ष प्रणाली साझा करते हैं। इनमें से, दो समान कोर की व्यवस्था लघु इकोसिहेमिडोडेकेड्रोन (त्रिकोणीय फलकों को सामान्य रूप से), और लघु डोडेकाहेमिडोडेकाहेड्रॉन (सामान्य में पंचकोणीय फलक) साझा करते हैं। शीर्ष प्रणाली को पांच अष्टफलकीय के सम्मिश्र और पांच टेट्राहेमीहेक्सहेड्रा के समान बहुफलक सम्मिश्र के साथ भी साझा किया जाता है।

इकोसिडोडेकाहेड्रॉन	लघु इकोसीहेमिडोडेकाहेड्रॉन	लघु डोडेकाहेमिडोडेकाहेड्रॉन
वृहत इकोसिडोडेकाहेड्रॉन	वृहत डोडेकाहेमिडोडेकाहेड्रॉन	वृहत आईकोसीहेमिडोडेकाहेडेरॉन
डोडेकाडोडेकाहेड्रॉन	लघु डोडेकेमिकोसाहेड्रोन	वृहत डोडेकेमिकोसाहेड्रोन
पांच अष्टफलकीय का सम्मिश्र	File:UC18-5 tetrahemihexahedron.png पाँच टेट्राहेमीहेक्सहेड्रा का सम्मिश्र

पॉलीकोरा संबंधित

चार-आयामी ज्यामिति में इकोसिडोडेकेड्रॉन समभुजकोणीय बहुतलीय 600-कक्ष में विषुवतीय भाग के रूप में प्रकट होता है जो 3 डी अंतरिक्ष के माध्यम से 600-कक्ष के शीर्ष-प्रथम मार्ग से संबंधित होता है। दूसरे शब्दों में: 600-कक्ष के 30 कोर जो इसके परिबद्ध अधिगोल क्षेत्र पर 90 डिग्री की चाप दूरी पर विपरीत शीर्षों की एक युग्म से स्थित होते हैं, एक इकोसिडोडेकेड्रॉन के शीर्ष होते हैं। 600-कक्ष के तार संरचना आकृति में 72 समतल सममित दशभुज होते हैं। इनमें से छह विपरीत शीर्षों के युग्म के लिए विषुवतीय दसभुज हैं। वे शुद्ध छह दशभुज हैं जो आईकोसिडोडेकहेड्रोन के तार संरचना आकृति बनाते हैं।

इकोसिडोडेकाहेड्रॉन आरेख

इकोसिडोडेकाहेड्रल आरेख
File:Icosidodecahedral graph.png 5-गुना समरूपता श्लेगल आरेख
Vertices	30
Edges	60
Automorphisms	120
Properties	क्वार्टिक ग्राफ, हैमिल्टनियन, नियमित
Table of graphs and parameters

आरेख सिद्धांत के गणित क्षेत्र में, एक इकोसिडोडेकाहेड्रा आरेख आर्किमिडीयन ठोस पदार्थों में से एक, इकोसिडोडेकाहेड्रा के शीर्ष और कोर का आरेख है। इसमें 30 शीर्ष और 60 कोर हैं, और यह एक चतुर्घाती आरेख आर्किमिडीयन आरेख है।

प्रकृति में इकोसिडोडेकेड्रा

होबरमैन क्षेत्र एक इकोसिडोडेकाहेड्रा है।

इकोसिडोडेकाहेड्रा मानव कोशिकाओं सहित सभी सुकैराटिनी कोशिका में पाया जा सकता है, जैसे कि Sec13/31 आवरण प्रोटीन सम्मिश्र II आवरण-प्रोटीन संरचनाएं होती है।

विविध-विषय

तारकीय स्थानांतरण समष्टि में, तर्क काल-तोह के वल्कन खेल का लक्ष्य एक स्वलिखित आईकोसाइडोडेकाहेड्रॉन बनाने का है।

द रॉंग स्टार्स में, टिम प्रैट की स्वयंसिद्ध श्रृंखला में से एक पुस्तक, ऐलेना के पास उसके दोनों ओर एक आईकोसिडोडेकहेड्रॉन यंत्र है। [पेपरबैक पृष्ठ 336]

यह भी देखें

• क्यूबोक्टाहेड्रोन
• वृहत विखंडित आईकोसाइडोडेकाहेड्रॉन
• विंशफलक
• रोम्बिकोसिडोडेकाहेड्रॉन
• खंडित आईकोसिडोडेकाहेड्रॉन

संदर्भ

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
• Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.

इस पेज में लापता आंतरिक लिंक की सूची

• आर्किमिडीज़ ठोस
• अर्ध-समभुजकोणीय पॉलीहेड्रॉन
• डोडेकाहेड्रॉन और आईकोसैहेड्रोन का सम्मिश्र
• दोहरी पॉलीहेड्रॉन
• रोम्बिक ट्राईकॉन्टाहेड्रोन
• तारकीय
• महान घेरा
• गोलाकार आइकोसैहेड्रॉन के 31 बड़े घेरे
• यहां तक ​​कि क्रमपरिवर्तन
• स्वर्ण त्रिभुज (गणित)
• गोलाकार टाइलिंग
• सुधार (ज्यामिति)
• पांच ऑक्टाहेड्रा का सम्मिश्र
• एकसमान तारा बहुफलक
• पाँच टेट्राहेमीहेक्सहेड्रा का सम्मिश्र
• कटा हुआ घन
• अंक शास्त्र
• शीर्ष (आरेख सिद्धांत)
• हॉबरमैन क्षेत्र
• ग्रेट ट्रंकेटेड आईकोसिडोडेकाहेड्रॉन

बाहरी संबंध

• Eric W. Weisstein, Icosidodecahedron (Archimedean solid) at MathWorld.
• Klitzing, Richard. "3D convex uniform polyhedra o3x5o - id".
• Editable printable net of an icosidodecahedron with interactive 3D view
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra