टॉरॉयडल पॉलीहेड्रॉन: Difference between revisions
No edit summary |
No edit summary |
||
| Line 148: | Line 148: | ||
{| class=wikitable align=right | {| class=wikitable align=right | ||
|- align=center | |- align=center | ||
|[[File:Octahemioctahedron.png|120px]]<br>[[ | |[[File:Octahemioctahedron.png|120px]]<br>[[Index.php?title=ऑक्टाहेमीऑक्टाहेड्रोन|ऑक्टाहेमीऑक्टाहेड्रोन]] | ||
|[[File:Small cubicuboctahedron.png|120px]]<br>[[ | |[[File:Small cubicuboctahedron.png|120px]]<br>[[Index.php?title=स्मॉल क्यूबिकुबोक्टाहेड्रोन|स्मॉल क्यूबिकुबोक्टाहेड्रोन]] | ||
|[[File:Great dodecahedron.png|120px]]<br>[[ | |[[File:Great dodecahedron.png|120px]]<br>[[Index.php?title=ग्रैट द्वादशफ़लक|ग्रैट द्वादशफ़लक]] | ||
|} | |} | ||
एक | एक बहुफलक जो क्रॉसिंग बहुभुज की एक प्रणाली द्वारा बनाई गई है, उसके बहुभुज और उनके साझा किनारों और कोने की प्रणाली द्वारा बनाई गई एक सार संस्थानिक बहुमुख से मेल खाती है, और बहुतल का प्रकार इस अमूर्त बहुमुख से निर्धारित किया जा सकता है। उदाहरणों में जीनस-1 [[Index.php?title=ऑक्टाहेमिओक्टाहेड्रॉन|ऑक्टाहेमिओक्टाहेड्रॉन]], जीनस-3 छोटा क्यूबिकुबोक्टाहेड्रोन और जीनस-4 [[Index.php?title=ग्रेट द्वादशफलक|ग्रेट द्वादशफलक]] सम्मलित हैं। | ||
उदाहरणों में जीनस-1 [[ | |||
{{Clear}} | {{Clear}} | ||
| Line 159: | Line 158: | ||
=== क्राउन पॉलीहेड्रा === | === क्राउन पॉलीहेड्रा === | ||
[[File:Stephanoid5.png|thumb|right|160px|पेंटागोनल स्टेफ़नॉइड। इस स्टेफ़नॉइड में पेंटागोनल [[डायहेड्रल समरूपता]] है और एक समान [[पंचकोणीय प्रिज्म]] के समान कोने हैं।]]एक | [[File:Stephanoid5.png|thumb|right|160px|पेंटागोनल स्टेफ़नॉइड। इस स्टेफ़नॉइड में पेंटागोनल [[डायहेड्रल समरूपता]] है और एक समान [[पंचकोणीय प्रिज्म]] के समान कोने हैं।]]एक शीर्ष बहुफलक या स्टेफ़नॉइड एक टॉरॉयडल पॉलीहेड्रॉन है, जो समकोणीय और आइसोहेड्रल दोनों होने के कारण भी बृहत है। [[Index.php?title=क्राउन पॉलीहेड्रॉन|क्राउन पॉलीहेड्रॉन]] स्व-प्रतिच्छेदी और [[Index.php?title=स्थलाकृतिक|स्थलाकृतिक]] रूप से स्व-द्वैत हैं। <ref>{{citation | ||
| last=Grünbaum | first=Branko | authorlink=Branko Grünbaum | | last=Grünbaum | first=Branko | authorlink=Branko Grünbaum | ||
| contribution=Polyhedra with Hollow Faces | | contribution=Polyhedra with Hollow Faces | ||
| Line 183: | Line 182: | ||
{{Reflist|30em}} | {{Reflist|30em}} | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
*{{MathWorld|urlname=ToroidalPolyhedron|title=Toroidal polyhedron}} | *{{MathWorld|urlname=ToroidalPolyhedron|title=Toroidal polyhedron}} | ||
Revision as of 23:14, 26 April 2023

ज्यामिति में, एक टोरॉयडल पॉलीहेड्रॉन होता है जो एक टोरॉयड (एक g-होलेड टोरस) भी होता है, जिसमें 1 या उससे अधिक का टोपोलॉजी वर्ग (g) होता है। उल्लेखनीय उदाहरणों में सेस्ज़ार और सिलासी बहुफलक सम्मलित हैं।
परिभाषा में स्थानान्तरण
टॉरॉयडल पॉलीहेड्रा को बहुभुजों के संग्रह के रूप में परिभाषित किया जाता है जो उनके किनारों और कोने पर मिलते हैं, जैसा कि वे करते हैं। अर्थात्, प्रत्येक किनारे को पूर्णतया दो बहुभुजों द्वारा सहभाजित किया जाना चाहिए, और प्रत्येक शीर्ष पर किनारे और फलक जो शीर्ष पर मिलते हैं, उन्हें वैकल्पिक किनारों और चेहरों के एक चक्र में एक साथ जोड़ा जाना चाहिए, शीर्ष का लिंक। टोरॉयडल पॉलीहेड्रा के लिए, यह कई गुना एक ओरिएंटेबल सतह है।[1] कुछ लेखक "टोरॉयडल पॉलीहेड्रा" वाक्यांश को अधिक विशेष रूप से पॉलीहेड्रा के रूप में (जीनस 1) टोरस के समतुल्य के रूप में प्रतिबंधित करते हैं।[2] इस क्षेत्र में, एम्बेडिंग टोरॉयडल पॉलीहेड्रा को अलग करना महत्वपूर्ण है, जिनके चेहरे त्रि-आयामी यूक्लिडियन अंतरिक्ष में समतल बहुभुज हैं जो खुद को या एक दूसरे को पार नहीं करते हैं, बिना किसी निर्दिष्ट ज्यामितीय प्राप्ति के सार पॉलीहेड्रा से, टोपोलॉजिकल सतहों से।[3] इन दो चरम सीमाओं के बीच इंटरमीडिएट यूक्लिडियन अंतरिक्ष में ज्यामितीय बहुभुज या स्टार बहुभुज द्वारा गठित पॉलीहेड्रा हैं जो एक दूसरे को पार करने की अनुमति देते हैं।
इन सभी स्थितियों में पॉलीहेड्रॉन की टोरॉयडल प्रकृति को इसकी उन्मुखता और इसकी यूलर विशेषता के गैर-सकारात्मक होने से सत्यापित किया जा सकता है। यूलर की विशेषता V − E + F = 2 − 2N, के लिए सामान्यीकृत होती है, जहां N आयोजनों की संख्या है।
ज़ाज़र और ज़िलास्सी पॉलीहेड्रा
 Interactive Csaszar polyhedron model – in the SVG image, move the mouse left and right to rotate it.[4] |
सबसे सरल संभव अंतः स्थापित टोरॉयडल पॉलीहेड्रा में से दो ज़ाज़र और ज़िलास्सी पॉलीहेड्रा हैं।
सेस्ज़ार पॉलीहेड्रॉन 21 किनारों और 14 त्रिकोणीय चेहरों वाला एक सात-शीर्ष टोरॉयडल पॉलीहेड्रॉन है।[6] यह और चतुष्फलक एकमात्र ज्ञात बहुफलक हैं जिसमें दो शीर्षों को जोड़ने वाला प्रत्येक संभव रेखा खंड बहुफलक योजक बनाता है।[7] इसके दोहरे, स्ज़ीलासी पॉलीहेड्रॉन में सात हेक्सागोनल चेहरे हैं जो सभी एक दूसरे से जुड़े हुए हैं,[8] इसलिए अस्तित्व को आधा प्रमेय प्रदान करते हैं कि एक (जीनस वन) टोरस पर एक मानचित्र के लिए आवश्यक रंगों की अधिकतम संख्या सात है। [9] ज़ाज़र पॉलीहेड्रॉन में किसी भी अंतः स्थापित टॉरॉयडल पॉलीहेड्रॉन के सबसे कम संभव कोने हैं, और स्ज़ीलासी पॉलीहेड्रॉन में किसी भी अंतः स्थापित टॉरॉयडल पॉलीहेड्रॉन के सबसे कम संभव बाह्य अर्थ हैं।
स्टीवर्ट टॉरॉयड्स
टोरॉयडल पॉलीहेड्रा की एक विशेष श्रेणी विशेष रूप से नियमित बहुभुज चेहरों द्वारा बनाई जाती है, प्रसंकरण के बिना, और एक और प्रतिबंध के साथ कि आसन्न चेहरे एक दूसरे के समान विमान में नहीं हो सकते हैं। इन्हें स्टीवर्ट टॉरॉयड्स कहा जाता है,[10] बोनी स्टीवर्ट के नाम पर रखा गया, जिन्होंने इनका गहन अध्ययन किया।[11] उत्तल पॉलीहेड्रॉन के स्थिति में वे जॉनसन ठोस के समान हैं; चूंकि, जॉनसन सॉलिड्स के विपरीत, असीम रूप से कई स्टीवर्ट टॉरॉयड्स हैं।[12] इनमें टॉरॉयडल डेल्टाहेड्रोन, पॉलीहेड्रा भी सम्मलित हैं जिनके चेहरे सभी समबाहु त्रिभुज हैं।
स्टीवर्ट टोरॉयड्स का एक प्रतिबंधित वर्ग, जिसे स्टीवर्ट द्वारा भी परिभाषित किया गया है, अर्ध-उत्तल टॉरॉयडल पॉलीहेड्रा हैं। ये स्टीवर्ट टॉरॉयड्स हैं जिनमें उनके उत्तल हल्स के सभी किनारे सम्मलित हैं। ऐसे बहुफलक के लिए, उत्तल पतवार का प्रत्येक फलक या तो टोरॉयड की सतह पर स्थित होता है, या एक बहुभुज होता है जिसके सभी किनारे टोरॉइड की सतह पर स्थित होते हैं। [13]
| जीनस | 1 | 1 |
|---|---|---|
| इमेज | 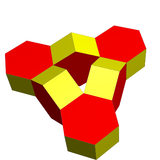
|
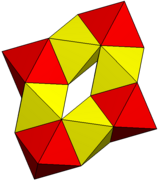
|
| पालिहीड्रन | 6 षट्कोणीय वर्णक्रम | 8 ऑक्टाहेड्रा |
| वर्टेक्स | 48 | 24 |
| एज | 84 | 72 |
| फेस | 36 | 48 |
| जीनस | 1 | 3 | 11 | 3 | 5 | 7 | 11 | |
|---|---|---|---|---|---|---|---|---|
| इमेज | 
|

|

|

|

|

|

|
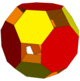
|
| पालिहीड्रन | 4 चौकोर गुंबद 8 चतुष्फलक |
6 त्रिकोणीय गुंबद 6 चौकोर पिरामिड |
4 त्रिकोणीय गुंबद 6 वर्ग पिरामिड |
24 त्रिकोणीय प्रिज्म 6 वर्ग पिरामिड 8 टेट्राहेड्रा |
6 चौकोर गुंबद 4 त्रिकोणीय गुंबद 12 घन |
8 त्रिकोणीय गुंबद 12 घन |
6 चौकोर गुंबद 12 घन |
6 चौकोर गुंबद 8 त्रिकोणीय गुंबद |
| कन्वेक्स हल | छोटा घन | संक्षिप्त ऑक्टाहेड्रॉन | संक्षिप्त ऑक्टाहेड्रॉन | विस्तारित क्यूबोक्टहेड्रॉन | संक्षिप्त क्यूबोक्टहेड्रॉन | संक्षिप्त क्यूबोक्टहेड्रॉन | संक्षिप्त क्यूबोक्टहेड्रॉन | संक्षिप्त क्यूबोक्टहेड्रॉन |
| वर्टेक्स | 32 | 30 | 30 | 62 | 72 | 72 | 72 | 72 |
| एज | 64 | 60 | 72 | 168 | 144 | 168 | 168 | 168 |
| फेस | 32 | 30 | 38 | 86 | 68 | 88 | 84 | 76 |
स्व-क्रॉसिंग पॉलीहेड्रा
 ऑक्टाहेमीऑक्टाहेड्रोन |
 स्मॉल क्यूबिकुबोक्टाहेड्रोन |
 ग्रैट द्वादशफ़लक |
एक बहुफलक जो क्रॉसिंग बहुभुज की एक प्रणाली द्वारा बनाई गई है, उसके बहुभुज और उनके साझा किनारों और कोने की प्रणाली द्वारा बनाई गई एक सार संस्थानिक बहुमुख से मेल खाती है, और बहुतल का प्रकार इस अमूर्त बहुमुख से निर्धारित किया जा सकता है। उदाहरणों में जीनस-1 ऑक्टाहेमिओक्टाहेड्रॉन, जीनस-3 छोटा क्यूबिकुबोक्टाहेड्रोन और जीनस-4 ग्रेट द्वादशफलक सम्मलित हैं।
क्राउन पॉलीहेड्रा

एक शीर्ष बहुफलक या स्टेफ़नॉइड एक टॉरॉयडल पॉलीहेड्रॉन है, जो समकोणीय और आइसोहेड्रल दोनों होने के कारण भी बृहत है। क्राउन पॉलीहेड्रॉन स्व-प्रतिच्छेदी और स्थलाकृतिक रूप से स्व-द्वैत हैं। [14]
यह भी देखें
- प्रक्षेपी बहुफलक
- तिरछा एपिरोहेड्रोन (अनंत तिरछा पॉलीहेड्रॉन)
- गोलाकार पॉलीहेड्रॉन
- टॉरॉयडल ग्राफ
संदर्भ
- ↑ Whiteley (1979); Stewart (1980), p. 15.
- ↑ Webber, William T. (1997), "Monohedral idemvalent polyhedra that are toroids", Geometriae Dedicata, 67 (1): 31–44, doi:10.1023/A:1004997029852, MR 1468859, S2CID 117884274.
- ↑ Whiteley, Walter (1979), "Realizability of polyhedra" (PDF), Structural Topology (1): 46–58, 73, MR 0621628.
- ↑ Ákos Császár, A Polyhedron Without Diagonals., Bolyai Institute, University of Szeged, 1949
- ↑ Grünbaum, Branko; Szilassi, Lajos (2009), "Geometric Realizations of Special Toroidal Complexes", Contributions to Discrete Mathematics, 4 (1): 21–39, doi:10.11575/cdm.v4i1.61986, ISSN 1715-0868
- ↑ Császár, A. (1949), "A polyhedron without diagonals", Acta Sci. Math. Szeged, 13: 140–142.
- ↑ Ziegler, Günter M. (2008), "Polyhedral Surfaces of High Genus", in Bobenko, A. I.; Schröder, P.; Sullivan, J. M.; Ziegler, G. M. (eds.), Discrete Differential Geometry, Oberwolfach Seminars, vol. 38, Springer-Verlag, pp. 191–213, arXiv:math.MG/0412093, doi:10.1007/978-3-7643-8621-4_10, ISBN 978-3-7643-8620-7, S2CID 15911143.
- ↑ Szilassi, Lajos (1986), "Regular toroids" (PDF), Structural Topology, 13: 69–80[permanent dead link].
- ↑ Heawood, P. J. (1890), "Map colouring theorems", Quarterly Journal of Mathematics, First Series, 24: 322–339
- ↑ Webb, Robert (2000), "Stella: polyhedron navigator", Symmetry: Culture and Science, 11 (1–4): 231–268, MR 2001419.
- ↑ Stewart, B. M. (1980), Adventures Among the Toroids: A Study of Orientable Polyhedra with Regular Faces (2nd ed.), B. M. Stewart, ISBN 978-0-686-11936-4.
- ↑ Stewart (1980), p. 15.
- ↑ Stewart (1980), "Quasi-convexity and weak quasi-convexity", pp. 76–79.
- ↑ Grünbaum, Branko (1994), "Polyhedra with Hollow Faces", Polytopes: Abstract, Convex and Computational, NATO ASI Series C: Mathematical and Physical Series, vol. 440, Kluwer Academic Publishers, pp. 43–70, doi:10.1007/978-94-011-0924-6_3. See in particular p. 60.
