रोम्बिक हेक्सेकोंटाहेड्रोन: Difference between revisions
No edit summary |
m (added Category:Vigyan Ready using HotCat) |
||
| Line 71: | Line 71: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 17/04/2023]] | [[Category:Created On 17/04/2023]] | ||
[[Category:Vigyan Ready]] | |||
Revision as of 17:49, 1 May 2023
| Rhombic hexecontahedron | |
|---|---|

| |
| Type | Stellation of rhombic triacontahedron |
| Vertices | 62 (12+20+30) |
| Edges | 120 (60+60) |
| Faces | 60 golden rhombi |
| Symmetry | Ih, [5,3], (*532) |
| Properties | non-convex, zonohedron |
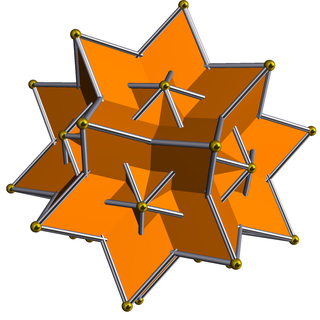
File:Rhombic hexecontahedron.stlज्यामिति में, एक रोम्बिक हेक्सेकोंटाहेड्रॉन, रोम्बिक ट्राईकॉन्टाहेड्रोन का एक तारा है। यह आइकोसाहेड्रल समरूपता के साथ 60 सुनहरे समचतुर्भुज चेहरों के साथ गैर-उत्तल है। यह 1940 में हेल्मुट अनकेलबैक द्वारा गणितीय रूप से वर्णित किया गया था।[1] यह सामयिक रूप से उत्तल डेल्टोइडल हेक्सेकोंटाहेड्रोन के समान है जिसमें पतंग (ज्यामिति) चेहरे हैं।
विच्छेदन
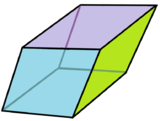
समचतुर्भुज षट्कोणीय फलक को एक केंद्रीय बिंदु पर 20 तीव्र स्वर्ण समचतुर्भुज बैठक में विच्छेदित किया जा सकता है। यह भुजा लंबाई a के हेक्सकॉन्टेहेड्रोन का आयतन और क्षेत्रफल देता है।.
निर्माण
एक समचतुर्भुज षट्कोणीय फलक एक नियमित द्वादशफलक से निर्मित किया जा सकता है, इसके शीर्षों, इसके फलक केंद्रों और इसके किनारे के केंद्रों को ले कर और उन्हें निकाय के केंद्र से अलग-अलग विस्तार तक स्केल करके बनाया जा सकता है। इस प्रकार, यदि द्वादशफलक के 20 शीर्षों को (सुनहरा अनुपात|ϕ+1)/2 ≈ 1.309 के गुणक द्वारा परिधि को बढ़ाने के लिए बाहर निकाला जाता है, तो 12 फलक केंद्रों को अंत:त्रिज्या को कम करने के लिए धकेल दिया जाता है इसके मूल मान का (3-ϕ) /2 ≈ 0.691,और 30 किनारों के केंद्रों को अपरिवर्तित छोड़ दिया जाता है, फिर एक समचतुर्भुज हेक्साकोंटाहेड्रॉन बनता है। (परिवृत्त में 30.9% की वृद्धि हुई है और अंतःत्रिज्या में समान 30.9% की कमी हुई है।) अलग-अलग राशियों द्वारा बिंदुओं को स्केल करने से पतंग के आकार वाले चेहरे या अन्य पॉलीहेड्रा के साथ हेक्सेकोंटाहेड्रा बनता है।
प्रत्येक सुनहरे समचतुर्भुज फलक का एक फलक केंद्र, एक शीर्ष और मूल द्वादशफलक के दो किनारे केंद्र होते हैं, जिसके किनारे केंद्र लघु विकर्ण बनाते हैं। प्रत्येक किनारा केंद्र दो शीर्षों और दो फलक केंद्रों से जुड़ा होता है। प्रत्येक फलक केंद्र पाँच किनारे वाले केंद्रों से जुड़ा है, और प्रत्येक शीर्ष तीन किनारे केंद्रों से जुड़ा है।
तारामंडल
रोम्बिक हेक्सेकोन्टाहेड्रोन, रोम्बिक ट्राइकॉन्टाहेड्रोन के 227 स्वावलंबी तारों में से एक है। इसका तारकीय आरेख इस तरह दिखता है, जिसमें मूल रोम्बिक ट्राइकॉन्टाहेड्रॉन चेहरे केंद्रीय रोम्बस के रूप में होते हैं।
संबंधित पॉलीहेड्रा
ग्रेट रोम्बिक ट्राईकॉन्टाहेड्रोन में 30 बड़े अन्तर्विभाजक रोम्बिक चेहरे होते हैं:
लोकप्रिय संस्कृति में
ब्राजील की संस्कृति में, हस्तकला रोम्बिक हेक्सेकोंटाहेड्रोन रंगीन कपड़े और कार्डबोर्ड से बनाया जाता था, जिसे कहा जाता है गीरामुंडोस (पुर्तगाली में वर्ल्ड टर्नर्स) या खुशी के सितारे, माताओं द्वारा सिले और उनकी बेटियों को शादी के तोहफे के रूप में दिए गए। ब्राजील के शहरीकरण के साथ यह रिवाज खत्म हो गया, चूँकि बीसवीं शताब्दी के पूर्वार्द्ध तक ब्राजील के ग्रामीण स्कूलों में हस्तशिल्प के उत्पादन की विधि अभी भी सिखाई जाती थी।[2]
वोल्फरम अल्फा वेबसाइट का लोगो एक लाल समचतुर्भुज हेक्साकॉन्टाहेड्रॉन है और संबंधित मेथेमेटिका सॉफ्टवेयर के लोगो से प्रेरित था।[3]
संदर्भ
- ↑ Grünbaum (1996b)
- ↑ Artesanato se antecipou à descoberta de poliedro [Handicraft anticipated the discovery of a polyhedron] (in Portuguese), IMPA, retrieved 2019-01-08
{{citation}}: CS1 maint: unrecognized language (link) - ↑ "What's in the Logo? That Which We Call a Rhombic Hexecontahedron—Wolfram|Alpha Blog".
ग्रन्थसूची
- Unkelbach, H. "Die kantensymmetrischen, gleichkantigen Polyeder. Deutsche Math. 5, 306-316, 1940.
- Grünbaum, B. (1996a). "A New Rhombic Hexecontahedron". Geombinatorics: 15–18.
- Grünbaum, B. (1996b). "A New Rhombic Hexecontahedron—Once More". Geombinatorics: 55–59.
- Grünbaum, B. (1997). "Still More Rhombic Hexecontahedra". Geombinatorics: 140–142.
- Grünbaum, B. Parallelogram-Faced Isohedra with Edges in Mirror-Planes. Discrete Math. 221, 93-100, 2000.
बाहरी संबंध
- Weisstein, Eric W. "Rhombic hexecontahedron". MathWorld.
- http://www.georgehart.com/virtual-polyhedra/zonohedra-info.html
- The Bilinski dodecahedron, and assorted parallelohedra, zonohedra, monohedra, isozonohedra and otherhedra. Branko Grünbaum