छोटा क्यूबिकुबोक्टाहेड्रोन: Difference between revisions
No edit summary |
No edit summary Tag: Manual revert |
| (2 intermediate revisions by 2 users not shown) | |
(No difference)
| |
Latest revision as of 17:02, 3 May 2023
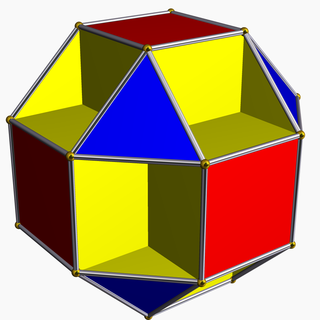
| Small cubicuboctahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 20, E = 48 V = 24 (χ = −4) |
| Faces by sides | 8{3}+6{4}+6{8} |
| Coxeter diagram | |
| Wythoff symbol | 3/2 4 | 4 3 4/3 | 4 |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U13, C38, W69 |
| Dual polyhedron | Small hexacronic icositetrahedron |
| Vertex figure |  4.8.3/2.8 |
| Bowers acronym | Socco |
File:Small cubicuboctahedron.stl ज्यामिति में, छोटा क्यूबिकुबोक्टाहेड्रोन एक समान तारा पॉलीहेड्रॉन है, जिसे U13 के रूप में अनुक्रमित किया गया है। इसके 20 फलक (8 त्रिभुज, 6 वर्ग और 6 अष्टभुज), 48 किनारे और 24 शीर्ष हैं।[1] इसकी शीर्ष आकृति एक रेखित चतुर्भुज है।
छोटाक्यूबिकुबोक्टाहेड्रोन,रोमबिकूबोक्टाहेड्रॉन का अग्रभाग है। इसके चौकोर भाग और इसके अष्टकोणीय भाग एक घन के समानांतर होते हैं, जबकि इसके त्रिकोणीय भाग एक ऑक्टाहेड्रॉन के समानांतर होते हैं: इसलिए इसका नाम क्यूबिकुबोक्टाहेड्रोन है। यह छोटा प्रत्यय इसे विशेष क्यूबुकोक्टाहेड्रॉन से अलग करता है, जिसमें उपरोक्त दिशाओं में भी भाग है।
संबंधित पॉलीहेड्रा
यह तारांकित छंटे हुए हेक्साहेड्रोन के साथ अपनी शीर्ष व्यवस्था को साझा करता है। इसके अतिरिक्त, यह रोम्बिकूबोक्टाहेड्रॉन (एक ही में त्रिकोणीय भाग और 6 वर्ग भाग वाले) के साथ और छोटे रोम्बिकूबोक्टाहेड्रॉन (सामान्यतः अष्टभुजाकार भाग वाले) के साथ अपनी साझा करता है।
 रोम्बिकूबोक्टाहेड्रॉन |
 छोटा क्यूबिकुबोक्टाहेड्रोन |
 छोटा रोम्बिकूबोक्टाहेड्रॉन |
 तारकीय संक्षिप्त हेक्साहेड्र |
संबंधित टाइलिंग
जैसा कि यूलर की विशेषता से पता चलता है, छोटा क्यूबिकुबोक्टाहेड्रोन जीनस 3 का एक टॉरॉयडल पॉलीहेड्रॉन है (स्थलीय रूप से यह जीनस 3 की सतह है), और इस प्रकार जीनस 3 पॉलीहेड्रल सतह के एक (पॉलीहेड्रल) निमज्जन (गणित) के रूप में व्याख्या की जा सकती है। इसके 24 शीर्षों का पूरक, 3- समष्टि में होती है। (किसी भी वर्टेक्स का पड़ोस एक आकृति-8 पर एक शंकु है, जो एक निमज्जन में नहीं हो सकता है। ध्यान दीजिए कि रिटर संदर्भ इस तथ्य को अनदेखा करता है।) अंतर्निहित पॉलीहेड्रॉन (स्वप्रतिच्छेदन की अनदेखी) इस सतह की एक समान टाइलिंग को परिभाषित करता है, और इसलिए छोटा क्यूबिकुबोक्टाहेड्रोन एक समान बहुफलक है। अमूर्त पॉलीटॉप्स की भाषा में, छोटे क्यूबिकूबोक्टाहेड्रॉन इस अमूर्त टोरोइडल पॉलीहेड्रॉन का एक यथार्थ कार्यान्वयन है, जिसका अर्थ है कि यह एक नॉन-जेनरेट पॉलीहेड्रोन है और उनके पास समान समरूपता समूह है। वास्तव में, इस टाइलिंग के साथ अमूर्त जीनस 3 सतह के प्रत्येक स्वचालित रूप को यूक्लिडियन समष्टि की एक सममिति द्वारा कार्यान्वयन किया जाता है।
उच्च जीनस सतहें (जीनस 2 या अधिक) नकारात्मक निरंतर वक्रता (एकरूपीकरण प्रमेय द्वारा) की एक मीट्रिक स्वीकार करती हैं, और परिणामी रीमैन सतह का सार्वभौमिक आवरण हाइपरबोलिक विमान के मॉडल हैं। हाइपरबोलिक समतल में संबंधित यूनिफ़ॉर्म टिलिंग में वर्टेक्स फिगर 3.8.4.8 (त्रिकोण, अष्टभुज, वर्ग, अष्टभुज) है। यदि सतह को वक्रता = -1 का उपयुक्त मीट्रिक दिया गया है, तो कवरिंग मैप एक स्थानीय सममिति है और इस प्रकार अमूर्त शीर्ष संख्या समान है। इस टाइलिंग को विथॉफ प्रतीक 3 4 | 4 द्वारा दर्शाया जा सकता है और दाईं ओर चित्रित किया गया है।

वैकल्पिक रूप से और अधिक सूक्ष्मता से, प्रत्येक चौकोर भाग को 2 त्रिभुजों में और प्रत्येक अष्टकोणीय भाग को 6 त्रिभुजों में काटकर, छोटे क्यूबिकुबोक्टाहेड्रोन को जीनस 3 सतह के संयोजन के नियमित (न केवल एक समान) टाइलिंग के गैर-नियमित रंग के रूप में व्याख्या की जा सकती है। 56 समबाहु त्रिभुज, 24 शीर्षों पर मिलते हैं, प्रत्येक की डिग्री 7 है।[2] यह नियमित टाइलिंग महत्वपूर्ण है क्योंकि यह क्लेन क्वार्टिक की टाइलिंग है, सबसे सममित मीट्रिक के साथ जीनस 3 सतह (सतह के इस टाइलिंग बराबर आइसोमेट्रीज़ के ऑटोमोर्फिज्म), और इस सतह का अभिविन्यास-संरक्षण ऑटोमोर्फिज्म समूह आइसोमोर्फिक है। प्रक्षेपी विशेष रैखिक समूह PSL(2,7), समतुल्य GL(3,2) (ऑर्डिनेशन-प्रिजर्विंग आइसोमेट्रीज का ऑर्डर 168 ग्रुप) है। ध्यान दें कि छोटे क्यूबिकुबोक्टाहेड्रॉन इस अमूर्त पॉलीहेड्रोन की प्राप्ति नहीं है, क्योंकि इसमें केवल 24 अभिविन्यास-प्रस्तुति-प्रस्तुत सममितियां हैं (हर अमूर्त स्वचालनताकृति को यूक्लिडियन सममिति द्वारा सिद्ध नहीं किया जाता है) - छोटे क्यूबिकूबोक्टाहेड्रॉन के आइसोमेट्री न केवल त्रिकोणीय टाइलिंग को संरक्षित करते हैं, बल्कि रंग भी करते हैं, और इसलिए यह पूर्ण सममिति समूह का एक उचित उपसमूह है।
हाइपरबोलिक समतल (यूनिवर्सल कवरिंग) की संबंधित टाइलिंग ऑर्डर -7 त्रिकोणीय टाइलिंग है। क्लेन क्वार्टिक के ऑटोमोर्फिज्म समूह को बढ़ाया जा सकता है (एक समरूपता द्वारा जिसे पॉलीहेड्रॉन की समरूपता द्वारा सिद्ध नहीं किया जाता है, अर्थात् किनारों के दो अंत बिंदुओं का आदान-प्रदान करना जो वर्गों और ऑक्टाहेड्रा को विभाजित करता है) मैथ्यू समूह M24 प्राप्त करने के लिए है।[3]
यह भी देखें
- पांच छोटे क्यूबिकुबोक्टाहेड्रोन का यौगिक
- एकसमान पॉलीहेड्रा की सूची
संदर्भ
- ↑ Maeder, Roman. "13: small cubicuboctahedron". MathConsult.
{{cite web}}: CS1 maint: url-status (link) - ↑ 2.0 2.1 (Richter) Note each face in the polyhedron consist of multiple faces in the tiling, hence the description as a "coloring" – two triangular faces constitute a square face and so forth, as per this explanatory image.
- ↑ (Richter)
- Richter, David A., How to Make the Mathieu Group M24, retrieved 2010-04-15
