सिमसन लाइन: Difference between revisions

Revision as of 18:22, 22 April 2023

परिवृत्त पर बिंदु

P

के संबंध में त्रिभुज

ABC

की सिमसन रेखा LN (लाल) है।

ज्यामिति में, त्रिभुज $ABC$ और इसके परिवृत्त पर बिंदु $P$ दिया गया है, रेखाओं $AB$ , $AC$ , और $BC$ पर $P$ के तीन निकटतम बिंदु संरेख हैं।^[1] इन बिंदुओं से होकर जाने वाली रेखा $P$ की सिमसन रेखा है, जिसका नाम रॉबर्ट सिमसन के नाम पर रखा गया है।^[2] चूँकि, इस अवधारणा को प्रथम बार 1799 में विलियम वालेस द्वारा प्रकाशित किया गया था।^[3]

इसका विपरीत भी सत्य है; यदि तीन रेखाओं पर $P$ के तीन निकटतम बिंदु समरेख हैं, और कोई भी दो रेखाएँ समानांतर नहीं हैं, तो $P$ तीन रेखाओं से बने त्रिभुज के परिवृत्त पर स्थित है, या दूसरे शब्दों में, त्रिभुज $ABC$ की सिमसन रेखा और बिंदु $P$ , $ABC$ और $P$ का सिर्फ पेडल त्रिकोण है, जो सीधी रेखा में पतित हो गया है और यह स्थिति त्रिभुज $ABC$ के परिवृत्त को ज्ञात करने के लिए $P$ को बाधित करती है।

समीकरण

त्रिभुज को जटिल तल में रखते हुए, त्रिकोण $ABC$ को इकाई परिवृत्त के साथ ऐसे शीर्ष होते हैं जिनके स्थानों में जटिल निर्देशांक $a$ , $b$ , $c$ होते हैं, और P को जटिल निर्देशांक $p$ के साथ परिवृत्त पर बिंदु हो। सिमसन रेखा बिंदु $z$ का समुच्चय है।^[4]^{: Proposition 4}

2abc{\bar {z}}-2pz+p^{2}+(a+b+c)p-(bc+ca+ab)-{\frac {abc}{p}}=0,

जहां ओवरबार जटिल संयुग्मन को प्रदर्शित करता है।

गुण

सिमसन रेखाएँ (लाल रंग में) स्टेनर डेल्टॉइड वक्र (नीले रंग में) की स्पर्शरेखाएँ हैं।

त्रिकोण के किसी शीर्ष की सिमसन रेखा उस शीर्ष से गिराए गए त्रिभुज की ऊँचाई (ज्यामिति) होती है, और शीर्ष के बिल्कुल विपरीत बिंदु की सिमसन रेखा उस शीर्ष के विपरीत त्रिभुज की भुजा होती है।

यदि $P$ और $Q$ परिवृत्त पर बिंदु हैं, तो $P$ और $Q$ की सिमसन रेखाओं के मध्य का कोण चाप $PQ$ के कोण का अर्ध है। विशेष रूप से, यदि बिंदु बिलकुल विपरीत हैं, तो उनकी सिमसन रेखाएँ लंबवत होती हैं और इस स्थिति में रेखाओं का प्रतिच्छेदन नौ-बिंदु वाले वृत्त पर स्थित होता है।
$H$ को त्रिभुज $ABC$ के लंबकेंद्र को निरूपित करें, की सिमसन रेखा $P$ खंड को समद्विभाजित करें $PH$ उस बिंदु पर जो नौ-बिंदु वाले वृत्त पर स्थित है।
एक ही परिवृत्त वाले दो त्रिभुज दिए गए हैं, दोनों त्रिभुजों के परिवृत्त पर बिंदु $P$ की सिमसन रेखाओं के मध्य का कोण $P$ पर निर्भर नहीं करता है।
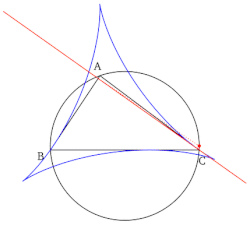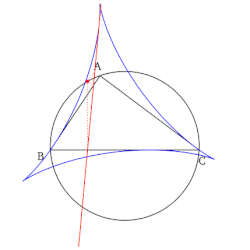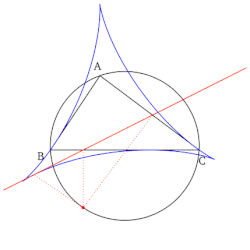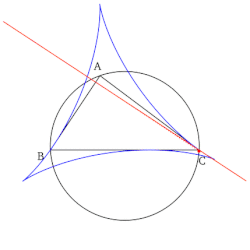
सभी सिमसन रेखाओं का समूह, जब खींचा जाता है, डेल्टोइड के आकार में लिफाफा बनाता है जिसे संदर्भ त्रिभुज के स्टीनर डेल्टोइड के रूप में जाना जाता है।
सिमसन रेखा का निर्माण जो संदर्भ त्रिकोण के पक्ष के साथ युग्मित होता है (ऊपर प्रथम संपत्ति देखें) इस पार्श्व रेखा पर गैर-अल्प बिंदु उत्पन्न करता है। यह बिंदु बनाई जा रही पार्श्व रेखा के मध्य बिंदु के सम्बंध में ऊंचाई के पैर (पार्श्व रेखा पर गिरा हुआ) का प्रतिबिंब है। इसके अतिरिक्त, यह बिंदु संदर्भ त्रिभुज की भुजा और उसके स्टेनर डेल्टॉइड के मध्य स्पर्शरेखा बिंदु है।
चतुर्भुज जो समांतर चतुर्भुज नहीं है, में केवल पेडल बिंदु होता है, जिसे सिमसन बिंदु कहा जाता है, जिसके संबंध में चतुर्भुज पर पैर समरेख होते हैं।^[5] समलम्ब चतुर्भुज का सिम्पसन बिंदु दो गैर समानांतर भुजाओं का प्रतिच्छेदन बिंदु है।^[6]^{: p. 186}
अल्प से अल्प 5 भुजाओं वाले किसी भी उत्तल बहुभुज में सिमसन रेखा नहीं होती है।^[7]

अस्तित्व का प्रमाण

प्रमाण का प्रकार यह दिखाना है, कि $\angle NMP+\angle PML=180^{\circ }$ $PCAB$ चक्रीय चतुर्भुज है, इसलिए $\angle PBA+\angle ACP=\angle PBN+\angle ACP=180^{\circ }$ $PMNB$ चक्रीय चतुर्भुज (थेल्स प्रमेय) है, इसलिए $\angle PBN+\angle NMP=180^{\circ }$ इस प्रकार $\angle NMP=\angle ACP$ है,अब $PLCM$ चक्रीय है, इसलिए $\angle PML=\angle PCL=180^{\circ }-\angle ACP$ इसलिए $\angle NMP+\angle PML=\angle ACP+(180^{\circ }-\angle ACP)=180^{\circ }$ है।

सामान्यीकरण

सामान्यीकरण 1

AP, Bp, Cp का BC, CA, AB पर प्रक्षेप तीन संरेख बिंदु हैं

मान लीजिए कि ABC त्रिभुज है, माना कि रेखा ℓ परिकेन्द्र O से होकर जाती है, और बिंदु P को परिवृत्त पर स्थित होने दें। माना AP, BP, CP क्रमशः A_p, B_p, C_p पर ℓ मिलते हैं। माना A₀, B₀, C₀ क्रमश: क्रमशः BC, CA, AB पर A_p, B_p, C_p के प्रक्षेप हैं। फिर A₀, B₀, C₀ संरेख हैं। इसके अतिरिक्त, नई रेखा PH के मध्य बिंदु से होकर निकलती है, जहाँ H ΔABC का लंबकेन्द्र है। यदि ℓ, P से होकर निकलती है, तो रेखा सिमसन रेखा के संपाती हो जाती है।^[8]^[9]^[10]

सिमसन लाइन का प्रक्षेपी संस्करण

सामान्यीकरण 2

मान लीजिए कि त्रिभुज ABC के शीर्ष शंकु Γ पर स्थित हैं, और Q, P को समतल में दो बिंदु होने देता है। माना PA, PB, PC शंकु को क्रमशः A₁, B₁, C₁ पर प्रतिच्छेद करते हैं। QA₁, BC को A₂ पर, QB₁ AC को B₂, और QC₁ AB को C₂ पर प्रतिछेदित करती है, तब चार बिंदु A₂, B₂, C₂, और P संरेख होते हैं, यदि केवल Q शंकु Γ पर स्थित है।^[11]

सामान्यीकरण 3

चक्रीय चतुर्भुज की सिमसन रेखाएँ में चक्रीय चतुर्भुजों के प्रमेय को आरएफ सिस्टर ने सामान्यीकरण किया।

यह भी देखें

पेडल त्रिकोण
रॉबर्ट सिमसन

संदर्भ

↑ H.S.M. Coxeter and S.L. Greitzer, Geometry revisited, Math. Assoc. America, 1967: p.41.
↑ "Gibson History 7 - Robert Simson". MacTutor History of Mathematics archive. 2008-01-30.
↑ "विलियम वॉलेस". MacTutor History of Mathematics archive.
↑ Todor Zaharinov, "The Simson triangle and its properties", Forum Geometricorum 17 (2017), 373--381. http://forumgeom.fau.edu/FG2017volume17/FG201736.pdf
↑ Daniela Ferrarello, Maria Flavia Mammana, and Mario Pennisi, "Pedal Polygons", Forum Geometricorum 13 (2013) 153–164: Theorem 4.
↑ Olga Radko and Emmanuel Tsukerman, "The Perpendicular Bisector Construction, the Isoptic point, and the Simson Line of a Quadrilateral", Forum Geometricorum 12 (2012). [1]
↑ Tsukerman, Emmanuel (2013). "पैराबोलस के असतत एनालॉग्स के रूप में एक सिमसन रेखा को स्वीकार करने वाले बहुभुजों पर" (PDF). Forum Geometricorum. 13: 197–208.
↑ "सिमसन लाइन का एक सामान्यीकरण". Cut-the-knot. April 2015.
↑ Nguyen Van Linh (2016), "Another synthetic proof of Dao's generalization of the Simson line theorem" (PDF), Forum Geometricorum, 16: 57–61
↑ Nguyen Le Phuoc and Nguyen Chuong Chi (2016). 100.24 A synthetic proof of Dao's generalisation of the Simson line theorem. The Mathematical Gazette, 100, pp 341-345. doi:10.1017/mag.2016.77. The Mathematical Gazette
↑ Smith, Geoff (2015), "99.20 A projective Simson line", The Mathematical Gazette, 99 (545): 339–341, doi:10.1017/mag.2015.47, S2CID 124965348

बाहरी संबंध

Simson Line at cut-the-knot.org
F. M. Jackson and Weisstein, Eric W. "Simson Line". MathWorld.
A generalization of Neuberg's theorem and the Simson-Wallace line at Dynamic Geometry Sketches, an interactive dynamic geometry sketch.

[1] H.S.M. Coxeter and S.L. Greitzer, Geometry revisited, Math. Assoc. America, 1967: p.41.

[2] "Gibson History 7 - Robert Simson". MacTutor History of Mathematics archive. 2008-01-30.

[3] "विलियम वॉलेस". MacTutor History of Mathematics archive.

[TZ-4] Todor Zaharinov, "The Simson triangle and its properties", Forum Geometricorum 17 (2017), 373--381. http://forumgeom.fau.edu/FG2017volume17/FG201736.pdf

[5] Daniela Ferrarello, Maria Flavia Mammana, and Mario Pennisi, "Pedal Polygons", Forum Geometricorum 13 (2013) 153–164: Theorem 4.

[6] Olga Radko and Emmanuel Tsukerman, "The Perpendicular Bisector Construction, the Isoptic point, and the Simson Line of a Quadrilateral", Forum Geometricorum 12 (2012). [1]

[7] Tsukerman, Emmanuel (2013). "पैराबोलस के असतत एनालॉग्स के रूप में एक सिमसन रेखा को स्वीकार करने वाले बहुभुजों पर" (PDF). Forum Geometricorum. 13: 197–208.

[8] "सिमसन लाइन का एक सामान्यीकरण". Cut-the-knot. April 2015.

[9] Nguyen Van Linh (2016), "Another synthetic proof of Dao's generalization of the Simson line theorem" (PDF), Forum Geometricorum, 16: 57–61

[NguyenLePhuocandNguyenChuongChi-10] Nguyen Le Phuoc and Nguyen Chuong Chi (2016). 100.24 A synthetic proof of Dao's generalisation of the Simson line theorem. The Mathematical Gazette, 100, pp 341-345. doi:10.1017/mag.2016.77. The Mathematical Gazette

[11] Smith, Geoff (2015), "99.20 A projective Simson line", The Mathematical Gazette, 99 (545): 339–341, doi:10.1017/mag.2015.47, S2CID 124965348

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

@@ Line 37: / Line 37: @@
 * मान लीजिए कि त्रिभुज ABC के शीर्ष [[शंकु खंड|शंकु]] Γ पर स्थित हैं, और Q, P को समतल में दो बिंदु होने देता है। माना PA, PB, PC शंकु को क्रमशः A<sub>1</sub>, B<sub>1</sub>, C<sub>1</sub> पर प्रतिच्छेद करते हैं। QA<sub>1</sub>, BC को A<sub>2</sub> पर, QB<sub>1</sub> AC को B<sub>2</sub>, और QC<sub>1</sub> AB को C<sub>2</sub> पर प्रतिछेदित करती है, तब चार बिंदु A<sub>2</sub>, B<sub>2</sub>, C<sub>2</sub>, और P संरेख होते हैं, यदि केवल Q शंकु Γ पर स्थित है।<ref>{{citation|url=http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=9834854&fulltextType=XX&fileId=S0025557215020549|first= Geoff|last= Smith|year=2015|title= 99.20 A projective Simson line|journal= The Mathematical Gazette|volume= 99|issue=545|pages=339–341|doi= 10.1017/mag.2015.47|s2cid= 124965348}}</ref>
 === सामान्यीकरण 3 ===
-* R. F. सिस्टर ने [https://www.jstor.org/stable/3606490 [[चक्रीय चतुर्भुज]] की सिमसन रेखाएँ] में चक्रीय चतुर्भुजों के लिए प्रमेय का सामान्यीकरण किया।
+* [https://www.jstor.org/stable/3606490 [[चक्रीय चतुर्भुज]] की सिमसन रेखाएँ] में चक्रीय चतुर्भुजों के प्रमेय को आरएफ सिस्टर ने सामान्यीकरण किया।
 == यह भी देखें ==

Anonymous

Search

सिमसन लाइन: Difference between revisions

Namespaces

More

Page actions

Revision as of 18:22, 22 April 2023

Contents

समीकरण

गुण

अस्तित्व का प्रमाण