जियोडेटिक प्रभाव: Difference between revisions
(Created page with "{{Short description|Precession of satellite orbits due to a celestial body's presence affecting spacetime}} {{about|precession of orbiting bodies|observing binary stars|de Sit...") |
No edit summary |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Precession of satellite orbits due to a celestial body's presence affecting spacetime}} | {{Short description|Precession of satellite orbits due to a celestial body's presence affecting spacetime}} | ||
{{about| | {{about|परिक्रमा करने वाले पिंडों का अग्रगमन|बाइनरी सितारों का अवलोकन|डी सिटर डबल स्टार प्रयोग}} | ||
[[File:Gravity_Probe_turning_axis.gif|thumb|236px|[[ग्रेविटी प्रोब बी]] के लिए मूल्यों के साथ जियोडेटिक प्रभाव का प्रतिनिधित्व।]]जियोडेटिक प्रभाव (जिओडेटिक प्रीसेशन, डी सिटर | [[File:Gravity_Probe_turning_axis.gif|thumb|236px|[[ग्रेविटी प्रोब बी|गुरुत्वाकर्षण प्रोब बी]] के लिए मूल्यों के साथ जियोडेटिक प्रभाव का प्रतिनिधित्व।]]जियोडेटिक प्रभाव (जिओडेटिक प्रीसेशन, डी सिटर पुरस्सरण या डी सिटर प्रभाव के रूप में भी जाना जाता है) एक कक्षीय पिंड के साथ-साथ किए गए वेक्टर पर सामान्य सापेक्षता द्वारा भविष्यवाणी की गई स्पेसटाइम की वक्रता के प्रभाव का प्रतिनिधित्व करता है। उदाहरण के लिए , सदिश वेक्टर पृथ्वी की परिक्रमा करने वाले जाइरोस्कोप का कोणीय संवेग हो सकता है, जैसा कि गुरुत्वाकर्षण प्रोब बी प्रयोग द्वारा किया गया है। 1916 में [[विलियम डी सिटर]] द्वारा पहली बार जियोडेटिक प्रभाव की भविष्यवाणी की गई थी, जिन्होंने पृथ्वी-चंद्रमा प्रणाली की गति को सापेक्ष सुधार प्रदान किया था। 1918 में जैन स्काउटन और 1920 में [[एड्रियन फोकर]] द्वारा डी सिटर के काम को बढ़ाया गया था।<ref name=Eisenstaedt>{{cite book |title=सामान्य सापेक्षता के इतिहास में अध्ययन|author1=Jean Eisenstaedt |author2=Anne J. Kox |url=https://books.google.com/books?id=vDHCF_3vIhUC&pg=PA42 |page=42 |isbn=0-8176-3479-7 |publisher=[[Birkhäuser]] |year=1988}}</ref> इसे लाप्लास-रेंज-लेनज़ वेक्टर के घूर्णन के सामान्य खगोलीय कक्षाओं के एक विशेष धर्मनिरपेक्ष पुरस्सरण पर भी प्रयुक्त किया जा सकता है।<ref>{{cite journal |last=de Sitter |first=W |year=1916 |title=आइंस्टीन के गुरुत्वाकर्षण के सिद्धांत और उसके खगोलीय परिणामों पर|journal=Mon. Not. R. Astron. Soc. |volume=77 |pages=155–184 |bibcode=1916MNRAS..77..155D|doi = 10.1093/mnras/77.2.155 |doi-access=free }}</ref> | ||
[[geodesic]] प्रभाव शब्द के दो अलग-अलग अर्थ हैं क्योंकि गतिमान पिंड | |||
डी सिटर | [[geodesic|जियोडेटिक]] प्रभाव शब्द के दो अलग-अलग अर्थ हैं क्योंकि गतिमान पिंड स्पिनिंग या गैर-स्पिनिंग हो सकता है। गैर-स्पिनिंग पिंड भूगर्भ विज्ञान में गति करते हैं, जबकि स्पिनिंग पिंड थोड़े अलग कक्षाओं में गति करते हैं।<ref>Rindler, p. 254.</ref> | ||
डी सिटर पुरस्सरण और लेंस-थिरिंग पुरस्सरण (फ्रेम ड्रैगिंग) के बीच का अंतर यह है कि डी सिटर प्रभाव केवल केंद्रीय द्रव्यमान की उपस्थिति के कारण होता है, जबकि लेंस-थिरिंग पुरस्सरण केंद्रीय द्रव्यमान के घूर्णन के कारण होता है। लेंस-थिरिंग पुरस्सरण के साथ डी सिटर पुरस्सरण को मिलाकर कुल पुरस्सरण की गणना की जाती है। | |||
== प्रायोगिक पुष्टि == | == प्रायोगिक पुष्टि == | ||
गुरुत्वाकर्षण प्रोब बी, एक प्रयोग जो पृथ्वी के चारों ओर कक्षा में [[जाइरोस्कोप]] के स्पिन अक्ष के झुकाव को मापता है, द्वारा जियोडेटिक प्रभाव को 0.5% प्रतिशत से बेहतर स्पष्ट के लिए सत्यापित किया गया था।<ref>{{cite web |author1=Everitt, C.W.F. |author2=Parkinson, B.W. |url=http://einstein.stanford.edu/content/final_report/GPB_Final_NASA_Report-020509-web.pdf |title=Gravity Probe B Science Results—NASA Final Report |year=2009 |access-date=2009-05-02}}</ref> पहला परिणाम 14 अप्रैल, 2007 को [[अमेरिकन फिजिकल सोसायटी]] की बैठक में घोषित किया गया।<ref>{{Cite news |last=Kahn |first=Bob |date=April 14, 2007 |title=Was Einstein right? Scientists provide first public peek at Gravity Probe B results |work=Stanford News |url=http://einstein.stanford.edu/content/press_releases/SU/pr-aps-041807.pdf |access-date=January 3, 2023}}</ref> | |||
| Line 13: | Line 15: | ||
{{General relativity sidebar |phenomena}} | {{General relativity sidebar |phenomena}} | ||
पुरस्सरण प्राप्त करने के लिए, मान लें कि | पुरस्सरण प्राप्त करने के लिए, मान लें कि प्रणाली घूर्णन [[श्वार्जस्चिल्ड मीट्रिक]] में है। अघूर्णन मीट्रिक है | ||
:<math>ds^2 = dt^2 \left(1-\frac{2m}{r}\right) - dr^2 \left(1 - \frac{2m}{r}\right)^{-1} - r^2 (d\theta^2 + \sin^2 \theta \, d\phi'^2) , | :<math>ds^2 = dt^2 \left(1-\frac{2m}{r}\right) - dr^2 \left(1 - \frac{2m}{r}\right)^{-1} - r^2 (d\theta^2 + \sin^2 \theta \, d\phi'^2) , | ||
</math> | </math> | ||
जहां | जहां ''c'' = ''G'' = 1. | ||
हम एक कोणीय वेग के साथ एक घूर्णन समन्वय प्रणाली का परिचय देते हैं | हम एक कोणीय वेग <math>\omega</math> के साथ एक घूर्णन समन्वय प्रणाली का परिचय देते हैं जैसे कि θ=π/2 समतल में एक गोलाकार कक्षा में एक उपग्रह विराम में रहता है। यह हमें देता है | ||
:<math>d\phi = d\phi' - \omega \, dt.</math> | :<math>d\phi = d\phi' - \omega \, dt.</math> | ||
इस समन्वय प्रणाली में, रेडियल स्थिति r पर एक पर्यवेक्षक r पर स्थित एक वेक्टर को कोणीय आवृत्ति ω के साथ घूमते हुए देखता है। | इस समन्वय प्रणाली में, रेडियल स्थिति r पर एक पर्यवेक्षक r पर स्थित एक वेक्टर को कोणीय आवृत्ति ω के साथ घूमते हुए देखता है। चूंकि , यह प्रेक्षक आर के किसी अन्य मान पर स्थित सदिश को सापेक्षिक समय फैलाव के कारण एक अलग दर पर घूर्णन के रूप में देखता है। श्वार्ज़स्चिल्ड मीट्रिक को घूर्णन फ्रेम में बदलना, और यह मानते हुए <math>\theta</math> एक स्थिरांक है, हम पाते हैं | ||
:<math> | :<math> | ||
| Line 30: | Line 32: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
<math>\beta = \sin^2(\theta)</math> के साथ। θ = π/2 समतल में परिक्रमा करने वाले पिंड के लिए हमारे पास β = 1 होगा और पिंड की विश्व-रेखा हर समय निरंतर स्थानिक निर्देशांक बनाए रखेगी। अब मीट्रिक विहित रूप में है | |||
:<math>ds^2 = e^{2\Phi}\left(dt - w_i \, dx^i \right)^2 - k_{ij} \, dx^i \, dx^j.</math> | :<math>ds^2 = e^{2\Phi}\left(dt - w_i \, dx^i \right)^2 - k_{ij} \, dx^i \, dx^j.</math> | ||
| Line 41: | Line 43: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहां अंतिम समानता केवल मुक्त रूप से गिरने वाले पर्यवेक्षकों के लिए सत्य है | जहां अंतिम समानता केवल मुक्त रूप से गिरने वाले पर्यवेक्षकों के लिए सत्य है जिसके लिए कोई त्वरण नहीं है और इस प्रकार <math> \Phi,_{i} = 0</math> इससे ये होता है | ||
कोई त्वरण नहीं है | |||
:<math> | :<math> | ||
\Phi,_i = \frac{2m/r^2 - 2r\beta\omega^2}{2(1-2m/r-r^2 \beta\omega^2)} = 0. | \Phi,_i = \frac{2m/r^2 - 2r\beta\omega^2}{2(1-2m/r-r^2 \beta\omega^2)} = 0. | ||
</math> | </math> | ||
ω | ω उपज के लिए इस समीकरण को हल करना | ||
:<math> | :<math> | ||
\omega^2 = \frac{m}{r^3 \beta}. | \omega^2 = \frac{m}{r^3 \beta}. | ||
</math> | </math> | ||
यह अनिवार्य रूप से केप्लर के नियम हैं। केप्लर के अवधियों के नियम, जो इस विशेष घूर्णन समन्वय प्रणाली के समय समन्वय | यह अनिवार्य रूप से केप्लर के नियम हैं। केप्लर के अवधियों के नियम, जो इस विशेष घूर्णन समन्वय प्रणाली के समय समन्वय t के संदर्भ में व्यक्त किए जाने पर सापेक्ष रूप से स्पष्ट होते हैं। घूर्णन फ्रेम में, उपग्रह आराम पर रहता है, किंतु उपग्रह पर सवार एक पर्यवेक्षक जाइरोस्कोप के कोणीय संवेग सदिश को ω दर से आगे बढ़ते हुए देखता है। यह प्रेक्षक दूर के तारों को घूर्णन के रूप में भी देखता है, किंतु वे समय के फैलाव के कारण थोड़ी भिन्न दर से घूमते हैं। मान लीजिए τ जाइरोस्कोप का [[उचित समय]] है। तब | ||
:<math> | :<math> | ||
\Delta \tau = \left(1-\frac{2m}{r} - r^2 \beta\omega^2 \right)^{1/2} \, dt = \left(1-\frac{3m}{r}\right)^{1/2} \, dt. | \Delta \tau = \left(1-\frac{2m}{r} - r^2 \beta\omega^2 \right)^{1/2} \, dt = \left(1-\frac{3m}{r}\right)^{1/2} \, dt. | ||
</math> | </math> | ||
−2m/r पद की व्याख्या गुरुत्वीय समय फैलाव के रूप में की जाती है, जबकि अतिरिक्त −m/r संदर्भ के इस फ्रेम के घूर्णन के कारण होता है। चलो α' घूर्णन फ्रेम में संचित पुरस्सरण हो। तब से <math>\alpha' = \Omega \Delta \tau</math>दूर के तारों के सापेक्ष, एक कक्षा के | −2m/r पद की व्याख्या गुरुत्वीय समय फैलाव के रूप में की जाती है, जबकि अतिरिक्त −m/r संदर्भ के इस फ्रेम के घूर्णन के कारण होता है। चलो α' घूर्णन फ्रेम में संचित पुरस्सरण हो। तब से <math>\alpha' = \Omega \Delta \tau</math>दूर के तारों के सापेक्ष, एक कक्षा के समय अग्रगमन द्वारा दिया जाता है: | ||
:<math> | :<math> | ||
| Line 71: | Line 72: | ||
== थॉमस रियायत == | == थॉमस रियायत == | ||
डी सिटर | डी सिटर पुरस्सरण को [[थॉमस प्रीसेशन|थॉमस]] पुरस्सरण नामक [[कीनेमेटीक्स का]] प्रभाव में तोड़ने का प्रयास किया जा सकता है, जो गुरुत्वाकर्षण के घुमावदार स्पेसटाइम के कारण होने वाले ज्यामितीय प्रभाव के साथ संयुक्त है। कम से कम एक लेखक<ref>Rindler, Page 234</ref> इसका इस तरह से वर्णन करता है, किंतु अन्य कहते हैं कि थॉमस पुरस्सरण पृथ्वी की सतह पर जाइरोस्कोप के लिए काम आता है ..., किंतु स्वतंत्र रूप से चलने वाले उपग्रह में जाइरोस्कोप के लिए नहीं होता है ।<ref>Misner, Thorne, and Wheeler, Gravitation, p. 1118</ref> पूर्व व्याख्या पर एक आपत्ति यह है कि आवश्यक थॉमस पुरस्सरण में गलत चिन्ह है। फर्मी-वाकर परिवहन समीकरण<ref>Misner, Thorne, and Wheeler, Gravitation, p. 165, pp. 175-176, pp. 1117-1121</ref> जियोडेटिक प्रभाव और थॉमस पुरस्सरण दोनों देता है और घुमावदार स्पेसटाइम में त्वरित गति के लिए स्पिन 4-वेक्टर के परिवहन का वर्णन करता है। स्पिन 4-वेक्टर वेग 4-वेक्टर के लिए ओर्थोगोनल है। फर्मी-वाकर परिवहन इस संबंध को बनाए रखता है। यदि कोई त्वरण नहीं है, तो फर्मी-वॉकर परिवहन एक जियोडेसिक के साथ समानांतर परिवहन है और जियोडेटिक प्रभाव के कारण स्पिन की पूर्वता देता है। फ्लैट मिन्कोव्स्की स्पेसटाइम में एकसमान परिपत्र गति के कारण त्वरण के लिए, फर्मी वाकर परिवहन थॉमस अग्रगमन देता है। | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 93: | Line 94: | ||
{{Relativity}} | {{Relativity}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Collapse templates]] | |||
[[Category:Created On 29/03/2023]] | [[Category:Created On 29/03/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with empty portal template]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Portal-inline template with redlinked portals]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Translated in Hindi]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:सामान्य सापेक्षता]] | |||
Latest revision as of 16:28, 16 May 2023
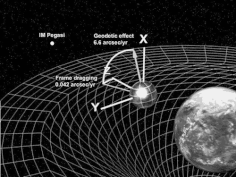
जियोडेटिक प्रभाव (जिओडेटिक प्रीसेशन, डी सिटर पुरस्सरण या डी सिटर प्रभाव के रूप में भी जाना जाता है) एक कक्षीय पिंड के साथ-साथ किए गए वेक्टर पर सामान्य सापेक्षता द्वारा भविष्यवाणी की गई स्पेसटाइम की वक्रता के प्रभाव का प्रतिनिधित्व करता है। उदाहरण के लिए , सदिश वेक्टर पृथ्वी की परिक्रमा करने वाले जाइरोस्कोप का कोणीय संवेग हो सकता है, जैसा कि गुरुत्वाकर्षण प्रोब बी प्रयोग द्वारा किया गया है। 1916 में विलियम डी सिटर द्वारा पहली बार जियोडेटिक प्रभाव की भविष्यवाणी की गई थी, जिन्होंने पृथ्वी-चंद्रमा प्रणाली की गति को सापेक्ष सुधार प्रदान किया था। 1918 में जैन स्काउटन और 1920 में एड्रियन फोकर द्वारा डी सिटर के काम को बढ़ाया गया था।[1] इसे लाप्लास-रेंज-लेनज़ वेक्टर के घूर्णन के सामान्य खगोलीय कक्षाओं के एक विशेष धर्मनिरपेक्ष पुरस्सरण पर भी प्रयुक्त किया जा सकता है।[2]
जियोडेटिक प्रभाव शब्द के दो अलग-अलग अर्थ हैं क्योंकि गतिमान पिंड स्पिनिंग या गैर-स्पिनिंग हो सकता है। गैर-स्पिनिंग पिंड भूगर्भ विज्ञान में गति करते हैं, जबकि स्पिनिंग पिंड थोड़े अलग कक्षाओं में गति करते हैं।[3]
डी सिटर पुरस्सरण और लेंस-थिरिंग पुरस्सरण (फ्रेम ड्रैगिंग) के बीच का अंतर यह है कि डी सिटर प्रभाव केवल केंद्रीय द्रव्यमान की उपस्थिति के कारण होता है, जबकि लेंस-थिरिंग पुरस्सरण केंद्रीय द्रव्यमान के घूर्णन के कारण होता है। लेंस-थिरिंग पुरस्सरण के साथ डी सिटर पुरस्सरण को मिलाकर कुल पुरस्सरण की गणना की जाती है।
प्रायोगिक पुष्टि
गुरुत्वाकर्षण प्रोब बी, एक प्रयोग जो पृथ्वी के चारों ओर कक्षा में जाइरोस्कोप के स्पिन अक्ष के झुकाव को मापता है, द्वारा जियोडेटिक प्रभाव को 0.5% प्रतिशत से बेहतर स्पष्ट के लिए सत्यापित किया गया था।[4] पहला परिणाम 14 अप्रैल, 2007 को अमेरिकन फिजिकल सोसायटी की बैठक में घोषित किया गया।[5]
सूत्र
| General relativity |
|---|
 |
पुरस्सरण प्राप्त करने के लिए, मान लें कि प्रणाली घूर्णन श्वार्जस्चिल्ड मीट्रिक में है। अघूर्णन मीट्रिक है
जहां c = G = 1.
हम एक कोणीय वेग के साथ एक घूर्णन समन्वय प्रणाली का परिचय देते हैं जैसे कि θ=π/2 समतल में एक गोलाकार कक्षा में एक उपग्रह विराम में रहता है। यह हमें देता है
इस समन्वय प्रणाली में, रेडियल स्थिति r पर एक पर्यवेक्षक r पर स्थित एक वेक्टर को कोणीय आवृत्ति ω के साथ घूमते हुए देखता है। चूंकि , यह प्रेक्षक आर के किसी अन्य मान पर स्थित सदिश को सापेक्षिक समय फैलाव के कारण एक अलग दर पर घूर्णन के रूप में देखता है। श्वार्ज़स्चिल्ड मीट्रिक को घूर्णन फ्रेम में बदलना, और यह मानते हुए एक स्थिरांक है, हम पाते हैं
के साथ। θ = π/2 समतल में परिक्रमा करने वाले पिंड के लिए हमारे पास β = 1 होगा और पिंड की विश्व-रेखा हर समय निरंतर स्थानिक निर्देशांक बनाए रखेगी। अब मीट्रिक विहित रूप में है
इस विहित रूप से, हम उचित समय में जाइरोस्कोप की घूर्णी दर को आसानी से निर्धारित कर सकते हैं
जहां अंतिम समानता केवल मुक्त रूप से गिरने वाले पर्यवेक्षकों के लिए सत्य है जिसके लिए कोई त्वरण नहीं है और इस प्रकार इससे ये होता है
ω उपज के लिए इस समीकरण को हल करना
यह अनिवार्य रूप से केप्लर के नियम हैं। केप्लर के अवधियों के नियम, जो इस विशेष घूर्णन समन्वय प्रणाली के समय समन्वय t के संदर्भ में व्यक्त किए जाने पर सापेक्ष रूप से स्पष्ट होते हैं। घूर्णन फ्रेम में, उपग्रह आराम पर रहता है, किंतु उपग्रह पर सवार एक पर्यवेक्षक जाइरोस्कोप के कोणीय संवेग सदिश को ω दर से आगे बढ़ते हुए देखता है। यह प्रेक्षक दूर के तारों को घूर्णन के रूप में भी देखता है, किंतु वे समय के फैलाव के कारण थोड़ी भिन्न दर से घूमते हैं। मान लीजिए τ जाइरोस्कोप का उचित समय है। तब
−2m/r पद की व्याख्या गुरुत्वीय समय फैलाव के रूप में की जाती है, जबकि अतिरिक्त −m/r संदर्भ के इस फ्रेम के घूर्णन के कारण होता है। चलो α' घूर्णन फ्रेम में संचित पुरस्सरण हो। तब से दूर के तारों के सापेक्ष, एक कक्षा के समय अग्रगमन द्वारा दिया जाता है:
प्रथम क्रम टेलर श्रृंखला के साथ हम पाते हैं
थॉमस रियायत
डी सिटर पुरस्सरण को थॉमस पुरस्सरण नामक कीनेमेटीक्स का प्रभाव में तोड़ने का प्रयास किया जा सकता है, जो गुरुत्वाकर्षण के घुमावदार स्पेसटाइम के कारण होने वाले ज्यामितीय प्रभाव के साथ संयुक्त है। कम से कम एक लेखक[6] इसका इस तरह से वर्णन करता है, किंतु अन्य कहते हैं कि थॉमस पुरस्सरण पृथ्वी की सतह पर जाइरोस्कोप के लिए काम आता है ..., किंतु स्वतंत्र रूप से चलने वाले उपग्रह में जाइरोस्कोप के लिए नहीं होता है ।[7] पूर्व व्याख्या पर एक आपत्ति यह है कि आवश्यक थॉमस पुरस्सरण में गलत चिन्ह है। फर्मी-वाकर परिवहन समीकरण[8] जियोडेटिक प्रभाव और थॉमस पुरस्सरण दोनों देता है और घुमावदार स्पेसटाइम में त्वरित गति के लिए स्पिन 4-वेक्टर के परिवहन का वर्णन करता है। स्पिन 4-वेक्टर वेग 4-वेक्टर के लिए ओर्थोगोनल है। फर्मी-वाकर परिवहन इस संबंध को बनाए रखता है। यदि कोई त्वरण नहीं है, तो फर्मी-वॉकर परिवहन एक जियोडेसिक के साथ समानांतर परिवहन है और जियोडेटिक प्रभाव के कारण स्पिन की पूर्वता देता है। फ्लैट मिन्कोव्स्की स्पेसटाइम में एकसमान परिपत्र गति के कारण त्वरण के लिए, फर्मी वाकर परिवहन थॉमस अग्रगमन देता है।
यह भी देखें
- फ्रेम खींच
- सामान्य सापेक्षता में भूगणित
- गुरुत्वाकर्षण अच्छी तरह से
- गुरुत्वाकर्षण भौतिकी और सापेक्षता की समयरेखा
टिप्पणियाँ
- ↑ Jean Eisenstaedt; Anne J. Kox (1988). सामान्य सापेक्षता के इतिहास में अध्ययन. Birkhäuser. p. 42. ISBN 0-8176-3479-7.
- ↑ de Sitter, W (1916). "आइंस्टीन के गुरुत्वाकर्षण के सिद्धांत और उसके खगोलीय परिणामों पर". Mon. Not. R. Astron. Soc. 77: 155–184. Bibcode:1916MNRAS..77..155D. doi:10.1093/mnras/77.2.155.
- ↑ Rindler, p. 254.
- ↑ Everitt, C.W.F.; Parkinson, B.W. (2009). "Gravity Probe B Science Results—NASA Final Report" (PDF). Retrieved 2009-05-02.
- ↑ Kahn, Bob (April 14, 2007). "Was Einstein right? Scientists provide first public peek at Gravity Probe B results" (PDF). Stanford News. Retrieved January 3, 2023.
- ↑ Rindler, Page 234
- ↑ Misner, Thorne, and Wheeler, Gravitation, p. 1118
- ↑ Misner, Thorne, and Wheeler, Gravitation, p. 165, pp. 175-176, pp. 1117-1121
संदर्भ
- Wolfgang Rindler (2006) Relativity: special, general, and cosmological (2nd Ed.), Oxford University Press, ISBN 978-0-19-856731-8
बाहरी संबंध
- Gravity Probe B websites at NASA and Stanford University
- Precession in Curved Space "The Geodetic Effect"
- Geodetic Effect
