गैलोज़ ज्यामिति: Difference between revisions

Latest revision as of 11:23, 17 May 2023

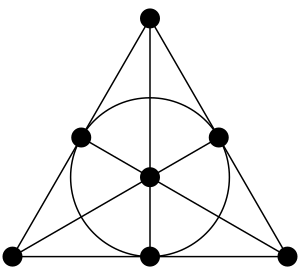
फानो समतल, दो तत्वों के साथ क्षेत्र के ऊपर प्रक्षेपी समतल, गैलोज़ ज्यामिति में सबसे सरल वस्तुओं में से एक है।

गैलोज़ ज्यामिति (19वीं सदी के फ्रांसीसी गणितज्ञ इवरिस्ट गैलोइस के नाम पर) परिमित ज्यामिति की शाखा है जोपरिमित क्षेत्र (या गैलोइस फ़ील्ड) पर बीजगणितीय ज्यामिति और विश्लेषणात्मक ज्यामिति से संबंधित है।^[1] अधिक संकीर्ण रूप से, गाल्वा ज्यामिति को परिमित क्षेत्र पर प्रक्षेपी समष्‍टि के रूप में परिभाषित किया जा सकता है।^[2]

अध्ययन की वस्तुओं में परिमित समष्‍टि और परिमित क्षेत्रों सजातीयउपसमष्‍टि (प्रक्षेपी ज्यामिति) और उनमें निहित विभिन्न संरचनाएं सम्मिलित हैं। विशेष रूप से, आर्क (प्रक्षेपी ज्योमेट्री), ओवल (प्रक्षेपी समतल), हाइपरोवाल्स, यूनिटल (ज्यामिति), अवरोधक समुच्चय, अंडाकार, कैप्स, स्प्रेड और गैर-परिमित ज्यामिति में पाए जाने वाले संरचनाओं के सभी परिमित एनालॉग हैं। परिमित क्षेत्रों में परिभाषित सदिश समष्‍टि विशेष रूप से निर्माण विधियों में महत्वपूर्ण भूमिका निभाते हैं।

परिमित क्षेत्रों पर प्रक्षेपी समष्‍टि

अंकन

चूंकि प्रक्षेपी ज्यामिति के सामान्य संकेतन का कभी-कभी उपयोग किया जाता है, परिमित क्षेत्रों पर प्रक्षेपी रिक्त समष्‍टि को निरूपित करना अधिक सामान्य है $PG(n, q)$ , जहाँ $n$ "ज्यामितीय" आयाम है (नीचे देखें), और $q$ परिमित क्षेत्र (या गैल्वा क्षेत्र) का क्रम है $GF(q)$ , जो पूर्णांक होना चाहिए जो एक प्रमुख या अभाज्य घात है।

उपरोक्त संकेतन में ज्यामितीय आयाम उस प्रणाली को संदर्भित करता है जिससे रेखाएं 1-आयामी होती हैं, समतल 2-आयामी होते हैं, बिंदु 0-आयामी होते हैं, आदि। संशोधक, कभी-कभी ज्यामितीय के अतिरिक्त प्रक्षेपी शब्द का उपयोग किया जाता है, इस अवधारणा के बाद से आवश्यक है आयाम की संख्या सदिश रिक्त समष्‍टि के लिए उपयोग की जाने वाली अवधारणा से भिन्न होती है (अर्थात, एक आधार में तत्वों की संख्या)। सामान्यतः एक ही नाम के साथ दो अलग-अलग अवधारणाएं होने से संदर्भ के कारण अलग-अलग क्षेत्रों में ज्यादा कठिनाई नहीं होती है, लेकिन इस विषय में सदिश समष्टि और प्रक्षेपी समष्टि दोनों महत्वपूर्ण भूमिका निभाते हैं और भ्रम की संभावना बहुत अधिक होती है। सदिश समष्‍टि अवधारणा को कभी-कभी बीजगणितीय आयाम के रूप में जाना जाता है।^[3]

निर्माण

मान लीजिए कि $V = V(n + 1, q)$ परिमित क्षेत्र $GF(q)$ पर परिभाषित (बीजीय) आयाम $n + 1$ के सदिश समष्‍टि को दर्शाता है। प्रक्षेप्य समष्‍टि $PG(n, q)$ में $V$ के सभी घनात्मक (बीजीय) आयामी सदिश उप-समष्‍टि होते हैं। निर्माण को देखने का वैकल्पिक तरीका $PG(n, q)$ बिंदुओं के के तुल्यता वर्ग के रूप में परिभाषित करना है। तुल्यता संबंध के अंतर्गत के $V$ के शून्य सदिश जिससे दो सदिश समतुल्य होते हैं यदि एक दूसरे का अदिश गुणक है। बिंदुओं के समुच्चय की रैखिक स्वतंत्रता की परिभाषा का उपयोग करके उप-समष्‍टि तब बिंदुओं से बनाए जाते हैं।

उप-समष्‍टि

बीजगणितीय आयाम $d + 1$ का $V$ का सदिश उपसमष्टि ज्यामितीय आयाम $d$ के $PG(n, q)$ (प्रक्षेपी) उपसमष्टि है। प्रक्षेपी उपस्थानों को सामान्य ज्यामितीय नाम दिए गए हैं; बिंदु, रेखाएँ, तल और ठोस क्रमशः 0,1,2 और 3-आयामी उपसमष्टि हैं। संपूर्ण समष्‍टि एक $n$ -आयामी उप-समष्‍टि और एक ( $n - 1$ )-आयामी उप-समष्‍टि को हाइपरप्लेन (या अभाज्य) कहा जाता है।

बीजगणितीय आयाम के सदिश उपस्थानों की संख्या $d$ सदिश समष्‍टि में $V(n, q)$ गाऊसी द्विपद गुणांक द्वारा दिया जाता है,

\left[{\begin{matrix}n\\d\end{matrix}}\right]_{q}={\frac {(q^{n}-1)(q^{n}-q)\cdots (q^{n}-q^{d-1})}{(q^{d}-1)(q^{d}-q)\cdots (q^{d}-q^{d-1})}}.

इसलिए, $k$ की संख्या आयामी प्रक्षेप्य उप-समष्‍टि $PG(n, q)$ द्वारा दिया गया है

\left[{\begin{matrix}n+1\\k+1\end{matrix}}\right]_{q}={\frac {(q^{n+1}-1)(q^{n+1}-q)\cdots (q^{n+1}-q^{k})}{(q^{k+1}-1)(q^{k+1}-q)\cdots (q^{k+1}-q^{k})}}.

इस प्रकार, उदाहरण के लिए, रेखाएँ की संख्या ( $k$ = 1) PG(3,2) में है

\left[{\begin{matrix}4\\2\end{matrix}}\right]_{2}={\frac {(2^{4}-1)(2^{4}-2)}{(2^{2}-1)(2^{2}-2)}}={\frac {(15)(14)}{(3)(2)}}=35.

यह इस प्रकार है कि अंकों की कुल संख्या ( $k$ = 0) का $P = PG(n, q)$ है

\left[{\begin{matrix}n+1\\1\end{matrix}}\right]_{q}={\frac {(q^{n+1}-1)}{(q-1)}}=q^{n}+q^{n-1}+\cdots +q+1.

यह $P$ के हाइपरप्लेन की संख्या के बराबर भी है।

$P$ के बिंदु के माध्यम से रेखाओं की संख्या की गणना की जा सकती है $q^{n-1}+q^{n-2}+\cdots +q+1$ और यह निश्चित बिंदु से गुजरने वाले हाइपरप्लेन की संख्या भी है।^[4]

$U$ और $W$ को गाल्वा ज्यामिति $P = PG(n, q)$ के उप-समष्‍टि होने दें। प्रतिच्छेदन $U \cap W$ , $P$ की उपसमष्टि है , लेकिन समुच्चय सैद्धांतिक संघ नहीं हो सकता है। $< U, W >$ द्वारा निरूपित इन उप-स्थानों का जुड़ाव, $P$ की सबसे छोटी उपसमष्टि है जिसमें दोनों $U$ और $W$ दोनों सम्मिलित हैं। इन दो उप-स्थानों के जुड़ने और प्रतिच्छेदन के आयाम सूत्र द्वारा संबंधित हैं,

|<U,W>|=|U|+|W|-|U\cap W|.

निर्देशांक

एक निश्चित आधार के संबंध में, $V$ में प्रत्येक सदिश में विशिष्ट रूप से $GF(q)$ के तत्वों के $n + 1$ -ट्यूपल द्वारा दर्शाया गया है। प्रक्षेप्य बिंदु सदिशों का तुल्यता वर्ग है, इसलिए कई अलग-अलग निर्देशांक (वैक्टरों के) हैं जो एक ही बिंदु के अनुरूप हैं। हालाँकि, ये सभी एक दूसरे से संबंधित हैं क्योंकि प्रत्येक दूसरों का गैर-शून्य अदिश गुणक है। यह प्रक्षेपी समष्‍टि के बिंदुओं का प्रतिनिधित्व करने के लिए उपयोग किए जाने वाले सजातीय निर्देशांक की अवधारणा को वृद्धि देता है।

इतिहास

गीनो फानो गैलोज़ ज्यामिति के क्षेत्र में प्रारंभिक लेखक थे। 1892 के अपने लेख में,^[5]प्रक्षेपी n-समष्टि के लिए स्वयंसिद्धों के अपने समुच्चय की स्वतंत्रता को सिद्ध करने पर,^[6] अन्य बातों के अतिरिक्त, उन्होंने प्रक्षेपी हार्मोनिक संयुग्म होने के परिणामों को इसके संयुग्म के बराबर माना हैं। यह 15 बिंदुओं, 35 रेखाओं और 15 समतलों के साथ परिमित त्रि-आयामी समष्टि में समाहित सात बिंदुओं और सात रेखाओं के विन्यास की ओर जाता है, जिसमें प्रत्येक पंक्ति में केवल तीन बिंदु होते हैं।^[5]^: 114 इस समष्टि में सभी समतलों में सात बिंदु और सात रेखाएँ होती हैं और अब इन्हें फानो समतलों के रूप में जाना जाता है। फ़ानो ने मनमाना आयाम और अभाज्य आदेशों के गाल्वा ज्यामिति का वर्णन किया था।

जॉर्ज कॉनवेल ने 1910 में गैलोज़ ज्यामिति का प्रारंभिक अनुप्रयोग दिया, जब उन्होंने पीजी (3,2) में तिरछी रेखाओं के समुच्चय के विभाजन के रूप में किर्कमैन की स्कूली छात्राओं की समस्या के समाधान की विशेषता बताई, गैलोज़ क्षेत्र GF(2) पर त्रि-आयामी प्रक्षेपी ज्यामिति हैं। .^[7]विशेषता 0 के क्षेत्र में समष्टि में रेखा ज्यामिति के तरीकों के समान, कॉनवेल ने PG (5,2) में प्लकर निर्देशांक का उपयोग किया और क्लेन क्वाड्रिक पर PG(3,2) में रेखाएँ का प्रतिनिधित्व करने वाले बिंदुओं की पहचान की थी।

1955 में बेनियामिनो सेग्रे ने q विषम के लिए अंडाकारों की विशेषता बताई थी। सेग्रे के प्रमेय में कहा गया है कि विषम क्रम के गैलोज़ ज्यामिति में (अर्थात, विषम विशेषता (क्षेत्र) के एक परिमित क्षेत्र पर परिभाषित एक प्रक्षेप्य समतल) प्रत्येक अंडाकार शंकु खंड है। इस परिणाम को अधिकांशतः अनुसंधान के महत्वपूर्ण क्षेत्र के रूप में गैलोइस ज्यामिति स्थापित करने का श्रेय दिया जाता है। 1958 में अंतर्राष्ट्रीय गणितीय कांग्रेस सेग्रे ने उस समय तक ज्ञात गैलोज़ ज्यामिति में परिणामों का एक सर्वेक्षण प्रस्तुत किया था।

यह भी देखें

घटना ज्यामिति

↑ SpringerLink
↑ "Projective spaces over a finite field, otherwise known as Galois geometries, ...", (Hirschfeld & Thas 1992)
↑ There are authors who use the term rank for algebraic dimension. Authors that do this frequently just use dimension when discussing geometric dimension.
↑ Beutelspacher & Rosenbaum 1998, pp. 24-25
↑ ^5.0 ^5.1 Fano, G. (1892), "Sui postulati fondamentali della geometria proiettiva", Giornale di Matematiche, 30: 106–132
↑ Collino, Conte & Verra 2013, p. 6
↑ George M. Conwell (1910) "The 3-space PG(3,2) and its Groups", Annals of Mathematics 11:60–76 doi:10.2307/1967582

संदर्भ

Beutelspacher, Albrecht; Rosenbaum, Ute (1998), Projective Geometry / From Foundations to Applications, Cambridge University Press, ISBN 978-0-521-48364-3
Collino, Alberto; Conte, Alberto; Verra, Alessandro (2013). "On the life and scientific work of Gino Fano". arXiv:1311.7177.
De Beule, Jan; Storme, Leo (2011), Current Research Topics in Galois Geometry, Nova Science Publishers, ISBN 978-1-61209-523-3
Hirschfeld, J. W. P. (1979), Projective Geometries Over Finite Fields, Oxford University Press, ISBN 978-0-19-850295-1, emphasizing dimensions one and two.{{citation}}: CS1 maint: postscript (link)
Hirschfeld, J. W. P. (1985), Finite Projective Spaces of Three Dimensions, Oxford University Press, ISBN 0-19-853536-8, dimension 3.{{citation}}: CS1 maint: postscript (link)
Hirschfeld, J. W. P.; Thas, J. A. (1992), General Galois Geometries, Oxford University Press, ISBN 978-0-19-853537-9, treating general dimension.{{citation}}: CS1 maint: postscript (link)

बाहरी संबंध

Galois geometry at Encyclopaedia of Mathematics, SpringerLink

[1] SpringerLink

[2] "Projective spaces over a finite field, otherwise known as Galois geometries, ...", (Hirschfeld & Thas 1992)

[3] There are authors who use the term rank for algebraic dimension. Authors that do this frequently just use dimension when discussing geometric dimension.

[4] Beutelspacher & Rosenbaum 1998, pp. 24-25

[Fano1-5] 5.0 ^5.1 Fano, G. (1892), "Sui postulati fondamentali della geometria proiettiva", Giornale di Matematiche, 30: 106–132

[6] Collino, Conte & Verra 2013, p. 6

[7] George M. Conwell (1910) "The 3-space PG(3,2) and its Groups", Annals of Mathematics 11:60–76 doi:10.2307/1967582

[1]

[2]

[3]

[4]

[5]

[6]

[7]

@@ Line 1: / Line 1: @@
-[[File:Fano plane.svg|thumb|[[फानो विमान]], दो तत्वों के साथ क्षेत्र के ऊपर [[प्रक्षेपी विमान]], गैलोज़ ज्यामिति में सबसे सरल वस्तुओं में से एक है।]]गैलोज़ ज्यामिति (इसलिए 19वीं सदी के फ्रांसीसी गणितज्ञ इवरिस्ट गैलोइस के नाम पर) [[परिमित ज्यामिति]] की शाखा है जो एक [[परिमित क्षेत्र]] (या ''गैलोइस फ़ील्ड'') पर [[बीजगणितीय ज्यामिति]] और [[विश्लेषणात्मक ज्यामिति]] से संबंधित है।<ref>SpringerLink</ref> अधिक संकीर्ण रूप से, एक गाल्वा ज्यामिति को एक परिमित क्षेत्र पर एक प्रक्षेपी स्थान के रूप में परिभाषित किया जा सकता है।<ref>"Projective spaces over a finite field, otherwise known as Galois geometries, ...", {{Harv|Hirschfeld|Thas|1992}}</ref>
+[[File:Fano plane.svg|thumb|[[फानो विमान|फानो समतल]], दो तत्वों के साथ क्षेत्र के ऊपर [[प्रक्षेपी विमान|प्रक्षेपी समतल]], गैलोज़ ज्यामिति में सबसे सरल वस्तुओं में से एक है।]]'''गैलोज़ ज्यामिति''' (19वीं सदी के फ्रांसीसी गणितज्ञ इवरिस्ट गैलोइस के नाम पर) [[परिमित ज्यामिति]] की शाखा है जो[[परिमित क्षेत्र]] (या ''गैलोइस फ़ील्ड'') पर [[बीजगणितीय ज्यामिति]] और [[विश्लेषणात्मक ज्यामिति]] से संबंधित है।<ref>SpringerLink</ref> अधिक संकीर्ण रूप से, गाल्वा ज्यामिति को परिमित क्षेत्र पर प्रक्षेपी समष्‍टि के रूप में परिभाषित किया जा सकता है।<ref>"Projective spaces over a finite field, otherwise known as Galois geometries, ...", {{Harv|Hirschfeld|Thas|1992}}</ref>
-अध्ययन की वस्तुओं में परिमित स्थान और परिमित क्षेत्रों [[चाप (प्रक्षेपी ज्यामिति)]] और उनमें निहित विभिन्न संरचनाएं शामिल हैं। विशेष रूप से, आर्क (प्रोजेक्टिव ज्योमेट्री) एस, [[ ओवल (प्रक्षेपी विमान) ]] एस, हाइपरोवाल्स, यूनिटल (ज्यामिति), [[ अवरोधक सेट ]], [[ अंडाकार ]]्स, कैप्स, स्प्रेड और गैर-परिमित ज्यामिति में पाए जाने वाले संरचनाओं के सभी परिमित एनालॉग। परिमित क्षेत्रों में परिभाषित सदिश स्थान विशेष रूप से निर्माण विधियों में महत्वपूर्ण भूमिका निभाते हैं।
+अध्ययन की वस्तुओं में परिमित समष्‍टि और परिमित क्षेत्रों  [[चाप (प्रक्षेपी ज्यामिति)|सजातीयउपसमष्‍टि (प्रक्षेपी ज्यामिति)]] और उनमें निहित विभिन्न संरचनाएं सम्मिलित हैं। विशेष रूप से, आर्क (प्रक्षेपी ज्योमेट्री), [[ ओवल (प्रक्षेपी विमान) |ओवल (प्रक्षेपी समतल)]], हाइपरोवाल्स, यूनिटल (ज्यामिति), [[ अवरोधक सेट |अवरोधक समुच्चय]], [[ अंडाकार | अंडाकार]], कैप्स, स्प्रेड और गैर-परिमित ज्यामिति में पाए जाने वाले संरचनाओं के सभी परिमित एनालॉग हैं। परिमित क्षेत्रों में परिभाषित सदिश समष्‍टि विशेष रूप से निर्माण विधियों में महत्वपूर्ण भूमिका निभाते हैं।
-== परिमित क्षेत्रों पर प्रक्षेपी स्थान ==
+== परिमित क्षेत्रों पर प्रक्षेपी समष्‍टि ==
 === अंकन ===
-हालांकि [[प्रक्षेपी ज्यामिति]] के सामान्य संकेतन का कभी-कभी उपयोग किया जाता है, परिमित क्षेत्रों पर प्रक्षेपी रिक्त स्थान को निरूपित करना अधिक सामान्य है{{math|PG(''n'', ''q'')}}, कहाँ {{mvar|n}} ज्यामितीय आयाम है (नीचे देखें), और {{mvar|q}} परिमित क्षेत्र (या गैल्वा क्षेत्र) का क्रम है {{math|GF(''q'')}}, जो एक पूर्णांक होना चाहिए जो एक प्रमुख या प्रधान शक्ति है।
+चूंकि [[प्रक्षेपी ज्यामिति]] के सामान्य संकेतन का कभी-कभी उपयोग किया जाता है, परिमित क्षेत्रों पर प्रक्षेपी रिक्त समष्‍टि को निरूपित करना अधिक सामान्य है {{math|PG(''n'', ''q'')}}, जहाँ {{mvar|n}} "ज्यामितीय" आयाम है (नीचे देखें), और {{mvar|q}} परिमित क्षेत्र (या गैल्वा क्षेत्र) का क्रम है {{math|GF(''q'')}}, जो पूर्णांक होना चाहिए जो एक प्रमुख या अभाज्य घात है।
-उपरोक्त संकेतन में ज्यामितीय आयाम उस प्रणाली को संदर्भित करता है जिससे रेखाएं 1-आयामी होती हैं, विमान 2-आयामी होते हैं, अंक 0-आयामी होते हैं, आदि। संशोधक, कभी-कभी ज्यामितीय के बजाय प्रक्षेपी शब्द का उपयोग किया जाता है, इस अवधारणा के बाद से आवश्यक है आयाम की संख्या वेक्टर रिक्त स्थान के लिए उपयोग की जाने वाली अवधारणा से भिन्न होती है (अर्थात, एक आधार में तत्वों की संख्या)। आम तौर पर एक ही नाम के साथ दो अलग-अलग अवधारणाएं होने से संदर्भ के कारण अलग-अलग क्षेत्रों में ज्यादा कठिनाई नहीं होती है, लेकिन इस विषय में वेक्टर स्पेस और प्रोजेक्टिव स्पेस दोनों महत्वपूर्ण भूमिका निभाते हैं और भ्रम की संभावना बहुत अधिक होती है। सदिश स्थान अवधारणा को कभी-कभी बीजगणितीय आयाम के रूप में जाना जाता है।<ref>There are authors who use the term ''rank'' for algebraic dimension. Authors that do this frequently just use ''dimension'' when discussing geometric dimension.</ref>
+उपरोक्त संकेतन में ज्यामितीय आयाम उस प्रणाली को संदर्भित करता है जिससे रेखाएं 1-आयामी होती हैं, समतल 2-आयामी होते हैं, बिंदु 0-आयामी होते हैं, आदि। संशोधक, कभी-कभी ज्यामितीय के अतिरिक्त प्रक्षेपी शब्द का उपयोग किया जाता है, इस अवधारणा के बाद से आवश्यक है आयाम की संख्या सदिश रिक्त समष्‍टि के लिए उपयोग की जाने वाली अवधारणा से भिन्न होती है (अर्थात, एक आधार में तत्वों की संख्या)। सामान्यतः एक ही नाम के साथ दो अलग-अलग अवधारणाएं होने से संदर्भ के कारण अलग-अलग क्षेत्रों में ज्यादा कठिनाई नहीं होती है, लेकिन इस विषय में सदिश समष्टि और प्रक्षेपी समष्टि दोनों महत्वपूर्ण भूमिका निभाते हैं और भ्रम की संभावना बहुत अधिक होती है। सदिश समष्‍टि अवधारणा को कभी-कभी बीजगणितीय आयाम के रूप में जाना जाता है।<ref>There are authors who use the term ''rank'' for algebraic dimension. Authors that do this frequently just use ''dimension'' when discussing geometric dimension.</ref>
 === निर्माण ===
-होने देना {{math|1=V = V(''n + 1'', ''q'')}} (बीजीय) आयाम के वेक्टर स्थान को दर्शाता है {{math|''n'' + 1}} परिमित क्षेत्र पर परिभाषित {{math|GF(''q'')}}. प्रक्षेप्य स्थान {{math|PG(''n'', ''q'')}} के सभी सकारात्मक (बीजीय) आयामी वेक्टर उप-स्थान होते हैं {{math|V}}. निर्माण को देखने का एक वैकल्पिक तरीका बिंदुओं को परिभाषित करना है {{math|PG(''n'', ''q'')}} के गैर-शून्य सदिशों के [[तुल्यता वर्ग]]ों के रूप में {{math|V}} [[तुल्यता संबंध]] के तहत जिससे दो सदिश समतुल्य होते हैं यदि एक दूसरे का [[अदिश गुणक]] है। बिंदुओं के सेट की [[रैखिक स्वतंत्रता]] की परिभाषा का उपयोग करके उप-स्थान तब बिंदुओं से बनाए जाते हैं।
+मान लीजिए कि {{math|1=V = V(''n + 1'', ''q'')}} परिमित क्षेत्र {{math|GF(''q'')}} पर परिभाषित (बीजीय) आयाम {{math|''n'' + 1}} के सदिश समष्‍टि को दर्शाता है। प्रक्षेप्य समष्‍टि {{math|PG(''n'', ''q'')}} में {{math|V}} के सभी घनात्मक (बीजीय) आयामी सदिश उप-समष्‍टि होते हैं। निर्माण को देखने का वैकल्पिक तरीका {{math|PG(''n'', ''q'')}} बिंदुओं के के [[तुल्यता वर्ग]] के रूप में परिभाषित करना है। [[तुल्यता संबंध]] के अंतर्गत के {{math|V}} के शून्य सदिश जिससे दो सदिश समतुल्य होते हैं यदि एक दूसरे का [[अदिश गुणक]] है। बिंदुओं के समुच्चय की [[रैखिक स्वतंत्रता]] की परिभाषा का उपयोग करके उप-समष्‍टि तब बिंदुओं से बनाए जाते हैं।
-=== उप-स्थान ===
+=== उप-समष्‍टि ===
-बीजीय आयाम की सदिश उपसमष्टि {{math|''d'' + 1}} का {{math|V}} की (प्रक्षेपी) उपसमष्टि है {{math|PG(''n'', ''q'')}} ज्यामितीय आयाम का {{mvar|d}}. प्रक्षेपी उपस्थानों को सामान्य ज्यामितीय नाम दिए गए हैं; बिंदु, रेखाएँ, तल और ठोस क्रमशः 0,1,2 और 3-आयामी उपसमष्टि हैं। संपूर्ण स्थान एक है {{mvar|n}}-आयामी उप-स्थान और एक ({{math|''n'' − 1}})-डायमेंशनल सबस्पेस को हाइपरप्लेन (या प्राइम) कहा जाता है।
+बीजगणितीय आयाम {{math|''d'' + 1}} का {{math|V}} का सदिश उपसमष्टि ज्यामितीय आयाम {{mvar|d}} के {{math|PG(''n'', ''q'')}}(प्रक्षेपी) उपसमष्टि है। प्रक्षेपी उपस्थानों को सामान्य ज्यामितीय नाम दिए गए हैं; बिंदु, रेखाएँ, तल और ठोस क्रमशः 0,1,2 और 3-आयामी उपसमष्टि हैं। संपूर्ण समष्‍टि एक {{mvar|n}}-आयामी उप-समष्‍टि और एक ({{math|''n'' − 1}})-आयामी उप-समष्‍टि को हाइपरप्लेन (या अभाज्य) कहा जाता है।
-बीजगणितीय आयाम के सदिश उपस्थानों की संख्या {{mvar|d}} सदिश स्थान में {{math|V(''n'', ''q'')}} [[गाऊसी द्विपद गुणांक]] द्वारा दिया जाता है,
+बीजगणितीय आयाम के सदिश उपस्थानों की संख्या {{mvar|d}} सदिश समष्‍टि में {{math|V(''n'', ''q'')}} [[गाऊसी द्विपद गुणांक]] द्वारा दिया जाता है,
 :<math>\left [ \begin{matrix} n \\ d \end{matrix} \right]_q = \frac{(q^n - 1)(q^n - q) \cdots (q^n - q^{d-1})}{(q^d -1)(q^d - q) \cdots (q^d - q^{d-1})}.</math>
-इसलिए, की संख्या {{mvar|k}} आयामी प्रक्षेप्य उप-स्थान {{math|PG(''n'', ''q'')}} द्वारा दिया गया है
+इसलिए, {{mvar|k}} की संख्या आयामी प्रक्षेप्य उप-समष्‍टि {{math|PG(''n'', ''q'')}} द्वारा दिया गया है
 :<math>\left [ \begin{matrix} n + 1 \\ k + 1 \end{matrix} \right]_q = \frac{(q^{n+1} - 1)(q^{n+1} - q) \cdots (q^{n+1} - q^k)}{(q^{k+1} -1)(q^{k+1} - q) \cdots (q^{k+1} - q^k)}.</math>
-इस प्रकार, उदाहरण के लिए, लाइनों की संख्या ({{mvar|k}} = 1) पीजी(3,2) में है
+इस प्रकार, उदाहरण के लिए, रेखाएँ की संख्या ({{mvar|k}} = 1) PG(3,2) में है
 :<math>\left [ \begin{matrix} 4 \\ 2 \end{matrix} \right]_2 = \frac{(2^4 - 1)(2^4 - 2)}{(2^2 -1)(2^2 - 2)} = \frac{(15)(14)}{(3)(2)} = 35.</math>
 यह इस प्रकार है कि अंकों की कुल संख्या ({{mvar|k}} = 0) का {{math|1='''P''' = PG(''n'', ''q'')}} है
 :<math>\left [ \begin{matrix} n + 1 \\ 1 \end{matrix} \right]_q = \frac{(q^{n+1} - 1)}{(q -1)} = q^n + q^{n-1} + \cdots + q + 1.</math>
-यह के हाइपरप्लेन की संख्या के बराबर भी है {{mvar|'''P'''}}.
+यह {{mvar|'''P'''}} के हाइपरप्लेन की संख्या के बराबर भी है।
-के एक बिंदु के माध्यम से लाइनों की संख्या {{mvar|'''P'''}} की गणना की जा सकती है <math>q^{n-1} + q^{n-2} + \cdots + q + 1</math> और यह एक निश्चित बिंदु से गुजरने वाले हाइपरप्लेन की संख्या भी है।<ref>{{harvnb|Beutelspacher|Rosenbaum|1998|loc=pp. 24-25}}</ref>
+{{mvar|'''P'''}} के बिंदु के माध्यम से रेखाओं की संख्या की गणना की जा सकती है <math>q^{n-1} + q^{n-2} + \cdots + q + 1</math> और यह निश्चित बिंदु से गुजरने वाले हाइपरप्लेन की संख्या भी है।<ref>{{harvnb|Beutelspacher|Rosenbaum|1998|loc=pp. 24-25}}</ref>
-होने देना {{mvar|U}} और {{mvar|W}} गाल्वा ज्यामिति के उप-स्थान बनें {{math|1='''P''' = PG(''n'', ''q'')}}. चौराहा {{math|''U'' ∩ ''W''}} की एक उपसमष्टि है {{math|'''P'''}}, लेकिन सेट सैद्धांतिक संघ नहीं हो सकता है। द्वारा निरूपित इन उप-स्थानों का जुड़ाव {{math|<''U'', ''W''>}}, की सबसे छोटी उपसमष्टि है {{math|'''P'''}} जिसमें दोनों शामिल हैं {{mvar|U}} और {{mvar|W}}. इन दो उप-स्थानों के जुड़ने और प्रतिच्छेदन के आयाम सूत्र द्वारा संबंधित हैं,
+{{mvar|U}} और {{mvar|W}} को गाल्वा ज्यामिति {{math|1='''P''' = PG(''n'', ''q'')}} के उप-समष्‍टि होने दें। प्रतिच्छेदन {{math|''U'' ∩ ''W''}}, {{math|'''P'''}} की उपसमष्टि है , लेकिन समुच्चय सैद्धांतिक संघ नहीं हो सकता है। {{math|<''U'', ''W''>}} द्वारा निरूपित इन उप-स्थानों का जुड़ाव, {{math|'''P'''}} की सबसे छोटी उपसमष्टि है  जिसमें दोनों {{mvar|U}} और {{mvar|W}} दोनों सम्मिलित हैं। इन दो उप-स्थानों के जुड़ने और प्रतिच्छेदन के आयाम सूत्र द्वारा संबंधित हैं,
 :<math>|<U,W>| = |U| + |W| - |U \cap W|.</math>
 === निर्देशांक ===
-{{main|Homogeneous coordinates}}
+{{main|सजातीय निर्देशांक}}
-एक निश्चित आधार के संबंध में, प्रत्येक वेक्टर में {{math|V}} विशिष्ट रूप से एक द्वारा दर्शाया गया है ({{math|''n'' + 1}})- के तत्वों का टपल {{math|GF(''q'')}}. एक प्रक्षेप्य बिंदु सदिशों का एक तुल्यता वर्ग है, इसलिए कई अलग-अलग निर्देशांक (वैक्टरों के) हैं जो एक ही बिंदु के अनुरूप हैं। हालाँकि, ये सभी एक दूसरे से संबंधित हैं क्योंकि प्रत्येक दूसरों का एक गैर-शून्य अदिश गुणक है। यह प्रक्षेपी स्थान के बिंदुओं का प्रतिनिधित्व करने के लिए उपयोग किए जाने वाले सजातीय निर्देशांक की अवधारणा को जन्म देता है।
+एक निश्चित आधार के संबंध में, {{math|V}} में प्रत्येक सदिश में विशिष्ट रूप से {{math|GF(''q'')}} के तत्वों के {{math|''n'' + 1}}-ट्यूपल द्वारा दर्शाया गया है। प्रक्षेप्य बिंदु सदिशों का तुल्यता वर्ग है, इसलिए कई अलग-अलग निर्देशांक (वैक्टरों के) हैं जो एक ही बिंदु के अनुरूप हैं। हालाँकि, ये सभी एक दूसरे से संबंधित हैं क्योंकि प्रत्येक दूसरों का गैर-शून्य अदिश गुणक है। यह प्रक्षेपी समष्‍टि के बिंदुओं का प्रतिनिधित्व करने के लिए उपयोग किए जाने वाले सजातीय निर्देशांक की अवधारणा को वृद्धि देता है।
 == इतिहास ==
-[[गीनो फानो]] गैलोज़ ज्यामिति के क्षेत्र में एक प्रारंभिक लेखक थे। 1892 के अपने लेख में,<ref name=Fano1>{{citation|first=G.|last=Fano|authorlink=Gino Fano|title=Sui postulati fondamentali della geometria proiettiva|url=http://www.bdim.eu/item?id=GM_Fano_1892_1|year=1892|journal=Giornale di Matematiche|volume= 30|pages=106–132}}</ref> प्रोजेक्टिव स्पेस | प्रोजेक्टिव एन-स्पेस के लिए स्वयंसिद्धों के अपने सेट की स्वतंत्रता को साबित करने पर,<ref>{{harvnb|Collino|Conte|Verra|2013|loc=p. 6}}</ref> अन्य बातों के अलावा, उन्होंने एक [[प्रक्षेपी हार्मोनिक संयुग्म]] होने के परिणामों को इसके संयुग्म के बराबर माना। यह 15 बिंदुओं, 35 रेखाओं और 15 विमानों के साथ परिमित त्रि-आयामी अंतरिक्ष में समाहित सात बिंदुओं और सात रेखाओं के विन्यास की ओर जाता है, जिसमें प्रत्येक पंक्ति में केवल तीन बिंदु होते हैं।<ref name=Fano1 />{{rp|114}} इस अंतरिक्ष में सभी विमानों में सात बिंदु और सात रेखाएँ होती हैं और अब इन्हें फानो विमानों के रूप में जाना जाता है। फ़ानो ने मनमाना आयाम और प्रधान आदेशों के गाल्वा ज्यामिति का वर्णन किया।
+[[गीनो फानो]] गैलोज़ ज्यामिति के क्षेत्र में प्रारंभिक लेखक थे। 1892 के अपने लेख में,<ref name=Fano1>{{citation|first=G.|last=Fano|authorlink=Gino Fano|title=Sui postulati fondamentali della geometria proiettiva|url=http://www.bdim.eu/item?id=GM_Fano_1892_1|year=1892|journal=Giornale di Matematiche|volume= 30|pages=106–132}}</ref>प्रक्षेपी ''n''-समष्टि के लिए स्वयंसिद्धों के अपने समुच्चय की स्वतंत्रता को सिद्ध करने पर,<ref>{{harvnb|Collino|Conte|Verra|2013|loc=p. 6}}</ref> अन्य बातों के अतिरिक्त, उन्होंने [[प्रक्षेपी हार्मोनिक संयुग्म]] होने के परिणामों को इसके संयुग्म के बराबर माना हैं। यह 15 बिंदुओं, 35 रेखाओं और 15 समतलों के साथ परिमित त्रि-आयामी समष्टि में समाहित सात बिंदुओं और सात रेखाओं के विन्यास की ओर जाता है, जिसमें प्रत्येक पंक्ति में केवल तीन बिंदु होते हैं।<ref name=Fano1 />{{rp|114}} इस समष्टि में सभी समतलों में सात बिंदु और सात रेखाएँ होती हैं और अब इन्हें फानो समतलों के रूप में जाना जाता है। फ़ानो ने मनमाना आयाम और अभाज्य आदेशों के गाल्वा ज्यामिति का वर्णन किया था।
-जॉर्ज कॉनवेल ने 1910 में गैलोज़ ज्यामिति का एक प्रारंभिक अनुप्रयोग दिया, जब उन्होंने पीजी (3,2) में तिरछी रेखाओं के सेट के विभाजन के रूप में किर्कमैन की स्कूली छात्राओं की समस्या के समाधान की विशेषता बताई, गैलोज़ क्षेत्र [[GF(2)]] पर त्रि-आयामी प्रक्षेपी ज्यामिति। .<ref>George M. Conwell (1910) "The 3-space PG(3,2) and its Groups", [[Annals of Mathematics]] 11:60–76 {{doi|10.2307/1967582}}</ref>
+जॉर्ज कॉनवेल ने 1910 में गैलोज़ ज्यामिति का प्रारंभिक अनुप्रयोग दिया, जब उन्होंने पीजी (3,2) में तिरछी रेखाओं के समुच्चय के विभाजन के रूप में किर्कमैन की स्कूली छात्राओं की समस्या के समाधान की विशेषता बताई, गैलोज़ क्षेत्र [[GF(2)]] पर त्रि-आयामी प्रक्षेपी ज्यामिति हैं। .<ref>George M. Conwell (1910) "The 3-space PG(3,2) and its Groups", [[Annals of Mathematics]] 11:60–76 {{doi|10.2307/1967582}}</ref>[[विशेषता 0]] के क्षेत्र में समष्टि में रेखा ज्यामिति के तरीकों के समान, कॉनवेल ने PG (5,2) में प्लकर निर्देशांक का उपयोग किया और [[क्लेन क्वाड्रिक]] पर PG(3,2) में रेखाएँ का प्रतिनिधित्व करने वाले बिंदुओं की पहचान की थी।
-[[विशेषता 0]] के क्षेत्र में अंतरिक्ष में लाइन ज्यामिति के तरीकों के समान, कॉनवेल ने पीजी (5,2) में प्लकर निर्देशांक का इस्तेमाल किया और [[क्लेन क्वाड्रिक]] पर पीजी (3,2) में लाइनों का प्रतिनिधित्व करने वाले बिंदुओं की पहचान की।
-में [[Beniamino Segre]] ने q विषम के लिए अंडाकारों की विशेषता बताई। सेग्रे के प्रमेय में कहा गया है कि विषम क्रम के एक गैलोज़ ज्यामिति में (अर्थात, विषम विशेषता (क्षेत्र) के एक परिमित क्षेत्र पर परिभाषित एक प्रक्षेप्य विमान) प्रत्येक अंडाकार एक [[शंकु खंड]] है। इस परिणाम को अक्सर अनुसंधान के एक महत्वपूर्ण क्षेत्र के रूप में गैलोइस ज्यामिति स्थापित करने का श्रेय दिया जाता है। 1958 में [[अंतर्राष्ट्रीय गणितीय कांग्रेस]] सेग्रे ने उस समय तक ज्ञात गैलोज़ ज्यामिति में परिणामों का एक सर्वेक्षण प्रस्तुत किया।
+में [[Beniamino Segre|बेनियामिनो सेग्रे]] ने q विषम के लिए अंडाकारों की विशेषता बताई थी। सेग्रे के प्रमेय में कहा गया है कि विषम क्रम के गैलोज़ ज्यामिति में (अर्थात, विषम विशेषता (क्षेत्र) के एक परिमित क्षेत्र पर परिभाषित एक प्रक्षेप्य समतल) प्रत्येक अंडाकार [[शंकु खंड]] है। इस परिणाम को अधिकांशतः अनुसंधान के महत्वपूर्ण क्षेत्र के रूप में गैलोइस ज्यामिति स्थापित करने का श्रेय दिया जाता है। 1958 में [[अंतर्राष्ट्रीय गणितीय कांग्रेस]] सेग्रे ने उस समय तक ज्ञात गैलोज़ ज्यामिति में परिणामों का एक सर्वेक्षण प्रस्तुत किया था।
 == यह भी देखें ==
@@ Line 94: / Line 90: @@
 * ''[https://encyclopediaofmath.org/wiki/Galois_geometry Galois geometry]'' at Encyclopaedia of Mathematics, SpringerLink
+[[Category:CS1 maint]]
-[[Category: परिमित ज्यामिति]] [[Category: परिमित क्षेत्र]] [[Category: बीजगणितीय ज्यामिति]] [[Category: विश्लेषणात्मक ज्यामिति]]
-[[Category: Machine Translated Page]]
 [[Category:Created On 08/05/2023]]
+[[Category:Machine Translated Page]]
+[[Category:Pages with script errors]]
+[[Category:Templates Vigyan Ready]]
+[[Category:परिमित क्षेत्र]]
+[[Category:परिमित ज्यामिति]]
+[[Category:बीजगणितीय ज्यामिति]]
+[[Category:विश्लेषणात्मक ज्यामिति]]

Anonymous

Search

गैलोज़ ज्यामिति: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 11:23, 17 May 2023

Contents

परिमित क्षेत्रों पर प्रक्षेपी समष्‍टि