बहुपद द्विपाशी: Difference between revisions
No edit summary |
No edit summary |
||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
[[Image:Cyc7.png|thumb| <math>|z^6+z^5+z^4+z^3+ </math> | [[Image:Cyc7.png|thumb| <math>|z^6+z^5+z^4+z^3+ </math> | ||
<math> z^2+z+1|=1</math>]]गणित में, एक बहुपद द्विपाशी या ''बहुपद स्तर वक्र'' घात 2n का एक [[बीजगणितीय वक्र]] है, जो घात ''n'' के जटिल गुणांक वाले बहुपद ''p'' से निर्मित होता है। | <math> z^2+z+1|=1</math>]]गणित में, एक बहुपद द्विपाशी या ''बहुपद स्तर वक्र'' घात 2n का एक [[बीजगणितीय वक्र]] है, जो घात ''n'' के जटिल गुणांक वाले बहुपद ''p'' से निर्मित होता है। | ||
ऐसे किसी बहुपद ''p'' और धनात्मक वास्तविक संख्या ''c'' के लिए, हम सम्मिश्र संख्याओं के समुच्चय को <math>|p(z)| = c</math> द्वारा परिभाषित कर सकते हैं संख्याओं के इस सम्मुच्चय को वास्तविक कार्तीय समतल में बिंदुओं के बराबर किया जा सकता है, जिससे एक बीजगणितीय वक्र ƒ(x, y) =c<sup>2 2n घात का होता है, जो z = x + iy के संदर्भ में | ऐसे किसी बहुपद ''p'' और धनात्मक वास्तविक संख्या ''c'' के लिए, हम सम्मिश्र संख्याओं के समुच्चय को <math>|p(z)| = c</math> द्वारा परिभाषित कर सकते हैं संख्याओं के इस सम्मुच्चय को वास्तविक कार्तीय समतल में बिंदुओं के बराबर किया जा सकता है, जिससे एक बीजगणितीय वक्र ƒ(x, y) =c<sup>2</sup> 2n घात का होता है, जो z = x + iy के संदर्भ में <math>p(z) \bar p(\bar z)</math>के विस्तार का परिणाम है। | ||
जब p घात 1 का बहुपद होता है तो परिणामी वक्र केवल एक वृत्त होता है जिसका केंद्र p का शून्य होता है। जब p घात 2 का बहुपद होता है तो वक्र [[कैसिनी अंडाकार]] होता है। | जब p घात 1 का बहुपद होता है तो परिणामी वक्र केवल एक वृत्त होता है जिसका केंद्र p का शून्य होता है। जब p घात 2 का बहुपद होता है तो वक्र [[कैसिनी अंडाकार]] होता है। | ||
| Line 9: | Line 8: | ||
== वन द्विपाशी == | == वन द्विपाशी == | ||
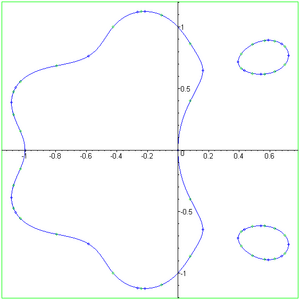
[[Image:Erdos5.png|thumb|घात दस और | [[Image:Erdos5.png|thumb|घात दस और प्रकार छह का एर्डोस द्विपाशी]]पॉल एर्डोस का एक अनुमान जिसने काफी रुचि आकर्षित की है, एक बहुपद लेमनिस्केट की अधिकतम लंबाई ƒ(x, y) = 1 घात 2n होती है जब p [[मोनिक बहुपद]] है, जो एर्डोस ने अनुमान लगाया था जब p(z) = zn - 1 प्राप्त किया गया था। | ||
यह अभी भी सिद्ध नहीं हुआ है लेकिन फ्रायंटोव और [[फेडर नाज़रोव]] ने | यह अभी भी सिद्ध नहीं हुआ है लेकिन फ्रायंटोव और [[फेडर नाज़रोव]] ने सिद्ध किया है कि p a स्थानीय अधिकतम देता है।<ref> | ||
{{cite journal| | {{cite journal| | ||
first1=A| | first1=A| | ||
| Line 23: | Line 21: | ||
pages=49–60| | pages=49–60| | ||
arxiv=0808.0717| | arxiv=0808.0717| | ||
bibcode=2008arXiv0808.0717F}}</ref> | bibcode=2008arXiv0808.0717F}}</ref> उस स्थिति में जब n = 2, एर्दोस [[लेम्निस्केट या बर्नौली|द्विपाशी या बर्नौली]] द्विपाशी है | ||
:<math>(x^2+y^2)^2=2(x^2-y^2)\,</math> | :<math>(x^2+y^2)^2=2(x^2-y^2)\,</math> | ||
और यह सिद्ध हो चुका है कि यह | और यह सिद्ध हो चुका है कि यह वस्तुतः घात चार में अधिकतम लंबाई है। एर्डोस द्विपाशी में तीन सामान्य n-गुना बिंदु हैं, जिनमें से एक मूल में है, और (n − 1)(n − 2)/2 का एक [[ज्यामितीय जीनस|ज्यामितीय प्रकार]] है। व्युत्क्रम ज्यामिति द्वारा ईकाई वृत में एर्डोस द्विपाशी, घात n का एक गैर-एकवचन वक्र प्राप्त करता है। | ||
== सामान्य बहुपद लेमनसेट == | == सामान्य बहुपद लेमनसेट == | ||
सामान्य तौर पर, एक बहुपद द्विपाशी मूल को स्पर्श नहीं करेगा, और केवल दो सामान्य n-गुना विलक्षणताएं होंगी, और इसलिए (n − 1) | सामान्य तौर पर, एक बहुपद द्विपाशी मूल को स्पर्श नहीं करेगा, और केवल दो सामान्य n-गुना विलक्षणताएं होंगी, और इसलिए (n − 1)<sup>2 का एक प्रकार होगा। वास्तविक वक्र के रूप में, इसमें कई असंबद्ध घटक हो सकते हैं। इसलिए, यह एक द्विपाशी की तरह नहीं लगेगा, जिससे नाम एक मिथ्या नाम बन जाएगा। | ||
इस तरह के बहुपद | इस तरह के बहुपद द्विपाशी का एक रोचक उदाहरण मैंडलब्रॉट वक्र हैं।अगर हम P<sub>0</sub> = z और P<sub>''n''</sub> = P<sub>''n''−1</sub><sup>2</sup> + z को सम्मुच्चय करते हैं, तब संगत बहुपद Mn को |pn(z)|= 2 द्वारा परिभाषित मैंडेलब्रॉट सेट की सीमा पर अभिसरण करता है।<ref>[https://www.desmos.com/calculator/coamqcajzq Desmos.com - The Mandelbrot Curves]</ref> मैंडेलब्रॉट वक्र 2n<sup>+1</sup> घात के हैं। <ref>{{citation|title=High-Dimensional Chaotic and Attractor Systems: A Comprehensive Introduction|publisher=Springer|year=2007|isbn=9781402054563|page=492|url=https://books.google.com/books?id=mbtCAAAAQBAJ&pg=PA492|first1=Vladimir G.|last1=Ivancevic|first2=Tijana T.|last2=Ivancevic}}.</ref> | ||
मैंडेलब्रॉट वक्र | |||
| Line 42: | Line 38: | ||
==संदर्भ== | ==संदर्भ== | ||
* | *एलेक्जेंडर एरेमेन्को और वाल्टर हेमैन, ऑन द लेंथ ऑफ लेम्निस्केट्स, मिशिगन मठ. जे. (1999), '''46''', no. 2, 409–415 [http://projecteuclid.org/Dienst/UI/1.0/Summarize/euclid.mmj/1030132418] | ||
* | *ओ एस कुज़नेत्सोवा और वी. जी. तकाचेव, लेम्निस्केट्स की लंबाई के कार्य, पांडुलिपि मठ., (2003), '''112''', 519–538 [https://arxiv.org/abs/math.CV/0306327] | ||
{{DEFAULTSORT:Polynomial Lemniscate}} | {{DEFAULTSORT:Polynomial Lemniscate}} | ||
[[Category:Created On 26/04/2023|Polynomial Lemniscate]] | |||
[[Category:Machine Translated Page|Polynomial Lemniscate]] | |||
[[Category: Machine Translated Page]] | [[Category:Pages with script errors|Polynomial Lemniscate]] | ||
[[Category: | [[Category:Templates Vigyan Ready]] | ||
[[Category:बीजगणितीय वक्र|Polynomial Lemniscate]] | |||
[[Category:समतल वक्र|Polynomial Lemniscate]] | |||
Latest revision as of 17:32, 17 May 2023
गणित में, एक बहुपद द्विपाशी या बहुपद स्तर वक्र घात 2n का एक बीजगणितीय वक्र है, जो घात n के जटिल गुणांक वाले बहुपद p से निर्मित होता है।
ऐसे किसी बहुपद p और धनात्मक वास्तविक संख्या c के लिए, हम सम्मिश्र संख्याओं के समुच्चय को द्वारा परिभाषित कर सकते हैं संख्याओं के इस सम्मुच्चय को वास्तविक कार्तीय समतल में बिंदुओं के बराबर किया जा सकता है, जिससे एक बीजगणितीय वक्र ƒ(x, y) =c2 2n घात का होता है, जो z = x + iy के संदर्भ में के विस्तार का परिणाम है।
जब p घात 1 का बहुपद होता है तो परिणामी वक्र केवल एक वृत्त होता है जिसका केंद्र p का शून्य होता है। जब p घात 2 का बहुपद होता है तो वक्र कैसिनी अंडाकार होता है।
वन द्विपाशी
पॉल एर्डोस का एक अनुमान जिसने काफी रुचि आकर्षित की है, एक बहुपद लेमनिस्केट की अधिकतम लंबाई ƒ(x, y) = 1 घात 2n होती है जब p मोनिक बहुपद है, जो एर्डोस ने अनुमान लगाया था जब p(z) = zn - 1 प्राप्त किया गया था।
यह अभी भी सिद्ध नहीं हुआ है लेकिन फ्रायंटोव और फेडर नाज़रोव ने सिद्ध किया है कि p a स्थानीय अधिकतम देता है।[1] उस स्थिति में जब n = 2, एर्दोस द्विपाशी या बर्नौली द्विपाशी है
और यह सिद्ध हो चुका है कि यह वस्तुतः घात चार में अधिकतम लंबाई है। एर्डोस द्विपाशी में तीन सामान्य n-गुना बिंदु हैं, जिनमें से एक मूल में है, और (n − 1)(n − 2)/2 का एक ज्यामितीय प्रकार है। व्युत्क्रम ज्यामिति द्वारा ईकाई वृत में एर्डोस द्विपाशी, घात n का एक गैर-एकवचन वक्र प्राप्त करता है।
सामान्य बहुपद लेमनसेट
सामान्य तौर पर, एक बहुपद द्विपाशी मूल को स्पर्श नहीं करेगा, और केवल दो सामान्य n-गुना विलक्षणताएं होंगी, और इसलिए (n − 1)2 का एक प्रकार होगा। वास्तविक वक्र के रूप में, इसमें कई असंबद्ध घटक हो सकते हैं। इसलिए, यह एक द्विपाशी की तरह नहीं लगेगा, जिससे नाम एक मिथ्या नाम बन जाएगा।
इस तरह के बहुपद द्विपाशी का एक रोचक उदाहरण मैंडलब्रॉट वक्र हैं।अगर हम P0 = z और Pn = Pn−12 + z को सम्मुच्चय करते हैं, तब संगत बहुपद Mn को |pn(z)|= 2 द्वारा परिभाषित मैंडेलब्रॉट सेट की सीमा पर अभिसरण करता है।[2] मैंडेलब्रॉट वक्र 2n+1 घात के हैं। [3]
टिप्पणियाँ
- ↑ Fryntov, A; Nazarov, F (2008). "New estimates for the length of the Erdos-Herzog-Piranian lemniscate". Linear and Complex Analysis. 226: 49–60. arXiv:0808.0717. Bibcode:2008arXiv0808.0717F.
- ↑ Desmos.com - The Mandelbrot Curves
- ↑ Ivancevic, Vladimir G.; Ivancevic, Tijana T. (2007), High-Dimensional Chaotic and Attractor Systems: A Comprehensive Introduction, Springer, p. 492, ISBN 9781402054563.