एकवचन समरूपता: Difference between revisions

Latest revision as of 17:53, 18 May 2023

बीजगणितीय सांस्थितिकी में, अद्वितीय समरूपता एक सांस्थितिक समष्टि 'x' के बीजगणितीय अचरों के एक निश्चित समुच्चयों के अध्ययन को संदर्भित करता है, तथाकथित समरूपता समूह $H_{n}(X)$ है। सहज रूप से, अद्वितीय समरूपता की गणना करता है, प्रत्येक आयाम n के लिए, समष्टि की n-आयामी रिक्तियां है। अद्वितीय समरूपता एक समरूपता सिद्धांत का एक विशेष उदाहरण है, जो अब सिद्धांतों का एक व्यापक संग्रह बन गया है। विभिन्न सिद्धांतों में से, यह समझने के लिए कदाचित सबसे सरल सिद्धांतों में से एक है, काफी ठोस निर्माणों पर बनाया जा रहा है (संबंधित सिद्धांत सरल समरूपता भी देखें)।

संक्षेप में, मानक n-संकेतन के प्रतिचित्रों को सांस्थितिक समष्टि की श्रेणी में ले जाकर किया जाता है और और उन्हें औपचारिक योगों में संयोजित कर अद्वितीय समरूपता का निर्माण किया जाता है, जिसे अद्वितीय श्रृंखला कहा जाता है। सीमा संचालन - प्रत्येक n-विमीय संकेतन को उसके (n-1) -विमीय सीमा संचालक से प्रतिचित्रण करना - अद्वितीय श्रृंखला समष्टि को प्रेरित करता है। अद्वितीय समरूपता तब श्रृंखला समष्टि की समरूपता है। परिणामी समरूपता समूह सभी समस्थेयता समतुल्य समष्टियों के लिए समान हैं, जो उनके अध्ययन का कारण है। इन निर्माणों को सभी सांस्थितिक समष्टियों पर अनुप्रयुक्त किया जा सकता है और इसलिए अद्वितीय समरूपता को सांस्थितिक समष्टियों की श्रेणी से श्रेणीबद्ध अबेलियन समूहों की श्रेणी के रूप में अभिव्यक्त किया जा सकता है।

अद्वितीय सरलता

R³ में मानक 2-संकेतन Δ² है।

एक सांस्थितिक समष्टि X में अद्वितीय n-संकेतन एक सांतत्य फलन है (जिसे प्रतिचित्र भी कहा जाता है) मानक $\sigma$ संकेतन से $\Delta ^{n}$ x के लिए, लिखित $\sigma :\Delta ^{n}\to X$ हैं। इस प्रतिचित्र को अंतःक्षेपक की आवश्यकता नहीं है और x में समान छवि के साथ गैर-समकक्ष अद्वितीय सरलताएं हो सकती हैं।

$\sigma$ की सीमा, $\partial _{n}\sigma$ के रूप में निरूपित अद्वितीय (n − 1)-सरलताओं के औपचारिक योग के रूप में परिभाषित किया गया है - जो कि प्रतिबंध द्वारा दर्शाए गए हैं। मानक n-संकेतन के पार्श्व पर $\sigma$ , अभिविन्यास को ध्यान में रखने के लिए एक वैकल्पिक संकेत के साथ है। औपचारिक योग सरलता पर मुक्त अबेलियन समूह का एक तत्व है। समूहों के लिए आधार सभी संभावित अद्वितीय सरलताओं का अनंत समुच्चय है। समूह संचालन "योग" है और संकेतन b के साथ संकेतन a का योग सामान्यतः केवल a + b निर्दिष्ट किया जाता है, परन्तु a + a = 2a और इसी तरह है। प्रत्येक संकेतन a में ऋणात्मक -a है। इस प्रकार, यदि हम $\sigma$ के शीर्ष द्वारा निर्दिष्ट करते हैं:

[p_{0},p_{1},\ldots ,p_{n}]=[\sigma (e_{0}),\sigma (e_{1}),\ldots ,\sigma (e_{n})]

शीर्षों $e_{k}$ के अनुरूप मानक n-संकेतन $\Delta ^{n}$ हैं (जो निश्चित रूप से निर्मित अद्वितीय संकेतन $\sigma$ को पूर्णतया से निर्दिष्ट नहीं करता है), तब

\partial _{n}\sigma =\partial _{n}[p_{0},p_{1},\ldots ,p_{n}]=\sum _{k=0}^{n}(-1)^{k}[p_{0},\ldots ,p_{k-1},p_{k+1},\ldots ,p_{n}]=\sum _{k=0}^{n}(-1)^{k}\sigma \mid _{e_{0},\ldots ,e_{k-1},e_{k+1},\ldots ,e_{n}}

एक विशिष्ट तरीके से निर्दिष्ट संकेतन छवि के पार्श्व का एक औपचारिक योग है^[1] (अर्थात, किसी विशेष पार्श्व $\sigma$ का प्रतिबंध होना चाहिए, एक पार्श्व $\Delta ^{n}$ के लिए जो उस क्रम पर निर्भर करता है जिसके शीर्ष सूचीबद्ध हैं)। इस प्रकार, उदाहरण के लिए, $\sigma =[p_{0},p_{1}]$ की सीमा (एक वक्र $p_{0}$ से $p_{1}$ को जा रहा है) औपचारिक योग (या औपचारिक अंतर) $[p_{1}]-[p_{0}]$ है।

अद्वितीय श्रृंखला समष्टि

सरलता के औपचारिक योगों को परिभाषित करके अद्वितीय समरूपता का सामान्य निर्माण आगे बढ़ता है, जिसे एक मुक्त अबेलियन समूह के तत्वों के रूप में समझा जा सकता है और फिर दर्शा रहा है कि हम एक निश्चित समूह को परिभाषित कर सकते हैं, सांस्थितिक समष्टि के समरूपता समूह, जिसमें सीमा संचालक सम्मिलित है।

पहले सभी संभव अद्वितीय n-सरलताओं $\sigma _{n}(X)$ के समुच्चय एक सांस्थितिक समष्टि X पर विचार करें। इस समुच्चय का उपयोग एक मुक्त अबेलियन समूह के आधार के रूप में किया जा सकता है, ताकि प्रत्येक अद्वितीय n-संकेतन समूह का जनक हो। जनक का यह समुच्चय निश्चित रूप से अनंत है, प्रायः अगणनीय होता है, क्योंकि एक विशिष्ट सांस्थितिक समष्टि में एक संकेतन को प्रतिचित्रण करने के कई तरीके हैं। इस आधार से उत्पन्न मुक्त अबेलियन समूह को सामान्य रूप $C_{n}(X)$ से निरूपित किया जाता है। घटक $C_{n}(X)$ को अद्वितीय n-श्रृंखला कहा जाता है; वे पूर्णांक गुणांक वाले अद्वितीय सरलीकरण के औपचारिक योग हैं।

सीमा $\partial$ अद्वितीय n-श्रृंखला पर कार्य करने के लिए सरलता से बढ़ाया जाता है। विस्तार, जिसे सीमा संचालक कहा जाता है, इस रूप में लिखा गया है,

\partial _{n}:C_{n}\to C_{n-1}

समूहों की एक समरूपता है। सीमा संचालक $C_{n}$ के साथ में, अबेलियन समूहों की एक श्रृंखला समष्टि बनाते हैं, जिसे अद्वितीय समष्टि कहा जाता है। इसे प्रायः $(C_{\bullet }(X),\partial _{\bullet })$ या अधिक सरलता से $C_{\bullet }(X)$ के रूप में दर्शाया जाता है।

सीमा संचालक $Z_{n}(X)=\ker(\partial _{n})$ की अष्ठि है और अद्वितीय n-चक्रों का समूह कहा जाता है। सीमा संचालक $B_{n}(X)=\operatorname {im} (\partial _{n+1})$ की छवि है और अद्वितीय n-सीमाओं का समूह कहा जाता है।

यह $\partial _{n}\circ \partial _{n+1}=0$ भी दर्शाया जा सकता है, अर्थात, $B_{n}(X)\subseteq Z_{n}(X)$ है। $n$ -वें समरूपता समूह $X$ को तब कारक समूह के रूप में परिभाषित किया जाता है।

H_{n}(X)=Z_{n}(X)/B_{n}(X)

$H_{n}(X)$ के तत्वों को समरूपता वर्ग कहा जाता है।^[2]

समस्थेयता निश्चरता

यदि X और Y एक ही समस्थेयता प्रकार के साथ दो सांस्थितिक समिष्टियाँ हैं (अर्थात, समस्थेयता समतुल्य हैं), तो

H_{n}(X)\cong H_{n}(Y)\,

सभी n ≥ 0 के लिए, इसका तात्पर्य है कि समरूपता समूह समस्थेयता अचर हैं और इसलिए सांस्थितिक अचर हैं।

विशेष रूप से, यदि X एक संयोजित अनुबंधित समिष्टि है, तब $H_{0}(X)\cong \mathbb {Z}$ के अतिरिक्त सभी समरूपता समूह 0 हैं

अद्वितीय समरूपता समूहों के समस्थेयता निश्चरता के लिए एक प्रमाण को निम्नानुसार आलिखित किया जा सकता है। एक सतत प्रतिचित्र f: X → Y एक समरूपता को प्रेरित करता है:

f_{\sharp }:C_{n}(X)\rightarrow C_{n}(Y)

इसे तत्काल सत्यापित किया जा सकता है।

\partial f_{\sharp }=f_{\sharp }\partial ,

अर्थात f_# एक श्रृंखला प्रतिचित्रण है,

f_{*}:H_{n}(X)\rightarrow H_{n}(Y)

अब हम दर्शाते हैं कि यदि f और g समस्थानिक रूप से समतुल्य हैं, तब f_* = g_* है। इससे यह पता चलता है कि यदि f एक समस्थेयता तुल्यता है, तो f_* एक समरूपता है।

मान लीजिए कि F: X × [0, 1] → Y एक समरूपता है जो f को g में ले जाती है। श्रृंखलाओं के स्तर पर, समाकारिता को परिभाषित कीजिए;

P:C_{n}(X)\rightarrow C_{n+1}(Y)

कि, ज्यामितीय रूप के अनुरूप, आधार तत्व σ: Δⁿ → X का C_n(X) "वर्णक्रम" P(σ): Δⁿ × I → Y के लिए: Δⁿ × I → Y पर ले जाता है। P(σ) की सीमा को इस प्रकार व्यक्त किया जा सकता है।

\partial P(\sigma )=f_{\sharp }(\sigma )-g_{\sharp }(\sigma )-P(\partial \sigma )

इसलिए यदि C_n(X) में α एक n-चक्र है, तो f_#(α ) और g_#(α) एक सीमा से भिन्न होते है:

f_{\sharp }(\alpha )-g_{\sharp }(\alpha )=\partial P(\alpha )

अर्थात, वे समरूप हैं। यह अनुरोध सिद्ध करता है।^[3]

सामान्य समष्टि के समरूपता समूह

नीचे दी गई तालिका k-वें समरूपता समूहों $H_{k}(X)$ को दर्शाती है, n-विमीय वास्तविक प्रक्षेपीय समष्टि RPⁿ, जटिल प्रक्षेपीय समष्टि CPⁿ, एक बिंदु, गोलाकार Sⁿ( $n\geq 1$ ) और एक 3-स्थूलक T³ पूर्णांक गुणांकों के साथ है।

समष्टि	समस्थेयता के प्रकार
RPⁿ^[4]	$\mathbf {Z}$	k = 0 और k = n विषम
	$\mathbf {Z} /2\mathbf {Z}$	k विषम, 0 < k < n
	0	अन्यथा
CPⁿ^[5]	$\mathbf {Z}$	k = 0,2,4,...,2n
CPⁿ^[5]	0	अन्यथा
बिंदु^[6]	$\mathbf {Z}$	k = 0
बिंदु^[6]	0	अन्यथा
Sⁿ	$\mathbf {Z}$	k = 0,n
Sⁿ	0	अन्यथा
T³^[7]	$\mathbf {Z}$	k = 0,3
	$\mathbf {Z}$ ³	k = 1,2
	0	अन्यथा

क्रियात्मकता

उपरोक्त निर्माण को किसी भी सांस्थितिक समष्टि के लिए परिभाषित किया जा सकता है और संतत प्रतिचित्रों की क्रिया द्वारा संरक्षित किया जाता है। इस व्यापकता का तात्पर्य है कि अद्वितीय समरूपता सिद्धांत को श्रेणी सिद्धांत की भाषा में पुनर्गठित किया जा सकता है। विशेष रूप से, समरूपता समूहों को सांस्थितिक समष्टि की श्रेणी से अबेलियन समूहों Ab की श्रेणी के लिए एक प्रकार्यक समझा जा सकता है।

सर्वप्रथम $X\mapsto C_{n}(X)$ पर विचार करें, सांस्थितिक समष्टि से मुक्त अबेलियन समूहों का एक प्रतिचित्र है। इससे पता चलता है, $C_{n}(X)$ को एक प्रकार्यक के रूप में लिया जा सकता है। बशर्ते, कोई शीर्ष के आकारिता पर अपनी क्रिया को समझ सके। अब, शीर्ष की आकारिता सांतत्य फलन हैं, इसलिए यदि $f:X\to Y$ सांस्थितिक समष्टि का एक सतत प्रतिचित्र है, इसे समूहों के समरूपता तक बढ़ाया जा सकता है।

f_{*}:C_{n}(X)\to C_{n}(Y)\,

परिभाषित करके;

f_{*}\left(\sum _{i}a_{i}\sigma _{i}\right)=\sum _{i}a_{i}(f\circ \sigma _{i})

जहाँ $\sigma _{i}:\Delta ^{n}\to X$ एक अद्वितीय संकेतन है, और $\sum _{i}a_{i}\sigma _{i}\,$ एक अद्वितीय n-श्रृंखला है, जो कि एक तत्व $C_{n}(X)$ है। इससे पता चलता है कि $C_{n}$ यह एक प्रकार्यक है।

C_{n}:\mathbf {Top} \to \mathbf {Ab}

सांस्थितिक समष्टि की श्रेणी से अबेलियन समूहों की श्रेणी तक है।

सीमा संचालक संतत प्रतिचित्रों के साथ आवागमन करता है, ताकि $\partial _{n}f_{*}=f_{*}\partial _{n}$ हो। यह संपूर्ण श्रृंखला समष्टि को एक प्रकार्यक के रूप में माना जाने की अनुमति प्रदान करता है। विशेष रूप से, यह दर्शाता है कि प्रतिचित्र $X\mapsto H_{n}(X)$ यह एक प्रकार्यक है।

H_{n}:\mathbf {Top} \to \mathbf {Ab}

सांस्थितिक समष्टि की श्रेणी से अबेलियन समूहों की श्रेणी तक, समस्थेयता स्वयंसिद्ध द्वारा, किसी के पास $H_{n}$ एक प्रकार्यक भी है, जिसे समरूपता प्रकार्यक कहा जाता है, hटॉप पर अभिनय करता है, भागफल समस्थेयता श्रेणी:

H_{n}:\mathbf {hTop} \to \mathbf {Ab}

यह अद्वितीय समरूपता को अन्य समरूपता सिद्धांतों से अलग करता है, जिसमें $H_{n}$ अभी भी एक प्रकार्यक है, परन्तु यह आवश्यक नहीं है कि सभी शीर्ष पर परिभाषित किया गया हो। कुछ अर्थों में, अद्वितीय समरूपता सबसे बड़ा समरूपता सिद्धांत है, जिसमें शीर्ष की एक उपश्रेणी पर प्रत्येक समरूपता सिद्धांत उस उपश्रेणी पर अद्वितीय समरूपता से अनुकूल है। दूसरी ओर, अद्वितीय समरूपता में सबसे साफ श्रेणीबद्ध गुण नहीं होते हैं; इस तरह की सफाई अन्य समरूपता सिद्धांतों जैसे कोष्ठात्मक समरूपता के विकास को प्रेरित करती है।

सामान्यतः, समरूपता प्रकार्यक को स्वयंसिद्ध रूप से परिभाषित किया जाता है, एक अबेलियन श्रेणी पर प्रकार्यक के रूप में, या वैकल्पिक रूप से, श्रृंखला समष्टियों पर एक प्रकार्यक के रूप में, संतोषजनक स्वयंसिद्धों के लिए एक सीमा आकारिकी की आवश्यकता होती है जो छोटे सटीक अनुक्रमों को लंबे सटीक अनुक्रमों में परिवर्तित कर देती है। अद्वितीय समरूपता कि स्थिति में, समरूपता प्रकार्यक को दो खंडों में विभाजित किया जा सकता है, एक सांस्थितिक खंड और एक बीजगणितीय खंड है। सांस्थितिक खंड द्वारा दिया गया है;

C_{\bullet }:\mathbf {Top} \to \mathbf {Comp}

जो सांस्थितिक समष्टि $X\mapsto (C_{\bullet }(X),\partial _{\bullet })$ को प्रतिचित्रण करता है और सांतत्य फलन $f\mapsto f_{*}$ है। यहाँ तो, $C_{\bullet }$ अद्वितीय श्रृंखला प्रकार्यक समझा जाता है, जो सांस्थितिक समष्टि को श्रृंखला समष्टि कॉम्प (या कॉम) की श्रेणी में प्रतिचित्रण करता है। श्रृंखला समष्टियों की श्रेणी में इसकी वस्तुओं के रूप में श्रृंखला समष्टि हैं और श्रृंखला प्रतिचित्र इसके आकारिकी के रूप में हैं।

दूसरा, बीजगणितीय भाग समरूपता प्रकार्यक है।

H_{n}:\mathbf {Comp} \to \mathbf {Ab}

कौन सा प्रतिचित्र

C_{\bullet }\mapsto H_{n}(C_{\bullet })=Z_{n}(C_{\bullet })/B_{n}(C_{\bullet })

और श्रृंखला प्रतिचित्रों को अबेलियन समूहों के प्रतिचित्रों तक ले जाता है। यह समरूपता प्रकार्यक है जिसे स्वयंसिद्ध रूप से परिभाषित किया जा सकता है, ताकि यह श्रृंखला समष्टियों की श्रेणी पर एक प्रकार्यक के रूप में स्वयं खड़ा हो।

समस्थेयता प्रतिचित्रण समरूप रूप से समतुल्य श्रृंखला प्रतिचित्रण को परिभाषित करके चित्र में पुनः प्रवेश करते हैं। इस प्रकार, कोई भागफल श्रेणी hकॉम्प या K को परिभाषित कर सकता है, श्रृंखला समष्टियों की समस्थेयता श्रेणी है।

R में गुणांक

किसी भी एकात्मक वलय R को देखते हुए, एक सांस्थितिक समष्टि पर अद्वितीय n-संकेतन के समुच्चय को मुक्त R-मापांक के जनक के रूप में लिया जा सकता है। अर्थात्, उपरोक्त निर्माणों को मुक्त अबेलियन समूहों के प्रारंभिक बिंदु से करने के बजाय, उनके स्थान पर मुक्त R-मापांक का उपयोग करता है। सभी निर्माण बहुत कम या बिना किसी परिवर्तन के होते हैं। इसका परिणाम है:

H_{n}(X;R)\

जो अब एक R-मापांक है। अवश्य ही, यह सामान्यतः एक मुक्त मापांक नहीं है। सामान्य समरूपता समूह को ध्यान में रखते हुए पुनः प्राप्त किया जाता है

H_{n}(X;\mathbb {Z} )=H_{n}(X)

जब कोई वलयों को पूर्णांकों का वलय मानता है। संकेतन H_n(X; R) को लगभग समान संकेतन H_n(X, A) के साथ भ्रमित नहीं होना चाहिए, जो सापेक्ष समरूपता (नीचे) को दर्शाता है।

सार्वभौमिक गुणांक प्रमेय लघु सटीक अनुक्रम का उपयोग करते हुए सामान्य पूर्णांक गुणांक वाले समरूपता के संदर्भ में R गुणांकों के साथ समरूपता की गणना करने के लिए एक प्रक्रिया प्रदान करता है।

0\to H_{n}(X;\mathbb {Z} )\otimes R\to H_{n}(X;R)\to Tor(H_{n-1}(X;\mathbb {Z} ),R)\to 0

जहाँ टॉर, टॉर प्रकार्यक है।^[8]ध्यान दें, यदि R विमोटन-मुक्त है, तो किसी भी G के लिए टॉर(G, R) = 0 है, इसलिए उपरोक्त लघु सटीक अनुक्रम एक समरूपता $H_{n}(X;\mathbb {Z} )\otimes R$ और $H_{n}(X;R)$ के मध्य कम हो जाता है।

सापेक्ष समरूपता

उपक्षेत्र $A\subset X$ के लिए, सापेक्ष समरूपता H_n(X, A) को श्रृंखला समष्टियों के भागफल की समरूपता को समझा जाता है, अर्थात,

H_{n}(X,A)=H_{n}(C_{\bullet }(X)/C_{\bullet }(A))

जहां शृंखला संकुलों का भागफल लघु सटीक अनुक्रम द्वारा दिया जाता है।

0\to C_{\bullet }(A)\to C_{\bullet }(X)\to C_{\bullet }(X)/C_{\bullet }(A)\to 0

^[9]

लघुकृत समरूपता

समष्टि x की लघुकृत समरूपता, ${\tilde {H}}_{n}(X)$ के रूप में सटीक की गई सामान्य समरूपता के लिए एक साधारण संशोधन है जो कुछ सम्बन्धो की अभिव्यक्ति को सरल करता है और अंतर्ज्ञान को पूर्ण करता है कि एक बिंदु के सभी समरूपता समूह शून्य होने चाहिए।

श्रृंखला समष्टि पर परिभाषित सामान्य समरूपता के लिए:

\dotsb {\overset {\partial _{n+1}}{\longrightarrow \,}}C_{n}{\overset {\partial _{n}}{\longrightarrow \,}}C_{n-1}{\overset {\partial _{n-1}}{\longrightarrow \,}}\dotsb {\overset {\partial _{2}}{\longrightarrow \,}}C_{1}{\overset {\partial _{1}}{\longrightarrow \,}}C_{0}{\overset {\partial _{0}}{\longrightarrow \,}}0

लघुकृत समरूपता को परिभाषित करने के लिए, हम श्रृंखला समष्टि को एक अतिरिक्त $\mathbb {Z}$ मध्य में $C_{0}$ और शून्य के साथ बढ़ाते हैं:

$\dotsb {\overset {\partial _{n+1}}{\longrightarrow \,}}C_{n}{\overset {\partial _{n}}{\longrightarrow \,}}C_{n-1}{\overset {\partial _{n-1}}{\longrightarrow \,}}\dotsb {\overset {\partial _{2}}{\longrightarrow \,}}C_{1}{\overset {\partial _{1}}{\longrightarrow \,}}C_{0}{\overset {\epsilon }{\longrightarrow \,}}\mathbb {Z} \to 0$

जहाँ $\epsilon \left(\sum _{i}n_{i}\sigma _{i}\right)=\sum _{i}n_{i}$ है। अपूरित समुच्चय को (-1)-संकेतन के रूप में व्याख्या करके इसे उचित ठहराया जा सकता है, जिसका अर्थ $C_{-1}\simeq \mathbb {Z}$ है।

लघुकृत समरूपता समूहों ${\tilde {H}}_{n}(X)=\ker(\partial _{n})/\mathrm {im} (\partial _{n+1})$ को धनात्मक n और ${\tilde {H}}_{0}(X)=\ker(\epsilon )/\mathrm {im} (\partial _{1})$ के लिए परिभाषित किया गया है।^[10]n > 0 के लिए, $H_{n}(X)={\tilde {H}}_{n}(X)$ है, जबकि n = 0 के लिए, $H_{0}(X)={\tilde {H}}_{0}(X)\oplus \mathbb {Z}$ है।

सह-समरूपता

समरूपता श्रृंखला समष्टि को दोहराकर (अर्थात प्रकार्यक होम(-, R), R को कोई भी वलय अनुप्रयुक्त करते हुए) हम सह-सीमा प्रतिचित्रण 𝛿 के साथ एक सह-श्रृंखला समष्टि प्राप्त करते हैं। X के सह-समरूपता समूहों को इस समष्टि के समरूपता समूहों के रूप में परिभाषित किया गया है; एक वाक्य में, सह-समरूपता सह-द्विक समष्टि की समरूपता है।

सह-समरूपता समूहों में समरूपता समूहों की तुलना में अधिक समृद्ध, या कम से कम अधिक परिचित, बीजगणितीय संरचना होती है। सर्वप्रथम, वे निम्नानुसार एक अवकलन श्रेणीबद्ध बीजगणित बनाते हैं:

समूहों का श्रेणीबद्ध समूह एक श्रेणीबद्ध R-मापांक बनाता है;
इसे बीज उत्पाद का उपयोग करके एक श्रेणीबद्ध R-बीजगणितीय की संरचना दी जा सकती है;
बॉकस्टीन समरूपता β एक अंतर प्रदान करता है।

अतिरिक्त सह-समरूपता संचालन हैं और सह-समरूपता बीजगणितीय में अतिरिक्त संरचना अत्याधुनिक p है (पूर्व की भांति, अत्याधुनिक p सह-समरूपता अत्याधुनिक p सह-श्रृंखला समष्टि की सह-समरूपता है, न कि अत्याधुनिक p सह-समरूपता की कमी), विशेष रूप से स्टीनरोड बीजगणितीय संरचना है।

बेट्टी समरूपता और सह-समरूपता

चूंकि समरूपता सिद्धांतों की संख्या बड़ी हो गई है (श्रेणी: समरूपता सिद्धांत देखें), बेट्टी समरूपता और बेट्टी सह-समरूपता शब्द कभी-कभी अद्वितीय सिद्धांत पर अनुप्रयुक्त होते हैं (विशेष रूप से, बीजगणितीय ज्यामिति पर लिखने वाले लेखकों द्वारा), बेट्टी संख्याओं के उत्थान के रूप में सबसे परिचित समष्टियों जैसे कि सरल समष्टि और संवृत्त बहुरूपता है।

असाधारण समरूपता

यदि कोई समरूपता सिद्धांत को स्वैच्छिक रूप से परिभाषित करता है (एलेनबर्ग-स्टीनरोड स्वयंसिद्धि के माध्यम से) और फिर स्वयंसिद्धि (आयाम स्वयंसिद्ध) में से एक को विश्रान्ति प्रदान करता है, तो एक सामान्यीकृत सिद्धांत प्राप्त होता है, जिसे असाधारण समरूपता सिद्धांत कहा जाता है। ये मूल रूप से असाधारण सह-समरूपता सिद्धांतों के रूप में उत्पन्न हुए, अर्थात् K-सिद्धांत और सह-सीमावाद सिद्धांत है। इस संदर्भ में, अद्वितीय समरूपता को साधारण समरूपता कहा जाता है।

यह भी देखें

संदर्भ

↑ Hatcher, 105
↑ Hatcher, 108
↑ Theorem 2.10. Hatcher, 111
↑ Hatcher, 144
↑ Hatcher, 140
↑ Hatcher, 110
↑ Hatcher, 142-143
↑ Hatcher, 264
↑ Hatcher, 115
↑ Hatcher, 110

Allen Hatcher, Algebraic topology. Cambridge University Press, ISBN 0-521-79160-X and ISBN 0-521-79540-0
J.P. May, A Concise Course in Algebraic Topology, Chicago University Press ISBN 0-226-51183-9
Joseph J. Rotman, An Introduction to Algebraic Topology, Springer-Verlag, ISBN 0-387-96678-1

[1] Hatcher, 105

[2] Hatcher, 108

[3] Theorem 2.10. Hatcher, 111

[4] Hatcher, 144

[5] Hatcher, 140

[6] Hatcher, 110

[7] Hatcher, 142-143

[8] Hatcher, 264

[9] Hatcher, 115

[10] Hatcher, 110

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Anonymous

Search

एकवचन समरूपता: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 17:53, 18 May 2023

Contents

अद्वितीय सरलता

अद्वितीय श्रृंखला समष्टि

समस्थेयता निश्चरता

सामान्य समष्टि के समरूपता समूह

क्रियात्मकता

R में गुणांक

सापेक्ष समरूपता

लघुकृत समरूपता

सह-समरूपता

बेट्टी समरूपता और सह-समरूपता

असाधारण समरूपता

यह भी देखें

संदर्भ

Navigation

Navigation

Wiki tools

Wiki tools

@@ Line 1: / Line 1: @@
 {{distinguish|सार बीजगणितीय विविधताओं की एकवचन समरूपता}}
 {{More footnotes|date=अगस्त 2018}}
-[[बीजगणितीय टोपोलॉजी|बीजगणितीय सांस्थितिकी]] में, एकवचन समरूपता एक [[टोपोलॉजिकल स्पेस|सांस्थितिक समष्टि]] 'x' के बीजगणितीय अचर के एक निश्चित समुच्चय के अध्ययन को संदर्भित करता है, तथाकथित समरूपता समूह <math>H_n(X).</math> है। सहज रूप से, एकवचन गृहविज्ञान मायने रखता है, प्रत्येक आयाम ''n'' के लिए, अंतरिक्ष के n-आयामी छिद्र। एकवचन समरूपता एक [[समरूपता सिद्धांत]] का एक विशेष उदाहरण है, जो अब सिद्धांतों का एक व्यापक संग्रह बन गया है। विभिन्न सिद्धांतों में से, यह समझने के लिए शायद सबसे सरल सिद्धांतों में से एक है, काफी ठोस निर्माणों पर बनाया जा रहा है (संबंधित सिद्धांत सरल समरूपता भी देखें)।
+[[बीजगणितीय टोपोलॉजी|बीजगणितीय सांस्थितिकी]] में, अद्वितीय समरूपता एक [[टोपोलॉजिकल स्पेस|सांस्थितिक समष्टि]] 'x' के बीजगणितीय अचरों के एक निश्चित समुच्चयों के अध्ययन को संदर्भित करता है, तथाकथित समरूपता समूह <math>H_n(X)</math> है। सहज रूप से, अद्वितीय समरूपता की गणना करता है, प्रत्येक आयाम ''n'' के लिए, समष्टि की n-आयामी रिक्तियां है। अद्वितीय समरूपता एक [[समरूपता सिद्धांत]] का एक विशेष उदाहरण है, जो अब सिद्धांतों का एक व्यापक संग्रह बन गया है। विभिन्न सिद्धांतों में से, यह समझने के लिए कदाचित सबसे सरल सिद्धांतों में से एक है, काफी ठोस निर्माणों पर बनाया जा रहा है (संबंधित सिद्धांत सरल समरूपता भी देखें)।
-संक्षेप में, एकवचन समरूपता का निर्माण प्रसमुच्चय | मानक n-प्रसमुच्चय के मानचित्रों [[टोपोलॉजिकल स्पेस की श्रेणी|सांस्थितिक समष्टि की श्रेणी]] में ले जाकर किया जाता है, और उन्हें फ्री एबेलियन ग्रुप # इंटेगर फ़ंक्शंस और औपचारिक योग में कंपोज़ किया जाता है, जिसे 'एकवचन श्रृंखला' कहा जाता है। सीमा संचालन - प्रत्येक n-विमीय प्रसमुच्चय को उसके (n-1) -विमीय [[ सीमा संचालक |सीमा संचालक]] से प्रतिचित्रण करना - एकवचन [[चेन कॉम्प्लेक्स|श्रृंखला समष्टि]] को प्रेरित करता है। एकवचन समरूपता तब श्रृंखला समष्टि की [[समरूपता (गणित)]] है। परिणामी समरूपता समूह सभी समस्थेयता # समस्थेयता समतुल्यता और अशक्त-समस्थेयता रिक्त स्थान के लिए समान हैं, जो उनके अध्ययन का कारण है। इन निर्माणों को सभी सांस्थितिक रिक्त स्थान पर अनुप्रयुक्त किया जा सकता है, और इसलिए एकवचन समरूपता को सांस्थितिक रिक्त स्थान की श्रेणी से ग्रेडेड [[एबेलियन समूह]]ों की श्रेणी के रूप में अभिव्यक्त किया जा सकता है।
+संक्षेप में, मानक n-संकेतन के प्रतिचित्रों को [[टोपोलॉजिकल स्पेस की श्रेणी|सांस्थितिक समष्टि की श्रेणी]] में ले जाकर किया जाता है और और उन्हें औपचारिक योगों में संयोजित कर अद्वितीय समरूपता का निर्माण किया जाता है, जिसे अद्वितीय श्रृंखला कहा जाता है। सीमा संचालन - प्रत्येक n-विमीय संकेतन को उसके (n-1) -विमीय [[ सीमा संचालक |सीमा संचालक]] से प्रतिचित्रण करना - अद्वितीय [[चेन कॉम्प्लेक्स|श्रृंखला समष्टि]] को प्रेरित करता है। अद्वितीय समरूपता तब श्रृंखला समष्टि की [[समरूपता (गणित)|समरूपता]] है। परिणामी समरूपता समूह सभी समस्थेयता समतुल्य समष्टियों के लिए समान हैं, जो उनके अध्ययन का कारण है। इन निर्माणों को सभी सांस्थितिक समष्टियों पर अनुप्रयुक्त किया जा सकता है और इसलिए अद्वितीय समरूपता को सांस्थितिक समष्टियों की श्रेणी से श्रेणीबद्ध [[एबेलियन समूह|अबेलियन समूहों]] की श्रेणी के रूप में अभिव्यक्त किया जा सकता है।
-== एकल सरल ==
+== अद्वितीय सरलता ==
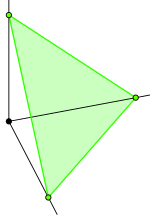
-[[Image:2D-simplex.svg|150px|thumb|right|मानक 2-प्रसमुच्चय Δ<sup>2</sup> R में<sup>3</उप>]]एक सांस्थितिक समष्टि में एक एकवचन n-प्रसमुच्चय | एकवचन n-प्रसमुच्चय एक [[निरंतर कार्य|सांतत्य फलन]] है (जिसे मानचित्र भी कहा जाता है) <math>\sigma</math> मानक [[संकेतन]] से <math>\Delta^n</math> x के लिए, लिखा <math>\sigma:\Delta^n\to X.</math> इस मानचित्र को [[इंजेक्शन]] की आवश्यकता नहीं है, और x में समान छवि के साथ गैर-समकक्ष एकवचन सरल हो सकते हैं।
+[[Image:2D-simplex.svg|150px|thumb|right|'''R'''<sup>3</sup> में मानक 2-संकेतन Δ<sup>2</sup> है।]]एक सांस्थितिक समष्टि ''X'' में अद्वितीय n-संकेतन एक [[निरंतर कार्य|सांतत्य फलन]] है (जिसे प्रतिचित्र भी कहा जाता है) मानक <math>\sigma</math> [[संकेतन]] से <math>\Delta^n</math> x के लिए, लिखित <math>\sigma:\Delta^n\to X</math> हैं। इस प्रतिचित्र को [[इंजेक्शन|अंतःक्षेपक]] की आवश्यकता नहीं है और x में समान छवि के साथ गैर-समकक्ष अद्वितीय सरलताएं हो सकती हैं।
-<math>\sigma,</math> की सीमा, इस रूप <math>\partial_n\sigma,</math> में घोषित किया गया एकवचन (n − 1) के औपचारिक योग के रूप में परिभाषित किया गया है - के प्रतिबंध द्वारा दर्शाए गए सरलीकरण <math>\sigma</math> मानक n-प्रसमुच्चय के पार्श्व पर, उन्मुखीकरण को ध्यान में रखने के लिए एक वैकल्पिक संकेत के साथ। (औपचारिक योग सरलता पर [[मुक्त एबेलियन समूह]] का एक तत्व है। समूह के लिए आधार सभी संभावित एकवचन सरलताओं का अनंत समुच्चय है। समूह संचालन अतिरिक्त है और प्रसमुच्चय बी के साथ प्रसमुच्चय ए का योग सामान्यतः बस नामित किया जाता है। + ''b'', परन्तु a + a = 2a और इसी तरह। प्रत्येक प्रसमुच्चय ए में नकारात्मक -ए है।) इस प्रकार, यदि हम नामित <math>\sigma</math> इसके शिखर द्वारा
+<math>\sigma</math> की सीमा, <math>\partial_n\sigma</math> के रूप में निरूपित अद्वितीय (n − 1)-सरलताओं के औपचारिक योग के रूप में परिभाषित किया गया है - जो कि प्रतिबंध द्वारा दर्शाए गए हैं। मानक n-संकेतन के पार्श्व पर <math>\sigma</math> , अभिविन्यास को ध्यान में रखने के लिए एक वैकल्पिक संकेत के साथ है। औपचारिक योग सरलता पर [[मुक्त एबेलियन समूह|मुक्त अबेलियन समूह]] का एक तत्व है। समूहों के लिए आधार सभी संभावित अद्वितीय सरलताओं का अनंत समुच्चय है। समूह संचालन "योग" है और संकेतन ''b'' के साथ संकेतन ''a'' का योग सामान्यतः केवल ''a'' + ''b'' निर्दिष्ट किया जाता है, परन्तु a + a = 2a और इसी तरह है। प्रत्येक संकेतन ''a'' में ऋणात्मक -''a'' है। इस प्रकार, यदि हम <math>\sigma</math> के शीर्ष द्वारा निर्दिष्ट करते हैं:
 :<math>[p_0,p_1,\ldots,p_n]=[\sigma(e_0),\sigma(e_1),\ldots,\sigma(e_n)]</math>
-शिखरों के अनुरूप <math>e_k</math> मानक n-प्रसमुच्चय का <math>\Delta^n</math> (जो निश्चित रूप से निर्मित एकवचन प्रसमुच्चय को पूर्णतया से निर्दिष्ट नहीं करता है <math>\sigma</math>), तब
+शीर्षों <math>e_k</math> के अनुरूप मानक n-संकेतन <math>\Delta^n</math> हैं (जो निश्चित रूप से निर्मित अद्वितीय संकेतन <math>\sigma</math> को पूर्णतया से निर्दिष्ट नहीं करता है), तब
 :<math>\partial_n\sigma=\partial_n[p_0,p_1,\ldots,p_n]=\sum_{k=0}^n(-1)^k [p_0,\ldots,p_{k-1},p_{k+1},\ldots ,p_n] = \sum_{k=0}^n (-1)^k \sigma\mid _{e_0,\ldots,e_{k-1},e_{k+1},\ldots ,e_n}</math>
-एक विशिष्ट तरीके से निर्दिष्ट प्रसमुच्चय छवि के पार्श्व का एक औपचारिक योग है।<ref>Hatcher, 105</ref> (अर्थात, किसी विशेष पार्श्व का प्रतिबंध होना चाहिए <math>\sigma</math> के एक पार्श्व के लिए <math>\Delta^n</math> जो उस क्रम पर निर्भर करता है जिसके शीर्ष सूचीबद्ध हैं।) इस प्रकार, उदाहरण के लिए, की सीमा <math>\sigma=[p_0,p_1]</math> (एक वक्र से जा रहा है <math>p_0</math> को <math>p_1</math>) औपचारिक योग (या औपचारिक अंतर) है <math>[p_1] - [p_0]</math>.
+एक विशिष्ट तरीके से निर्दिष्ट संकेतन छवि के पार्श्व का एक औपचारिक योग है<ref>Hatcher, 105</ref> (अर्थात, किसी विशेष पार्श्व <math>\sigma</math> का प्रतिबंध होना चाहिए, एक पार्श्व <math>\Delta^n</math> के लिए जो उस क्रम पर निर्भर करता है जिसके शीर्ष सूचीबद्ध हैं)। इस प्रकार, उदाहरण के लिए, <math>\sigma=[p_0,p_1]</math> की सीमा (एक वक्र <math>p_0</math> से <math>p_1</math>को जा रहा है) औपचारिक योग (या औपचारिक अंतर) <math>[p_1] - [p_0]</math>है।
-== एकवचन श्रृंखला समष्टि ==
+== अद्वितीय श्रृंखला समष्टि ==
-सरलता के औपचारिक योगों को परिभाषित करके एकवचन समरूपता का सामान्य निर्माण आगे बढ़ता है, जिसे एक मुक्त एबेलियन समूह के तत्वों के रूप में समझा जा सकता है, और फिर दर्शा रहा है कि हम एक निश्चित समूह को परिभाषित कर सकते हैं, सांस्थितिक समष्टि का समरूपता समूह, जिसमें सीमा संचालक सम्मिलित है। .
+सरलता के औपचारिक योगों को परिभाषित करके अद्वितीय समरूपता का सामान्य निर्माण आगे बढ़ता है, जिसे एक मुक्त अबेलियन समूह के तत्वों के रूप में समझा जा सकता है और फिर दर्शा रहा है कि हम एक निश्चित समूह को परिभाषित कर सकते हैं, सांस्थितिक समष्टि के समरूपता समूह, जिसमें सीमा संचालक सम्मिलित है।
-पहले सभी संभव एकवचन ''n''-सरलताओं के समुच्चय पर विचार करें <math>\sigma_n(X)</math> एक सांस्थितिक समष्टि x पर। इस समुच्चय का उपयोग एक मुक्त एबेलियन समूह के आधार के रूप में किया जा सकता है, ताकि प्रत्येक एकवचन n-प्रसमुच्चय समूह का जनक हो। जनक का यह समुच्चय निश्चित रूप से अनंत है, प्रायः [[बेशुमार]] होता है, क्योंकि एक विशिष्ट सांस्थितिक समष्टि में एक प्रसमुच्चय को प्रतिचित्रण करने के कई तरीके हैं। इस आधार से उत्पन्न मुक्त आबेली समूह को सामान्य रूप से निरूपित किया जाता है <math>C_n(X)</math>. घटक <math>C_n(X)</math> एकवचन ''n''-श्रृंखला कहलाते हैं; वे पूर्णांक गुणांक वाले एकवचन सरलीकरण के औपचारिक योग हैं।
+पहले सभी संभव अद्वितीय ''n''-सरलताओं <math>\sigma_n(X)</math> के समुच्चय एक सांस्थितिक समष्टि ''X'' पर विचार करें। इस समुच्चय का उपयोग एक मुक्त अबेलियन समूह के आधार के रूप में किया जा सकता है, ताकि प्रत्येक अद्वितीय n-संकेतन समूह का जनक हो। जनक का यह समुच्चय निश्चित रूप से अनंत है, प्रायः [[बेशुमार|अगणनीय]] होता है, क्योंकि एक विशिष्ट सांस्थितिक समष्टि में एक संकेतन को प्रतिचित्रण करने के कई तरीके हैं। इस आधार से उत्पन्न मुक्त अबेलियन समूह को सामान्य रूप <math>C_n(X)</math> से निरूपित किया जाता है। घटक <math>C_n(X)</math> को अद्वितीय ''n''-श्रृंखला कहा जाता है; वे पूर्णांक गुणांक वाले अद्वितीय सरलीकरण के औपचारिक योग हैं।
-सीमा संचालक <math>\partial</math> एकवचन n-श्रृंखला पर कार्य करने के लिए सरलता से बढ़ाया जाता है। विस्तार, जिसे सीमा संचालक कहा जाता है, के रूप में लिखा गया है
+सीमा <math>\partial</math> अद्वितीय n-श्रृंखला पर कार्य करने के लिए सरलता से बढ़ाया जाता है। विस्तार, जिसे सीमा संचालक कहा जाता है, इस रूप में लिखा गया है,
-:<math>\partial_n:C_n\to C_{n-1},</math>
+:<math>\partial_n:C_n\to C_{n-1}</math>
-समूहों का एक [[समरूपता]] है। सीमा संचालक, साथ में <math>C_n</math>, एबेलियन समूहों का एक श्रृंखला समष्टि बनाते हैं, जिसे एकवचन समष्टि कहा जाता है। इसे प्रायः के रूप में दर्शाया जाता है <math>(C_\bullet(X),\partial_\bullet)</math> या अधिक सरलता से <math>C_\bullet(X)</math>.
+समूहों की एक [[समरूपता]] है। सीमा संचालक <math>C_n</math>के साथ में, अबेलियन समूहों की एक श्रृंखला समष्टि बनाते हैं, जिसे अद्वितीय समष्टि कहा जाता है। इसे प्रायः <math>(C_\bullet(X),\partial_\bullet)</math> या अधिक सरलता से <math>C_\bullet(X)</math> के रूप में दर्शाया जाता है।
-सीमा संचालक का कर्नेल है <math>Z_n(X)=\ker (\partial_{n})</math>, और एकवचन ''n''-चक्रों का समूह कहलाता है। सीमा संचालक की छवि है <math>B_n(X)=\operatorname{im} (\partial_{n+1})</math>, और एकवचन ''n''-सीमाओं का समूह कहलाता है।
+सीमा संचालक <math>Z_n(X)=\ker (\partial_{n})</math> की अष्ठि है और अद्वितीय ''n''-चक्रों का समूह कहा जाता है। सीमा संचालक <math>B_n(X)=\operatorname{im} (\partial_{n+1})</math> की छवि है और अद्वितीय ''n''-सीमाओं का समूह कहा जाता है।
-यह भी दर्शाया जा सकता है <math>\partial_n\circ \partial_{n+1}=0</math>, तात्पर्य <math>B_n(X) \subseteq Z_n(X)</math>. <math>n</math>वें>-वें समरूपता समूह <math>X</math> फिर [[कारक समूह]] के रूप में परिभाषित किया गया है
+यह <math>\partial_n\circ \partial_{n+1}=0</math> भी दर्शाया जा सकता है, अर्थात, <math>B_n(X) \subseteq Z_n(X)</math> है। <math>n</math>-वें समरूपता समूह <math>X</math> को तब कारक समूह के रूप में परिभाषित किया जाता है।
-:<math>H_{n}(X) = Z_n(X) / B_n(X).</math>
+:<math>H_{n}(X) = Z_n(X) / B_n(X)</math>
-के तत्व <math>H_n(X)</math> समरूपता वर्ग कहलाते हैं।<ref>Hatcher, 108</ref>
+<math>H_n(X)</math> के तत्वों को समरूपता वर्ग कहा जाता है।<ref>Hatcher, 108</ref>
 == समस्थेयता निश्चरता ==
-यदि X और Y एक ही [[होमोटॉपी प्रकार|समस्थेयता प्रकार]] के साथ दो सांस्थितिक समष्टि हैं (अर्थात समस्थेयता समतुल्य हैं), तो
+यदि X और Y एक ही [[होमोटॉपी प्रकार|समस्थेयता प्रकार]] के साथ दो सांस्थितिक समिष्टियाँ हैं (अर्थात, समस्थेयता समतुल्य हैं), तो
 :<math>H_n(X) \cong H_n(Y)\,</math>
-सभी n ≥ 0 के लिए। इसका तात्पर्य है कि समरूपता समूह समस्थेयता अचर हैं, और इसलिए [[टोपोलॉजिकल इनवेरिएंट|सांस्थितिक अचर]] हैं।
+सभी n ≥ 0 के लिए, इसका तात्पर्य है कि समरूपता समूह समस्थेयता अचर हैं और इसलिए [[टोपोलॉजिकल इनवेरिएंट|सांस्थितिक अचर]] हैं।
-विशेष रूप से, यदि X एक जुड़ा हुआ अनुबंधित स्थान है, तो इसके सभी समरूपता समूह 0 हैं, अतिरिक्त <math>H_0(X) \cong \mathbb{Z}</math>.
+विशेष रूप से, यदि X एक संयोजित अनुबंधित समिष्टि है, तब <math>H_0(X) \cong \mathbb{Z}</math> के अतिरिक्त सभी समरूपता समूह 0 हैं
-एकवचन समरूपता समूहों के समस्थेयता निश्चरता के लिए एक प्रमाण को निम्नानुसार आलिखित किया जा सकता है। एक सतत प्रतिचित्र f: X → Y एक समरूपता को प्रेरित करता है
+अद्वितीय समरूपता समूहों के समस्थेयता निश्चरता के लिए एक प्रमाण को निम्नानुसार आलिखित किया जा सकता है। एक सतत प्रतिचित्र f: X → Y एक समरूपता को प्रेरित करता है:
-:<math>f_{\sharp} : C_n(X) \rightarrow C_n(Y).</math>
+:<math>f_{\sharp} : C_n(X) \rightarrow C_n(Y)</math>
-इसे तुरंत सत्यापित किया जा सकता है
+इसे तत्काल सत्यापित किया जा सकता है।
 :<math>\partial f_{\sharp} = f_{\sharp} \partial,</math>
-अर्थात एफ<sub>#</sub> एक श्रृंखला समष्टि # श्रृंखला प्रतिचित्रण है, जो समरूपता पर समरूपता तक उतरता है
+अर्थात ''f''<sub>#</sub> एक श्रृंखला प्रतिचित्रण है,
-:<math>f_* : H_n(X) \rightarrow H_n(Y).</math>
+:<math>f_* : H_n(X) \rightarrow H_n(Y)</math>
-अब हम दिखाते हैं कि यदि f और g समस्थानिक रूप से समतुल्य हैं, तो f<sub>*</sub> = जी<sub>*</sub>. इससे यह पता चलता है कि यदि f एक समस्थेयता तुल्यता है, तो f<sub>*</sub> एक समरूपता है।
+अब हम दर्शाते हैं कि यदि f और g समस्थानिक रूप से समतुल्य हैं, तब ''f''<sub>*</sub> = ''g''<sub>*</sub> है। इससे यह पता चलता है कि यदि f एक समस्थेयता तुल्यता है, तो f<sub>*</sub> एक समरूपता है।
-मान लीजिए F : X × [0, 1] → Y एक समरूपता है जो f को g में ले जाती है। श्रृंखला के स्तर पर, समाकारिता को परिभाषित कीजिए
+मान लीजिए कि F: X × [0, 1] → Y एक समरूपता है जो f को g में ले जाती है। श्रृंखलाओं के स्तर पर, समाकारिता को परिभाषित कीजिए;
 :<math>P : C_n(X) \rightarrow C_{n+1}(Y)</math>
-वह, ज्यामितीय रूप से बोलते हुए, आधार तत्व σ: Δ लेता है<sup>n</sup> → C का X<sub>n</sub>(x) प्रिज्म पी (σ) के लिए: Δ<sup>n</sup> × I → Y. P(σ) की सीमा को इस प्रकार व्यक्त किया जा सकता है
+कि, ज्यामितीय रूप के अनुरूप, आधार तत्व  σ: Δ<sup>''n''</sup> → ''X'' का ''C<sub>n</sub>''(''X'') "वर्णक्रम" ''P''(σ): Δ<sup>''n''</sup> × ''I'' → ''Y'' के लिए: Δ<sup>n</sup> × I → Y पर ले जाता है। P(σ) की सीमा को इस प्रकार व्यक्त किया जा सकता है।
-:<math>\partial P(\sigma) = f_{\sharp}(\sigma) - g_{\sharp}(\sigma) - P(\partial \sigma).</math>
+:<math>\partial P(\sigma) = f_{\sharp}(\sigma) - g_{\sharp}(\sigma) - P(\partial \sigma)</math>
-तो अगर α में''C<sub>n</sub>''(''X'') एक n-चक्र है, फिर ''f''<sub>#</sub>(''α'' ) और ''g''<sub>#</sub>(α) एक सीमा से भिन्न होता है:
+इसलिए यदि ''C<sub>n</sub>''(''X'') में α एक n-चक्र है, तो ''f''<sub>#</sub>(''α'' ) और ''g''<sub>#</sub>(α) एक सीमा से भिन्न होते है:
-:<math> f_{\sharp} (\alpha) - g_{\sharp}(\alpha) = \partial P(\alpha),</math>
+:<math> f_{\sharp} (\alpha) - g_{\sharp}(\alpha) = \partial P(\alpha)</math>
-अर्थात वे समरूप हैं। यह अनुरोध सिद्ध करता है।<ref>Theorem 2.10. Hatcher, 111</ref>
+अर्थात, वे समरूप हैं। यह अनुरोध सिद्ध करता है।<ref>Theorem 2.10. Hatcher, 111</ref>
-== कॉमन समष्टि के समरूपता समूह ==
+== सामान्य समष्टि के समरूपता समूह ==
-नीचे दी गई तालिका k-वें समरूपता समूहों को दर्शाती है <math>H_k(X)</math> n-विमीय वास्तविक प्रक्षेपीय समष्टि Rपी<sup>n</sup>, जटिल प्रक्षेप्य स्थान, 'CP'<sup>n</sup>, एक बिंदु, गोले S<sup>n</sup>(<math>n\ge 1</math>), और एक 3-टोरस टी<sup>3</sup> पूर्णांक गुणांकों के साथ।
+नीचे दी गई तालिका k-वें समरूपता समूहों <math>H_k(X)</math> को दर्शाती है, n-विमीय वास्तविक प्रक्षेपीय समष्टि RP<sup>n</sup>, जटिल प्रक्षेपीय समष्टि CP<sup>n</sup>, एक बिंदु, गोलाकार S<sup>n</sup>(<math>n\ge 1</math>) और एक 3-स्थूलक ''T''<sup>3</sup> पूर्णांक गुणांकों के साथ है।
 {| class="wikitable"
-!Space
+!समष्टि
-!colspan="2"|Homotopy type
+!colspan="2"|समस्थेयता के प्रकार
 |-
 |rowspan="3"|'''RP'''<sup>''n''</sup><ref>Hatcher, 144</ref>
@@ Line 115: / Line 115: @@
-== कार्यात्मकता ==
+== क्रियात्मकता ==
-उपरोक्त निर्माण को किसी भी सामयिक स्थान के लिए परिभाषित किया जा सकता है, और निरंतर मानचित्रों की क्रिया द्वारा संरक्षित किया जाता है। इस व्यापकता का तात्पर्य है कि एकवचन समरूपता सिद्धांत को [[श्रेणी सिद्धांत]] की भाषा में पुनर्गठित किया जा सकता है। विशेष रूप से, समरूपता समूह को सांस्थितिक रिक्त स्थान की श्रेणी से एबेलियन समूह एब की श्रेणी के लिए एक मज़ेदार समझा जा सकता है।
+उपरोक्त निर्माण को किसी भी सांस्थितिक समष्टि के लिए परिभाषित किया जा सकता है और संतत प्रतिचित्रों की क्रिया द्वारा संरक्षित किया जाता है। इस व्यापकता का तात्पर्य है कि अद्वितीय समरूपता सिद्धांत को [[श्रेणी सिद्धांत]] की भाषा में पुनर्गठित किया जा सकता है। विशेष रूप से, समरूपता समूहों को सांस्थितिक समष्टि की श्रेणी से अबेलियन समूहों Ab की श्रेणी के लिए एक प्रकार्यक समझा जा सकता है।
-पहले उस पर विचार करें <math>X\mapsto C_n(X)</math> सांस्थितिक समष्टि से मुक्त एबेलियन समूहों का एक प्रतिचित्र है। इससे पता चलता है <math>C_n(X)</math> एक functor के रूप में लिया जा सकता है, बशर्ते कोई शीर्ष के [[morphism|आकारिता]] पर अपनी कार्रवाई को समझ सके। अब, शीर्ष के आकारिता सांतत्य फलन हैं, इसलिए यदि <math>f:X\to Y</math> सांस्थितिक समष्टि का एक सतत प्रतिचित्र है, इसे समूहों के समरूपता तक बढ़ाया जा सकता है
+सर्वप्रथम <math>X\mapsto C_n(X)</math> पर विचार करें, सांस्थितिक समष्टि से मुक्त अबेलियन समूहों का एक प्रतिचित्र है। इससे पता चलता है, <math>C_n(X)</math> को एक प्रकार्यक के रूप में लिया जा सकता है। बशर्ते, कोई शीर्ष के [[morphism|आकारिता]] पर अपनी क्रिया को समझ सके। अब, शीर्ष की आकारिता सांतत्य फलन हैं, इसलिए यदि <math>f:X\to Y</math> सांस्थितिक समष्टि का एक सतत प्रतिचित्र है, इसे समूहों के समरूपता तक बढ़ाया जा सकता है।
 :<math>f_*:C_n(X)\to C_n(Y)\,</math>
-परिभाषित करके
+परिभाषित करके;
 :<math>f_*\left(\sum_i a_i\sigma_i\right)=\sum_i a_i (f\circ \sigma_i)</math>
-कहाँ <math>\sigma_i:\Delta^n\to X</math> एक विलक्षण प्रसमुच्चय है, और <math>\sum_i a_i\sigma_i\,</math> एक विलक्षण n-श्रृंखला है, जो कि एक तत्व है <math>C_n(X)</math>. इससे पता चलता है कि <math>C_n</math> यह एक प्रकार्यक है
+जहाँ <math>\sigma_i:\Delta^n\to X</math> एक अद्वितीय संकेतन है, और <math>\sum_i a_i\sigma_i\,</math> एक अद्वितीय n-श्रृंखला है, जो कि एक तत्व <math>C_n(X)</math> है। इससे पता चलता है कि <math>C_n</math> यह एक प्रकार्यक है।
 :<math>C_n:\mathbf{Top} \to \mathbf{Ab}</math>
-सांस्थितिक समष्टि की श्रेणी से एबेलियन समूहों की श्रेणी तक।
+सांस्थितिक समष्टि की श्रेणी से अबेलियन समूहों की श्रेणी तक है।
-सीमा संचालक निरंतर मानचित्रों के साथ आवागमन करता है, ताकि <math>\partial_n f_*=f_*\partial_n</math>. यह संपूर्ण श्रृंखला समष्टि को एक मज़ेदार के रूप में माना जाने की अनुमति देता है। विशेष रूप से, यह दर्शाता है कि map <math>X\mapsto H_n (X)</math> यह एक प्रकार्यक है
+सीमा संचालक संतत प्रतिचित्रों के साथ आवागमन करता है, ताकि <math>\partial_n f_*=f_*\partial_n</math>हो। यह संपूर्ण श्रृंखला समष्टि को एक प्रकार्यक के रूप में माना जाने की अनुमति प्रदान करता है। विशेष रूप से, यह दर्शाता है कि प्रतिचित्र <math>X\mapsto H_n (X)</math> यह एक प्रकार्यक है।
 :<math>H_n:\mathbf{Top}\to\mathbf{Ab}</math>
-सांस्थितिक समष्टि की श्रेणी से एबेलियन समूहों की श्रेणी तक। समस्थेयता स्वयंसिद्ध द्वारा, किसी के पास वह है <math>H_n</math> एक प्रकार्यक भी है, जिसे समरूपता प्रकार्यक कहा जाता है, hTop पर अभिनय करता है, भागफल समस्थेयता श्रेणी:
+सांस्थितिक समष्टि की श्रेणी से अबेलियन समूहों की श्रेणी तक, समस्थेयता स्वयंसिद्ध द्वारा, किसी के पास <math>H_n</math> एक प्रकार्यक भी है, जिसे समरूपता प्रकार्यक कहा जाता है, hटॉप पर अभिनय करता है, भागफल समस्थेयता श्रेणी:
-:<math>H_n:\mathbf{hTop}\to\mathbf{Ab}.</math>
+:<math>H_n:\mathbf{hTop}\to\mathbf{Ab}</math>
-यह एकवचन समरूपता को अन्य समरूपता सिद्धांतों से अलग करता है, जिसमें <math>H_n</math> अभी भी एक मज़ेदार है, परन्तु यह आवश्यक नहीं है कि सभी शीर्ष पर परिभाषित किया गया हो। कुछ अर्थों में, एकवचन समरूपता सबसे बड़ा समरूपता सिद्धांत है, जिसमें शीर्ष के एक [[उपश्रेणी]] पर हर समरूपता सिद्धांत उस उपश्रेणी पर एकवचन समरूपता से सहमत है। दूसरी ओर, एकवचन समरूपता में सबसे साफ श्रेणीबद्ध गुण नहीं होते हैं; इस तरह की सफाई अन्य समरूपता सिद्धांतों जैसे [[सेलुलर समरूपता]] के विकास को प्रेरित करती है।
+यह अद्वितीय समरूपता को अन्य समरूपता सिद्धांतों से अलग करता है, जिसमें <math>H_n</math> अभी भी एक प्रकार्यक है, परन्तु यह आवश्यक नहीं है कि सभी शीर्ष पर परिभाषित किया गया हो। कुछ अर्थों में, अद्वितीय समरूपता सबसे बड़ा समरूपता सिद्धांत है, जिसमें शीर्ष की एक [[उपश्रेणी]] पर प्रत्येक समरूपता सिद्धांत उस उपश्रेणी पर अद्वितीय समरूपता से अनुकूल है। दूसरी ओर, अद्वितीय समरूपता में सबसे साफ श्रेणीबद्ध गुण नहीं होते हैं; इस तरह की सफाई अन्य समरूपता सिद्धांतों जैसे [[सेलुलर समरूपता|कोष्ठात्मक समरूपता]] के विकास को प्रेरित करती है।
-अधिक सामान्यतः, समरूपता प्रकार्यक को स्वयंसिद्ध रूप से परिभाषित किया जाता है, एक [[एबेलियन श्रेणी]] पर प्रकार्यक के रूप में, या, वैकल्पिक रूप से, श्रृंखला समष्टिों पर एक प्रकार्यक के रूप में, संतोषजनक स्वयंसिद्धों के लिए एक [[सीमा आकारिकी]] की आवश्यकता होती है जो छोटे सटीक अनुक्रमों को लंबे सटीक अनुक्रमों में परिवर्तित कर देती है। एकवचन समरूपता के मामले में, समरूपता प्रकार्यक को दो टुकड़ों में विभाजित किया जा सकता है, एक सांस्थितिक खंड और एक बीजगणितीय खंड। सांस्थितिक खंड द्वारा दिया गया है
+सामान्यतः, समरूपता प्रकार्यक को स्वयंसिद्ध रूप से परिभाषित किया जाता है, एक [[एबेलियन श्रेणी|अबेलियन श्रेणी]] पर प्रकार्यक के रूप में, या वैकल्पिक रूप से, श्रृंखला समष्टियों पर एक प्रकार्यक के रूप में, संतोषजनक स्वयंसिद्धों के लिए एक [[सीमा आकारिकी]] की आवश्यकता होती है जो छोटे सटीक अनुक्रमों को लंबे सटीक अनुक्रमों में परिवर्तित कर देती है। अद्वितीय समरूपता कि स्थिति में, समरूपता प्रकार्यक को दो खंडों में विभाजित किया जा सकता है, एक सांस्थितिक खंड और एक बीजगणितीय खंड है। सांस्थितिक खंड द्वारा दिया गया है;
 :<math>C_\bullet:\mathbf{Top}\to\mathbf{Comp}</math>
-जो सांस्थितिक समष्टि को प्रतिचित्रण करता है <math>X\mapsto (C_\bullet(X),\partial_\bullet)</math> और सांतत्य फलन करता है <math>f\mapsto f_*</math>. यहाँ तो, <math>C_\bullet</math> एकवचन श्रृंखला प्रकार्यक समझा जाता है, जो सांस्थितिक समष्टि को श्रृंखला समष्टि कॉम्प (या कॉम) की श्रेणी में प्रतिचित्रण करता है। [[श्रृंखला परिसरों की श्रेणी|श्रृंखला समष्टिों की श्रेणी]] में इसकी [[वस्तु (श्रेणी सिद्धांत)]] के रूप में श्रृंखला समष्टि हैं, और श्रृंखला मानचित्र इसके आकारिकी के रूप में हैं।
+जो सांस्थितिक समष्टि <math>X\mapsto (C_\bullet(X),\partial_\bullet)</math> को प्रतिचित्रण करता है और सांतत्य फलन <math>f\mapsto f_*</math> है। यहाँ तो, <math>C_\bullet</math> अद्वितीय श्रृंखला प्रकार्यक समझा जाता है, जो सांस्थितिक समष्टि को श्रृंखला समष्टि कॉम्प (या कॉम) की श्रेणी में प्रतिचित्रण करता है। [[श्रृंखला परिसरों की श्रेणी|श्रृंखला समष्टियों की श्रेणी]] में इसकी [[वस्तु (श्रेणी सिद्धांत)|वस्तुओं]] के रूप में श्रृंखला समष्टि हैं और श्रृंखला प्रतिचित्र इसके आकारिकी के रूप में हैं।
-दूसरा, बीजगणितीय भाग समरूपता प्रकार्यक है
+दूसरा, बीजगणितीय भाग समरूपता प्रकार्यक है।
 :<math>H_n:\mathbf{Comp}\to\mathbf{Ab}</math>
-कौन सा मानचित्र
+कौन सा प्रतिचित्र
 :<math>C_\bullet\mapsto H_n(C_\bullet)=Z_n(C_\bullet)/B_n(C_\bullet)</math>
-और श्रृंखला मानचित्रों को एबेलियन समूहों के मानचित्रों तक ले जाता है। यह समरूपता प्रकार्यक है जिसे स्वयंसिद्ध रूप से परिभाषित किया जा सकता है, ताकि यह श्रृंखला समष्टिों की श्रेणी पर एक प्रकार्यक के रूप में स्वयं खड़ा हो।
+और श्रृंखला प्रतिचित्रों को अबेलियन समूहों के प्रतिचित्रों तक ले जाता है। यह समरूपता प्रकार्यक है जिसे स्वयंसिद्ध रूप से परिभाषित किया जा सकता है, ताकि यह श्रृंखला समष्टियों की श्रेणी पर एक प्रकार्यक के रूप में स्वयं खड़ा हो।
-समस्थेयता प्रतिचित्रण्स समरूप रूप से समतुल्य श्रृंखला प्रतिचित्रण्स को परिभाषित करके चित्र में फिर से प्रवेश करते हैं। इस प्रकार, कोई [[भागफल श्रेणी]] hComp या K को परिभाषित कर सकता है, [[श्रृंखला परिसरों की होमोटोपी श्रेणी|श्रृंखला समष्टिों की समस्थेयता श्रेणी]]।
+समस्थेयता प्रतिचित्रण समरूप रूप से समतुल्य श्रृंखला प्रतिचित्रण को परिभाषित करके चित्र में पुनः प्रवेश करते हैं। इस प्रकार, कोई [[भागफल श्रेणी]] hकॉम्प या K को परिभाषित कर सकता है, [[श्रृंखला परिसरों की होमोटोपी श्रेणी|श्रृंखला समष्टियों की समस्थेयता श्रेणी]] है।
 == R में गुणांक ==
-किसी भी एकात्मक वलय (गणित) R को देखते हुए, एक सांस्थितिक समष्टि पर एकवचन n-सिम्पलिस के समुच्चय को फ्री मापांक के जनक के रूप में लिया जा सकता है। फ्री R-मापांक। अर्थात्, उपरोक्त निर्माणों को मुक्त एबेलियन समूहों के प्रारंभिक बिंदु से करने के बजाय, उनके स्थान पर मुफ्त R-मापांक का उपयोग करता है। सभी निर्माण बहुत कम या बिना किसी परिवर्तित कराव के होते हैं। इसका परिणाम है
+किसी भी एकात्मक वलय R को देखते हुए, एक सांस्थितिक समष्टि पर अद्वितीय n-संकेतन के समुच्चय को मुक्त R-मापांक के जनक के रूप में लिया जा सकता है। अर्थात्, उपरोक्त निर्माणों को मुक्त अबेलियन समूहों के प्रारंभिक बिंदु से करने के बजाय, उनके स्थान पर मुक्त R-मापांक का उपयोग करता है। सभी निर्माण बहुत कम या बिना किसी परिवर्तन के होते हैं। इसका परिणाम है:
 :<math>H_n(X; R)\ </math>
-जो अब एक मापांक (गणित) है | R-मापांक। बेशक, यह सामान्यतः एक मुफ्त मापांक नहीं है। सामान्य समरूपता समूह को ध्यान में रखते हुए पुनः प्राप्त किया जाता है
+जो अब एक R-मापांक है। अवश्य ही, यह सामान्यतः एक मुक्त मापांक नहीं है। सामान्य समरूपता समूह को ध्यान में रखते हुए पुनः प्राप्त किया जाता है
 :<math>H_n(X;\mathbb{Z})=H_n(X)</math>
-जब कोई वलय को पूर्णांकों का वलय मानता है। संकेतन एच<sub>''n''</sub>(x; R) को लगभग समान अंकन एच के साथ भ्रमित नहीं होना चाहिए<sub>''n''</sub>(x, ए), जो रिश्तेदार समरूपता (नीचे) को दर्शाता है।
+जब कोई वलयों को पूर्णांकों का वलय मानता है। संकेतन ''H<sub>n</sub>''(''X''; ''R'') को लगभग समान संकेतन ''H<sub>n</sub>''(''X'', ''A'') के साथ भ्रमित नहीं होना चाहिए, जो सापेक्ष समरूपता (नीचे) को दर्शाता है।
-[[सार्वभौमिक गुणांक प्रमेय]] लघु सटीक अनुक्रम का उपयोग करते हुए सामान्य पूर्णांक गुणांक वाले समरूपता के संदर्भ में R गुणांकों के साथ समरूपता की गणना करने के लिए एक तंत्र प्रदान करता है।
+[[सार्वभौमिक गुणांक प्रमेय]] लघु सटीक अनुक्रम का उपयोग करते हुए सामान्य पूर्णांक गुणांक वाले समरूपता के संदर्भ में R गुणांकों के साथ समरूपता की गणना करने के लिए एक प्रक्रिया प्रदान करता है।
-:<math>0\to H_n(X; \mathbb{Z}) \otimes R \to H_n(X; R) \to Tor(H_{n-1}(X; \mathbb{Z}), R) \to 0.</math>
+:<math>0\to H_n(X; \mathbb{Z}) \otimes R \to H_n(X; R) \to Tor(H_{n-1}(X; \mathbb{Z}), R) \to 0</math>
-जहाँ Tor, [[Tor functor]] है।<ref>Hatcher, 264</ref>
+जहाँ टॉर, [[Tor functor|टॉर प्रकार्यक]] है।<ref>Hatcher, 264</ref>ध्यान दें, यदि R विमोटन-मुक्त है, तो किसी भी G के लिए टॉर(G, R) = 0 है, इसलिए उपरोक्त लघु सटीक अनुक्रम एक समरूपता <math>H_n(X; \mathbb{Z}) \otimes R</math> और <math>H_n(X; R)</math> के मध्य कम हो जाता है।
-ध्यान दें, यदि R मरोड़-मुक्त है, तो किसी भी G के लिए Tor(G, R) = 0 है, इसलिए उपरोक्त लघु सटीक अनुक्रम एक समरूपता के मध्य कम हो जाता है <math>H_n(X; \mathbb{Z}) \otimes R</math> और <math>H_n(X; R).</math>
-== रिलेटिव समरूपता ==
+== सापेक्ष समरूपता ==
-{{main|Relative homology}}
+{{main|सापेक्ष समरूपता}}
-उपक्षेत्र के लिए <math>A\subset X</math>, रिश्तेदार समरूपता एच<sub>''n''</sub>(x, ए) को श्रृंखला समष्टिों के भागफल के समरूपता के रूप में समझा जाता है, अर्थात
+उपक्षेत्र <math>A\subset X</math> के लिए, सापेक्ष समरूपता ''H<sub>n</sub>''(''X'', ''A'') को श्रृंखला समष्टियों के भागफल की समरूपता को समझा जाता है, अर्थात,
 :<math>H_n(X,A)=H_n(C_\bullet(X)/C_\bullet(A))</math>
-जहां शृंखला संकुलों का भागफल लघु सटीक अनुक्रम द्वारा दिया जाता है
+जहां शृंखला संकुलों का भागफल लघु सटीक अनुक्रम द्वारा दिया जाता है।
-:<math>0\to C_\bullet(A) \to C_\bullet(X) \to C_\bullet(X)/C_\bullet(A) \to 0.</math><ref>Hatcher, 115</ref>
+:<math>0\to C_\bullet(A) \to C_\bullet(X) \to C_\bullet(X)/C_\bullet(A) \to 0</math><ref>Hatcher, 115</ref>
-== कम समरूपता ==
+== लघुकृत समरूपता ==
-{{main|Reduced homology}}
+{{main|लघुकृत समरूपता}}
-समष्टि x की घटी हुई समरूपता, के रूप में nोटेट की गई <math> \tilde{H}_n(X)</math> सामान्य समरूपता के लिए एक  साधारण संशोधन है जो कुछ रिश्तों की अभिव्यक्ति को सरल करता है और इस बात को पूर्ण करता है कि एक बिंदु के सभी समरूपता समूह शून्य होने चाहिए।
+समष्टि x की लघुकृत समरूपता, <math> \tilde{H}_n(X)</math> के रूप में सटीक की गई सामान्य समरूपता के लिए एक साधारण संशोधन है जो कुछ सम्बन्धो की अभिव्यक्ति को सरल करता है और अंतर्ज्ञान को पूर्ण करता है कि एक बिंदु के सभी समरूपता समूह शून्य होने चाहिए।
 श्रृंखला समष्टि पर परिभाषित सामान्य समरूपता के लिए:
@@ Line 191: / Line 192: @@
 \overset{\partial_1}{\longrightarrow\,}
 C_0\overset{\partial_0}{\longrightarrow\,} 0</math>
-घटी हुई समरूपता को परिभाषित करने के लिए, हम श्रृंखला समष्टि को एक अतिरिक्त के साथ बढ़ाते हैं <math>\mathbb{Z}</math> मध्य में <math>C_0</math> और शून्य:
+लघुकृत समरूपता को परिभाषित करने के लिए, हम श्रृंखला समष्टि को एक अतिरिक्त <math>\mathbb{Z}</math> मध्य में <math>C_0</math> और शून्य के साथ बढ़ाते हैं:
 <math>\dotsb\overset{\partial_{n+1}}{\longrightarrow\,}C_n
@@ Line 202: / Line 203: @@
 C_0\overset{\epsilon}{\longrightarrow\,} \mathbb{Z} \to 0
 </math>
-कहाँ <math>\epsilon \left( \sum_i n_i \sigma_i \right) = \sum_i n_i </math>. खाली समुच्चय को (-1)-simplex के रूप में व्याख्या करके इसे उचित ठहराया जा सकता है, जिसका अर्थ है <math>C_{-1} \simeq \Z</math>.
-घटे हुए समरूपता समूहों को अब परिभाषित किया गया है <math> \tilde{H}_n(X) = \ker(\partial_n) / \mathrm{im}(\partial_{n+1})</math> सकारात्मक n और के लिए <math>\tilde{H}_0(X) = \ker(\epsilon) / \mathrm{im}(\partial_1)</math>. <ref>Hatcher, 110</ref>
+जहाँ <math>\epsilon \left( \sum_i n_i \sigma_i \right) = \sum_i n_i </math> है। अपूरित समुच्चय को (-1)-संकेतन के रूप में व्याख्या करके इसे उचित ठहराया जा सकता है, जिसका अर्थ <math>C_{-1} \simeq \Z</math> है।
-n > 0 के लिए, <math> H_n(X) = \tilde{H}_n(X) </math>, जबकि n = 0 के लिए, <math> H_0(X) = \tilde{H}_0(X) \oplus \mathbb{Z}. </math>
+लघुकृत समरूपता समूहों <math> \tilde{H}_n(X) = \ker(\partial_n) / \mathrm{im}(\partial_{n+1})</math> को धनात्मक n और <math>\tilde{H}_0(X) = \ker(\epsilon) / \mathrm{im}(\partial_1)</math> के लिए परिभाषित किया गया है।<ref>Hatcher, 110</ref>n > 0 के लिए, <math> H_n(X) = \tilde{H}_n(X) </math> है, जबकि n = 0 के लिए, <math> H_0(X) = \tilde{H}_0(X) \oplus \mathbb{Z} </math> है।
-== सह समरूपता ==
+== सह-समरूपता ==
-{{main|सह समरूपता}}
+{{main|सह-समरूपता}}
-समरूपता श्रृंखला समष्टि को दोहराकर (अर्थात प्रकार्यक होम (-, R), R को कोई भी वलय अनुप्रयुक्त करते हुए) हम कोबाउंड्री प्रतिचित्रण के साथ एक [[कोचेन कॉम्प्लेक्स|कोश्रृंखला समष्टि]] प्राप्त करते हैं <math>\delta</math>. ''X'' के सह समरूपता समूहों को इस समष्टि के समरूपता समूहों के रूप में परिभाषित किया गया है; एक चुटकी में, सह समरूपता सह [द्वैत समष्टि] की समरूपता है।
+समरूपता श्रृंखला समष्टि को दोहराकर (अर्थात प्रकार्यक होम(-, R), R को कोई भी वलय अनुप्रयुक्त करते हुए) हम सह-सीमा प्रतिचित्रण 𝛿 के साथ एक [[कोचेन कॉम्प्लेक्स|सह-श्रृंखला समष्टि]] प्राप्त करते हैं। ''X'' के सह-समरूपता समूहों को इस समष्टि के समरूपता समूहों के रूप में परिभाषित किया गया है; एक वाक्य में, सह-समरूपता सह-द्विक समष्टि की समरूपता है।
-कोसमरूपता समूहों में समरूपता समूहों की तुलना में अधिक समृद्ध, या कम से कम अधिक परिचित, बीजगणितीय संरचना होती है। सबसे पहले, वे निम्नानुसार एक अवकलन ग्रेडेड बीजगणित बनाते हैं:
+सह-समरूपता समूहों में समरूपता समूहों की तुलना में अधिक समृद्ध, या कम से कम अधिक परिचित, बीजगणितीय संरचना होती है। सर्वप्रथम, वे निम्नानुसार एक अवकलन श्रेणीबद्ध बीजगणित बनाते हैं:
-* समूहों का श्रेणीबद्ध समूह एक श्रेणीबद्ध ''R''-[[मॉड्यूल (गणित)|मापांक (गणित)]] बनाता है;
+* समूहों का श्रेणीबद्ध समूह एक श्रेणीबद्ध ''R''-[[मॉड्यूल (गणित)|मापांक]] बनाता है;
-* इसे [[कप उत्पाद]] का उपयोग करके एक श्रेणीबद्ध ''R''-[[बीजगणित (अंगूठी सिद्धांत)]] की संरचना दी जा सकती है;
+* इसे [[कप उत्पाद|बीज उत्पाद]] का उपयोग करके एक श्रेणीबद्ध ''R''-[[बीजगणित (अंगूठी सिद्धांत)|बीजगणितीय]] की संरचना दी जा सकती है;
-* [[बॉकस्टीन समरूपता]] ''β'' एक अंतर देता है।
+* [[बॉकस्टीन समरूपता]] ''β'' एक अंतर प्रदान करता है।
-अतिरिक्त [[कोहोलॉजी ऑपरेशन|सह समरूपता संचालन]] हैं, और सह समरूपता बीजगणित में अतिरिक्त संरचना मॉड ''पी'' है (पहले की तरह, मॉड ''पी'' सह समरूपता मॉड ''पी'' कोश्रृंखला समष्टि का सह समरूपता है, न कि मॉड '' पी'' सह समरूपता की कमी), विशेष रूप से स्टीनरोड बीजगणित संरचना।
+अतिरिक्त [[कोहोलॉजी ऑपरेशन|सह-समरूपता संचालन]] हैं और सह-समरूपता बीजगणितीय में अतिरिक्त संरचना अत्याधुनिक ''p'' है (पूर्व की भांति, अत्याधुनिक ''p'' सह-समरूपता अत्याधुनिक ''p'' सह-श्रृंखला समष्टि की सह-समरूपता है, न कि अत्याधुनिक ''p'' सह-समरूपता की कमी), विशेष रूप से स्टीनरोड बीजगणितीय संरचना है।
-== बेट्टी समरूपता और सह समरूपता ==
+== बेट्टी समरूपता और सह-समरूपता ==
-चूंकि [[समरूपता सिद्धांत]]ों की संख्या बड़ी हो गई है (देखें: श्रेणी: समरूपता सिद्धांत), 'बेट्टी समरूपता' और 'बेटी सह समरूपता' शब्द कभी-कभी एकवचन सिद्धांत पर अनुप्रयुक्त होते हैं (विशेष रूप से [[बीजगणितीय ज्यामिति]] पर लिखने वाले लेखकों द्वारा), सरल समष्टिों और बंद मैनिफोल्ड्स जैसे सबसे परिचित स्थानों की बेट्टी संख्या को जन्म देने के रूप में।
+चूंकि [[समरूपता सिद्धांत|समरूपता सिद्धांतों]] की संख्या बड़ी हो गई है (श्रेणी: समरूपता सिद्धांत देखें), बेट्टी समरूपता और बेट्टी सह-समरूपता शब्द कभी-कभी अद्वितीय सिद्धांत पर अनुप्रयुक्त होते हैं (विशेष रूप से, [[बीजगणितीय ज्यामिति]] पर लिखने वाले लेखकों द्वारा), बेट्टी संख्याओं के उत्थान के रूप में सबसे परिचित समष्टियों जैसे कि सरल समष्टि और संवृत्त बहुरूपता है।
 == असाधारण समरूपता ==
 {{main|असाधारण समरूपता सिद्धांत}}
-यदि कोई समरूपता सिद्धांत को स्वैच्छिक रूप से परिभाषित करता है (एलेनबर्ग-स्टीनरोड xिओम्स के माध्यम से), और फिर xिओम्स (आयाम स्वयंसिद्ध) में से एक को Rाम देता है, तो एक सामान्यीकृत सिद्धांत प्राप्त होता है, जिसे असाधारण समरूपता सिद्धांत कहा जाता है। ये मूल रूप से [[असाधारण कोहोलॉजी सिद्धांत|असाधारण सह समरूपता सिद्धांत]]ों के रूप में उत्पन्न हुए, अर्थात् के-सिद्धांत और कोबर्डिज्म सिद्धांत। इस संदर्भ में, एकवचन समरूपता को 'साधारण समरूपता' कहा जाता है।
+यदि कोई समरूपता सिद्धांत को स्वैच्छिक रूप से परिभाषित करता है (एलेनबर्ग-स्टीनरोड स्वयंसिद्धि के माध्यम से) और फिर स्वयंसिद्धि (आयाम स्वयंसिद्ध) में से एक को विश्रान्ति प्रदान करता है, तो एक सामान्यीकृत सिद्धांत प्राप्त होता है, जिसे असाधारण समरूपता सिद्धांत कहा जाता है। ये मूल रूप से [[असाधारण कोहोलॉजी सिद्धांत|असाधारण सह-समरूपता सिद्धांतों]] के रूप में उत्पन्न हुए, अर्थात् K-सिद्धांत और सह-सीमावाद सिद्धांत है। इस संदर्भ में, अद्वितीय समरूपता को साधारण समरूपता कहा जाता है।
 == यह भी देखें ==
@@ Line 240: / Line 242: @@
 * J.P. May, ''A Concise Course in Algebraic Topology'', Chicago University Press {{isbn|0-226-51183-9}}
 * Joseph J. Rotman, ''An Introduction to Algebraic Topology'', Springer-Verlag, {{isbn|0-387-96678-1}}
-[[Category: होमोलॉजी सिद्धांत]]
-[[Category: Machine Translated Page]]
+[[Category:All articles lacking in-text citations]]
+[[Category:Articles lacking in-text citations from अगस्त 2018]]
+[[Category:Articles with hatnote templates targeting a nonexistent page]]
+[[Category:Articles with invalid date parameter in template]]
 [[Category:Created On 08/05/2023]]
+[[Category:Machine Translated Page]]
+[[Category:Pages with script errors]]
+[[Category:Templates Vigyan Ready]]
+[[Category:होमोलॉजी सिद्धांत]]

Anonymous

Search

एकवचन समरूपता: Difference between revisions

Latest revision as of 17:53, 18 May 2023

अद्वितीय सरलता

अद्वितीय श्रृंखला समष्टि

समस्थेयता निश्चरता

सामान्य समष्टि के समरूपता समूह

क्रियात्मकता

R में गुणांक

सापेक्ष समरूपता

लघुकृत समरूपता

सह-समरूपता

बेट्टी समरूपता और सह-समरूपता

असाधारण समरूपता

यह भी देखें

संदर्भ

Navigation

Wiki tools

Page tools

Other projects

Categories