कोणीय संवेग व प्रचक्रण: Difference between revisions
(→उदाहरण) |
No edit summary |
||
| (33 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
कोणीय संवेग एक भौतिक मात्रा है जो एक अक्ष के चारों ओर किसी वस्तु की घूर्णी गति का वर्णन करती है। इसे किसी वस्तु के जड़त्व आघूर्ण और उसके कोणीय वेग के उत्पाद के रूप में परिभाषित किया जाता है। जड़ता का क्षण किसी वस्तु के घूर्णी गति के प्रतिरोध का एक उपाय है, और कोणीय वेग वह दर है जिस पर वस्तु अक्ष के चारों ओर घूमती है। | कोणीय संवेग एक भौतिक मात्रा है जो एक अक्ष के चारों ओर किसी वस्तु की घूर्णी गति का वर्णन करती है। इसे किसी वस्तु के जड़त्व आघूर्ण और उसके कोणीय वेग के उत्पाद के रूप में परिभाषित किया जाता है। जड़ता का क्षण किसी वस्तु के घूर्णी गति के प्रतिरोध का एक उपाय है, और कोणीय वेग वह दर है जिस पर वस्तु अक्ष के चारों ओर घूमती है। | ||
[[File:Gyroskop.jpg|thumb|प्रयोगशाला | [[File:Gyroskop.jpg|thumb|प्रयोगशाला में प्रयोग में आने वाला ,जाइरोस्कोप,कोणीय संवेग व प्रचक्रण को समझने में सहायक है ।]] | ||
गणितीय रूप से, कोणीय संवेग <math>(L)</math> को <math>L = I * \omega</math> के रूप में व्यक्त किया जाता है, जहाँ <math>I</math> जड़ता का क्षण है और <math>\omega</math> कोणीय वेग है। कोणीय संवेग की इकाई किलोग्राम मीटर वर्ग प्रति सेकंड <math>(kg\centerdot m^2/s)</math> है। | गणितीय रूप से, कोणीय संवेग <math>(L)</math> को <math>L = I * \omega</math> के रूप में व्यक्त किया जाता है, जहाँ <math>I</math> जड़ता का क्षण है और <math>\omega</math> कोणीय वेग है। कोणीय संवेग की इकाई किलोग्राम मीटर वर्ग प्रति सेकंड <math>(kg\centerdot m^2/s)</math> है। | ||
एक बंद प्रणाली में कोणीय संवेग,संरक्षित रहता है ,जहां उस प्रणाली पर कोई बाहरी बलाघूर्ण कार्य नहीं कर रहा हो। भौतिकी में,इस संरक्षण नियम के महत्वपूर्ण अनुप्रयोग हैं, जैसे आकाशीय यांत्रिकी, परमाणु भौतिकी और क्वांटम यांत्रिकी के अध्ययन में। विशेष रूप से, कोणीय संवेग का संरक्षण कई अवलोकित परिघटनाओं की व्याख्या करने में मदद करता है, जैसे की एक प्रचक्रित लट्टू के पुरस्सरण में, सौर मंडल में ग्रहों की गति, और उपपरमाण्विक कणों का व्यवहार।[[File:Spin One-Half (Slow).gif|thumb]] | एक बंद प्रणाली में कोणीय संवेग,संरक्षित रहता है ,जहां उस प्रणाली पर कोई बाहरी बलाघूर्ण कार्य नहीं कर रहा हो। भौतिकी में,इस संरक्षण नियम के महत्वपूर्ण अनुप्रयोग हैं, जैसे आकाशीय यांत्रिकी, परमाणु भौतिकी और क्वांटम यांत्रिकी के अध्ययन में। विशेष रूप से, कोणीय संवेग का संरक्षण कई अवलोकित परिघटनाओं की व्याख्या करने में मदद करता है, जैसे की एक प्रचक्रित लट्टू के पुरस्सरण में, सौर मंडल में ग्रहों की गति, और उपपरमाण्विक कणों का व्यवहार।[[File:Spin One-Half (Slow).gif|thumb|अंतरिक्ष में एक बिंदु बिना उलझे लगातार घूम सकता है। ध्यान दें कि 360 डिग्री घूमने के बाद, सर्पिल दक्षिणावर्त और वामावर्त झुकाव के बीच फ़्लिप करता है। पूर्ण 720 डिग्री घूमने के बाद यह अपने मूल विन्यास में लौट आता है।]] | ||
== मुख्य प्रकार == | == मुख्य प्रकार == | ||
| Line 9: | Line 9: | ||
कोणीय संवेग के दो मुख्य प्रकार हैं: | कोणीय संवेग के दो मुख्य प्रकार हैं: | ||
* | * कक्षीय कोणीय संवेग: इस प्रकार का कोणीय संवेग किसी केंद्रीय बिंदु या अक्ष के चारों ओर कक्षा में किसी वस्तु की गति से जुड़ा होता है। यह वस्तु के द्रव्यमान, गति और केंद्रीय बिंदु से दूरी पर निर्भर करता है। किसी वस्तु का कक्षीय कोणीय संवेग उसके कक्षीय तल के लंबवत होता है। | ||
* | * प्रचक्रित कोणीय संवेग: इस प्रकार की कोणीय गति एक कण के आंतरिक प्रचक्रण से जुड़ी होती है, जैसे कि इलेक्ट्रॉन, प्रोटॉन या न्यूट्रॉन। यह इन कणों का मूलभूत गुण है और अंतरिक्ष में उनकी गति से संबंधित नहीं है। किसी कण का प्रचक्रण कोणीय संवेग भी उसके प्रचक्रण अक्ष के लम्बवत् होता है। | ||
दोनों प्रकार के कोणीय गति के भौतिकी में महत्वपूर्ण अनुप्रयोग हैं, जैसे कि क्वांटम यांत्रिकी, परमाणु और आणविक भौतिकी और खगोल विज्ञान के अध्ययन में। कोणीय गति का संरक्षण कई भौतिक प्रणालियों में एक महत्वपूर्ण भूमिका निभाता है, और यह शास्त्रीय यांत्रिकी और क्वांटम यांत्रिकी में एक महत्वपूर्ण सिद्धांत है। | दोनों प्रकार के कोणीय गति के भौतिकी में महत्वपूर्ण अनुप्रयोग हैं, जैसे कि क्वांटम यांत्रिकी, परमाणु और आणविक भौतिकी और खगोल विज्ञान के अध्ययन में। कोणीय गति का संरक्षण कई भौतिक प्रणालियों में एक महत्वपूर्ण भूमिका निभाता है, और यह शास्त्रीय यांत्रिकी और क्वांटम यांत्रिकी में एक महत्वपूर्ण सिद्धांत है। | ||
== कोणीय संवेग और प्रचक्रण में संबंध == | == कोणीय संवेग और प्रचक्रण में संबंध == | ||
[[कोणीय गति]], जिसे कभी-कभी स्पिन के रूप में संदर्भित किया जाता है, किसी वस्तु के द्रव्यमान, उसके वेग और द्रव्यमान के घूमने के बिंदु से कितनी दूर तक फैला हुआ है, द्वारा निर्धारित किया जाता है। द्रव्यमान अपने अक्ष बिंदु के जितना निकट होता है - या जितना अधिक समेकित वह उस अक्ष के चारों ओर होता है - उसका वेग उतना ही अधिक होता है। | |||
किसी कण का स्पिन कोणीय संवेग परिमाणित होता है, जिसका अर्थ है कि | प्रचक्रण (स्पिन) कोणीय गति, एक कण, जैसे कि एक इलेक्ट्रॉन,प्रोटॉन या न्यूट्रॉन, की आंतरिक कोणीय गति<ref>{{Cite book|last=आर. इल्गे और वी. वुन्श|title=Relativistic Wave Equations Including Higher Spin Fields Encyclopedia of Mathematical Physics|publisher=अकादमिक प्रेस एल्सेवियर लिमिटेड|year=2006|pages=391-398|doi=10.1016/B0-12-512666-2/00161-9}}</ref> (वेग) से जुड़ी होती है। प्रचक्रण (स्पिन) कोणीय गति,किसी भी माध्यम से कण की गति से संबंधित नहीं है। एक कण की गतिमान व्यवस्था में,कण की गति के, तात्कालिक व बाहय पहलु होते हैं,यहां ये याद रखना होगा की एक प्र्चक्रित कण की प्रचक्रण गति तात्कालिक होने के साथ साथ उसका आंतरिक गुण है। ध्यान देने योग्य बात यह भी है की इस गतिशील व्यवस्था में वेग मात्र चक्रित, मात्र कोणीय, मात्र रैखिक अथवा वेग के इन रूपों के विभिन्न संयोजनों में हो सकता है। | ||
किसी कण का स्पिन कोणीय संवेग, परिमाणित होता है, जिसका अर्थ है कि इस के केवल कुछ असतत मान हो सकते हैं, जो कण के गुणों पर निर्भर करते हैं। उदाहरण के लिए, एक इलेक्ट्रॉन का स्पिन 1/2 होता है, जिसका अर्थ है कि इसके स्पिन कोणीय गति के केवल दो संभावित मान हो सकते हैं: प्लैंक स्थिरांक की इकाइयों में <math>1/2</math> या <math>-1/2</math> को <math>2\pi</math> से विभाजित किया जाता है। | |||
चक्रण के अतिरिक्त, कणों में कक्षीय कोणीय संवेग भी हो सकता है, जो एक केंद्रीय बिंदु या अक्ष के चारों ओर उनकी गति से जुड़ा होता है। किसी कण का कुल कोणीय संवेग उसके प्रचक्रण और कक्षीय कोणीय संवेग का योग होता है। | चक्रण के अतिरिक्त, कणों में कक्षीय कोणीय संवेग भी हो सकता है, जो एक केंद्रीय बिंदु या अक्ष के चारों ओर उनकी गति से जुड़ा होता है। किसी कण का कुल कोणीय संवेग उसके प्रचक्रण और कक्षीय कोणीय संवेग का योग होता है। | ||
स्पिन और कक्षीय कोणीय गति सहित कोणीय गति की अवधारणा क्वांटम यांत्रिकी, परमाणु और | स्पिन और कक्षीय कोणीय गति सहित कोणीय गति की अवधारणा [https://en-m-wikipedia-org.translate.goog/wiki/Quantum_mechanics?_x_tr_sl=en&_x_tr_tl=hi&_x_tr_hl=hi&_x_tr_pto=tc क्वांटम यांत्रिकी], [https://en-m-wikipedia-org.translate.goog/wiki/Atomic,_molecular,_and_optical_physics?_x_tr_sl=en&_x_tr_tl=hi&_x_tr_hl=hi&_x_tr_pto=tc परमाणु,आणविक और ऑप्टिकल भौतिकी] और [https://en-m-wikipedia-org.translate.goog/wiki/Astronomy?_x_tr_sl=en&_x_tr_tl=hi&_x_tr_hl=hi&_x_tr_pto=tc खगोल विज्ञान] सहित भौतिकी के कई क्षेत्रों के लिए मौलिक है। इन क्षेत्रों में कोणीय संवेग का संरक्षण एक महत्वपूर्ण सिद्धांत है, और इसका उपयोग कई देखी गई घटनाओं की व्याख्या करने के लिए किया जाता है। | ||
== उदाहरण == | == उदाहरण == | ||
एक कक्षा में किसी पिंड के कोणीय संवेग L | किसी वस्तु के कोणीय संवेग <math>L</math> को मापते समय यह देखा जाता है की वह वस्तु किस व्यवस्था का अंग है। ऐसी स्थिति में सौर्य मंडल में प्रचक्रण करते,कक्षीय अवस्था में पाए आने वाले ग्रह (जैसे की सूर्य की परिक्रमा करती पृथ्वी) और एक परमाणु के नाभिक प्रभाव क्षेत्र के इर्द गिर्द पाए जाने वाले इलेक्ट्रान के कोणीय संवेग के दो हिज्जे (प्र्चक्रित एवं कक्षीय पहलु ) को नापने की विधि मूलतः एक सी होने पर भी, दृष्टिकोण भेद से ग्रसित है। | ||
गणना सापेक्षतावादी विचारों पर भी निर्भर करती है। सूर्य के चारों ओर पृथ्वी की गति के सरल (आ-सापेक्ष) मामले पर विचार करें | |||
एक कक्षा में किसी <math>M</math> द्रव्यमान के पिंड, के कोणीय संवेग <math>L</math> का साधारण सम्बन्ध | |||
<math>L = 2 \pi M f r^2</math> | <math>L = 2 \pi M f r^2</math> | ||
द्वारा दिया जाता है | |||
इसके बजाय अपनी धुरी के चारों ओर घूमने वाले एक समान कठोर गोले का कोणीय संवेग <math>L</math> | जहाँ ,<math>f</math> कक्षा की आवृत्ति है और <math>r</math> की त्रिज्या है। | ||
इसके बजाय अपनी धुरी के चारों ओर घूमने वाले एक समान कठोर गोले का कोणीय संवेग <math>L</math> | |||
<math>{\displaystyle L={\frac {4}{5}}\pi Mfr^{2}}</math> | <math>{\displaystyle L={\frac {4}{5}}\pi Mfr^{2}}</math> | ||
द्वारा दिया जाता है | |||
जहाँ <math>M</math> गोले का द्रव्यमान है, <math>f</math> घूर्णन की आवृत्ति है और <math>r</math> गोले की त्रिज्या है। | जहाँ <math>M</math> गोले का द्रव्यमान है, <math>f</math> घूर्णन की आवृत्ति है और <math>r</math> गोले की त्रिज्या है। | ||
इस प्रकार, उदाहरण के लिए, सूर्य के संबंध में पृथ्वी का कक्षीय कोणीय संवेग लगभग 2.66 × 10<sup>40</sup> kg⋅m<sup>2</sup>⋅s<sup>−1</sup> | इस प्रकार, उदाहरण के लिए, सूर्य के संबंध में पृथ्वी का कक्षीय कोणीय संवेग <math>L</math> लगभग 2.66 × 10<sup>40</sup> kg⋅m<sup>2</sup>⋅s<sup>−1</sup> है<ref>{{Cite web|title=Angular Momentum|url=https://www.vanderbilt.edu/AnS/physics/astrocourses/ast201/angular_momentum.html}}</ref>, जबकि इसका प्रचक्रण (घूर्णी) कोणीय संवेग लगभग 7.05 × 10<sup>33</sup> kg⋅m<sup>2</sup>⋅s<sup>−1</sup> है। | ||
अपनी धुरी के चारों ओर घूमने वाले एकसमान कठोर गोले के मामले में, यदि इसके द्रव्यमान के बजाय, इसका घनत्व ज्ञात हो, तो कोणीय संवेग द्वारा दिया जाता है | |||
[[File:Moment of inertia examples.gif|thumb|कुछ आकृतियों के जड़त्व आघूर्ण ]] | |||
<math>{\displaystyle L={\frac {16}{15}}\pi ^{2}\rho fr^{5}}</math> | |||
जहाँ <math>\rho</math> गोले का घनत्व है, <math>f</math> घूर्णन की आवृत्ति है और <math>r</math> गोले की त्रिज्या है। | |||
स्पिनिंग डिस्क के सरलतम मामले में, कोणीय संवेग <math>L</math> द्वारा दिया जाता है <ref name=":0" /> | |||
<math>{\displaystyle L=\pi Mfr^{2}}</math> | |||
जहाँ <math>M</math> डिस्क का द्रव्यमान है, <math>f</math> घूर्णन की आवृत्ति है और <math>r</math> डिस्क की त्रिज्या है। | |||
यदि इसके बजाय डिस्क अपने व्यास के बारे में घूमती है (जैसे सिक्के का लट्टू के रूप में घूर्ण ), तो इसका कोणीय संवेग <math>L</math> <ref name=":0">{{Cite web|title=भौतिकी और खगोल विज्ञान विभाग, जॉर्जिया स्टेट यूनिवर्सिटी। "Moment of Inertia: Thin Disk" हाइपरफिजिक्स 17 मार्च 2023 को पुनःप्राप्त|url=http://hyperphysics.phy-astr.gsu.edu/hbase/tdisc.html}}</ref> द्वारा दिया जाता है | |||
<math>{\displaystyle L={\frac {1}{2}}\pi Mfr^{2}}</math> | |||
समान द्रव्यमान के रहते हुए भी ,वस्तु के विभिन्न आकारों के कारण, घूर्णी और कोणीय संवेग,अलग अलग हो सकते हैं।ऐसा उस द्रव्यमान वस्तु के आकार भेद से उतपन्न जड़त्व आघूर्ण के बदलाव के कारण होता है (जैसा की संलग्न चित्र में दिखलाया गया है)। | |||
== छोटे पैमाने की प्रणालियों के लिए : इलेक्ट्रॉनों के लिए उदाहरण == | |||
कक्षीय इलेक्ट्रॉन,अपनी चलित ऊर्जा को निष्कासित करते हूए, नाभिक में नहीं गिरते, कई वर्षों तक वैज्ञानिकों को हैरान करता रहा और नाभिक में पॉजिटिव चार्ज होने पर भी,में पॉजिटिव चार्ज होने पर भी परमाणु का मॉडल सं रचित रहता है। यह तथ्य क्वांटम यांत्रिकी विकसित होने के कई कारणों में से एक बना। | |||
हिसेनबर्ग के [[:hi:अनिश्चितता_सिद्धान्त|अनिश्चितता सिद्धांत]] का सहारा लेते हुए ,बाध्य इलेक्ट्रॉनों के लिए ,निर्धारित सीमाओं के भीतर एक परमाणु कक्षा में ,इलेक्ट्रॉन को खोजने की संभावना परिभाषित की जाती है। ऐसे जटिल परिदृश्य में कोणीय गति का स्पिन और कक्षीय घटक,शास्त्रीय और क्वांटम-मैकेनिकल गुणों का उपयोग कर यह स्थापित करते हैं की न सिर्फ यह इलेक्ट्रान इस सम्भवना क्षेत्र में पाया जा सकता है बल्कि यह उस इलेक्ट्रान को ढूढ़ने की यह प्रयास ही एक मात्र सही प्रयास है। | |||
एल = | क्वांटम यांत्रिकी में इसकी घटाक्रम की समीक्षा,कणों को [[तरंग फलन]]<ref>{{Cite web|title=वेव फंक्शन क्या है?|url=https://www-thoughtco-com.translate.goog/definition-of-wavefunction-605790?_x_tr_sl=en&_x_tr_tl=hi&_x_tr_hl=hi&_x_tr_pto=rq}}</ref> [[तरंग फलन|का]] उपयोग कर वर्णित की जा सकती है। इलेक्ट्रॉन के पाए जाने वाले सम्भावना क्षेत्र को वर्णित करने के लिये यह प्रश्न पूंछा जा सकता है की "जब पानी में कुछ गिरकर लहर बनाती है, तो वह लहर किस स्थान पर होती है?" इसके उत्तर में कहा जा सकता है की तरंग का कोई निश्चित स्थान निर्धारित नहीं किया जा सकता है ,परन्तु सही उत्तर यह है की तरंग के पाए जाने वाले स्थान को एक समभावित क्षेत्र में निर्धारित किया जाता है,यही स्थिति इलेक्ट्रान की है जिसको क्वांटम मैकेनिक्स में एक तरंग फलन के रूप में देखा जा सकता है,इस प्रकार के चित्रण में इलेक्ट्रॉन अंतरिक्ष में फैले हुए हैं। जिस तरह से यह इलेक्ट्रॉन तरंग<ref>{{Cite web|last=आर नैव|first=|title=इलेक्ट्रॉन की तरंग प्रकृति|url=https://hyperphysics-phy--astr-gsu-edu.translate.goog/hbase/debrog.html?_x_tr_sch=http&_x_tr_sl=en&_x_tr_tl=hi&_x_tr_hl=hi&_x_tr_pto=tc|website=hyperphysics-phy--astr-gsu-edu}}</ref> चलती है उसका वर्णन श्रोडिंगर समीकरण<ref>{{Cite book|last=एल.डी. लन्दौ, ईएम लाइफशिट्ज,|title=Quantum Mechanics: A Shorter Course of Theoretical Physics SCHRÖDINGER'S EQUATION|publisher=पेर्गमॉन एल्सेवियर लिमिटेड|year=1974|isbn=978-0-08-017801-1}}</ref> द्वारा किया जाता है। | ||
< | कोणीय गति, क्वांटम संख्या, जिसे <math>l</math> द्वारा दर्शाया गया है, सामान्य आकार या क्षेत्र का वर्णन करता है,जिसमें एक इलेक्ट्रॉन होता है-इसकी कक्षीय आकृति <math>l</math> का मान मुख्य क्वांटम संख्या, <math>n</math> के मान पर निर्भर करता है। कोणीय गति क्वांटम संख्या में शून्य से <math>n-1</math> के धनात्मक मान हो सकते हैं। अगर <math>n=2, </math>तो <math>l</math> या तो <math>0</math> अथवा <math>1</math> हो सकता है। | ||
== शास्त्रीय और क्वांटम-मैकेनिकल गुणों का समानता मापन == | |||
आम तौर पर यह मापन, मानचित्रण समानता पर निर्भर करता है, जो शास्त्रीय पैमाने (बड़ी प्रणालियों) पर मान्य है लेकिन ,परमाणु स्तर पर जाने पर कुछ अंतर्ज्ञान टूट सकते हैं। | |||
शास्त्रीय कोणीय गति, वास्तविक गति (विशेष रूप से परिपत्र गति) का वर्णन करती है, जो कि समय के संबंध में स्थिति में परिवर्तन है। क्वांटम यांत्रिकी में गति की धारणा थोड़ी अस्पष्ट है,एक कण की स्थिति को अच्छी तरह से परिभाषित नहीं किया जा सकता है। विभिन्न संभावनाओं के समीकरण,क्वांटम कोणीय संवेग और शास्त्रीय शैली, संभाव्यता वितरण<ref>{{Cite web|title=संभाव्यता वितरण|url=https://www-simplilearn-com.translate.goog/tutorials/statistics-tutorial/what-is-probability-distribution?_x_tr_sl=en&_x_tr_tl=hi&_x_tr_hl=hi&_x_tr_pto=tc}}</ref> का उपयोग कर,अलग-अलग स्थितियों पर अवस्था, जहां उच्च संभावना के साथ इलेक्ट्रॉन (कण) पाया जा सकता है, को, वर्णित करते हैं। | |||
शास्त्रीय भौतिकी स्थूलता (मेकोरस्कोपिक) से संबंधित है,यहां उन घटनाक्रम की चर्चा, जहां कणों का आकार,<math>{{10^{-8}}}m</math> से अधिक और कण वेग <math>108 m/s</math> से कम ,और पर्याप्त गुरुत्वाकर्षण व विद्युत चुम्बकीय बल,विद्यमान रहते हैं । | |||
क्वांटम यांत्रिकी सूक्ष्मता से संबंधित है, यहां परमाणुओं,अणुओं नाभिक घटनाओं की व्याख्या होती है। इस पैमाने की भौतिक घटनाओं पर क्षीण और दृढ़,परमाणु बल हावी रहते हैं । | |||
कुछ विद्वान,शास्त्रीय को क्वांटम यांत्रिकी का एक विशेष संदर्भ मानते हैं<ref>{{Cite journal|last=डिर्क एर्ट्स|date=1983|title=Classical theories and nonclassical theories as special cases of a more general theory|journal=Journal of Mathematical Physics|volume=24,|pages=2441–2453|doi=10.1063/1.525626}}</ref>। | |||
== निष्कर्ष == | |||
कोणीय संवेग व प्रचक्रण,भौतिक विज्ञान के महत्व पूर्ण उपक्रम, यांत्रिकी, के शास्त्रीय और क्वांटम पहलू को जोड़ते हैं । सापेक्षता के सिद्धांत को साथ में रख कर, ये तीन विधाएँ आधुनिक काल में भौतिकी के आधार स्थंभ माने जा सकते हैं। | |||
== संदर्भ == | |||
<references /> | |||
[[Category:CS1 maint]] | |||
[[Category:Organic Articles]] | |||
[[Category:Templates Vigyan Ready]] | |||
Latest revision as of 10:03, 22 May 2023
कोणीय संवेग एक भौतिक मात्रा है जो एक अक्ष के चारों ओर किसी वस्तु की घूर्णी गति का वर्णन करती है। इसे किसी वस्तु के जड़त्व आघूर्ण और उसके कोणीय वेग के उत्पाद के रूप में परिभाषित किया जाता है। जड़ता का क्षण किसी वस्तु के घूर्णी गति के प्रतिरोध का एक उपाय है, और कोणीय वेग वह दर है जिस पर वस्तु अक्ष के चारों ओर घूमती है।
गणितीय रूप से, कोणीय संवेग को के रूप में व्यक्त किया जाता है, जहाँ जड़ता का क्षण है और कोणीय वेग है। कोणीय संवेग की इकाई किलोग्राम मीटर वर्ग प्रति सेकंड है।
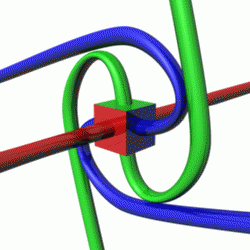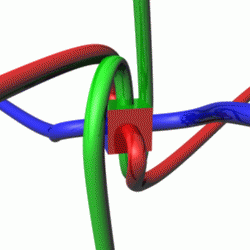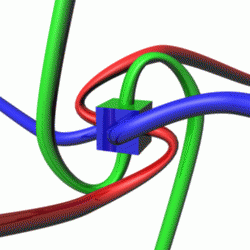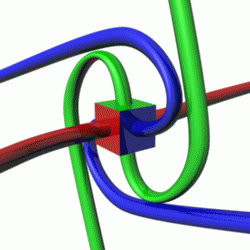
एक बंद प्रणाली में कोणीय संवेग,संरक्षित रहता है ,जहां उस प्रणाली पर कोई बाहरी बलाघूर्ण कार्य नहीं कर रहा हो। भौतिकी में,इस संरक्षण नियम के महत्वपूर्ण अनुप्रयोग हैं, जैसे आकाशीय यांत्रिकी, परमाणु भौतिकी और क्वांटम यांत्रिकी के अध्ययन में। विशेष रूप से, कोणीय संवेग का संरक्षण कई अवलोकित परिघटनाओं की व्याख्या करने में मदद करता है, जैसे की एक प्रचक्रित लट्टू के पुरस्सरण में, सौर मंडल में ग्रहों की गति, और उपपरमाण्विक कणों का व्यवहार।
मुख्य प्रकार
कोणीय संवेग के दो मुख्य प्रकार हैं:
- कक्षीय कोणीय संवेग: इस प्रकार का कोणीय संवेग किसी केंद्रीय बिंदु या अक्ष के चारों ओर कक्षा में किसी वस्तु की गति से जुड़ा होता है। यह वस्तु के द्रव्यमान, गति और केंद्रीय बिंदु से दूरी पर निर्भर करता है। किसी वस्तु का कक्षीय कोणीय संवेग उसके कक्षीय तल के लंबवत होता है।
- प्रचक्रित कोणीय संवेग: इस प्रकार की कोणीय गति एक कण के आंतरिक प्रचक्रण से जुड़ी होती है, जैसे कि इलेक्ट्रॉन, प्रोटॉन या न्यूट्रॉन। यह इन कणों का मूलभूत गुण है और अंतरिक्ष में उनकी गति से संबंधित नहीं है। किसी कण का प्रचक्रण कोणीय संवेग भी उसके प्रचक्रण अक्ष के लम्बवत् होता है।
दोनों प्रकार के कोणीय गति के भौतिकी में महत्वपूर्ण अनुप्रयोग हैं, जैसे कि क्वांटम यांत्रिकी, परमाणु और आणविक भौतिकी और खगोल विज्ञान के अध्ययन में। कोणीय गति का संरक्षण कई भौतिक प्रणालियों में एक महत्वपूर्ण भूमिका निभाता है, और यह शास्त्रीय यांत्रिकी और क्वांटम यांत्रिकी में एक महत्वपूर्ण सिद्धांत है।
कोणीय संवेग और प्रचक्रण में संबंध
कोणीय गति, जिसे कभी-कभी स्पिन के रूप में संदर्भित किया जाता है, किसी वस्तु के द्रव्यमान, उसके वेग और द्रव्यमान के घूमने के बिंदु से कितनी दूर तक फैला हुआ है, द्वारा निर्धारित किया जाता है। द्रव्यमान अपने अक्ष बिंदु के जितना निकट होता है - या जितना अधिक समेकित वह उस अक्ष के चारों ओर होता है - उसका वेग उतना ही अधिक होता है।
प्रचक्रण (स्पिन) कोणीय गति, एक कण, जैसे कि एक इलेक्ट्रॉन,प्रोटॉन या न्यूट्रॉन, की आंतरिक कोणीय गति[1] (वेग) से जुड़ी होती है। प्रचक्रण (स्पिन) कोणीय गति,किसी भी माध्यम से कण की गति से संबंधित नहीं है। एक कण की गतिमान व्यवस्था में,कण की गति के, तात्कालिक व बाहय पहलु होते हैं,यहां ये याद रखना होगा की एक प्र्चक्रित कण की प्रचक्रण गति तात्कालिक होने के साथ साथ उसका आंतरिक गुण है। ध्यान देने योग्य बात यह भी है की इस गतिशील व्यवस्था में वेग मात्र चक्रित, मात्र कोणीय, मात्र रैखिक अथवा वेग के इन रूपों के विभिन्न संयोजनों में हो सकता है।
किसी कण का स्पिन कोणीय संवेग, परिमाणित होता है, जिसका अर्थ है कि इस के केवल कुछ असतत मान हो सकते हैं, जो कण के गुणों पर निर्भर करते हैं। उदाहरण के लिए, एक इलेक्ट्रॉन का स्पिन 1/2 होता है, जिसका अर्थ है कि इसके स्पिन कोणीय गति के केवल दो संभावित मान हो सकते हैं: प्लैंक स्थिरांक की इकाइयों में या को से विभाजित किया जाता है।
चक्रण के अतिरिक्त, कणों में कक्षीय कोणीय संवेग भी हो सकता है, जो एक केंद्रीय बिंदु या अक्ष के चारों ओर उनकी गति से जुड़ा होता है। किसी कण का कुल कोणीय संवेग उसके प्रचक्रण और कक्षीय कोणीय संवेग का योग होता है।
स्पिन और कक्षीय कोणीय गति सहित कोणीय गति की अवधारणा क्वांटम यांत्रिकी, परमाणु,आणविक और ऑप्टिकल भौतिकी और खगोल विज्ञान सहित भौतिकी के कई क्षेत्रों के लिए मौलिक है। इन क्षेत्रों में कोणीय संवेग का संरक्षण एक महत्वपूर्ण सिद्धांत है, और इसका उपयोग कई देखी गई घटनाओं की व्याख्या करने के लिए किया जाता है।
उदाहरण
किसी वस्तु के कोणीय संवेग को मापते समय यह देखा जाता है की वह वस्तु किस व्यवस्था का अंग है। ऐसी स्थिति में सौर्य मंडल में प्रचक्रण करते,कक्षीय अवस्था में पाए आने वाले ग्रह (जैसे की सूर्य की परिक्रमा करती पृथ्वी) और एक परमाणु के नाभिक प्रभाव क्षेत्र के इर्द गिर्द पाए जाने वाले इलेक्ट्रान के कोणीय संवेग के दो हिज्जे (प्र्चक्रित एवं कक्षीय पहलु ) को नापने की विधि मूलतः एक सी होने पर भी, दृष्टिकोण भेद से ग्रसित है।
गणना सापेक्षतावादी विचारों पर भी निर्भर करती है। सूर्य के चारों ओर पृथ्वी की गति के सरल (आ-सापेक्ष) मामले पर विचार करें
एक कक्षा में किसी द्रव्यमान के पिंड, के कोणीय संवेग का साधारण सम्बन्ध
द्वारा दिया जाता है
जहाँ , कक्षा की आवृत्ति है और की त्रिज्या है।
इसके बजाय अपनी धुरी के चारों ओर घूमने वाले एक समान कठोर गोले का कोणीय संवेग
द्वारा दिया जाता है
जहाँ गोले का द्रव्यमान है, घूर्णन की आवृत्ति है और गोले की त्रिज्या है।
इस प्रकार, उदाहरण के लिए, सूर्य के संबंध में पृथ्वी का कक्षीय कोणीय संवेग लगभग 2.66 × 1040 kg⋅m2⋅s−1 है[2], जबकि इसका प्रचक्रण (घूर्णी) कोणीय संवेग लगभग 7.05 × 1033 kg⋅m2⋅s−1 है।
अपनी धुरी के चारों ओर घूमने वाले एकसमान कठोर गोले के मामले में, यदि इसके द्रव्यमान के बजाय, इसका घनत्व ज्ञात हो, तो कोणीय संवेग द्वारा दिया जाता है
जहाँ गोले का घनत्व है, घूर्णन की आवृत्ति है और गोले की त्रिज्या है।
स्पिनिंग डिस्क के सरलतम मामले में, कोणीय संवेग द्वारा दिया जाता है [3]
जहाँ डिस्क का द्रव्यमान है, घूर्णन की आवृत्ति है और डिस्क की त्रिज्या है।
यदि इसके बजाय डिस्क अपने व्यास के बारे में घूमती है (जैसे सिक्के का लट्टू के रूप में घूर्ण ), तो इसका कोणीय संवेग [3] द्वारा दिया जाता है
समान द्रव्यमान के रहते हुए भी ,वस्तु के विभिन्न आकारों के कारण, घूर्णी और कोणीय संवेग,अलग अलग हो सकते हैं।ऐसा उस द्रव्यमान वस्तु के आकार भेद से उतपन्न जड़त्व आघूर्ण के बदलाव के कारण होता है (जैसा की संलग्न चित्र में दिखलाया गया है)।
छोटे पैमाने की प्रणालियों के लिए : इलेक्ट्रॉनों के लिए उदाहरण
कक्षीय इलेक्ट्रॉन,अपनी चलित ऊर्जा को निष्कासित करते हूए, नाभिक में नहीं गिरते, कई वर्षों तक वैज्ञानिकों को हैरान करता रहा और नाभिक में पॉजिटिव चार्ज होने पर भी,में पॉजिटिव चार्ज होने पर भी परमाणु का मॉडल सं रचित रहता है। यह तथ्य क्वांटम यांत्रिकी विकसित होने के कई कारणों में से एक बना।
हिसेनबर्ग के अनिश्चितता सिद्धांत का सहारा लेते हुए ,बाध्य इलेक्ट्रॉनों के लिए ,निर्धारित सीमाओं के भीतर एक परमाणु कक्षा में ,इलेक्ट्रॉन को खोजने की संभावना परिभाषित की जाती है। ऐसे जटिल परिदृश्य में कोणीय गति का स्पिन और कक्षीय घटक,शास्त्रीय और क्वांटम-मैकेनिकल गुणों का उपयोग कर यह स्थापित करते हैं की न सिर्फ यह इलेक्ट्रान इस सम्भवना क्षेत्र में पाया जा सकता है बल्कि यह उस इलेक्ट्रान को ढूढ़ने की यह प्रयास ही एक मात्र सही प्रयास है।
क्वांटम यांत्रिकी में इसकी घटाक्रम की समीक्षा,कणों को तरंग फलन[4] का उपयोग कर वर्णित की जा सकती है। इलेक्ट्रॉन के पाए जाने वाले सम्भावना क्षेत्र को वर्णित करने के लिये यह प्रश्न पूंछा जा सकता है की "जब पानी में कुछ गिरकर लहर बनाती है, तो वह लहर किस स्थान पर होती है?" इसके उत्तर में कहा जा सकता है की तरंग का कोई निश्चित स्थान निर्धारित नहीं किया जा सकता है ,परन्तु सही उत्तर यह है की तरंग के पाए जाने वाले स्थान को एक समभावित क्षेत्र में निर्धारित किया जाता है,यही स्थिति इलेक्ट्रान की है जिसको क्वांटम मैकेनिक्स में एक तरंग फलन के रूप में देखा जा सकता है,इस प्रकार के चित्रण में इलेक्ट्रॉन अंतरिक्ष में फैले हुए हैं। जिस तरह से यह इलेक्ट्रॉन तरंग[5] चलती है उसका वर्णन श्रोडिंगर समीकरण[6] द्वारा किया जाता है।
कोणीय गति, क्वांटम संख्या, जिसे द्वारा दर्शाया गया है, सामान्य आकार या क्षेत्र का वर्णन करता है,जिसमें एक इलेक्ट्रॉन होता है-इसकी कक्षीय आकृति का मान मुख्य क्वांटम संख्या, के मान पर निर्भर करता है। कोणीय गति क्वांटम संख्या में शून्य से के धनात्मक मान हो सकते हैं। अगर तो या तो अथवा हो सकता है।
शास्त्रीय और क्वांटम-मैकेनिकल गुणों का समानता मापन
आम तौर पर यह मापन, मानचित्रण समानता पर निर्भर करता है, जो शास्त्रीय पैमाने (बड़ी प्रणालियों) पर मान्य है लेकिन ,परमाणु स्तर पर जाने पर कुछ अंतर्ज्ञान टूट सकते हैं।
शास्त्रीय कोणीय गति, वास्तविक गति (विशेष रूप से परिपत्र गति) का वर्णन करती है, जो कि समय के संबंध में स्थिति में परिवर्तन है। क्वांटम यांत्रिकी में गति की धारणा थोड़ी अस्पष्ट है,एक कण की स्थिति को अच्छी तरह से परिभाषित नहीं किया जा सकता है। विभिन्न संभावनाओं के समीकरण,क्वांटम कोणीय संवेग और शास्त्रीय शैली, संभाव्यता वितरण[7] का उपयोग कर,अलग-अलग स्थितियों पर अवस्था, जहां उच्च संभावना के साथ इलेक्ट्रॉन (कण) पाया जा सकता है, को, वर्णित करते हैं।
शास्त्रीय भौतिकी स्थूलता (मेकोरस्कोपिक) से संबंधित है,यहां उन घटनाक्रम की चर्चा, जहां कणों का आकार, से अधिक और कण वेग से कम ,और पर्याप्त गुरुत्वाकर्षण व विद्युत चुम्बकीय बल,विद्यमान रहते हैं ।
क्वांटम यांत्रिकी सूक्ष्मता से संबंधित है, यहां परमाणुओं,अणुओं नाभिक घटनाओं की व्याख्या होती है। इस पैमाने की भौतिक घटनाओं पर क्षीण और दृढ़,परमाणु बल हावी रहते हैं ।
कुछ विद्वान,शास्त्रीय को क्वांटम यांत्रिकी का एक विशेष संदर्भ मानते हैं[8]।
निष्कर्ष
कोणीय संवेग व प्रचक्रण,भौतिक विज्ञान के महत्व पूर्ण उपक्रम, यांत्रिकी, के शास्त्रीय और क्वांटम पहलू को जोड़ते हैं । सापेक्षता के सिद्धांत को साथ में रख कर, ये तीन विधाएँ आधुनिक काल में भौतिकी के आधार स्थंभ माने जा सकते हैं।
संदर्भ
- ↑ आर. इल्गे और वी. वुन्श (2006). Relativistic Wave Equations Including Higher Spin Fields Encyclopedia of Mathematical Physics. अकादमिक प्रेस एल्सेवियर लिमिटेड. pp. 391–398. doi:10.1016/B0-12-512666-2/00161-9.
- ↑ "Angular Momentum".
- ↑ 3.0 3.1 "भौतिकी और खगोल विज्ञान विभाग, जॉर्जिया स्टेट यूनिवर्सिटी। "Moment of Inertia: Thin Disk" हाइपरफिजिक्स 17 मार्च 2023 को पुनःप्राप्त".
- ↑ "वेव फंक्शन क्या है?".
- ↑ आर नैव. "इलेक्ट्रॉन की तरंग प्रकृति". hyperphysics-phy--astr-gsu-edu.
- ↑ एल.डी. लन्दौ, ईएम लाइफशिट्ज, (1974). Quantum Mechanics: A Shorter Course of Theoretical Physics SCHRÖDINGER'S EQUATION. पेर्गमॉन एल्सेवियर लिमिटेड. ISBN 978-0-08-017801-1.
{{cite book}}: CS1 maint: extra punctuation (link) CS1 maint: multiple names: authors list (link) - ↑ "संभाव्यता वितरण".
- ↑ डिर्क एर्ट्स (1983). "Classical theories and nonclassical theories as special cases of a more general theory". Journal of Mathematical Physics. 24, : 2441–2453. doi:10.1063/1.525626.
{{cite journal}}: CS1 maint: extra punctuation (link)