स्नेक लेम्मा: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by 4 users not shown) | |||
| Line 11: | Line 11: | ||
जहाँ d एक समरूपता है, जिसे संयोजक समरूपता के रूप में जाना जाता है। | जहाँ d एक समरूपता है, जिसे संयोजक समरूपता के रूप में जाना जाता है। | ||
इसके अतिरिक्त, यदि आकृतिवाद f एक [[एकरूपता]] है, तो आकारिकी भी <math>\ker a ~{\color{Gray}\longrightarrow}~ \ker b</math>,है | इसके अतिरिक्त, यदि आकृतिवाद f एक [[एकरूपता]] है, तो आकारिकी भी <math>\ker a ~{\color{Gray}\longrightarrow}~ \ker b</math>,है और यदि g' [[ अधिरूपता |अधिरूपता]] है, तो ऐसा <math>\operatorname{coker} b ~{\color{Gray}\longrightarrow}~ \operatorname{coker} c</math>.है | ||
यहाँ कोकर्नेल <math>\operatorname{coker}a = A'/\operatorname{im}a</math>, <math>\operatorname{coker}b = B'/\operatorname{im}b</math>, <math>\operatorname{coker}c = C'/\operatorname{im}c</math> हैं: | यहाँ कोकर्नेल <math>\operatorname{coker}a = A'/\operatorname{im}a</math>, <math>\operatorname{coker}b = B'/\operatorname{im}b</math>, <math>\operatorname{coker}c = C'/\operatorname{im}c</math> हैं: | ||
| Line 21: | Line 21: | ||
== नक्शों का निर्माण == | == नक्शों का निर्माण == | ||
[[File:Snake lemma map construction.gif|alt=An animation of the diagram chase to construct the map d by finding d(x) ker c|thumb|361x361px|मानचित्र d के निर्माण का एक एनीमेशन में कुछ x दिया गया है]]आरेख की क्रमविनिमेयता के कारण दिए गए (क्षैतिज) मानचित्रों द्वारा गुठली और कोकर्नेल के बीच के मानचित्रों के बीच के मानचित्रों को प्राकृतिक विधि से प्रेरित किया जाता है। मूल आरेख की पंक्तियों की स्पष्टता से दो प्रेरित अनुक्रमों की स्पष्टता | [[File:Snake lemma map construction.gif|alt=An animation of the diagram chase to construct the map d by finding d(x) ker c|thumb|361x361px|मानचित्र d के निर्माण का एक एनीमेशन में कुछ x दिया गया है]]आरेख की क्रमविनिमेयता के कारण दिए गए (क्षैतिज) मानचित्रों द्वारा गुठली और कोकर्नेल के बीच के मानचित्रों के बीच के मानचित्रों को प्राकृतिक विधि से प्रेरित किया जाता है। मूल आरेख की पंक्तियों की स्पष्टता से दो प्रेरित अनुक्रमों की स्पष्टता सीधे विधि से होती है। लेम्मा का महत्वपूर्ण कथन यह है कि एक कनेक्टिंग होमोमोर्फिज्म ''d'' उपस्थित है जो स्पष्ट अनुक्रम को पूरा करता है। | ||
कुछ [[अंगूठी (गणित)|रिंग (गणित)]] पर एबेलियन समूहों या [[मॉड्यूल (गणित)]] के स्थिति में नक्शा ''d'' निम्नानुसार बनाया जा सकता है: | कुछ [[अंगूठी (गणित)|रिंग (गणित)]] पर एबेलियन समूहों या [[मॉड्यूल (गणित)]] के स्थिति में नक्शा ''d'' निम्नानुसार बनाया जा सकता है: | ||
केर C में एक तत्व एक्स चुनें और इसे सी के एक तत्व के रूप में देखें; चूँकि g आच्छादक है, इसलिए B में g(y) = x के साथ y उपस्थित है। आरेख की क्रमविनिमेयता के कारण, हमारे पास g'(b(y)) = c(g(y)) = c(x) = 0 है (क्योंकि x, c के कर्नेल में है), और इसलिए b(y) g' के कर्नेल में है। चूंकि नीचे की पंक्ति बिल्कुल स्पष्ट है, इसलिए हमें A' में f '(z) = b(y) के साथ एक तत्व z मिलता है। f' के इंजेक्शन द्वारा z अद्वितीय है। फिर हम d(x) = z + im(a) को परिभाषित करते हैं। अब किसी को यह जांचना है कि ''d'' | केर C में एक तत्व एक्स चुनें और इसे सी के एक तत्व के रूप में देखें; चूँकि g आच्छादक है, इसलिए B में g(y) = x के साथ y उपस्थित है। आरेख की क्रमविनिमेयता के कारण, हमारे पास g'(b(y)) = c(g(y)) = c(x) = 0 है (क्योंकि x, c के कर्नेल में है), और इसलिए b(y) g' के कर्नेल में है। चूंकि नीचे की पंक्ति बिल्कुल स्पष्ट है, इसलिए हमें A' में f '(z) = b(y) के साथ एक तत्व z मिलता है। f' के इंजेक्शन द्वारा z अद्वितीय है। फिर हम d(x) = z + im(a) को परिभाषित करते हैं। अब किसी को यह जांचना है कि ''d'' अच्छी तरह से परिभाषित है (अर्थात ''d''(''x'') केवल ''x'' पर निर्भर करता है और ''y'' की पसंद पर नहीं), यह एक समरूपता है, और परिणामी लंबा अनुक्रम वास्तव में स्पष्ट है। क्रमविनिमेय रेखाचित्र या आरेख का पीछा करते हुए नियमित रूप से स्पष्टता को सत्यापित किया जा सकता है (प्रमेयिका 9.1 का प्रमाण देखें) <ref>{{harvnb|Lang|2002|p=159}}</ref>). | ||
एक बार ऐसा हो जाने के बाद, रिंग के ऊपर एबेलियन समूहों या मॉड्यूल के लिए प्रमेय सिद्ध हो जाता है। सामान्य स्थिति के लिए, तर्क को तत्वों के अतिरिक्त तीरों और रद्दीकरण के गुणों के संदर्भ में दोहराया जा सकता है। वैकल्पिक रूप से, कोई मिशेल के एम्बेडिंग प्रमेय का आह्वान कर सकता है। | एक बार ऐसा हो जाने के बाद, रिंग के ऊपर एबेलियन समूहों या मॉड्यूल के लिए प्रमेय सिद्ध हो जाता है। सामान्य स्थिति के लिए, तर्क को तत्वों के अतिरिक्त तीरों और रद्दीकरण के गुणों के संदर्भ में दोहराया जा सकता है। वैकल्पिक रूप से, कोई मिशेल के एम्बेडिंग प्रमेय का आह्वान कर सकता है। | ||
| Line 39: | Line 39: | ||
== उदाहरण == | == उदाहरण == | ||
मान लीजिए <math>k</math> क्षेत्र है, <math>V</math> <math>k</math>-वेक्टर स्थान है। <math>V</math>, <math>k[t]</math>-मॉड्यूल द्वारा | मान लीजिए <math>k</math> क्षेत्र है, <math>V</math> <math>k</math>-वेक्टर स्थान है। <math>V</math>, <math>k[t]</math>-मॉड्यूल द्वारा <math>t:V \to V</math> एक <math>k</math>-रैखिक परिवर्तन है, इसलिए हम <math>k[t]</math> पर <math>V</math> और <math>k</math> को टेन्सर कर सकते हैं। | ||
: <math>V \otimes_{k[t]} k = V \otimes_{k[t]} (k[t]/(t)) = V/tV = \operatorname{coker}(t) .</math> | : <math>V \otimes_{k[t]} k = V \otimes_{k[t]} (k[t]/(t)) = V/tV = \operatorname{coker}(t) .</math> | ||
का संक्षिप्त स्पष्ट क्रम दिया गया है <math>k</math>-वेक्टर रिक्त स्थान <math>0 \to M \to N \to P \to 0</math>, हम एक स्पष्ट अनुक्रम प्रेरित कर सकते हैं <math>M \otimes_{k[t]} k \to N \otimes_{k[t]} k \to P \otimes_{k[t]} k \to 0</math> टेंसर उत्पाद की सही स्पष्टता | का संक्षिप्त स्पष्ट क्रम दिया गया है <math>k</math>-वेक्टर रिक्त स्थान <math>0 \to M \to N \to P \to 0</math>, हम एक स्पष्ट अनुक्रम प्रेरित कर सकते हैं <math>M \otimes_{k[t]} k \to N \otimes_{k[t]} k \to P \otimes_{k[t]} k \to 0</math> टेंसर उत्पाद की सही स्पष्टता से किंतु क्रम <math>0 \to M \otimes_{k[t]} k \to N \otimes_{k[t]} k \to P \otimes_{k[t]} k \to 0</math> सामान्यतः स्पष्ट नहीं है। इसलिए स्वाभाविक प्रश्न उठता है। यह क्रम स्पष्ट क्यों नहीं है? | ||
[[File:Snklem.png|430x430 पीएक्स]]उपरोक्त आरेख के अनुसार, हम एक स्पष्ट अनुक्रम प्रेरित कर सकते हैं <math>\ker(t_M) \to \ker(t_N) \to \ker(t_P) \to M \otimes_{k[t]} k \to N \otimes_{k[t]} k \to P \otimes_{k[t]} k \to 0</math> स्नेक लेम्मा लगाने से इस प्रकार, सांप लेम्मा टेन्सर उत्पाद की स्पष्ट होने में विफलता को दर्शाता है। | [[File:Snklem.png|430x430 पीएक्स]]उपरोक्त आरेख के अनुसार, हम एक स्पष्ट अनुक्रम प्रेरित कर सकते हैं <math>\ker(t_M) \to \ker(t_N) \to \ker(t_P) \to M \otimes_{k[t]} k \to N \otimes_{k[t]} k \to P \otimes_{k[t]} k \to 0</math> स्नेक लेम्मा लगाने से इस प्रकार, सांप लेम्मा टेन्सर उत्पाद की स्पष्ट होने में विफलता को दर्शाता है। | ||
== समूहों की श्रेणी में == | == समूहों की श्रेणी में == | ||
जबकि होमोलॉजिकल बीजगणित के कई परिणाम, जैसे कि पांच लेम्मा या [[नौ लेम्मा]], एबेलियन श्रेणियों के साथ-साथ समूहों की श्रेणी में भी हैं, साँप लेम्मा नहीं है। वास्तव में, इच्छानुसार कोकर्नेल उपस्थित नहीं है। चूंकि, कोकर्नेल को (बाएं) कोसेट द्वारा प्रतिस्थापित किया जा सकता है <math>A'/\operatorname{im} a</math>, <math>B'/\operatorname{im} b</math>, और <math>C'/\operatorname{im} c</math>.फिर कनेक्टिंग होमोमोर्फिज्म को अभी भी परिभाषित किया जा सकता है, और सांप लेम्मा के कथन के रूप में अनुक्रम लिख सकते हैं। यह सदैव | जबकि होमोलॉजिकल बीजगणित के कई परिणाम, जैसे कि पांच लेम्मा या [[नौ लेम्मा]], एबेलियन श्रेणियों के साथ-साथ समूहों की श्रेणी में भी हैं, साँप लेम्मा नहीं है। वास्तव में, इच्छानुसार कोकर्नेल उपस्थित नहीं है। चूंकि, कोकर्नेल को (बाएं) कोसेट द्वारा प्रतिस्थापित किया जा सकता है <math>A'/\operatorname{im} a</math>, <math>B'/\operatorname{im} b</math>, और <math>C'/\operatorname{im} c</math>.फिर कनेक्टिंग होमोमोर्फिज्म को अभी भी परिभाषित किया जा सकता है, और सांप लेम्मा के कथन के रूप में अनुक्रम लिख सकते हैं। यह सदैव एक चेन कॉम्प्लेक्स होगा, किंतु यह स्पष्ट होने में विफल हो सकता है। स्पष्टता का प्रमाणित किया जा सकता है, चूँकि जब आरेख में लंबवत अनुक्रम स्पष्ट होते हैं, अर्थात , जब ''a'', ''b'', और ''c'' की छवियां [[सामान्य उपसमूह]] होती हैं। | ||
=== प्रति उदाहरण === | === प्रति उदाहरण === | ||
| Line 63: | Line 63: | ||
== लोकप्रिय संस्कृति में == | == लोकप्रिय संस्कृति में == | ||
सर्प प्रमेयिका के प्रमाण को [[जिल क्लेबर्ग]] के चरित्र द्वारा 1980 की फिल्म इट्स माई टर्न की प्रारंभ | सर्प प्रमेयिका के प्रमाण को [[जिल क्लेबर्ग]] के चरित्र द्वारा 1980 की फिल्म इट्स माई टर्न की प्रारंभ में सिखाया गया है।।<ref>{{cite journal |first=C. L. |last=Schochet |title=सामयिक साँप लेम्मा और कोरोना बीजगणित|journal=New York Journal of Mathematics |volume=5 |year=1999 |pages=131–7 |url=http://www.emis.de/journals/NYJM/j/1999/5-11.pdf |archive-url=https://ghostarchive.org/archive/20221009/http://www.emis.de/journals/NYJM/j/1999/5-11.pdf |archive-date=2022-10-09 |url-status=live |citeseerx=10.1.1.73.1568 }}</ref> | ||
'''सर्प प्रमेयिका के प्रमाण को [[जिल क्लेबर्ग]] के चरित्र द्वारा 1980 की फिल्म इट्स माई टर्न की प्रारंभ | '''सर्प प्रमेयिका के प्रमाण को [[जिल क्लेबर्ग]] के चरित्र द्वारा 1980 की फिल्म इट्स माई टर्न की प्रारंभ में''' | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[ज़िगज़ैग लेम्मा]] | * [[ज़िगज़ैग लेम्मा]] | ||
| Line 82: | Line 82: | ||
*[http://planetmath.org/encyclopedia/SnakeLemma.html Snake Lemma] at [[PlanetMath]] | *[http://planetmath.org/encyclopedia/SnakeLemma.html Snake Lemma] at [[PlanetMath]] | ||
*[https://www.youtube.com/watch?v=etbcKWEKnvg Proof of the Snake Lemma] in the film [https://www.imdb.com/title/tt0080936/ It's My Turn] | *[https://www.youtube.com/watch?v=etbcKWEKnvg Proof of the Snake Lemma] in the film [https://www.imdb.com/title/tt0080936/ It's My Turn] | ||
[[Category:Created On 08/05/2023]] | [[Category:Created On 08/05/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:श्रेणी सिद्धांत में नींबू]] | |||
[[Category:समरूप बीजगणित]] | |||
Latest revision as of 10:09, 22 May 2023
स्नेक लेम्मा एक उपकरण है जिसका उपयोग गणित में किया जाता है, विशेष रूप से होमोलॉजिकल बीजगणित में, लंबे स्पष्ट अनुक्रमों के निर्माण के लिए स्नेक लेम्मा हर एबेलियन श्रेणी में मान्य है और होमोलॉजिकल बीजगणित और इसके अनुप्रयोगों में एक महत्वपूर्ण उपकरण है, उदाहरण के लिए बीजगणितीय टोपोलॉजी में इसकी सहायता से निर्मित होमोमोर्फिज्म को सामान्यतः 'कनेक्टिंग होमोमोर्फिज्म' कहा जाता है।
कथन
एबेलियन श्रेणी में (जैसे कि एबेलियन समूह की श्रेणी या किसी दिए गए क्षेत्र (बीजगणित) पर वेक्टर रिक्त स्थान की श्रेणी), एक कम्यूटेटिव आरेख पर विचार करें:
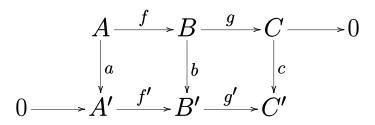 जहाँ पंक्तियाँ स्पष्ट क्रम हैं और 0 शून्य वस्तु है।
जहाँ पंक्तियाँ स्पष्ट क्रम हैं और 0 शून्य वस्तु है।
फिर a, b और c के कर्नेल (श्रेणी सिद्धांत) और कोकेर्नल से संबंधित एक स्पष्ट अनुक्रम है:
जहाँ d एक समरूपता है, जिसे संयोजक समरूपता के रूप में जाना जाता है।
इसके अतिरिक्त, यदि आकृतिवाद f एक एकरूपता है, तो आकारिकी भी ,है और यदि g' अधिरूपता है, तो ऐसा .है
यहाँ कोकर्नेल , , हैं:
नाम की व्याख्या
यह देखने के लिए कि स्नेक लेम्मा को इसका नाम कहां मिलता है, उपरोक्त आरेख को इस प्रकार विस्तृत करें:

- और फिर स्पष्ट क्रम जो कि लेम्मा का निष्कर्ष है, इस विस्तारित आरेख पर एक रेंगने वाले सांप के उल्टे S आकार में खींचा जा सकता है।
नक्शों का निर्माण
आरेख की क्रमविनिमेयता के कारण दिए गए (क्षैतिज) मानचित्रों द्वारा गुठली और कोकर्नेल के बीच के मानचित्रों के बीच के मानचित्रों को प्राकृतिक विधि से प्रेरित किया जाता है। मूल आरेख की पंक्तियों की स्पष्टता से दो प्रेरित अनुक्रमों की स्पष्टता सीधे विधि से होती है। लेम्मा का महत्वपूर्ण कथन यह है कि एक कनेक्टिंग होमोमोर्फिज्म d उपस्थित है जो स्पष्ट अनुक्रम को पूरा करता है।
कुछ रिंग (गणित) पर एबेलियन समूहों या मॉड्यूल (गणित) के स्थिति में नक्शा d निम्नानुसार बनाया जा सकता है:
केर C में एक तत्व एक्स चुनें और इसे सी के एक तत्व के रूप में देखें; चूँकि g आच्छादक है, इसलिए B में g(y) = x के साथ y उपस्थित है। आरेख की क्रमविनिमेयता के कारण, हमारे पास g'(b(y)) = c(g(y)) = c(x) = 0 है (क्योंकि x, c के कर्नेल में है), और इसलिए b(y) g' के कर्नेल में है। चूंकि नीचे की पंक्ति बिल्कुल स्पष्ट है, इसलिए हमें A' में f '(z) = b(y) के साथ एक तत्व z मिलता है। f' के इंजेक्शन द्वारा z अद्वितीय है। फिर हम d(x) = z + im(a) को परिभाषित करते हैं। अब किसी को यह जांचना है कि d अच्छी तरह से परिभाषित है (अर्थात d(x) केवल x पर निर्भर करता है और y की पसंद पर नहीं), यह एक समरूपता है, और परिणामी लंबा अनुक्रम वास्तव में स्पष्ट है। क्रमविनिमेय रेखाचित्र या आरेख का पीछा करते हुए नियमित रूप से स्पष्टता को सत्यापित किया जा सकता है (प्रमेयिका 9.1 का प्रमाण देखें) [1]).
एक बार ऐसा हो जाने के बाद, रिंग के ऊपर एबेलियन समूहों या मॉड्यूल के लिए प्रमेय सिद्ध हो जाता है। सामान्य स्थिति के लिए, तर्क को तत्वों के अतिरिक्त तीरों और रद्दीकरण के गुणों के संदर्भ में दोहराया जा सकता है। वैकल्पिक रूप से, कोई मिशेल के एम्बेडिंग प्रमेय का आह्वान कर सकता है।
स्वाभाविकता
अनुप्रयोगों में, अधिकांशतः यह दिखाने की आवश्यकता होती है कि लंबे स्पष्ट अनुक्रम प्राकृतिक हैं (प्राकृतिक परिवर्तन के अर्थ में)। यह सर्प लेम्मा द्वारा निर्मित अनुक्रम की स्वाभाविकता से अनुसरण करता है।
यदि

- स्पष्ट पंक्तियों के साथ एक क्रमविनिमेय आरेख है, तो सांप लेम्मा को दो बार आगे और पीछे दो बार प्रयुक्त किया जा सकता है, जिससे दो लंबे स्पष्ट क्रम मिलते हैं; ये प्रपत्र के क्रमविनिमेय आरेख द्वारा संबंधित हैं

उदाहरण
मान लीजिए क्षेत्र है, -वेक्टर स्थान है। , -मॉड्यूल द्वारा एक -रैखिक परिवर्तन है, इसलिए हम पर और को टेन्सर कर सकते हैं।
का संक्षिप्त स्पष्ट क्रम दिया गया है -वेक्टर रिक्त स्थान , हम एक स्पष्ट अनुक्रम प्रेरित कर सकते हैं टेंसर उत्पाद की सही स्पष्टता से किंतु क्रम सामान्यतः स्पष्ट नहीं है। इसलिए स्वाभाविक प्रश्न उठता है। यह क्रम स्पष्ट क्यों नहीं है?
 उपरोक्त आरेख के अनुसार, हम एक स्पष्ट अनुक्रम प्रेरित कर सकते हैं स्नेक लेम्मा लगाने से इस प्रकार, सांप लेम्मा टेन्सर उत्पाद की स्पष्ट होने में विफलता को दर्शाता है।
उपरोक्त आरेख के अनुसार, हम एक स्पष्ट अनुक्रम प्रेरित कर सकते हैं स्नेक लेम्मा लगाने से इस प्रकार, सांप लेम्मा टेन्सर उत्पाद की स्पष्ट होने में विफलता को दर्शाता है।
समूहों की श्रेणी में
जबकि होमोलॉजिकल बीजगणित के कई परिणाम, जैसे कि पांच लेम्मा या नौ लेम्मा, एबेलियन श्रेणियों के साथ-साथ समूहों की श्रेणी में भी हैं, साँप लेम्मा नहीं है। वास्तव में, इच्छानुसार कोकर्नेल उपस्थित नहीं है। चूंकि, कोकर्नेल को (बाएं) कोसेट द्वारा प्रतिस्थापित किया जा सकता है , , और .फिर कनेक्टिंग होमोमोर्फिज्म को अभी भी परिभाषित किया जा सकता है, और सांप लेम्मा के कथन के रूप में अनुक्रम लिख सकते हैं। यह सदैव एक चेन कॉम्प्लेक्स होगा, किंतु यह स्पष्ट होने में विफल हो सकता है। स्पष्टता का प्रमाणित किया जा सकता है, चूँकि जब आरेख में लंबवत अनुक्रम स्पष्ट होते हैं, अर्थात , जब a, b, और c की छवियां सामान्य उपसमूह होती हैं।
प्रति उदाहरण
वैकल्पिक समूह पर विचार करें: इसमें सममित समूह के लिए एक उपसमूह आइसोमॉर्फिक सम्मिलित है, जो बदले में चक्रीय समूहों के अर्ध-प्रत्यक्ष उत्पाद के रूप में लिखा जा सकता है: यह निम्नलिखित आरेख को स्पष्ट पंक्तियों के साथ जन्म देता है:[2]
ध्यान दें कि मध्य स्तंभ स्पष्ट नहीं है: अर्ध-प्रत्यक्ष उत्पाद में सामान्य उपसमूह नहीं है।
चूँकि सरल है, दाएँ लंबवत तीर में तुच्छ कोकर्नेल है। इस बीच भागफल समूह , के लिए समरूप है। सर्प प्रमेयिका के कथन में क्रम इसलिए है
- ,
जो वास्तव में स्पष्ट होने में विफल रहता है।
लोकप्रिय संस्कृति में
सर्प प्रमेयिका के प्रमाण को जिल क्लेबर्ग के चरित्र द्वारा 1980 की फिल्म इट्स माई टर्न की प्रारंभ में सिखाया गया है।।[3]
सर्प प्रमेयिका के प्रमाण को जिल क्लेबर्ग के चरित्र द्वारा 1980 की फिल्म इट्स माई टर्न की प्रारंभ में
यह भी देखें
संदर्भ
- ↑ Lang 2002, p. 159
- ↑ "Extensions of C2 by C3". GroupNames. Retrieved 2021-11-06.
- ↑ Schochet, C. L. (1999). "सामयिक साँप लेम्मा और कोरोना बीजगणित" (PDF). New York Journal of Mathematics. 5: 131–7. CiteSeerX 10.1.1.73.1568. Archived (PDF) from the original on 2022-10-09.
- Lang, Serge (2002). "III §9 The Snake Lemma". Algebra (3rd ed.). Springer. pp. 157–9. ISBN 978-0-387-95385-4.
- Atiyah, M.F.; Macdonald, I. G. (1969). Introduction to Commutative Algebra. Addison–Wesley. ISBN 0-201-00361-9.
- Hilton, P.; Stammbach, U. (1997). A course in homological algebra. Graduate Texts in Mathematics. Springer. p. 99. ISBN 0-387-94823-6.
