वर्टेक्स कवर: Difference between revisions

Revision as of 00:00, 16 May 2023

उदाहरण ग्राफ़ जिसमें वर्टेक्स कवर होता है जिसमें 2 कोने (नीचे) होते हैं, लेकिन कम के साथ कोई नहीं।

किनारा (ग्राफ सिद्धांत), ग्राफ़ (असतत गणित) का वर्टेक्स कवर (कभी-कभी नोड कवर) वर्टेक्स का सेट होता है जिसमें ग्राफ़ के प्रत्येक एज (ग्राफ़ थ्योरी) का कम से कम समापन बिंदु शामिल होता है।

कंप्यूटर विज्ञान में, न्यूनतम वर्टेक्स कवर खोजने की समस्या शास्त्रीय अनुकूलन समस्या है। यह एनपी कठिन है, इसलिए यदि पी ≠ एनपी है तो इसे बहुपद-समय एल्गोरिदम द्वारा हल नहीं किया जा सकता है। इसके अलावा, इसका अंदाज़ा लगाना कठिन है - यदि अद्वितीय खेलों का अनुमान सही है तो इसे 2 से छोटे कारक तक अनुमानित नहीं किया जा सकता है। दूसरी ओर, इसके कई सरल 2-कारक सन्निकटन हैं। यह एनपी-हार्ड ऑप्टिमाइज़ेशन समस्या का विशिष्ट उदाहरण है जिसमें सन्निकटन एल्गोरिथम है। इसकी निर्णय समस्या, वर्टेक्स कवर समस्या, कार्प की 21 एनपी-पूर्ण समस्याओं में से थी और इसलिए कम्प्यूटेशनल जटिलता सिद्धांत में शास्त्रीय एनपी-पूर्ण समस्या है। इसके अलावा, वर्टेक्स कवर समस्या फिक्स्ड-पैरामीटर ट्रैक्टेबल है और पैरामिट्रीकृत जटिलता में केंद्रीय समस्या है।

न्यूनतम वर्टेक्स कवर समस्या को आधा-पूर्णांक | आधा-अभिन्न, रैखिक कार्यक्रम के रूप में तैयार किया जा सकता है जिसका दोहरा रैखिक कार्यक्रम अधिकतम मिलान समस्या है।

वर्टेक्स कवर की समस्याओं को hypergraph के लिए सामान्यीकृत किया गया है, देखें हाइपरग्राफ में वर्टेक्स कवर।

परिभाषा

वर्टेक्स कवर के उदाहरण

न्यूनतम वर्टेक्स कवर के उदाहरण

औपचारिक रूप से, वर्टेक्स कवर $V'$ अप्रत्यक्ष ग्राफ का $G=(V,E)$ का उपसमुच्चय है $V$ ऐसा है कि $uv\in E\Rightarrow u\in V'\lor v\in V'$ , अर्थात यह शीर्षों का समूह है $V'$ जहां प्रत्येक किनारे के शीर्ष कवर में कम से कम समापन बिंदु होता है $V'$ . इस तरह के सेट के किनारों को कवर करने के लिए कहा जाता है $G$ . ऊपरी आंकड़ा वर्टेक्स कवर के दो उदाहरण दिखाता है, कुछ वर्टेक्स कवर के साथ $V'$ लाल रंग में चिह्नित।

न्यूनतम वर्टेक्स कवर सबसे छोटे संभव आकार का वर्टेक्स कवर है। वर्टेक्स कवर नंबर $\tau$ न्यूनतम वर्टेक्स कवर का आकार है, अर्थात $\tau =|V'|$ . निचला आंकड़ा पिछले ग्राफ़ में न्यूनतम वर्टेक्स कवर के उदाहरण दिखाता है।

उदाहरण

सभी शीर्षों का समुच्चय शीर्ष आवरण है।
किसी भी अधिकतम मिलान के समापन बिंदु वर्टेक्स कवर बनाते हैं।
पूरा द्विपक्षीय ग्राफ $K_{m,n}$ आकार का न्यूनतम वर्टेक्स कवर है $\tau (K_{m,n})=\min\{\,m,n\,\}$ .

गुण

वर्टिकल का सेट वर्टेक्स कवर है अगर और केवल अगर इसका पूरक (सेट थ्योरी) स्वतंत्र सेट (ग्राफ थ्योरी) है।
नतीजतन, ग्राफ के शीर्षों की संख्या इसके न्यूनतम शीर्ष आवरण संख्या और अधिकतम स्वतंत्र सेट के आकार के बराबर होती है (तिबोर सकता है 1959)।

कम्प्यूटेशनल समस्या

न्यूनतम वर्टेक्स कवर समस्या किसी दिए गए ग्राफ़ में सबसे छोटा वर्टेक्स कवर खोजने की अनुकूलन समस्या है।

उदाहरण: ग्राफ

G

आउटपुट: सबसे छोटी संख्या

k

ऐसा है कि

G

आकार का वर्टेक्स कवर है

k

.

यदि समस्या को निर्णय समस्या के रूप में कहा जाता है, तो इसे वर्टेक्स कवर समस्या कहा जाता है:

उदाहरण: ग्राफ

G

और सकारात्मक पूर्णांक

k

.

प्रश्न: करता है

G

अधिकतम आकार का वर्टेक्स कवर है

k

?

वर्टेक्स कवर समस्या एनपी-पूर्ण समस्या है: यह कार्प की 21 एनपी-पूर्ण समस्याओं में से थी। यह अक्सर कम्प्यूटेशनल जटिलता सिद्धांत में एनपी-कठोरता प्रमाण के लिए प्रारंभिक बिंदु के रूप में उपयोग किया जाता है।

आईएलपी सूत्रीकरण

मान लें कि प्रत्येक शीर्ष की संबद्ध लागत है $c(v)\geq 0$ . (भारित) न्यूनतम वर्टेक्स कवर समस्या को निम्नलिखित पूर्णांक रेखीय कार्यक्रम (ILP) के रूप में तैयार किया जा सकता है।^[1]

minimize	$\textstyle \sum _{v\in V}c(v)x_{v}$		(minimize the total cost)
subject to	$x_{u}+x_{v}\geq 1$	for all $\{u,v\}\in E$	(cover every edge of the graph),
	$x_{v}\in \{0,1\}$	for all $v\in V$ .	(every vertex is either in the vertex cover or not)

यह ILP समस्याओं को कवर करने के लिए ILPs के अधिक सामान्य वर्ग से संबंधित है। इस ILP का लीनियर प्रोग्रामिंग रिलैक्सेशन# सन्निकटन और इंटीग्रेलिटी गैप है $2$ , इसलिए इसकी रैखिक प्रोग्रामिंग छूट (प्रत्येक चर को 0 से 1 के अंतराल में होने की अनुमति देता है, न कि केवल 0 या 1 होने के लिए चर की आवश्यकता होती है) कारक देता है- $2$ न्यूनतम वर्टेक्स कवर समस्या के लिए सन्निकटन एल्गोरिथम। इसके अलावा, उस आईएलपी की रैखिक प्रोग्रामिंग छूट आधा-अभिन्न है, यानी, इष्टतम समाधान मौजूद है जिसके लिए प्रत्येक प्रविष्टि $x_{v}$ या तो 0, 1/2, या 1 है। इस भिन्नात्मक समाधान से 2-अनुमानित वर्टेक्स कवर प्राप्त किया जा सकता है, जिसके वेरिएबल्स नॉनज़रो हैं।

सटीक मूल्यांकन

वर्टेक्स कवर समस्या का निर्णय समस्या संस्करण एनपी-पूर्ण है, जिसका अर्थ है कि यह संभावना नहीं है कि मनमाने ढंग से ग्राफ के लिए इसे हल करने के लिए कुशल एल्गोरिदम है। एनपी-पूर्णता को बूलियन संतुष्टि समस्या से घटाकर सिद्ध किया जा सकता है|3-संतोषजनकता या, जैसा कि कार्प ने किया, क्लिक समस्या से कमी करके। क्यूबिक ग्राफ में भी वर्टेक्स कवर एनपी-पूर्ण रहता है^[2] और डिग्री के प्लेनर ग्राफ में भी अधिकतम 3.^[3] द्विदलीय रेखांकन के लिए, कोनिग प्रमेय (ग्राफ सिद्धांत) द्वारा वर्णित वर्टेक्स कवर और अधिकतम मिलान के बीच समानता | कोनिग प्रमेय द्विदलीय वर्टेक्स कवर समस्या को बहुपद समय में हल करने की अनुमति देता है।

पेड़ का ग्राफ ़ के लिए, एल्गोरिद्म ट्री में पहला पत्ता खोजकर और उसके पैरेंट को न्यूनतम वर्टेक्स कवर में जोड़कर बहुपद समय में न्यूनतम वर्टेक्स कवर ढूंढता है, फिर लीफ और पैरेंट और सभी संबंधित किनारों को हटा देता है और तब तक जारी रखता है जब तक कि कोई किनारा शेष न रह जाए। पेड़।

फिक्स्ड-पैरामीटर ट्रैक्टेबिलिटी

क्रूर-बल खोज एल्गोरिदम समय 2 में समस्या को हल कर सकता है, जहां k वर्टेक्स कवर का आकार है। वर्टेक्स कवर इसलिए निश्चित-पैरामीटर ट्रैक्टेबल है, और यदि हम केवल छोटे के में रुचि रखते हैं, तो हम बहुपद समय में समस्या को हल कर सकते हैं। एल्गोरिथम तकनीक जो यहां काम करती है, उसे बाउंडेड सर्च ट्री एल्गोरिथम कहा जाता है, और इसका विचार बार-बार कुछ शीर्ष और पुनरावर्ती शाखा को चुनना है, प्रत्येक चरण में दो मामलों के साथ: या तो वर्तमान शीर्ष या उसके सभी पड़ोसियों को शीर्ष आवरण में रखें। वर्टेक्स कवर को हल करने के लिए एल्गोरिथम जो पैरामीटर पर सर्वोत्तम स्पर्शोन्मुख निर्भरता प्राप्त करता है, समय में चलता है इस समयबद्ध का क्लैम मान (सबसे बड़े पैरामीटर मान के लिए अनुमान जिसे उचित समय में हल किया जा सकता है) लगभग 190 है। यानी, जब तक कि अतिरिक्त एल्गोरिथम सुधार नहीं पाया जा सकता है, यह एल्गोरिथम केवल उन उदाहरणों के लिए उपयुक्त है जिनके शीर्ष कवर संख्या 190 या उससे कम है। उचित जटिलता-सैद्धांतिक मान्यताओं के तहत, अर्थात् घातीय समय परिकल्पना, चलने का समय 2 में सुधार नहीं किया जा सकता, तब भी जब .

हालाँकि, प्लानर ग्राफ़ के लिए, और अधिक सामान्यतः, कुछ निश्चित ग्राफ़ को माइनर के रूप में छोड़कर ग्राफ़ के लिए, आकार k का वर्टेक्स कवर समय पर पाया जा सकता है, यानी, समस्या सबएक्सपोनेंशियल फिक्स्ड-पैरामीटर ट्रैक्टेबल है। यह एल्गोरिदम फिर से इष्टतम है, इस अर्थ में कि, घातीय समय परिकल्पना के तहत, कोई एल्गोरिदम समय में प्लानर ग्राफ पर वर्टेक्स कवर को हल नहीं कर सकता है।

अनुमानित मूल्यांकन

किनारे के दोनों समापन बिंदुओं को बार-बार वर्टेक्स कवर में ले जाकर, फिर उन्हें ग्राफ़ से हटाकर कारक -2 सन्निकटन एल्गोरिथम पा सकता है। अन्यथा रखो, हम लालची एल्गोरिथ्म के साथ अधिकतम मिलान एम पाते हैं और वर्टेक्स कवर सी का निर्माण करते हैं जिसमें एम में किनारों के सभी समापन बिंदु होते हैं। निम्नलिखित आकृति में, अधिकतम मिलान एम को लाल रंग से चिह्नित किया गया है, और वर्टेक्स कवर सी है नीले रंग से चिह्नित।

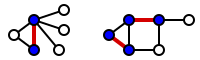इस तरह से निर्मित सेट सी वर्टेक्स कवर है: मान लीजिए कि किनारा ई सी द्वारा कवर नहीं किया गया है; तो M ∪ {e} मिलान है और e ∉ M, जो इस धारणा के विपरीत है कि M अधिकतम है। इसके अलावा, यदि e = {u, v} ∈ M, तो किसी भी वर्टेक्स कवर - इष्टतम वर्टेक्स कवर सहित - में u या v (या दोनों) होना चाहिए; अन्यथा किनारा ई ढका नहीं है। यही है, इष्टतम कवर में एम में प्रत्येक किनारे का कम से कम समापन बिंदु होता है; कुल मिलाकर, सेट सी इष्टतम वर्टेक्स कवर के रूप में अधिकतम 2 गुना बड़ा है।

यह सरल एल्गोरिथम स्वतंत्र रूप से फैनिका गैवरिल और माइकलिस यानाकाकिस द्वारा खोजा गया था।^[4] अधिक शामिल तकनीकों से पता चलता है कि थोड़ा बेहतर सन्निकटन कारक के साथ सन्निकटन एल्गोरिदम हैं। उदाहरण के लिए, सन्निकटन एल्गोरिथम सन्निकटन कारक के साथ ${\textstyle 2-\Theta \left(1/{\sqrt {\log |V|}}\right)}$ ज्ञात है।^[5] समस्या को सन्निकटन कारक के साथ अनुमानित किया जा सकता है $2/(1+\delta )$ में $\delta$ - घने रेखांकन।^[6]

अनुपयुक्तता

उपरोक्त की तुलना में कोई बेहतर स्थिर-कारक सन्निकटन एल्गोरिथम ज्ञात नहीं है। न्यूनतम वर्टेक्स कवर समस्या APX|APX-पूर्ण है, अर्थात, इसे मनमाने ढंग से अच्छी तरह से अनुमानित नहीं किया जा सकता है जब तक कि P = NP समस्या|P = NP। पीसीपी प्रमेय की तकनीकों का उपयोग करते हुए, इरिट दिनूर और शमूएल सफरा ने 2005 में साबित किया कि किसी भी पर्याप्त बड़ी शीर्ष डिग्री के लिए 1.3606 के कारक के भीतर न्यूनतम वर्टेक्स कवर का अनुमान नहीं लगाया जा सकता है जब तक कि पी = एनपी नहीं।^[7] बाद में, कारक में सुधार किया गया ${\sqrt {2}}-\epsilon$ किसी के लिए $\epsilon >0$ .^[8]^[9] इसके अलावा, यदि अद्वितीय खेलों का अनुमान सही है, तो न्यूनतम वर्टेक्स कवर को 2 से बेहतर किसी भी स्थिर कारक के भीतर अनुमानित नहीं किया जा सकता है।^[10] यद्यपि न्यूनतम-आकार के वर्टेक्स कवर को खोजना अधिकतम-आकार के स्वतंत्र सेट को खोजने के बराबर है, जैसा कि ऊपर वर्णित है, दो समस्याएं सन्निकटन-संरक्षण के तरीके के बराबर नहीं हैं: स्वतंत्र सेट समस्या का कोई स्थिर-कारक सन्निकटन नहीं है जब तक कि 'पी' = 'एनपी'।

स्यूडोकोड

APPROXIMATION-VERTEX-COVER(G)
C = ∅
E'= G.E

while E' ≠ ∅:
    let (u, v) be an arbitrary edge of E'
    C = C ∪ {u, v}
    remove from E' every edge incident on either u or v

return C

^[11] ^[12]

अनुप्रयोग

वर्टेक्स कवर ऑप्टिमाइज़ेशन कई वास्तविक दुनिया और एनपी-पूर्णता समस्याओं के लिए गणितीय मॉडल के रूप में कार्य करता है। उदाहरण के लिए, फर्श पर सभी कमरों (नोड्स) को जोड़ने वाले सभी हॉलवे (किनारों) को कवर करने वाले कम से कम संभव क्लोज़्ड सर्किट टेलीविज़न स्थापित करने में रुचि रखने वाला व्यावसायिक प्रतिष्ठान उद्देश्य को वर्टेक्स कवर न्यूनीकरण समस्या के रूप में मॉडल कर सकता है। समस्या का उपयोग संश्लेषित जीव विज्ञान विज्ञान और चयापचय इंजीनियरिंग अनुप्रयोगों के लिए दोहराए गए अनुक्रम (डीएनए) के उन्मूलन के मॉडल के लिए भी किया गया है।^[13]^[14]

↑ Vazirani 2003, pp. 121–122
↑ Garey, Johnson & Stockmeyer 1974
↑ Garey & Johnson 1977; Garey & Johnson 1979, pp. 190 and 195.
↑ Papadimitriou & Steiglitz 1998, p. 432, mentions both Gavril and Yannakakis. Garey & Johnson 1979, p. 134, cites Gavril.
↑ Karakostas 2009
↑ Karpinski & Zelikovsky 1998
↑ Dinur & Safra 2005
↑ Khot, Minzer & Safra 2017^{[full citation needed]}
↑ Dinur et al. 2018^{[full citation needed]}
↑ Khot & Regev 2008
↑ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "Section 35.1: The vertex-cover problem". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 1024–1027. ISBN 0-262-03293-7.
↑ Chakrabarti, Amit (Winter 2005). "Approximation Algorithms: Vertex Cover" (PDF). Computer Science 105. Dartmouth College. Retrieved 21 February 2005.
↑ Hossain, Ayaan; Lopez, Eriberto; Halper, Sean M.; Cetnar, Daniel P.; Reis, Alexander C.; Strickland, Devin; Klavins, Eric; Salis, Howard M. (2020-07-13). "इंजीनियरिंग स्थिर आनुवंशिक प्रणालियों के लिए हजारों गैर-दोहराव वाले भागों का स्वचालित डिजाइन". Nature Biotechnology (in English). 38 (12): 1466–1475. doi:10.1038/s41587-020-0584-2. ISSN 1087-0156. PMID 32661437. S2CID 220506228.
↑ Reis, Alexander C.; Halper, Sean M.; Vezeau, Grace E.; Cetnar, Daniel P.; Hossain, Ayaan; Clauer, Phillip R.; Salis, Howard M. (November 2019). "गैर-दोहराव वाले अतिरिक्त-लंबे sgRNA सरणियों का उपयोग करके कई जीवाणु जीनों का एक साथ दमन". Nature Biotechnology (in English). 37 (11): 1294–1301. doi:10.1038/s41587-019-0286-9. ISSN 1546-1696. OSTI 1569832. PMID 31591552. S2CID 203852115.

संदर्भ

Chen, Jianer; Kanj, Iyad A.; Xia, Ge (2006). "Improved Parameterized Upper Bounds for Vertex Cover". Mathematical Foundations of Computer Science 2006: 31st International Symposium, MFCS 2006, Stará Lesná, Slovakia, August 28-September 1, 2006, Proceedings (PDF). Lecture Notes in Computer Science. Vol. 4162. Springer-Verlag. pp. 238–249. doi:10.1007/11821069_21. ISBN 978-3-540-37791-7.
Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms. Cambridge, Mass.: MIT Press and McGraw-Hill. pp. 1024–1027. ISBN 0-262-03293-7.
Demaine, Erik; Fomin, Fedor V.; Hajiaghayi, Mohammad Taghi; Thilikos, Dimitrios M. (2005). "Subexponential parameterized algorithms on bounded-genus graphs and H-minor-free graphs". Journal of the ACM. 52 (6): 866–893. doi:10.1145/1101821.1101823. S2CID 6238832. Retrieved 2010-03-05.
Dinur, Irit; Safra, Samuel (2005). "On the hardness of approximating minimum vertex cover". Annals of Mathematics. 162 (1): 439–485. CiteSeerX 10.1.1.125.334. doi:10.4007/annals.2005.162.439.
Flum, Jörg; Grohe, Martin (2006). Parameterized Complexity Theory. Springer. ISBN 978-3-540-29952-3. Retrieved 2010-03-05.
Garey, Michael R.; Johnson, David S. (1977). "The rectilinear Steiner tree problem is NP-complete". SIAM Journal on Applied Mathematics. 32 (4): 826–834. doi:10.1137/0132071.
Garey, Michael R.; Johnson, David S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN 0-7167-1045-5. A1.1: GT1, pg.190.
Garey, Michael R.; Johnson, David S.; Stockmeyer, Larry (1974). "Some simplified NP-complete problems". Proceedings of the Sixth Annual ACM Symposium on Theory of Computing. pp. 47–63. doi:10.1145/800119.803884.
Gallai, Tibor (1959). "Über extreme Punkt- und Kantenmengen". Ann. Univ. Sci. Budapest, Eötvös Sect. Math. 2: 133–138.
Karakostas, George (November 2009). "A better approximation ratio for the vertex cover problem" (PDF). ACM Transactions on Algorithms. 5 (4): 41:1–41:8. CiteSeerX 10.1.1.649.7407. doi:10.1145/1597036.1597045. S2CID 2525818. ECCC TR04-084.
Karpinski, Marek; Zelikovsky, Alexander (1998). "Approximating dense cases of covering problems". Proceedings of the DIMACS Workshop on Network Design: Connectivity and Facilities Location. DIMACS Series in Discrete Mathematics and Theoretical Computer Science. Vol. 40. American Mathematical Society. pp. 169–178.
Khot, Subhash; Regev, Oded (2008). "Vertex cover might be hard to approximate to within 2−ε". Journal of Computer and System Sciences. 74 (3): 335–349. doi:10.1016/j.jcss.2007.06.019.
O'Callahan, Robert; Choi, Jong-Deok (2003). "Hybrid dynamic data race detection". ACM SIGPLAN Notices. 38 (10): 167–178. doi:10.1145/966049.781528.
Papadimitriou, Christos H.; Steiglitz, Kenneth (1998). Combinatorial Optimization: Algorithms and Complexity. Dover.
Vazirani, Vijay V. (2003). Approximation Algorithms. Springer-Verlag. ISBN 978-3-662-04565-7.

बाहरी संबंध

[1] Vazirani 2003, pp. 121–122

[2] Garey, Johnson & Stockmeyer 1974

[3] Garey & Johnson 1977; Garey & Johnson 1979, pp. 190 and 195.

[4] Papadimitriou & Steiglitz 1998, p. 432, mentions both Gavril and Yannakakis. Garey & Johnson 1979, p. 134, cites Gavril.

[5] Karakostas 2009

[6] Karpinski & Zelikovsky 1998

[7] Dinur & Safra 2005

[8] Khot, Minzer & Safra 2017^{[full citation needed]}

[9] Dinur et al. 2018^{[full citation needed]}

[kr08-10] Khot & Regev 2008

[11] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "Section 35.1: The vertex-cover problem". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 1024–1027. ISBN 0-262-03293-7.

[12] Chakrabarti, Amit (Winter 2005). "Approximation Algorithms: Vertex Cover" (PDF). Computer Science 105. Dartmouth College. Retrieved 21 February 2005.

[13] Hossain, Ayaan; Lopez, Eriberto; Halper, Sean M.; Cetnar, Daniel P.; Reis, Alexander C.; Strickland, Devin; Klavins, Eric; Salis, Howard M. (2020-07-13). "इंजीनियरिंग स्थिर आनुवंशिक प्रणालियों के लिए हजारों गैर-दोहराव वाले भागों का स्वचालित डिजाइन". Nature Biotechnology (in English). 38 (12): 1466–1475. doi:10.1038/s41587-020-0584-2. ISSN 1087-0156. PMID 32661437. S2CID 220506228.

[14] Reis, Alexander C.; Halper, Sean M.; Vezeau, Grace E.; Cetnar, Daniel P.; Hossain, Ayaan; Clauer, Phillip R.; Salis, Howard M. (November 2019). "गैर-दोहराव वाले अतिरिक्त-लंबे sgRNA सरणियों का उपयोग करके कई जीवाणु जीनों का एक साथ दमन". Nature Biotechnology (in English). 37 (11): 1294–1301. doi:10.1038/s41587-019-0286-9. ISSN 1546-1696. OSTI 1569832. PMID 31591552. S2CID 203852115.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

@@ Line 1: / Line 1: @@
-[[File:Couverture de sommets.svg|thumb|उदाहरण ग्राफ़ जिसमें एक वर्टेक्स कवर होता है जिसमें 2 कोने (नीचे) होते हैं, लेकिन कम के साथ कोई नहीं।]]किनारा ([[ग्राफ सिद्धांत]]), ग्राफ़ (असतत गणित) का एक वर्टेक्स कवर (कभी-कभी नोड कवर) वर्टेक्स (ग्राफ़ थ्योरी) का एक सेट होता है जिसमें ग्राफ़ के प्रत्येक एज (ग्राफ़ थ्योरी) का कम से कम एक समापन बिंदु शामिल होता है।
+[[File:Couverture de sommets.svg|thumb|उदाहरण ग्राफ़ जिसमें  वर्टेक्स कवर होता है जिसमें 2 कोने (नीचे) होते हैं, लेकिन कम के साथ कोई नहीं।]]किनारा ([[ग्राफ सिद्धांत]]), ग्राफ़ (असतत गणित) का  वर्टेक्स कवर (कभी-कभी नोड कवर) वर्टेक्स का  सेट होता है जिसमें ग्राफ़ के प्रत्येक एज (ग्राफ़ थ्योरी) का कम से कम  समापन बिंदु शामिल होता है।
-[[कंप्यूटर विज्ञान]] में, न्यूनतम वर्टेक्स कवर खोजने की समस्या शास्त्रीय [[अनुकूलन समस्या]] है। यह [[ एनपी कठिन |एनपी कठिन]] है, इसलिए यदि पी ≠ एनपी है तो इसे बहुपद-समय एल्गोरिदम द्वारा हल नहीं किया जा सकता है। इसके अलावा, इसका अंदाज़ा लगाना कठिन है - यदि अद्वितीय खेलों का अनुमान सही है तो इसे 2 से छोटे कारक तक अनुमानित नहीं किया जा सकता है। दूसरी ओर, इसके कई सरल 2-कारक सन्निकटन हैं। यह एनपी-हार्ड ऑप्टिमाइज़ेशन समस्या का एक विशिष्ट उदाहरण है जिसमें सन्निकटन एल्गोरिथम है। इसकी [[निर्णय समस्या]], वर्टेक्स कवर समस्या, कार्प की 21 एनपी-पूर्ण समस्याओं में से एक थी और इसलिए [[कम्प्यूटेशनल जटिलता सिद्धांत]] में एक शास्त्रीय एनपी-पूर्ण समस्या है। इसके अलावा, वर्टेक्स कवर समस्या [[फिक्स्ड-पैरामीटर ट्रैक्टेबल]] है और पैरामिट्रीकृत जटिलता में एक केंद्रीय समस्या है।
+[[कंप्यूटर विज्ञान]] में, न्यूनतम वर्टेक्स कवर खोजने की समस्या शास्त्रीय [[अनुकूलन समस्या]] है। यह [[ एनपी कठिन |एनपी कठिन]] है, इसलिए यदि पी ≠ एनपी है तो इसे बहुपद-समय एल्गोरिदम द्वारा हल नहीं किया जा सकता है। इसके अलावा, इसका अंदाज़ा लगाना कठिन है - यदि अद्वितीय खेलों का अनुमान सही है तो इसे 2 से छोटे कारक तक अनुमानित नहीं किया जा सकता है। दूसरी ओर, इसके कई सरल 2-कारक सन्निकटन हैं। यह एनपी-हार्ड ऑप्टिमाइज़ेशन समस्या का  विशिष्ट उदाहरण है जिसमें सन्निकटन एल्गोरिथम है। इसकी [[निर्णय समस्या]], वर्टेक्स कवर समस्या, कार्प की 21 एनपी-पूर्ण समस्याओं में से  थी और इसलिए [[कम्प्यूटेशनल जटिलता सिद्धांत]] में  शास्त्रीय एनपी-पूर्ण समस्या है। इसके अलावा, वर्टेक्स कवर समस्या [[फिक्स्ड-पैरामीटर ट्रैक्टेबल]] है और पैरामिट्रीकृत जटिलता में  केंद्रीय समस्या है।
 न्यूनतम वर्टेक्स कवर समस्या को [[आधा-पूर्णांक]] | आधा-अभिन्न, [[रैखिक कार्यक्रम]] के रूप में तैयार किया जा सकता है जिसका दोहरा रैखिक कार्यक्रम [[अधिकतम मिलान समस्या]] है।
@@ Line 12: / Line 12: @@
 [[File:Vertex-cover.svg|thumb|वर्टेक्स कवर के उदाहरण]]
-[[File:Minimum-vertex-cover.svg|thumb|न्यूनतम वर्टेक्स कवर के उदाहरण]]औपचारिक रूप से, एक वर्टेक्स कवर <math>V'</math> एक अप्रत्यक्ष ग्राफ का <math>G=(V, E)</math> का उपसमुच्चय है <math>V</math> ऐसा है कि <math> uv \in E \Rightarrow  u \in V' \lor v \in V'</math>, अर्थात यह शीर्षों का समूह है <math>V'</math> जहां प्रत्येक किनारे के शीर्ष कवर में कम से कम एक समापन बिंदु होता है <math>V'</math>. इस तरह के एक सेट के किनारों को कवर करने के लिए कहा जाता है <math>G</math>. ऊपरी आंकड़ा वर्टेक्स कवर के दो उदाहरण दिखाता है, कुछ वर्टेक्स कवर के साथ <math>V'</math> लाल रंग में चिह्नित।
+[[File:Minimum-vertex-cover.svg|thumb|न्यूनतम वर्टेक्स कवर के उदाहरण]]औपचारिक रूप से,  वर्टेक्स कवर <math>V'</math>  अप्रत्यक्ष ग्राफ का <math>G=(V, E)</math> का उपसमुच्चय है <math>V</math> ऐसा है कि <math> uv \in E \Rightarrow  u \in V' \lor v \in V'</math>, अर्थात यह शीर्षों का समूह है <math>V'</math> जहां प्रत्येक किनारे के शीर्ष कवर में कम से कम  समापन बिंदु होता है <math>V'</math>. इस तरह के  सेट के किनारों को कवर करने के लिए कहा जाता है <math>G</math>. ऊपरी आंकड़ा वर्टेक्स कवर के दो उदाहरण दिखाता है, कुछ वर्टेक्स कवर के साथ <math>V'</math> लाल रंग में चिह्नित।
 न्यूनतम वर्टेक्स कवर सबसे छोटे संभव आकार का वर्टेक्स कवर है। वर्टेक्स कवर नंबर <math>\tau</math> न्यूनतम वर्टेक्स कवर का आकार है, अर्थात <math>\tau = |V'|</math>. निचला आंकड़ा पिछले ग्राफ़ में न्यूनतम वर्टेक्स कवर के उदाहरण दिखाता है।
@@ Line 18: / Line 18: @@
 === उदाहरण ===
-* सभी शीर्षों का समुच्चय एक शीर्ष आवरण है।
+* सभी शीर्षों का समुच्चय  शीर्ष आवरण है।
-* किसी भी [[अधिकतम मिलान]] के समापन बिंदु एक वर्टेक्स कवर बनाते हैं।
+* किसी भी [[अधिकतम मिलान]] के समापन बिंदु  वर्टेक्स कवर बनाते हैं।
 * पूरा द्विपक्षीय ग्राफ <math>K_{m,n}</math> आकार का न्यूनतम वर्टेक्स कवर है <math>\tau(K_{m,n})=\min\{\,m,n\,\}</math>.
 === गुण ===
-* वर्टिकल का एक सेट एक वर्टेक्स कवर है अगर और केवल अगर इसका पूरक (सेट थ्योरी) एक स्वतंत्र सेट (ग्राफ थ्योरी) है।
+* वर्टिकल का  सेट  वर्टेक्स कवर है अगर और केवल अगर इसका पूरक (सेट थ्योरी)  स्वतंत्र सेट (ग्राफ थ्योरी) है।
-* नतीजतन, एक ग्राफ के शीर्षों की संख्या इसके न्यूनतम शीर्ष आवरण संख्या और अधिकतम स्वतंत्र सेट के आकार के बराबर होती है ([[तिबोर सकता है]] 1959)।
+* नतीजतन,  ग्राफ के शीर्षों की संख्या इसके न्यूनतम शीर्ष आवरण संख्या और अधिकतम स्वतंत्र सेट के आकार के बराबर होती है ([[तिबोर सकता है]] 1959)।
 == कम्प्यूटेशनल समस्या ==
@@ Line 31: / Line 31: @@
 न्यूनतम वर्टेक्स कवर समस्या किसी दिए गए ग्राफ़ में सबसे छोटा वर्टेक्स कवर खोजने की अनुकूलन समस्या है।
 : उदाहरण: ग्राफ <math>G</math>
-:आउटपुट: सबसे छोटी संख्या <math>k</math> ऐसा है कि <math>G</math> आकार का एक वर्टेक्स कवर है <math>k</math>.
+:आउटपुट: सबसे छोटी संख्या <math>k</math> ऐसा है कि <math>G</math> आकार का  वर्टेक्स कवर है <math>k</math>.
 यदि समस्या को निर्णय समस्या के रूप में कहा जाता है, तो इसे वर्टेक्स कवर समस्या कहा जाता है:
 : उदाहरण: ग्राफ <math>G</math> और सकारात्मक पूर्णांक <math>k</math>.
 : प्रश्न: करता है <math>G</math> अधिकतम आकार का वर्टेक्स कवर है <math>k</math>?
-वर्टेक्स कवर समस्या एक एनपी-पूर्ण समस्या है: यह कार्प की 21 एनपी-पूर्ण समस्याओं में से एक थी। यह अक्सर कम्प्यूटेशनल जटिलता सिद्धांत में एनपी-कठोरता प्रमाण के लिए एक प्रारंभिक बिंदु के रूप में उपयोग किया जाता है।
+वर्टेक्स कवर समस्या  एनपी-पूर्ण समस्या है: यह कार्प की 21 एनपी-पूर्ण समस्याओं में से  थी। यह अक्सर कम्प्यूटेशनल जटिलता सिद्धांत में एनपी-कठोरता प्रमाण के लिए  प्रारंभिक बिंदु के रूप में उपयोग किया जाता है।
 === आईएलपी सूत्रीकरण ===
@@ Line 60: / Line 60: @@
 |}
 यह ILP समस्याओं को कवर करने के लिए ILPs के अधिक सामान्य वर्ग से संबंधित है।
-इस ILP का लीनियर प्रोग्रामिंग रिलैक्सेशन# सन्निकटन और इंटीग्रेलिटी गैप है <math>2</math>, इसलिए इसकी [[रैखिक प्रोग्रामिंग छूट]] (प्रत्येक चर को 0 से 1 के अंतराल में होने की अनुमति देता है, न कि केवल 0 या 1 होने के लिए चर की आवश्यकता होती है) एक कारक देता है-<math>2</math> न्यूनतम वर्टेक्स कवर समस्या के लिए सन्निकटन एल्गोरिथम।
+इस ILP का लीनियर प्रोग्रामिंग रिलैक्सेशन# सन्निकटन और इंटीग्रेलिटी गैप है <math>2</math>, इसलिए इसकी [[रैखिक प्रोग्रामिंग छूट]] (प्रत्येक चर को 0 से 1 के अंतराल में होने की अनुमति देता है, न कि केवल 0 या 1 होने के लिए चर की आवश्यकता होती है)  कारक देता है-<math>2</math> न्यूनतम वर्टेक्स कवर समस्या के लिए सन्निकटन एल्गोरिथम।
-इसके अलावा, उस आईएलपी की रैखिक प्रोग्रामिंग छूट आधा-अभिन्न है, यानी, एक इष्टतम समाधान मौजूद है जिसके लिए प्रत्येक प्रविष्टि <math>x_v</math> या तो 0, 1/2, या 1 है। इस भिन्नात्मक समाधान से एक 2-अनुमानित वर्टेक्स कवर प्राप्त किया जा सकता है, जिसके वेरिएबल्स नॉनज़रो हैं।
+इसके अलावा, उस आईएलपी की रैखिक प्रोग्रामिंग छूट आधा-अभिन्न है, यानी,  इष्टतम समाधान मौजूद है जिसके लिए प्रत्येक प्रविष्टि <math>x_v</math> या तो 0, 1/2, या 1 है। इस भिन्नात्मक समाधान से  2-अनुमानित वर्टेक्स कवर प्राप्त किया जा सकता है, जिसके वेरिएबल्स नॉनज़रो हैं।
 === सटीक मूल्यांकन ===
-वर्टेक्स कवर समस्या का निर्णय समस्या संस्करण एनपी-पूर्ण है, जिसका अर्थ है कि यह संभावना नहीं है कि मनमाने ढंग से ग्राफ के लिए इसे हल करने के लिए एक कुशल एल्गोरिदम है। एनपी-पूर्णता को [[बूलियन संतुष्टि समस्या]] से घटाकर सिद्ध किया जा सकता है|3-संतोषजनकता या, जैसा कि कार्प ने किया, [[क्लिक समस्या]] से कमी करके। [[क्यूबिक ग्राफ]] में भी वर्टेक्स कवर एनपी-पूर्ण रहता है<ref>{{harvnb|Garey|Johnson|Stockmeyer|1974}}</ref> और डिग्री के [[ प्लेनर ग्राफ |प्लेनर ग्राफ]] में भी अधिकतम 3.<ref>{{harvnb|Garey|Johnson|1977}}; {{harvnb|Garey|Johnson|1979}}, pp. 190 and 195.</ref>
+वर्टेक्स कवर समस्या का निर्णय समस्या संस्करण एनपी-पूर्ण है, जिसका अर्थ है कि यह संभावना नहीं है कि मनमाने ढंग से ग्राफ के लिए इसे हल करने के लिए  कुशल एल्गोरिदम है। एनपी-पूर्णता को [[बूलियन संतुष्टि समस्या]] से घटाकर सिद्ध किया जा सकता है|3-संतोषजनकता या, जैसा कि कार्प ने किया, [[क्लिक समस्या]] से कमी करके। [[क्यूबिक ग्राफ]] में भी वर्टेक्स कवर एनपी-पूर्ण रहता है<ref>{{harvnb|Garey|Johnson|Stockmeyer|1974}}</ref> और डिग्री के [[ प्लेनर ग्राफ |प्लेनर ग्राफ]] में भी अधिकतम 3.<ref>{{harvnb|Garey|Johnson|1977}}; {{harvnb|Garey|Johnson|1979}}, pp. 190 and 195.</ref>
 द्विदलीय रेखांकन के लिए, कोनिग प्रमेय (ग्राफ सिद्धांत) द्वारा वर्णित वर्टेक्स कवर और अधिकतम मिलान के बीच समानता | कोनिग प्रमेय द्विदलीय वर्टेक्स कवर समस्या को बहुपद समय में हल करने की अनुमति देता है।
-[[ पेड़ का ग्राफ ]]़ के लिए, एक एल्गोरिद्म ट्री में पहला पत्ता खोजकर और उसके पैरेंट को न्यूनतम वर्टेक्स कवर में जोड़कर बहुपद समय में एक न्यूनतम वर्टेक्स कवर ढूंढता है, फिर लीफ और पैरेंट और सभी संबंधित किनारों को हटा देता है और तब तक जारी रखता है जब तक कि कोई किनारा शेष न रह जाए। पेड़।
+[[ पेड़ का ग्राफ ]]़ के लिए,  एल्गोरिद्म ट्री में पहला पत्ता खोजकर और उसके पैरेंट को न्यूनतम वर्टेक्स कवर में जोड़कर बहुपद समय में  न्यूनतम वर्टेक्स कवर ढूंढता है, फिर लीफ और पैरेंट और सभी संबंधित किनारों को हटा देता है और तब तक जारी रखता है जब तक कि कोई किनारा शेष न रह जाए। पेड़।
 ==== फिक्स्ड-पैरामीटर ट्रैक्टेबिलिटी ====
-[[ क्रूर-बल खोज | क्रूर-बल खोज]] एल्गोरिदम समय 2 में समस्या को हल कर सकता है, जहां k वर्टेक्स कवर का आकार है। वर्टेक्स कवर इसलिए निश्चित-पैरामीटर ट्रैक्टेबल है, और यदि हम केवल छोटे के में रुचि रखते हैं, तो हम बहुपद समय में समस्या को हल कर सकते हैं। एक एल्गोरिथम तकनीक जो यहां काम करती है, उसे बाउंडेड सर्च ट्री एल्गोरिथम कहा जाता है, और इसका विचार बार-बार कुछ शीर्ष और पुनरावर्ती शाखा को चुनना है, प्रत्येक चरण में दो मामलों के साथ: या तो वर्तमान शीर्ष या उसके सभी पड़ोसियों को शीर्ष आवरण में रखें।
+[[ क्रूर-बल खोज | क्रूर-बल खोज]] एल्गोरिदम समय 2 में समस्या को हल कर सकता है, जहां k वर्टेक्स कवर का आकार है। वर्टेक्स कवर इसलिए निश्चित-पैरामीटर ट्रैक्टेबल है, और यदि हम केवल छोटे के में रुचि रखते हैं, तो हम बहुपद समय में समस्या को हल कर सकते हैं।  एल्गोरिथम तकनीक जो यहां काम करती है, उसे बाउंडेड सर्च ट्री एल्गोरिथम कहा जाता है, और इसका विचार बार-बार कुछ शीर्ष और पुनरावर्ती शाखा को चुनना है, प्रत्येक चरण में दो मामलों के साथ: या तो वर्तमान शीर्ष या उसके सभी पड़ोसियों को शीर्ष आवरण में रखें।
-वर्टेक्स कवर को हल करने के लिए एल्गोरिथम जो पैरामीटर पर सर्वोत्तम स्पर्शोन्मुख निर्भरता प्राप्त करता है, समय में चलता है इस समयबद्ध का क्लैम मान (सबसे बड़े पैरामीटर मान के लिए एक अनुमान जिसे उचित समय में हल किया जा सकता है) लगभग 190 है। यानी, जब तक कि अतिरिक्त एल्गोरिथम सुधार नहीं पाया जा सकता है, यह एल्गोरिथम केवल उन उदाहरणों के लिए उपयुक्त है जिनके शीर्ष कवर संख्या 190 या उससे कम है। उचित जटिलता-सैद्धांतिक मान्यताओं के तहत, अर्थात् [[घातीय समय परिकल्पना]], चलने का समय 2 में सुधार नहीं किया जा सकता, तब भी जब .
+वर्टेक्स कवर को हल करने के लिए एल्गोरिथम जो पैरामीटर पर सर्वोत्तम स्पर्शोन्मुख निर्भरता प्राप्त करता है, समय में चलता है इस समयबद्ध का क्लैम मान (सबसे बड़े पैरामीटर मान के लिए  अनुमान जिसे उचित समय में हल किया जा सकता है) लगभग 190 है। यानी, जब तक कि अतिरिक्त एल्गोरिथम सुधार नहीं पाया जा सकता है, यह एल्गोरिथम केवल उन उदाहरणों के लिए उपयुक्त है जिनके शीर्ष कवर संख्या 190 या उससे कम है। उचित जटिलता-सैद्धांतिक मान्यताओं के तहत, अर्थात् [[घातीय समय परिकल्पना]], चलने का समय 2 में सुधार नहीं किया जा सकता, तब भी जब .
-हालाँकि, प्लानर ग्राफ़ के लिए, और अधिक सामान्यतः, कुछ निश्चित ग्राफ़ को माइनर के रूप में छोड़कर ग्राफ़ के लिए, आकार k का एक वर्टेक्स कवर समय पर पाया जा सकता है, यानी, समस्या सबएक्सपोनेंशियल फिक्स्ड-पैरामीटर ट्रैक्टेबल है। यह एल्गोरिदम फिर से इष्टतम है, इस अर्थ में कि, घातीय समय परिकल्पना के तहत, कोई एल्गोरिदम समय में प्लानर ग्राफ पर वर्टेक्स कवर को हल नहीं कर सकता है।
+हालाँकि, प्लानर ग्राफ़ के लिए, और अधिक सामान्यतः, कुछ निश्चित ग्राफ़ को माइनर के रूप में छोड़कर ग्राफ़ के लिए, आकार k का  वर्टेक्स कवर समय पर पाया जा सकता है, यानी, समस्या सबएक्सपोनेंशियल फिक्स्ड-पैरामीटर ट्रैक्टेबल है। यह एल्गोरिदम फिर से इष्टतम है, इस अर्थ में कि, घातीय समय परिकल्पना के तहत, कोई एल्गोरिदम समय में प्लानर ग्राफ पर वर्टेक्स कवर को हल नहीं कर सकता है।
 [[Category:All articles with incomplete citations]]
@@ Line 90: / Line 90: @@
 === अनुमानित मूल्यांकन ===
-एक किनारे के दोनों समापन बिंदुओं को बार-बार वर्टेक्स कवर में ले जाकर, फिर उन्हें ग्राफ़ से हटाकर एक कारक -2 सन्निकटन एल्गोरिथम पा सकता है। अन्यथा रखो, हम एक लालची एल्गोरिथ्म के साथ एक अधिकतम मिलान एम पाते हैं और एक वर्टेक्स कवर सी का निर्माण करते हैं जिसमें एम में किनारों के सभी समापन बिंदु होते हैं। निम्नलिखित आकृति में, एक अधिकतम मिलान एम को लाल रंग से चिह्नित किया गया है, और वर्टेक्स कवर सी है नीले रंग से चिह्नित।
+किनारे के दोनों समापन बिंदुओं को बार-बार वर्टेक्स कवर में ले जाकर, फिर उन्हें ग्राफ़ से हटाकर  कारक -2 सन्निकटन एल्गोरिथम पा सकता है। अन्यथा रखो, हम  लालची एल्गोरिथ्म के साथ  अधिकतम मिलान एम पाते हैं और  वर्टेक्स कवर सी का निर्माण करते हैं जिसमें एम में किनारों के सभी समापन बिंदु होते हैं। निम्नलिखित आकृति में,  अधिकतम मिलान एम को लाल रंग से चिह्नित किया गया है, और वर्टेक्स कवर सी है नीले रंग से चिह्नित।
-:[[File:Vertex-cover-from-maximal-matching.svg]]इस तरह से निर्मित सेट सी एक वर्टेक्स कवर है: मान लीजिए कि एक किनारा ई सी द्वारा कवर नहीं किया गया है; तो M ∪ {e} एक मिलान है और e ∉ M, जो इस धारणा के विपरीत है कि M अधिकतम है। इसके अलावा, यदि e = {u, v} ∈ M, तो किसी भी वर्टेक्स कवर - एक इष्टतम वर्टेक्स कवर सहित - में u या v (या दोनों) होना चाहिए; अन्यथा किनारा ई ढका नहीं है। यही है, एक इष्टतम कवर में एम में प्रत्येक किनारे का कम से कम एक समापन बिंदु होता है; कुल मिलाकर, सेट सी इष्टतम वर्टेक्स कवर के रूप में अधिकतम 2 गुना बड़ा है।
+:[[File:Vertex-cover-from-maximal-matching.svg]]इस तरह से निर्मित सेट सी  वर्टेक्स कवर है: मान लीजिए कि  किनारा ई सी द्वारा कवर नहीं किया गया है; तो M ∪ {e}  मिलान है और e ∉ M, जो इस धारणा के विपरीत है कि M अधिकतम है। इसके अलावा, यदि e = {u, v} ∈ M, तो किसी भी वर्टेक्स कवर -  इष्टतम वर्टेक्स कवर सहित - में u या v (या दोनों) होना चाहिए; अन्यथा किनारा ई ढका नहीं है। यही है,  इष्टतम कवर में एम में प्रत्येक किनारे का कम से कम  समापन बिंदु होता है; कुल मिलाकर, सेट सी इष्टतम वर्टेक्स कवर के रूप में अधिकतम 2 गुना बड़ा है।
 यह सरल एल्गोरिथम स्वतंत्र रूप से फैनिका गैवरिल और [[माइकलिस यानाकाकिस]] द्वारा खोजा गया था।<ref>{{harvnb|Papadimitriou|Steiglitz|1998}}, p. 432, mentions both Gavril and Yannakakis. {{harvnb|Garey|Johnson|1979}}, p. 134, cites Gavril.</ref>
-अधिक शामिल तकनीकों से पता चलता है कि थोड़ा बेहतर सन्निकटन कारक के साथ सन्निकटन एल्गोरिदम हैं। उदाहरण के लिए, एक सन्निकटन एल्गोरिथम एक सन्निकटन कारक के साथ <math display="inline">2 - \Theta \left( 1 / \sqrt{\log |V|} \right)</math> ज्ञात है।<ref>{{harvnb|Karakostas|2009}}</ref> समस्या को एक सन्निकटन कारक के साथ अनुमानित किया जा सकता है <math>2/(1 + \delta)</math> में <math>\delta</math> - घने रेखांकन।<ref>{{harvnb|Karpinski|Zelikovsky|1998}}</ref>
+अधिक शामिल तकनीकों से पता चलता है कि थोड़ा बेहतर सन्निकटन कारक के साथ सन्निकटन एल्गोरिदम हैं। उदाहरण के लिए,  सन्निकटन एल्गोरिथम  सन्निकटन कारक के साथ <math display="inline">2 - \Theta \left( 1 / \sqrt{\log |V|} \right)</math> ज्ञात है।<ref>{{harvnb|Karakostas|2009}}</ref> समस्या को  सन्निकटन कारक के साथ अनुमानित किया जा सकता है <math>2/(1 + \delta)</math> में <math>\delta</math> - घने रेखांकन।<ref>{{harvnb|Karpinski|Zelikovsky|1998}}</ref>
@@ Line 101: / Line 101: @@
 उपरोक्त की तुलना में कोई बेहतर [[स्थिर-कारक सन्निकटन एल्गोरिथम]] ज्ञात नहीं है।
 न्यूनतम वर्टेक्स कवर समस्या [[APX]]|APX-पूर्ण है, अर्थात, इसे मनमाने ढंग से अच्छी तरह से अनुमानित नहीं किया जा सकता है जब तक कि P = NP समस्या|P = NP।
-[[पीसीपी प्रमेय]] की तकनीकों का उपयोग करते हुए, [[इरिट दिनूर]] और [[शमूएल सफरा]] ने 2005 में साबित किया कि किसी भी पर्याप्त बड़ी शीर्ष डिग्री के लिए 1.3606 के एक कारक के भीतर न्यूनतम वर्टेक्स कवर का अनुमान नहीं लगाया जा सकता है जब तक कि पी = एनपी नहीं।<ref>{{harvnb|Dinur|Safra|2005}}</ref> बाद में, कारक में सुधार किया गया <math>\sqrt{2} - \epsilon</math> किसी के लिए <math>\epsilon > 0</math>.<ref>{{harvnb|Khot|Minzer|Safra|2017}}{{full citation needed|date=July 2020}}</ref><ref>{{harvnb|Dinur|Khot|Kindler|Minzer|Safra|2018}}{{full citation needed|date=July 2020}}</ref>
+[[पीसीपी प्रमेय]] की तकनीकों का उपयोग करते हुए, [[इरिट दिनूर]] और [[शमूएल सफरा]] ने 2005 में साबित किया कि किसी भी पर्याप्त बड़ी शीर्ष डिग्री के लिए 1.3606 के  कारक के भीतर न्यूनतम वर्टेक्स कवर का अनुमान नहीं लगाया जा सकता है जब तक कि पी = एनपी नहीं।<ref>{{harvnb|Dinur|Safra|2005}}</ref> बाद में, कारक में सुधार किया गया <math>\sqrt{2} - \epsilon</math> किसी के लिए <math>\epsilon > 0</math>.<ref>{{harvnb|Khot|Minzer|Safra|2017}}{{full citation needed|date=July 2020}}</ref><ref>{{harvnb|Dinur|Khot|Kindler|Minzer|Safra|2018}}{{full citation needed|date=July 2020}}</ref>
 इसके अलावा, यदि अद्वितीय खेलों का अनुमान सही है, तो न्यूनतम वर्टेक्स कवर को 2 से बेहतर किसी भी स्थिर कारक के भीतर अनुमानित नहीं किया जा सकता है।<ref name="kr08">{{harvnb|Khot|Regev|2008}}</ref>
 यद्यपि न्यूनतम-आकार के वर्टेक्स कवर को खोजना अधिकतम-आकार के स्वतंत्र सेट को खोजने के बराबर है, जैसा कि ऊपर वर्णित है, दो समस्याएं सन्निकटन-संरक्षण के तरीके के बराबर नहीं हैं: स्वतंत्र सेट समस्या का कोई स्थिर-कारक सन्निकटन नहीं है जब तक कि 'पी' = 'एनपी'।
@@ Line 125: / Line 125: @@
 == अनुप्रयोग ==
-वर्टेक्स कवर ऑप्टिमाइज़ेशन कई वास्तविक दुनिया और एनपी-पूर्णता समस्याओं के लिए एक गणितीय मॉडल के रूप में कार्य करता है। उदाहरण के लिए, फर्श पर सभी कमरों (नोड्स) को जोड़ने वाले सभी हॉलवे (किनारों) को कवर करने वाले कम से कम संभव [[क्लोज़्ड सर्किट टेलीविज़न]] स्थापित करने में रुचि रखने वाला एक व्यावसायिक प्रतिष्ठान उद्देश्य को वर्टेक्स कवर न्यूनीकरण समस्या के रूप में मॉडल कर सकता है। समस्या का उपयोग [[संश्लेषित जीव विज्ञान]] विज्ञान और [[चयापचय इंजीनियरिंग]] अनुप्रयोगों के लिए दोहराए गए अनुक्रम (डीएनए) के उन्मूलन के मॉडल के लिए भी किया गया है।<ref>{{Cite journal|last1=Hossain|first1=Ayaan|last2=Lopez|first2=Eriberto|last3=Halper|first3=Sean M.|last4=Cetnar|first4=Daniel P.|last5=Reis|first5=Alexander C.|last6=Strickland|first6=Devin|last7=Klavins|first7=Eric|last8=Salis|first8=Howard M.|date=2020-07-13|title=इंजीनियरिंग स्थिर आनुवंशिक प्रणालियों के लिए हजारों गैर-दोहराव वाले भागों का स्वचालित डिजाइन|url=http://www.nature.com/articles/s41587-020-0584-2|journal=Nature Biotechnology|volume=38|issue=12|pages=1466–1475|language=en|doi=10.1038/s41587-020-0584-2|pmid=32661437|s2cid=220506228|issn=1087-0156}}</ref><ref>{{Cite journal|last1=Reis|first1=Alexander C.|last2=Halper|first2=Sean M.|last3=Vezeau|first3=Grace E.|last4=Cetnar|first4=Daniel P.|last5=Hossain|first5=Ayaan|last6=Clauer|first6=Phillip R.|last7=Salis|first7=Howard M.|date=November 2019|title=गैर-दोहराव वाले अतिरिक्त-लंबे sgRNA सरणियों का उपयोग करके कई जीवाणु जीनों का एक साथ दमन|url=https://www.nature.com/articles/s41587-019-0286-9|journal=Nature Biotechnology|language=en|volume=37|issue=11|pages=1294–1301|doi=10.1038/s41587-019-0286-9|pmid=31591552|osti=1569832 |s2cid=203852115|issn=1546-1696}}</ref>
+वर्टेक्स कवर ऑप्टिमाइज़ेशन कई वास्तविक दुनिया और एनपी-पूर्णता समस्याओं के लिए  गणितीय मॉडल के रूप में कार्य करता है। उदाहरण के लिए, फर्श पर सभी कमरों (नोड्स) को जोड़ने वाले सभी हॉलवे (किनारों) को कवर करने वाले कम से कम संभव [[क्लोज़्ड सर्किट टेलीविज़न]] स्थापित करने में रुचि रखने वाला  व्यावसायिक प्रतिष्ठान उद्देश्य को वर्टेक्स कवर न्यूनीकरण समस्या के रूप में मॉडल कर सकता है। समस्या का उपयोग [[संश्लेषित जीव विज्ञान]] विज्ञान और [[चयापचय इंजीनियरिंग]] अनुप्रयोगों के लिए दोहराए गए अनुक्रम (डीएनए) के उन्मूलन के मॉडल के लिए भी किया गया है।<ref>{{Cite journal|last1=Hossain|first1=Ayaan|last2=Lopez|first2=Eriberto|last3=Halper|first3=Sean M.|last4=Cetnar|first4=Daniel P.|last5=Reis|first5=Alexander C.|last6=Strickland|first6=Devin|last7=Klavins|first7=Eric|last8=Salis|first8=Howard M.|date=2020-07-13|title=इंजीनियरिंग स्थिर आनुवंशिक प्रणालियों के लिए हजारों गैर-दोहराव वाले भागों का स्वचालित डिजाइन|url=http://www.nature.com/articles/s41587-020-0584-2|journal=Nature Biotechnology|volume=38|issue=12|pages=1466–1475|language=en|doi=10.1038/s41587-020-0584-2|pmid=32661437|s2cid=220506228|issn=1087-0156}}</ref><ref>{{Cite journal|last1=Reis|first1=Alexander C.|last2=Halper|first2=Sean M.|last3=Vezeau|first3=Grace E.|last4=Cetnar|first4=Daniel P.|last5=Hossain|first5=Ayaan|last6=Clauer|first6=Phillip R.|last7=Salis|first7=Howard M.|date=November 2019|title=गैर-दोहराव वाले अतिरिक्त-लंबे sgRNA सरणियों का उपयोग करके कई जीवाणु जीनों का एक साथ दमन|url=https://www.nature.com/articles/s41587-019-0286-9|journal=Nature Biotechnology|language=en|volume=37|issue=11|pages=1294–1301|doi=10.1038/s41587-019-0286-9|pmid=31591552|osti=1569832 |s2cid=203852115|issn=1546-1696}}</ref>

Anonymous

Search

वर्टेक्स कवर: Difference between revisions

Namespaces

More

Page actions

Revision as of 00:00, 16 May 2023

Contents