बीजगणितीय कॉम्बिनेटरिक्स: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Area of combinatorics}} | {{Short description|Area of combinatorics}} | ||
{{for|the academic journal|Algebraic Combinatorics (journal)}} | {{for|the academic journal|Algebraic Combinatorics (journal)}} | ||
[[File:fano plane.svg|thumb|फ़ानो [[ matroid ]], फ़ानो विमान से निकला है। | [[File:fano plane.svg|thumb|फ़ानो [[ matroid | मैट्रॉइड]] , फ़ानो विमान से निकला है। मैट्रॉइड, बीजगणितीय साहचर्य में अध्ययन की जाने वाली कई प्रकार की वस्तुओं में से एक है।]] | ||
{{use dmy dates|date=January 2022}} | {{use dmy dates|date=January 2022}} | ||
| Line 21: | Line 21: | ||
{{main|संघीय योजनाएं}} | {{main|संघीय योजनाएं}} | ||
संघ योजना कुछ अनुकूलता आवश्यकताओं को पूरा करने वाले [[द्विआधारी संबंध|द्विआधारी संबंधों]] का संग्रह है। | संघ योजना कुछ अनुकूलता आवश्यकताओं को पूरा करने वाले [[द्विआधारी संबंध|द्विआधारी संबंधों]] का संग्रह है। संघीय योजनाएँ कई विषयों के लिए एकीकृत दृष्टिकोण प्रदान करती हैं उदाहरण के लिए [[संयोजन डिजाइन|संयोजन प्रारूप]] और [[कोडिंग सिद्धांत]]।{{sfn|Bannai|Ito|1984}}{{sfn|Godsil|1993}} बीजगणित में साहचर्य योजनाएँ [[समूह (गणित)]] का सामान्यीकरण करती हैं और साहचर्य योजनाओं का सिद्धांत समूहों के [[समूह प्रतिनिधित्व]] के [[समूह चरित्र]] का सामान्यीकरण करता है।{{sfn|Bailey|2004|p=387}}{{sfn|Zieschang|2005b}}{{sfn|Zieschang|2005a}} | ||
=== शक्तिशाली नियमित ग्राफ़ === | === शक्तिशाली नियमित ग्राफ़ === | ||
| Line 33: | Line 33: | ||
इस प्रकार के ग्राफ को कभी-कभी srg(v, k, λ, μ) कहा जाता है। | इस प्रकार के ग्राफ को कभी-कभी srg(v, k, λ, μ) कहा जाता है। | ||
कुछ लेखक उन | कुछ लेखक उन ग्राफों को सम्मिलित नहीं करते हैं जो परिभाषा को बिना प्रयास किये संतुष्ट करते हैं अर्थात् वे ग्राफ जो एक या अधिक समान आकार के पूर्ण ग्राफ और उनके [[पूरक ग्राफ]], तुरान ग्राफ के असंबद्ध मिलन हैं।{{sfn|Brouwer|Haemers|n.d.|p=101}}{{sfn|Godsil|Royle|2001|p=218}} | ||
=== | === यंग टेबलाउ === | ||
{{main| | {{main|यंग टेबलाउ}} | ||
[[युवा झाँकी|यंग टेबलाउ]] (pl .:टेबलाउ) प्रतिनिधित्व सिद्धांत और [[शुबर्ट कैलकुलस]] में उपयोगी संयोजन वस्तु है। यह [[सममित समूह]] और [[सामान्य रैखिक समूह]] समूहों के समूह निरूपण का वर्णन करने और उनके गुणों का अध्ययन करने का एक सुविधाजनक उपाय प्रदान करता है। सन 1900 में [[कैम्ब्रिज विश्वविद्यालय]] के [[गणितज्ञ]] [[अल्फ्रेड यंग (गणितज्ञ)]] द्वारा यंग टेबलाउ प्रस्तुत किया गया था। इसके पश्चात इसे सन 1903 में [[जॉर्ज फ्रोबेनियस]] द्वारा सममित समूह के अध्ययन के लिए लागू किया गया था। उनके सिद्धांत को कई गणितज्ञों द्वारा विकसित किया गया था जिसमें [[पर्सी मैकमोहन]], डब्ल्यू. वी. डी. हॉज, गिल्बर्ट डी ब्योरेगार्ड रॉबिन्सन, [[जियान-कार्लो रोटा]], [[एलेन लास्कौक्स]], मार्सेल-पॉल शुट्ज़ेनबर्गर और रिचर्ड पी स्टेनली भी सम्मिलित थे। | |||
=== मैट्रोइड्स === | === मैट्रोइड्स === | ||
{{main| | {{main|मैट्रॉइड}} | ||
मैट्रॉइड एक संरचना है जो वेक्टर रिक्त स्थान में [[रैखिक स्वतंत्रता]] की धारणा को नियंत्रित और सामान्य करती है। मैट्रॉइड को कई समान प्रकार से परिभाषित किया जा सकता है जिसमें स्वतंत्र समुच्चय, आधार, सर्किट, बंद समुच्चय या फ्लैट, क्लोजर ऑपरेटर और रैंक फ़ंक्शन के संदर्भ में सबसे महत्वपूर्ण हैं। | |||
मैट्रॉइड सिद्धांत बड़े पैमाने पर रैखिक बीजगणित और [[ग्राफ सिद्धांत]] की शब्दावली से उधार लेता है | मैट्रॉइड सिद्धांत बड़े पैमाने पर रैखिक बीजगणित और [[ग्राफ सिद्धांत]] की शब्दावली से उधार लेता है क्योंकि यह इन क्षेत्रों में केंद्रीय महत्व के विभिन्न विचारों का सार है। मैट्रोइड्स में ज्यामिति, [[टोपोलॉजी]], संयोजी अनुकूलन, [[नेटवर्क सिद्धांत]] और कोडिंग सिद्धांत में अनुप्रयोग किये गये है।{{sfn|Neel|Neudauer|2009|pp=26–41}}{{sfn|Kashyap|Soljanin|Vontobel|2009}} | ||
=== परिमित ज्यामिति === | === परिमित ज्यामिति === | ||
{{main| | {{main|परिमित ज्यामिति}} | ||
परिचित [[यूक्लिडियन ज्यामिति]] परिमित नहीं है | कोई भी ज्यामिति प्रणाली, परिमित [[ज्यामिति]] है जिसमें केवल [[बिंदु (ज्यामिति)]] की एक सीमित संख्या होती है। | ||
परिचित [[यूक्लिडियन ज्यामिति]] परिमित नहीं है क्योंकि यूक्लिडियन रेखा में असीम रूप से कई बिंदु होते हैं। कंप्यूटर स्क्रीन पर प्रदर्शित ग्राफ़िक्स पर आधारित ज्यामिति जहाँ [[पिक्सेल]] को बिंदु माना जाता है यह परिमित ज्यामिति होगी। जबकि ऐसी कई प्रणालियाँ हैं जिन्हें परिमित ज्यामिति कहा जा सकता है एवं उनकी नियमितता और सरलता के कारण परिमित प्रक्षेप्य स्थान और परिशोधित स्थानों पर ध्यान दिया जाता है। परिमित ज्यामिति के अन्य महत्वपूर्ण प्रकार हैं परिमित मोबियस तल और लैगुएरे तल जो एक सामान्य प्रकार के उदाहरण हैं जिन्हें बेंज़ तल कहा जाता है और उनके उच्च-आयामी अनुरूप जैसे उच्च परिमित व्युत्क्रमणीय ज्यामिति कहा जाता है। | |||
रेखीय बीजगणित के माध्यम से परिमित ज्यामिति का निर्माण किया जा सकता है | रेखीय बीजगणित के माध्यम से परिमित ज्यामिति का निर्माण किया जा सकता है जो [[परिमित क्षेत्र]] पर सदिश स्थानों से आरम्भ होता है तथा इस प्रकार निर्मित संबधित और प्रक्षेपी तलों को गैल्वा ज्यामिति कहा जाता है। परिमित ज्यामिति को विशुद्ध रूप से स्वयंसिद्ध रूप से भी परिभाषित किया जा सकता है। अधिकांश सामान्य परिमित ज्यामिति गाल्वा ज्यामिति हैं क्योंकि तीन या अधिक आयाम के किसी भी परिमित प्रक्षेप्य स्थान परिमित क्षेत्र पर [[प्रक्षेपण स्थान]] के लिए समरूप है (अर्थात परिमित क्षेत्र पर सदिश स्थान का प्रक्षेपण)। जबकि आयाम दो में एफ़िन और [[ प्रक्षेपी विमान |प्रक्षेपी तल]] हैं जो [[गैलोज़ ज्यामिति]] के लिए [[समाकृतिकता]] नहीं हैं अर्थात् [[गैर-Desarguesian विमान|गैर-डेसार्गेसियन तल]] प्रकार के परिणाम अन्य प्रकार की परिमित ज्यामिति के लिए भी लागू होते हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 20:16, 17 May 2023
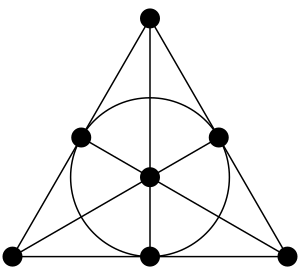
बीजगणितीय साहचर्य गणित का क्षेत्र है जो अमूर्त बीजगणित के उपायों को नियोजित करता है विशेष रूप से समूह सिद्धांत और प्रतिनिधित्व सिद्धांत, विभिन्न साहचर्य संदर्भों में और इसके विपरीत, सार बीजगणित में समस्याओं हेतु सांयोगिक तकनीक लागू करता है।
इतिहास
1970 के दशक के अंत में बीजगणितीय साहचर्य शब्द प्रस्तुत किया गया था।[1] 1990 के दशक के आरंभिक या मध्य के समय बीजगणितीय साहचर्य में रुचि के विशिष्ट संयोजी वस्तुओं ने या तो बहुत अधिक समरूपता (गणित) (संघ योजना, दृढ़ता से नियमित ग्राफ, समूह क्रिया (गणित) के साथ पॉसेट्स) को स्वीकार किया या अधिकतर प्रतिनिधित्व सैद्धांतिक उत्पत्ति (सममित कार्य, युवा झांकी) समृद्ध बीजगणितीय संरचना धारण की। यह अवधि सन 1991 में प्रारम्भ की गई अमेरिकी गणितीय सोसायटी गणित विषय वर्गीकरण के क्षेत्र 05E बीजगणितीय साहचर्य में परिलक्षित होती है।
विस्तार
बीजगणितीय साहचर्य को गणित के क्षेत्र के रूप में अधिक व्यापक रूप से देखा जाने लगा है जहां कॉम्बिनेटरियल और बीजगणितीय तरीकों की बातचीत विशेष रूप से मजबूत और महत्वपूर्ण है। इस प्रकार सांयोगिक विषय प्रकृति में गणनात्मक साहचर्य हो सकते हैं या इसमें मैट्रोइड्स, पॉलीटोप्स, आंशिक रूप से क्रमबद्ध समुच्चय या परिमित ज्यामिति सम्मिलित हो सकते हैं। बीजगणितीय पक्ष में समूह सिद्धांत और प्रतिनिधित्व सिद्धांत के अतिरिक्त जाली सिद्धांत और क्रमविनिमेय बीजगणित का सामान्य रूप से उपयोग किया जाता है।
महत्वपूर्ण विषय
सममित कार्य
सममित कार्यों के वृत्त n अनिश्चित में सममित बहुपदों के वृत्तों की विशिष्ट सीमा है क्योंकि n अनंत तक जाता है। ये वृत्त सार्वभौमिक संरचना के रूप में कार्य करता है जिसमें सममित बहुपदों के मध्य संबंधों को निर्धारकों की संख्या n से स्वतंत्रतापूर्वक व्यक्त किया जा सकता है (परन्तु इसके तत्व न तो बहुपद हैं और न ही कार्य)। अन्य बातों के अतिरिक्त ये वृत्त सममित समूहों के प्रतिनिधित्व सिद्धांत में महत्वपूर्ण भूमिका निभाता है।
संघीय योजनाएं
संघ योजना कुछ अनुकूलता आवश्यकताओं को पूरा करने वाले द्विआधारी संबंधों का संग्रह है। संघीय योजनाएँ कई विषयों के लिए एकीकृत दृष्टिकोण प्रदान करती हैं उदाहरण के लिए संयोजन प्रारूप और कोडिंग सिद्धांत।[2][3] बीजगणित में साहचर्य योजनाएँ समूह (गणित) का सामान्यीकरण करती हैं और साहचर्य योजनाओं का सिद्धांत समूहों के समूह प्रतिनिधित्व के समूह चरित्र का सामान्यीकरण करता है।[4][5][6]
शक्तिशाली नियमित ग्राफ़
शक्तिशाली नियमित ग्राफ को निम्नानुसार परिभाषित किया गया है। मान लीजिए कि G = (V, E) v शीर्षों और घात k के साथ नियमित ग्राफ है। जी को 'दृढ़ता से नियमित' कहा जाता है यदि पूर्णांक λ और μ भी हैं:
- प्रत्येक दो सन्निकट शीर्षों के λ उभयनिष्ठ पड़ोसी होते हैं।
- प्रत्येक दो गैर-निकटवर्ती शीर्षों में μ उभयनिष्ठ पड़ोसी होते हैं।
इस प्रकार के ग्राफ को कभी-कभी srg(v, k, λ, μ) कहा जाता है।
कुछ लेखक उन ग्राफों को सम्मिलित नहीं करते हैं जो परिभाषा को बिना प्रयास किये संतुष्ट करते हैं अर्थात् वे ग्राफ जो एक या अधिक समान आकार के पूर्ण ग्राफ और उनके पूरक ग्राफ, तुरान ग्राफ के असंबद्ध मिलन हैं।[7][8]
यंग टेबलाउ
यंग टेबलाउ (pl .:टेबलाउ) प्रतिनिधित्व सिद्धांत और शुबर्ट कैलकुलस में उपयोगी संयोजन वस्तु है। यह सममित समूह और सामान्य रैखिक समूह समूहों के समूह निरूपण का वर्णन करने और उनके गुणों का अध्ययन करने का एक सुविधाजनक उपाय प्रदान करता है। सन 1900 में कैम्ब्रिज विश्वविद्यालय के गणितज्ञ अल्फ्रेड यंग (गणितज्ञ) द्वारा यंग टेबलाउ प्रस्तुत किया गया था। इसके पश्चात इसे सन 1903 में जॉर्ज फ्रोबेनियस द्वारा सममित समूह के अध्ययन के लिए लागू किया गया था। उनके सिद्धांत को कई गणितज्ञों द्वारा विकसित किया गया था जिसमें पर्सी मैकमोहन, डब्ल्यू. वी. डी. हॉज, गिल्बर्ट डी ब्योरेगार्ड रॉबिन्सन, जियान-कार्लो रोटा, एलेन लास्कौक्स, मार्सेल-पॉल शुट्ज़ेनबर्गर और रिचर्ड पी स्टेनली भी सम्मिलित थे।
मैट्रोइड्स
मैट्रॉइड एक संरचना है जो वेक्टर रिक्त स्थान में रैखिक स्वतंत्रता की धारणा को नियंत्रित और सामान्य करती है। मैट्रॉइड को कई समान प्रकार से परिभाषित किया जा सकता है जिसमें स्वतंत्र समुच्चय, आधार, सर्किट, बंद समुच्चय या फ्लैट, क्लोजर ऑपरेटर और रैंक फ़ंक्शन के संदर्भ में सबसे महत्वपूर्ण हैं।
मैट्रॉइड सिद्धांत बड़े पैमाने पर रैखिक बीजगणित और ग्राफ सिद्धांत की शब्दावली से उधार लेता है क्योंकि यह इन क्षेत्रों में केंद्रीय महत्व के विभिन्न विचारों का सार है। मैट्रोइड्स में ज्यामिति, टोपोलॉजी, संयोजी अनुकूलन, नेटवर्क सिद्धांत और कोडिंग सिद्धांत में अनुप्रयोग किये गये है।[9][10]
परिमित ज्यामिति
कोई भी ज्यामिति प्रणाली, परिमित ज्यामिति है जिसमें केवल बिंदु (ज्यामिति) की एक सीमित संख्या होती है।
परिचित यूक्लिडियन ज्यामिति परिमित नहीं है क्योंकि यूक्लिडियन रेखा में असीम रूप से कई बिंदु होते हैं। कंप्यूटर स्क्रीन पर प्रदर्शित ग्राफ़िक्स पर आधारित ज्यामिति जहाँ पिक्सेल को बिंदु माना जाता है यह परिमित ज्यामिति होगी। जबकि ऐसी कई प्रणालियाँ हैं जिन्हें परिमित ज्यामिति कहा जा सकता है एवं उनकी नियमितता और सरलता के कारण परिमित प्रक्षेप्य स्थान और परिशोधित स्थानों पर ध्यान दिया जाता है। परिमित ज्यामिति के अन्य महत्वपूर्ण प्रकार हैं परिमित मोबियस तल और लैगुएरे तल जो एक सामान्य प्रकार के उदाहरण हैं जिन्हें बेंज़ तल कहा जाता है और उनके उच्च-आयामी अनुरूप जैसे उच्च परिमित व्युत्क्रमणीय ज्यामिति कहा जाता है।
रेखीय बीजगणित के माध्यम से परिमित ज्यामिति का निर्माण किया जा सकता है जो परिमित क्षेत्र पर सदिश स्थानों से आरम्भ होता है तथा इस प्रकार निर्मित संबधित और प्रक्षेपी तलों को गैल्वा ज्यामिति कहा जाता है। परिमित ज्यामिति को विशुद्ध रूप से स्वयंसिद्ध रूप से भी परिभाषित किया जा सकता है। अधिकांश सामान्य परिमित ज्यामिति गाल्वा ज्यामिति हैं क्योंकि तीन या अधिक आयाम के किसी भी परिमित प्रक्षेप्य स्थान परिमित क्षेत्र पर प्रक्षेपण स्थान के लिए समरूप है (अर्थात परिमित क्षेत्र पर सदिश स्थान का प्रक्षेपण)। जबकि आयाम दो में एफ़िन और प्रक्षेपी तल हैं जो गैलोज़ ज्यामिति के लिए समाकृतिकता नहीं हैं अर्थात् गैर-डेसार्गेसियन तल प्रकार के परिणाम अन्य प्रकार की परिमित ज्यामिति के लिए भी लागू होते हैं।
यह भी देखें
- बीजगणितीय ग्राफ सिद्धांत
- कॉम्बिनेटरियल कम्यूटेटिव बीजगणित
- बीजगणितीय साहचर्य (जर्नल)|बीजगणितीय साहचर्य (जर्नल)
- बीजगणितीय साहचर्य का जर्नल
- पॉलीहेड्रल साहचर्य
उद्धरण
- ↑ Bannai 2012.
- ↑ Bannai & Ito 1984.
- ↑ Godsil 1993.
- ↑ Bailey 2004, p. 387.
- ↑ Zieschang 2005b.
- ↑ Zieschang 2005a.
- ↑ Brouwer & Haemers n.d., p. 101.
- ↑ Godsil & Royle 2001, p. 218.
- ↑ Neel & Neudauer 2009, pp. 26–41.
- ↑ Kashyap, Soljanin & Vontobel 2009.
उद्धृत कार्य
- Bailey, Rosemary A. (2004). एसोसिएशन स्कीम्स: डिज़ाइन किए गए प्रयोग, बीजगणित और कॉम्बिनेटरिक्स. Cambridge University Press. ISBN 978-0-521-82446-0. MR 2047311.. (प्रारंभिक मसौदे के अध्याय ऑन-लाइन उपलब्ध हैं हैं।)
- Bannai, Eiichi (2012). "बीजगणितीय कॉम्बिनेटरिक्स" (PDF). School of Mathematical Sciences Shanghai Jiao Tong University. Retrieved 30 January 2022.
- Bannai, Eiichi; Ito, Tatsuro (1984). बीजगणितीय कॉम्बिनेटरिक्स I: एसोसिएशन योजनाएं. Menlo Park, CA: The Benjamin/Cummings Publishing Co. ISBN 0-8053-0490-8. MR 0882540.
- Brouwer, Andries E.; Haemers, Willem H. (n.d.). रेखांकन का स्पेक्ट्रा (PDF). p. 101. Archived from the original (PDF) on 16 March 2012.
- Godsil, Chris; Royle, Gordon (2001). बीजगणितीय ग्राफ सिद्धांत. Graduate Texts in Mathematics. New York: Springer-Verlag. p. 218. ISBN 978-0-387-95241-3.
- Godsil, Chris D. (1993). बीजगणितीय कॉम्बिनेटरिक्स. New York: Chapman and Hall. ISBN 0-412-04131-6. MR 1220704.
- Kashyap, Navin; Soljanin, Emina; Vontobel, Pascal (2–7 August 2009). "सूचना और कोडिंग सिद्धांत के लिए मैट्रोइड थ्योरी और कॉम्बिनेटरियल ऑप्टिमाइज़ेशन के अनुप्रयोग" (PDF). BIRS. Retrieved 4 October 2014.
- Neel, David L.; Neudauer, Nancy Ann (2009). "मैट्रोइड्स जिन्हें आप जानते हैं" (PDF). Mathematics Magazine. 82 (1): 26–41. doi:10.4169/193009809x469020.
- Zieschang, Paul-Hermann (2005a). "एसोसिएशन स्कीम्स: डिज़ाइन्ड एक्सपेरिमेंट्स, अलजेब्रा एंड कॉम्बिनेटरिक्स रोज़मेरी ए बेली द्वारा, समीक्षा" (PDF). Bulletin of the American Mathematical Society. 43 (2): 249–253. doi:10.1090/S0273-0979-05-01077-3.
- Zieschang, Paul-Hermann (2005b). संघ योजनाओं का सिद्धांत. Springer. ISBN 3-540-26136-2.
अग्रिम पठन
- Billera, Louis J.; Björner, Anders; Greene, Curtis; Simion, Rodica; Stanley, Richard P., eds. (1999). New Perspectives in Algebraic Combinatorics. MSRI Publications. Vol. 38. Cambridge University Press. ISBN 052177087-4.
- Hibi, Takayuki (1992). Algebraic combinatorics on convex polytopes. Glebe, Australia: Carslaw Publications. ISBN 1875399046. OCLC 29023080.
- Hochster, Melvin (1977). "Cohen–Macaulay rings, combinatorics, and simplicial complexes". Ring Theory II: Proceedings of the Second Oklahoma Conference. Lecture Notes in Pure and Applied Mathematics. Vol. 26. Dekker. pp. 171–223. ISBN 0-8247-6575-3. OCLC 610144046. Zbl 0351.13009.
- Miller, Ezra; Sturmfels, Bernd (2005). Combinatorial commutative algebra. Graduate Texts in Mathematics. Vol. 227. Springer. ISBN 0-387-22356-8. Zbl 1066.13001.
- Stanley, Richard P. (1996). Combinatorics and commutative algebra. Progress in Mathematics. Vol. 41 (2nd ed.). Birkhäuser. ISBN 0-8176-3836-9. Zbl 0838.13008.
- Sturmfels, Bernd (1996). Gröbner bases and convex polytopes. University Lecture Series. Vol. 8. American Mathematical Society. ISBN 0-8218-0487-1. OCLC 907364245. Zbl 0856.13020 – via Internet Archive.
- Zeilberger, Doron (2008). "Enumerative and Algebraic Combinatorics" (PDF). The Princeton Companion to Mathematics. Princeton University Press.
बाहरी संबंध
 Media related to बीजगणितीय कॉम्बिनेटरिक्स at Wikimedia Commons
Media related to बीजगणितीय कॉम्बिनेटरिक्स at Wikimedia Commons