ह्रासक प्रतिपुष्टि प्रवर्धक

चित्र 1: आदर्श नकारात्मक-फीडबैक एम्पलीफायर

एक नकारात्मक-प्रतिपुष्टि प्रवर्धक (एम्पलीफायर) (या प्रतिपुष्टि प्रवर्धक) एक इलेक्ट्रॉनिक प्रवर्धक है जो अपने निविष्ट (इनपुट) से इसके उत्पादन (आउटपुट) के एक अंश को घटाता है, ताकि नकारात्मक प्रतिपुष्टि मूल संकेत का विरोध करे। प्रयुक्त नकारात्मक प्रतिपुष्टि इसके प्रदर्शन (स्थिरता, रैखिकता, आवृत्ति प्रतिक्रिया, चरण प्रतिक्रिया) में सुधार कर सकती है और विनिर्माण या पर्यावरण के कारण प्राचल (पैरामीटर) विविधताओं के प्रति संवेदनशीलता को कम करती है। इन फायदों के कारण, कई प्रवर्धक (एम्पलीफायरों) और नियंत्रण प्रणाली नकारात्मक प्रतिपुष्टि का उपयोग करते हैं।

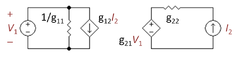
एक आदर्श नकारात्मक-प्रतिपुष्टि प्रवर्धक, जैसा कि चित्र में दिखाया गया है, तीन तत्वों की एक प्रणाली है (चित्र 1 देखें):

• AOL, लाभ के साथ एक प्रवर्धक एक प्रतिपुष्टि तंत्र (फीडबैक नेटवर्क) β, जो उत्पादन (आउटपुट) संकेत को महसूस करता है और संभवतः इसे किसी तरह से बदल देता है (उदाहरण के लिए इसे क्षीण या निस्पंदन (फ़िल्टर) करके), एक योग परिपथ (समनिंग सर्किट) जो एक घटाव (चित्र में वृत्त) के रूप में कार्य करता है, जो निविष्ट (इनपुट) और रूपांतरित उत्पादन (आउटपुट) को जोड़ता है।

अवलोकन

मौलिक रूप से, सभी इलेक्ट्रॉनिक उपकरण (डिवाइस) जो शक्ति लाभ प्रदान करते हैं (जैसे, शून्यक नली, द्विध्रुवी ट्रांजिस्टर, एमओएस ट्रांजिस्टर) अरेखीय हैं।नकारात्मक प्रतिपुष्टि लेन-देन उच्च रैखिकता (विरूपण को कम करने) के लिए लाभ अन्य लाभ प्रदान कर सकते है।यदि सही ढंग से नहीं रूपांकित किया गया है, तो नकारात्मक प्रतिपुष्टि वाले प्रवर्धक (एम्पलीफायर) कुछ परिस्थितियों में प्रतिपुष्टि के सकारात्मक होने के कारण अस्थिर हो सकते हैं, जिसके परिणामस्वरूप अवांछित व्यवहार जैसे दोलन होता है।बेल लेबोरेटरीज के हैरी नाइक्विस्ट द्वारा विकसित नाइक्विस्ट स्थिरता मानदंड का उपयोग प्रतिपुष्टि प्रवर्धक की स्थिरता का अध्ययन करने के लिए किया जाता है।

प्रतिपुष्टि प्रवर्धक इन गुणों को साझा करते हैं:

पेशेवरों:

• निविष्ट (इनपुट) प्रतिबाधा को बढ़ा या घटा सकता है (प्रतिपुष्टि के प्रकार के आधार पर)।
• उत्पादन (आउटपुट) प्रतिबाधा को बढ़ा या घटा सकता है (प्रतिपुष्टि के प्रकार के आधार पर)।
• पर्याप्त रूप से लागू होने पर कुल विकृति को कम करता है (रैखिकता बढ़ाता है)।
• बैंडविड्थ को बढ़ाता है।
• घटक विविधताओं के लिए लाभ को कम करता है।
• प्रवर्धक के चरण प्रतिक्रिया को नियंत्रित कर सकते हैं।

दोष:

• यदि सावधानी से रूपांकित नहीं किया गया तो अस्थिरता हो सकती है।
• प्रवर्धक का लाभ कम हो जाता है।
• एक नकारात्मक-प्रतिपुष्टि प्रवर्धक (संवृत पाश प्रतिपुष्टि) के निविष्ट (इनपुट) और उत्पादन (आउटपुट) प्रतिबाधा प्रतिपुष्टि के बिना एक प्रवर्धक के लाभ के प्रति संवेदनशील हो जाते हैं (अनावृत पाश प्रतिपुष्टि) - जो इन प्रतिबाधाओं को अनावृत पाश लाभ में भिन्नता के लिए उजागर करता है, उदाहरण के लिए, प्राचल (पैरामीटर) विविधताओं या अनावृत पाश लाभ की गैर-रेखीयता के कारण।
• अपर्याप्त रूप से लागू होने पर विरूपण (बढ़ती श्रव्यता) की संरचना को बदल देता है।

इतिहास

पॉल वोइगट ने जनवरी 1924 में एक नकारात्मक-प्रतिपुष्टि प्रवर्धक (एम्पलीफायर) का एकस्व (पेटेंट) कराया, हालांकि उनके सिद्धांत में विस्तार का अभाव था। हेरोल्ड स्टीफन ब्लैक ने स्वतंत्र रूप से नकारात्मक-प्रतिपुष्टि प्रवर्धक (एम्पलीफायर) का आविष्कार किया था, जबकि वह 2 अगस्त, 1927 को बेल लेबोरेटरीज (न्यू जर्सी के बजाय मैनहट्टन में स्थित) में काम करने के लिए अपने रास्ते पर लैकवाना फेरी (होबोकेन टर्मिनल से मैनहट्टन तक) में एक यात्री थे।। (यूएस एकस्व (पेटेंट) 2,102,671, 1937 में जारी किया गया)।ब्लैक टेलीफोन प्रसारण के लिए उपयोग किए जाने वाले पुनरावर्तक प्रवर्धक में विकृति को कम करने पर काम कर रहा थे।न्यूयॉर्क टाइम्स की अपनी प्रति में एक रिक्त स्थान पर, उन्होंने चित्र 1 में पाए गए आरेख और नीचे दिए गए समीकरणों को दर्ज किया। 8 अगस्त, 1928 को, ब्लैक ने अपना आविष्कार यू.एस. एकस्व (पेटेंट) कार्यालय को प्रस्तुत किया, जिसे पेटेंट जारी करने में 9 वर्ष से अधिक का समय लगा। ब्लैक ने बाद में लिखा: "देरी का एक कारण यह था कि अवधारणा स्थापित मान्यताओं के इतने विपरीत थी कि एकस्व (पेटेंट) कार्यालय को शुरू में विश्वास नहीं था कि यह काम करेगा।

शास्त्रीय प्रतिक्रिया

दो एकतरफा ब्लॉक के मॉडल का उपयोग करते हुए, प्रतिपुष्टि के कई परिणाम आसानी से प्राप्त होते हैं।

लाभ में कमी

नीचे, प्रतिपुष्टि के साथ प्रवर्धक (एम्पलीफायर) का वोल्टेज लाभ, संवृत पाश लाभ AFB, प्रतिपुष्टि के बिना प्रवर्धक (एम्पलीफायर) के लाभ के संदर्भ में प्राप्त किया जाता है, अनावृत पाश लाभ AOL और प्रतिपुष्टि कारक β, जो यह नियंत्रित करता है कि निविष्ट (इनपुट) पर उत्पादन (आउटपुट) संकेत कितना लागू होता है (चित्र 1 देखें)।अनावृत पाश लाभ AOL सामान्य तौर पर आवृत्ति और वोल्टेज दोनों का एक कार्य हो सकता है;प्रतिपुष्टि प्राचल (पैरामीटर) प्रतिपुष्टि तंत्र द्वारा निर्धारित किया जाता है जो प्रवर्धक (एम्पलीफायर) के आसपास जुड़ा हुआ है।एक परिचालन प्रवर्धक के लिए, वोल्टेज विभक्त बनाने वाले दो प्रतिरोधों का उपयोग प्रतिपुष्टि तंत्र के लिए 0 और 1 के बीच निर्धारित करने के लिए किया जा सकता है। इस तंत्र (नेटवर्क) को संधारित्र (कैपेसिटर) या कुचालक (इंडक्टर्स) जैसे प्रतिक्रियाशील तत्वों का उपयोग करके संशोधित किया जा सकता है (ए) आवृत्ति-निर्भर संवृत पाश (बंद-लूप) लाभ देता है जैसा कि समीकरण/स्वर नियंत्रण परिपथ (टोन-कंट्रोल सर्किट) या (बी) कांपनेवाला (ऑसिलेटर) का निर्माण करते हैं।प्रतिक्रिया के साथ प्रवर्धक (एम्पलीफायर) का लाभ विद्युत दाब (वोल्टेज) प्रतिक्रिया के साथ विद्युत दाब प्रवर्धक (वोल्टेज एम्पलीफायर) के मामले में नीचे प्राप्त होता है।

प्रतिक्रिया के बिना, निविष्ट विद्युत दाब (इनपुट वोल्टेज) v ′in सीधे प्रवर्धक (एम्पलीफायर) निविष्ट (इनपुट) पर लागू होता है। उत्पादन विद्युत दाब (आउटपुट वोल्टेज) के अनुसार है

$V_{\text{out}}=A_{\text{OL}}\cdot V'_{\text{in}}.$

अब मान लीजिए कि एक क्षीणन प्रतिक्रिया पाश (एटेंटिंग फीडबैक लूप) एक अंश लागू करता है $\beta \cdot V_{\text{out}}$में से किसी एक घटाव (सबट्रेक्टर) पर लागू होता है निविष्ट (इनपुट) ताकि यह परिपथ निविष्ट विद्युत दाब (सर्किट इनपुट वोल्टेज) से घटाया जा सके Vin अन्य घटाव निविष्ट (इनपुट) पर लागू होता है। प्रवर्धक (एम्पलीफायर) निविष्ट (इनपुट) पर लागू घटाव का परिणाम है

$V'_{\text{in}}=V_{\text{in}}-\beta \cdot V_{\text{out}}.$

प्रथम व्यंजक में V′in के स्थान पर,

$V_{\text{out}}=A_{\text{OL}}(V_{\text{in}}-\beta \cdot V_{\text{out}}).$

पुनर्व्यवस्थित:

$V_{\text{out}}(1+\beta \cdot A_{\text{OL}})=V_{\text{in}}\cdot A_{\text{OL}}.$

फिर प्रतिक्रिया के साथ प्रवर्धक (एम्पलीफायर) का वृद्धि, संवृत पाश (बंद-लूप) वृद्धि कहा जाता है, A_FB द्वारा दिया जाता है

$A_{\text{FB}}={\frac {V_{\text{out}}}{V_{\text{in}}}}={\frac {A_{\text{OL}}}{1+\beta \cdot A_{\text{OL}}}}.$

यदि AOL ≫ 1, फिर AFB ≈ 1 / β, और प्रभावी प्रवर्धन (या संवृत पाश लाभ) AFB प्रतिपुष्टि स्थिरांक द्वारा निर्धारित किया गया है, और इसलिए प्रतिपुष्टि तंत्र द्वारा निर्धारित किया गया है, आमतौर पर एक सरल प्रतिलिपि प्रस्तुत करने योग्य तंत्र, इस प्रकार प्रवर्धन विशेषताओं को रैखिक और स्थिर करना सीधा बनाता है।।यदि ऐसी स्थितियां हैं जहां β AOL = −1, प्रवर्धक में अनंत प्रवर्धन है - यह एक कांपनेवाला बन गया है, लाभ प्रतिपुष्टि उत्पाद की स्थिरता विशेषताओं β AOL को अक्सर नाइक्विस्ट प्लॉट पर प्रदर्शित और जांचा जाता है (लाभ का एक ध्रुवीय भूखंड/आवृत्ति के प्राचल (पैरामीटर) कार्य के रूप में चरण बदलाव) ।एक सरल, लेकिन कम सामान्य तकनीक, बोड प्लॉट का उपयोग करती है।

संयोजन L = −β AOL आमतौर पर प्रतिपुष्टि विश्लेषण में दिखाई देता है और इसे पाश लाभ (लूप गेन) कहा जाता है।संयोजन (1 + β AOL) भी आमतौर पर प्रकट होता है और इसे विभिन्न रूप से असंवेदनशीलता कारक, वापसी अंतर, या सुधार कारक के रूप में नामित किया जाता है।

शर्तों का सारांश

• अनावृत पाश लाभ = $A_{\text{OL}}$
• संवृत पाश लाभ = ${\frac {A_{\text{OL}}}{1+\beta \cdot A_{\text{OL}}}}$
• प्रतिपुष्टि कारक = $\beta$
• ध्वनि लाभ = $1/\beta$
• पाश लाभ = $-\beta \cdot A_{\text{OL}}$
• असंवेदनशीलता कारक = $1+\beta \cdot A_{\text{OL}}$

बैंडविड्थ एक्सटेंशन

चित्रा 2: फीडबैक के साथ और बिना एकल-पोल एम्पलीफायर के लिए बनाम आवृत्ति प्राप्त करें;कोने की आवृत्तियों को लेबल किया जाता है

प्रवर्धक के लाभ को कम करने की कीमत पर प्रवर्धक की बैंडविड्थ को बढ़ाने के लिए प्रतिपुष्टि का उपयोग किया जा सकता है। चित्रा 2 इस तरह की तुलना दिखाता है।आकृति को निम्नानुसार समझा जाता है। प्रतिपुष्टि के बिना इस उदाहरण में तथाकथित अनावृत पाश लाभ में एक एकल-समय-स्थिर आवृत्ति प्रतिक्रिया दी गई है

$A_{\text{OL}}(f)={\frac {A_{0}}{1+jf/f_{\text{C}}}},$

जहां f_C प्रवर्धक की कटऑफ या कोने की आवृत्ति है: इस उदाहरण में f_C = 104 Hz, और शून्य आवृत्ति पर लाभ A0 = 105 V/V। आकृति दर्शाती है कि लाभ कोने की आवृत्ति के लिए सपाट है और फिर गिरता है। जब प्रतिपुष्टि मौजूद होती है, तो तथाकथित संवृत पाश लाभ, जैसा कि पिछले अनुभाग के सूत्र में दिखाया गया है, बन जाता है

${\begin{aligned}A_{\text{FB}}(f)&={\frac {A_{\text{OL}}}{1+\beta A_{\text{OL}}}}\\&={\frac {A_{0}/(1+jf/f_{\text{C}})}{1+\beta A_{0}/(1+jf/f_{\text{C}})}}\\&={\frac {A_{0}}{1+jf/f_{\text{C}}+\beta A_{0}}}\\&={\frac {A_{0}}{(1+\beta A_{0})\left(1+j{\frac {f}{(1+\beta A_{0})f_{\text{C}}}}\right)}}.\end{aligned}}$

अंतिम अभिव्यक्ति से पता चलता है कि प्रतिपुष्टि प्रवर्धक में अभी भी एकल-समय-निरंतर व्यवहार है, लेकिन कोने की आवृत्ति अब सुधार कारक (1 + β A₀) द्वारा बढ़ी है, और शून्य आवृत्ति पर लाभ ठीक उसी कारक से गिरा है।इस व्यवहार को लाभ-बैंडविड्थ ट्रेडऑफ कहा जाता है (GAIN -BANDWIDTH TRADEOFF) ।चित्रा 2 में, (1 + β A₀) = 10³, इसलिए A_FB(0) = 10⁵ / 10³ = 100 V/V, और f_C बढ़कर 10⁴ × 10³ = 10⁷ Hz हो जाता है।

मल्टीपल डंडे

जब संवृत पाश लाभ लाभ में कई ध्रुव होते हैं, उपरोक्त उदाहरण के एकल ध्रुव के बजाय, प्रतिक्रिया के परिणामस्वरूप जटिल ध्रुव (वास्तविक और काल्पनिक भाग) हो सकते हैं। दो ध्रुवों के मामले में, परिणाम अपने कोने की आवृत्ति के पास प्रतिपुष्टि प्रवर्धक की आवृत्ति प्रतिक्रिया में चरम पर है और इसके चरण प्रतिक्रिया में वलयीकरण (ringing) और लक्ष्य से बाहर (overshoot) है। दो से अधिक ध्रुवों के मामले में, प्रतिपुष्टि प्रवर्धक अस्थिर और दोलन हो सकता है।लाभ अंतर और चरण अंतर की चर्चा देखें।पूरी चर्चा के लिए, सेंसन देखें।

सिग्नल-फ्लो विश्लेषण

परिचय के निर्माण के पीछे एक प्रमुख आदर्शीकरण दो स्वायत्त ब्लॉकों में नेटवर्क का विभाजन है (यानी, अपने स्वयं के व्यक्तिगत रूप से निर्धारित हस्तांतरण कार्यों के साथ), जिसे अक्सर सर्किट विभाजन कहा जाता है, इसका एक सरल उदाहरण, जिसे अक्सर सर्किट विभाजन कहा जाता है, जो इस उदाहरण में डिवीजन को एक फॉरवर्ड प्रवर्धन ब्लॉक और एक फीडबैक ब्लॉक में संदर्भित करता है।व्यावहारिक एम्पलीफायरों में, सूचना प्रवाह अप्रत्यक्ष नहीं है जैसा कि यहां दिखाया गया है। अक्सर इन ब्लॉकों को द्विपक्षीय सूचना हस्तांतरण को शामिल करने की अनुमति देने के लिए दो-पोर्ट नेटवर्क के रूप में लिया जाता है। इस रूप में एक एम्पलीफायर को कास्ट करना एक गैर-तुच्छ कार्य है, हालांकि, विशेष रूप से जब इसमें शामिल प्रतिक्रिया वैश्विक नहीं होती है (जो सीधे आउटपुट से इनपुट तक है) लेकिन स्थानीय (यानी, नेटवर्क के भीतर प्रतिक्रिया, नोड्स शामिल नोड्स जो नहीं करते हैंइनपुट और/या आउटपुट टर्मिनलों के साथ संयोग)।

एक नियंत्रण चर पी के आधार पर नकारात्मक-फीडबैक एम्पलीफायर के लिए एक संभावित सिग्नल-फ्लो ग्राफ दो आंतरिक चर से संबंधित: एक्स_j = पीएक्स_i।D'Amico et al के बाद पैटर्न।

इन अधिक सामान्य मामलों में, एम्पलीफायर को आरेख में उन ब्लॉकों में विभाजन के बिना सीधे विश्लेषण किया जाता है, सिग्नल-फ्लो ग्राफ के आधार पर कुछ विश्लेषण का उपयोग करके सिग्नल-फ्लो विश्लेषण, जैसे कि रिटर्न-अनुपात विधि या एसिम्प्टोटिक लाभनमूना। सिग्नल-फ्लो दृष्टिकोण पर टिप्पणी करते हुए, चोमा कहते हैं:

फीडबैक नेटवर्क विश्लेषण समस्या के लिए आरेख और दो-पोर्ट दृष्टिकोण को ब्लॉक करने के विपरीत, सिग्नल फ्लो विधियाँ खुले लूप और फीडबैक सबसिर्किट्स के एकतरफा या द्विपक्षीय गुणों के रूप में एक प्राथमिक मान्यताओं को अनिवार्य करती हैं।इसके अलावा, वे पारस्परिक रूप से स्वतंत्र खुले लूप और फीडबैक सबसिरकूट ट्रांसफर फ़ंक्शंस पर समर्पित नहीं हैं, और उन्हें यह आवश्यक नहीं है कि फीडबैक को केवल विश्व स्तर पर लागू किया जाए।वास्तव में सिग्नल फ्लो तकनीकों को भी खुले लूप और फीडबैक सबसिर्किट्स की स्पष्ट पहचान की आवश्यकता नहीं होती है।सिग्नल फ्लो इस प्रकार पारंपरिक प्रतिक्रिया नेटवर्क विश्लेषण के विकृतियों को हटा देता है, लेकिन इसके अलावा, यह कम्प्यूटेशनल रूप से कुशल साबित होता है।

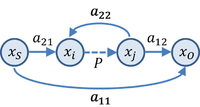
इस सुझाव के बाद, एक नकारात्मक-फीडबैक एम्पलीफायर के लिए एक सिग्नल-फ्लो ग्राफ को आंकड़े में दिखाया गया है, जो कि डी'एमिको एट अल द्वारा एक के बाद पैटर्न किया गया है। इन लेखकों के बाद, संकेतन इस प्रकार है:

चर एक्स_S, एक्स_O इनपुट और आउटपुट सिग्नल का प्रतिनिधित्व करें, इसके अलावा, दो अन्य जेनेरिक चर, एक्स_i, एक्स_jनियंत्रण (या महत्वपूर्ण) पैरामीटर पी के माध्यम से एक साथ जुड़ा हुआ है, स्पष्ट रूप से दिखाया गया है।पैरामीटर ए_ijवजन शाखाएं हैं।चर x_i, एक्स_jऔर नियंत्रण पैरामीटर, पी, मॉडल एक नियंत्रित जनरेटर, या सर्किट के दो नोड्स में वोल्टेज और वर्तमान के बीच संबंध।

शब्द ए₁₁ इनपुट और आउटपुट के बीच स्थानांतरण फ़ंक्शन है [बाद] नियंत्रण पैरामीटर, पी, शून्य से सेट करना;टर्म ए₁₂ आउटपुट और नियंत्रित चर एक्स के बीच स्थानांतरण फ़ंक्शन है_j[के बाद] इनपुट स्रोत सेट करना, x_S, शून्य के लिए;टर्म ए₂₁ स्रोत चर और आंतरिक चर, एक्स के बीच हस्तांतरण फ़ंक्शन का प्रतिनिधित्व करता है_iजब नियंत्रित चर एक्स_jशून्य पर सेट है (यानी, जब नियंत्रण पैरामीटर, पी शून्य पर सेट होता है);टर्म ए₂₂ स्वतंत्र और नियंत्रित आंतरिक चर सेटिंग नियंत्रण पैरामीटर, पी और इनपुट चर, एक्स के बीच संबंध देता है_S, शून्य के लिए।

इस ग्राफ का उपयोग करते हुए, ये लेखक नियंत्रण पैरामीटर P के संदर्भ में सामान्यीकृत लाभ अभिव्यक्ति को प्राप्त करते हैं जो नियंत्रित स्रोत संबंध x को परिभाषित करता है_j= पीएक्स_i:

$x_{\text{O}}=a_{11}x_{\text{S}}+a_{12}x_{j},$

$x_{i}=a_{21}x_{\text{S}}+a_{22}x_{j},$

$x_{j}=Px_{i}.$

इन परिणामों को मिलाकर, लाभ द्वारा दिया गया है

${\frac {x_{\text{O}}}{x_{\text{S}}}}=a_{11}+{\frac {a_{12}a_{21}P}{1-Pa_{22}}}.$

इस सूत्र को नियोजित करने के लिए, किसी को हाथ में विशेष एम्पलीफायर सर्किट के लिए एक महत्वपूर्ण नियंत्रित स्रोत की पहचान करनी होगी।उदाहरण के लिए, P दो-पोर्ट नेटवर्क में नियंत्रित स्रोतों में से एक का नियंत्रण पैरामीटर हो सकता है, जैसा कि D'Amico et al में एक विशेष मामले के लिए दिखाया गया है।एक अलग उदाहरण के रूप में, यदि हम एक लेते हैं₁₂ = a₂₁ = 1, पी = ए, ए₂₂ = - & बीटा;(नकारात्मक प्रतिक्रिया) और ए₁₁ = 0 (कोई फीडफॉर्म नहीं), हम दो यूनिडायरेक्शनल ब्लॉकों के साथ सरल परिणाम प्राप्त करते हैं।

प्रतिक्रिया का दो-पोर्ट विश्लेषण

दो-पोर्ट्स का उपयोग करके एक नकारात्मक-फीडबैक एम्पलीफायर के लिए विभिन्न टोपोलॉजी।शीर्ष बाएं: वर्तमान एम्पलीफायर टोपोलॉजी;शीर्ष अधिकार: transconductance;नीचे बाएं: ट्रांसरेसिस्टेंस;नीचे दाएं: वोल्टेज-एम्पलीफायर टोपोलॉजी।

हालांकि, जैसा कि अनुभाग #सिग्नल-फ्लो विश्लेषण में उल्लेख किया गया है। सिग्नल-फ्लो विश्लेषण, सिग्नल-फ्लो विश्लेषण के कुछ रूप नकारात्मक-फीडबैक एम्पलीफायर के इलाज के लिए सबसे सामान्य तरीका है, दो दो-पोर्ट नेटवर्क के रूप में प्रतिनिधित्व। दृष्टिकोण सबसे अधिक बार पाठ्यपुस्तकों में प्रस्तुत किया जाता है और यहां प्रस्तुत किया जाता है। यह एम्पलीफायर के दो-ब्लॉक सर्किट विभाजन को बरकरार रखता है, लेकिन ब्लॉकों को द्विपक्षीय होने की अनुमति देता है। इस पद्धति की कुछ कमियां #IS हैं जो मुख्य एम्पलीफायर एक दो-पोर्ट ब्लॉक हैं? अंत में वर्णित है।

इलेक्ट्रॉनिक एम्पलीफायरों इनपुट और आउटपुट के रूप में वर्तमान या वोल्टेज का उपयोग करते हैं, इसलिए चार प्रकार के एम्पलीफायर संभव हैं (दो संभावित इनपुट में से कोई भी दो संभावित आउटपुट के साथ)। एम्पलीफायरों का वर्गीकरण देखें। फीडबैक एम्पलीफायर के लिए उद्देश्य चार प्रकार के एम्पलीफायर में से एक हो सकता है और जरूरी नहीं कि ओपन-लूप एम्पलीफायर के समान ही हो, जो स्वयं इन प्रकारों में से कोई भी हो सकता है। इसलिए, उदाहरण के लिए, एक ओपी एएमपी (वोल्टेज एम्पलीफायर) को इसके बजाय एक वर्तमान एम्पलीफायर बनाने के लिए व्यवस्थित किया जा सकता है।

किसी भी प्रकार के नकारात्मक-फीडबैक एम्पलीफायरों को दो-पोर्ट नेटवर्क के संयोजन का उपयोग करके लागू किया जा सकता है। चार प्रकार के दो-पोर्ट नेटवर्क हैं, और एम्पलीफायर के प्रकार वांछित दो-पोर्ट की पसंद और आरेख में दिखाए गए चार अलग-अलग कनेक्शन टोपोलॉजी में से एक का चयन करते हैं। इन कनेक्शनों को आमतौर पर श्रृंखला या शंट (समानांतर) कनेक्शन के रूप में संदर्भित किया जाता है। आरेख में, बाएं कॉलम शंट इनपुट दिखाता है;सही कॉलम श्रृंखला इनपुट दिखाता है।शीर्ष पंक्ति श्रृंखला आउटपुट दिखाती है;नीचे की पंक्ति शंट आउटपुट दिखाती है।कनेक्शन और दो-पोर्ट के विभिन्न संयोजनों को नीचे दी गई तालिका में सूचीबद्ध किया गया है।

Feedback amplifier type	Input connection	Output connection	Ideal feedback	Two-port feedback
Current	Shunt	Series	CCCS	g-parameter
Transresistance	Shunt	Shunt	CCVS	y-parameter
Transconductance	Series	Series	VCCS	z-parameter
Voltage	Series	Shunt	VCVS	h-parameter

उदाहरण के लिए, एक वर्तमान-फीडबैक एम्पलीफायर के लिए, आउटपुट से वर्तमान को प्रतिक्रिया के लिए नमूना लिया जाता है और इनपुट पर वर्तमान के साथ संयुक्त होता है।इसलिए, प्रतिक्रिया आदर्श रूप से एक (आउटपुट) वर्तमान-नियंत्रित वर्तमान स्रोत (CCCS) का उपयोग करके की जाती है, और दो-पोर्ट नेटवर्क का उपयोग करके इसका अपूर्ण अहसास भी CCCS को शामिल करना होगा, अर्थात, फीडबैक नेटवर्क के लिए उपयुक्त विकल्प एक दो है-पोर्ट नेटवर्क#उलटा हाइब्रिड पैरामीटर .28G-parameters.29 | G-Parameter दो-पोर्ट।यहां अधिकांश पाठ्यपुस्तकों में उपयोग की जाने वाली दो-पोर्ट विधि प्रस्तुत की गई है, एसिम्प्टोटिक गेन मॉडल#टू-स्टेज ट्रांजिस्टर एम्पलीफायर पर लेख में इलाज किए गए सर्किट का उपयोग करना | एसिम्प्टोटिक गेन मॉडल।

चित्र 3: एक शंट-सीरीज़ फीडबैक एम्पलीफायर

चित्रा 3 एक प्रतिक्रिया रोकनेवाला आर के साथ एक दो-ट्रांसिस्टर एम्पलीफायर दिखाता है_f।इसका उद्देश्य तीन वस्तुओं को खोजने के लिए इस सर्किट का विश्लेषण करना है: लाभ, आउटपुट प्रतिबाधा लोड से एम्पलीफायर में देख रहे हैं, और स्रोत से एम्पलीफायर में देख रहे इनपुट प्रतिबाधा।

=== दो-पोर्ट === के साथ प्रतिक्रिया नेटवर्क का प्रतिस्थापन पहला कदम दो-पोर्ट नेटवर्क द्वारा फीडबैक नेटवर्क का प्रतिस्थापन है। दो-पोर्ट।बस कौन से घटक दो-पोर्ट में जाते हैं?

दो-पोर्ट के इनपुट पक्ष पर हमारे पास आर है_f।यदि आर के दाईं ओर वोल्टेज_f परिवर्तन, यह आर में वर्तमान को बदलता है_f यह इनपुट ट्रांजिस्टर के आधार में प्रवेश करने वाले करंट से घटाया जाता है।अर्थात्, दो-पोर्ट का इनपुट पक्ष एक आश्रित वर्तमान स्रोत है जो वोल्टेज द्वारा नियंत्रित किया गया है जो रोकनेवाला आर के शीर्ष पर है₂।

कोई कह सकता है कि एम्पलीफायर का दूसरा चरण सिर्फ एक वोल्टेज अनुयायी है, जो इन इनपुट ट्रांजिस्टर के कलेक्टर पर वोल्टेज को आर के शीर्ष पर पहुंचाता है₂।यही है, मॉनिटर आउटपुट सिग्नल वास्तव में इनपुट ट्रांजिस्टर के कलेक्टर में वोल्टेज है।यह दृश्य वैध है, लेकिन फिर वोल्टेज अनुयायी चरण प्रतिक्रिया नेटवर्क का हिस्सा बन जाता है।यह प्रतिक्रिया का विश्लेषण अधिक जटिल बनाता है।

चित्र 4: जी-पैरामीटर फीडबैक नेटवर्क

एक वैकल्पिक दृश्य यह है कि आर के शीर्ष पर वोल्टेज₂ आउटपुट ट्रांजिस्टर के एमिटर करंट द्वारा सेट किया गया है।यह दृश्य आर से बना एक पूरी तरह से निष्क्रिय प्रतिक्रिया नेटवर्क की ओर जाता है₂ और आर_f।प्रतिक्रिया को नियंत्रित करने वाला चर एमिटर करंट है, इसलिए फीडबैक एक वर्तमान-नियंत्रित वर्तमान स्रोत (CCCS) है।हम चार उपलब्ध दो-पोर्ट नेटवर्क के माध्यम से खोज करते हैं और एक सीसीसी के साथ केवल एक ही पाते हैं, जी-पैरामीटर टू-पोर्ट है, चित्रा 4 में दिखाया गया है। अगला कार्य जी-पैरामीटर का चयन करना है ताकि दो-पोर्ट का आंकड़ा4 विद्युत रूप से आर से बने एल-सेक्शन के बराबर है₂ और आर_f।यह चयन एक बीजीय प्रक्रिया है जो दो व्यक्तिगत मामलों को देखकर सबसे अधिक बनाई गई है: वी के साथ मामला₁ = 0, जो दो-पोर्ट के दाईं ओर एक शॉर्ट-सर्किट के दाईं ओर वीसीवी बनाता है;और मैं के साथ मामला₂ = 0. जो बाईं ओर CCCs को एक खुला सर्किट बनाता है।इन दो मामलों में बीजगणित सरल है, एक बार में सभी चर के लिए हल करने की तुलना में बहुत आसान है।जी-पैरामीटर की पसंद जो दो-पोर्ट और एल-सेक्शन को बनाती है, उसी तरह से नीचे दी गई तालिका में दिखाया गया है।

g11	g12	g21	g22
${\frac {1}{R_{\mathrm {f} }+R_{2}}}$	$-{\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}$	${\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}$	$R_{2}||R_{\mathrm {f} }\$

चित्रा 5: फीडबैक नेटवर्क के लिए दो-पोर्ट के साथ छोटे-सिग्नल सर्किट;ऊपरी छायांकित बॉक्स: मुख्य एम्पलीफायर;लोअर शेडेड बॉक्स: फीडबैक टू-पोर्ट आर से बने एल-सेक्शन की जगह_f और आर₂।

छोटा-सिग्नल सर्किट

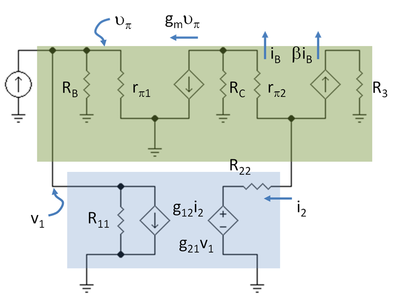
अगला कदम ट्रांजिस्टर के लिए हाइब्रिड-पीआई मॉडल का उपयोग करके दो-पोर्ट के साथ एम्पलीफायर के लिए छोटे-सिग्नल योजनाबद्ध को आकर्षित करना है।चित्रा 5 संकेतन आर के साथ योजनाबद्ध दिखाता है₃ = आर_C2 ||आर_L और आर₁₁ = 1 / जी₁₁, आर₂₂ = जी₂₂।

लोडेड ओपन-लूप गेन

चित्रा 3 आउटपुट नोड को इंगित करता है, लेकिन आउटपुट चर की पसंद नहीं।एक उपयोगी विकल्प एम्पलीफायर का शॉर्ट-सर्किट वर्तमान आउटपुट है (शॉर्ट-सर्किट वर्तमान लाभ के लिए अग्रणी)।क्योंकि यह चर किसी भी अन्य विकल्पों में से किसी की ओर जाता है (उदाहरण के लिए, वोल्टेज लोड या लोड करंट), शॉर्ट-सर्किट वर्तमान लाभ नीचे पाया गया है।

पहले लोडेड ओपन-लूप लाभ पाया जाता है।प्रतिक्रिया को जी सेट करके बंद कर दिया जाता है₁₂ = जी₂₁ = 0. विचार यह है कि फीडबैक नेटवर्क में प्रतिरोधों के कारण एम्पलीफायर का लाभ कितना बदल जाता है, प्रतिक्रिया बंद हो जाती है।यह गणना बहुत आसान है क्योंकि आर₁₁, आर_B, और आर_π1 सभी समानांतर और वी में हैं₁ = वी_π।आर₁ = आर₁₁ ||आर_B ||आर_π1।इसके अलावा, मैं₂ = - ((+1) मैं_B।ओपन-लूप वर्तमान लाभ के लिए परिणाम_OL है:

$A_{\mathrm {OL} }={\frac {\beta i_{\mathrm {B} }}{i_{\mathrm {S} }}}=g_{m}R_{\mathrm {C} }\left({\frac {\beta }{\beta +1}}\right)\left({\frac {R_{1}}{R_{22}+{\frac {r_{\pi 2}+R_{\mathrm {C} }}{\beta +1}}}}\right)\ .$

प्रतिक्रिया के साथ लाभ

प्रतिक्रिया के लिए शास्त्रीय दृष्टिकोण में, VCVs द्वारा प्रतिनिधित्व किए गए फीडफॉर्वर्ड₂₁ v₁) उपेक्षित है। यह चित्रा 5 के सर्किट को चित्र 1 के ब्लॉक आरेख से मिलता -जुलता है, और प्रतिक्रिया के साथ लाभ तब है:

$A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}{1+{\beta }_{\mathrm {FB} }A_{\mathrm {OL} }}}$

$A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}{1+{\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}A_{\mathrm {OL} }}}\ ,$

जहां प्रतिक्रिया कारक β_FB = −g₁₂।नोटेशन बी_FB प्रतिक्रिया कारक के लिए इसे ट्रांजिस्टर से अलग करने के लिए पेश किया गया है।

इनपुट और आउटपुट प्रतिरोध

चित्रा 6: प्रतिक्रिया एम्पलीफायर इनपुट प्रतिरोध खोजने के लिए सर्किट सेट-अप

फीडबैक का उपयोग उनके लोड के लिए सिग्नल स्रोतों से बेहतर मैच करने के लिए किया जाता है।उदाहरण के लिए, एक प्रतिरोधक लोड के लिए वोल्टेज स्रोत के प्रत्यक्ष संबंध से वोल्टेज डिवीजन के कारण सिग्नल लॉस हो सकता है, लेकिन एक नकारात्मक प्रतिक्रिया एम्पलीफायर को हस्तक्षेप करने से स्रोत द्वारा देखे गए स्पष्ट लोड को बढ़ाया जा सकता है, और लोड द्वारा देखे गए स्पष्ट ड्राइवर प्रतिबाधा को कम किया जा सकता हैवोल्टेज डिवीजन द्वारा सिग्नल क्षीणन से परहेज करना।यह लाभ वोल्टेज एम्पलीफायरों के लिए प्रतिबंधित नहीं है, लेकिन मिलान में अनुरूप सुधार को वर्तमान एम्पलीफायरों, ट्रांसकॉन्डक्टेंस एम्पलीफायरों और ट्रांसरेसिस्टेंस एम्पलीफायरों के लिए व्यवस्थित किया जा सकता है।

प्रतिबाधा पर प्रतिक्रिया के इन प्रभावों को समझाने के लिए, पहले दो-पोर्ट सिद्धांत प्रतिरोध निर्धारण के दृष्टिकोण पर एक विषयांतर, और फिर हाथ में एम्पलीफायर के लिए इसका आवेदन कैसे होता है।

प्रतिरोध निर्धारण पर पृष्ठभूमि

चित्रा 6 एक फीडबैक वोल्टेज एम्पलीफायर (बाएं) के इनपुट प्रतिरोध को खोजने के लिए और एक प्रतिक्रिया वर्तमान एम्पलीफायर (दाएं) के इनपुट प्रतिरोध को खोजने के लिए एक समान सर्किट दिखाता है।ये व्यवस्थाएं विशिष्ट मिलर प्रमेय अनुप्रयोग हैं।

वोल्टेज एम्पलीफायर के मामले में, आउटपुट वोल्टेज, वी_out फीडबैक नेटवर्क को श्रृंखला में और इनपुट वोल्टेज वी के विपरीत ध्रुवीयता के साथ लागू किया जाता है_xलूप पर यात्रा करना (लेकिन जमीन के संबंध में, ध्रुवीय समान हैं)।नतीजतन, एम्पलीफायर इनपुट प्रतिरोध आर के माध्यम से प्रभावी वोल्टेज और वर्तमान में प्रभावी वोल्टेज_in कमी ताकि सर्किट इनपुट प्रतिरोध बढ़े (कोई कह सकता है कि आर_in जाहिरा तौर पर बढ़ता है)।इसके नए मूल्य की गणना मिलर प्रमेय (वोल्टेज के लिए) या बुनियादी सर्किट कानूनों को लागू करके की जा सकती है।इस प्रकार Kirchhoff के सर्किट कानून | Kirchhoff का वोल्टेज कानून प्रदान करता है:

$V_{x}=I_{x}R_{\mathrm {in} }+\beta v_{\mathrm {out} }\ ,$

जहां वी_out = A_v v_in = A_v I_x R_in।उपरोक्त समीकरण में इस परिणाम को प्रतिस्थापित करना और प्रतिक्रिया एम्पलीफायर के इनपुट प्रतिरोध के लिए हल करना, परिणाम है:

$R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}}=\left(1+\beta A_{v}\right)R_{\mathrm {in} }\ .$

इस उदाहरण से सामान्य निष्कर्ष और आउटपुट प्रतिरोध मामले के लिए एक समान उदाहरण है: इनपुट (आउटपुट) पर एक श्रृंखला प्रतिक्रिया कनेक्शन एक कारक द्वारा इनपुट (आउटपुट) प्रतिरोध को बढ़ाता है (1 + β ए ए_OL ), जहाँ एक_OL = खुला लूप लाभ।

दूसरी ओर, वर्तमान एम्पलीफायर के लिए, आउटपुट करंट βi_out फीडबैक नेटवर्क को समानांतर में और इनपुट करंट के विपरीत दिशा के साथ लागू किया जाता है_x।नतीजतन, सर्किट इनपुट के माध्यम से कुल वर्तमान बहता है (न केवल इनपुट प्रतिरोध आर के माध्यम से_in) बढ़ता है और इसके पार वोल्टेज कम हो जाता है ताकि सर्किट इनपुट प्रतिरोध कम हो जाए (आर)_in जाहिरा तौर पर घटता है)।इसके नए मूल्य की गणना दोहरी मिलर प्रमेय (धाराओं के लिए) या मूल किरचॉफ के कानूनों को लागू करके की जा सकती है:

$I_{x}={\frac {V_{\mathrm {in} }}{R_{\mathrm {in} }}}+\beta i_{\mathrm {out} }\ .$

जहां मैं_out = A_i i_in = A_i V_x / आर_in।उपरोक्त समीकरण में इस परिणाम को प्रतिस्थापित करना और प्रतिक्रिया एम्पलीफायर के इनपुट प्रतिरोध के लिए हल करना, परिणाम है:

$R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}}={\frac {R_{\mathrm {in} }}{\left(1+\beta A_{i}\right)}}\ .$

इस उदाहरण से सामान्य निष्कर्ष और आउटपुट प्रतिरोध मामले के लिए एक समान उदाहरण है: इनपुट (आउटपुट) पर एक समानांतर प्रतिक्रिया कनेक्शन एक कारक द्वारा इनपुट (आउटपुट) प्रतिरोध को कम करता है (1 + β ए_OL ), जहाँ एक_OL = खुला लूप लाभ।

इन निष्कर्षों को मनमाने ढंग से नॉर्टन के प्रमेय के साथ मामलों का इलाज करने के लिए सामान्यीकृत किया जा सकता है।हालाँकि, परिणाम दो-पोर्ट के रूप में एक प्रतिनिधित्व वाले मुख्य एम्पलीफायर पर निर्भर करते हैं-अर्थात, परिणाम इनपुट टर्मिनलों को प्रवेश करने और छोड़ने के लिए एक ही वर्तमान पर निर्भर करते हैं, और इसी तरह, एक ही करंट जो एक आउटपुट टर्मिनल को छोड़ देता हैअन्य आउटपुट टर्मिनल।

एक व्यापक निष्कर्ष, मात्रात्मक विवरण से स्वतंत्र, यह है कि प्रतिक्रिया का उपयोग इनपुट और आउटपुट प्रतिबाधा को बढ़ाने या कम करने के लिए किया जा सकता है।

उदाहरण के लिए आवेदन एम्पलीफायर

ये प्रतिरोध परिणाम अब चित्रा 3 और चित्रा 5 के एम्पलीफायर पर लागू होते हैं। सुधार कारक जो लाभ को कम करता है, अर्थात् (1 + β_FB A_OL), सीधे एम्पलीफायर के इनपुट और आउटपुट प्रतिरोध पर प्रतिक्रिया के प्रभाव को तय करता है।एक शंट कनेक्शन के मामले में, इस कारक द्वारा इनपुट प्रतिबाधा कम हो जाता है;और श्रृंखला कनेक्शन के मामले में, प्रतिबाधा इस कारक से गुणा किया जाता है।हालांकि, प्रतिक्रिया द्वारा संशोधित प्रतिबाधा चित्र 5 में एम्पलीफायर का प्रतिबाधा है, जिसमें प्रतिक्रिया बंद हो गई है, और इसमें प्रतिक्रिया नेटवर्क के प्रतिरोधों के कारण प्रतिबाधा में संशोधन शामिल हैं।

इसलिए, प्रतिक्रिया के साथ स्रोत द्वारा देखा गया इनपुट प्रतिबाधा आर है_in = आर₁ = आर₁₁ ||आर_B ||आर_π1, और प्रतिक्रिया के साथ चालू (लेकिन कोई फीडफॉर्म नहीं)

$R_{\mathrm {in} }={\frac {R_{1}}{1+{\beta }_{\mathrm {FB} }A_{\mathrm {OL} }}}\ ,$

जहां डिवीजन का उपयोग किया जाता है क्योंकि इनपुट कनेक्शन शंट है: प्रतिक्रिया दो-पोर्ट एम्पलीफायर के इनपुट पक्ष में सिग्नल स्रोत के साथ समानांतर में है।एक अनुस्मारक: ए_OL लोडेड ओपन लूप गेन नेगेटिव फीडबैक एम्पलीफायर#लोडेड ओपन-लूप गेन | ऊपर पाया गया, जैसा कि फीडबैक नेटवर्क के प्रतिरोधों द्वारा संशोधित किया गया है।

लोड द्वारा देखे गए प्रतिबाधा को आगे की चर्चा की आवश्यकता है।चित्रा 5 में लोड आउटपुट ट्रांजिस्टर के कलेक्टर से जुड़ा हुआ है, और इसलिए आउटपुट वर्तमान स्रोत के अनंत प्रतिबाधा द्वारा एम्पलीफायर के शरीर से अलग किया जाता है।इसलिए, फीडबैक का आउटपुट प्रतिबाधा पर कोई प्रभाव नहीं पड़ता है, जो बस आर रहता है_C2 जैसा कि लोड रोकनेवाला आर द्वारा देखा गया है_L चित्रा 3 में। यदि इसके बजाय हम आउटपुट ट्रांजिस्टर (इसके कलेक्टर के बजाय) के एमिटर पर प्रस्तुत प्रतिबाधा को ढूंढना चाहते थे, जो कि फीडबैक नेटवर्क से जुड़ी श्रृंखला है, तो फीडबैक इस प्रतिरोध को सुधार कारक (1 + β (1 +) द्वारा बढ़ाएगा_FB A_OL)।

लोड वोल्टेज और लोड करंट

ऊपर प्राप्त लाभ आउटपुट ट्रांजिस्टर के कलेक्टर में वर्तमान लाभ है।जब वोल्टेज एम्पलीफायर का आउटपुट होता है, तो इस लाभ को प्राप्त करने के लिए, ध्यान दें कि लोड आर पर आउटपुट वोल्टेज_L v के रूप में ओम के नियम द्वारा कलेक्टर करंट से संबंधित है_L = मैं_C (आर_C2 ||आर_L)।नतीजतन, ट्रांसरेसिस्टेंस लाभ v_L / मैं_S आर द्वारा वर्तमान लाभ को गुणा करके पाया जाता है_C2 ||आर_L:

${\frac {v_{\mathrm {L} }}{i_{\mathrm {S} }}}=A_{\mathrm {FB} }(R_{\mathrm {C2} }\parallel R_{\mathrm {L} })\ .$

इसी तरह, यदि एम्पलीफायर के आउटपुट को लोड रोकनेवाला आर में वर्तमान के रूप में लिया जाता है_L, वर्तमान डिवीजन लोड करंट को निर्धारित करता है, और लाभ तब होता है:

${\frac {i_{\mathrm {L} }}{i_{\mathrm {S} }}}=A_{\mathrm {FB} }{\frac {R_{\mathrm {C2} }}{R_{\mathrm {C2} }+R_{\mathrm {L} }}}\ .$

मुख्य एम्पलीफायर एक दो-पोर्ट ब्लॉक है?

चित्र 7: जी द्वारा लेबल किए गए ग्राउंड कनेक्शन के साथ एम्पलीफायर। फीडबैक नेटवर्क पोर्ट स्थितियों को संतुष्ट करता है।

दो दो-पोर्ट दृष्टिकोण की कुछ कमियां फॉलो करती हैं, जो चौकस पाठक के लिए होती हैं।

चित्रा 7 मुख्य एम्पलीफायर के साथ छोटे-सिग्नल योजनाबद्ध और छायांकित बक्से में दो-पोर्ट को दिखाता है।फीडबैक टू-पोर्ट दो-पोर्ट नेटवर्क को संतुष्ट करता है | पोर्ट शर्तें: इनपुट पोर्ट पर, मैं_in प्रवेश करता है और बंदरगाह को छोड़ देता है, और इसी तरह आउटपुट पर, मैं_out प्रवेश करता है और छोड़ देता है।

क्या मुख्य एम्पलीफायर ब्लॉक भी दो-पोर्ट है?मुख्य एम्पलीफायर को ऊपरी छायांकित बॉक्स में दिखाया गया है।ग्राउंड कनेक्शन लेबल किए जाते हैं।चित्रा 7 दिलचस्प तथ्य को दर्शाता है कि मुख्य एम्पलीफायर अपने इनपुट और आउटपुट पर पोर्ट स्थितियों को संतुष्ट नहीं करता है जब तक कि ऐसा करने के लिए जमीन कनेक्शन नहीं चुना जाता है।उदाहरण के लिए, इनपुट पक्ष पर, मुख्य एम्पलीफायर में प्रवेश करने वाला वर्तमान मैं है_S।यह वर्तमान तीन तरीकों से विभाजित है: प्रतिक्रिया नेटवर्क के लिए, पूर्वाग्रह रोकनेवाला आर के लिए_B और इनपुट ट्रांजिस्टर आर के आधार प्रतिरोध के लिए_π।मुख्य एम्पलीफायर के लिए पोर्ट की स्थिति को संतुष्ट करने के लिए, सभी तीन घटकों को मुख्य एम्पलीफायर के इनपुट पक्ष में लौटा दिया जाना चाहिए, जिसका अर्थ है कि सभी ग्राउंड लीड लेबल जी जी।₁ जुड़ा होना चाहिए, साथ ही एमिटर लीड जी_E1।इसी तरह, आउटपुट पक्ष पर, सभी ग्राउंड कनेक्शन जी₂ कनेक्ट होना चाहिए और ग्राउंड कनेक्शन जी भी होना चाहिए_E2।फिर, योजनाबद्ध के निचले भाग में, फीडबैक दो-पोर्ट के नीचे और एम्पलीफायर ब्लॉक के बाहर, जी₁ जी से जुड़ा हुआ है₂।यह जमीन की धाराओं को इनपुट और आउटपुट पक्षों के बीच योजना के अनुसार विभाजित करने के लिए मजबूर करता है।ध्यान दें कि यह कनेक्शन व्यवस्था इनपुट ट्रांजिस्टर के एमिटर को बेस-साइड और एक कलेक्टर-साइड में विभाजित करती है-एक शारीरिक रूप से असंभव बात करने के लिए, लेकिन विद्युत रूप से सर्किट सभी जमीनी कनेक्शन को एक नोड के रूप में देखता है, इसलिए इस कल्पना की अनुमति है।

बेशक, जिस तरह से ग्राउंड लीड कनेक्ट होते हैं, वह एम्पलीफायर से कोई फर्क नहीं पड़ता (वे सभी एक नोड हैं), लेकिन यह पोर्ट स्थितियों में फर्क पड़ता है।यह कृत्रिमता इस दृष्टिकोण की एक कमजोरी है: विधि को सही ठहराने के लिए बंदरगाह की स्थिति की आवश्यकता होती है, लेकिन सर्किट वास्तव में अप्रभावित है कि धाराओं को जमीनी कनेक्शन के बीच कैसे कारोबार किया जाता है।

हालांकि, यदि जमीन की स्थिति की 'कोई संभावित व्यवस्था' कोई संभव नहीं है, तो बंदरगाह की स्थिति की ओर जाता है, सर्किट उसी तरह से व्यवहार नहीं कर सकता है। सुधार कारक (1 + β_FB A_OL) इनपुट और आउटपुट प्रतिबाधा का निर्धारण करने के लिए काम नहीं कर सकता है। यह स्थिति अजीब है, क्योंकि दो-पोर्ट बनाने में विफलता एक वास्तविक समस्या को प्रतिबिंबित कर सकती है (यह बस संभव नहीं है), या कल्पना की कमी को प्रतिबिंबित कर सकता है (उदाहरण के लिए, बस दो में एमिटर नोड को विभाजित करने के बारे में नहीं सोचा था)।परिणामस्वरूप, जब पोर्ट की स्थिति संदेह में होती है, तो कम से कम दो दृष्टिकोण यह स्थापित करने के लिए संभव हैं कि क्या सुधार कारक सटीक हैं: या तो मसाले का उपयोग करके एक उदाहरण का अनुकरण करें और एक सुधार कारक के उपयोग के साथ परिणामों की तुलना करें, या एक परीक्षण स्रोत का उपयोग करके प्रतिबाधा की गणना करेंऔर परिणामों की तुलना करें।

एक अधिक व्यावहारिक विकल्प दो-पोर्ट दृष्टिकोण को पूरी तरह से गिराना है, और सिग्नल-फ्लो ग्राफ के आधार पर विभिन्न विकल्पों का उपयोग करना है। सिग्नल फ्लो ग्राफ सिद्धांत, जिसमें रोसेनस्टार्क विधि, चोमा विधि और ब्लैकमैन के प्रमेय का उपयोग शामिल है। यदि छोटे-सिग्नल डिवाइस मॉडल जटिल हैं, या उपलब्ध नहीं हैं, तो यह विकल्प उचित हो सकता है (उदाहरण के लिए, उपकरण केवल संख्यात्मक रूप से, शायद माप से या मसाले सिमुलेशन से) ज्ञात हैं।

प्रतिक्रिया एम्पलीफायर सूत्र

फीडबैक के दो-पोर्ट विश्लेषण को संक्षेप में, किसी को सूत्रों की यह तालिका मिल सकती है।

Feedback Amplifier	Source Signal	Output Signal	Transfer Function	Input Resistance	Output Resistance
Series-Shunt (voltage amplifier)	Voltage	Voltage	$A_{vf}={\frac {V_{o}}{V_{i}}}={\frac {A_{v}}{1+\beta _{v}A_{v}}}$	$R_{i}(1+\beta _{v}A_{v})$	${\frac {R_{o}}{1+\beta _{v}A_{v}}}$
Shunt-Series (current amplifier)	Current	Current	$A_{if}={\frac {I_{o}}{I_{i}}}={\frac {A_{i}}{1+\beta _{i}A_{i}}}$	${\frac {R_{i}}{1+\beta _{i}A_{i}}}$	$R_{o}(1+\beta _{i}A_{i})$
Series-Series(transconductance amplifier)	Voltage	Current	$A_{gf}={\frac {I_{o}}{V_{i}}}={\frac {A_{g}}{1+\beta _{z}A_{g}}}$	$R_{i}(1+\beta _{z}A_{g})$	$R_{o}(1+\beta _{z}A_{g})$
Shunt-Shunt (transresistance amplifier)	Current	Voltage	$A_{zf}={\frac {V_{o}}{I_{i}}}={\frac {A_{z}}{1+\beta _{g}A_{z}}}$	${\frac {R_{i}}{1+\beta _{g}A_{z}}}$	${\frac {R_{o}}{1+\beta _{g}A_{z}}}$

चर और उनके अर्थ हैं

$A$- बढ़त, $I$- वर्तमान, $V$- वोल्टेज,$\beta$- प्रतिक्रिया लाभ और $R$- प्रतिरोध।

सदस्यता और उनके अर्थ हैं

$f$- प्रतिक्रिया एम्पलीफायर, $v$- वोल्टेज,$g$- transconductance, $Z$- transresistance, $o$- आउटपुट और $i$- लाभ और प्रतिक्रिया के लिए वर्तमान और $i$- प्रतिरोधों के लिए इनपुट।

उदाहरण के लिए $A_{vf}$वोल्टेज प्रतिक्रिया एम्पलीफायर लाभ का मतलब है।

विरूपण

सामान्य एमिटर कॉन्फ़िगरेशन जैसे सरल एम्पलीफायरों में मुख्य रूप से कम-क्रम विरूपण होता है, जैसे कि 2 और 3 हार्मोनिक्स।ऑडियो सिस्टम में, ये न्यूनतम श्रव्य हो सकते हैं क्योंकि संगीत संकेत आमतौर पर पहले से ही एक हार्मोनिक श्रृंखला हैं, और कम-क्रम विरूपण उत्पाद मानव श्रवण प्रणाली के मास्किंग प्रभाव से छिपे हुए हैं। नकारात्मक प्रतिक्रिया (10-15 & nbsp; DB) की मध्यम मात्रा को लागू करने के बाद, कम-ऑर्डर हार्मोनिक्स कम हो जाते हैं, लेकिन उच्च-क्रम हार्मोनिक्स पेश किए जाते हैं। चूंकि ये नकाबपोश नहीं हैं, इसलिए विरूपण श्रव्य रूप से बदतर हो जाता है, भले ही समग्र THD नीचे जा सकता है। इसने एक लगातार मिथक का नेतृत्व किया है कि ऑडियो एम्पलीफायरों में नकारात्मक प्रतिक्रिया हानिकारक है,अग्रणी ऑडीओफाइल निर्माताओं ने अपने एम्पलीफायरों को शून्य प्रतिक्रिया के रूप में विपणन करने के लिए (यहां तक कि जब वे प्रत्येक चरण को रैखिक करने के लिए स्थानीय प्रतिक्रिया का उपयोग करते हैं)। हालांकि, जैसे-जैसे नकारात्मक प्रतिक्रिया की मात्रा में और वृद्धि हुई है, सभी हार्मोनिक्स कम हो जाते हैं, विकृति को अमानवीयता में वापस कर देते हैं, और फिर इसे मूल शून्य-फीडबैक चरण से परे सुधारते हैं (बशर्ते सिस्टम सख्ती से स्थिर हो)। इसलिए समस्या नकारात्मक प्रतिक्रिया नहीं है, लेकिन इसकी अपर्याप्त मात्रा है।

यह भी देखें

• Asymptotic लाभ मॉडल
• ब्लैकमैन का प्रमेय
• बोड प्लॉट
• बफर एम्पलीफायर नकारात्मक प्रतिक्रिया के साथ बुनियादी ओपी-एम्पी एम्पलीफाइंग चरण पर विचार करता है
• कॉमन कलेक्टर (एमिटर फॉलोअर) नकारात्मक प्रतिक्रिया के साथ बुनियादी ट्रांजिस्टर एम्पलीफाइंग चरण के लिए समर्पित है
• अतिरिक्त तत्व प्रमेय
• आवृत्ति मुआवजा
• मिलर प्रमेय नकारात्मक प्रतिक्रिया सर्किट के इनपुट/आउटपुट प्रतिबाधा का निर्धारण करने के लिए एक शक्तिशाली उपकरण है
• ऑपरेशनल एम्पलीफायर मूल ओप-एम्प ऑपरेशनल एम्पलीफायर प्रस्तुत करता है#नॉन-इनवर्टिंग एम्पलीफायर | नॉन-इनवर्टिंग एम्पलीफायर और इनवर्टिंग एम्पलीफायर
• ऑपरेशनल एम्पलीफायर एप्लिकेशन नकारात्मक प्रतिक्रिया के साथ सबसे विशिष्ट ऑप-एम्प सर्किट दिखाते हैं
• चरण मार्जिन
• पोल विभाजन
• वापसी अनुपात
• कदम की प्रतिक्रिया

संदर्भ और नोट्स

]]

डी: नकारात्मक rückkopplung]]]] एनएल: Tegenkoppeling]] [नहीं: नेगेटिव तिलबेककोबलिंग]] आरयू: नकारात्मक प्रतिक्रिया ] एसवी: नेगेटिव Återkoppling]]