वेव शोलिंग: Difference between revisions
m (added Category:Vigyan Ready using HotCat) |
m (12 revisions imported from alpha:वेव_शोलिंग) |
(No difference)
| |
Revision as of 11:36, 26 May 2023


पृथ्वी के गुरुत्वाकर्षण g और आवृत्ति T का उपयोग करके मात्राओं को आयाम रहित बनाया गया है, L0 = gT2/(2π) और गहरे पानी की चरण गति c0 = L0/T। द्वारा दी गई गहरे पानी की तरंग दैर्ध्य के साथ। ग्रे लाइन कम-पानी की सीमा cp =cg = √(gh) से मेल खाती है।
चरण की गति - और इस प्रकार तरंग दैर्ध्य L = cpT घटती गहराई के साथ नीरस रूप से घट जाती है। हालाँकि, समूह का वेग पहले इसके गहरे पानी के मूल्य (cg = 1/2सी0= gT/(4π)) कम गहराई में घटने से पहले है।[1]
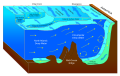
द्रव गतिविज्ञान में, वेव शोलिंग का प्रभाव है जिसके द्वारा बाहरी तरंगें, उथले पानी में प्रवेश करती हैं, और लहर की ऊँचाई में परिवर्तन करती हैं। यह इस तथ्य के कारण होता है कि समूह वेग, जो तरंग-ऊर्जा परिवहन वेग भी है, जो पानी की गहराई के साथ बदलता है। स्थिर परिस्थितियों में, निरंतर ऊर्जा प्रवाह बनाए रखने के लिए परिवहन गति में कमी को ऊर्जा घनत्व में वृद्धि द्वारा प्रतिकरात्मक होना चाहिए। [2] वेव शोलिंग और तरंग दैर्ध्य के अभाव में कमी होती है जबकि आवृत्ति स्थिर रहती है।
दूसरे शब्दों में, जैसे-जैसे लहरें तट के पास पहुँचती हैं और पानी कम होता जाता है, लहरें ऊँची होती जाती हैं, और धीमी होती जाती हैं, और एक-दूसरे के समीप आती जाती हैं।
उथले पानी और समानांतर गहराई की रूपरेखाओं में, तरंग उथले पानी में प्रवेश करते ही लहर की ऊंचाई में गैर-लुप्त तरंगें बढ़ जाती है। [3] यह सूनामी के लिए विशेष रूप से स्पष्ट है चूंकि विनाशकारी परिणामों के साथ समुद्र तट के पास पहुंचने पर वे ऊंचाई में बढ़ जाती हैं।
अवलोकन
तट के पास आने वाली लहरें विभिन्न प्रभावों के माध्यम से लहर की ऊँचाई को बदल देती हैं। कुछ महत्वपूर्ण तरंग प्रक्रियाएं अपवर्तन, विवर्तन, परावर्तन, तरंग विभंजन, वेव-जल धारा पारस्परिक प्रभाव, घर्षण, हवा के कारण तरंग वृद्धि और वेव शोलिंग हैं। अन्य प्रभावों की अनुपस्थिति में, वेव शोलिंग लहर की ऊंचाई में परिवर्तन है जो पूरी तरह से औसत पानी की गहराई में परिवर्तन के कारण होता है - लहर प्रसार दिशा और अपव्यय में परिवर्तन के बिना शुद्ध लहर शोलिंग लंबी-शिखर वाली लहरों के लिए होती है। जो हल्के से समतल वाले समुद्र-तल की समानांतर गहराई समोच्च रेखाओं के लंबवत फैलती हैं। फिर लहर की ऊंचाई एक निश्चित स्थान पर व्यक्त किया जा सकता है:[2][3]: साथ शोलिंग गुणांक और गहरे पानी में लहर की ऊंचाई शोलिंग गुणांक स्थानीय जल गहराई पर निर्भर करती है। और तरंग आवृत्ति (या समकक्ष पर और लहर अवधि ). गहरे पानी का अर्थ है कि लहरें समुद्र तल से प्रभावित होती हैं, जो गहराई होने पर होता है जो लगभग आधे गहरे पानी की तरंग दैर्ध्य से बड़ा होता है
भौतिकी


गैर-विच्छेद तरंगों के लिए, तरंग गति से जुड़ा ऊर्जा प्रवाह, जो दो तरंग किरणों के बीच समूह वेग के साथ तरंग ऊर्जा घनत्व का उत्पाद है, और एक संरक्षित मात्रा है। जो स्थिर स्थितियों के तहत कुल ऊर्जा परिवहन तरंग किरण के साथ स्थिर होती है - जैसा कि पहली बार 1915 में विलियम बर्नसाइड द्वारा दिखाया गया था।[4]
अपवर्तन और वेव शोलिंग से प्रभावित तरंगों के लिए, तरंग ऊर्जा परिवहन के परिवर्तन की दर है।[3]
जहाँ तरंग किरण के साथ समन्वय है और प्रति इकाई शिखर लंबाई ऊर्जा प्रवाह है। समूह गति में कमी और तरंग किरणों के बीच की दूरी ऊर्जा घनत्व में वृद्धि द्वारा प्रतिकरात्मक होना जाना चाहिए . इसे गहरे पानी में लहर की ऊंचाई के सापेक्ष वेल शोलिंग गुणांक के रूप में उपस्थित किया जाता है।[3][2]
उथले पानी के लिए, जब तरंग दैर्ध्य पानी की गहराई से बहुत बड़ा होता है - तो एक निरंतर किरण दूरी के स्थिति में तरंग वेव शोलिंग ग्रीन के नियम को सरल बनाती है:
साथ ही औसत पानी की गहराई, लहर की ऊंचाई और का चौथा मूल होता है।
जल तरंग अपवर्तन
फिलिप्स (1977) और मेई (1989) के बाद,[5][6] तरंग किरण के चरण को निरूपित करते हैं
- .
स्थानीय तरंग संख्या वेक्टर चरण फलन का प्रवणता है,
- ,
और कोणीय आवृत्ति इसके परिवर्तन की स्थानीय दर के समानुपाती होती है,
- .
एक आयाम को सरल बनाना और इसे अनुप्रस्थ- अंतरात्मक देखा जा सकता है कि उपरोक्त परिभाषाएँ केवल यह दर्शाती हैं कि तरंग संख्या के परिवर्तन की दर एक किरण के साथ आवृत्ति के अभिसरण द्वारा संतुलित होती है;
- .
स्थिर स्थिति मानकर (), इसका तात्पर्य है कि तरंग शिखर संरक्षित हैं और तरंग किरण के साथ आवृत्ति स्थिर रहनी चाहिए चूंकि . जैसे ही लहरें उथले पानी में प्रवेश करती हैं, पानी की गहराई में कमी के कारण समूह वेग में कमी से लहर की लंबाई में कमी आती है चूंकि लहर चरण की गति के लिए विस्तार संबंध की अविच्छिन्न उथली जल सीमा निर्देश देती है।
- ,
अर्थात् , एक स्थिर वृद्धि (में कमी ) के रूप में चरण की गति स्थिर के तहत घट जाती है। .
यह भी देखें
टिप्पणियाँ
- ↑ Wiegel, R.L. (2013). समुद्र विज्ञान इंजीनियरिंग. Dover Publications. p. 17, Figure 2.4. ISBN 978-0-486-16019-1.
- ↑ 2.0 2.1 Goda, Y. (2010). यादृच्छिक समुद्र और समुद्री संरचनाओं का डिजाइन. Advanced Series on Ocean Engineering. Vol. 33 (3 ed.). Singapore: World Scientific. pp. 10–13 & 99–102. ISBN 978-981-4282-39-0.
- ↑ 3.0 3.1 3.2 3.3 Dean, R.G.; Dalrymple, R.A. (1991). इंजीनियरों और वैज्ञानिकों के लिए जल तरंग यांत्रिकी. Advanced Series on Ocean Engineering. Vol. 2. Singapore: World Scientific. ISBN 978-981-02-0420-4.
- ↑ Burnside, W. (1915). "लहरों की एक ट्रेन के संशोधन पर क्योंकि यह उथले पानी में आगे बढ़ती है". Proceedings of the London Mathematical Society. Series 2. 14: 131–133. doi:10.1112/plms/s2_14.1.131.
- ↑ Phillips, Owen M. (1977). The dynamics of the upper ocean (2nd ed.). Cambridge University Press. ISBN 0-521-29801-6.
- ↑ Mei, Chiang C. (1989). महासागर की सतह की लहरों की एप्लाइड डायनेमिक्स. Singapore: World Scientific. ISBN 9971-5-0773-0.