हेल्महोल्ट्ज़ समीकरण: Difference between revisions
No edit summary |
|||
| (6 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Eigenvalue problem for the Laplace operator}} | {{Short description|Eigenvalue problem for the Laplace operator}} | ||
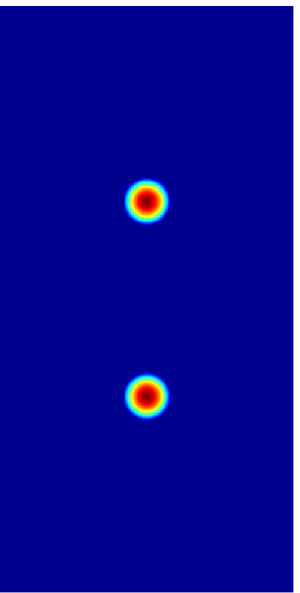
[[Image:Helmholtz source.png|right|thumb|समतल में विकिरण के दो स्रोत, गणितीय रूप से एक फलन {{math|''f''}} द्वारा दिए गए, जो नीले क्षेत्र में शून्य है]] | [[Image:Helmholtz source.png|right|thumb|समतल में विकिरण के दो स्रोत, गणितीय रूप से एक फलन {{math|''f''}} द्वारा दिए गए, जो नीले क्षेत्र में शून्य है]] | ||
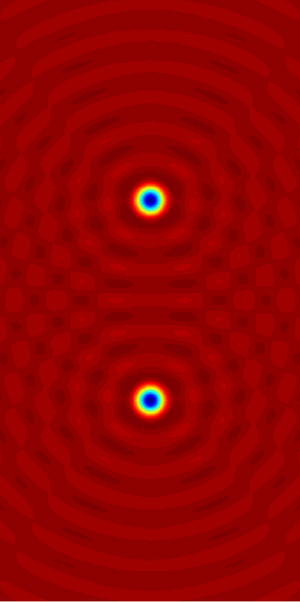
[[Image:Helmholtz solution.png|right|thumb|परिणामी क्षेत्र का [[ वास्तविक भाग ]] {{mvar|A}}, {{mvar|A}} विषम हेल्महोल्ट्ज समीकरण का हल है {{math|1= (∇<sup>2</sup> − ''k''<sup>2</sup>) ''A'' = −''f''.}}]]गणित में, [[ लाप्लास ऑपरेटर ]] के लिए [[ eigenvalue |अभिलक्षणिक मान]] समस्या को[[ हरमन वॉन हेल्महोल्ट्ज़ | '''हेल्महोल्ट्ज़''']] '''समीकरण''' के रूप में जाना जाता है। यह रैखिक आंशिक अवकल समीकरण से मेल खाती है<math display="block">\nabla^2 f = -k^2 f,</math>कहां {{math|∇<sup>2</sup>}} लाप्लास ऑपरेटर (या <nowiki>''लाप्लासियन''</nowiki>) है, {{math|''k''<sup>2</sup>}} अभिलक्षणिक मान है, और {{mvar|f}} (अभिलक्षणिक) फलन है। जब समीकरण तरंगों पर लागू होता है, {{mvar|k}} [[ तरंग संख्या |तरंग संख्या]] के रूप में जाना जाता है। हेल्महोल्त्ज़ समीकरण में भौतिकी में विभिन्न प्रकार के अनुप्रयोग हैं, जिसमें[[ तरंग समीकरण | तरंग समीकरण]] और [[ प्रसार समीकरण | प्रसार समीकरण]] सम्मिलित हैं, और इसका अन्य विज्ञानों में उपयोग होता है। | [[Image:Helmholtz solution.png|right|thumb|परिणामी क्षेत्र का [[ वास्तविक भाग ]] {{mvar|A}}, {{mvar|A}} विषम हेल्महोल्ट्ज समीकरण का हल है {{math|1= (∇<sup>2</sup> − ''k''<sup>2</sup>) ''A'' = −''f''.}}]]गणित में, [[ लाप्लास ऑपरेटर | लाप्लास ऑपरेटर]] के लिए [[ eigenvalue |अभिलक्षणिक मान]] समस्या को[[ हरमन वॉन हेल्महोल्ट्ज़ | '''हेल्महोल्ट्ज़''']] '''समीकरण''' के रूप में जाना जाता है। यह रैखिक आंशिक अवकल समीकरण से मेल खाती है<math display="block">\nabla^2 f = -k^2 f,</math>कहां {{math|∇<sup>2</sup>}} लाप्लास ऑपरेटर (या <nowiki>''लाप्लासियन''</nowiki>) है, {{math|''k''<sup>2</sup>}} अभिलक्षणिक मान है, और {{mvar|f}} (अभिलक्षणिक) फलन है। जब समीकरण तरंगों पर लागू होता है, {{mvar|k}} [[ तरंग संख्या |तरंग संख्या]] के रूप में जाना जाता है। हेल्महोल्त्ज़ समीकरण में भौतिकी में विभिन्न प्रकार के अनुप्रयोग हैं, जिसमें[[ तरंग समीकरण | तरंग समीकरण]] और[[ प्रसार समीकरण | प्रसार समीकरण]] सम्मिलित हैं, और इसका अन्य विज्ञानों में उपयोग होता है। | ||
== प्रेरणा और उपयोग == | == प्रेरणा और उपयोग == | ||
हेल्महोल्त्ज़ समीकरण प्रायः अंतरिक्ष और समय दोनों में आंशिक अवकल समीकरणों (पीडीई) से जुड़ी भौतिक समस्याओं के अध्ययन में उत्पन्न होता है। हेल्महोल्त्ज़ समीकरण, जो तरंग समीकरण के एक '''समय-स्वतंत्र''' रूप का प्रतिनिधित्व करता है, विश्लेषण की जटिलता को कम करने के लिए | हेल्महोल्त्ज़ समीकरण प्रायः अंतरिक्ष और समय दोनों में आंशिक अवकल समीकरणों (पीडीई) से जुड़ी भौतिक समस्याओं के अध्ययन में उत्पन्न होता है। हेल्महोल्त्ज़ समीकरण, जो तरंग समीकरण के एक '''समय-स्वतंत्र''' रूप का प्रतिनिधित्व करता है, विश्लेषण की जटिलता को कम करने के लिए वेरिएबल के पृथक्करण की तकनीक को लागू करने का परिणाम है। | ||
उदाहरण के लिए, तरंग समीकरण पर विचार करें | उदाहरण के लिए, तरंग समीकरण पर विचार करें | ||
<math display="block">\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right) u(\mathbf{r},t)=0.</math> | <math display="block">\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right) u(\mathbf{r},t)=0.</math> | ||
वेरिएबलों का पृथक्करण यह मानकर प्रारम्भ होता है कि तरंग फलन {{math|''u''('''r''', ''t'')}} असलियत में वियोज्य है: | |||
<math display="block">u(\mathbf{r},t) =A (\mathbf{r}) T(t).</math> | <math display="block">u(\mathbf{r},t) =A (\mathbf{r}) T(t).</math> | ||
इस रूप को तरंग समीकरण में प्रतिस्थापित करने और फिर सरल करने पर, हम निम्नलिखित समीकरण प्राप्त करते हैं: | इस रूप को तरंग समीकरण में प्रतिस्थापित करने और फिर सरल करने पर, हम निम्नलिखित समीकरण प्राप्त करते हैं: | ||
<math display="block">\frac{\nabla^2 A}{A} = \frac{1}{c^2 T} \frac{\mathrm{d}^2 T}{\mathrm{d} t^2}.</math> | <math display="block">\frac{\nabla^2 A}{A} = \frac{1}{c^2 T} \frac{\mathrm{d}^2 T}{\mathrm{d} t^2}.</math> | ||
ध्यान दें कि बाईं ओर का व्यंजक केवल {{math|'''r'''}} पर निर्भर करता है, जबकि दाएँ पक्ष का व्यंजक केवल {{mvar|t}} पर निर्भर करता है। फलस्वरूप, यह समीकरण सामान्य स्थिति में मान्य है यदि और केवल यदि समीकरण के दोनों पक्ष समान स्थिर मान के बराबर हैं। यह तर्क | ध्यान दें कि बाईं ओर का व्यंजक केवल {{math|'''r'''}} पर निर्भर करता है, जबकि दाएँ पक्ष का व्यंजक केवल {{mvar|t}} पर निर्भर करता है। फलस्वरूप, यह समीकरण सामान्य स्थिति में मान्य है यदि और केवल यदि समीकरण के दोनों पक्ष समान स्थिर मान के बराबर हैं। यह तर्क वेरिएबलों को अलग करके रैखिक आंशिक अवकल समीकरणों को हल करने की तकनीक में महत्वपूर्ण है। इस अवलोकन से हमें दो समीकरण प्राप्त होते हैं, एक {{math|''A''('''r''')}} के लिए, दूसरे {{math|''T''(''t'')}} के लिए: | ||
<math display="block">\frac{\nabla^2 A}{A} = -k^2</math> | <math display="block">\frac{\nabla^2 A}{A} = -k^2</math><math display="block">\frac{1}{c^2 T} \frac{\mathrm{d}^2 T}{\mathrm{d}t^2} = -k^2,</math> | ||
<math display="block">\frac{1}{c^2 T} \frac{\mathrm{d}^2 T}{\mathrm{d}t^2} = -k^2,</math> | |||
जहां हमने व्यापकता को खोए बिना स्थिरांक के मान के लिए {{math|−''k''<sup>2</sup>}} व्यंजक को चुना है। स्थिरांक के मान के लिए। (यह किसी भी स्थिरांक {{mvar|k}} को पृथक्करण स्थिरांक के रूप में उपयोग करने के लिए समान रूप से मान्य है; {{math|−''k''<sup>2</sup>}} केवल परिणामी समाधानों में सुविधा के लिए ही चुना जाता है।) | जहां हमने व्यापकता को खोए बिना स्थिरांक के मान के लिए {{math|−''k''<sup>2</sup>}} व्यंजक को चुना है। स्थिरांक के मान के लिए। (यह किसी भी स्थिरांक {{mvar|k}} को पृथक्करण स्थिरांक के रूप में उपयोग करने के लिए समान रूप से मान्य है; {{math|−''k''<sup>2</sup>}} केवल परिणामी समाधानों में सुविधा के लिए ही चुना जाता है।) | ||
पहले समीकरण को पुनर्व्यवस्थित करने पर, हम हेल्महोल्ट्ज़ समीकरण प्राप्त करते हैं: | पहले समीकरण को पुनर्व्यवस्थित करने पर, हम हेल्महोल्ट्ज़ समीकरण प्राप्त करते हैं: | ||
<math display="block">\nabla^2 A + k^2 A = (\nabla^2 + k^2) A = 0.</math> | <math display="block">\nabla^2 A + k^2 A = (\nabla^2 + k^2) A = 0.</math> | ||
इसी तरह, प्रतिस्थापन करने के बाद {{math|1= ''ω'' = ''kc''}}, जहाँ {{mvar|k}} [[ वेवनंबर |तरंग संख्या]] है, और {{mvar|ω}} [[ कोणीय आवृत्ति ]](एकवर्णीय क्षेत्र मानकर) है, तो दूसरा समीकरण बन जाता है | इसी तरह, प्रतिस्थापन करने के बाद {{math|1= ''ω'' = ''kc''}}, जहाँ {{mvar|k}} [[ वेवनंबर |तरंग संख्या]] है, और {{mvar|ω}} [[ कोणीय आवृत्ति |कोणीय आवृत्ति]] (एकवर्णीय क्षेत्र मानकर) है, तो दूसरा समीकरण बन जाता है | ||
<math display="block">\frac{\mathrm{d}^2 T}{\mathrm{d}t^2} + \omega^2T = \left( \frac{\mathrm{d}^2}{\mathrm{d}t^2} + \omega^2 \right) T = 0.</math> | <math display="block">\frac{\mathrm{d}^2 T}{\mathrm{d}t^2} + \omega^2T = \left( \frac{\mathrm{d}^2}{\mathrm{d}t^2} + \omega^2 \right) T = 0.</math> | ||
अब हमारे पास स्थानिक | अब हमारे पास स्थानिक वेरिएबल {{math|'''r'''}} के लिए हेल्महोल्त्ज़ का समीकरण और समय में एक दूसरे क्रम का [[ साधारण अंतर समीकरण |साधारण अवकल समीकरण]] है। समय में समाधान ज्या और [[ कोज्या |कोज्या]] फलनों का एक [[ रैखिक संयोजन ]]होगा, जिसका सटीक रूप प्रारंभिक स्थितियों से निर्धारित होता है, जबकि अंतरिक्ष में समाधान का रूप सीमा स्थितियों पर निर्भर करेगा। वैकल्पिक रूप से, [[ अभिन्न परिवर्तन |समाकल रूपांतरण]], जैसे[[ लाप्लास रूपांतरण | लाप्लास]] या [[ फूरियर रूपांतरण |फूरियर रूपांतरण]], का उपयोग प्रायः [[ अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण |अतिपरवलयिक पीडीई]] को हेल्महोल्ट्ज़ समीकरण के रूप में बदलने के लिए उपयोग किया जाता है। | ||
तरंग समीकरण से इसके संबंध के कारण, हेल्महोल्त्ज़ समीकरण भौतिकी के ऐसे क्षेत्रों में समस्याओं में उत्पन्न होता है जैसे [[ विद्युत चुम्बकीय विकिरण |विद्युत चुम्बकीय विकिरण]], [[ भूकंप विज्ञान |भूकंप विज्ञान]]और ध्वनिकी का अध्ययन। | तरंग समीकरण से इसके संबंध के कारण, हेल्महोल्त्ज़ समीकरण भौतिकी के ऐसे क्षेत्रों में समस्याओं में उत्पन्न होता है जैसे [[ विद्युत चुम्बकीय विकिरण |विद्युत चुम्बकीय विकिरण]], [[ भूकंप विज्ञान |भूकंप विज्ञान]] और ध्वनिकी का अध्ययन। | ||
== | == वेरिएबलों के पृथक्करण का उपयोग करके हेल्महोल्ट्ज़ समीकरण को हल करना == | ||
स्थानिक हेल्महोल्ट्ज़ समीकरण का समाधान: | स्थानिक हेल्महोल्ट्ज़ समीकरण का समाधान: | ||
<math display="block"> \nabla^2 A = -k^2 A </math> | <math display="block"> \nabla^2 A = -k^2 A </math> | ||
वेरिएबलों के पृथक्करण का उपयोग करके सरल ज्यामिति के लिए प्राप्त किया जा सकता है। | |||
=== कंपन झिल्ली === | === कंपन झिल्ली === | ||
कंपन स्ट्रिंग का द्वि-आयामी एनालॉग कंपन झिल्ली है, जिसके किनारों को गतिहीन होने के लिए जकड़ा जाता है। हेल्महोल्ट्ज़ समीकरण को 19वीं शताब्दी में कई बुनियादी आकृतियों के लिए हल किया गया था: 1829 में सिमोन डेनिस पोइसन द्वारा आयताकार झिल्ली, 1852 में गेब्रियल लैम द्वारा समबाहु त्रिभुज, और 1862 में [[ अल्फ्रेड क्लेब्सच |अल्फ्रेड क्लेबश]] द्वारा गोलाकार झिल्ली। अण्डाकार ड्रमहेड का अध्ययन एमिले मैथ्यू द्वारा किया गया था। जिससे मैथ्यू | कंपन स्ट्रिंग का द्वि-आयामी एनालॉग कंपन झिल्ली है, जिसके किनारों को गतिहीन होने के लिए जकड़ा जाता है। हेल्महोल्ट्ज़ समीकरण को 19वीं शताब्दी में कई बुनियादी आकृतियों के लिए हल किया गया था: 1829 में सिमोन डेनिस पोइसन द्वारा आयताकार झिल्ली, 1852 में गेब्रियल लैम द्वारा समबाहु त्रिभुज, और 1862 में [[ अल्फ्रेड क्लेब्सच |अल्फ्रेड क्लेबश]] द्वारा गोलाकार झिल्ली। अण्डाकार ड्रमहेड का अध्ययन एमिले मैथ्यू द्वारा किया गया था। जिससे मैथ्यू का अवकल समीकरण उत्पन्न हुआ। | ||
यदि किसी आकृति के किनारे सीधी रेखा खंड हैं, तो एक समाधान केवल समाकलनीय या बंद रूप में जानने योग्य है, यदि यह समतल तरंगों के परिमित रैखिक संयोजन के रूप में अभिव्यक्त होता है जो सीमा की स्थिति को पूरा करता है (सीमा पर शून्य, यानी, झिल्ली जकड़ी हुई)। | यदि किसी आकृति के किनारे सीधी रेखा खंड हैं, तो एक समाधान केवल समाकलनीय या बंद रूप में जानने योग्य है, यदि यह समतल तरंगों के परिमित रैखिक संयोजन के रूप में अभिव्यक्त होता है जो सीमा की स्थिति को पूरा करता है (सीमा पर शून्य, यानी, झिल्ली जकड़ी हुई)। | ||
| Line 43: | Line 42: | ||
हम सीमा अनुबंध लगा सकते हैं कि {{mvar|A}} अगर लुप्त हो जाता है यदि {{math|1= ''r'' = ''a''}}; इस प्रकार | हम सीमा अनुबंध लगा सकते हैं कि {{mvar|A}} अगर लुप्त हो जाता है यदि {{math|1= ''r'' = ''a''}}; इस प्रकार | ||
<math display="block">A(a,\theta) = 0.</math> | <math display="block">A(a,\theta) = 0.</math> | ||
वेरिएबलों के पृथक्करण की विधि प्रपत्र के परीक्षण समाधान की ओर ले जाती है | |||
<math display="block">A(r,\theta) = R(r)\Theta(\theta),</math> | <math display="block">A(r,\theta) = R(r)\Theta(\theta),</math> | ||
कहां {{math|Θ}} अवधि {{math|2''π''}} के आवधिक होना चाहिए। इससे यह होता है | कहां {{math|Θ}} अवधि {{math|2''π''}} के आवधिक होना चाहिए। इससे यह होता है | ||
<math display="block">\Theta'' +n^2 \Theta =0,</math> | <math display="block">\Theta'' +n^2 \Theta =0,</math><math display="block"> r^2 R'' + r R' + r^2 k^2 R - n^2 R=0.</math> | ||
<math display="block"> r^2 R'' + r R' + r^2 k^2 R - n^2 R=0.</math> | |||
यह आवधिकता की स्थिति से निम्नानुसार है | यह आवधिकता की स्थिति से निम्नानुसार है | ||
<math display="block"> \Theta = \alpha \cos n\theta + \beta \sin n\theta,</math> | <math display="block"> \Theta = \alpha \cos n\theta + \beta \sin n\theta,</math> | ||
| Line 55: | Line 53: | ||
जहां बेसेल फलन {{math|''J<sub>n</sub>''(''ρ'')}} बेसेल के समीकरण को संतुष्ट करता है | जहां बेसेल फलन {{math|''J<sub>n</sub>''(''ρ'')}} बेसेल के समीकरण को संतुष्ट करता है | ||
<math display="block"> \rho^2 J_n'' + \rho J_n' +(\rho^2 - n^2)J_n =0, </math> | <math display="block"> \rho^2 J_n'' + \rho J_n' +(\rho^2 - n^2)J_n =0, </math> | ||
और {{math|1= ''ρ'' = ''kr''}}। रेडियल फलन {{math|''J<sub>n</sub>''}} में {{mvar|n}} के प्रत्येक मान के लिए अपरिमित रूप से अनेक मूल होते हैं, जिन्हें {{math|''ρ''<sub>''m'',''n''</sub>}} | और {{math|1= ''ρ'' = ''kr''}}। रेडियल फलन {{math|''J<sub>n</sub>''}} में {{mvar|n}} के प्रत्येक मान के लिए अपरिमित रूप से अनेक मूल होते हैं, जिन्हें {{math|''ρ''<sub>''m'',''n''</sub>}} द्वारा दर्शाया गया है। सीमा अनुबंध है कि {{mvar|A}} लुप्त हो जाता है जहां {{math|1= ''r'' = ''a''}} संतुष्ट हो जाएगा यदि संबंधित तरंगों को दिया जाता है | ||
<math display="block">k_{m,n} = \frac{1}{a} \rho_{m,n}.</math> | <math display="block">k_{m,n} = \frac{1}{a} \rho_{m,n}.</math> | ||
सामान्य समाधान {{mvar|A}} तब {{math|''J<sub>n</sub>''(''k<sub>m,n</sub>r'')}} और {{math|''nθ''}} की ज्या (या कोसाइन) के फिर उत्पादों को | सामान्य समाधान {{mvar|A}} तब {{math|''J<sub>n</sub>''(''k<sub>m,n</sub>r'')}} और {{math|''nθ''}} की ज्या (या कोसाइन) के फिर उत्पादों को सम्मिलित करने वाली अनुबंधों की [[सामान्यीकृत फूरियर श्रृंखला]] का रूप लेता है। ये समाधान एक वृत्ताकार ड्रमहेड के कंपन के तरीके हैं। | ||
=== त्रि-आयामी समाधान === | === त्रि-आयामी समाधान === | ||
| Line 75: | Line 73: | ||
{{Further|मंदता परिवर्ती आवरण सन्निकटन}} | {{Further|मंदता परिवर्ती आवरण सन्निकटन}} | ||
हेल्महोल्ट्ज़ समीकरण के | हेल्महोल्ट्ज़ समीकरण के पैराएक्सियल सन्निकटन में,<ref>{{cite book |title=फूरियर ऑप्टिक्स का परिचय|edition=2nd |author=J. W. Goodman |pages=61–62 }}</ref> [[ जटिल आयाम | जटिल आयाम]] {{mvar|A}} रूप में अभिव्यक्त किया जाता है | ||
<math display="block">A(\mathbf{r}) = u(\mathbf{r}) e^{ikz} </math> | <math display="block">A(\mathbf{r}) = u(\mathbf{r}) e^{ikz} </math> | ||
जहाँ {{mvar|u}} जटिल-मूल्यवान आयाम का प्रतिनिधित्व करता है जो घातीय कारक द्वारा दर्शाए गए ज्यावक्रीय समतल तरंग को नियंत्रित करता है। फिर एक उपयुक्त धारणा के तहत, {{mvar|u}} लगभग हल करता है | जहाँ {{mvar|u}} जटिल-मूल्यवान आयाम का प्रतिनिधित्व करता है जो घातीय कारक द्वारा दर्शाए गए ज्यावक्रीय समतल तरंग को नियंत्रित करता है। फिर एक उपयुक्त धारणा के तहत, {{mvar|u}} लगभग हल करता है | ||
| Line 86: | Line 84: | ||
<math display="block"> \left| \frac{ \partial^2 u }{ \partial z^2 } \right| \ll \left| k \frac{\partial u}{\partial z} \right| .</math> | <math display="block"> \left| \frac{ \partial^2 u }{ \partial z^2 } \right| \ll \left| k \frac{\partial u}{\partial z} \right| .</math> | ||
यह स्थिति कहने के बराबर है कि तरंग वेक्टर {{math|'''k'''}} के बीच और ऑप्टिकल अक्ष {{mvar|z}} के बीच कोण {{mvar|θ}} छोटा है: {{math|''θ'' ≪ 1}} | यह स्थिति कहने के बराबर है कि तरंग वेक्टर {{math|'''k'''}} के बीच और ऑप्टिकल अक्ष {{mvar|z}} के बीच कोण {{mvar|θ}} छोटा है: {{math|''θ'' ≪ 1}}। | ||
हेल्महोल्ट्ज़ समीकरण के | हेल्महोल्ट्ज़ समीकरण के पैराएक्सियल रूप को हेल्महोल्ट्ज़ समीकरण के सामान्य रूप में जटिल आयाम के लिए उपर्युक्त अभिव्यक्ति को निम्नानुसार प्रतिस्थापित करके पाया जाता है: | ||
<math display="block">\nabla^{2}(u\left( x,y,z \right) e^{ikz}) + k^2 u\left( x,y,z \right) e^{ikz} = 0.</math> | <math display="block">\nabla^{2}(u\left( x,y,z \right) e^{ikz}) + k^2 u\left( x,y,z \right) e^{ikz} = 0.</math> | ||
| Line 94: | Line 92: | ||
<math display="block">\left( \frac {\partial^2}{\partial x^2} + \frac {\partial^2}{\partial y^2} \right) u(x,y,z) e^{ikz} + \left( \frac {\partial^2}{\partial z^2} u (x,y,z) \right) e^{ikz} + 2 \left( \frac \partial {\partial z} u(x,y,z) \right) ik{e^{ikz}}=0.</math> | <math display="block">\left( \frac {\partial^2}{\partial x^2} + \frac {\partial^2}{\partial y^2} \right) u(x,y,z) e^{ikz} + \left( \frac {\partial^2}{\partial z^2} u (x,y,z) \right) e^{ikz} + 2 \left( \frac \partial {\partial z} u(x,y,z) \right) ik{e^{ikz}}=0.</math> | ||
ऊपर बताई गई | ऊपर बताई गई पैराएक्सियल असमानता के कारण, {{math|∂<sup>2</sup>''u''/∂''z''<sup>2</sup>}} शब्द {{math|''k''·∂''u''/∂''z''}} पद की तुलना में उपेक्षित है। इससे पैराएक्सियल हेल्महोल्ट्ज समीकरण प्राप्त होता है। {{math|1= ''u''('''r''') = ''A''('''r''') ''e''<sup>−''ikz''</sup>}} को प्रतिस्थापित करने पर मूल जटिल आयाम A के लिए पराक्षीय समीकरण देता है:<math display="block">\nabla_{\perp}^2 A + 2ik\frac{\partial A}{\partial z} = 0.</math> | ||
फ़्रेस्नेल विवर्तन समाकल | फ़्रेस्नेल विवर्तन समाकल पैराएक्सियल हेल्महोल्ट्ज़ समीकरण का एक सटीक समाधान है।<ref>{{Cite journal |doi = 10.1088/0150-536X/13/6/006|title = फ्रेस्नेल प्रसार और विवर्तन और पैराएक्सियल तरंग समीकरण|journal = Journal of Optics|volume = 13|issue = 6|pages = 367–374|year = 1982|last1 = Grella|first1 = R.| bibcode=1982JOpt...13..367G }}</ref> | ||
== विषम हेल्महोल्ट्ज़ समीकरण == | == विषम हेल्महोल्ट्ज़ समीकरण == | ||
'''विषम हेल्महोल्ट्ज़ समीकरण''' समीकरण है | '''विषम हेल्महोल्ट्ज़ समीकरण''' समीकरण है | ||
<math display="block">\nabla^2 A(x) + k^2 A(x) = -f(x) \ \text { in } \R^n,</math> | <math display="block">\nabla^2 A(x) + k^2 A(x) = -f(x) \ \text { in } \R^n,</math> | ||
जहाँ {{math|''ƒ'' : '''R'''<sup>''n''</sup> → '''C'''}} [[ कॉम्पैक्ट समर्थन ]]वाला एक फलन है, और {{math|1= ''n'' = 1, 2, 3.}} यह समीकरण स्क्रीन किए गए पोइसन समीकरण के समान है, और समान होगा यदि धन चिह्न ({{mvar|k}} शब्द के सामने) को ऋणात्मक चिह्न में बदल दिया गया। | जहाँ {{math|''ƒ'' : '''R'''<sup>''n''</sup> → '''C'''}} [[ कॉम्पैक्ट समर्थन | कॉम्पैक्ट क्रम]] वाला एक फलन है, और {{math|1= ''n'' = 1, 2, 3.}} यह समीकरण स्क्रीन किए गए पोइसन समीकरण के समान है, और समान होगा यदि धन चिह्न ({{mvar|k}} शब्द के सामने) को ऋणात्मक चिह्न में बदल दिया गया। | ||
इस समीकरण को विशिष्ट रूप से हल करने के लिए, अनंत पर एक सीमा स्थिति निर्दिष्ट करने की आवश्यकता है, जो प्रायः [[सोमरफेल्ड विकिरण स्थिति]] है | इस समीकरण को विशिष्ट रूप से हल करने के लिए, अनंत पर एक सीमा स्थिति निर्दिष्ट करने की आवश्यकता है, जो प्रायः [[सोमरफेल्ड विकिरण स्थिति]] है | ||
| Line 107: | Line 105: | ||
<math display="block">\lim_{r \to \infty} r^{\frac{n-1}{2}} \left( \frac{\partial}{\partial r} - ik \right) A({x}) = 0</math> | <math display="block">\lim_{r \to \infty} r^{\frac{n-1}{2}} \left( \frac{\partial}{\partial r} - ik \right) A({x}) = 0</math> | ||
<math>n</math> स्थानिक आयामों में, सभी कोणों के लिए (अर्थात <math>\theta, \phi</math> का कोई मान)हैं। यहाँ<math>r = \sqrt{\sum_{i=1}^n x_i^2} </math> जहाँ <math>x_i</math> सदिश <math>\mathbf{x}</math> के निर्देशांक हैं। | |||
इस अनुबंध के साथ, विषम हेल्महोल्ट्ज़ समीकरण का हल है | |||
<math display="block">{\displaystyle A(\mathbf {x} )=\int _{\mathbb {R} ^{n}}\!G(\mathbf {x} ,\mathbf {x'} )f(\mathbf {x'} )\,\mathrm {d} \mathbf {x'} }</math> | <math display="block">{\displaystyle A(\mathbf {x} )=\int _{\mathbb {R} ^{n}}\!G(\mathbf {x} ,\mathbf {x'} )f(\mathbf {x'} )\,\mathrm {d} \mathbf {x'} }</math> | ||
(ध्यान दें कि यह इंटीग्रल | (ध्यान दें कि यह इंटीग्रल सचमुच एक परिमित क्षेत्र पर है, क्योंकि {{mvar|f}} सघन क्रम है)। यहां, {{mvar|G}} इस समीकरण का ग्रीन फलन है, अर्थात्, [[ डिराक डेल्टा समारोह |डिराक डेल्टा फलन]] के बराबर {{math|''f''}} के साथ विषम हेल्महोल्त्ज़ समीकरण का समाधान करता है, इसलिए {{mvar|G}} संतुष्ट करता है | ||
<math display="block">\nabla^2 G(x) + k^2 G(x) = -\delta(x) \in \R^n. </math> | <math display="block">\nabla^2 G(x) + k^2 G(x) = -\delta(x) \in \R^n. </math> | ||
ग्रीन के फलन के लिए व्यंजक स्थान के आयाम {{mvar|n}} पर निर्भर करता है। किसी के पास | |||
<math display="block">G(x) = \frac{ie^{ik|x|}}{2k}</math> | <math display="block">G(x,x') = \frac{ie^{ik|x - x'|}}{2k}</math> | ||
के लिए {{math|1= ''n'' = 1}}, | {{math|1= ''n'' = 1}} के लिए , | ||
<math display="block">G(\mathbf{x},\mathbf{x'}) = -\frac{i}{4}H^{(1)}_0(k|\mathbf{x}-\mathbf{x'}|)</math> | |||
{{math|1= ''n'' = 2}} के लिए ,<ref>ftp://ftp.math.ucla.edu/pub/camreport/cam14-71.pdf</ref> जहाँ {{math|''H''{{su|p=(1)|b=0}}}} एक हैंकेल फलन है, और | |||
<math display="block">G(\mathbf{x},\mathbf{x'}) = \frac{e^{ik|\mathbf{x}-\mathbf{x'}|}}{4\pi |\mathbf{x}-\mathbf{x'}|}</math> | |||
{{math|1= ''n'' = 3}} के लिए। ध्यान दें कि हमने सीमा अनुबंध को चुना है जिसके लिए ग्रीन फलन एक बाहर जाने वाली तरंग है {{math|{{mabs|''x''}} → ∞}}. | |||
<math display="block">G(\mathbf{x},\mathbf{x'}) = c_d k^p \frac{H_p^{(1)}(k|\mathbf{x}-\mathbf{x'}|)}{|\mathbf{x}-\mathbf{x'}|^p}</math> | |||
जहाँ <math> p = \frac{n - 2}{2} </math> और <math>c_d = \frac{1}{2i(2\pi)^p} </math> । | |||
== यह भी देखें == | == यह भी देखें == | ||
* लाप्लास का समीकरण (हेल्महोल्ट्ज़ समीकरण का एक विशेष | * लाप्लास का समीकरण (हेल्महोल्ट्ज़ समीकरण का एक विशेष स्थिति) | ||
* वीइल विस्तार | * वीइल विस्तार | ||
| Line 219: | Line 231: | ||
{{Authority control}} | {{Authority control}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Created On 27/12/2022]] | [[Category:Created On 27/12/2022]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with broken file links]] | |||
[[Category:Pages with maths render errors]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Template documentation pages|Short description/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
Latest revision as of 16:19, 29 May 2023
गणित में, लाप्लास ऑपरेटर के लिए अभिलक्षणिक मान समस्या को हेल्महोल्ट्ज़ समीकरण के रूप में जाना जाता है। यह रैखिक आंशिक अवकल समीकरण से मेल खाती है
प्रेरणा और उपयोग
हेल्महोल्त्ज़ समीकरण प्रायः अंतरिक्ष और समय दोनों में आंशिक अवकल समीकरणों (पीडीई) से जुड़ी भौतिक समस्याओं के अध्ययन में उत्पन्न होता है। हेल्महोल्त्ज़ समीकरण, जो तरंग समीकरण के एक समय-स्वतंत्र रूप का प्रतिनिधित्व करता है, विश्लेषण की जटिलता को कम करने के लिए वेरिएबल के पृथक्करण की तकनीक को लागू करने का परिणाम है।
उदाहरण के लिए, तरंग समीकरण पर विचार करें
पहले समीकरण को पुनर्व्यवस्थित करने पर, हम हेल्महोल्ट्ज़ समीकरण प्राप्त करते हैं:
तरंग समीकरण से इसके संबंध के कारण, हेल्महोल्त्ज़ समीकरण भौतिकी के ऐसे क्षेत्रों में समस्याओं में उत्पन्न होता है जैसे विद्युत चुम्बकीय विकिरण, भूकंप विज्ञान और ध्वनिकी का अध्ययन।
वेरिएबलों के पृथक्करण का उपयोग करके हेल्महोल्ट्ज़ समीकरण को हल करना
स्थानिक हेल्महोल्ट्ज़ समीकरण का समाधान:
कंपन झिल्ली
कंपन स्ट्रिंग का द्वि-आयामी एनालॉग कंपन झिल्ली है, जिसके किनारों को गतिहीन होने के लिए जकड़ा जाता है। हेल्महोल्ट्ज़ समीकरण को 19वीं शताब्दी में कई बुनियादी आकृतियों के लिए हल किया गया था: 1829 में सिमोन डेनिस पोइसन द्वारा आयताकार झिल्ली, 1852 में गेब्रियल लैम द्वारा समबाहु त्रिभुज, और 1862 में अल्फ्रेड क्लेबश द्वारा गोलाकार झिल्ली। अण्डाकार ड्रमहेड का अध्ययन एमिले मैथ्यू द्वारा किया गया था। जिससे मैथ्यू का अवकल समीकरण उत्पन्न हुआ।
यदि किसी आकृति के किनारे सीधी रेखा खंड हैं, तो एक समाधान केवल समाकलनीय या बंद रूप में जानने योग्य है, यदि यह समतल तरंगों के परिमित रैखिक संयोजन के रूप में अभिव्यक्त होता है जो सीमा की स्थिति को पूरा करता है (सीमा पर शून्य, यानी, झिल्ली जकड़ी हुई)।
यदि डोमेन त्रिज्या a का एक वृत्त है, तो ध्रुवीय निर्देशांक r और θ परिचय देना उचित है. हेल्महोल्ट्ज़ समीकरण रूप लेता है
त्रि-आयामी समाधान
गोलाकार निर्देशांक में समाधान है:
ℓ(θ, φ) गोलाकार हार्मोनिक्स हैं (अब्रामोविट्ज़ और स्टेगुन, 1964)। ध्यान दें कि ये प्रपत्र सामान्य समाधान हैं, और किसी विशिष्ट स्थिति में उपयोग करने के लिए सीमा अनुबंधों को निर्दिष्ट करने की आवश्यकता होती है। अनंत बाहरी डोमेन के लिए, विकिरण की स्थिति भी आवश्यक हो सकती है (सोमरफेल्ड, 1949)।
लेखन r0 = (x, y, z) फलन A(r0) स्पर्शोन्मुखता है
पैराएक्सियल सन्निकटन
हेल्महोल्ट्ज़ समीकरण के पैराएक्सियल सन्निकटन में,[1] जटिल आयाम A रूप में अभिव्यक्त किया जाता है
प्रकाशिकी के विज्ञान में इस समीकरण के महत्वपूर्ण अनुप्रयोग हैं, जहाँ यह ऐसे समाधान प्रदान करता है जो परवलय तरंगों या गाऊसी बीम के रूप में विद्युत चुम्बकीय तरंगों (प्रकाश) के प्रसार का वर्णन करता है। अधिकांश लेज़र ऐसे बीम उत्सर्जित करते हैं जो इस रूप को लेते हैं।
धारणा जिसके तहत पैराएक्सियल सन्निकटन मान्य है, आयाम फलन u का z व्युत्पन्न z का धीरे-धीरे बदलता फलन है :
हेल्महोल्ट्ज़ समीकरण के पैराएक्सियल रूप को हेल्महोल्ट्ज़ समीकरण के सामान्य रूप में जटिल आयाम के लिए उपर्युक्त अभिव्यक्ति को निम्नानुसार प्रतिस्थापित करके पाया जाता है:
फ़्रेस्नेल विवर्तन समाकल पैराएक्सियल हेल्महोल्ट्ज़ समीकरण का एक सटीक समाधान है।[2]
विषम हेल्महोल्ट्ज़ समीकरण
विषम हेल्महोल्ट्ज़ समीकरण समीकरण है
इस समीकरण को विशिष्ट रूप से हल करने के लिए, अनंत पर एक सीमा स्थिति निर्दिष्ट करने की आवश्यकता है, जो प्रायः सोमरफेल्ड विकिरण स्थिति है
स्थानिक आयामों में, सभी कोणों के लिए (अर्थात का कोई मान)हैं। यहाँ जहाँ सदिश के निर्देशांक हैं।
इस अनुबंध के साथ, विषम हेल्महोल्ट्ज़ समीकरण का हल है
0 एक हैंकेल फलन है, और
जहाँ और ।
यह भी देखें
- लाप्लास का समीकरण (हेल्महोल्ट्ज़ समीकरण का एक विशेष स्थिति)
- वीइल विस्तार
टिप्पणियाँ
- ↑ J. W. Goodman. फूरियर ऑप्टिक्स का परिचय (2nd ed.). pp. 61–62.
- ↑ Grella, R. (1982). "फ्रेस्नेल प्रसार और विवर्तन और पैराएक्सियल तरंग समीकरण". Journal of Optics. 13 (6): 367–374. Bibcode:1982JOpt...13..367G. doi:10.1088/0150-536X/13/6/006.
- ↑ ftp://ftp.math.ucla.edu/pub/camreport/cam14-71.pdf
संदर्भ
- Abramowitz, Milton; Stegun, Irene, eds. (1964). Handbook of Mathematical functions with Formulas, Graphs and Mathematical Tables. New York: Dover Publications. ISBN 978-0-486-61272-0.
- Riley, K. F.; Hobson, M. P.; Bence, S. J. (2002). "Chapter 19". Mathematical methods for physics and engineering. New York: Cambridge University Press. ISBN 978-0-521-89067-0.
- Riley, K. F. (2002). "Chapter 16". Mathematical Methods for Scientists and Engineers. Sausalito, California: University Science Books. ISBN 978-1-891389-24-5.
- Saleh, Bahaa E. A.; Teich, Malvin Carl (1991). "Chapter 3". Fundamentals of Photonics. Wiley Series in Pure and Applied Optics. New York: John Wiley & Sons. pp. 80–107. ISBN 978-0-471-83965-1.
- Sommerfeld, Arnold (1949). "Chapter 16". Partial Differential Equations in Physics. New York: Academic Press. ISBN 978-0126546569.
- Howe, M. S. (1998). Acoustics of fluid-structure interactions. New York: Cambridge University Press. ISBN 978-0-521-63320-8.
बाहरी कड़ियाँ
- Helmholtz Equation at EqWorld: The World of Mathematical Equations.
- "Helmholtz equation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Vibrating Circular Membrane by Sam Blake, The Wolfram Demonstrations Project.
- Green's functions for the wave, Helmholtz and Poisson equations in a two-dimensional boundless domain