वर्णक्रमीय क्रम: Difference between revisions
No edit summary |
No edit summary |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{For|खगोल विज्ञान में तारों का वर्गीकरण|तारकीय वर्गीकरण}} | {{For|खगोल विज्ञान में तारों का वर्गीकरण|तारकीय वर्गीकरण}} | ||
{{Short description|Tool in homological algebra}} | {{Short description|Tool in homological algebra}} | ||
तुल्य बीजगणित और [[बीजगणितीय टोपोलॉजी|बीजगणितीय]] सांस्थिति में, | तुल्य बीजगणित और [[बीजगणितीय टोपोलॉजी|बीजगणितीय]] सांस्थिति में, वर्णक्रमीय अनुक्रम क्रमिक सन्निकटन लेकर अनुरूपता समूहों की गणना करने का एक साधन है। वर्णक्रमीय अनुक्रम यथार्थ अनुक्रमों का एक सामान्यीकरण है, और {{harvs|txt|authorlink=Jean Leray|first=Jean|last=Leray |year=1946a|year2=1946b}} द्वारा उनके परिचय के बाद से, वे महत्वपूर्ण संगणनात्मक उपकरण बन गए हैं, विशेष रूप से बीजीय सांस्थिति, [[बीजगणितीय ज्यामिति]] और समरूप बीजगणित में है। | ||
== आविष्कार और प्रेरणा == | == आविष्कार और प्रेरणा == | ||
बीजगणितीय सांस्थिति में समस्याओं से प्रेरित, जीन लेरे ने एक [[शीफ (गणित)|शेफ (गणित | बीजगणितीय सांस्थिति में समस्याओं से प्रेरित, जीन लेरे ने एक [[शीफ (गणित)|शेफ (गणित]]) की धारणा प्रस्तुत की और स्वयं को संगणना शेफ सह समरूपता की समस्या का सामना करना पड़ा। [[शेफ कोहोलॉजी|शेफ सह समरूपता]] की गणना करने के लिए, लेरे ने संगणनात्मक तकनीक प्रस्तुत की जिसे अब [[लेरे वर्णक्रमीय अनुक्रम]] के रूप में जाना जाता है। इसने एक शेफ के सह समरूपता समूहों और एक शेफ की प्रत्यक्ष प्रतिरूप के सह समरूपता समूहों के बीच एक संबंध दिया। संबंध में एक अनंत प्रक्रिया सम्मिलित थी। लेरे ने पाया कि ज़ारी रखने के सह समरूपता समूहों ने प्राकृतिक श्रृंखला सम्मिश्र का गठन किया, ताकि वह सह समरूपता के सह समरूपता को ले सकें। यह अभी भी मूल शेफ की सह समरूपता नहीं थी, परन्तु यह एक अर्थ में एक चरण और निकट था। सह समरूपता के सह समरूपता ने फिर से एक [[चेन कॉम्प्लेक्स|मिश्रित शृंखला]] का गठन किया, और इसके सह समरूपता ने मिश्रित शृंखला का निर्माण किया, और इसी प्रकार। इस अनंत प्रक्रिया की सीमा अनिवार्य रूप से वही थी जो मूल शेफ की सह समरूपता समूहों के रूप में थी। | ||
शीघ्र ही यह समझा गया किया गया कि लेरे की संगणनात्मक तकनीक | शीघ्र ही यह समझा गया किया गया कि लेरे की संगणनात्मक तकनीक अधिक सामान्य घटना का एक उदाहरण थी। विभिन्न स्थितियों में वर्णक्रमीय अनुक्रम पाए गए, और उन्होंने अनुरूपता और सह समरूपता समूहों के बीच सम्मिश्र संबंध दिए, जो ज्यामितीय स्थितियों जैसे [[कंपन]] और बीजगणितीय स्थितियों से व्युत्पन्न प्रकार्यक से जुड़े थे। जबकि [[व्युत्पन्न श्रेणी]] की प्रारंभ के बाद से उनका सैद्धांतिक महत्व कम हो गया है, वे अभी भी सबसे प्रभावी संगणनात्मक उपकरण उपलब्ध हैं। यह तब भी सत्य है जब वर्णक्रमीय अनुक्रम के कई पद अगणनीय हैं। | ||
दुर्भाग्य से, बड़ी मात्रा में सूचना वर्णक्रमीय अनुक्रमों में ले जाने के कारण, उन्हें समझना जटिल है। यह सूचना सामान्यतः [[एबेलियन समूह|एबेलियन समूहों]] या [[मॉड्यूल (गणित)]] के पद तीन जाली में निहित होती है। निपटने के लिए सबसे सरल स्थिति वे हैं जिनमें वर्णक्रमीय अनुक्रम अंततः पतन हो जाता है, जिसका अर्थ है कि अनुक्रम में आगे जाने से कोई नवीन सूचना नहीं मिलती है। यहां तक कि जब ऐसा नहीं होता है, तब भी विभिन्न क्रमभंग से वर्णक्रमीय अनुक्रम से उपयोगी सूचना प्राप्त करना प्रायः संभव होता है। | दुर्भाग्य से, बड़ी मात्रा में सूचना वर्णक्रमीय अनुक्रमों में ले जाने के कारण, उन्हें समझना जटिल है। यह सूचना सामान्यतः [[एबेलियन समूह|एबेलियन समूहों]] या [[मॉड्यूल (गणित)|मॉड्यूल (गणित]]) के पद तीन जाली में निहित होती है। निपटने के लिए सबसे सरल स्थिति वे हैं जिनमें वर्णक्रमीय अनुक्रम अंततः पतन हो जाता है, जिसका अर्थ है कि अनुक्रम में आगे जाने से कोई नवीन सूचना नहीं मिलती है। यहां तक कि जब ऐसा नहीं होता है, तब भी विभिन्न क्रमभंग से वर्णक्रमीय अनुक्रम से उपयोगी सूचना प्राप्त करना प्रायः संभव होता है। | ||
== औपचारिक परिभाषा == | == औपचारिक परिभाषा == | ||
=== सह समरूपी वर्णक्रमीय अनुक्रम === | === सह समरूपी वर्णक्रमीय अनुक्रम === | ||
एक [[एबेलियन श्रेणी]] को ठीक करें, जैसे कि एक [[अंगूठी (गणित)|वलय (गणित | एक [[एबेलियन श्रेणी]] को ठीक करें, जैसे कि एक [[अंगूठी (गणित)|वलय (गणित]]) पर मॉड्यूल (गणित) की श्रेणी, और गैर-ऋणात्मक पूर्णांक <math>r_0</math>। सह समरूपी वर्णक्रमीय अनुक्रम वस्तु <math> E_r </math> और समरूपता <math> d_r : E_r \to E_r </math> का अनुक्रम <math> \{E_r, d_r\}_{r\geq r_0} </math> है, जैसे कि प्रत्येक <math> r\geq r_0 </math> के लिए, | ||
# <math> d_r \circ d_r = 0 </math>, | # <math> d_r \circ d_r = 0 </math>, | ||
# <math> E_{r+1} \cong H_{*}(E_r, d_r) </math>, <math>d_r</math> के संबंध में <math>E_r</math> की [[समरूपता (गणित)]]। | # <math> E_{r+1} \cong H_{*}(E_r, d_r) </math>, <math>d_r</math> के संबंध में <math>E_r</math> की [[समरूपता (गणित)|समरूपता (गणित]])। | ||
सामान्यतः समरूपताओं को दबा दिया जाता है और हम इसके अतिरिक्त <math> E_{r+1} = H_{*}(E_r, d_r) </math> लिखते हैं। एक वस्तु <math> E_r </math>को पत्रक (पृष्ठ के पत्रक के रूप में), या कभी-कभी एक पृष्ठ या पद कहा जाता है; एक समरूपता <math> d_r </math> को सीमा प्रतिचित्र या अवकलन कहा जाता है। कभी-कभी <math>E_{r+1}</math> को <math>E_r</math> की व्युत्पन्न वस्तु कहा जाता है।{{citation needed|date=June 2015}} | सामान्यतः समरूपताओं को दबा दिया जाता है और हम इसके अतिरिक्त <math> E_{r+1} = H_{*}(E_r, d_r) </math> लिखते हैं। एक वस्तु <math> E_r </math>को पत्रक (पृष्ठ के पत्रक के रूप में), या कभी-कभी एक पृष्ठ या पद कहा जाता है; एक समरूपता <math> d_r </math> को सीमा प्रतिचित्र या अवकलन कहा जाता है। कभी-कभी <math>E_{r+1}</math> को <math>E_r</math> की व्युत्पन्न वस्तु कहा जाता है।{{citation needed|date=June 2015}} | ||
=== द्वि वर्गीकृत वर्णक्रमीय अनुक्रम === | === द्वि वर्गीकृत वर्णक्रमीय अनुक्रम === | ||
वस्तुतः वर्णक्रमीय अनुक्रम अधिकतर एक वलय (गणित) R (या द्वि वर्गीकृत शेफ (गणित) मॉड्यूल के वलय के एक शेफ पर) पर द्वि वर्गीकृत मॉड्यूल (गणित) की श्रेणी में होते हैं, अर्थात प्रत्येक पत्रक एक द्वि वर्गीकृत R-मॉड्यूल <math display="inline"> E_r = \bigoplus_{p,q \in \mathbb{Z}^2} E_r^{p,q} </math> है। तो इस स्थिति में | वस्तुतः वर्णक्रमीय अनुक्रम अधिकतर एक वलय (गणित) R (या द्वि वर्गीकृत शेफ (गणित) मॉड्यूल के वलय के एक शेफ पर) पर द्वि वर्गीकृत मॉड्यूल (गणित) की श्रेणी में होते हैं, अर्थात प्रत्येक पत्रक एक द्वि वर्गीकृत R-मॉड्यूल <math display="inline"> E_r = \bigoplus_{p,q \in \mathbb{Z}^2} E_r^{p,q} </math> है। तो इस स्थिति में सह-समरूपता वर्णक्रमीय अनुक्रम द्वि वर्गीकृत R-मॉड्यूल <math> \{E_r^{p,q}\}_{p,q} </math> का अनुक्रम <math> \{E_r, d_r\}_{r\geq r_0} </math> है और प्रत्येक मॉड्यूल के लिए द्वि वर्गीकृत <math> (r,1-r) </math> के समरूपता <math> d_r = (d_r^{p,q} : E_r^{p,q} \to E_r^{p+r,q-r+1})_{p,q \in \mathbb{Z}^2} </math> का प्रत्यक्ष योग है, जैसे कि प्रत्येक <math> r\geq r_0 </math> के लिए यह धारण करते है: | ||
# <math> d_r^{p+r,q-r+1} \circ d_r^{p,q} = 0 </math>, | # <math> d_r^{p+r,q-r+1} \circ d_r^{p,q} = 0 </math>, | ||
# <math> E_{r+1} \cong H_{*}(E_r, d_r) </math>। | # <math> E_{r+1} \cong H_{*}(E_r, d_r) </math>। | ||
यहाँ प्रयुक्त अंकन को पूरक घात कहा जाता है। कुछ लेखक इसके अतिरिक्त <math> E_r^{d,q} </math> लिखते हैं , जहाँ <math> d = p + q </math> कुल घात है। वर्णक्रमीय अनुक्रम के आधार पर, पहली पत्रक पर सीमा प्रतिचित्र में एक घात हो सकती है जो R = 0, R = 1, या R = 2 से मेल खाती है। उदाहरण के लिए, निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम के लिए, नीचे वर्णित, R<sub>0</sub> = 0, परन्तु [[ग्रोथेंडिक स्पेक्ट्रल अनुक्रम|ग्रोथेंडिक वर्णक्रमीय अनुक्रम]] के लिए, R<sub>0</sub> = 2। सामान्यतः R<sub>0</sub> शून्य, एक या दो है। ऊपर वर्णित अश्रेणीकृत स्थिति में, r<sub>0</sub> अप्रासंगिक है। | यहाँ प्रयुक्त अंकन को पूरक घात कहा जाता है। कुछ लेखक इसके अतिरिक्त <math> E_r^{d,q} </math> लिखते हैं, जहाँ <math> d = p + q </math> कुल घात है। वर्णक्रमीय अनुक्रम के आधार पर, पहली पत्रक पर सीमा प्रतिचित्र में एक घात हो सकती है जो R = 0, R = 1, या R = 2 से मेल खाती है। उदाहरण के लिए, निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम के लिए, नीचे वर्णित, R<sub>0</sub> = 0, परन्तु [[ग्रोथेंडिक स्पेक्ट्रल अनुक्रम|ग्रोथेंडिक वर्णक्रमीय अनुक्रम]] के लिए, R<sub>0</sub> = 2। सामान्यतः R<sub>0</sub> शून्य, एक या दो है। ऊपर वर्णित अश्रेणीकृत स्थिति में, r<sub>0</sub> अप्रासंगिक है। | ||
=== सजातीय वर्णक्रमीय अनुक्रम === | === सजातीय वर्णक्रमीय अनुक्रम === | ||
अधिकतर जिन वस्तुओं के विषय में हम बात कर रहे हैं वे मिश्रित शृंखला हैं, जो अवरोही (जैसे ऊपर) या आरोही क्रम में होते हैं। बाद की स्थिति में, <math> E_r^{p,q} </math> को <math> E^r_{p,q} </math> और <math> d_r^{p,q} : E_r^{p,q} \to E_r^{p+r,q-r+1} </math> के साथ <math> d^r_{p,q} : E^r_{p,q} \to E^r_{p-r,q+r-1} </math>, ( | अधिकतर जिन वस्तुओं के विषय में हम बात कर रहे हैं वे मिश्रित शृंखला हैं, जो अवरोही (जैसे ऊपर) या आरोही क्रम में होते हैं। बाद की स्थिति में, <math> E_r^{p,q} </math> को <math> E^r_{p,q} </math> और <math> d_r^{p,q} : E_r^{p,q} \to E_r^{p+r,q-r+1} </math> के साथ <math> d^r_{p,q} : E^r_{p,q} \to E^r_{p-r,q+r-1} </math>, (द्विपद <math> (-r,r-1) </math>) के साथ प्रतिस्थापित करके, सह समरूपी स्थिति के अनुरूप तुल्य वर्णक्रमीय अनुक्रम की परिभाषा प्राप्त करते है। | ||
==== एक श्रृंखला सम्मिश्र से वर्णक्रमीय अनुक्रम ==== | ==== एक श्रृंखला सम्मिश्र से वर्णक्रमीय अनुक्रम ==== | ||
अक्रमिक स्थिति में सबसे प्राथमिक उदाहरण एक मिश्रित शृंखला C• है। | अक्रमिक स्थिति में सबसे प्राथमिक उदाहरण एक मिश्रित शृंखला C• है। वस्तु C• मिश्रित शृंखला की एबेलियन श्रेणी में स्वाभाविक रूप से एक अवकलन d के साथ आता है। मान लीजिए R<sub>0</sub> = 0, और मान लीजिए E<sub>0</sub> C<sub>•</sub> है। यह E<sub>1</sub> को सम्मिश्र H (C•) होने के लिए बाध्य करते है: iवें स्थान पर यह C <sub>•</sub> का iवां समरूपता समूह है। इस नवीन सम्मिश्र पर एकमात्र प्राकृतिक अवकलन शून्य प्रतिचित्र है, इसलिए हम d<sub>1</sub> = 0 करते हैं। यह <math>E_2</math> को <math>E_1</math>के बराबर बनाता है, और फिर से हमारा एकमात्र प्राकृतिक अवकलन शून्य प्रतिचित्र है। हमारी शेष सभी पत्रकों पर शून्य अवकलन डालने से वर्णक्रमीय क्रम मिलता है जिसकी पद हैं: | ||
* E<sub>0</sub> = C• | * E<sub>0</sub> = C• | ||
*सभी R ≥ 1 के लिए E<sub>r</sub>= H (C•)। | *सभी R ≥ 1 के लिए E<sub>r</sub>= H (C•)। | ||
इस वर्णक्रमीय अनुक्रम की | इस वर्णक्रमीय अनुक्रम की पद पहली पत्रक पर स्थिर होती हैं क्योंकि इसका एकमात्र असतहीय अवकल शून्यवाँ पत्रक पर था। फलस्वरूप, हम बाद के चरणों में और अधिक सूचना प्राप्त नहीं कर सकते हैं। सामान्यतः, बाद की पत्रक से उपयोगी सूचना प्राप्त करने के लिए, हमें <math>E_r</math> पर अतिरिक्त संरचना की आवश्यकता होती है। | ||
== प्रत्यक्षण == | == प्रत्यक्षण == | ||
[[Image:SpectralSequence.png|frame|E<sub>2</sub> सह समरूपी वर्णक्रमीय अनुक्रम की पत्रक]]एक द्वि वर्गीकृत वर्णक्रमीय अनुक्रम में ट्रैक रखने के लिए डेटा की विलक्षण मात्रा होती है, परन्तु | [[Image:SpectralSequence.png|frame|E<sub>2</sub> सह समरूपी वर्णक्रमीय अनुक्रम की पत्रक]]एक द्वि वर्गीकृत वर्णक्रमीय अनुक्रम में ट्रैक रखने के लिए डेटा की विलक्षण मात्रा होती है, परन्तु सामान्य प्रत्यक्षण तकनीक है जो वर्णक्रमीय अनुक्रम की संरचना को स्पष्ट बनाती है। हमारे निकट तीन सूचकांक हैं, R, पी और q। एक वस्तु <math>E_r</math>को पुस्तक के <math>r^{th}</math> विविध पृष्ठ के रूप में देखा जा सकता है। इन पत्रकों पर, हम p को क्षैतिज दिशा और q को उर्ध्वाधर दिशा मानेंगे। प्रत्येक जाली बिंदु पर हमारे निकट वस्तु <math>E_r^{p,q}</math> है। अब अगले पृष्ठ की ओर मुड़ने का अर्थ है समरूपता लेना, अर्थात <math>r^{th}</math> पृष्ठ <math>(r+1)^{th}</math> पृष्ठ का एक उपभाग है। कुल घात n = p + q प्रत्येक पत्रक के पार तिरछे, उत्तर-पश्चिम से दक्षिण-पूर्व तक चलता है। समरूपी स्थिति में, अवकलों का द्विपद (−r, r − 1) होता है, इसलिए वे n से घटाते हैं। सह समरूपी स्थिति में, n एक से बढ़ जाता है। r के संबंध में अवकल प्रत्येक मोड़ के साथ अपनी दिशा बदलते हैं। | ||
[[File:Spectral Sequence Visualization.jpg|thumb|center|upright=3.0|सह समरूपी वर्णक्रमीय अनुक्रम के चार पृष्ठ]]लाल तीर पहले चतुर्थांश अनुक्रम की स्थिति को प्रदर्शित | [[File:Spectral Sequence Visualization.jpg|thumb|center|upright=3.0|सह समरूपी वर्णक्रमीय अनुक्रम के चार पृष्ठ]]लाल तीर पहले चतुर्थांश अनुक्रम की स्थिति को प्रदर्शित करते है (उदाहरण वर्णक्रमीय अनुक्रम देखें), जहां मात्र पहले चतुर्थांश की वस्तुएं गैर-शून्य हैं। पृष्ठों को पलटते समय, सभी अवकलनों का प्रांत या उपप्रांत शून्य हो जाता है। | ||
== गुण == | == गुण == | ||
| Line 47: | Line 47: | ||
=== गुणक संरचना === | === गुणक संरचना === | ||
एक [[कप उत्पाद]] सह समरूपता समूह को एक वलय (गणित) देता है, इसे | एक [[कप उत्पाद]] सह समरूपता समूह को एक वलय (गणित) देता है, इसे [[कोहोलॉजी रिंग|सह समरूपता वलय]] में बदल देते है। इस प्रकार, वलय संरचना के साथ-साथ वर्णक्रमीय अनुक्रम पर विचार करना स्वाभाविक है। <math>E^{p, q}_r</math> को सह समरूपी प्रकार का एक वर्णक्रमीय अनुक्रम होने दें। हम कहते हैं कि इसकी गुणात्मक संरचना है यदि (i) <math>E_r</math> (द्वि वर्गीकृत) [[अंतर वर्गीकृत बीजगणित|अवकल वर्गीकृत बीजगणित]] और (ii) <math>E_{r+1}</math> पर गुणा सह समरूपता केमाध्यम से <math>E_r</math> पर प्रेरित किया जाता है। | ||
एक विशिष्ट उदाहरण एक कंपन <math>F \to E \to B</math> के लिए उपयोग [[सेरे स्पेक्ट्रल अनुक्रम|सेरे वर्णक्रमीय अनुक्रम]] है , जब गुणांक समूह एक वलय R है। इसमें फाइबर <math>E_{2}</math>-पृष्ठ के कप उत्पादों और आधार पर गुणक संरचना होती | एक विशिष्ट उदाहरण एक कंपन <math>F \to E \to B</math> के लिए उपयोग [[सेरे स्पेक्ट्रल अनुक्रम|सेरे वर्णक्रमीय अनुक्रम]] है, जब गुणांक समूह एक वलय R है। इसमें फाइबर <math>E_{2}</math>-पृष्ठ के कप उत्पादों और आधार पर गुणक संरचना होती है।{{sfn|McCleary|2001|p={{pn|date=August 2021}}}} यद्यपि, सामान्यतःसीमित पद <math>E_{\infty}</math> H (E; R) के लिए वर्गीकृत बीजगणित के रूप मेंसमरूपी नहीं है।{{sfn|Hatcher|loc=Example 1.17}} गुणात्मक संरचना अनुक्रम पर अवकलन की गणना के लिए बहुत उपयोगी हो सकती है।{{sfn|Hatcher|loc=Example 1.18}} | ||
== वर्णक्रमीय अनुक्रमों का निर्माण == | == वर्णक्रमीय अनुक्रमों का निर्माण == | ||
| Line 56: | Line 56: | ||
=== एक यथार्थ युग्म का वर्णक्रमीय अनुक्रम === | === एक यथार्थ युग्म का वर्णक्रमीय अनुक्रम === | ||
{{main|यथार्थ युगल}} | {{main|यथार्थ युगल}} | ||
[[Image:Exact couple.png|right]]वर्णक्रमीय अनुक्रमों के निर्माण के लिए एक और तकनीक [[विलियम शूमाकर मैसी]] की यथार्थ युग्मों की विधि है। बीजगणितीय सांस्थिति में यथार्थ युग्म विशेष रूप से सामान्य हैं। इसके | [[Image:Exact couple.png|right]]वर्णक्रमीय अनुक्रमों के निर्माण के लिए एक और तकनीक [[विलियम शूमाकर मैसी]] की यथार्थ युग्मों की विधि है। बीजगणितीय सांस्थिति में यथार्थ युग्म विशेष रूप से सामान्य हैं। इसके अतिरिक्त वे अमूर्त बीजगणित में अलोकप्रिय हैं, जहां अधिकांश वर्णक्रमीय अनुक्रम निस्यंदित किए गए सम्मिश्रों से आते हैं। | ||
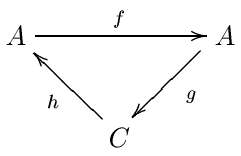
यथार्थ युग्मों को परिभाषित करने के लिए, हम फिर से एक एबेलियन श्रेणी से | यथार्थ युग्मों को परिभाषित करने के लिए, हम फिर से एक एबेलियन श्रेणी से प्रारंभ करते हैं। पहले के जैसे, व्यवहार में यह सामान्यतः वलय के ऊपर दोगुने क्रमिक वाले मॉड्यूल की श्रेणी है। एक यथार्थ युग्म वस्तुओं की युग्म है (''A'', ''C''), साथ में इन वस्तुओं के बीच तीन समरूपताएं हैं: ''f'' : ''A'' → ''A'', ''g'' : ''A'' → ''C'' और ''h'' : ''C'' → ''A'' कुछ यथार्थ प्रतिबन्धों के अधीन: | ||
*[[छवि (गणित)|प्रतिरूप (गणित | *[[छवि (गणित)|प्रतिरूप (गणित]]) ''f'' = [[कर्नेल (बीजगणित)|कर्नेल (बीजगणित]]) ''g'' | ||
*प्रतिरूप ''g'' = कर्नेल ''H'' | *प्रतिरूप ''g'' = कर्नेल ''H'' | ||
*प्रतिरूप ''H'' = कर्नेल ''f'' | *प्रतिरूप ''H'' = कर्नेल ''f'' | ||
हम इस डेटा को (''A'', ''C'', ''f'', ''g'', ''h'') द्वारा संक्षिप्त करेंगे। यथार्थ युग्म को सामान्यतः त्रिकोण के रूप में दर्शाया जाता है। हम देखेंगे | हम इस डेटा को (''A'', ''C'', ''f'', ''g'', ''h'') द्वारा संक्षिप्त करेंगे। यथार्थ युग्म को सामान्यतः त्रिकोण के रूप में दर्शाया जाता है। हम देखेंगे कि C वर्णक्रमीय अनुक्रम के ''E'' <sub>0</sub> वपद से मेल खाता है और A कुछ सहायक डेटा है। | ||
वर्णक्रमीय अनुक्रम की अगली पत्रक पर जाने के लिए, हम 'व्युत्पन्न युग्म' बनाएंगे। हम लोग तैयार हैं: | वर्णक्रमीय अनुक्रम की अगली पत्रक पर जाने के लिए, हम 'व्युत्पन्न युग्म' बनाएंगे। हम लोग तैयार हैं: | ||
*d = g <small>o</small> H | *d = g <small>o</small> H | ||
*A<nowiki>'</nowiki> = f(A) | *A<nowiki>'</nowiki> = f (A) | ||
*C<nowiki>'</nowiki> = Ker d / Im d | *C<nowiki>'</nowiki> = Ker d / Im d | ||
*f<nowiki>'</nowiki> = f|<sub>''A<nowiki>'</nowiki>''</sub>, f से A<nowiki>'</nowiki> का प्रतिबंध | *f<nowiki>'</nowiki> = f|<sub>''A<nowiki>'</nowiki>''</sub>, f से A<nowiki>'</nowiki> का प्रतिबंध | ||
*h<nowiki>'</nowiki> : C<nowiki>'</nowiki> → A<nowiki>'</nowiki> h से प्रेरित है। यह देखना सरल है कि h ऐसे प्रतिचित्र को प्रेरित | *h<nowiki>'</nowiki> : C<nowiki>'</nowiki> → A<nowiki>'</nowiki> h से प्रेरित है। यह देखना सरल है कि h ऐसे प्रतिचित्र को प्रेरित करते है। | ||
*g<nowiki>'</nowiki> : A<nowiki>'</nowiki> → C<nowiki>'</nowiki> को तत्वों पर इस प्रकार परिभाषित किया गया है: A<nowiki>'</nowiki> में प्रत्येक के लिए , A में कुछ b के लिए a को f(b) के रूप में लिखें। g<nowiki>'</nowiki>(a) को C<nowiki>'</nowiki> में g(b) की प्रतिरूप के रूप में परिभाषित किया गया है। सामान्यतः , एबेलियन श्रेणियों के लिए एम्बेडिंग प्रमेयों में से एक का उपयोग करके g<nowiki>'</nowiki> का निर्माण किया जा सकता है। | *g<nowiki>'</nowiki> : A<nowiki>'</nowiki> → C<nowiki>'</nowiki> को तत्वों पर इस प्रकार परिभाषित किया गया है: A<nowiki>'</nowiki> में प्रत्येक के लिए, A में कुछ b के लिए a को f (b) के रूप में लिखें। g<nowiki>'</nowiki> (a) को C<nowiki>'</nowiki> में g (b) की प्रतिरूप के रूप में परिभाषित किया गया है। सामान्यतः, एबेलियन श्रेणियों के लिए एम्बेडिंग प्रमेयों में से एक का उपयोग करके g<nowiki>'</nowiki> का निर्माण किया जा सकता है। | ||
यहां से यह जांचना सरल है कि (A<nowiki>'</nowiki>, C<nowiki>'</nowiki>, f<nowiki>'</nowiki>, g<nowiki>'</nowiki>, h <nowiki>'</nowiki>) | यहां से यह जांचना सरल है कि (A<nowiki>'</nowiki>, C<nowiki>'</nowiki>, f<nowiki>'</nowiki>, g<nowiki>'</nowiki>, h <nowiki>'</nowiki>) यथार्थ युग्म है। C' वर्णक्रमीय अनुक्रम के E<sub>1</sub> पद से मेल खाता है। हम यथार्थ युग्म (A <sup>(n</sup>), सी <sup>(n</sup>), f <sup>(n</sup>), g <sup>(n</sup>), H <sup>(n)</sup>) प्राप्त करने के लिए इस प्रक्रिया को दोहरा सकते हैं। | ||
वर्णक्रमीय अनुक्रम बनाने के लिए, E<sub>n</sub> को C<sup>(n | वर्णक्रमीय अनुक्रम बनाने के लिए, E<sub>n</sub> को C <sup>(n</sup>) और D<sub>n</sub> को G <sup>(n) o h (n) होने दें। | ||
==== इस पद्धति से निर्मित वर्णक्रमीय अनुक्रम ==== | ==== इस पद्धति से निर्मित वर्णक्रमीय अनुक्रम ==== | ||
| Line 88: | Line 88: | ||
=== निस्यंदित किए गए सम्मिश्र का वर्णक्रमीय अनुक्रम === | === निस्यंदित किए गए सम्मिश्र का वर्णक्रमीय अनुक्रम === | ||
एक बहुत ही सामान्य प्रकार का वर्णक्रमीय अनुक्रम निस्यंदित (अमूर्त बीजगणित) उपशृंखला मिश्रित से आता है, क्योंकि यह स्वाभाविक रूप से एक बड़ी श्रेणी वाली वस्तु को प्रेरित | एक बहुत ही सामान्य प्रकार का वर्णक्रमीय अनुक्रम निस्यंदित (अमूर्त बीजगणित) उपशृंखला मिश्रित से आता है, क्योंकि यह स्वाभाविक रूप से एक बड़ी श्रेणी वाली वस्तु को प्रेरित करते है। अवरोही निस्पंदन <math display="inline"> ... \supset\, F^{-2}C^{\bullet} \,\supset\, F^{-1}C^{\bullet} \supset F^{0}C^{\bullet} \,\supset\, F^{1}C^{\bullet} \,\supset\, F^{2}C^{\bullet} \,\supset\, F^{3}C^{\bullet} \,\supset... \, </math> के साथ एक उपशृंखला मिश्रित <math> (C^{\bullet}, d) </math> पर विचार करें। हमें आवश्यकता है कि सीमा प्रतिचित्र निस्पंदन के अनुकूल हो, अर्थात <math display="inline"> d(F^pC^n) \subset F^pC^{n+1}</math>, और यह कि निस्पंदन संपूर्ण है, अर्थात सभी <math display="inline">F^pC^{\bullet}</math> के समुच्चय का मिलन संपूर्ण श्रृंखला सम्मिश्र <math display="inline">C^{\bullet}</math> है। फिर <math display="inline"> E_0^{p,q} = F^{p}C^{p+q}/F^{p+1}C^{p+q} </math> और <math display="inline"> E_1^{p,q} = H^{p+q}(F^{p}C^{\bullet}/F^{p+1}C^{\bullet}) </math> के साथ एक वर्णक्रमीय अनुक्रम स्थित है।।<ref>{{citation|surname1=[[Serge Lang]]|title=Algebra|edition=Überarbeitete 3.|series=Graduate Texts in Mathematics 211|publisher=[[Springer Science+Business Media|Springer-Verlag]]|publication-place=New York|isbn=038795385X|date=2002|language=German | ||
}}</ref> बाद में, हम यह भी मान लेंगे कि निस्पंदन हॉसडॉर्फ या अलग है, अर्थात सभी <math display="inline">F^pC^{\bullet}</math> के सम्मुचय का प्रतिच्छेदन शून्य है। | }}</ref> बाद में, हम यह भी मान लेंगे कि निस्पंदन हॉसडॉर्फ या अलग है, अर्थात सभी <math display="inline">F^pC^{\bullet}</math> के सम्मुचय का प्रतिच्छेदन शून्य है। | ||
| Line 100: | Line 100: | ||
:<math>E_0^{p,q} = \frac{Z_0^{p,q}}{B_0^{p,q} + Z_{-1}^{p+1,q-1}} = \frac{F^p C^{p+q}}{F^{p+1} C^{p+q}}</math> | :<math>E_0^{p,q} = \frac{Z_0^{p,q}}{B_0^{p,q} + Z_{-1}^{p+1,q-1}} = \frac{F^p C^{p+q}}{F^{p+1} C^{p+q}}</math> | ||
:<math>E_0 = \bigoplus_{p,q\in\mathbf{Z}} E_0^{p,q}</math> | :<math>E_0 = \bigoplus_{p,q\in\mathbf{Z}} E_0^{p,q}</math> | ||
चूँकि हमने माना कि सीमा प्रतिचित्र निस्पंदन के साथ संगत था, <math> E_0 </math> एक दोगुनी वर्गीकृत वस्तु है और <math> E_0 </math> पर | चूँकि हमने माना कि सीमा प्रतिचित्र निस्पंदन के साथ संगत था, <math> E_0 </math> एक दोगुनी वर्गीकृत वस्तु है और <math> E_0 </math> पर प्राकृतिक दोगुनी वर्गीकृत सीमा प्रतिचित्र <math> d_0 </math> है। <math> E_1 </math>प्राप्त करने के लिए <math> E_0 </math> की समरूपता लेते हैं। | ||
:<math>\bar{Z}_1^{p,q} = \ker d_0^{p,q} : E_0^{p,q} \rightarrow E_0^{p,q+1} = \ker d_0^{p,q} : F^p C^{p+q}/F^{p+1} C^{p+q} \rightarrow F^p C^{p+q+1}/F^{p+1} C^{p+q+1}</math> | :<math>\bar{Z}_1^{p,q} = \ker d_0^{p,q} : E_0^{p,q} \rightarrow E_0^{p,q+1} = \ker d_0^{p,q} : F^p C^{p+q}/F^{p+1} C^{p+q} \rightarrow F^p C^{p+q+1}/F^{p+1} C^{p+q+1}</math> | ||
| Line 136: | Line 136: | ||
=== एक दोहरे सम्मिश्र का वर्णक्रमीय अनुक्रम === | === एक दोहरे सम्मिश्र का वर्णक्रमीय अनुक्रम === | ||
अन्य सामान्य वर्णक्रमीय अनुक्रम एक दोहरे सम्मिश्र का वर्णक्रमीय क्रम है। एक द्वि सम्मिश्र ''सभी पूर्णांकों i और j के लिए दो अवकलन,'' वस्तुओं का एक संग्रह है ''C<sub>i,j</sub> के साथ, d <sup>I</sup> और d <sup>II के साथ वस्तुओं Cij का एक संग्रह है। d I को i घटता माना जाता है, और d II को j घटता हुआ माना जाता है। इसके अतिरिक्त, हम मानते हैं कि अवकलन विरोधी आवागमन है, ताकि d <sup>i</sup> d <sup>II</sup> + d <sup>II</sup> d <sup>I</sup> = 0। हमारा लक्ष्य पुनरावृत्त समरूपता <math>H^I_i(H^{II}_j(C_{\bullet,\bullet}))</math> और <math>H^{II}_j(H^I_i(C_{\bullet,\bullet}))</math> की तुलना करना है। हम अपने द्वि सम्मिश्र को दो अलग-अलग विधियों से निस्यंदित करके ऐसा करेंगे। यहां हमारे निस्यंदित हैं:'' | |||
:<math>(C_{i,j}^I)_p = \begin{cases} | :<math>(C_{i,j}^I)_p = \begin{cases} | ||
| Line 144: | Line 144: | ||
0 & \text{if } j < p \\ | 0 & \text{if } j < p \\ | ||
C_{i,j} & \text{if } j \ge p \end{cases}</math> | C_{i,j} & \text{if } j \ge p \end{cases}</math> | ||
वर्णक्रमीय अनुक्रम प्राप्त करने के लिए, हम पिछले उदाहरण को कम कर देंगे। हम कुल सम्मिश्र T(C<sub>•,•</sub>) को उस सम्मिश्र के रूप में परिभाषित करते हैं जिसका n'वाँ पद<math>\bigoplus_{i+j=n} C_{i,j}</math> और जिसका अवकलन d''<sup>I''+ d''<sup>II'' है। <sup>यह एक सम्मिश्र है क्योंकि d <sup>I</sup> और d <sup>II</sup> विरोधी आवागमन अवकल हैं। C<sub>i,j पर दो निस्यंदित</sub> कुल सम्मिश्र पर दो <sub>निस्यंदक</sub> देते हैं: | वर्णक्रमीय अनुक्रम प्राप्त करने के लिए, हम पिछले उदाहरण को कम कर देंगे। हम कुल सम्मिश्र T (C<sub>•,•</sub>) को उस सम्मिश्र के रूप में परिभाषित करते हैं जिसका n'वाँ पद<math>\bigoplus_{i+j=n} C_{i,j}</math> और जिसका अवकलन d''<sup>I''+ d''<sup>II'' है। <sup>यह एक सम्मिश्र है क्योंकि d <sup>I</sup> और d <sup>II</sup> विरोधी आवागमन अवकल हैं। C<sub>i,j पर दो निस्यंदित</sub> कुल सम्मिश्र पर दो <sub>निस्यंदक</sub> देते हैं: | ||
:<math>T_n(C_{\bullet,\bullet})^I_p = \bigoplus_{i+j=n \atop i > p-1} C_{i,j}</math> | :<math>T_n(C_{\bullet,\bullet})^I_p = \bigoplus_{i+j=n \atop i > p-1} C_{i,j}</math> | ||
:<math>T_n(C_{\bullet,\bullet})^{II}_p = \bigoplus_{i+j=n \atop j > p-1} C_{i,j}</math> | :<math>T_n(C_{\bullet,\bullet})^{II}_p = \bigoplus_{i+j=n \atop j > p-1} C_{i,j}</math> | ||
यह दिखाने के लिए कि ये वर्णक्रमीय अनुक्रम पुनरावृत्त समरूपता के विषय में सूचना देते हैं, हम T(C•,•) पर I निस्पंदन के E<sup>0, E<sup>1</sup>, औरE<sup>2</sup> के प्रतिबन्ध पर काम करेंगे। E<sup>0</sup> पद स्पष्ट है: | यह दिखाने के लिए कि ये वर्णक्रमीय अनुक्रम पुनरावृत्त समरूपता के विषय में सूचना देते हैं, हम T (C•,•) पर I निस्पंदन के E<sup>0, E<sup>1</sup>, औरE<sup>2</sup> के प्रतिबन्ध पर काम करेंगे। E<sup>0</sup> पद स्पष्ट है: | ||
:<math>{}^IE^0_{p,q} = | :<math>{}^IE^0_{p,q} = | ||
| Line 183: | Line 183: | ||
=== चक्रों और सीमाओं के निस्पंदन के रूप में व्याख्या === | === चक्रों और सीमाओं के निस्पंदन के रूप में व्याख्या === | ||
माना कि R = 1 से प्रारंभ होकर E<sub>''r''</sub> | माना कि R = 1 से प्रारंभ होकर E<sub>''r''</sub> वर्णक्रमीय क्रम है। फिर उपवस्तु | ||
:<math>0 = B_0 \subset B_1 \subset B_{2} \subset \dots \subset B_r \subset \dots \subset Z_r \subset \dots \subset Z_2 \subset Z_1 \subset Z_0 = E_1</math> | :<math>0 = B_0 \subset B_1 \subset B_{2} \subset \dots \subset B_r \subset \dots \subset Z_r \subset \dots \subset Z_2 \subset Z_1 \subset Z_0 = E_1</math> | ||
का अनुक्रम होता है जैसे कि <math>E_r \simeq Z_{r-1}/B_{r-1}</math>; वस्तुतः, पुनरावर्ती रूप से हम <math>Z_0 = E_1, B_0 = 0</math> और <math>Z_r, B_r</math> होने देते हैं ताकि <math>E_r \overset{d_r}\to E_r</math> कर्नेल और<math>Z_r/B_{r-1}, B_r/B_{r-1}</math> की प्रतिरूप हो। | का अनुक्रम होता है जैसे कि <math>E_r \simeq Z_{r-1}/B_{r-1}</math>; वस्तुतः, पुनरावर्ती रूप से हम <math>Z_0 = E_1, B_0 = 0</math> और <math>Z_r, B_r</math> होने देते हैं ताकि <math>E_r \overset{d_r}\to E_r</math> कर्नेल और<math>Z_r/B_{r-1}, B_r/B_{r-1}</math> की प्रतिरूप हो। | ||
| Line 189: | Line 189: | ||
फिर हम <math>Z_{\infty} = \cap_r Z_r, B_{\infty} = \cup_r B_r</math> और | फिर हम <math>Z_{\infty} = \cap_r Z_r, B_{\infty} = \cup_r B_r</math> और | ||
:<math>E_{\infty} = Z_{\infty}/B_{\infty}</math>; | :<math>E_{\infty} = Z_{\infty}/B_{\infty}</math>; | ||
देते हैं: इसे सीमांत पद कहते हैं। (अवश्य, इस प्रकार के <math>E_{\infty}</math> को श्रेणी में मौजूद होने की आवश्यकता नहीं है, परन्तु यह सामान्यतः एक गैर-समस्या है क्योंकि उदाहरण के लिए मॉड्यूल की श्रेणी में ऐसी सीमाएं स्थित हैं या चूंकि व्यवहार में | देते हैं: इसे सीमांत पद कहते हैं। (अवश्य, इस प्रकार के <math>E_{\infty}</math> को श्रेणी में मौजूद होने की आवश्यकता नहीं है, परन्तु यह सामान्यतः एक गैर-समस्या है क्योंकि उदाहरण के लिए मॉड्यूल की श्रेणी में ऐसी सीमाएं स्थित हैं या चूंकि व्यवहार में वर्णक्रमीय अनुक्रम पतित होने की प्रवृत्ति के साथ काम करते है; ऊपर दिए गए क्रम में मात्र सूक्ष्म रूप से कई समावेशन हैं।) | ||
=== अभिसरण की | === अभिसरण की पद === | ||
हम कहते हैं कि वर्णक्रमीय अनुक्रम निर्बल रूप से अभिसरण करता है यदि प्रत्येक <math> n </math> के लिए एक निस्पंदन <math> F^{\bullet} H^{n} </math> के साथ | हम कहते हैं कि वर्णक्रमीय अनुक्रम निर्बल रूप से अभिसरण करता है यदि प्रत्येक <math> n </math> के लिए एक निस्पंदन <math> F^{\bullet} H^{n} </math> के साथ वर्गीकृत वस्तु <math> H^{\bullet} </math> है, और प्रत्येक <math> p </math> के लिए एक समरूपता <math> E_{\infty}^{p,q} \cong F^pH^{p+q}/F^{p+1}H^{p+q} </math> स्थित है। यह <math> H^{\bullet} </math> में परिवर्तित हो जाता है यदि निस्पंदन <math> F^{\bullet} H^{n} </math> हौसडॉर्फ है, अर्थात<math> \cap_{p}F^pC^{\bullet}=0 </math>। हम | ||
:<math>E_r^{p,q} \Rightarrow_p E_\infty^n</math> | :<math>E_r^{p,q} \Rightarrow_p E_\infty^n</math> | ||
लिखते हैं जिसका अर्थ है कि जब भी p + q = n, <math>E_r^{p,q}</math> ,<math>E_\infty^{p,q}</math> में परिवर्तित होता है। हम कहते हैं कि | लिखते हैं जिसका अर्थ है कि जब भी p + q = n, <math>E_r^{p,q}</math>,<math>E_\infty^{p,q}</math> में परिवर्तित होता है। हम कहते हैं कि वर्णक्रमीय अनुक्रम <math>E_r^{p,q}</math> <math>E_\infty^{p,q}</math> से जुड़ा हुआ है यदि प्रत्येक <math> p,q </math> के लिए <math> r(p,q) </math> ऐसा है कि सभी <math>r \geq r(p,q)</math>, <math>E_r^{p,q} = E_{r(p,q)}^{p,q}</math>के लिए। तब <math>E_{r(p,q)}^{p,q} = E_\infty^{p,q}</math> सीमित पद है। वर्णक्रमीय क्रम नियमित है या <math> r_0 </math> पर पतित होता है यदि अवकलन <math>d_r^{p,q}</math> सभी <math> r \geq r_0 </math> के लिए शून्य है। यदि विशेष रूप से <math> r_0 \geq 2 </math> है, जैसे कि <math> r_0^{th} </math> पत्रक एक पंक्ति या एक स्तंभ पर केंद्रित होती है, तो हम कहते हैं कि यह पतित हो जाती है। प्रतीकों में हम लिखते हैं: | ||
:<math>E_r^{p,q} \Rightarrow_p E_\infty^{p,q}</math> | :<math>E_r^{p,q} \Rightarrow_p E_\infty^{p,q}</math> | ||
p निस्पंदन सूचकांक को इंगित करता है। <math>E_2^{p,q}</math> पद आधार के बाईं ओर लिखना बहुत सामान्य है, क्योंकि यह अधिकांश वर्णक्रमीय अनुक्रमों का सबसे उपयोगी पद है। | p निस्पंदन सूचकांक को इंगित करता है। <math>E_2^{p,q}</math> पद आधार के बाईं ओर लिखना बहुत सामान्य है, क्योंकि यह अधिकांश वर्णक्रमीय अनुक्रमों का सबसे उपयोगी पद है। अनिस्यंदित मिश्रित शृंखला का वर्णक्रमीय अनुक्रम पहली पत्रक पर घटता है (पहला उदाहरण देखें) : चूँकि शून्यवाँ पत्रक के बाद कुछ भी नहीं होता है, प्रतिबंधक पत्रक <math> E_{\infty} </math> <math> E_1 </math> के समान है। | ||
वर्णक्रमीय अनुक्रम का पांच-पद का यथार्थ अनुक्रम कुछ निम्न-घात प्रतिबन्धों और E<sub>∞</sub> प्रतिबन्धों से संबंधित है। | वर्णक्रमीय अनुक्रम का पांच-पद का यथार्थ अनुक्रम कुछ निम्न-घात प्रतिबन्धों और E<sub>∞</sub> प्रतिबन्धों से संबंधित है। | ||
| Line 220: | Line 220: | ||
:<math>Z_\infty^{p,q} = \bigcap_{r=0}^\infty Z_r^{p,q} = \bigcap_{r=0}^\infty \ker(F^p C^{p+q} \rightarrow C^{p+q+1}/F^{p+r} C^{p+q+1})</math> | :<math>Z_\infty^{p,q} = \bigcap_{r=0}^\infty Z_r^{p,q} = \bigcap_{r=0}^\infty \ker(F^p C^{p+q} \rightarrow C^{p+q+1}/F^{p+r} C^{p+q+1})</math> | ||
:<math>B_\infty^{p,q} = \bigcup_{r=0}^\infty B_r^{p,q} = \bigcup_{r=0}^\infty (\mbox{im } d^{p,q-r} : F^{p-r} C^{p+q-1} \rightarrow C^{p+q}) \cap F^p C^{p+q}</math> | :<math>B_\infty^{p,q} = \bigcup_{r=0}^\infty B_r^{p,q} = \bigcup_{r=0}^\infty (\mbox{im } d^{p,q-r} : F^{p-r} C^{p+q-1} \rightarrow C^{p+q}) \cap F^p C^{p+q}</math> | ||
यह देखने के लिए कि <math>Z_\infty^{p,q}</math> का क्या तात्पर्य है याद रखें कि हमने मान लिया था कि निस्पंदन अलग हो गया था। इसका तात्पर्य यह है कि जैसे-जैसे r बढ़ता है, कर्नेल सिकुड़ती जाती है, जब तक कि हमारे निकट <math>Z_\infty^{p,q} = \ker(F^p C^{p+q} \rightarrow C^{p+q+1})</math> नहीं रह जाती। <math>B_\infty^{p,q}</math> के लिए , याद रखें कि हमने माना था कि निस्यंदित संपूर्ण था। इसका तात्पर्य यह है कि जैसे-जैसे r बढ़ता है, तब तक प्रतिरूप बढ़ते हैं जब तक हम <math>B_\infty^{p,q} = \text{im }(C^{p+q-1} \rightarrow C^{p+q}) \cap F^p C^{p+q}</math> तक नहीं पहुँच जाते। हम निष्कर्ष निकालते हैं कि | यह देखने के लिए कि <math>Z_\infty^{p,q}</math> का क्या तात्पर्य है याद रखें कि हमने मान लिया था कि निस्पंदन अलग हो गया था। इसका तात्पर्य यह है कि जैसे-जैसे r बढ़ता है, कर्नेल सिकुड़ती जाती है, जब तक कि हमारे निकट <math>Z_\infty^{p,q} = \ker(F^p C^{p+q} \rightarrow C^{p+q+1})</math> नहीं रह जाती। <math>B_\infty^{p,q}</math> के लिए, याद रखें कि हमने माना था कि निस्यंदित संपूर्ण था। इसका तात्पर्य यह है कि जैसे-जैसे r बढ़ता है, तब तक प्रतिरूप बढ़ते हैं जब तक हम <math>B_\infty^{p,q} = \text{im }(C^{p+q-1} \rightarrow C^{p+q}) \cap F^p C^{p+q}</math> तक नहीं पहुँच जाते। हम निष्कर्ष निकालते हैं कि | ||
:<math>E_\infty^{p,q} = \mbox{gr}_p H^{p+q}(C^\bull)</math>, | :<math>E_\infty^{p,q} = \mbox{gr}_p H^{p+q}(C^\bull)</math>, | ||
अर्थात्, वर्णक्रमीय अनुक्रम का निरसन, C के (p+q)वें अनुरूपता का pवां श्रेणीबद्ध भाग है। यदि हमारा वर्णक्रमीय अनुक्रम अभिसरण करता है, तो हम यह निष्कर्ष निकालते हैं कि: | अर्थात्, वर्णक्रमीय अनुक्रम का निरसन, C के (p+q) वें अनुरूपता का pवां श्रेणीबद्ध भाग है। यदि हमारा वर्णक्रमीय अनुक्रम अभिसरण करता है, तो हम यह निष्कर्ष निकालते हैं कि: | ||
:<math>E_r^{p,q} \Rightarrow_p H^{p+q}(C^\bull)</math> | :<math>E_r^{p,q} \Rightarrow_p H^{p+q}(C^\bull)</math> | ||
| Line 231: | Line 231: | ||
==== लंबे यथार्थ क्रम ==== | ==== लंबे यथार्थ क्रम ==== | ||
निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम का उपयोग करके, हम लंबे यथार्थ अनुक्रमों के अस्तित्व को प्राप्त कर सकते हैं। उपशृंखला मिश्रित का संक्षिप्त यथार्थ अनुक्रम | निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम का उपयोग करके, हम लंबे यथार्थ अनुक्रमों के अस्तित्व को प्राप्त कर सकते हैं। उपशृंखला मिश्रित का संक्षिप्त यथार्थ अनुक्रम 0 → A <sup>•</sup> → B<sup>•</sup> → C• → 0 चुनें, और पहले प्रतिचित्र को f<sup>•</sup> :A<sup>•</sup> → B<sup>•</sup> कहते हैं। हमें अनुरूपता वस्तु H<sup>n</sup> (A<sup>•</sup>) → H<sup>n</sup> (B<sup>•</sup>) → H<sup>n</sup> (C•) के प्राकृतिक प्रतिचित्र मिलते हैं, और हम जानते हैं कि यह ठीक बीच में है। हम संयोजक समरूपता को खोजने के लिए निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम का उपयोग करेंगे और यह सिद्ध करने के लिए कि परिणामी अनुक्रम यथार्थ है। प्रारंभ करने के लिए, हम B<sup>•</sup>: | ||
:<math>F^0 B^n = B^n</math> | :<math>F^0 B^n = B^n</math> | ||
:<math>F^1 B^n = A^n</math> | :<math>F^1 B^n = A^n</math> | ||
:<math>F^2 B^n = 0</math> | :<math>F^2 B^n = 0</math> निस्यंदित करते हैं | ||
यह | यह: | ||
:<math>E^{p,q}_0 | :<math>E^{p,q}_0 | ||
| Line 247: | Line 247: | ||
0 & \text{if } p < 0 \text{ or } p > 1 \\ | 0 & \text{if } p < 0 \text{ or } p > 1 \\ | ||
H^q(C^\bull) & \text{if } p = 0 \\ | H^q(C^\bull) & \text{if } p = 0 \\ | ||
H^{q+1}(A^\bull) & \text{if } p = 1 \end{cases}</math> | H^{q+1}(A^\bull) & \text{if } p = 1 \end{cases}</math> देता है | ||
अवकल में | अवकल में द्विपद (1, 0) होता है, इसलिए d<sub>0,q</sub>: H<sup>q</sup> (C•) → H<sup>q+1</sup> (A)। ये स्नेक लेम्मा से संयोजक समरूपता हैं, और प्रतिचित्र A<sup>•</sup> → B<sup>•</sup> → C• के साथ, वे एक क्रम देते हैं: | ||
:<math>\cdots\rightarrow H^q(B^\bull) \rightarrow H^q(C^\bull) \rightarrow H^{q+1}(A^\bull) \rightarrow H^{q+1}(B^\bull) \rightarrow\cdots</math> | :<math>\cdots\rightarrow H^q(B^\bull) \rightarrow H^q(C^\bull) \rightarrow H^{q+1}(A^\bull) \rightarrow H^{q+1}(B^\bull) \rightarrow\cdots</math> | ||
यह दिखाना | यह दिखाना शेष है कि यह क्रम A और C स्थान पर यथार्थ है। ध्यान दें कि यह वर्णक्रमीय क्रम E<sub>2</sub> पद पर पतित होता है क्योंकि अवकलों का द्विपद (2, −1) होता है। फलस्वरूप, E<sub>2</sub> पद E<sub>∞</sub> पद के समान है : | ||
:<math>E^{p,q}_2 | :<math>E^{p,q}_2 | ||
| Line 259: | Line 259: | ||
H^q(B^\bull)/H^q(A^\bull) & \text{if } p = 0 \\ | H^q(B^\bull)/H^q(A^\bull) & \text{if } p = 0 \\ | ||
\text{im } H^{q+1}f^\bull : H^{q+1}(A^\bull) \rightarrow H^{q+1}(B^\bull) &\text{if } p = 1 \end{cases}</math> | \text{im } H^{q+1}f^\bull : H^{q+1}(A^\bull) \rightarrow H^{q+1}(B^\bull) &\text{if } p = 1 \end{cases}</math> | ||
परन्तु हमारे निकट | परन्तु हमारे निकट E<sub>2</sub> पद का प्रत्यक्ष वर्णन E<sub>1</sub> पद की समरूपता के रूप में भी है। ये दो विवरण समरूपी होने चाहिए: | ||
:<math> H^q(B^\bull)/H^q(A^\bull) \cong \ker d^1_{0,q} : H^q(C^\bull) \rightarrow H^{q+1}(A^\bull)</math> | :<math> H^q(B^\bull)/H^q(A^\bull) \cong \ker d^1_{0,q} : H^q(C^\bull) \rightarrow H^{q+1}(A^\bull)</math> | ||
:<math> \text{im } H^{q+1}f^\bull : H^{q+1}(A^\bull) \rightarrow H^{q+1}(B^\bull) \cong H^{q+1}(A^\bull) / (\mbox{im } d^1_{0,q} : H^q(C^\bull) \rightarrow H^{q+1}(A^\bull))</math> | :<math> \text{im } H^{q+1}f^\bull : H^{q+1}(A^\bull) \rightarrow H^{q+1}(B^\bull) \cong H^{q+1}(A^\bull) / (\mbox{im } d^1_{0,q} : H^q(C^\bull) \rightarrow H^{q+1}(A^\bull))</math> | ||
पूर्व C स्थान पर यथार्थता देता है, और बाद वाला | पूर्व C स्थान पर यथार्थता देता है, और बाद वाला A स्थान पर यथार्थता देता है। | ||
=== एक दोहरे सम्मिश्र का वर्णक्रमीय अनुक्रम, जारी === | === एक दोहरे सम्मिश्र का वर्णक्रमीय अनुक्रम, जारी === | ||
निस्यंदित सम्मिश्र के लिए आधार का उपयोग करते हुए, हम पाते हैं कि: | |||
:<math>H^I_p(H^{II}_q(C_{\bull,\bull})) \Rightarrow_p H^{p+q}(T(C_{\bull,\bull}))</math> | :<math>H^I_p(H^{II}_q(C_{\bull,\bull})) \Rightarrow_p H^{p+q}(T(C_{\bull,\bull}))</math> | ||
:<math>H^{II}_q(H^I_p(C_{\bull,\bull})) \Rightarrow_q H^{p+q}(T(C_{\bull,\bull}))</math> | :<math>H^{II}_q(H^I_p(C_{\bull,\bull})) \Rightarrow_q H^{p+q}(T(C_{\bull,\bull}))</math> | ||
सामान्यतः , H | सामान्यतः, H<sup>p+q</sup> (T (C•<sub>,•</sub>)) पर दो श्रेणीकरण अलग हैं। इसके अतिरिक्त, इन दो वर्णक्रमीय अनुक्रमों से उपयोगी सूचना प्राप्त करना अभी भी संभव है। | ||
==== Tor की क्रमविनिमेयता ==== | ==== Tor की क्रमविनिमेयता ==== | ||
R को वलय होने दें, | R को वलय होने दें, M को दाएँ R-मॉड्यूल और n को बाएँ R-मॉड्यूल होने दें। याद रखें कि टेंसर उत्पाद के व्युत्पन्न प्रकार्यक को [[टोर काम करता है|टॉर फलन]] के रूप में दर्शाया गया है। टॉर को इसके पहले तर्क के प्रक्षेपी संकल्प का उपयोग करके परिभाषित किया गया है। यद्यपि, यह पता चला है कि <math>\operatorname{Tor}_i(M,N) =\operatorname{Tor}_i(N,M)</math>। जबकि यह वर्णक्रमीय अनुक्रम के बिना सत्यापित किया जा सकता है, यह वर्णक्रमीय अनुक्रमों के साथ बहुत सरल है। | ||
क्रमशः M और N के प्रक्षेपी विभेदन <math>P_\bull</math> और <math>Q_\bull</math> चुनें। इन्हें ऐसे सम्मिश्रों के रूप में मानें जो क्रमशः d और ई के अवकलन वाले ऋणात्मक घात में लुप्त हो जाते हैं। हम एक द्वि सम्मिश्र का निर्माण कर सकते हैं जिसकी पद <math>C_{i,j} = P_i \otimes Q_j</math> हैं और जिनके अवकलन <math>d \otimes 1</math> और <math>(-1)^i(1 \otimes e)</math> हैं। (-1 का कारक इतना है कि अवकलन विरोधी आवागमन है।) चूंकि प्रक्षेपी मॉड्यूल समतल हैं, प्रक्षेपी मॉड्यूल के साथ टेंसर उत्पाद लेना अनुरूपता लेने के साथ प्रारंभ होता है, इसलिए हम प्राप्त करते हैं: | |||
:<math>H^I_p(H^{II}_q(P_\bull \otimes Q_\bull)) = H^I_p(P_\bull \otimes H^{II}_q(Q_\bull))</math> | :<math>H^I_p(H^{II}_q(P_\bull \otimes Q_\bull)) = H^I_p(P_\bull \otimes H^{II}_q(Q_\bull))</math> | ||
:<math>H^{II}_q(H^I_p(P_\bull \otimes Q_\bull)) = H^{II}_q(H^I_p(P_\bull) \otimes Q_\bull)</math> | :<math>H^{II}_q(H^I_p(P_\bull \otimes Q_\bull)) = H^{II}_q(H^I_p(P_\bull) \otimes Q_\bull)</math> | ||
चूंकि दो सम्मिश्र संकल्प हैं, उनकी अनुरूपता घात शून्य के बाहर | चूंकि दो सम्मिश्र संकल्प हैं, उनकी अनुरूपता घात शून्य के बाहर लुप्त हो जाती है। घात शून्य में, हम | ||
:<math>H^I_p(P_\bull \otimes N) = \operatorname{Tor}_p(M,N)</math> | :<math>H^I_p(P_\bull \otimes N) = \operatorname{Tor}_p(M,N)</math> | ||
:<math>H^{II}_q(M \otimes Q_\bull) = \operatorname{Tor}_q(N,M)</math> | :<math>H^{II}_q(M \otimes Q_\bull) = \operatorname{Tor}_q(N,M)</math> के साथ रह जाते हैं | ||
विशेष रूप से, <math>E^2_{p,q}</math> | विशेष रूप से, <math>E^2_{p,q}</math> पद पंक्ति q = 0 (I वर्णक्रमीय अनुक्रम के लिए) और p = 0 (II वर्णक्रमीय अनुक्रम के लिए) को छोड़कर लुप्त हो जाते हैं। इसका तात्पर्य यह है कि वर्णक्रमीय क्रम दूसरी पत्रक पर पतित हो जाता है, इसलिए E<sup>∞</sup> पद E <sup>2</sup> प्रतिबन्धों के लिए तुल्याकारी हैं: | ||
:<math>\operatorname{Tor}_p(M,N) \cong E^\infty_p = H_p(T(C_{\bull,\bull}))</math> | :<math>\operatorname{Tor}_p(M,N) \cong E^\infty_p = H_p(T(C_{\bull,\bull}))</math> | ||
| Line 291: | Line 291: | ||
अंत में, जब p और q बराबर होते हैं, तो दाएँ हाथ की दो भुजाएँ बराबर होती हैं, और Tor की क्रमविनिमेयता इस प्रकार होती है। | अंत में, जब p और q बराबर होते हैं, तो दाएँ हाथ की दो भुजाएँ बराबर होती हैं, और Tor की क्रमविनिमेयता इस प्रकार होती है। | ||
== | == हल निकालने के उदाहरण == | ||
=== प्रथम-चतुर्थांश पत्रक === | === प्रथम-चतुर्थांश पत्रक === | ||
एक वर्णक्रमीय अनुक्रम पर विचार करें जहाँ <math>E_r^{p,q}</math> | एक वर्णक्रमीय अनुक्रम पर विचार करें जहाँ <math>E_r^{p,q}</math> कुछ <math> p_0 </math> से कम सभी <math> p </math> के लिए और कुछ <math> q_0 </math> से कम सभी <math> q </math> के लिए लुप्त हो जाता है। यदि <math> p_0 </math> और <math> q_0 </math> को शून्य के रूप में चुना जा सकता है, तो इसे प्रथम-चतुर्थांश वर्णक्रमीय अनुक्रम कहा जाता है। क्रम समाप्त हो जाता है क्योंकि <math> E_{r+i}^{p,q} = E_r^{p,q} </math> सभी <math> i\geq 0 </math> के लिए धारण करते है यदि <math> r>p </math> और <math> r>q+1 </math>। इसे देखने के लिए, ध्यान दें कि माने गए स्थितियों के लिए या तो अवकलन का प्रांत या उपप्रांत शून्य है। दृश्य पदों में, पत्रक एक बढ़ती हुई आयत में स्थिर हो जाती हैं (ऊपर चित्र देखें)। यद्यपि, वर्णक्रमीय अनुक्रम को पतित होने की आवश्यकता नहीं है, क्योंकि अवकलन प्रतिचित्र सभी एक बार में शून्य नहीं हो सकते हैं। इसी प्रकार, वर्णक्रमीय क्रम भी अभिसरण करता है यदि <math>E_r^{p,q}</math> कुछ <math> p_0 </math>से अधिक सभी <math> p </math> के लिए लुप्त हो जाता है और कुछ <math> q_0 </math> से अधिक सभी <math> q </math> के लिए लुप्त हो जाता है। | ||
क्रम समाप्त हो जाता है क्योंकि <math> E_{r+i}^{p,q} = E_r^{p,q} </math> सभी | |||
=== 2 गैर-शून्य आसन्न | === 2 गैर-शून्य आसन्न स्तंभ === | ||
मान लीजिए कि <math>E^r_{p, q}</math> एक सजातीय वर्णक्रमीय अनुक्रम है जैसे कि <math>E^2_{p, q} = 0</math> 0, 1 को छोड़कर सभी p के लिए है। दृष्टिगत रूप से, यह <math>E^2</math>-पृष्ठ | |||
:<math>\begin{matrix} | :<math>\begin{matrix} | ||
& \vdots & \vdots & \vdots & \vdots & \\ | & \vdots & \vdots & \vdots & \vdots & \\ | ||
| Line 306: | Line 305: | ||
\cdots & 0 & E^2_{0,-1} & E^2_{1,-1} & 0 & \cdots \\ | \cdots & 0 & E^2_{0,-1} & E^2_{1,-1} & 0 & \cdots \\ | ||
& \vdots & \vdots & \vdots & \vdots & | & \vdots & \vdots & \vdots & \vdots & | ||
\end{matrix}</math> | \end{matrix}</math> के साथ वर्णक्रमीय अनुक्रम है | ||
दूसरे पृष्ठ पर अवकलन की घात (-2, 1) है, इसलिए वे | दूसरे पृष्ठ पर अवकलन की घात (-2, 1) है, इसलिए वे | ||
:<math>d^2_{p,q}:E^2_{p,q} \to E^2_{p-2,q+1}</math> | :<math>d^2_{p,q}:E^2_{p,q} \to E^2_{p-2,q+1}</math> के रूप में हैं | ||
ये प्रतिचित्र सभी शून्य हैं क्योंकि वे | ये प्रतिचित्र सभी शून्य हैं क्योंकि वे | ||
:<math>d^2_{0,q}:E^2_{0,q} \to 0</math>, <math>d^2_{1,q}:E^2_{1,q} \to 0</math> | :<math>d^2_{0,q}:E^2_{0,q} \to 0</math>, <math>d^2_{1,q}:E^2_{1,q} \to 0</math> | ||
इसलिए वर्णक्रमीय अनुक्रम पतित होता है: <math>E^{\infty} = E^2</math>। कहते हैं, यह | हैं इसलिए वर्णक्रमीय अनुक्रम पतित होता है: <math>E^{\infty} = E^2</math>। कहते हैं, यह एक निस्पंदन | ||
:<math>0 = F_{-1} H_n \subset F_0 H_n \subset \dots \subset F_n H_n = H_n</math> | :<math>0 = F_{-1} H_n \subset F_0 H_n \subset \dots \subset F_n H_n = H_n</math> | ||
के साथ <math>H_*</math> में परिवर्तित होता है जैसे कि <math>E^{\infty}_{p, q} = F_p H_{p+q}/F_{p-1} H_{p+q}</math>। तब <math>F_0 H_n = E^2_{0, n}</math>, <math>F_1 H_n / F_0 H_n = E^2_{1, n -1}</math>, <math>F_2 H_n / F_1 H_n = 0</math>, <math>F_3 H_n / F_2 H_n = 0</math>, आदि। इस प्रकार, यथार्थ क्रम है:<ref>{{harvnb|Weibel|1994|loc=Exercise 5.2.1.}}; there are typos in the exact sequence, at least in the 1994 edition.</ref> | |||
:<math>0 \to E^2_{0, n} \to H_n \to E^2_{1, n - 1} \to 0</math>। | :<math>0 \to E^2_{0, n} \to H_n \to E^2_{1, n - 1} \to 0</math>। | ||
अगला, | अगला, मान लीजिए कि <math>E^r_{p, q}</math> वर्णक्रमीय अनुक्रम है जिसके दूसरे पृष्ठ में मात्र दो पंक्तियाँ q = 0, 1 हैं। यह दूसरे पृष्ठ पर पतित होने की आवश्यकता नहीं है, परन्तु यह अभी भी तीसरे पृष्ठ पर पतित होता है क्योंकि अवकलन में घात (-3, 2) होती है। टिप्पणी <math>E^3_{p, 0} = \operatorname{ker} (d: E^2_{p, 0} \to E^2_{p - 2, 1})</math>, क्योंकि भाजक शून्य है। इसी प्रकार, <math>E^3_{p, 1} = \operatorname{coker}(d: E^2_{p+2, 0} \to E^2_{p, 1})</math>। इस प्रकार, | ||
:<math>0 \to E^{\infty}_{p, 0} \to E^2_{p, 0} \overset{d}\to E^2_{p-2, 1} \to E^{\infty}_{p-2, 1} \to 0</math>। | :<math>0 \to E^{\infty}_{p, 0} \to E^2_{p, 0} \overset{d}\to E^2_{p-2, 1} \to E^{\infty}_{p-2, 1} \to 0</math>। | ||
अब, कहते हैं, वर्णक्रमीय अनुक्रम पिछले उदाहरण के जैसे एक निस्पंदन f के साथ H में परिवर्तित हो जाता है। | अब, कहते हैं, वर्णक्रमीय अनुक्रम पिछले उदाहरण के जैसे एक निस्पंदन f के साथ H में परिवर्तित हो जाता है। चूंकि <math>F_{p-2} H_{p} / F_{p-3} H_{p} = E^{\infty}_{p-2, 2} = 0</math>, <math>F_{p-3} H_p / F_{p-4} H_p = 0</math>, आदि, हमारे निकट है: <math>0 \to E^{\infty}_{p - 1, 1} \to H_p \to E^{\infty}_{p, 0} \to 0</math>। सब कुछ एक साथ रखकर, एक मिलता है:<ref>{{harvnb|Weibel|1994|loc=Exercise 5.2.2.}}</ref> | ||
:<math>\cdots \to H_{p+1} \to E^2_{p + 1, 0} \overset{d}\to E^2_{p - 1, 1} \to H_p \to E^2_{p, 0} \overset{d}\to E^2_{p - 2, 1} \to H_{p-1} \to \dots.</math> | :<math>\cdots \to H_{p+1} \to E^2_{p + 1, 0} \overset{d}\to E^2_{p - 1, 1} \to H_p \to E^2_{p, 0} \overset{d}\to E^2_{p - 2, 1} \to H_{p-1} \to \dots.</math> | ||
=== वांग अनुक्रम === | === वांग अनुक्रम === | ||
पिछले खंड में की गई गणना | पिछले खंड में की गई गणना सरल विधि से सामान्यीकरण करती है। एक क्षेत्र पर कंपन पर विचार करें: | ||
:<math>F \overset{i}\to E \overset{p}\to S^n</math> | :<math>F \overset{i}\to E \overset{p}\to S^n</math> | ||
n | जिसमें n कम से कम 2 हो। सेरे वर्णक्रमीय अनुक्रम है: | ||
:<math>E^2_{p, q} = H_p(S^n; H_q(F)) \Rightarrow H_{p+q}(E)</math>; | :<math>E^2_{p, q} = H_p(S^n; H_q(F)) \Rightarrow H_{p+q}(E)</math>; | ||
यही कहना है, <math>E^{\infty}_{p, q} = F_p H_{p+q}(E)/F_{p-1} H_{p+q}(E)</math> कुछ निस्पंदन <math>F_\bullet</math> के साथ। | |||
चूँकि <math>H_p(S^n)</math> मात्र शून्य नहीं है जब p शून्य या n है और उस स्थिति में 'Z' के बराबर है, हम देखते हैं कि <math>E^2_{p, q}</math> में मात्र दो रेखाएँ <math>p = 0,n</math> हैं, इसलिए <math>E^2</math>-पृष्ठ | |||
:<math>\begin{matrix} | :<math>\begin{matrix} | ||
& \vdots & \vdots & \vdots & & \vdots & \vdots & \vdots & \\ | & \vdots & \vdots & \vdots & & \vdots & \vdots & \vdots & \\ | ||
| Line 334: | Line 333: | ||
\cdots & 0 & E^2_{0,1} & 0 & \cdots & 0 & E^2_{n,1} & 0 & \cdots \\ | \cdots & 0 & E^2_{0,1} & 0 & \cdots & 0 & E^2_{n,1} & 0 & \cdots \\ | ||
\cdots & 0 & E^2_{0,0} & 0 & \cdots & 0 & E^2_{n,0} & 0 & \cdots \\ | \cdots & 0 & E^2_{0,0} & 0 & \cdots & 0 & E^2_{n,0} & 0 & \cdots \\ | ||
\end{matrix}</math> | \end{matrix}</math> द्वारा दिया गया है। | ||
इसके अतिरिक्त, | इसके अतिरिक्त [[सार्वभौमिक गुणांक प्रमेय]] द्वारा <math>p = 0,n</math> के लिए | ||
:<math>E^2_{p, q} = H_p(S^n;H_q(F)) = H_q(F)</math> | :<math>E^2_{p, q} = H_p(S^n;H_q(F)) = H_q(F)</math> | ||
के | के बाद से, <math>E^2</math> पृष्ठ | ||
:<math>\begin{matrix} | :<math>\begin{matrix} | ||
& \vdots & \vdots & \vdots & & \vdots & \vdots & \vdots & \\ | & \vdots & \vdots & \vdots & & \vdots & \vdots & \vdots & \\ | ||
| Line 343: | Line 342: | ||
\cdots & 0 & H_1(F) & 0 & \cdots & 0 & H_1(F) & 0 & \cdots \\ | \cdots & 0 & H_1(F) & 0 & \cdots & 0 & H_1(F) & 0 & \cdots \\ | ||
\cdots & 0 & H_0(F) & 0 & \cdots & 0 & H_0(F) & 0 & \cdots \\ | \cdots & 0 & H_0(F) & 0 & \cdots & 0 & H_0(F) & 0 & \cdots \\ | ||
\end{matrix}</math> | \end{matrix}</math> जैसा दिखता है। | ||
चूंकि | चूंकि <math>E^n</math>-पृष्ठ मात्र गैर-शून्य अवकलन हैं, | ||
:<math>d^n_{n,q}:E^n_{n,q} \to E^n_{0,q+n-1}</math> | :<math>d^n_{n,q}:E^n_{n,q} \to E^n_{0,q+n-1}</math> | ||
जो | द्वारा दिया गया है जो कि | ||
:<math>d^n_{n,q}:H_q(F) \to H_{q+n-1}(F)</math> | :<math>d^n_{n,q}:H_q(F) \to H_{q+n-1}(F)</math> | ||
वर्णक्रमीय अनुक्रम | है वर्णक्रमीय अनुक्रम <math>E^{n+1} = E^{\infty}</math>पर अभिसरण करता है। <math>E^{n+1}</math> की गणना करके हम यथार्थ क्रम | ||
:<math>0 \to E^{\infty}_{n, q-n} \to E^n_{n, q-n} \overset{d}\to E^n_{0, q-1} \to E^{\infty}_{0, q-1} \to 0 | :<math>0 \to E^{\infty}_{n, q-n} \to E^n_{n, q-n} \overset{d}\to E^n_{0, q-1} \to E^{\infty}_{0, q-1} \to 0</math> प्राप्त करते हैं। | ||
और अनुरूपता समूहों का उपयोग करके लिखा गया है, यह | और अनुरूपता समूहों का उपयोग करके लिखा गया है, यह | ||
:<math>0 \to E^{\infty}_{n, q-n} \to H_{q-n}(F) \overset{d}\to H_{q-1}(F) \to E^{\infty}_{0, q-1} \to 0 | :<math>0 \to E^{\infty}_{n, q-n} \to H_{q-n}(F) \overset{d}\to H_{q-1}(F) \to E^{\infty}_{0, q-1} \to 0</math> है। | ||
यह स्थापित करने के लिए कि दो <math>E^\infty</math>-पद क्या हैं, <math>H = H(E)</math>, लिखें, और चूंकि <math>F_1 H_q/F_0 H_q = E^{\infty}_{1, q - 1} = 0</math>, आदि, हमारे निकट: <math>E^{\infty}_{n, q-n} = F_n H_q / F_0 H_q</math> और इस प्रकार, के बाद से <math>F_n H_q = H_q</math>, | |||
:<math>0 \to E^{\infty}_{0, q} \to H_q \to E^{\infty}_{n, q - n} \to 0 | :<math>0 \to E^{\infty}_{0, q} \to H_q \to E^{\infty}_{n, q - n} \to 0</math> है। | ||
यह ठीक क्रम | यह ठीक क्रम | ||
:<math>0 \to H_q(F) \to H_q(E) \to H_{q-n}(F)\to 0 | :<math>0 \to H_q(F) \to H_q(E) \to H_{q-n}(F)\to 0</math> है | ||
सभी गणनाओं को एक साथ रखकर, एक प्राप्त होता है:<ref>{{harvnb|Weibel|1994|loc=Application 5.3.5.}}</ref> | सभी गणनाओं को एक साथ रखकर, एक प्राप्त होता है:<ref>{{harvnb|Weibel|1994|loc=Application 5.3.5.}}</ref> | ||
:<math>\dots \to H_q(F) \overset{i_*}\to H_q(E) \to H_{q-n}(F) \overset{d}\to H_{q-1}(F) \overset{i_*}\to H_{q-1}(E) \to H_{q-n -1}(F) \to \dots</math> | :<math>\dots \to H_q(F) \overset{i_*}\to H_q(E) \to H_{q-n}(F) \overset{d}\to H_{q-1}(F) \overset{i_*}\to H_{q-1}(E) \to H_{q-n -1}(F) \to \dots</math> | ||
(ग्य्सिन अनुक्रम इसी प्रकार से प्राप्त किया जाता है।) | (ग्य्सिन अनुक्रम इसी प्रकार से प्राप्त किया जाता है।) | ||
=== कम-घात | === कम-घात पद === | ||
एक स्पष्ट सांकेतिक परिवर्तन के साथ, पिछले उदाहरणों में संगणना के प्रकार को उपयोग वर्णक्रमीय अनुक्रम के लिए भी किया जा सकता है। | एक स्पष्ट सांकेतिक परिवर्तन के साथ, पिछले उदाहरणों में संगणना के प्रकार को उपयोग वर्णक्रमीय अनुक्रम के लिए भी किया जा सकता है। माना <math>E_r^{p, q}</math> घटते निस्पंदन | ||
:<math>0 = F^{n+1} H^n \subset F^n H^n \subset \dots \subset F^0 H^n = H^n</math> | :<math>0 = F^{n+1} H^n \subset F^n H^n \subset \dots \subset F^0 H^n = H^n</math> | ||
ताकि <math>E_{\infty}^{p,q} = F^p H^{p+q}/F^{p+1} H^{p+q}.</math> | के साथ H में परिवर्तित होने वाला प्रथम-चतुर्थांश वर्णक्रमीय अनुक्रम है ताकि <math>E_{\infty}^{p,q} = F^p H^{p+q}/F^{p+1} H^{p+q}.</math> | ||
चूँकि <math>E_2^{p, q}</math> शून्य है यदि p या q ऋणात्मक है, तो हमारे निकट: | |||
:<math>0 \to E^{0, 1}_{\infty} \to E^{0, 1}_2 \overset{d}\to E^{2, 0}_2 \to E^{2, 0}_{\infty} \to 0.</math> | :<math>0 \to E^{0, 1}_{\infty} \to E^{0, 1}_2 \overset{d}\to E^{2, 0}_2 \to E^{2, 0}_{\infty} \to 0.</math> | ||
चूँकि <math>E_{\infty}^{1, 0} = E_2^{1, 0}</math> उसी कारण से और चूँकि <math>F^2 H^1 = 0,</math> | |||
:<math>0 \to E_2^{1, 0} \to H^1 \to E^{0, 1}_{\infty} \to 0</math>। | :<math>0 \to E_2^{1, 0} \to H^1 \to E^{0, 1}_{\infty} \to 0</math>। | ||
<math>F^3 H^2 = 0</math>, <math>E^{2, 0}_{\infty} \subset H^2</math> के बाद से। अनुक्रमों को एक साथ जोड़कर, हम तथाकथित पांच-पद यथार्थ अनुक्रम प्राप्त करते हैं: | |||
:<math>0 \to E^{1, 0}_2 \to H^1 \to E^{0, 1}_2 \overset{d}\to E^{2, 0}_2 \to H^2.</math> | :<math>0 \to E^{1, 0}_2 \to H^1 \to E^{0, 1}_2 \overset{d}\to E^{2, 0}_2 \to H^2.</math> | ||
== किनारे के | == किनारे के प्रतिचित्र और अतिक्रमण == | ||
=== तुल्य वर्णक्रमीय अनुक्रम === | === तुल्य वर्णक्रमीय अनुक्रम === | ||
मान लीजिए कि <math>E^r_{p, q}</math> एक वर्णक्रमीय क्रम है। यदि प्रत्येक q < 0 के लिए <math>E^r_{p, q} = 0</math> है, तो यह होना चाहिए: r ≥ 2 के लिए, भाजक के रूप में | |||
:<math>E^{r+1}_{p, 0} = \operatorname{ker}(d: E^r_{p, 0} \to E^r_{p-r, r-1})</math> | :<math>E^{r+1}_{p, 0} = \operatorname{ker}(d: E^r_{p, 0} \to E^r_{p-r, r-1})</math> | ||
शून्य है। इसलिए, एकरूपता का एक क्रम है: | |||
:<math>E^{r}_{p, 0} \to E^{r-1}_{p, 0} \to \dots \to E^3_{p, 0} \to E^2_{p, 0}</math>। | :<math>E^{r}_{p, 0} \to E^{r-1}_{p, 0} \to \dots \to E^3_{p, 0} \to E^2_{p, 0}</math>। | ||
उन्हें किनारे के | उन्हें किनारे के प्रतिचित्र कहा जाता है। इसी प्रकार, यदि प्रत्येक p <0 के लिए <math>E^r_{p, q} = 0</math> तो समाकारिता का एक क्रम होता है (जिसे किनारे के प्रतिचित्र भी कहा जाता है) : | ||
:<math>E^2_{0, q} \to E^3_{0, q} \to \dots \to E^{r-1}_{0, q} \to E^r_{0, q}</math>। | :<math>E^2_{0, q} \to E^3_{0, q} \to \dots \to E^{r-1}_{0, q} \to E^r_{0, q}</math>। | ||
अतिक्रमण प्रतिचित्र आंशिक रूप से परिभाषित प्रतिचित्र है (अधिक यथार्थ, एक उपवस्तु से एक भागफल तक का प्रतिचित्र) | |||
:<math>\tau: E^2_{p, 0} \to E^2_{0, p - 1}</math> | :<math>\tau: E^2_{p, 0} \to E^2_{0, p - 1}</math> | ||
रचना | को एक रचना <math>E^2_{p, 0} \to E^p_{p, 0} \overset{d}\to E^p_{0, p-1} \to E^2_{0, p - 1}</math> के रूप में दिया गया है, पहला और अंतिम प्रतिचित्र किनारे के प्रतिचित्र के व्युत्क्रम हैं।{{sfn|May|loc=§ 1}} | ||
=== सह समरूपी वर्णक्रमीय अनुक्रम === | === सह समरूपी वर्णक्रमीय अनुक्रम === | ||
वर्णक्रमीय अनुक्रम | सह समरूपी प्रकार के वर्णक्रमीय अनुक्रम <math>E_r^{p, q}</math> के लिए, अनुरूप कथन धारण करते हैं। यदि प्रत्येक q <0 के लिए <math>E_r^{p, q} = 0</math> है, तो समाकारिता | ||
:<math>E_{2}^{p, 0} \to E_{3}^{p, 0} \to \dots \to E_{r-1}^{p, 0} \to E_r^{p, 0}</math> | :<math>E_{2}^{p, 0} \to E_{3}^{p, 0} \to \dots \to E_{r-1}^{p, 0} \to E_r^{p, 0}</math>का एक क्रम है। | ||
और यदि <math>E_r^{p, q} = 0</math> | और यदि प्रत्येक p < 0 के लिए <math>E_r^{p, q} = 0</math>, तो एकरूपता का एक क्रम होता है: | ||
:<math>E_{r}^{0, q} \to E_{r-1}^{0, q} \to \dots \to E_{3}^{0, q} \to E_2^{0, q}</math>। | :<math>E_{r}^{0, q} \to E_{r-1}^{0, q} \to \dots \to E_{3}^{0, q} \to E_2^{0, q}</math>। | ||
अतिक्रमण आवश्यक ठीक रूप से परिभाषित प्रतिचित्र नहीं है: | |||
:<math>\tau: E_2^{0, q-1} \to E_2^{q, 0}</math> | :<math>\tau: E_2^{0, q-1} \to E_2^{q, 0}</math> | ||
द्वारा प्रेरित <math>d: E_q^{0, q-1} \to E_q^{q, 0}</math>। | |||
=== | === अनुप्रयोग === | ||
इन प्रतिचित्रों का निर्धारण | इन प्रतिचित्रों का निर्धारण सेरे वर्णक्रमीय अनुक्रम में कई अवकलनों की गणना के लिए मौलिक है। उदाहरण के लिए अतिक्रमण प्रतिचित्र तुल्य वर्णक्रमीय अनुक्रम के लिए अवकलन{{sfn|Hatcher|pp=540, 564}} | ||
:<math>d_n:E_{n,0}^n \to E_{0,n-1}^n</math> | :<math>d_n:E_{n,0}^n \to E_{0,n-1}^n</math> | ||
को निर्धारित करता है, इसलिए कंपन <math>F \to E \to B</math> के लिए सेरे वर्णक्रमीय अनुक्रम पर प्रतिचित्र | |||
:<math>d_n:H_n(B) \to H_{n-1}(F)</math> | :<math>d_n:H_n(B) \to H_{n-1}(F)</math> देते है। | ||
== | == और अधिक उदाहरण == | ||
कुछ उल्लेखनीय वर्णक्रमीय अनुक्रम हैं: | कुछ उल्लेखनीय वर्णक्रमीय अनुक्रम हैं: | ||
| Line 406: | Line 406: | ||
=== सांस्थिति और ज्यामिति === | === सांस्थिति और ज्यामिति === | ||
* एक [[असाधारण कोहोलॉजी सिद्धांत| | * एक [[असाधारण कोहोलॉजी सिद्धांत|विशेष सह समरूपता सिद्धांत]] का अतियाह-हिर्जेब्रुक वर्णक्रमीय अनुक्रम | ||
* एक समूह के वर्गीकरण स्थान की समरूपता के लिए [[बार वर्णक्रमीय अनुक्रम]]। | * एक समूह के वर्गीकरण स्थान की समरूपता के लिए [[बार वर्णक्रमीय अनुक्रम]]। | ||
* बॉकस्टीन वर्णक्रमीय अनुक्रम, मॉड | * बॉकस्टीन वर्णक्रमीय अनुक्रम, मॉड p गुणांक के साथ अनुरूपता से संबंधित है और अनुरूपता ने मॉड p को कम कर दिया है। | ||
*कार्टन-लेरे वर्णक्रमीय अनुक्रम भागफल स्थान के अनुरूपता में परिवर्तित हो रहा है। | *कार्टन-लेरे वर्णक्रमीय अनुक्रम भागफल स्थान के अनुरूपता में परिवर्तित हो रहा है। | ||
* एक कंपन के [[ ठहराना | | * एक कंपन के [[ ठहराना |बाधा]] के [[एकवचन कोहोलॉजी|विलक्षणता सह समरूपता]] के लिए ईलेनबर्ग-मूर वर्णक्रमीय अनुक्रम | ||
* एक कंपन का गंभीर वर्णक्रमीय क्रम | * एक कंपन का गंभीर वर्णक्रमीय क्रम | ||
=== | === समस्थेयता सिद्धांत === | ||
* [[स्थिर समरूपता सिद्धांत]] में [[ईएचपी वर्णक्रमीय अनुक्रम| | * [[स्थिर समरूपता सिद्धांत]] में [[ईएचपी वर्णक्रमीय अनुक्रम|एडम्स वर्णक्रमीय अनुक्रम]] | ||
*एडम्स-नोविकोव वर्णक्रमीय अनुक्रम, असाधारण सह समरूपता सिद्धांत के लिए एक सामान्यीकरण। | *एडम्स-नोविकोव वर्णक्रमीय अनुक्रम, असाधारण सह समरूपता सिद्धांत के लिए एक सामान्यीकरण। | ||
* बैराट वर्णक्रमीय अनुक्रम एक | * बैराट वर्णक्रमीय अनुक्रम एक सहभाजन के प्रारंभिक स्थान के समस्थेयता में परिवर्तित हो रहा है। | ||
* बाउसफ़ील्ड-कान वर्णक्रमीय अनुक्रम एक | * बाउसफ़ील्ड-कान वर्णक्रमीय अनुक्रम एक प्रकार्यक के समस्थेयता सह सीमा में परिवर्तित हो रहा है। | ||
* एडम्स-नोविकोव वर्णक्रमीय अनुक्रम की प्रारंभिक प्रतिबन्धों की गणना [[होमोटॉपी निश्चित बिंदु वर्णक्रमीय अनुक्रम]] | * एडम्स-नोविकोव वर्णक्रमीय अनुक्रम की प्रारंभिक प्रतिबन्धों की गणना [[होमोटॉपी निश्चित बिंदु वर्णक्रमीय अनुक्रम|समस्थेयता निश्चित बिंदु वर्णक्रमीय अनुक्रम]] | ||
* कोबर वर्णक्रमीय अनुक्रम | * कोबर वर्णक्रमीय अनुक्रम | ||
* | *EHP वर्णक्रमीय अनुक्रम क्षेत्रों के स्थिर समस्थेयता समूहों में परिवर्तित हो रहा है | ||
*फेडरर वर्णक्रमीय अनुक्रम एक | *फेडरर वर्णक्रमीय अनुक्रम एक फलन समष्टि के समस्थेयता समूहों में परिवर्तित हो रहा है। | ||
* | * समस्थेयता नियत [[फेडरर वर्णक्रमीय अनुक्रम]]<ref>{{cite journal |arxiv=math/0406081|first1=Robert R. |last1=Bruner |first2=John |last2=Rognes |title=होमोलॉजिकल होमोटॉपी फिक्स्ड पॉइंट स्पेक्ट्रल सीक्वेंस में डिफरेंशियल|journal=Algebr. Geom. Topol. |volume=5 |issue=2 |date=2005 |pages=653–690 |doi=10.2140/agt.2005.5.653 |doi-access=free}}</ref> | ||
* | *ह्यूरविक्ज़ वर्णक्रमीय अनुक्रम किसी स्थान की समरूपता की समरूपता की गणना के लिए। | ||
* [[मिलर वर्णक्रमीय अनुक्रम]] एक | * [[मिलर वर्णक्रमीय अनुक्रम]] एक अभिसारी के मॉड p स्थिर अनुरूपता में परिवर्तित हो रहा है। | ||
* मिल्नोर वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है। | * मिल्नोर वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है। | ||
* मूर वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है। | * मूर वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है। | ||
* एक साधारण समूह की | * एक साधारण समूह की समस्थेयता की गणना के लिए [[क्विलन वर्णक्रमीय अनुक्रम]] | ||
* रोथेनबर्ग-स्टीनरोड वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है। | * रोथेनबर्ग-स्टीनरोड वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है। | ||
*वैन कम्पेन वर्णक्रमीय अनुक्रम रिक्त स्थान की कील की | *वैन कम्पेन वर्णक्रमीय अनुक्रम रिक्त स्थान की कील की समस्थेयता की गणना के लिए। | ||
=== बीजगणित === | === बीजगणित === | ||
* चेक सह समरूपता से शेफ सह समरूपता तक चेक- | * चेक सह समरूपता से शेफ सह समरूपता तक चेक-से-व्युत्पन्न प्रकार्यक वर्णक्रमीय अनुक्रम। | ||
* मॉड्यूल के | * मॉड्यूल के टॉर और Ext समूहों की गणना के लिए वलय वर्णक्रमीय अनुक्रमों का परिवर्तन। | ||
* एक बीजगणित के चक्रीय समरूपता में अभिसरण कोन्स वर्णक्रमीय अनुक्रम। | * एक बीजगणित के चक्रीय समरूपता में अभिसरण कोन्स वर्णक्रमीय अनुक्रम। | ||
* गेर्स्टन-विट वर्णक्रमीय अनुक्रम | * गेर्स्टन-विट वर्णक्रमीय अनुक्रम | ||
* [[कोहोलॉजी शर्ट|सह समरूपता शर्ट]] के लिए ग्रीन का वर्णक्रमीय अनुक्रम | * [[कोहोलॉजी शर्ट|सह समरूपता शर्ट]] के लिए ग्रीन का वर्णक्रमीय अनुक्रम | ||
*व्युत्पन्न | *व्युत्पन्न प्रकार्यक बनाने के लिए ग्रोथेंडिक वर्णक्रमीय अनुक्रम | ||
* | *अतिअनुरूपता की गणना के लिए [[हाइपरहोमोलॉजी वर्णक्रमीय अनुक्रम|अतिअनुरूपता वर्णक्रमीय अनुक्रम]] | ||
*अवकलन बीजगणित के टेंसर उत्पाद के अनुरूपता की गणना के लिए कुनेथ वर्णक्रमीय अनुक्रम। | *अवकलन बीजगणित के टेंसर उत्पाद के अनुरूपता की गणना के लिए कुनेथ वर्णक्रमीय अनुक्रम। | ||
* लेरे वर्णक्रमीय अनुक्रम एक शेफ के सह समरूपता में परिवर्तित हो रहा है। | * लेरे वर्णक्रमीय अनुक्रम एक शेफ के सह समरूपता में परिवर्तित हो रहा है। | ||
*[[स्थानीय-से-वैश्विक एक्सट स्पेक्ट्रल अनुक्रम|स्थानीय-से-वैश्विक | *[[स्थानीय-से-वैश्विक एक्सट स्पेक्ट्रल अनुक्रम|स्थानीय-से-वैश्विक Ext वर्णक्रमीय अनुक्रम]] | ||
*लिंडन-होच्स्चाइल्ड-सेरे वर्णक्रमीय सीक्वेंस इन [[ समूह कोहोलॉजी |समूह सह समरूपता]] | *लिंडन-होच्स्चाइल्ड-सेरे वर्णक्रमीय सीक्वेंस इन [[ समूह कोहोलॉजी |समूह सह समरूपता]] अनुरूपता | ||
*एक बीजगणित के Tor या Ext समूहों की गणना के लिए [[मई वर्णक्रमीय अनुक्रम]] | *एक बीजगणित के Tor या Ext समूहों की गणना के लिए [[मई वर्णक्रमीय अनुक्रम|मे वर्णक्रमीय अनुक्रम]] | ||
* एक विभेदक निस्यंदित समूह का वर्णक्रमीय क्रम: इस लेख में वर्णित है। | * एक विभेदक निस्यंदित समूह का वर्णक्रमीय क्रम: इस लेख में वर्णित है। | ||
*एक दोहरे सम्मिश्र का वर्णक्रमीय क्रम: इस लेख में वर्णित है। | *एक दोहरे सम्मिश्र का वर्णक्रमीय क्रम: इस लेख में वर्णित है। | ||
| Line 453: | Line 453: | ||
=== सम्मिश्र और बीजगणितीय ज्यामिति === | === सम्मिश्र और बीजगणितीय ज्यामिति === | ||
* | *विलक्षणता सिद्धांत में अर्नोल्ड का वर्णक्रमीय क्रम। | ||
* बलोच-लिक्टेनबौम वर्णक्रमीय अनुक्रम एक क्षेत्र के बीजगणितीय के-सिद्धांत में परिवर्तित हो रहा है। | * बलोच-लिक्टेनबौम वर्णक्रमीय अनुक्रम एक क्षेत्र के बीजगणितीय के-सिद्धांत में परिवर्तित हो रहा है। | ||
* | *फ्रोलिचेर वर्णक्रमीय अनुक्रम [[Dolbeault cohomology|डोलबौल्ट सह-समरूपता]] से प्रारंभ होता है और विभिन्न प्रकार के बीजगणितीय डी राम सह-समरूपता में परिवर्तित होता है। | ||
* हॉज-डी राम वर्णक्रमीय अनुक्रम विभिन्न प्रकार के बीजगणितीय d राम सह समरूपता में परिवर्तित हो रहा है। | * हॉज-डी राम वर्णक्रमीय अनुक्रम विभिन्न प्रकार के बीजगणितीय d राम सह समरूपता में परिवर्तित हो रहा है। | ||
*मोटिविक- | *मोटिविक-से-के-सिद्धांत वर्णक्रमीय अनुक्रम | ||
== टिप्पणियाँ == | == टिप्पणियाँ == | ||
| Line 502: | Line 502: | ||
* {{cite web|url=https://mathoverflow.net/q/17357|title= What is so "spectral" about spectral sequences?| publisher= [[MathOverflow]]}} | * {{cite web|url=https://mathoverflow.net/q/17357|title= What is so "spectral" about spectral sequences?| publisher= [[MathOverflow]]}} | ||
* {{cite web|url=https://faculty.math.illinois.edu/Macaulay2/doc/Macaulay2-1.15/share/doc/Macaulay2/SpectralSequences/html/|title=SpectralSequences — a package for working with filtered complexes and spectral sequences| publisher=[[Macaulay2]]}} | * {{cite web|url=https://faculty.math.illinois.edu/Macaulay2/doc/Macaulay2-1.15/share/doc/Macaulay2/SpectralSequences/html/|title=SpectralSequences — a package for working with filtered complexes and spectral sequences| publisher=[[Macaulay2]]}} | ||
[[Category: | [[Category:All articles with unsourced statements]] | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Articles with unsourced statements from June 2015]] | |||
[[Category:CS1 maint]] | |||
[[Category:Created On 08/05/2023]] | [[Category:Created On 08/05/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia articles needing page number citations from August 2021]] | |||
[[Category:स्पेक्ट्रल अनुक्रम|*]] | |||
Latest revision as of 10:44, 30 May 2023
तुल्य बीजगणित और बीजगणितीय सांस्थिति में, वर्णक्रमीय अनुक्रम क्रमिक सन्निकटन लेकर अनुरूपता समूहों की गणना करने का एक साधन है। वर्णक्रमीय अनुक्रम यथार्थ अनुक्रमों का एक सामान्यीकरण है, और Jean Leray (1946a, 1946b) द्वारा उनके परिचय के बाद से, वे महत्वपूर्ण संगणनात्मक उपकरण बन गए हैं, विशेष रूप से बीजीय सांस्थिति, बीजगणितीय ज्यामिति और समरूप बीजगणित में है।
आविष्कार और प्रेरणा
बीजगणितीय सांस्थिति में समस्याओं से प्रेरित, जीन लेरे ने एक शेफ (गणित) की धारणा प्रस्तुत की और स्वयं को संगणना शेफ सह समरूपता की समस्या का सामना करना पड़ा। शेफ सह समरूपता की गणना करने के लिए, लेरे ने संगणनात्मक तकनीक प्रस्तुत की जिसे अब लेरे वर्णक्रमीय अनुक्रम के रूप में जाना जाता है। इसने एक शेफ के सह समरूपता समूहों और एक शेफ की प्रत्यक्ष प्रतिरूप के सह समरूपता समूहों के बीच एक संबंध दिया। संबंध में एक अनंत प्रक्रिया सम्मिलित थी। लेरे ने पाया कि ज़ारी रखने के सह समरूपता समूहों ने प्राकृतिक श्रृंखला सम्मिश्र का गठन किया, ताकि वह सह समरूपता के सह समरूपता को ले सकें। यह अभी भी मूल शेफ की सह समरूपता नहीं थी, परन्तु यह एक अर्थ में एक चरण और निकट था। सह समरूपता के सह समरूपता ने फिर से एक मिश्रित शृंखला का गठन किया, और इसके सह समरूपता ने मिश्रित शृंखला का निर्माण किया, और इसी प्रकार। इस अनंत प्रक्रिया की सीमा अनिवार्य रूप से वही थी जो मूल शेफ की सह समरूपता समूहों के रूप में थी।
शीघ्र ही यह समझा गया किया गया कि लेरे की संगणनात्मक तकनीक अधिक सामान्य घटना का एक उदाहरण थी। विभिन्न स्थितियों में वर्णक्रमीय अनुक्रम पाए गए, और उन्होंने अनुरूपता और सह समरूपता समूहों के बीच सम्मिश्र संबंध दिए, जो ज्यामितीय स्थितियों जैसे कंपन और बीजगणितीय स्थितियों से व्युत्पन्न प्रकार्यक से जुड़े थे। जबकि व्युत्पन्न श्रेणी की प्रारंभ के बाद से उनका सैद्धांतिक महत्व कम हो गया है, वे अभी भी सबसे प्रभावी संगणनात्मक उपकरण उपलब्ध हैं। यह तब भी सत्य है जब वर्णक्रमीय अनुक्रम के कई पद अगणनीय हैं।
दुर्भाग्य से, बड़ी मात्रा में सूचना वर्णक्रमीय अनुक्रमों में ले जाने के कारण, उन्हें समझना जटिल है। यह सूचना सामान्यतः एबेलियन समूहों या मॉड्यूल (गणित) के पद तीन जाली में निहित होती है। निपटने के लिए सबसे सरल स्थिति वे हैं जिनमें वर्णक्रमीय अनुक्रम अंततः पतन हो जाता है, जिसका अर्थ है कि अनुक्रम में आगे जाने से कोई नवीन सूचना नहीं मिलती है। यहां तक कि जब ऐसा नहीं होता है, तब भी विभिन्न क्रमभंग से वर्णक्रमीय अनुक्रम से उपयोगी सूचना प्राप्त करना प्रायः संभव होता है।
औपचारिक परिभाषा
सह समरूपी वर्णक्रमीय अनुक्रम
एक एबेलियन श्रेणी को ठीक करें, जैसे कि एक वलय (गणित) पर मॉड्यूल (गणित) की श्रेणी, और गैर-ऋणात्मक पूर्णांक । सह समरूपी वर्णक्रमीय अनुक्रम वस्तु और समरूपता का अनुक्रम है, जैसे कि प्रत्येक के लिए,
- ,
- , के संबंध में की समरूपता (गणित)।
सामान्यतः समरूपताओं को दबा दिया जाता है और हम इसके अतिरिक्त लिखते हैं। एक वस्तु को पत्रक (पृष्ठ के पत्रक के रूप में), या कभी-कभी एक पृष्ठ या पद कहा जाता है; एक समरूपता को सीमा प्रतिचित्र या अवकलन कहा जाता है। कभी-कभी को की व्युत्पन्न वस्तु कहा जाता है।[citation needed]
द्वि वर्गीकृत वर्णक्रमीय अनुक्रम
वस्तुतः वर्णक्रमीय अनुक्रम अधिकतर एक वलय (गणित) R (या द्वि वर्गीकृत शेफ (गणित) मॉड्यूल के वलय के एक शेफ पर) पर द्वि वर्गीकृत मॉड्यूल (गणित) की श्रेणी में होते हैं, अर्थात प्रत्येक पत्रक एक द्वि वर्गीकृत R-मॉड्यूल है। तो इस स्थिति में सह-समरूपता वर्णक्रमीय अनुक्रम द्वि वर्गीकृत R-मॉड्यूल का अनुक्रम है और प्रत्येक मॉड्यूल के लिए द्वि वर्गीकृत के समरूपता का प्रत्यक्ष योग है, जैसे कि प्रत्येक के लिए यह धारण करते है:
- ,
- ।
यहाँ प्रयुक्त अंकन को पूरक घात कहा जाता है। कुछ लेखक इसके अतिरिक्त लिखते हैं, जहाँ कुल घात है। वर्णक्रमीय अनुक्रम के आधार पर, पहली पत्रक पर सीमा प्रतिचित्र में एक घात हो सकती है जो R = 0, R = 1, या R = 2 से मेल खाती है। उदाहरण के लिए, निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम के लिए, नीचे वर्णित, R0 = 0, परन्तु ग्रोथेंडिक वर्णक्रमीय अनुक्रम के लिए, R0 = 2। सामान्यतः R0 शून्य, एक या दो है। ऊपर वर्णित अश्रेणीकृत स्थिति में, r0 अप्रासंगिक है।
सजातीय वर्णक्रमीय अनुक्रम
अधिकतर जिन वस्तुओं के विषय में हम बात कर रहे हैं वे मिश्रित शृंखला हैं, जो अवरोही (जैसे ऊपर) या आरोही क्रम में होते हैं। बाद की स्थिति में, को और के साथ , (द्विपद ) के साथ प्रतिस्थापित करके, सह समरूपी स्थिति के अनुरूप तुल्य वर्णक्रमीय अनुक्रम की परिभाषा प्राप्त करते है।
एक श्रृंखला सम्मिश्र से वर्णक्रमीय अनुक्रम
अक्रमिक स्थिति में सबसे प्राथमिक उदाहरण एक मिश्रित शृंखला C• है। वस्तु C• मिश्रित शृंखला की एबेलियन श्रेणी में स्वाभाविक रूप से एक अवकलन d के साथ आता है। मान लीजिए R0 = 0, और मान लीजिए E0 C• है। यह E1 को सम्मिश्र H (C•) होने के लिए बाध्य करते है: iवें स्थान पर यह C • का iवां समरूपता समूह है। इस नवीन सम्मिश्र पर एकमात्र प्राकृतिक अवकलन शून्य प्रतिचित्र है, इसलिए हम d1 = 0 करते हैं। यह को के बराबर बनाता है, और फिर से हमारा एकमात्र प्राकृतिक अवकलन शून्य प्रतिचित्र है। हमारी शेष सभी पत्रकों पर शून्य अवकलन डालने से वर्णक्रमीय क्रम मिलता है जिसकी पद हैं:
- E0 = C•
- सभी R ≥ 1 के लिए Er= H (C•)।
इस वर्णक्रमीय अनुक्रम की पद पहली पत्रक पर स्थिर होती हैं क्योंकि इसका एकमात्र असतहीय अवकल शून्यवाँ पत्रक पर था। फलस्वरूप, हम बाद के चरणों में और अधिक सूचना प्राप्त नहीं कर सकते हैं। सामान्यतः, बाद की पत्रक से उपयोगी सूचना प्राप्त करने के लिए, हमें पर अतिरिक्त संरचना की आवश्यकता होती है।
प्रत्यक्षण
एक द्वि वर्गीकृत वर्णक्रमीय अनुक्रम में ट्रैक रखने के लिए डेटा की विलक्षण मात्रा होती है, परन्तु सामान्य प्रत्यक्षण तकनीक है जो वर्णक्रमीय अनुक्रम की संरचना को स्पष्ट बनाती है। हमारे निकट तीन सूचकांक हैं, R, पी और q। एक वस्तु को पुस्तक के विविध पृष्ठ के रूप में देखा जा सकता है। इन पत्रकों पर, हम p को क्षैतिज दिशा और q को उर्ध्वाधर दिशा मानेंगे। प्रत्येक जाली बिंदु पर हमारे निकट वस्तु है। अब अगले पृष्ठ की ओर मुड़ने का अर्थ है समरूपता लेना, अर्थात पृष्ठ पृष्ठ का एक उपभाग है। कुल घात n = p + q प्रत्येक पत्रक के पार तिरछे, उत्तर-पश्चिम से दक्षिण-पूर्व तक चलता है। समरूपी स्थिति में, अवकलों का द्विपद (−r, r − 1) होता है, इसलिए वे n से घटाते हैं। सह समरूपी स्थिति में, n एक से बढ़ जाता है। r के संबंध में अवकल प्रत्येक मोड़ के साथ अपनी दिशा बदलते हैं।
लाल तीर पहले चतुर्थांश अनुक्रम की स्थिति को प्रदर्शित करते है (उदाहरण वर्णक्रमीय अनुक्रम देखें), जहां मात्र पहले चतुर्थांश की वस्तुएं गैर-शून्य हैं। पृष्ठों को पलटते समय, सभी अवकलनों का प्रांत या उपप्रांत शून्य हो जाता है।
गुण
श्रेणीबद्ध गुण
उपयोग वर्णक्रमीय अनुक्रमों का सम्मुचय एक श्रेणी बनाता है: वर्णक्रमीय अनुक्रमों का एक रूपवाद परिभाषा के अनुसार प्रतिचित्रों का एक संग्रह हैजो अवकलन के साथ संगत हैं, अर्थात , और दिए गए समरूपताओं के साथ क्रमशः E और E' के Rवें चरण और (R + 1) वें पत्रक के सह समरूपता के बीच: । द्वि वर्गीकृत स्थिति में, उन्हेंक्रमस्थापनका भी सम्मान करना चाहिए:
गुणक संरचना
एक कप उत्पाद सह समरूपता समूह को एक वलय (गणित) देता है, इसे सह समरूपता वलय में बदल देते है। इस प्रकार, वलय संरचना के साथ-साथ वर्णक्रमीय अनुक्रम पर विचार करना स्वाभाविक है। को सह समरूपी प्रकार का एक वर्णक्रमीय अनुक्रम होने दें। हम कहते हैं कि इसकी गुणात्मक संरचना है यदि (i) (द्वि वर्गीकृत) अवकल वर्गीकृत बीजगणित और (ii) पर गुणा सह समरूपता केमाध्यम से पर प्रेरित किया जाता है।
एक विशिष्ट उदाहरण एक कंपन के लिए उपयोग सेरे वर्णक्रमीय अनुक्रम है, जब गुणांक समूह एक वलय R है। इसमें फाइबर -पृष्ठ के कप उत्पादों और आधार पर गुणक संरचना होती है।[1] यद्यपि, सामान्यतःसीमित पद H (E; R) के लिए वर्गीकृत बीजगणित के रूप मेंसमरूपी नहीं है।[2] गुणात्मक संरचना अनुक्रम पर अवकलन की गणना के लिए बहुत उपयोगी हो सकती है।[3]
वर्णक्रमीय अनुक्रमों का निर्माण
वर्णक्रमीय दृश्यों का निर्माण विभिन्न विधियों से किया जा सकता है। बीजगणितीय सांस्थिति में, एक यथार्थ युग्म संभवतः निर्माण के लिए सबसे सामान्य उपकरण है। बीजगणितीय ज्यामिति में, वर्णक्रमीय अनुक्रम सामान्यतः उप शृंखला सम्मिश्रों के निस्पंदन से निर्मित होते हैं।
एक यथार्थ युग्म का वर्णक्रमीय अनुक्रम
वर्णक्रमीय अनुक्रमों के निर्माण के लिए एक और तकनीक विलियम शूमाकर मैसी की यथार्थ युग्मों की विधि है। बीजगणितीय सांस्थिति में यथार्थ युग्म विशेष रूप से सामान्य हैं। इसके अतिरिक्त वे अमूर्त बीजगणित में अलोकप्रिय हैं, जहां अधिकांश वर्णक्रमीय अनुक्रम निस्यंदित किए गए सम्मिश्रों से आते हैं।
यथार्थ युग्मों को परिभाषित करने के लिए, हम फिर से एक एबेलियन श्रेणी से प्रारंभ करते हैं। पहले के जैसे, व्यवहार में यह सामान्यतः वलय के ऊपर दोगुने क्रमिक वाले मॉड्यूल की श्रेणी है। एक यथार्थ युग्म वस्तुओं की युग्म है (A, C), साथ में इन वस्तुओं के बीच तीन समरूपताएं हैं: f : A → A, g : A → C और h : C → A कुछ यथार्थ प्रतिबन्धों के अधीन:
- प्रतिरूप (गणित) f = कर्नेल (बीजगणित) g
- प्रतिरूप g = कर्नेल H
- प्रतिरूप H = कर्नेल f
हम इस डेटा को (A, C, f, g, h) द्वारा संक्षिप्त करेंगे। यथार्थ युग्म को सामान्यतः त्रिकोण के रूप में दर्शाया जाता है। हम देखेंगे कि C वर्णक्रमीय अनुक्रम के E 0 वपद से मेल खाता है और A कुछ सहायक डेटा है।
वर्णक्रमीय अनुक्रम की अगली पत्रक पर जाने के लिए, हम 'व्युत्पन्न युग्म' बनाएंगे। हम लोग तैयार हैं:
- d = g o H
- A' = f (A)
- C' = Ker d / Im d
- f' = f|A', f से A' का प्रतिबंध
- h' : C' → A' h से प्रेरित है। यह देखना सरल है कि h ऐसे प्रतिचित्र को प्रेरित करते है।
- g' : A' → C' को तत्वों पर इस प्रकार परिभाषित किया गया है: A' में प्रत्येक के लिए, A में कुछ b के लिए a को f (b) के रूप में लिखें। g' (a) को C' में g (b) की प्रतिरूप के रूप में परिभाषित किया गया है। सामान्यतः, एबेलियन श्रेणियों के लिए एम्बेडिंग प्रमेयों में से एक का उपयोग करके g' का निर्माण किया जा सकता है।
यहां से यह जांचना सरल है कि (A', C', f', g', h ') यथार्थ युग्म है। C' वर्णक्रमीय अनुक्रम के E1 पद से मेल खाता है। हम यथार्थ युग्म (A (n), सी (n), f (n), g (n), H (n)) प्राप्त करने के लिए इस प्रक्रिया को दोहरा सकते हैं।
वर्णक्रमीय अनुक्रम बनाने के लिए, En को C (n) और Dn को G (n) o h (n) होने दें।
इस पद्धति से निर्मित वर्णक्रमीय अनुक्रम
- सेरे वर्णक्रमीय अनुक्रम[4] - एक कंपन की समरूपता की गणना (सह) करने के लिए उपयोग किया जाता है
- अत्यायाह-हिर्जेब्रूच वर्णक्रमीय अनुक्रम - असाधारण सह समरूपता सिद्धांतों की गणना (सह) समरूपता के लिए उपयोग किया जाता है, जैसे कि K-सिद्धांत
- बॉकस्टीन वर्णक्रमीय अनुक्रम।
- निस्यंदित किए गए सम्मिश्रों के वर्णक्रमीय क्रम
निस्यंदित किए गए सम्मिश्र का वर्णक्रमीय अनुक्रम
एक बहुत ही सामान्य प्रकार का वर्णक्रमीय अनुक्रम निस्यंदित (अमूर्त बीजगणित) उपशृंखला मिश्रित से आता है, क्योंकि यह स्वाभाविक रूप से एक बड़ी श्रेणी वाली वस्तु को प्रेरित करते है। अवरोही निस्पंदन के साथ एक उपशृंखला मिश्रित पर विचार करें। हमें आवश्यकता है कि सीमा प्रतिचित्र निस्पंदन के अनुकूल हो, अर्थात , और यह कि निस्पंदन संपूर्ण है, अर्थात सभी के समुच्चय का मिलन संपूर्ण श्रृंखला सम्मिश्र है। फिर और के साथ एक वर्णक्रमीय अनुक्रम स्थित है।।[5] बाद में, हम यह भी मान लेंगे कि निस्पंदन हॉसडॉर्फ या अलग है, अर्थात सभी के सम्मुचय का प्रतिच्छेदन शून्य है।
निस्यंदन उपयोगी है क्योंकि यह शून्य की निकटता का माप देता है: जैसे-जैसे p बढ़ता है, शून्य के और निकट आता जाता है। हम इस निस्यंदित से एक वर्णक्रमीय अनुक्रम का निर्माण करेंगे जहां बाद की पत्रक में उपसीमाओं और उपचक्र मूल सम्मिश्र में उपसीमाओं और उपचक्र के निकट और निकट आते हैं। इस वर्णक्रमीय अनुक्रम को निस्पंदन घात p और पूरक घात q = n − p द्वारा दोगुना वर्गीकृत किया गया है।
निर्माण
में मात्र एक श्रेणीकरण और एक निस्यंदित है, इसलिए हम पहले वर्णक्रमीय अनुक्रम के पहले पृष्ठ के लिए एक दोगुनी श्रेणीबद्ध वस्तु का निर्माण करते हैं। दूसरी श्रेणीकरण प्राप्त करने के लिए, हम निस्यंदित के संबंध में संबंधित क्रमिक वस्तु लेंगे। हम इसे एक असामान्य विधि से लिखेंगे जो चरण पर उचित होगा:
चूँकि हमने माना कि सीमा प्रतिचित्र निस्पंदन के साथ संगत था, एक दोगुनी वर्गीकृत वस्तु है और पर प्राकृतिक दोगुनी वर्गीकृत सीमा प्रतिचित्र है। प्राप्त करने के लिए की समरूपता लेते हैं।
ध्यान दें कि और को
के में प्रतिरूपों के रूप में लिखा जा सकता है और फिर हमारे निकट
- है।
वस्तुतः वे तत्व हैं जो अवकलन निस्पंदन में एक स्तर ऊपर धकेलते हैं, और वस्तुतः उन तत्वों की प्रतिरूप हैं जो अवकलन निस्पंदन में शून्य स्तर ऊपर धकेलते हैं। इससे पता चलता है कि हमें को उन तत्वों के रूप में चुनना चाहिए जो अवकलन निस्पंदन में r स्तरों को ऊपर धकेलता है और उन तत्वों की प्रतिरूप है जो अवकलन निस्पंदन में r-1 स्तरों को ऊपर धकेलता है। दूसरे पदों में, वर्णक्रमीय अनुक्रम को
को संतुष्ट करना चाहिए और हमारे निकट संबंध
- होना चाहिए।
इसे समझने के लिए, हमें प्रत्येक पर एक अवकलन खोजना होगा और यह सत्यापित करना होगा कि यह समरूपी समरूपता को की ओर ले जाता है। अवकलन
को पर परिभाषित मूल अवकलन d को उपवस्तु तक सीमित करके परिभाषित किया गया है। यह जाँचना सरल है कि इस अवकलन के संबंध में की समरूपता है, इसलिए यह वर्णक्रमीय अनुक्रम देता है। दुर्भाग्य से, अवकलन बहुत स्पष्ट नहीं है। वर्णक्रमीय अनुक्रम को सफलतापूर्वक लागू करने के लिए अवकलन निर्धारित करना या उनके निकट काम करने के विधि खोजना मुख्य चुनौतियों में से एक है।
इस पद्धति से निर्मित वर्णक्रमीय अनुक्रम
- हॉज-डे राम वर्णक्रमीय अनुक्रम
- एक दोहरे सम्मिश्र का वर्णक्रमीय क्रम
- मिश्रित हॉज संरचनाओं के निर्माण के लिए उपयोग किया जा सकता है[6]
एक दोहरे सम्मिश्र का वर्णक्रमीय अनुक्रम
अन्य सामान्य वर्णक्रमीय अनुक्रम एक दोहरे सम्मिश्र का वर्णक्रमीय क्रम है। एक द्वि सम्मिश्र सभी पूर्णांकों i और j के लिए दो अवकलन, वस्तुओं का एक संग्रह है Ci,j के साथ, d I और d II के साथ वस्तुओं Cij का एक संग्रह है। d I को i घटता माना जाता है, और d II को j घटता हुआ माना जाता है। इसके अतिरिक्त, हम मानते हैं कि अवकलन विरोधी आवागमन है, ताकि d i d II + d II d I = 0। हमारा लक्ष्य पुनरावृत्त समरूपता और की तुलना करना है। हम अपने द्वि सम्मिश्र को दो अलग-अलग विधियों से निस्यंदित करके ऐसा करेंगे। यहां हमारे निस्यंदित हैं:
वर्णक्रमीय अनुक्रम प्राप्त करने के लिए, हम पिछले उदाहरण को कम कर देंगे। हम कुल सम्मिश्र T (C•,•) को उस सम्मिश्र के रूप में परिभाषित करते हैं जिसका n'वाँ पद और जिसका अवकलन dI+ dII है। यह एक सम्मिश्र है क्योंकि d I और d II विरोधी आवागमन अवकल हैं। Ci,j पर दो निस्यंदित कुल सम्मिश्र पर दो निस्यंदक देते हैं:
यह दिखाने के लिए कि ये वर्णक्रमीय अनुक्रम पुनरावृत्त समरूपता के विषय में सूचना देते हैं, हम T (C•,•) पर I निस्पंदन के E0, E1, औरE2 के प्रतिबन्ध पर काम करेंगे। E0 पद स्पष्ट है:
जहाँ n = p + q।
E1 ज्ञात करने के लिए, हमें E0 पर dI + d II निर्धारित करने की आवश्यकता है। पर द्वितीय </उप>। ध्यान दें कि n के संबंध में अवकलन की घात -1 होनी चाहिए, इसलिए हमें एक प्रतिचित्र
- मिलता है
फलस्वरूप, E0 पर अवकलन प्रतिचित्र Cp,q → सीp,q−1 d I + dII द्वारा प्रेरित है। परन्तु d I के निकट ऐसे प्रतिचित्र को प्रेरित करने के लिए अनुचित घात है, इसलिए d I को E0 पर शून्य होना चाहिए। इसका अर्थ है कि अवकलन पूर्णतः dII है, इसलिए हमें
- मिलता है।
E2 ज्ञात करने के लिए, हमें
- ज्ञात करना होगा
क्योंकि E1 यथार्थ में d II के संबंध में समरूपता थी, d II E1 पर शून्य है। फलस्वरूप, हमें
- मिलता है।
अन्य निस्पंदन का उपयोग करने से हमें समान E2 पद
- के साथ एक अलग वर्णक्रमीय क्रम मिलता है :
इन दो वर्णक्रमीय अनुक्रमों के बीच संबंध खोजने के लिए क्या बचा है। यह पता चलेगा कि जैसे-जैसे r बढ़ता है, उपयोगी तुलना की अनुमति देने के लिए दो क्रम समान हो जाएंगे।
अभिसरण, पतन और अभिसरण
चक्रों और सीमाओं के निस्पंदन के रूप में व्याख्या
माना कि R = 1 से प्रारंभ होकर Er वर्णक्रमीय क्रम है। फिर उपवस्तु
का अनुक्रम होता है जैसे कि ; वस्तुतः, पुनरावर्ती रूप से हम और होने देते हैं ताकि कर्नेल और की प्रतिरूप हो।
फिर हम और
- ;
देते हैं: इसे सीमांत पद कहते हैं। (अवश्य, इस प्रकार के को श्रेणी में मौजूद होने की आवश्यकता नहीं है, परन्तु यह सामान्यतः एक गैर-समस्या है क्योंकि उदाहरण के लिए मॉड्यूल की श्रेणी में ऐसी सीमाएं स्थित हैं या चूंकि व्यवहार में वर्णक्रमीय अनुक्रम पतित होने की प्रवृत्ति के साथ काम करते है; ऊपर दिए गए क्रम में मात्र सूक्ष्म रूप से कई समावेशन हैं।)
अभिसरण की पद
हम कहते हैं कि वर्णक्रमीय अनुक्रम निर्बल रूप से अभिसरण करता है यदि प्रत्येक के लिए एक निस्पंदन के साथ वर्गीकृत वस्तु है, और प्रत्येक के लिए एक समरूपता स्थित है। यह में परिवर्तित हो जाता है यदि निस्पंदन हौसडॉर्फ है, अर्थात। हम
लिखते हैं जिसका अर्थ है कि जब भी p + q = n, , में परिवर्तित होता है। हम कहते हैं कि वर्णक्रमीय अनुक्रम से जुड़ा हुआ है यदि प्रत्येक के लिए ऐसा है कि सभी , के लिए। तब सीमित पद है। वर्णक्रमीय क्रम नियमित है या पर पतित होता है यदि अवकलन सभी के लिए शून्य है। यदि विशेष रूप से है, जैसे कि पत्रक एक पंक्ति या एक स्तंभ पर केंद्रित होती है, तो हम कहते हैं कि यह पतित हो जाती है। प्रतीकों में हम लिखते हैं:
p निस्पंदन सूचकांक को इंगित करता है। पद आधार के बाईं ओर लिखना बहुत सामान्य है, क्योंकि यह अधिकांश वर्णक्रमीय अनुक्रमों का सबसे उपयोगी पद है। अनिस्यंदित मिश्रित शृंखला का वर्णक्रमीय अनुक्रम पहली पत्रक पर घटता है (पहला उदाहरण देखें) : चूँकि शून्यवाँ पत्रक के बाद कुछ भी नहीं होता है, प्रतिबंधक पत्रक के समान है।
वर्णक्रमीय अनुक्रम का पांच-पद का यथार्थ अनुक्रम कुछ निम्न-घात प्रतिबन्धों और E∞ प्रतिबन्धों से संबंधित है।
अध: पतन के उदाहरण
निस्यंदित किए गए सम्मिश्र का वर्णक्रमीय अनुक्रम, जारी
ध्यान दें कि हमारे निकट समावेशन की एक श्रृंखला है:
हम पूछ सकते हैं कि क्या होता है यदि हम
- को परिभाषित करते हैं।
इस वर्णक्रमीय अनुक्रम के निरस्तीकरण के लिए एक स्वाभाविक प्रत्याशी है। अभिसरण स्वत: नहीं होता है, परन्तु कई स्थितियों में होता है। विशेष रूप से, यदि निस्पंदन परिमित है और इसमें ठीक r असतहीय चरण होते हैं, तो वर्णक्रमीय क्रम rवे पत्रक के बाद पतित हो जाता है। अभिसरण तब भी होता है जब सम्मिश्र और निस्यंदित दोनों नीचे से बंधे होते हैं या दोनों ऊपर से बंधे होते हैं।
अधिक विस्तार से हमारे वर्णक्रमीय अनुक्रम के निरस्तीकरण का वर्णन करने के लिए, ध्यान दें कि हमारे निकट सूत्र हैं:
यह देखने के लिए कि का क्या तात्पर्य है याद रखें कि हमने मान लिया था कि निस्पंदन अलग हो गया था। इसका तात्पर्य यह है कि जैसे-जैसे r बढ़ता है, कर्नेल सिकुड़ती जाती है, जब तक कि हमारे निकट नहीं रह जाती। के लिए, याद रखें कि हमने माना था कि निस्यंदित संपूर्ण था। इसका तात्पर्य यह है कि जैसे-जैसे r बढ़ता है, तब तक प्रतिरूप बढ़ते हैं जब तक हम तक नहीं पहुँच जाते। हम निष्कर्ष निकालते हैं कि
- ,
अर्थात्, वर्णक्रमीय अनुक्रम का निरसन, C के (p+q) वें अनुरूपता का pवां श्रेणीबद्ध भाग है। यदि हमारा वर्णक्रमीय अनुक्रम अभिसरण करता है, तो हम यह निष्कर्ष निकालते हैं कि:
लंबे यथार्थ क्रम
निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम का उपयोग करके, हम लंबे यथार्थ अनुक्रमों के अस्तित्व को प्राप्त कर सकते हैं। उपशृंखला मिश्रित का संक्षिप्त यथार्थ अनुक्रम 0 → A • → B• → C• → 0 चुनें, और पहले प्रतिचित्र को f• :A• → B• कहते हैं। हमें अनुरूपता वस्तु Hn (A•) → Hn (B•) → Hn (C•) के प्राकृतिक प्रतिचित्र मिलते हैं, और हम जानते हैं कि यह ठीक बीच में है। हम संयोजक समरूपता को खोजने के लिए निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम का उपयोग करेंगे और यह सिद्ध करने के लिए कि परिणामी अनुक्रम यथार्थ है। प्रारंभ करने के लिए, हम B•:
- निस्यंदित करते हैं
यह:
- देता है
अवकल में द्विपद (1, 0) होता है, इसलिए d0,q: Hq (C•) → Hq+1 (A)। ये स्नेक लेम्मा से संयोजक समरूपता हैं, और प्रतिचित्र A• → B• → C• के साथ, वे एक क्रम देते हैं:
यह दिखाना शेष है कि यह क्रम A और C स्थान पर यथार्थ है। ध्यान दें कि यह वर्णक्रमीय क्रम E2 पद पर पतित होता है क्योंकि अवकलों का द्विपद (2, −1) होता है। फलस्वरूप, E2 पद E∞ पद के समान है :
परन्तु हमारे निकट E2 पद का प्रत्यक्ष वर्णन E1 पद की समरूपता के रूप में भी है। ये दो विवरण समरूपी होने चाहिए:
पूर्व C स्थान पर यथार्थता देता है, और बाद वाला A स्थान पर यथार्थता देता है।
एक दोहरे सम्मिश्र का वर्णक्रमीय अनुक्रम, जारी
निस्यंदित सम्मिश्र के लिए आधार का उपयोग करते हुए, हम पाते हैं कि:
सामान्यतः, Hp+q (T (C•,•)) पर दो श्रेणीकरण अलग हैं। इसके अतिरिक्त, इन दो वर्णक्रमीय अनुक्रमों से उपयोगी सूचना प्राप्त करना अभी भी संभव है।
Tor की क्रमविनिमेयता
R को वलय होने दें, M को दाएँ R-मॉड्यूल और n को बाएँ R-मॉड्यूल होने दें। याद रखें कि टेंसर उत्पाद के व्युत्पन्न प्रकार्यक को टॉर फलन के रूप में दर्शाया गया है। टॉर को इसके पहले तर्क के प्रक्षेपी संकल्प का उपयोग करके परिभाषित किया गया है। यद्यपि, यह पता चला है कि । जबकि यह वर्णक्रमीय अनुक्रम के बिना सत्यापित किया जा सकता है, यह वर्णक्रमीय अनुक्रमों के साथ बहुत सरल है।
क्रमशः M और N के प्रक्षेपी विभेदन और चुनें। इन्हें ऐसे सम्मिश्रों के रूप में मानें जो क्रमशः d और ई के अवकलन वाले ऋणात्मक घात में लुप्त हो जाते हैं। हम एक द्वि सम्मिश्र का निर्माण कर सकते हैं जिसकी पद हैं और जिनके अवकलन और हैं। (-1 का कारक इतना है कि अवकलन विरोधी आवागमन है।) चूंकि प्रक्षेपी मॉड्यूल समतल हैं, प्रक्षेपी मॉड्यूल के साथ टेंसर उत्पाद लेना अनुरूपता लेने के साथ प्रारंभ होता है, इसलिए हम प्राप्त करते हैं:
चूंकि दो सम्मिश्र संकल्प हैं, उनकी अनुरूपता घात शून्य के बाहर लुप्त हो जाती है। घात शून्य में, हम
- के साथ रह जाते हैं
विशेष रूप से, पद पंक्ति q = 0 (I वर्णक्रमीय अनुक्रम के लिए) और p = 0 (II वर्णक्रमीय अनुक्रम के लिए) को छोड़कर लुप्त हो जाते हैं। इसका तात्पर्य यह है कि वर्णक्रमीय क्रम दूसरी पत्रक पर पतित हो जाता है, इसलिए E∞ पद E 2 प्रतिबन्धों के लिए तुल्याकारी हैं:
अंत में, जब p और q बराबर होते हैं, तो दाएँ हाथ की दो भुजाएँ बराबर होती हैं, और Tor की क्रमविनिमेयता इस प्रकार होती है।
हल निकालने के उदाहरण
प्रथम-चतुर्थांश पत्रक
एक वर्णक्रमीय अनुक्रम पर विचार करें जहाँ कुछ से कम सभी के लिए और कुछ से कम सभी के लिए लुप्त हो जाता है। यदि और को शून्य के रूप में चुना जा सकता है, तो इसे प्रथम-चतुर्थांश वर्णक्रमीय अनुक्रम कहा जाता है। क्रम समाप्त हो जाता है क्योंकि सभी के लिए धारण करते है यदि और । इसे देखने के लिए, ध्यान दें कि माने गए स्थितियों के लिए या तो अवकलन का प्रांत या उपप्रांत शून्य है। दृश्य पदों में, पत्रक एक बढ़ती हुई आयत में स्थिर हो जाती हैं (ऊपर चित्र देखें)। यद्यपि, वर्णक्रमीय अनुक्रम को पतित होने की आवश्यकता नहीं है, क्योंकि अवकलन प्रतिचित्र सभी एक बार में शून्य नहीं हो सकते हैं। इसी प्रकार, वर्णक्रमीय क्रम भी अभिसरण करता है यदि कुछ से अधिक सभी के लिए लुप्त हो जाता है और कुछ से अधिक सभी के लिए लुप्त हो जाता है।
2 गैर-शून्य आसन्न स्तंभ
मान लीजिए कि एक सजातीय वर्णक्रमीय अनुक्रम है जैसे कि 0, 1 को छोड़कर सभी p के लिए है। दृष्टिगत रूप से, यह -पृष्ठ
- के साथ वर्णक्रमीय अनुक्रम है
दूसरे पृष्ठ पर अवकलन की घात (-2, 1) है, इसलिए वे
- के रूप में हैं
ये प्रतिचित्र सभी शून्य हैं क्योंकि वे
- ,
हैं इसलिए वर्णक्रमीय अनुक्रम पतित होता है: । कहते हैं, यह एक निस्पंदन
के साथ में परिवर्तित होता है जैसे कि । तब , , , , आदि। इस प्रकार, यथार्थ क्रम है:[7]
- ।
अगला, मान लीजिए कि वर्णक्रमीय अनुक्रम है जिसके दूसरे पृष्ठ में मात्र दो पंक्तियाँ q = 0, 1 हैं। यह दूसरे पृष्ठ पर पतित होने की आवश्यकता नहीं है, परन्तु यह अभी भी तीसरे पृष्ठ पर पतित होता है क्योंकि अवकलन में घात (-3, 2) होती है। टिप्पणी , क्योंकि भाजक शून्य है। इसी प्रकार, । इस प्रकार,
- ।
अब, कहते हैं, वर्णक्रमीय अनुक्रम पिछले उदाहरण के जैसे एक निस्पंदन f के साथ H में परिवर्तित हो जाता है। चूंकि , , आदि, हमारे निकट है: । सब कुछ एक साथ रखकर, एक मिलता है:[8]
वांग अनुक्रम
पिछले खंड में की गई गणना सरल विधि से सामान्यीकरण करती है। एक क्षेत्र पर कंपन पर विचार करें:
जिसमें n कम से कम 2 हो। सेरे वर्णक्रमीय अनुक्रम है:
- ;
यही कहना है, कुछ निस्पंदन के साथ।
चूँकि मात्र शून्य नहीं है जब p शून्य या n है और उस स्थिति में 'Z' के बराबर है, हम देखते हैं कि में मात्र दो रेखाएँ हैं, इसलिए -पृष्ठ
- द्वारा दिया गया है।
इसके अतिरिक्त सार्वभौमिक गुणांक प्रमेय द्वारा के लिए
के बाद से, पृष्ठ
- जैसा दिखता है।
चूंकि -पृष्ठ मात्र गैर-शून्य अवकलन हैं,
द्वारा दिया गया है जो कि
है वर्णक्रमीय अनुक्रम पर अभिसरण करता है। की गणना करके हम यथार्थ क्रम
- प्राप्त करते हैं।
और अनुरूपता समूहों का उपयोग करके लिखा गया है, यह
- है।
यह स्थापित करने के लिए कि दो -पद क्या हैं, , लिखें, और चूंकि , आदि, हमारे निकट: और इस प्रकार, के बाद से ,
- है।
यह ठीक क्रम
- है
सभी गणनाओं को एक साथ रखकर, एक प्राप्त होता है:[9]
(ग्य्सिन अनुक्रम इसी प्रकार से प्राप्त किया जाता है।)
कम-घात पद
एक स्पष्ट सांकेतिक परिवर्तन के साथ, पिछले उदाहरणों में संगणना के प्रकार को उपयोग वर्णक्रमीय अनुक्रम के लिए भी किया जा सकता है। माना घटते निस्पंदन
के साथ H में परिवर्तित होने वाला प्रथम-चतुर्थांश वर्णक्रमीय अनुक्रम है ताकि
चूँकि शून्य है यदि p या q ऋणात्मक है, तो हमारे निकट:
चूँकि उसी कारण से और चूँकि
- ।
, के बाद से। अनुक्रमों को एक साथ जोड़कर, हम तथाकथित पांच-पद यथार्थ अनुक्रम प्राप्त करते हैं:
किनारे के प्रतिचित्र और अतिक्रमण
तुल्य वर्णक्रमीय अनुक्रम
मान लीजिए कि एक वर्णक्रमीय क्रम है। यदि प्रत्येक q < 0 के लिए है, तो यह होना चाहिए: r ≥ 2 के लिए, भाजक के रूप में
शून्य है। इसलिए, एकरूपता का एक क्रम है:
- ।
उन्हें किनारे के प्रतिचित्र कहा जाता है। इसी प्रकार, यदि प्रत्येक p <0 के लिए तो समाकारिता का एक क्रम होता है (जिसे किनारे के प्रतिचित्र भी कहा जाता है) :
- ।
अतिक्रमण प्रतिचित्र आंशिक रूप से परिभाषित प्रतिचित्र है (अधिक यथार्थ, एक उपवस्तु से एक भागफल तक का प्रतिचित्र)
को एक रचना के रूप में दिया गया है, पहला और अंतिम प्रतिचित्र किनारे के प्रतिचित्र के व्युत्क्रम हैं।[10]
सह समरूपी वर्णक्रमीय अनुक्रम
सह समरूपी प्रकार के वर्णक्रमीय अनुक्रम के लिए, अनुरूप कथन धारण करते हैं। यदि प्रत्येक q <0 के लिए है, तो समाकारिता
- का एक क्रम है।
और यदि प्रत्येक p < 0 के लिए , तो एकरूपता का एक क्रम होता है:
- ।
अतिक्रमण आवश्यक ठीक रूप से परिभाषित प्रतिचित्र नहीं है:
द्वारा प्रेरित ।
अनुप्रयोग
इन प्रतिचित्रों का निर्धारण सेरे वर्णक्रमीय अनुक्रम में कई अवकलनों की गणना के लिए मौलिक है। उदाहरण के लिए अतिक्रमण प्रतिचित्र तुल्य वर्णक्रमीय अनुक्रम के लिए अवकलन[11]
को निर्धारित करता है, इसलिए कंपन के लिए सेरे वर्णक्रमीय अनुक्रम पर प्रतिचित्र
- देते है।
और अधिक उदाहरण
कुछ उल्लेखनीय वर्णक्रमीय अनुक्रम हैं:
सांस्थिति और ज्यामिति
- एक विशेष सह समरूपता सिद्धांत का अतियाह-हिर्जेब्रुक वर्णक्रमीय अनुक्रम
- एक समूह के वर्गीकरण स्थान की समरूपता के लिए बार वर्णक्रमीय अनुक्रम।
- बॉकस्टीन वर्णक्रमीय अनुक्रम, मॉड p गुणांक के साथ अनुरूपता से संबंधित है और अनुरूपता ने मॉड p को कम कर दिया है।
- कार्टन-लेरे वर्णक्रमीय अनुक्रम भागफल स्थान के अनुरूपता में परिवर्तित हो रहा है।
- एक कंपन के बाधा के विलक्षणता सह समरूपता के लिए ईलेनबर्ग-मूर वर्णक्रमीय अनुक्रम
- एक कंपन का गंभीर वर्णक्रमीय क्रम
समस्थेयता सिद्धांत
- स्थिर समरूपता सिद्धांत में एडम्स वर्णक्रमीय अनुक्रम
- एडम्स-नोविकोव वर्णक्रमीय अनुक्रम, असाधारण सह समरूपता सिद्धांत के लिए एक सामान्यीकरण।
- बैराट वर्णक्रमीय अनुक्रम एक सहभाजन के प्रारंभिक स्थान के समस्थेयता में परिवर्तित हो रहा है।
- बाउसफ़ील्ड-कान वर्णक्रमीय अनुक्रम एक प्रकार्यक के समस्थेयता सह सीमा में परिवर्तित हो रहा है।
- एडम्स-नोविकोव वर्णक्रमीय अनुक्रम की प्रारंभिक प्रतिबन्धों की गणना समस्थेयता निश्चित बिंदु वर्णक्रमीय अनुक्रम
- कोबर वर्णक्रमीय अनुक्रम
- EHP वर्णक्रमीय अनुक्रम क्षेत्रों के स्थिर समस्थेयता समूहों में परिवर्तित हो रहा है
- फेडरर वर्णक्रमीय अनुक्रम एक फलन समष्टि के समस्थेयता समूहों में परिवर्तित हो रहा है।
- समस्थेयता नियत फेडरर वर्णक्रमीय अनुक्रम[12]
- ह्यूरविक्ज़ वर्णक्रमीय अनुक्रम किसी स्थान की समरूपता की समरूपता की गणना के लिए।
- मिलर वर्णक्रमीय अनुक्रम एक अभिसारी के मॉड p स्थिर अनुरूपता में परिवर्तित हो रहा है।
- मिल्नोर वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है।
- मूर वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है।
- एक साधारण समूह की समस्थेयता की गणना के लिए क्विलन वर्णक्रमीय अनुक्रम
- रोथेनबर्ग-स्टीनरोड वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है।
- वैन कम्पेन वर्णक्रमीय अनुक्रम रिक्त स्थान की कील की समस्थेयता की गणना के लिए।
बीजगणित
- चेक सह समरूपता से शेफ सह समरूपता तक चेक-से-व्युत्पन्न प्रकार्यक वर्णक्रमीय अनुक्रम।
- मॉड्यूल के टॉर और Ext समूहों की गणना के लिए वलय वर्णक्रमीय अनुक्रमों का परिवर्तन।
- एक बीजगणित के चक्रीय समरूपता में अभिसरण कोन्स वर्णक्रमीय अनुक्रम।
- गेर्स्टन-विट वर्णक्रमीय अनुक्रम
- सह समरूपता शर्ट के लिए ग्रीन का वर्णक्रमीय अनुक्रम
- व्युत्पन्न प्रकार्यक बनाने के लिए ग्रोथेंडिक वर्णक्रमीय अनुक्रम
- अतिअनुरूपता की गणना के लिए अतिअनुरूपता वर्णक्रमीय अनुक्रम
- अवकलन बीजगणित के टेंसर उत्पाद के अनुरूपता की गणना के लिए कुनेथ वर्णक्रमीय अनुक्रम।
- लेरे वर्णक्रमीय अनुक्रम एक शेफ के सह समरूपता में परिवर्तित हो रहा है।
- स्थानीय-से-वैश्विक Ext वर्णक्रमीय अनुक्रम
- लिंडन-होच्स्चाइल्ड-सेरे वर्णक्रमीय सीक्वेंस इन समूह सह समरूपता अनुरूपता
- एक बीजगणित के Tor या Ext समूहों की गणना के लिए मे वर्णक्रमीय अनुक्रम
- एक विभेदक निस्यंदित समूह का वर्णक्रमीय क्रम: इस लेख में वर्णित है।
- एक दोहरे सम्मिश्र का वर्णक्रमीय क्रम: इस लेख में वर्णित है।
- एक यथार्थ युग्म का वर्णक्रमीय क्रम: इस लेख में वर्णित है।
- सार्वभौमिक गुणांक वर्णक्रमीय अनुक्रम
- वैन एस्ट वर्णक्रमीय अनुक्रम सापेक्ष लाई बीजगणित सह समरूपता में परिवर्तित हो रहा है।
सम्मिश्र और बीजगणितीय ज्यामिति
- विलक्षणता सिद्धांत में अर्नोल्ड का वर्णक्रमीय क्रम।
- बलोच-लिक्टेनबौम वर्णक्रमीय अनुक्रम एक क्षेत्र के बीजगणितीय के-सिद्धांत में परिवर्तित हो रहा है।
- फ्रोलिचेर वर्णक्रमीय अनुक्रम डोलबौल्ट सह-समरूपता से प्रारंभ होता है और विभिन्न प्रकार के बीजगणितीय डी राम सह-समरूपता में परिवर्तित होता है।
- हॉज-डी राम वर्णक्रमीय अनुक्रम विभिन्न प्रकार के बीजगणितीय d राम सह समरूपता में परिवर्तित हो रहा है।
- मोटिविक-से-के-सिद्धांत वर्णक्रमीय अनुक्रम
टिप्पणियाँ
- ↑ McCleary 2001, p. [page needed].
- ↑ Hatcher, Example 1.17.
- ↑ Hatcher, Example 1.18.
- ↑ May.
- ↑ Serge Lang (2002), Algebra, Graduate Texts in Mathematics 211 (in German) (Überarbeitete 3. ed.), New York: Springer-Verlag, ISBN 038795385X
{{citation}}: CS1 maint: unrecognized language (link) - ↑ Elzein, Fouad; Trang, Lê Dung (2013-02-23). "मिश्रित हॉज संरचनाएं". pp. 40, 4.0.2. arXiv:1302.5811 [math.AG].
- ↑ Weibel 1994, Exercise 5.2.1.; there are typos in the exact sequence, at least in the 1994 edition.
- ↑ Weibel 1994, Exercise 5.2.2.
- ↑ Weibel 1994, Application 5.3.5.
- ↑ May, § 1.
- ↑ Hatcher, pp. 540, 564.
- ↑ Bruner, Robert R.; Rognes, John (2005). "होमोलॉजिकल होमोटॉपी फिक्स्ड पॉइंट स्पेक्ट्रल सीक्वेंस में डिफरेंशियल". Algebr. Geom. Topol. 5 (2): 653–690. arXiv:math/0406081. doi:10.2140/agt.2005.5.653.
संदर्भ
परिचयात्मक
- Fomenko, Anatoly; Fuchs, Dmitry, Homotopical Topology
- Hatcher, Allen. "बीजगणितीय टोपोलॉजी में वर्णक्रमीय अनुक्रम" (PDF).
संदर्भ
- Leray, Jean (1946a), "L'anneau d'homologie d'une représentation", Les Comptes rendus de l'Académie des sciences, 222: 1366–1368
- Leray, Jean (1946b), "Structure de l'anneau d'homologie d'une représentation", Les Comptes rendus de l'Académie des sciences, 222: 1419–1422
- Koszul, Jean-Louis (1947). "Sur les opérateurs de dérivation dans un anneau". Comptes rendus de l'Académie des Sciences. 225: 217–219.
- Massey, William S. (1952). "Exact couples in algebraic topology. I, II". Annals of Mathematics. Second Series. Annals of Mathematics. 56 (2): 363–396. doi:10.2307/1969805. JSTOR 1969805.
- Massey, William S. (1953). "Exact couples in algebraic topology. III, IV, V". Annals of Mathematics. Second Series. Annals of Mathematics. 57 (2): 248–286. doi:10.2307/1969858. JSTOR 1969858.
- May, J. Peter. "A primer on spectral sequences" (PDF). Archived (PDF) from the original on 21 Jun 2020. Retrieved 21 Jun 2020.
- McCleary, John (2001). A User's Guide to Spectral Sequences. Cambridge Studies in Advanced Mathematics. Vol. 58 (2nd ed.). Cambridge University Press. ISBN 978-0-521-56759-6. MR 1793722.
- Mosher, Robert; Tangora, Martin (1968), Cohomology Operations and Applications in Homotopy Theory, Harper and Row, ISBN 978-0-06-044627-7
- Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.
अग्रिम पठन
- Chow, Timothy Y. (2006). "You Could Have Invented Spectral Sequences" (PDF). Notices of the American Mathematical Society. 53: 15–19.