प्रवाह संतुलन विश्लेषण: Difference between revisions

Revision as of 08:53, 4 June 2023

अपशिष्ट संतुलन विश्लेषण (एफबीए) उपापचय प्रक्रिया नेटवर्क के जीनोम-मापक्रम पुनर्निर्माण में उपापचय प्रक्रिया का अनुकरण करने के लिए एक गणितीय विधि है। प्रतिरूपण के सैद्धांतिक प्रक्रियाओं की तुलना में, प्रतिरूप के निर्माण के लिए आवश्यक इनपुट डेटा के सन्दर्भ में एफबीए कम प्रकृष्ट है। एफबीए का उपयोग करके किए गए अनुरूपण अभिकलनीय रूप से सस्ते हैं और आधुनिक व्यक्तिगत कंप्यूटरों पर कुछ सेकंड में बड़े प्रतिरूप (2000 से अधिक प्रतिक्रियाओं) के लिए स्थिर-अवस्था उपापचय प्रक्रिया प्रवाह की गणना कर सकते हैं। उपापचयी मार्ग विश्लेषण की संबंधित विधि उपापचय प्रक्रियाओं के बीच सभी संभावित मार्गों को ढूंढने और सूचीबद्ध करने का प्रयास करती है।

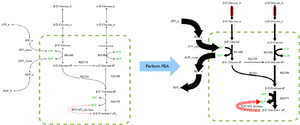
ग्लाइको – अपघटन की शीर्ष छह प्रतिक्रियाओं के तैयार उपापचय प्रक्रिया नेटवर्क पर एफबीए के परिणाम। प्रत्येक प्रतिक्रिया के माध्यम से अनुमानित प्रवाह रेखा की चौड़ाई के समानुपाती होता है। लाल रंग में उद्देश्य फलन, अल्फा-डी-ग्लूकोज और बीटा-डी-ग्लूकोज आयात पर बाधाएं लाल सलाखों के रूप में प्रस्तुत की जाती हैं।^[1]

एफबीए जैव प्रक्रम इंजीनियरिंग में अनुप्रयोग प्राप्त करता है जिससे कि किण्वन प्रक्रियाओं में उपयोग किए जाने वाले रोगाणुओं के उपापचय प्रक्रिया नेटवर्क में व्यवस्थित रूप से संशोधनों की पहचान की जा सके जो इथेनॉल और सक्सिनिक अम्ल जैसे औद्योगिक रूप से महत्वपूर्ण रसायनों के उत्पाद की पैदावार में सुधार करते हैं।^[2] इसका उपयोग कैंसर में उपचारात्मक दवा लक्ष्यों की पहचान के लिए ^[3] और रोगजनक, ^[4] संस्कृति मीडिया का तर्कसंगत डिज़ाइन, ^[5] और मेज़बान-रोगज़नक़ पारस्परिक क्रिया के लिए भी किया गया है। ^[6] एफबीए के परिणामों को दाहिनी ओर की छवि के समान प्रवाह मानचित्रों का उपयोग करके देखा जा सकता है, जो ग्लाइको – अपघटन में प्रतिक्रियाओं द्वारा किए गए स्थिर-अवस्था के प्रवाह को दिखाता है। तीरों की अंतराल मान प्रतिक्रिया के माध्यम से प्रवाह के समानुपाती होती है।

एफबीए एक उपापचय प्रक्रिया नेटवर्क में एकाग्रता परिवर्तन का वर्णन करने वाले समीकरणों की प्रणाली को उचित तत्वानुपातकीय गुणांक (स्टोइकियोमेट्रिक आव्यूह एस) और अनसुलझी अपशिष्ट के सदिश वी के आव्यूह के डॉट उत्पाद के रूप में औपचारिक रूप देता है। डॉट उत्पाद का दाहिना हाथ शून्य का एक सदिश है जो स्थिर अवस्था में क्रमव्यवस्था का प्रतिनिधित्व करता है। रैखिक कार्यरचना का उपयोग तब स्थिर अवस्था के अनुरूप अपशिष्ट के समाधान की गणना के लिए किया जाता है।

इतिहास

अपशिष्ट संतुलन विश्लेषण में कुछ प्रारंभिक काम 1980 के दशक की शुरुआत के हैं। पापौतसकिस^[7] प्रदर्शित किया कि उपापचय प्रक्रिया मानचित्र का उपयोग करके प्रवाह संतुलन समीकरणों का निर्माण करना संभव था। यह वाटसन था,^[8] हालांकि, जिन्होंने सबसे पहले मार्ग में अपशिष्ट को हल करने के लिए रैखिक कार्यरचना और एक उद्देश्य फलन का उपयोग करने का विचार प्रस्तुत किया। पहला महत्वपूर्ण अध्ययन बाद में फेल और स्मॉल द्वारा प्रकाशित किया गया था,^[9] जिन्होंने वसा संश्लेषण में बाधाओं का अध्ययन करने के लिए अधिक विस्तृत उद्देश्य कार्यों के साथ प्रवाह संतुलन विश्लेषण का उपयोग किया।

अनुरूपण

एफबीए द्वारा गणना के अनुसार प्रतिक्रिया लाइनों के वजन द्वारा दिखाए गए अपशिष्ट के साथ एक नमूना उपापचय प्रक्रिया नेटवर्क में एक गैर घातक जीन विलोपन का एक उदाहरण। यहां उद्देश्य फलन के माध्यम से प्रवाह आधा हो गया है लेकिन अभी भी उपलब्ध है।^[1]

एफबीए द्वारा गणना के अनुसार प्रतिक्रिया लाइनों के वजन द्वारा दिखाए गए अपशिष्ट के साथ एक नमूना उपापचय प्रक्रिया नेटवर्क में घातक जीन विलोपन का एक उदाहरण। यहाँ उद्देश्य फलन के माध्यम से कोई प्रवाह नहीं है, यह अनुकरण करते हुए कि मार्ग अब कार्यात्मक नहीं है।^[1]

प्रतिक्रिया निषेध: एक ई.कोली एफबीए प्रतिरूप में ऑक्सीजन (एक्स-अक्ष) के घटते प्रवाह के लिए एफबीए की अनुमानित विकास दर (वाई-अक्ष) का प्लॉट।^{[citation needed]}

माइकोबैक्टीरियम ट्यूबरकुलोसिस की वृद्धि दर पर अलग-अलग ग्लूकोज और ग्लिसरॉल इनपुट अपशिष्ट के प्रभाव को दर्शाने वाला एक 3-डी लक्षणप्ररूप फेज प्लेन। एक्स अक्ष ग्लिसरॉल प्रवाह का प्रतिनिधित्व करता है और वाई अक्ष ग्लूकोज प्रवाह का प्रतिनिधित्व करता है, सतह की ऊंचाई (लाल) इनपुट प्रवाह के प्रत्येक संयोजन के लिए विकास प्रवाह के मूल्य का प्रतिनिधित्व करती है।^{[citation needed]}

File:Phenotypic Phase Plane for M.tb, on Glycerol and Glucose.png

माइकोबैक्टीरियम ट्यूबरकुलोसिस की वृद्धि दर पर अलग-अलग ग्लूकोज और ग्लिसरॉल इनपुट अपशिष्ट के प्रभाव को दिखाते हुए लक्षणप्ररूप फेज प्लेन का एक लेवलप्लॉट संस्करण। एक्स अक्ष ग्लिसरॉल प्रवाह का प्रतिनिधित्व करता है और वाई अक्ष ग्लूकोज प्रवाह का प्रतिनिधित्व करता है, रंग विकास प्रवाह के मूल्य का प्रतिनिधित्व करता है।^{[citation needed]}

ई.कोलाई (बाएं) और एम.ट्यूबरकुलोसिस (दाएं) के लिए विभिन्न उपप्रणालियों में घातक युग्मित प्रतिक्रिया विलोपन के सहसंबंध भूखंडों की तुलना।^{[citation needed]}

अपशिष्ट संतुलन विश्लेषण अभिकलनीय रूप से प्रकृष्ट नहीं है, एक विशिष्ट नेटवर्क (लगभग 2000 प्रतिक्रियाओं) के लिए जैव ईंधन उत्पादन के लिए इष्टतम प्रवाह की गणना करने के लिए सेकंड के क्रम में उपयोग किया जा सकता है। इसका तात्पर्य यह है कि नेटवर्क से प्रतिक्रियाओं को हटाने और/या अपशिष्ट बाधाओं को रूपांतरित करने का प्रभाव एक ही कंप्यूटर पर समझदारी से तैयार किया जा सकता है।

जीन/प्रतिक्रिया विलोपन और त्रुटि अध्ययन

एकल प्रतिक्रिया विलोपन

जैव ईंधन के उत्पादन के लिए विशेष रूप से महत्वपूर्ण प्रतिक्रियाओं के लिए एक उपापचय प्रक्रिया नेटवर्क की खोज करने के लिए अधिकांशतः उपयोग की जाने वाली तकनीक का प्रयोग किया जाता है। उसके स्थान पर एक नेटवर्क में प्रत्येक प्रतिक्रिया को हटाकर और जैव ईंधन फलन के माध्यम से अनुमानित प्रवाह को मापकर, (यदि जैव ईंधन फलन के माध्यम से प्रवाह काफी कम हो जाता है) या गैर-आवश्यक (यदि जैव ईंधन के माध्यम से प्रवाह) कार्य अपरिवर्तित है या केवल थोड़ा कम है) प्रत्येक प्रतिक्रिया को या तो आवश्यक रूप से वर्गीकृत किया जा सकता है।

जोड़ो में प्रतिक्रिया विलोपन

दवाओं के लक्ष्यों की तलाश करते समय सभी संभावित जोड़े प्रतिक्रियाओं का युग्मित प्रतिक्रिया विलोपन उपयोगी होता है, क्योंकि यह बहु-लक्षित उपचारों के अनुकरण की अनुमति देता है, या तो एक ही दवा द्वारा कई लक्ष्यों के साथ या दवा संयोजनों द्वारा अनुमति देता है। दोहरे विलोपन अध्ययन भी विभिन्न मार्गों के बीच सिंथेटिक घातक अंतःक्रियाओं की मात्रा निर्धारित कर सकते हैं जो समग्र नेटवर्क मजबूती के लिए मार्ग के योगदान का एक उपाय प्रदान करते हैं।

एकल और एकाधिक जीन विलोपन

जीन जीन-प्रोटीन-प्रतिक्रिया अभिव्यक्ति (जीपीआर) के रूप में जाने वाले बूलियन अभिव्यक्ति द्वारा प्रकिण्व -उत्प्रेरित प्रतिक्रियाओं से जुड़े होते हैं। सामान्यतः एक जीपीआर यह इंगित करने के लिए (जीन ए और जीन बी) रूप लेता है कि जीन ए और बी के उत्पाद प्रोटीन उप-इकाइयां हैं जो पूर्ण प्रोटीन बनाने के लिए संग्रहित होते हैं और इसलिए किसी की अनुपस्थिति के परिणामस्वरूप प्रतिक्रिया को हटा दिया जाएगा। दूसरी ओर, यदि जीपीआर (जीन ए या जीन बी) है तो इसका तात्पर्य है कि जीन ए और बी के उत्पाद सम प्रकिण्व हैं। इसलिए, बूलियन अभिव्यक्ति के रूप में जीपीआर के मूल्यांकन द्वारा एकल या एकाधिक जीन विलोपन के प्रभाव का मूल्यांकन करना संभव है। यदि जीपीआर गलत का मूल्यांकन करता है, तो प्रतिक्रिया एफबीए करने से पहले प्रतिरूप में शून्य तक सीमित है। इस प्रकार जीन नॉकआउट को अपशिष्ट संतुलन विश्लेषण का उपयोग करके अनुरूपित किया जा सकता है।

जीन की व्याख्या और प्रतिक्रिया विलोपन परिणाम

एफबीए के साथ अध्ययन किए जा रहे नेटवर्क के लिए जीन-प्रोटीन-प्रतिक्रिया आव्यूह को संग्रहित किया गया है, तो प्रतिक्रिया अवरोधन और विलोपन विश्लेषण की उपयोगिता सबसे स्पष्ट हो जाती है। जीन-प्रोटीन-प्रतिक्रिया आव्यूह एक बाइनरी आव्यूह है जो जीन को उनसे बने प्रोटीन से जोड़ता है। इस आव्यूह का उपयोग करके, प्रतिक्रिया अनिवार्यता को जीन अनिवार्यता में परिवर्तित किया जा सकता है जो जीन अवगुण का संकेत देता है जो एक निश्चित रोग लक्षणप्ररूप या प्रोटीन/प्रकिण्व (और इस प्रकार रोगजनकों में सबसे आशाजनक दवा लक्ष्य हैं) जो आवश्यक हैं। हालांकि, जीन-प्रोटीन-प्रतिक्रिया आव्यूह प्रकिण्व के संबंध में जीन के बीच बूलियन संबंध को निर्दिष्ट नहीं करता है, इसके अतिरिक्त यह केवल उनके बीच संबंध को इंगित करता है। इसलिए, इसका उपयोग केवल तभी किया जाना चाहिए जब बूलियन जीपीआर अभिव्यक्ति अनुपलब्ध हो।

प्रतिक्रिया निषेध

प्रतिक्रिया को पूरी तरह से हटाने के अतिरिक्त इसे रोकने के प्रभाव को इसके माध्यम से अनुमत प्रवाह को प्रतिबंधित करके एफबीए में अनुरूपित किया जा सकता है। एक निषेध के प्रभाव को घातक या गैर-घातक के रूप में वर्गीकृत किया जा सकता है, जैसा कि विलोपन के सन्दर्भ में होता है, जहां "थोड़ा कम" से "काफी कम" को अलग करने के लिए एक उपयुक्त सीमा का उपयोग किया जाता है। सामान्यतः दहलीज का चुनाव मनमाना होता है लेकिन विकास प्रयोगों से एक उचित अनुमान प्राप्त किया जा सकता है जहां अनुरूपित अवरोध/विलोपन वास्तव में किया जाता है और विकास दर को मापा जाता है।

विकास मीडिया अनुकूलन

बढ़ी हुई विकास दर या उपयोगी उप-उत्पाद स्राव के संबंध में इष्टतम विकास मीडिया को डिजाइन करने के लिए, लक्षणप्ररूप चरण विमान विश्लेषण के रूप में ज्ञात विधि का उपयोग करना संभव है। पीएचपीपी में प्रतिरूप पर बार-बार एफबीए लागू करना सम्मिलित है, जबकि पोषक तत्व तेज बाधाओं को अलग-अलग करते हैं और उद्देश्य फलन (या उप-उत्पाद प्रवाह) के मूल्य को देखते हैं। पीएचपीपी उन पोषक तत्वों के इष्टतम संयोजन को खोजना संभव बनाता है जो किसी विशेष लक्षणप्ररूप या उपापचय प्रक्रिया के एक तरीके का पक्ष लेते हैं जिसके परिणामस्वरूप उच्च विकास दर या औद्योगिक रूप से उपयोगी उप-उत्पादों का स्राव होता है। अलग-अलग मीडिया में बैक्टीरिया की अनुमानित विकास दर प्रयोगात्मक परिणामों के साथ अच्छी तरह से सहसंबंधित दिखाई गई है,^[10]साथ ही साल्मोनेला टाइफिम्यूरियम की संस्कृति के लिए सटीक न्यूनतम मीडिया को परिभाषित करने के लिए दिखाई गई है।^[11]

उच्च पोषक -रोगज़नक़ पारस्परिक क्रिया

मानव सूक्ष्मजीविता एक जटिल प्रणाली है जिसमें 400 ट्रिलियन सूक्ष्म जीव और बैक्टीरिया एक दूसरे और उच्च पोषक के साथ पारस्परिक क्रिया करते हैं। इस सन्दर्भ में, जैव ईंधन उद्देश्य फलन को अधिकतम करने के लिए उपापचय प्रक्रिया प्रणाली को अनुकूलित किया गया था। इस प्रणाली में प्रमुख कारकों को समझने के लिए; एक बहु-स्तरीय, गतिशील प्रवाह-संतुलन विश्लेषण प्रस्तावित है क्योंकि अपशिष्ट संतुलन विश्लेषण को कम अभिकलनीय रूप से प्रकृष्ट के रूप में वर्गीकृत किया गया है।^[12]

गणितीय विवरण

युग्मित साधारण अंतर समीकरणों का उपयोग करते हुए उपापचय प्रक्रिया प्रतिरूपण के सैद्धांतिक दृष्टिकोण के विपरीत, प्रवाह संतुलन विश्लेषण के लिए प्रकिण्व गतिज मापदंडों और प्रणाली में उपापचय प्रक्रियाओं की एकाग्रता के संदर्भ में बहुत कम जानकारी की आवश्यकता होती है। यह दो धारणाएं, स्थिर अवस्था और इष्टतमता बनाकर इसे प्राप्त करता है। पहली धारणा यह है कि प्रतिरूप की गई प्रणाली एक स्थिर स्थिति में प्रवेश कर चुकी है, जहां उपापचय सांद्रता अब नहीं बदलती है, अर्थात प्रत्येक उपापचय नोड में उत्पादक और उपभोग करने वाले अपशिष्ट एक दूसरे को निष्क्रिय कर देते हैं। दूसरी धारणा यह है कि जीव को कुछ जैविक लक्ष्य के लिए विकास के माध्यम से अनुकूलित किया गया है, जैसे इष्टतम विकास या संसाधनों का संरक्षण इत्यादि। स्थिर-अवस्था धारणा प्रणाली को रेखीय समीकरणों के एक सेट तक कम कर देती है, जिसे तब प्रवाह वितरण ढूंढने के लिए हल किया जाता है जो छद्म-प्रतिक्रिया (उद्देश्य फलन) के मान को अधिकतम करते हुए उचित तत्वानुपातकीय बाधाओं के अधीन स्थिर-अवस्था की स्थिति को संतुष्ट करता है। जैव ईंधन अग्रदूतों के जैव ईंधन में रूपांतरण का प्रतिनिधित्व करता है।

जैव प्रक्रम इंजीनियरिंग में किण्वकों में सूक्ष्मजैविकी कोशिकाओं के विकास को प्रतिरूप करने के लिए विकसित सामग्री संतुलन के विचारों के लिए स्थिर-अवस्था की धारणा है। सूक्ष्मजैविकी विकास के समय, जैव ईंधन उत्पन्न करने के लिए ट्रेस तत्वों के साथ कार्बन, हाइड्रोजन, ऑक्सीजन और नाइट्रोजन स्रोतों के एक जटिल मिश्रण से युक्त एक कार्यद्रव्य का सेवन किया जाता है।

इस प्रक्रिया के लिए सामग्री संतुलन प्रतिरूप बन जाता है:

\mathrm {Input} =\mathrm {Output} +\mathrm {Accumulation}

यदि हम सूक्ष्मजैविकी कोशिकाओं की प्रणाली को स्थिर अवस्था में मानते हैं तो हम संचय अवधि को शून्य पर सेट कर सकते हैं और भौतिक संतुलन समीकरणों को सरल बीजगणितीय समीकरणों में कम कर सकते हैं। ऐसी प्रणाली में, कार्यद्रव्य उस प्रणाली का इनपुट बन जाता है जिसका उपभोग किया जाता है और जैव ईंधन का उत्पादन क्रमव्यवस्था से आउटपुट बन जाता है। भौतिक संतुलन को तब इस प्रकार दर्शाया जा सकता है:

\mathrm {Input} =\mathrm {Output}

\mathrm {Input} -\mathrm {Output} =\mathrm {0}

गणितीय रूप से, बीजगणितीय समीकरणों को गुणांकों के आव्यूह और अज्ञात के सदिश के डॉट उत्पाद के रूप में दर्शाया जा सकता है। चूंकि स्थिर-अवस्था धारणा संचय अवधि को शून्य पर रखती है। क्रमव्यवस्था को इस प्रकार लिखा जा सकता है:

\qquad A\cdot \mathbf {x} =\mathbf {0}

इस विचार को उपापचय प्रक्रिया नेटवर्क तक विस्तारित करना, समीकरणों के उचित तत्वानुपातकीय संतुलित सेट के रूप में एक उपापचय प्रक्रिया नेटवर्क का प्रतिनिधित्व करना संभव है। आव्यूह की औपचारिकता पर चलते हुए, हम समीकरणों को उचित तत्वानुपातकीय गुणांक (उचित तत्वानुपातकीय आव्यूह) के आव्यूह के डॉट उत्पाद के रूप में प्रस्तुत कर सकते हैं $S$ ) और अपशिष्ट का सदिश $\mathbf {v}$ अज्ञात के रूप में और स्थिर स्थिति को लागू करने के लिए दाहिने हाथ की ओर 0 सेट करें।

\qquad S\cdot \mathbf {v} =\mathbf {0}

उपापचयी नेटवर्क में सामान्यतः उपापचयज की तुलना में अधिक प्रतिक्रियाएं होती हैं और यह समीकरणों की तुलना में अधिक चर वाले रैखिक समीकरणों की एक निर्धारित प्रणाली देता है। ऐसे अंडर-निर्धारित क्रमव्यवस्था को हल करने के लिए मानक दृष्टिकोण रैखिक कार्यरचना को लागू करना है।

रैखिक कार्यक्रम ऐसी समस्याएं हैं जिन्हें विहित रूप में व्यक्त किया जा सकता है:

{\begin{aligned}&{\text{maximize}}&&\mathbf {c} ^{\mathrm {T} }\mathbf {x} \\&{\text{subject to}}&&A\mathbf {x} \leq \mathbf {b} \\&{\text{and}}&&\mathbf {x} \geq \mathbf {0} \end{aligned}}

जहाँ x चर राशियों के सदिश को दर्शाता है (निर्धारित किया जाना है), c और b (ज्ञात) गुणांकों के सदिश स्थल हैं, A गुणांकों का एक (ज्ञात) आव्यूह (गणित) है, और ^टीx इस सन्दर्भ में) $(\cdot )^{\mathrm {T} }$ आव्यूह स्थानान्तरण है। अधिकतम या न्यूनतम किए जाने वाले व्यंजक को उद्देश्य फलन ('c') कहा जाता है असमानताएँ Ax ≤ b वे बाधाएँ हैं जो एक उत्तल पॉलीटॉप निर्दिष्ट करती हैं जिसके ऊपर उद्देश्य फलन को अनुकूलित किया जाना है।

रैखिक कार्यरचना के लिए एक उद्देश्य फलन की परिभाषा की आवश्यकता होती है। एलपी समस्या का इष्टतम समाधान उस समाधान के रूप में माना जाता है जो बिंदु के सन्दर्भ के आधार पर उद्देश्य फलन के मूल्य को अधिकतम या कम करता है। प्रवाह संतुलन विश्लेषण के सन्दर्भ में, एलपी के लिए उद्देश्य फलन जेड को अधिकांशतः जैव ईंधन उत्पादन के रूप में परिभाषित किया जाता है। जैव ईंधन उत्पादन एक गांठ वाली प्रतिक्रिया का प्रतिनिधित्व करने वाले समीकरण द्वारा अनुरूपित होता है जो विभिन्न जैव ईंधन अग्रदूतों को जैव ईंधन की एक इकाई में परिवर्तित करता है।

इसलिए, अपशिष्ट संतुलन विश्लेषण समस्या का विहित रूप होगा:

{\begin{aligned}&{\text{maximize}}&&\mathbf {c} ^{\mathrm {T} }\mathbf {v} \\&{\text{subject to}}&&S\mathbf {v} =\mathbf {0} \\&{\text{and}}&&\mathbf {lowerbound} \leq \mathbf {v} \leq \mathbf {upperbound} \end{aligned}}

जहाँ $\mathbf {v}$ अपशिष्ट के सदिश का प्रतिनिधित्व करता है (निर्धारित किया जाना), $S$ गुणांकों का एक (ज्ञात) आव्यूह (गणित) है। अधिकतम या न्यूनतम किए जाने वाले व्यंजक को उद्देश्य फलन कहते हैं ( $\mathbf {c} ^{\mathrm {T} }\mathbf {v}$ इस सन्दर्भ में)। असमानताएं $\mathbf {lowerbound} \leq \mathbf {v}$ और $\mathbf {v} \leq \mathbf {upperbound}$ के स्तंभों के अनुरूप प्रत्येक प्रतिक्रिया के लिए प्रवाह की न्यूनतम और अधिकतम दरों को क्रमशः परिभाषित करें $S$ आव्यूह। इन दरों को प्रयोगात्मक रूप से प्रतिरूप की भविष्यवाणिय सटीकता को और भी बेहतर बनाने के लिए निर्धारित किया जा सकता है या उन्हें मनमाने ढंग से उच्च मूल्य के लिए निर्दिष्ट किया जा सकता है जो प्रतिक्रिया के माध्यम से प्रवाह पर कोई बाधा नहीं दर्शाता है।

प्रवाह संतुलन दृष्टिकोण का मुख्य लाभ यह है कि इसके लिए उपापचय सांद्रता, या इससे भी महत्वपूर्ण बात, क्रमव्यवस्था के प्रकिण्व गतिकी के ज्ञान की आवश्यकता नहीं होती है; समस्थिति धारणा किसी भी समय उपापचय सांद्रता के ज्ञान की आवश्यकता को रोकती है जब तक कि मात्रा स्थिर रहती है, और इसके अतिरिक्त यह विशिष्ट दर समीकरण की आवश्यकता को हटा देता है क्योंकि यह मानता है कि स्थिर अवस्था में, उपापचय के आकार में कोई परिवर्तन नहीं होता है। किसी विशिष्ट उद्देश्य फलन के गणितीय अधिकतमकरण के लिए अकेले उचित तत्वानुपातकीय गुणांक पर्याप्त हैं।

वस्तुनिष्ठ कार्य अनिवार्य रूप से इस बात का माप है कि क्रमव्यवस्था में प्रत्येक घटक वांछित उत्पाद के उत्पादन में कैसे योगदान देता है। उत्पाद स्वयं प्रतिरूप के उद्देश्य पर निर्भर करता है, लेकिन सबसे आम उदाहरणों में से एक कुल जैव ईंधन का अध्ययन है। अपशिष्ट संतुलन विश्लेषण की सफलता का एक उल्लेखनीय उदाहरण विभिन्न परिस्थितियों में सुसंस्कृत होने पर प्रोकैरियोट ई. कोलाई की विकास दर का सटीक अनुमान लगाने की क्षमता है।^[10] इस सन्दर्भ में, जैव ईंधन उद्देश्य फलन को अधिकतम करने के लिए उपापचय प्रक्रिया प्रणाली को अनुकूलित किया गया था। हालांकि इस प्रतिरूप का उपयोग किसी भी उत्पाद के उत्पादन को अनुकूलित करने के लिए किया जा सकता है, और अधिकांशतः कुछ जैव प्रौद्योगिकी प्रासंगिक उत्पाद के आउटपुट स्तर को निर्धारित करने के लिए उपयोग किया जाता है। यह सुनिश्चित करने के लिए कि पोषक तत्वों की सांद्रता स्थिर है, प्रतिरूप को रसायन स्थापी या इसी तरह के उपकरणों का उपयोग करके जीवों की खेती करके प्रयोगात्मक रूप से सत्यापित किया जा सकता है। वांछित उद्देश्य के उत्पादन के मापन का उपयोग तब प्रतिरूप को सही करने के लिए किया जा सकता है।

अपशिष्ट संतुलन विश्लेषण की साधारण अवधारणाओं का एक अच्छा विवरण एडवर्ड्स एट अल को स्वतंत्र रूप से उपलब्ध पूरक सामग्री में पाया जा सकता है। 2001^[10]जो नेचर वेबसाइट पर पाया जा सकता है।^[13] अन्य स्रोतों में इस विषय को समर्पित बी. पाल्सन की पुस्तक सिस्टम्स जीव विज्ञान सम्मिलित है^[14] और जे. ऑर्थ द्वारा एक उपयोगी ट्यूटोरियल और पेपर सम्मिलित है।^[15] तकनीक पर जानकारी के कई अन्य स्रोत ली एट 2006, फिस्ट एट अल और लुईस एट अल सहित प्रकाशित वैज्ञानिक साहित्य में उपलब्ध हैं। ^[16] ^[17] .^[18]

प्रतिरूप की तैयारी और शोधन

प्रतिरूप तैयार करने के प्रमुख भाग हैं: बिना अंतराल के एक उपापचयी नेटवर्क बनाना, प्रतिरूप में बाधाएँ जोड़ना, और अंत में एक उद्देश्य फलन (जिसे अधिकांशतः जैव ईंधन फलन कहा जाता है) जोड़ना, सामान्यतः प्रतिरूप किए जा रहे जीव के विकास का अनुकरण करना इत्यादि।

उपापचय प्रक्रिया नेटवर्क और सॉफ्टवेयर उपकरण

ग्लाइको – अपघटन में पहली छह प्रतिक्रियाएँ एफबीए के लिए एक वस्तुनिष्ठ कार्य (लाल) और पोषक तत्वों के आयात और निर्यात (एटीपी, एडीपी, बीडीजी, एडीजी) के माध्यम से क्रमव्यवस्था सीमा (डैश्ड ग्रीन लाइन) के माध्यम से तैयार की गईं।^[1]

कोशिका (जीव विज्ञान), ऊतक (जीव विज्ञान) या जीव तक एकल उपापचयी मार्ग का वर्णन करने वालों से उपापचयी नेटवर्क दायरे में भिन्न हो सकते हैं। एफबीए-तैयार नेटवर्क का आधार बनाने वाले उपापचयी नेटवर्क की मुख्य आवश्यकता यह है कि इसमें कोई अंतराल न हो। इसका सामान्यतः तात्पर्य है कि व्यापक शारीरिक क्यूरेशन की आवश्यकता होती है, जिससे अपशिष्ट -संतुलन विश्लेषण के लिए एक उपापचयी नेटवर्क की तैयारी एक ऐसी प्रक्रिया बन जाती है जिसमें महीनों या वर्ष लग सकते हैं। हालाँकि, हाल की प्रगति जैसे तथाकथित गैप-फिलिंग भरने के तरीकों जैसे हाल के अग्रिम आवश्यक समय को हफ्तों या महीनों तक कम कर सकते हैं।

एफबीए प्रतिरूप बनाने के लिए सॉफ्टवेयर पैकेज में सम्मिलित हैं: पाथवे टूल्स/मेटाअपशिष्ट ,^[19]^[20] सिम्फनी,^[21]^[22] मेटनेटमेकर,^[23] कोबरापी,^[24] कार्वमे,^[25] एमआईओएम,^[26] या कब्रिक्सा इत्यादि।^[27]

सामान्यतः प्रतिरूप बायोपैक्स या एसबीएमएल प्रारूप में बनाए जाते हैं जिससे कि अन्य सॉफ़्टवेयर में आगे का विश्लेषण या प्रत्यक्षण हो सके, हालांकि यह एक आवश्यकता नहीं है।

बाधाएं

एफबीए का एक महत्वपूर्ण हिस्सा नेटवर्क के अंतर्गत प्रतिक्रियाओं की प्रवाह दर में बाधाओं को जोड़ने की क्षमता है, जिससे उन्हें चयनित मूल्यों की एक सीमा के अंतर्गत रहने के लिए मजबूर किया जा सकता है। यह प्रतिरूप को वास्तविक उपापचय प्रक्रिया को अधिक सटीक रूप से अनुकरण करने देता है। बाधाएं जैविक दृष्टिकोण से दो उपसेट से संबंधित हैं; सीमा बाधाएँ जो पोषक तत्वों के सेवन/उत्सर्जन को सीमित करती हैं और आंतरिक बाधाएँ जो जीव के अंतर्गत प्रतिक्रियाओं के माध्यम से प्रवाह को सीमित करती हैं। गणितीय शब्दों में, एफबीए प्रतिरूप के समाधान स्थान को कम करने के लिए बाधाओं के आवेदन पर विचार किया जा सकता है। एक उपापचय प्रक्रिया नेटवर्क के किनारों पर लागू बाधाओं के अतिरिक्त, नेटवर्क के अंतर्गत गहरी प्रतिक्रियाओं पर बाधाओं को लागू किया जा सकता है। ये बाधाएँ सामान्यतः सरल होती हैं; वे ऊर्जा संबंधी विचारों के कारण प्रतिक्रिया की दिशा को बाधित कर सकते हैं या प्रकृति में सभी प्रतिक्रियाओं की परिमित गति के कारण प्रतिक्रिया की अधिकतम गति को बाधित कर सकते हैं।

विकास मीडिया की कमी

जीवों और अन्य सभी उपापचय प्रक्रिया प्रणालियों को पोषक तत्वों के कुछ इनपुट की आवश्यकता होती है। उदाहरण के लिए जब किसी जीव के विकास का प्रतिरूपण करते हैं तो उद्देश्य फलन को सामान्यतः जैव ईंधन के रूप में परिभाषित किया जाता है। सामान्यतः पोषक तत्वों के ग्रहण की दर उनकी उपलब्धता (एक पोषक तत्व जो उपलब्ध नहीं है, अवशोषित नहीं किया जा सकता है), उनकी एकाग्रता और प्रसार स्थिरांक (तेजी से फैलाने वाले उपापचयज की उच्च सांद्रता अधिक तेज़ी से अवशोषित होती है) और अवशोषण की विधि (जैसे) सक्रिय परिवहन या सुगम प्रसार बनाम सरल प्रसार) द्वारा निर्धारित की जाती है।

यदि कुछ पोषक तत्वों के अवशोषण (और/या उत्सर्जन) की दर को प्रयोगात्मक रूप से मापा जा सकता है तो इस जानकारी को उपापचय प्रक्रिया प्रतिरूप के किनारों पर अपशिष्ट दर पर बाधा के रूप में जोड़ा जा सकता है। यह सुनिश्चित करता है कि पोषक तत्व जो उपलब्ध नहीं हैं या जीव द्वारा अवशोषित नहीं होते हैं, वे इसके उपापचय प्रक्रिया में प्रवेश नहीं करते हैं (प्रवाह दर शून्य तक सीमित है) और इसका तात्पर्य यह भी है कि ज्ञात पोषक तत्वों की तेज दरों का अनुकरण द्वारा पालन किया जाता है। यह सुनिश्चित करने का एक द्वितीयक तरीका प्रदान करता है कि अनुरूपित उपापचय प्रक्रिया में गणितीय रूप से स्वीकार्य गुणों के अतिरिक्त प्रायोगिक रूप से सत्यापित गुण हैं।

ऊष्मप्रवैगिकी प्रतिक्रिया बाधाएँ

सिद्धांत रूप में, सभी प्रतिक्रियाएँ उत्क्रमणीय होती हैं लेकिन व्यवहार में प्रतिक्रियाएँ अधिकांशतः प्रभावी रूप से केवल एक ही दिशा में होती हैं। यह प्रतिक्रिया के उत्पादों की एकाग्रता की तुलना में अभिकारकों की काफी अधिक सांद्रता के कारण हो सकता है। लेकिन अधिक बार ऐसा इसलिए होता है क्योंकि प्रतिक्रिया के उत्पादों में अभिकारकों की तुलना में बहुत कम मुक्त ऊर्जा होती है और इसलिए प्रतिक्रिया की आगे की दिशा अधिक अनुकूल होती है।

आदर्श प्रतिक्रियाओं के लिए,

-\infty <v_{i}<\infty \,

कुछ प्रतिक्रियाओं के लिए एक थर्मोडायनामिक बाधा लागू की जा सकती है (इस सन्दर्भ में आगे)

0<v_{i}<\infty \,

वास्तविक रूप से एक प्रतिक्रिया के माध्यम से प्रवाह अनंत नहीं हो सकता है (यह देखते हुए कि वास्तविक प्रणाली में प्रकिण्व परिमित हैं) जिसका तात्पर्य है कि,

0<v_{i}<v_{\max }\,

प्रायोगिक रूप से मापे गए प्रवाह की कमी

कुछ प्रवाह दरों को प्रयोगात्मक रूप से मापा जा सकता है ( $v_{i,m}\,$ ) और एक उपापचय प्रक्रिया प्रतिरूप के अंतर्गत प्रवाह को कुछ त्रुटि के अंतर्गत विवश किया जा सकता है ( $\varepsilon \,$ ), यह सुनिश्चित करने के लिए कि इन ज्ञात प्रवाह दरों को अनुरूपण में सटीक रूप से पुन: प्रस्तुत किया गया है।

v_{i,m}-\varepsilon <v_{i}<v_{i,m}+\varepsilon \,

नेटवर्क के किनारे पर पोषक तत्वों के अवशोषण के लिए अपशिष्ट दरों को सबसे आसानी से मापा जाता है। रेडियोधर्मी रूप से लेबल किए गए या एनएमआर दृश्यमान उपापचयज का उपयोग करके आंतरिक अपशिष्ट का मापन संभव है।

सीओबीआरए टूलबॉक्स जैसे सॉफ़्टवेयर का उपयोग करके विवश एफबीए-तैयार उपापचय प्रक्रिया प्रतिरूप ^[28] (एमएटीएलबी और पायथन (कार्यरचना भाषा) में उपलब्ध कार्यान्वयन), सरेएफबीए,^[29] या वेब आधारित फेम का विश्लेषण किया जा सकता है।^[30] अतिरिक्त सॉफ़्टवेयर पैकेज अन्यत्र सूचीबद्ध किए गए हैं।^[31] ऐसे सभी सॉफ्टवेयर और उनकी कार्यप्रणाली की व्यापक समीक्षा हाल ही में की गई है।^[32]

पैकेज के रूप में आर (कार्यरचना भाषा) में एक ओपन-सोर्स विकल्प उपलब्ध है एबीसीडीई एफबीए या सिबिल^[33] एफबीए और अन्य बाधा आधारित प्रतिरूपण तकनीकों के प्रदर्शन के ओपन-सोर्स लिए उपलब्ध है।^[34]

उद्देश्य फलन

एफबीए स्थिर-अवस्था समस्या के लिए बड़ी संख्या में गणितीय रूप से स्वीकार्य समाधान दे सकता है $(S{\vec {v}}=0)$ . हालाँकि जैविक हित के समाधान वे हैं जो वांछित उपापचय प्रक्रियाओं को सही अनुपात में उत्पन्न करते हैं। उद्देश्य फलन इन उपापचय प्रक्रियाओं के अनुपात को परिभाषित करता है। उदाहरण के लिए जब किसी जीव के विकास का प्रतिरूपण करते हैं तो उद्देश्य फलन को सामान्यतः जैव ईंधन के रूप में परिभाषित किया जाता है। गणितीय रूप से, यह उचित तत्वानुपातकीय आव्यूह में एक स्तंभ है, जिसकी प्रविष्टियां एस आव्यूह की संबंधित पंक्तियों पर उपलब्ध फैटी एसिड, अमीनो अम्ल और कोशिका वॉल घटकों जैसे जीव संश्लेषण अग्रदूतों के लिए एक सिंक के रूप में मांग या कार्य करती हैं। ये प्रविष्टियां कोशिकीय घटकों के प्रयोगात्मक रूप से मापे गए शुष्क भार अनुपातों का प्रतिनिधित्व करती हैं। इसलिए, यह स्तंभ एक गांठदार प्रतिक्रिया बन जाता है जो विकास और प्रजनन का अनुकरण करता है। इसलिए, प्रायोगिक माप की सटीकता जैव ईंधन फलन की सही परिभाषा में एक आवश्यक भूमिका निभाती है और यह सुनिश्चित करके एफबीए के परिणामों को जैविक रूप से लागू करती है कि उपापचयज का सही अनुपात उपापचय प्रक्रिया द्वारा उत्पादित होता है।

जब छोटे नेटवर्क की प्रतिरूपण की जाती है तो ऑब्जेक्टिव फलन को तदनुसार बदला जा सकता है। इसका एक उदाहरण ग्लाइको – अपघटन पाथवे के अध्ययन में होगा जहां उद्देश्य कार्य को संभवतः एडेनोसाइन ट्रायफ़ोस्फेट और एनएडीएच के एक निश्चित अनुपात के रूप में परिभाषित किया जाएगा और इस प्रकार इस मार्ग द्वारा उच्च ऊर्जा उपापचयज के उत्पादन का अनुकरण किया जाएगा।

उद्देश्य/जैव ईंधन फलन का अनुकूलन

एकल इष्टतम समाधान ढूंढने के लिए रैखिक कार्यरचना का उपयोग किया जा सकता है। एफबीए होमोस्टैटिक धारणा को लागू करके इस बाधा से बचता है, जो जैविक प्रणालियों का एक यथोचित अनुमानित विवरण है। पूरे जीव के उपापचय प्रक्रिया नेटवर्क के लिए सबसे आम जैविक अनुकूलन लक्ष्य अपशिष्ट सदिश का चयन करना होगा ${\vec {v}}$ जो जीव के घटक उपापचयज से बने जैव ईंधन फलन के माध्यम से अपशिष्ट को अधिकतम करता है जिसे उचित तत्वानुपातकीय आव्यूह में रखा जाता है और $v_{\textrm {biomass}}$ या केवल $v_{b}$ निरूपित किया जाता है

\max _{\vec {v}}\ v_{b}\qquad {\textrm {s.t.}}\qquad \mathbf {S} \,{\vec {v}}=0

अधिक सामान्य सन्दर्भ में किसी भी प्रतिक्रिया को परिभाषित किया जा सकता है और जैव ईंधन फलन में जोड़ा जा सकता है या तो शर्त के साथ कि इसे अधिकतम या कम किया जा सकता है यदि एक "इष्टतम" समाधान वांछित है। वैकल्पिक रूप से, और सबसे सामान्य सन्दर्भ में, एक सदिश ${\vec {c}}$ प्रस्तुत किया जा सकता है, जो प्रतिक्रियाओं के भारित सेट को परिभाषित करता है कि रैखिक कार्यरचना प्रतिरूप को अधिकतम या कम करने का लक्ष्य रखना चाहिए,

\max _{\vec {v}}\ {\vec {v}}\cdot {\vec {c}}\qquad {\textrm {s.t.}}\qquad \mathbf {S} \,{\vec {v}}=0.

उचित तत्वानुपातकीय आव्यूह के अंतर्गत केवल एक अलग जैव ईंधन फलन/प्रतिक्रिया होने के सन्दर्भ में ${\vec {c}}$ उस जैव ईंधन फलन के अनुरूप स्थिति में 1 (या कोई गैर-शून्य मान) के मान के साथ सभी शून्यों को सरल करेगा। जहां कई अलग-अलग वस्तुनिष्ठ कार्य थे ${\vec {c}}$ सभी उद्देश्य कार्यों के अनुरूप पदों में भारित मूल्यों के साथ सभी शून्यों को सरल करेगा।

समाधान स्थान को कम करना - क्रमव्यवस्था के लिए जैविक विचार

मैटलैब और ऑक्टेव जैसे आव्यूह संचालन के लिए विशेष सॉफ्टवेयर पैकेजों में मेट्रिसेस के शून्य स्थान का विश्लेषण लागू किया गया है। के शून्य स्थान का निर्धारण $\scriptstyle \mathbf {S}$ हमें अपशिष्ट वैक्टर (या उसके रैखिक संयोजन) के सभी संभावित संग्रह बताता है जो जैविक नेटवर्क के अंतर्गत प्रवाह को संतुलित करता है। इस दृष्टिकोण का लाभ जैविक प्रणालियों में स्पष्ट हो जाता है जो कई अज्ञात के साथ विभेदक समीकरण प्रणालियों द्वारा वर्णित हैं। उपरोक्त अवकल समीकरणों में वेग - $v_{1}$ और $v_{2}$ - अंतर्निहित समीकरणों की प्रतिक्रिया दरों पर निर्भर हैं। वेग सामान्यतः माइकलिस-मेंटेन गतिकी | माइकलिस-मेंटेन काइनेटिक सिद्धांत से लिए जाते हैं, जिसमें प्रतिक्रियाओं को उत्प्रेरित करने वाले प्रकिण्व के गतिज पैरामीटर और स्वयं उपापचयज की एकाग्रता सम्मिलित होती है। जीवित जीवों से प्रकिण्व को अलग करना और उनके गतिज मापदंडों को मापना एक कठिन कार्य है, जैसा कि एक जीव के अंतर्गत आंतरिक सांद्रता और उपापचयज के प्रसार स्थिरांक को मापना है। यह एक ऐसी समस्या है जिससे गतिशील उपापचय प्रक्रिया अनुरूपण अनुमानतः बचेंगे। इसलिए, उपापचयी प्रतिरूपण के लिए अंतर समीकरण दृष्टिकोण विज्ञान के वर्तमान दायरे से परे है, लेकिन सबसे अधिक अध्ययन किए गए जीवों के लिए।^[35] एफबीए होमोस्टैटिक धारणा को लागू करके इस बाधा से बचता है, जो जैविक प्रणालियों का एक यथोचित अनुमानित विवरण है।

हालांकि एफबीए उस जैविक बाधा से बचता है, एक बड़े समाधान स्थान का गणितीय मुद्दा बना रहता है। एफबीए का दोहरा उद्देश्य है। क्रमव्यवस्था की जैविक सीमाओं का सटीक रूप से प्रतिनिधित्व करना और लक्ष्य प्रणाली/जीव के अंतर्गत प्राकृतिक अपशिष्ट के निकटतम अपशिष्ट वितरण को वापस करना। मीडिया पर नॉकआउट या विकास का अनुकरण करते समय, एफबीए अंतिम स्थिर-अवस्था फ़्लक्स वितरण देता है। कुछ जैविक सिद्धांत गणितीय कठिनाइयों को दूर करने में मदद कर सकते हैं। जबकि उचित तत्वानुपातकीय आव्यूह लगभग सदैव प्रारंभिक रूप से निर्धारित होता है (जिसका तात्पर्य है कि समाधान स्थान $\scriptstyle \mathbf {S} \,{\vec {v}}=0$ बहुत बड़ा है), समाधान स्थान के आकार को कम किया जा सकता है और समाधान पर कुछ बाधाओं के आवेदन के माध्यम से समस्या के जीव विज्ञान के प्रति अधिक चिंतनशील बनाया जा सकता है।

विस्तारण

एफबीए की सफलता और इसकी सीमाओं की प्राप्ति ने उन विस्तारों को जन्म दिया है जो तकनीक की सीमाओं की मध्यस्थता करने का प्रयास करते हैं।

प्रवाह परिवर्तनशीलता विश्लेषण

संपूर्ण नेटवर्क पर एफवीए का दृश्य और संख्यात्मक प्रतिनिधित्व।^[1]

अपशिष्ट -संतुलन समस्या का इष्टतम समाधान कई संभावित, और समान रूप से इष्टतम, उपलब्ध समाधानों के साथ अनुमानतः ही कभी अनूठा होता है। अपशिष्ट वेरिएबिलिटी विश्लेषण (एफवीए), कुछ विश्लेषण सॉफ्टवेयर में निर्मित, प्रत्येक प्रतिक्रिया के माध्यम से अपशिष्ट के लिए सीमाएं लौटाता है, जो अन्य अपशिष्ट के सही संयोजन के साथ जोड़ा जा सकता है, इष्टतम समाधान का अनुमान लगाता है।

गैर-घातक विलोपन वाले नेटवर्क पर एफवीए का दृश्य और संख्यात्मक प्रतिनिधित्व।^[1]

प्रतिक्रियाएँ जो उनके माध्यम से अपशिष्ट की कम परिवर्तनशीलता का समर्थन कर सकती हैं, एक जीव के लिए उच्च महत्व की होने की संभावना है और एफवीए महत्वपूर्ण प्रतिक्रियाओं की पहचान के लिए एक आशाजनक तकनीक है।

उपापचय प्रक्रिया समायोजन का न्यूनीकरण (एमओएमए)

मीडिया पर नॉकआउट या विकास का अनुकरण करते समय, एफबीए अंतिम स्थिर-अवस्था फ़्लक्स वितरण देता है। यह अंतिम स्थिर अवस्था अलग-अलग समय-मानों में पहुँचती है। उदाहरण के लिए, प्राथमिक कार्बन स्रोत के रूप में ग्लिसरॉल पर ई. कोलाई की अनुमानित विकास दर एफबीए भविष्यवाणियों से मेल नहीं खाती; हालाँकि, 40 दिनों या 700 पीढ़ियों के लिए उप-संवर्धन पर, विकास दर अनुकूल रूप से एफबीए भविष्यवाणी से मेल खाने के लिए विकसित हुई।^[36]

कभी-कभी यह पता लगाने में रुचि होती है कि त्रुटि या नॉकआउट का तत्काल प्रभाव क्या होता है, क्योंकि विनियामक परिवर्तन होने में समय लगता है और जीव के लिए अपशिष्ट को पुनः व्यवस्थित करने के लिए एक अलग कार्बन स्रोत का उपयोग करने या प्रभाव को रोकने के लिए नॉक आउट। एमओएमए जंगली प्रकार के एफबीए प्रवाह वितरण और द्विघात कार्यरचना का उपयोग करते हुए उत्परिवर्ती प्रवाह वितरण के बीच की दूरी (यूक्लिडियन) को कम करके त्रुटि के बाद तत्काल उप-इष्टतम प्रवाह वितरण की भविष्यवाणी करता है। यह फॉर्म की अनुकूलन समस्या उत्पन्न करता है।

$\min \ ||\mathbf {v_{w}} -\mathbf {v_{d}} ||^{2}\qquad s.t.\quad \mathbf {S} \cdot \mathbf {v_{d}} =0$ जहाँ $\mathbf {v_{w}}$ जंगली प्रकार (या अपरंपरागत अवस्था) प्रवाह वितरण का प्रतिनिधित्व करता है और $\mathbf {v_{d}}$ जीन विलोपन पर प्रवाह वितरण का प्रतिनिधित्व करता है जिसे हल किया जाना है। यह सरल करता है:

$\min \ {\frac {1}{2}}\,{\mathbf {v_{d}} }^{T}\,\mathbf {I} \,\mathbf {v_{d}} +(\mathbf {-v_{w}} )\cdot \mathbf {v_{d}} \qquad s.t.\quad \mathbf {S} \cdot \mathbf {v_{d}} =0$

यह एमओएमए समाधान है जो त्रुटि के तुरंत बाद अपशिष्ट वितरण का प्रतिनिधित्व करता है।^[37]

विनियामक ऑन-ऑफ न्यूनीकरण (आरओओएम)

आरओओएम एक जीन नॉकआउट के बाद किसी जीव की उपापचय प्रक्रिया स्थिति की भविष्यवाणी में सुधार करने का प्रयास करता है। यह एमओएमए के समान आधार का पालन करता है कि एक जीव नॉकआउट के बाद जंगली प्रकार के जितना संभव हो सके अपशिष्ट वितरण को बहाल करने का प्रयास करेगा। हालाँकि यह आगे परिकल्पना करता है कि नियामक नेटवर्क द्वारा क्षणिक उपापचय प्रक्रिया परिवर्तनों की एक श्रृंखला के माध्यम से इस स्थिर स्थिति तक पहुँचा जा सकता है और जीव जंगली प्रकार की स्थिति तक पहुँचने के लिए आवश्यक नियामक परिवर्तनों की संख्या को कम करने की कोशिश करेगा। दूरी मीट्रिक न्यूनीकरण का उपयोग करने के अतिरिक्त यह एक मिश्रित पूर्णांक रैखिक कार्यरचना विधि का उपयोग करता है।^[38]

सक्रिय एफबीए

सक्रिय एफबीए समय के साथ प्रतिरूप को रूपांतरित करने की क्षमता को जोड़ने का प्रयास करता है, इस प्रकार कुछ प्रक्रियाओं से शुद्ध एफबीए की सख्त स्थिर स्थिति से बचा जाता है। यह संभावना नहीं है कि एफबीए, उदाहरण के लिए, एक तंत्रिका कोशिका के कार्य का अनुकरण कर सकता है। सामान्यतः तकनीक में एक एफबीए अनुरूपण चलाना, उस अनुरूपण के आउटपुट के आधार पर प्रतिरूप को बदलना और अनुरूपण को पुनः चलाना सम्मिलित होता है। इस प्रक्रिया को दोहराने से समय के साथ फीडबैक का एक तत्व प्राप्त होता है।

अन्य तकनीकों के साथ तुलना

एफबीए चोक प्वाइंट विश्लेषण की तुलना में कम सरलीकृत विश्लेषण प्रदान करता है जबकि प्रतिक्रिया दरों पर बहुत कम जानकारी की आवश्यकता होती है और एक पूर्ण गतिशील अनुरूपण की तुलना में बहुत कम पूर्ण नेटवर्क पुनर्निर्माण की आवश्यकता होती है। यह एक ऐसी समस्या है जिससे गतिशील उपापचय प्रक्रिया अनुरूपण अनुमानतः बचेंगे। एफबीए होमोस्टैटिक धारणा को लागू करके इस बाधा से बचता है, जो जैविक प्रणालियों का एक यथोचित अनुमानित विवरण है। इस स्थान को भरने में, एफबीए को सेलुलर क्रमव्यवस्था की उपापचय प्रक्रिया क्षमताओं के विश्लेषण के लिए एक बहुत ही उपयोगी तकनीक के रूप में दिखाया गया है।

चोक पॉइंट विश्लेषण

चोक पॉइंट विश्लेषण के विपरीत, जो केवल नेटवर्क में उन बिंदुओं पर विचार करता है जहां उपापचयज का उत्पादन होता है लेकिन उपभोग नहीं किया जाता है या इसके विपरीत, एफबीए उपापचय प्रक्रिया नेटवर्क प्रतिरूपण का एक वास्तविक रूप है क्योंकि यह उपापचयी नेटवर्क को सभी चरणों में एक पूर्ण इकाई ( उचित तत्वानुपातकीय आव्यूह) के रूप में मानता है। विश्लेषण। इसका तात्पर्य है कि नेटवर्क प्रभाव, जैसे कि एक दूसरे को प्रभावित करने वाले दूर के रास्ते में रासायनिक प्रतिक्रियाएं, प्रतिरूप में पुन: उत्पन्न की जा सकती हैं। नेटवर्क प्रभावों का अनुकरण करने के लिए चोक पॉइंट विश्लेषण की अक्षमता का उल्टा यह है कि यह एक नेटवर्क के अंतर्गत प्रत्येक प्रतिक्रिया को अलगाव में मानता है और इस प्रकार एक नेटवर्क में महत्वपूर्ण प्रतिक्रियाओं का सुझाव दे सकता है, भले ही नेटवर्क अत्यधिक खंडित हो और इसमें कई अंतराल हों।

गतिशील उपापचय प्रक्रिया अनुरूपण

सक्रिय उपापचयी अनुरूपण के विपरीत, एफबीए मानता है कि क्रमव्यवस्था के अंतर्गत उपापचयज की आंतरिक सांद्रता समय के साथ स्थिर रहती है और इस प्रकार स्थिर-अवस्था समाधान के अतिरिक्त कुछ भी प्रदान करने में असमर्थ है। यह संभावना नहीं है कि एफबीए, उदाहरण के लिए, एक तंत्रिका कोशिका के कार्य का अनुकरण कर सकता है। चूंकि एक प्रतिरूप के अंतर्गत उपापचयज की आंतरिक एकाग्रता पर विचार नहीं किया जाता है, यह संभव है कि एक एफबीए समाधान में जैविक रूप से स्वीकार्य होने के लिए बहुत अधिक एकाग्रता में उपापचयज हो सकते हैं। यह एक ऐसी समस्या है जिससे गतिशील उपापचय प्रक्रिया अनुरूपण अनुमानतः बचेंगे। गतिशील अनुरूपण पर एफबीए की सादगी का एक फायदा यह है कि वे अभिकलनीय रूप से बहुत कम खर्चीले हैं, जिससे नेटवर्क में बड़ी संख्या में त्रुटि का अनुकरण हो सकता है। एक दूसरा लाभ यह है कि प्रकिण्व दर और प्रकिण्व गतिकी पर जटिल अंतःक्रियाओं के प्रभाव पर विचार करने की आवश्यकता से बचकर पुनर्निर्मित प्रतिरूप काफी सरल हो सकता है।

यह भी देखें

संदर्भ

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 Forth, Thomas (2012). मलेरिया परजीवी का मेटाबोलिक सिस्टम बायोलॉजी. Leeds, UK: University of Leeds. ISBN 978-0-85731-297-6.
↑ Ranganathan, Sridhar; Suthers, Patrick F.; Maranas, Costas D. (2010). "OptForce: An Optimization Procedure for Identifying All Genetic Manipulations Leading to Targeted Overproductions". PLOS Comput Biol. 6 (4): e1000744. Bibcode:2010PLSCB...6E0744R. doi:10.1371/journal.pcbi.1000744. PMC 2855329. PMID 20419153.
↑ Lewis, NE; Abdel-Haleem, AM (2013). "कैंसर चयापचय के जीनोम-स्केल मॉडल का विकास". Front. Physiol. 4: 237. doi:10.3389/fphys.2013.00237. PMC 3759783. PMID 24027532.
↑ Raman, Karthik; Yeturu, Kalidas; Chandra, Nagasuma (2008). "targetTB: इंटरएक्टोम, रिएक्टोम और जीनोम-स्केल स्ट्रक्चरल विश्लेषण के माध्यम से माइकोबैक्टीरियम ट्यूबरकुलोसिस के लिए एक लक्ष्य पहचान पाइपलाइन". BMC Systems Biology. 2 (1): 109. doi:10.1186/1752-0509-2-109. PMC 2651862. PMID 19099550.
↑ {{cite journal | last1 = Yang | first1 = Hong | last2 = Roth | first2 = Charles M. | last3 = Ierapetritou | first3 = Marianthi G. | year = 2009 | title = हेपेटोसाइट संस्कृति में अमीनो एसिड पूरकता के लिए एक तर्कसंगत डिजाइन दृष्टिकोण| journal = Biotechnology and Bioengineering | volume = 103 | issue = 6| pages = 1176–1191 | doi = 10.1002/bit.22342 | pmid = 19422042 | s2cid = 13230467 }
↑ {{cite journal | last1 = Raghunathan | first1 = Anu | last2 = Shin | first2 = Sookil | last3 = Daefler | first3 = Simon | year = 2010 | title = बायोथ्रेट एजेंट फ्रांसिसैला के साथ संक्रमण में मेजबान-रोगज़नक़ की बातचीत की जांच करने के लिए सिस्टम दृष्टिकोण। फ्रांसिसैला तुलारेन्सिस का प्रतिबन्ध आधारित मॉडल| journal = BMC Systems Biology | volume = 4 | issue = 1| page = 118 | doi = 10.1186/1752-0509-4-118 | pmid = 20731870 | pmc = 2933595 }
↑ Papoutsakis, ET (1984). "ब्यूटिरिक एसिड बैक्टीरिया के किण्वन के लिए समीकरण और गणना". Biotechnology and Bioengineering. 26 (2): 174–187. doi:10.1002/bit.260260210. PMID 18551704. S2CID 25023799.
↑ Watson MR (1984) Metabolic maps for the Apple II. 12, 1093-1094
↑ Fell, DA; Small, JR (1986). "वसा ऊतक में वसा संश्लेषण। रससमीकरणमितीय बाधाओं की एक परीक्षा". Biochem J. 238 (3): 781–786. doi:10.1042/bj2380781. PMC 1147204. PMID 3800960.
↑ ^10.0 ^10.1 ^10.2 Edwards, J.; Ibarra, R.; Palsson, B. (2001). "Escherichia कोलाई चयापचय क्षमताओं की 'इन सिलिको' भविष्यवाणियां प्रयोगात्मक डेटा के अनुरूप हैं". Nature Biotechnology. 19 (2): 125–130. doi:10.1038/84379. PMID 11175725. S2CID 1619105.
↑ Raghunathan, A.; et al. (2009). "मेजबान-रोगज़नक़ बातचीत के दौरान साल्मोनेला टाइफीम्यूरियम की चयापचय क्षमता का विश्लेषण आधारित विश्लेषण". BMC Systems Biology. 3: 38. doi:10.1186/1752-0509-3-38. PMC 2678070. PMID 19356237.
↑ Hoek, Milan J. A. van; Merks, Roeland M. H. (2017-05-16). "आंत माइक्रोबियल चयापचय के एक स्थानिक मॉडल में क्रॉस-फीडिंग इंटरैक्शन के कारण माइक्रोबियल विविधता का उद्भव". BMC Systems Biology. 11 (1): 56. doi:10.1186/s12918-017-0430-4. ISSN 1752-0509. PMC 5434578. PMID 28511646.
↑ "संग्रहीत प्रति". Archived from the original on 2008-02-01. Retrieved 2007-12-01.
↑ Palsson, B.O. Systems Biology: Properties of Reconstructed Networks. 334(Cambridge University Press: 2006).
↑ Orth, J.D.; Thiele, I.; Palsson, B.Ø. (2010). "What is flux balance analysis?". Nature Biotechnology. 28 (3): 245–248. doi:10.1038/nbt.1614. PMC 3108565. PMID 20212490.
↑ Lee, J.M.; Gianchandani, E.P.; Papin, J.A. (2006). "चयापचयों के युग में प्रवाह संतुलन विश्लेषण". Briefings in Bioinformatics. 7 (2): 140–50. doi:10.1093/bib/bbl007. PMID 16772264.
↑ Feist, A.M.; Palsson, B.Ø. (2008). "Escherichia कोलाई का उपयोग करके जीनोम-स्केल चयापचय पुनर्निर्माण के अनुप्रयोगों का बढ़ता दायरा". Nature Biotechnology. 26 (6): 659–67. doi:10.1038/nbt1401. PMC 3108568. PMID 18536691.
↑ Lewis, N.E.; Nagarajan, H.; Palsson, B.Ø. (2012). "Constraining the metabolic genotype–phenotype relationship using a phylogeny of in silico methods". Nature Reviews Microbiology. 10 (4): 291–305. doi:10.1038/nrmicro2737. PMC 3536058. PMID 22367118.
↑ Karp, P.D.; Paley, S.M.; Krummenacker, M.; et al. (2010). "Pathway Tools version 13.0: Integrated Software for Pathway/Genome Informatics and Systems Biology". Briefings in Bioinformatics. 11 (1): 40–79. arXiv:1510.03964. doi:10.1093/bib/bbp043. PMC 2810111. PMID 19955237.
↑ Latendresse, M.; Krummenacker, M.; Trupp, M.; Karp, P.D. (2012). "पाथवे डेटाबेस से फ्लक्स बैलेंस मॉडल का निर्माण और पूर्णता". Bioinformatics. 28 (388–96): 388–96. doi:10.1093/bioinformatics/btr681. PMC 3268246. PMID 22262672.
↑ Schilling, C.H. et al. SimPheny: A Computational Infrastructure for Systems Biology. (2008).
↑ "Genomatica | Technology: Technology Suite". Archived from the original on 2010-04-21. Retrieved 2010-03-11.
↑ "MetNetMaker on Tom's Personal Page".
↑ "COBRApy: Constraint-Based Reconstruction and Analysis in Python". GitHub. 2013.
↑ "CarveMe के साथ जीनोम-स्केल मेटाबोलिक मॉडल पुनर्निर्माण". GitHub. 28 October 2021.
↑ "MIOM: Constraint-based modeling of metabolism using Mixed Integer Optimization". GitHub. 26 July 2021.
↑ "बाधा-आधारित पुनर्निर्माण और एक्सास्केल विश्लेषण". GitHub. 16 May 2021.
↑ Becker, S.A.; et al. (2007). "Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox". Nature Protocols. 2 (3): 727–38. doi:10.1038/nprot.2007.99. PMID 17406635. S2CID 5687582.
↑ Gevorgyan, A; Bushell, ME; Avignone-Rossa, C; Kierzek, AM (2011). "SurreyFBA: a command line tool and graphics user interface for constraint-based modeling of genome-scale metabolic reaction networks". Bioinformatics. 27 (3): 433–4. doi:10.1093/bioinformatics/btq679. PMID 21148545.
↑ Boele, J; Olivier, BG; Teusink, B (2012). "FAME: the Flux Analysis and Modeling Environment". BMC Syst Biol. 6 (1): 8. doi:10.1186/1752-0509-6-8. PMC 3317868. PMID 22289213.
↑ "CoBRA Methods - Constraint-based analysis".
↑ Lakshmanan, M; Koh, G; Chung, BK; Lee, DY (Jan 2014). "प्रवाह संतुलन विश्लेषण के लिए सॉफ्टवेयर अनुप्रयोग।". Briefings in Bioinformatics. 15 (1): 108–22. doi:10.1093/bib/bbs069. PMID 23131418.
↑ Gelius-Dietrich, G.; Amer Desouki, A.; Fritzemeier, C.J.; Lercher, M.J. (2013). "sybil – Efficient constraint-based modelling in R." BMC Systems Biology. 7 (1): 125. doi:10.1186/1752-0509-7-125. PMC 3843580. PMID 24224957. Software available at https://cran.r-project.org/package=sybil
↑ Gangadharan A. Rohatgi N. abcdeFBA: Functions for Constraint Based Simulation using Flux Balance Analysis and informative analysis of the data generated during simulation. Available at: https://cran.r-project.org/web/packages/abcdeFBA/
↑ Kotte, O.; Zaugg, J. B.; Heinemann, M. (2010). "चयापचय प्रवाह के वितरित संवेदन के माध्यम से जीवाणु अनुकूलन". Molecular Systems Biology. 6 (355): 355. doi:10.1038/msb.2010.10. PMC 2858440. PMID 20212527.
↑ Ibarra, Rafael U.; Edwards, Jeremy S.; Palsson, Bernhard O. (2002). "Escherichia Coli K-12 Undergoes Adaptive Evolution to Achieve in Silico Predicted Optimal Growth". Nature. 420 (6912): 186–189. Bibcode:2002Natur.420..186I. doi:10.1038/nature01149. PMID 12432395. S2CID 4415915.
↑ Segrè, Daniel; Vitkup, Dennis; Church, George M. (2002). "प्राकृतिक और परेशान मेटाबोलिक नेटवर्क में इष्टतमता का विश्लेषण". Proceedings of the National Academy of Sciences. 99 (23): 15112–15117. Bibcode:2002PNAS...9915112S. doi:10.1073/pnas.232349399. PMC 137552. PMID 12415116.
↑ Shlomi, Tomer, Omer Berkman, and Eytan Ruppin. "Regulatory On/off Minimization of Metabolic Flux Changes After Genetic Perturbations." Proceedings of the National Academy of Sciences of the United States of America 102, no. 21 (May 24, 2005): 7695–7700. doi:10.1073/pnas.0406346102.

[:0-1] 1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 Forth, Thomas (2012). मलेरिया परजीवी का मेटाबोलिक सिस्टम बायोलॉजी. Leeds, UK: University of Leeds. ISBN 978-0-85731-297-6.

[2] Ranganathan, Sridhar; Suthers, Patrick F.; Maranas, Costas D. (2010). "OptForce: An Optimization Procedure for Identifying All Genetic Manipulations Leading to Targeted Overproductions". PLOS Comput Biol. 6 (4): e1000744. Bibcode:2010PLSCB...6E0744R. doi:10.1371/journal.pcbi.1000744. PMC 2855329. PMID 20419153.

[genome_scale-3] Lewis, NE; Abdel-Haleem, AM (2013). "कैंसर चयापचय के जीनोम-स्केल मॉडल का विकास". Front. Physiol. 4: 237. doi:10.3389/fphys.2013.00237. PMC 3759783. PMID 24027532.

[4] Raman, Karthik; Yeturu, Kalidas; Chandra, Nagasuma (2008). "targetTB: इंटरएक्टोम, रिएक्टोम और जीनोम-स्केल स्ट्रक्चरल विश्लेषण के माध्यम से माइकोबैक्टीरियम ट्यूबरकुलोसिस के लिए एक लक्ष्य पहचान पाइपलाइन". BMC Systems Biology. 2 (1): 109. doi:10.1186/1752-0509-2-109. PMC 2651862. PMID 19099550.

[5] {{cite journal | last1 = Yang | first1 = Hong | last2 = Roth | first2 = Charles M. | last3 = Ierapetritou | first3 = Marianthi G. | year = 2009 | title = हेपेटोसाइट संस्कृति में अमीनो एसिड पूरकता के लिए एक तर्कसंगत डिजाइन दृष्टिकोण| journal = Biotechnology and Bioengineering | volume = 103 | issue = 6| pages = 1176–1191 | doi = 10.1002/bit.22342 | pmid = 19422042 | s2cid = 13230467 }

[6] {{cite journal | last1 = Raghunathan | first1 = Anu | last2 = Shin | first2 = Sookil | last3 = Daefler | first3 = Simon | year = 2010 | title = बायोथ्रेट एजेंट फ्रांसिसैला के साथ संक्रमण में मेजबान-रोगज़नक़ की बातचीत की जांच करने के लिए सिस्टम दृष्टिकोण। फ्रांसिसैला तुलारेन्सिस का प्रतिबन्ध आधारित मॉडल| journal = BMC Systems Biology | volume = 4 | issue = 1| page = 118 | doi = 10.1186/1752-0509-4-118 | pmid = 20731870 | pmc = 2933595 }

[Papoutsakis,_ET._1984-7] Papoutsakis, ET (1984). "ब्यूटिरिक एसिड बैक्टीरिया के किण्वन के लिए समीकरण और गणना". Biotechnology and Bioengineering. 26 (2): 174–187. doi:10.1002/bit.260260210. PMID 18551704. S2CID 25023799.

[Watson,_MR._1984-8] Watson MR (1984) Metabolic maps for the Apple II. 12, 1093-1094

[Fell_DA_and_Small_JR._1986-9] Fell, DA; Small, JR (1986). "वसा ऊतक में वसा संश्लेषण। रससमीकरणमितीय बाधाओं की एक परीक्षा". Biochem J. 238 (3): 781–786. doi:10.1042/bj2380781. PMC 1147204. PMID 3800960.

[Edwards,_J._2001-10] 10.0 ^10.1 ^10.2 Edwards, J.; Ibarra, R.; Palsson, B. (2001). "Escherichia कोलाई चयापचय क्षमताओं की 'इन सिलिको' भविष्यवाणियां प्रयोगात्मक डेटा के अनुरूप हैं". Nature Biotechnology. 19 (2): 125–130. doi:10.1038/84379. PMID 11175725. S2CID 1619105.

[11] Raghunathan, A.; et al. (2009). "मेजबान-रोगज़नक़ बातचीत के दौरान साल्मोनेला टाइफीम्यूरियम की चयापचय क्षमता का विश्लेषण आधारित विश्लेषण". BMC Systems Biology. 3: 38. doi:10.1186/1752-0509-3-38. PMC 2678070. PMID 19356237.

[12] Hoek, Milan J. A. van; Merks, Roeland M. H. (2017-05-16). "आंत माइक्रोबियल चयापचय के एक स्थानिक मॉडल में क्रॉस-फीडिंग इंटरैक्शन के कारण माइक्रोबियल विविधता का उद्भव". BMC Systems Biology. 11 (1): 56. doi:10.1186/s12918-017-0430-4. ISSN 1752-0509. PMC 5434578. PMID 28511646.

[13] "संग्रहीत प्रति". Archived from the original on 2008-02-01. Retrieved 2007-12-01.

[14] Palsson, B.O. Systems Biology: Properties of Reconstructed Networks. 334(Cambridge University Press: 2006).

[ref1-15] Orth, J.D.; Thiele, I.; Palsson, B.Ø. (2010). "What is flux balance analysis?". Nature Biotechnology. 28 (3): 245–248. doi:10.1038/nbt.1614. PMC 3108565. PMID 20212490.

[16] Lee, J.M.; Gianchandani, E.P.; Papin, J.A. (2006). "चयापचयों के युग में प्रवाह संतुलन विश्लेषण". Briefings in Bioinformatics. 7 (2): 140–50. doi:10.1093/bib/bbl007. PMID 16772264.

[17] Feist, A.M.; Palsson, B.Ø. (2008). "Escherichia कोलाई का उपयोग करके जीनोम-स्केल चयापचय पुनर्निर्माण के अनुप्रयोगों का बढ़ता दायरा". Nature Biotechnology. 26 (6): 659–67. doi:10.1038/nbt1401. PMC 3108568. PMID 18536691.

[18] Lewis, N.E.; Nagarajan, H.; Palsson, B.Ø. (2012). "Constraining the metabolic genotype–phenotype relationship using a phylogeny of in silico methods". Nature Reviews Microbiology. 10 (4): 291–305. doi:10.1038/nrmicro2737. PMC 3536058. PMID 22367118.

[19] Karp, P.D.; Paley, S.M.; Krummenacker, M.; et al. (2010). "Pathway Tools version 13.0: Integrated Software for Pathway/Genome Informatics and Systems Biology". Briefings in Bioinformatics. 11 (1): 40–79. arXiv:1510.03964. doi:10.1093/bib/bbp043. PMC 2810111. PMID 19955237.

[20] Latendresse, M.; Krummenacker, M.; Trupp, M.; Karp, P.D. (2012). "पाथवे डेटाबेस से फ्लक्स बैलेंस मॉडल का निर्माण और पूर्णता". Bioinformatics. 28 (388–96): 388–96. doi:10.1093/bioinformatics/btr681. PMC 3268246. PMID 22262672.

[21] Schilling, C.H. et al. SimPheny: A Computational Infrastructure for Systems Biology. (2008).

[22] "Genomatica | Technology: Technology Suite". Archived from the original on 2010-04-21. Retrieved 2010-03-11.

[23] "MetNetMaker on Tom's Personal Page".

[24] "COBRApy: Constraint-Based Reconstruction and Analysis in Python". GitHub. 2013.

[25] "CarveMe के साथ जीनोम-स्केल मेटाबोलिक मॉडल पुनर्निर्माण". GitHub. 28 October 2021.

[26] "MIOM: Constraint-based modeling of metabolism using Mixed Integer Optimization". GitHub. 26 July 2021.

[27] "बाधा-आधारित पुनर्निर्माण और एक्सास्केल विश्लेषण". GitHub. 16 May 2021.

[28] Becker, S.A.; et al. (2007). "Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox". Nature Protocols. 2 (3): 727–38. doi:10.1038/nprot.2007.99. PMID 17406635. S2CID 5687582.

[29] Gevorgyan, A; Bushell, ME; Avignone-Rossa, C; Kierzek, AM (2011). "SurreyFBA: a command line tool and graphics user interface for constraint-based modeling of genome-scale metabolic reaction networks". Bioinformatics. 27 (3): 433–4. doi:10.1093/bioinformatics/btq679. PMID 21148545.

[30] Boele, J; Olivier, BG; Teusink, B (2012). "FAME: the Flux Analysis and Modeling Environment". BMC Syst Biol. 6 (1): 8. doi:10.1186/1752-0509-6-8. PMC 3317868. PMID 22289213.

[31] "CoBRA Methods - Constraint-based analysis".

[32] Lakshmanan, M; Koh, G; Chung, BK; Lee, DY (Jan 2014). "प्रवाह संतुलन विश्लेषण के लिए सॉफ्टवेयर अनुप्रयोग।". Briefings in Bioinformatics. 15 (1): 108–22. doi:10.1093/bib/bbs069. PMID 23131418.

[33] Gelius-Dietrich, G.; Amer Desouki, A.; Fritzemeier, C.J.; Lercher, M.J. (2013). "sybil – Efficient constraint-based modelling in R." BMC Systems Biology. 7 (1): 125. doi:10.1186/1752-0509-7-125. PMC 3843580. PMID 24224957. Software available at https://cran.r-project.org/package=sybil

[34] Gangadharan A. Rohatgi N. abcdeFBA: Functions for Constraint Based Simulation using Flux Balance Analysis and informative analysis of the data generated during simulation. Available at: https://cran.r-project.org/web/packages/abcdeFBA/

[35] Kotte, O.; Zaugg, J. B.; Heinemann, M. (2010). "चयापचय प्रवाह के वितरित संवेदन के माध्यम से जीवाणु अनुकूलन". Molecular Systems Biology. 6 (355): 355. doi:10.1038/msb.2010.10. PMC 2858440. PMID 20212527.

[36] Ibarra, Rafael U.; Edwards, Jeremy S.; Palsson, Bernhard O. (2002). "Escherichia Coli K-12 Undergoes Adaptive Evolution to Achieve in Silico Predicted Optimal Growth". Nature. 420 (6912): 186–189. Bibcode:2002Natur.420..186I. doi:10.1038/nature01149. PMID 12432395. S2CID 4415915.

[37] Segrè, Daniel; Vitkup, Dennis; Church, George M. (2002). "प्राकृतिक और परेशान मेटाबोलिक नेटवर्क में इष्टतमता का विश्लेषण". Proceedings of the National Academy of Sciences. 99 (23): 15112–15117. Bibcode:2002PNAS...9915112S. doi:10.1073/pnas.232349399. PMC 137552. PMID 12415116.

[38] Shlomi, Tomer, Omer Berkman, and Eytan Ruppin. "Regulatory On/off Minimization of Metabolic Flux Changes After Genetic Perturbations." Proceedings of the National Academy of Sciences of the United States of America 102, no. 21 (May 24, 2005): 7695–7700. doi:10.1073/pnas.0406346102.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

Revision as of 14:56, 2 June 2023 (view source) alpha>Neeraja m (added Category:Vigyan Ready using HotCat) ← Older edit	Revision as of 08:53, 4 June 2023 (view source) Indicwiki (talk \| contribs) m (13 revisions imported from alpha:प्रवाह_संतुलन_विश्लेषण) Newer edit →
(No difference)

Anonymous

Search