अर्ध-अंतर्निहित यूलर विधि: Difference between revisions
(Created page with "गणित में, सेमी-इंप्लिसिट यूलर मेथड, जिसे सिम्पलेक्टिक यूलर, सेमी-एक...") |
(text) |
||
| Line 1: | Line 1: | ||
गणित में, | गणित में, अर्ध-अंतर्निहित यूलर विधि, जिसे सिम्पलेक्टिक यूलर, अर्ध-सुस्पष्ट यूलर, यूलर-क्रोमर, और न्यूटन-स्टॉर्मर-वर्लेट (NSV) भी कहा जाता है, हैमिल्टन के समीकरणों को हल करने के लिए [[ यूलर एकीकरण |यूलर एकीकरण]], सामान्य की एक प्रणाली [[शास्त्रीय यांत्रिकी|पारम्परिक यांत्रिकी]] में उत्पन्न होने वाले अंतर समीकरण का एक संशोधन है। यह एक सहानुभूतिपूर्ण समाकलक है और इसलिए यह मानक यूलर विधि की तुलना में बेहतर परिणाम देता है। | ||
== | == समायोजन == | ||
अर्ध-अंतर्निहित यूलर विधि को | अर्ध-अंतर्निहित यूलर विधि को निम्न प्ररूप के [[अंतर समीकरण]]ों की एक जोड़ी पर लागू किया जा सकता है{{citation needed|date=September 2019}} | ||
:<math>\begin{align} | :<math>\begin{align} | ||
{dx \over dt} &= f(t,v) \\ | {dx \over dt} &= f(t,v) \\ | ||
{dv \over dt} &= g(t,x), | {dv \over dt} &= g(t,x), | ||
\end{align}</math> | \end{align}</math> | ||
जहाँ f और g फलन दिए गए हैं। यहाँ, x और v या तो अदिश या सदिश हो सकते हैं। [[हैमिल्टनियन यांत्रिकी]] में गति के समीकरण इस रूप को लेते हैं यदि हैमिल्टनियन रूप का है | जहाँ f और g फलन दिए गए हैं। यहाँ, x और v या तो अदिश या सदिश हो सकते हैं। [[हैमिल्टनियन यांत्रिकी]] में गति के समीकरण इस रूप को लेते हैं यदि हैमिल्टनियन निम्न रूप का है | ||
:<math> H = T(t,v) + V(t,x). \, </math> | :<math> H = T(t,v) + V(t,x). \, </math> | ||
| Line 23: | Line 23: | ||
x_{n+1} &= x_n + f(t_n, v_{n+1}) \, \Delta t | x_{n+1} &= x_n + f(t_n, v_{n+1}) \, \Delta t | ||
\end{align}</math> | \end{align}</math> | ||
जहां Δt समय कदम है और | जहां Δt समय कदम है और t<sub>n</sub>= t<sub>0</sub> + nΔt n चरणों के बाद का समय है। | ||
मानक यूलर विधि से अंतर यह है कि अर्ध-अंतर्निहित यूलर विधि | मानक यूलर विधि से अंतर यह है कि अर्ध-अंतर्निहित यूलर विधि x<sub>''n''+1</sub> के लिए समीकरण में v<sub>''n''+1</sub> का उपयोग करती है, जबकि यूलर विधि v<sub>n</sub> का उपयोग करती है। | ||
<math>(x_n, v_n)</math> से <math>(x_{n+1}, v_{n+1})</math> की गणना के लिए ऋणात्मक समय कदम के साथ विधि को लागू करना और पुनर्व्यवस्थित करना अर्ध-अंतर्निहित यूलर विधि का दूसरा रूपांतर होता है | |||
:<math>\begin{align} | :<math>\begin{align} | ||
x_{n+1} &= x_n + f(t_n, v_n) \, \Delta t\\[0.3ex] | x_{n+1} &= x_n + f(t_n, v_n) \, \Delta t\\[0.3ex] | ||
v_{n+1} &= v_n + g(t_n, x_{n+1}) \, \Delta t | v_{n+1} &= v_n + g(t_n, x_{n+1}) \, \Delta t | ||
\end{align}</math> | \end{align}</math> | ||
जिसके समान गुण | जिसके समान गुण हैं। | ||
अर्ध-अंतर्निहित यूलर मानक यूलर विधि के रूप में एक संख्यात्मक साधारण अंतर समीकरण | अर्ध-अंतर्निहित यूलर मानक यूलर विधि के रूप में एक संख्यात्मक साधारण अंतर समीकरण प्रथम-क्रम समाकलक है। इसका अर्थ यह है कि यह Δt के आदेश की वैश्विक त्रुटि करता है। हालांकि, मानक विधि के विपरीत, अर्ध-अंतर्निहित यूलर विधि एक सहानुभूतिपूर्ण समाकलक है। परिणामस्वरूप, अर्ध-अंतर्निहित यूलर विधि लगभग ऊर्जा का संरक्षण करती है (जब हैमिल्टनियन समय-स्वतंत्र होता है)। प्रायः, जब मानक यूलर विधि लागू की जाती है तो ऊर्जा प्रवाहित होती है, जिससे यह बहुत कम सटीक हो जाती है। | ||
अर्ध-अंतर्निहित यूलर विधि के दो रूपों के बीच बारी-बारी से स्टॉर्मर-वर्लेट एकीकरण के लिए एक सरलीकरण और [[लीपफ्रॉग एकीकरण]] के लिए थोड़ा अलग सरलीकरण होता है, जिससे त्रुटि के क्रम और ऊर्जा के संरक्षण के क्रम दोनों में वृद्धि होती है।<ref name="hairer2003" /> | अर्ध-अंतर्निहित यूलर विधि के दो रूपों के बीच बारी-बारी से स्टॉर्मर-वर्लेट एकीकरण के लिए एक सरलीकरण और [[लीपफ्रॉग एकीकरण|प्लुति एकीकरण]] के लिए थोड़ा अलग सरलीकरण होता है, जिससे त्रुटि के क्रम और ऊर्जा के संरक्षण के क्रम दोनों में वृद्धि होती है। <ref name="hairer2003" /> | ||
अर्ध-अंतर्निहित विधि का स्थिरता क्षेत्र नीरनेन द्वारा प्रस्तुत किया गया था<ref>[https://www.researchgate.net/publication/268034494_Fast_and_accurate_symmetric_Euler_algorithm_for_electromechanical_simulations_NOTE_The_method_became_later_known_as_Symplectic_Euler Niiranen, Jouko: Fast and accurate symmetric Euler algorithm for electromechanical simulations] Proceedings of the Electrimacs'99, Sept. 14-16, 1999 Lisboa, Portugal, Vol. 1, pages 71 - 78.</ref> हालांकि अर्ध-अंतर्निहित यूलर को उनके | अर्ध-अंतर्निहित विधि का स्थिरता क्षेत्र नीरनेन द्वारा प्रस्तुत किया गया था, <ref>[https://www.researchgate.net/publication/268034494_Fast_and_accurate_symmetric_Euler_algorithm_for_electromechanical_simulations_NOTE_The_method_became_later_known_as_Symplectic_Euler Niiranen, Jouko: Fast and accurate symmetric Euler algorithm for electromechanical simulations] Proceedings of the Electrimacs'99, Sept. 14-16, 1999 Lisboa, Portugal, Vol. 1, pages 71 - 78.</ref> हालांकि अर्ध-अंतर्निहित यूलर को उनके लेख में भ्रामक रूप से सममित यूलर कहा गया था। अर्ध-अंतर्निहित विधि कृत्रिम प्रणाली को सही ढंग से प्रतिरूप करती है यदि विशेषता समीकरण की सम्मिश्र मूल नीचे दिखाए गए वृत्त के भीतर हैं। यथार्थ मूल के लिए स्थिरता क्षेत्र उस वृत्त के बाहर विस्तारित होता है जिसके लिए मानदंड <math>s > - 2/\Delta t</math> है। | ||
[[Image:Symplectic Euler stability region.jpeg]]जैसा कि देखा जा सकता है, अर्ध-अंतर्निहित विधि दोनों स्थिर प्रणालियों को सही ढंग से अनुकरण कर सकती है | [[Image:Symplectic Euler stability region.jpeg]]जैसा कि देखा जा सकता है, अर्ध-अंतर्निहित विधि दोनों स्थिर प्रणालियों को सही ढंग से अनुकरण कर सकती है जिनके मूल बाएं अर्ध समतल में हैं और अस्थिर प्रणाली जिनके मूल दाएं अर्ध समतल में हैं। यह आगे (मानक) यूलर और पिछड़े यूलर पर स्पष्ट लाभ है। जब जड़ों के नकारात्मक वास्तविक भाग काल्पनिक अक्ष के निकट आ जाते हैं तो प्रगल्भ यूलर में वास्तविक प्रणाली की तुलना में कम अवमंदन होता है और जब मूल दाहिने आधे तल में हों तब पश्च यूलर प्रणाली को तब भी स्थिर दिखा सकता है। | ||
== उदाहरण == | == उदाहरण == | ||
हुक के नियम को संतुष्ट करने वाली [[वसंत (उपकरण)]] | हुक के नियम को संतुष्ट करने वाली [[वसंत (उपकरण)|कमानी (उपकरण)]] की गति किसके द्वारा दी जाती है | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 56: | Line 56: | ||
x_{n+1} &= x_n + v_{n+1} \,\Delta t. | x_{n+1} &= x_n + v_{n+1} \,\Delta t. | ||
\end{align}</math> | \end{align}</math> | ||
स्थानापन्न <math>v_{n+1}</math> पहले समीकरण द्वारा दी गई अभिव्यक्ति के साथ दूसरे समीकरण में, पुनरावृत्ति को निम्नलिखित | स्थानापन्न <math>v_{n+1}</math> पहले समीकरण द्वारा दी गई अभिव्यक्ति के साथ दूसरे समीकरण में, पुनरावृत्ति को निम्नलिखित आव्यूह रूप में व्यक्त किया जा सकता है। | ||
:<math>\begin{bmatrix} x_{n+1} \\v_{n+1}\end{bmatrix} = | :<math>\begin{bmatrix} x_{n+1} \\v_{n+1}\end{bmatrix} = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 62: | Line 62: | ||
-\omega^2 \Delta t & 1 | -\omega^2 \Delta t & 1 | ||
\end{bmatrix} \begin{bmatrix} x_{n} \\ v_{n} \end{bmatrix},</math> | \end{bmatrix} \begin{bmatrix} x_{n} \\ v_{n} \end{bmatrix},</math> | ||
और चूंकि | और चूंकि आव्यूह का निर्धारक 1 है, परिवर्तन क्षेत्र-संरक्षण है। | ||
पुनरावृति संशोधित ऊर्जा को कार्यात्मक | पुनरावृति संशोधित ऊर्जा को यथार्थत: कार्यात्मक <math>E_h(x,v)=\tfrac12\left(v^2+\omega^2\,x^2-\omega^2\Delta t\,vx\right)</math> बनाए रखती है, स्थिर आवधिक कक्षाओं के लिए अग्रणी (पर्याप्त रूप से छोटे चरण आकार के लिए) जो सटीक कक्षाओं से <math>O(\Delta t)</math> से विचलित होते हैं। सटीक परिपत्र आवृत्ति <math>\omega</math> के एक कारक <math>1+\tfrac1{24}\omega^2\Delta t^2+O(\Delta t^4)</math> द्वारा संख्यात्मक सन्निकटन में वृद्धि करता है। | ||
== संदर्भ == | == संदर्भ == | ||
| Line 83: | Line 83: | ||
}}</ref> | }}</ref> | ||
</references> | </references> | ||
* {{cite web|last=Nikolic|first= | * {{cite web|last=Nikolic|first=ब्रानिस्लाव के.|title=यूलर-क्रोमर विधि|publisher=[[डेलावेयर विश्वविद्यालय]] | url=http://www.physics.udel.edu/~bnikolic/teaching/phys660/numerical_ode/node2.html|url-status=live|accessdate=2021-09-29}} | ||
* {{cite book |last= Vesely|first= Franz J.|title= | * {{cite book |last= Vesely|first= Franz J.|title= कम्प्यूटेशनल भौतिकी: एक परिचय|url= https://archive.org/details/computationalphy00vese_143|url-access= limited|edition= 2nd|publisher= Springer|year= 2001|isbn= 978-0-306-46631-1|pages=[https://archive.org/details/computationalphy00vese_143/page/n125 117]}} | ||
* {{cite book |last= Giordano|first= Nicholas J.|author2= | * {{cite book |last= Giordano|first= Nicholas J.|author2=हिसाव नाकानिशी|title= कम्प्यूटेशनल भौतिकी|edition= 2nd|publisher= बेंजामिन कमिंग्स|date=July 2005|isbn= 0-13-146990-8 }} | ||
{{Numerical integrators}} | {{Numerical integrators}} | ||
Revision as of 10:44, 26 May 2023
गणित में, अर्ध-अंतर्निहित यूलर विधि, जिसे सिम्पलेक्टिक यूलर, अर्ध-सुस्पष्ट यूलर, यूलर-क्रोमर, और न्यूटन-स्टॉर्मर-वर्लेट (NSV) भी कहा जाता है, हैमिल्टन के समीकरणों को हल करने के लिए यूलर एकीकरण, सामान्य की एक प्रणाली पारम्परिक यांत्रिकी में उत्पन्न होने वाले अंतर समीकरण का एक संशोधन है। यह एक सहानुभूतिपूर्ण समाकलक है और इसलिए यह मानक यूलर विधि की तुलना में बेहतर परिणाम देता है।
समायोजन
अर्ध-अंतर्निहित यूलर विधि को निम्न प्ररूप के अंतर समीकरणों की एक जोड़ी पर लागू किया जा सकता है[citation needed]
जहाँ f और g फलन दिए गए हैं। यहाँ, x और v या तो अदिश या सदिश हो सकते हैं। हैमिल्टनियन यांत्रिकी में गति के समीकरण इस रूप को लेते हैं यदि हैमिल्टनियन निम्न रूप का है
प्रारंभिक स्थिति के साथ अंतर समीकरणों को हल किया जाना है
विधि
अर्ध-अंतर्निहित यूलर विधि पुनरावृति द्वारा अनुमानित असतत गणित समाधान उत्पन्न करती है
जहां Δt समय कदम है और tn= t0 + nΔt n चरणों के बाद का समय है।
मानक यूलर विधि से अंतर यह है कि अर्ध-अंतर्निहित यूलर विधि xn+1 के लिए समीकरण में vn+1 का उपयोग करती है, जबकि यूलर विधि vn का उपयोग करती है।
से की गणना के लिए ऋणात्मक समय कदम के साथ विधि को लागू करना और पुनर्व्यवस्थित करना अर्ध-अंतर्निहित यूलर विधि का दूसरा रूपांतर होता है
जिसके समान गुण हैं।
अर्ध-अंतर्निहित यूलर मानक यूलर विधि के रूप में एक संख्यात्मक साधारण अंतर समीकरण प्रथम-क्रम समाकलक है। इसका अर्थ यह है कि यह Δt के आदेश की वैश्विक त्रुटि करता है। हालांकि, मानक विधि के विपरीत, अर्ध-अंतर्निहित यूलर विधि एक सहानुभूतिपूर्ण समाकलक है। परिणामस्वरूप, अर्ध-अंतर्निहित यूलर विधि लगभग ऊर्जा का संरक्षण करती है (जब हैमिल्टनियन समय-स्वतंत्र होता है)। प्रायः, जब मानक यूलर विधि लागू की जाती है तो ऊर्जा प्रवाहित होती है, जिससे यह बहुत कम सटीक हो जाती है।
अर्ध-अंतर्निहित यूलर विधि के दो रूपों के बीच बारी-बारी से स्टॉर्मर-वर्लेट एकीकरण के लिए एक सरलीकरण और प्लुति एकीकरण के लिए थोड़ा अलग सरलीकरण होता है, जिससे त्रुटि के क्रम और ऊर्जा के संरक्षण के क्रम दोनों में वृद्धि होती है। [1]
अर्ध-अंतर्निहित विधि का स्थिरता क्षेत्र नीरनेन द्वारा प्रस्तुत किया गया था, [2] हालांकि अर्ध-अंतर्निहित यूलर को उनके लेख में भ्रामक रूप से सममित यूलर कहा गया था। अर्ध-अंतर्निहित विधि कृत्रिम प्रणाली को सही ढंग से प्रतिरूप करती है यदि विशेषता समीकरण की सम्मिश्र मूल नीचे दिखाए गए वृत्त के भीतर हैं। यथार्थ मूल के लिए स्थिरता क्षेत्र उस वृत्त के बाहर विस्तारित होता है जिसके लिए मानदंड है।
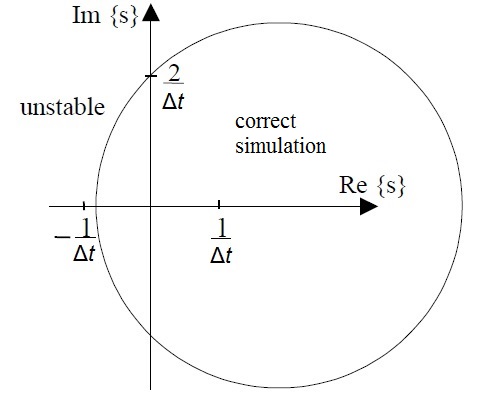 जैसा कि देखा जा सकता है, अर्ध-अंतर्निहित विधि दोनों स्थिर प्रणालियों को सही ढंग से अनुकरण कर सकती है जिनके मूल बाएं अर्ध समतल में हैं और अस्थिर प्रणाली जिनके मूल दाएं अर्ध समतल में हैं। यह आगे (मानक) यूलर और पिछड़े यूलर पर स्पष्ट लाभ है। जब जड़ों के नकारात्मक वास्तविक भाग काल्पनिक अक्ष के निकट आ जाते हैं तो प्रगल्भ यूलर में वास्तविक प्रणाली की तुलना में कम अवमंदन होता है और जब मूल दाहिने आधे तल में हों तब पश्च यूलर प्रणाली को तब भी स्थिर दिखा सकता है।
जैसा कि देखा जा सकता है, अर्ध-अंतर्निहित विधि दोनों स्थिर प्रणालियों को सही ढंग से अनुकरण कर सकती है जिनके मूल बाएं अर्ध समतल में हैं और अस्थिर प्रणाली जिनके मूल दाएं अर्ध समतल में हैं। यह आगे (मानक) यूलर और पिछड़े यूलर पर स्पष्ट लाभ है। जब जड़ों के नकारात्मक वास्तविक भाग काल्पनिक अक्ष के निकट आ जाते हैं तो प्रगल्भ यूलर में वास्तविक प्रणाली की तुलना में कम अवमंदन होता है और जब मूल दाहिने आधे तल में हों तब पश्च यूलर प्रणाली को तब भी स्थिर दिखा सकता है।
उदाहरण
हुक के नियम को संतुष्ट करने वाली कमानी (उपकरण) की गति किसके द्वारा दी जाती है
इस समीकरण के लिए अर्ध-अंतर्निहित यूलर है
स्थानापन्न पहले समीकरण द्वारा दी गई अभिव्यक्ति के साथ दूसरे समीकरण में, पुनरावृत्ति को निम्नलिखित आव्यूह रूप में व्यक्त किया जा सकता है।
और चूंकि आव्यूह का निर्धारक 1 है, परिवर्तन क्षेत्र-संरक्षण है।
पुनरावृति संशोधित ऊर्जा को यथार्थत: कार्यात्मक बनाए रखती है, स्थिर आवधिक कक्षाओं के लिए अग्रणी (पर्याप्त रूप से छोटे चरण आकार के लिए) जो सटीक कक्षाओं से से विचलित होते हैं। सटीक परिपत्र आवृत्ति के एक कारक द्वारा संख्यात्मक सन्निकटन में वृद्धि करता है।
संदर्भ
- ↑ Hairer, Ernst; Lubich, Christian; Wanner, Gerhard (2003). "Geometric numerical integration illustrated by the Störmer/Verlet method". Acta Numerica. 12: 399–450. Bibcode:2003AcNum..12..399H. CiteSeerX 10.1.1.7.7106. doi:10.1017/S0962492902000144. S2CID 122016794.
- ↑ Niiranen, Jouko: Fast and accurate symmetric Euler algorithm for electromechanical simulations Proceedings of the Electrimacs'99, Sept. 14-16, 1999 Lisboa, Portugal, Vol. 1, pages 71 - 78.
- Nikolic, ब्रानिस्लाव के. "यूलर-क्रोमर विधि". डेलावेयर विश्वविद्यालय. Retrieved 2021-09-29.
{{cite web}}: CS1 maint: url-status (link) - Vesely, Franz J. (2001). कम्प्यूटेशनल भौतिकी: एक परिचय (2nd ed.). Springer. pp. 117. ISBN 978-0-306-46631-1.
- Giordano, Nicholas J.; हिसाव नाकानिशी (July 2005). कम्प्यूटेशनल भौतिकी (2nd ed.). बेंजामिन कमिंग्स. ISBN 0-13-146990-8.