पथ (ग्राफ सिद्धांत): Difference between revisions
(Created page with "{{Short description|Sequence of edges which join a sequence of nodes on a given graph}} {{For|the family of graphs known as paths|Path graph}} File:Snake-in-the-box and Ham...") |
mNo edit summary |
||
| Line 2: | Line 2: | ||
{{For|the family of graphs known as paths|Path graph}} | {{For|the family of graphs known as paths|Path graph}} | ||
[[File:Snake-in-the-box and Hamiltonian path.svg|thumb|right|एक त्रि-आयामी [[हाइपरक्यूब ग्राफ]]़ लाल रंग में [[हैमिल्टनियन पथ]] और बोल्ड ब्लैक में एक [[सांप-इन-द-बॉक्स]] दिखा रहा है।]]ग्राफ़ सिद्धांत में, | [[File:Snake-in-the-box and Hamiltonian path.svg|thumb|right|एक त्रि-आयामी [[हाइपरक्यूब ग्राफ]]़ लाल रंग में [[हैमिल्टनियन पथ]] और बोल्ड ब्लैक में एक [[सांप-इन-द-बॉक्स]] दिखा रहा है।]]ग्राफ़ सिद्धांत में, ग्राफ़ में एक पथ किनारों का एक परिमित या अनंत अनुक्रम होता है जो शीर्षों के अनुक्रम में शामिल होता है, जो कि अधिकांश परिभाषाओं से अलग होते हैं (और चूंकि कोने अलग होते हैं, इसलिए किनारे भी होते हैं)। एक निर्देशित पथ (कभी-कभी द्विपथ {{sfn|Bender|Williamson|2010|p=162}} कहा जाता है) एक निर्देशित ग्राफ में किनारों का एक परिमित या अनंत अनुक्रम होता है जो अलग-अलग शीर्षों के अनुक्रम में शामिल होता है, लेकिन अतिरिक्त प्रतिबंध के साथ कि किनारों को एक ही दिशा में निर्देशित किया जाता है। | ||
पथ | पथ ग्राफ सिद्धांत की मूलभूत अवधारणाएँ हैं, जिनका वर्णन अधिकांश ग्राफ सिद्धांत ग्रंथों के परिचयात्मक खंडों में वर्णित है। उदाहरण देखें बॉन्डी और मूर्ति (1976), गिबन्स (1985), या डायस्टेल (2005) कोर्टे एट अल। (1990) रेखांकन में पथों से संबंधित अधिक उन्नत [[ कलन विधि |कलन विधि]] विषयों को कवर करते हैं। | ||
== परिभाषाएँ == | == परिभाषाएँ == | ||
=== चलना, निशान, और पथ === | === चलना, निशान, और पथ === | ||
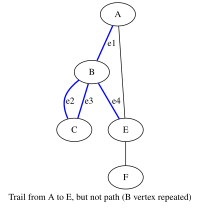
[[File:Trail but not path.svg|200px|thumb|right]]* | [[File:Trail but not path.svg|200px|thumb|right]]* चलना किनारों का एक परिमित या अनंत क्रम है जो शीर्षों के अनुक्रम में शामिल होता है{{sfn|Bender|Williamson|2010|p=162}} | ||
: | : मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित चाल किनारों (e1, e2, …, en − 1) का एक क्रम है जिसके लिए वर्टिकल (v1, v2, …, vn) का एक क्रम है जैसे कि ϕ(ei) = {vi, vi 1} के लिए i = 1, 2, …, n − 1. (v1, v2, …, vn) चलने का शीर्ष अनुक्रम है।चलना बंद है अगर v1 = vn, और यह अन्यथा खुला है। एक अनंत चलना यहाँ वर्णित एक ही प्रकार के किनारों का एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंत चलना (या किरण) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है | ||
* एक 'पथ' एक ऐसा मार्ग है जिसमें सभी किनारे अलग-अलग होते हैं।{{sfn|Bender|Williamson|2010|p=162}} | * एक 'पथ' एक ऐसा मार्ग है जिसमें सभी किनारे अलग-अलग होते हैं।{{sfn|Bender|Williamson|2010|p=162}} | ||
* एक पथ एक पगडंडी है जिसमें सभी कोने (और इसलिए सभी किनारे भी) अलग-अलग हैं।{{sfn|Bender|Williamson|2010|p=162}} | * एक पथ एक पगडंडी है जिसमें सभी कोने (और इसलिए सभी किनारे भी) अलग-अलग हैं।{{sfn|Bender|Williamson|2010|p=162}} | ||
Revision as of 16:08, 25 May 2023

ग्राफ़ सिद्धांत में, ग्राफ़ में एक पथ किनारों का एक परिमित या अनंत अनुक्रम होता है जो शीर्षों के अनुक्रम में शामिल होता है, जो कि अधिकांश परिभाषाओं से अलग होते हैं (और चूंकि कोने अलग होते हैं, इसलिए किनारे भी होते हैं)। एक निर्देशित पथ (कभी-कभी द्विपथ [1] कहा जाता है) एक निर्देशित ग्राफ में किनारों का एक परिमित या अनंत अनुक्रम होता है जो अलग-अलग शीर्षों के अनुक्रम में शामिल होता है, लेकिन अतिरिक्त प्रतिबंध के साथ कि किनारों को एक ही दिशा में निर्देशित किया जाता है।
पथ ग्राफ सिद्धांत की मूलभूत अवधारणाएँ हैं, जिनका वर्णन अधिकांश ग्राफ सिद्धांत ग्रंथों के परिचयात्मक खंडों में वर्णित है। उदाहरण देखें बॉन्डी और मूर्ति (1976), गिबन्स (1985), या डायस्टेल (2005) कोर्टे एट अल। (1990) रेखांकन में पथों से संबंधित अधिक उन्नत कलन विधि विषयों को कवर करते हैं।
परिभाषाएँ
चलना, निशान, और पथ
* चलना किनारों का एक परिमित या अनंत क्रम है जो शीर्षों के अनुक्रम में शामिल होता है[1]
- मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित चाल किनारों (e1, e2, …, en − 1) का एक क्रम है जिसके लिए वर्टिकल (v1, v2, …, vn) का एक क्रम है जैसे कि ϕ(ei) = {vi, vi 1} के लिए i = 1, 2, …, n − 1. (v1, v2, …, vn) चलने का शीर्ष अनुक्रम है।चलना बंद है अगर v1 = vn, और यह अन्यथा खुला है। एक अनंत चलना यहाँ वर्णित एक ही प्रकार के किनारों का एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंत चलना (या किरण) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है
- एक 'पथ' एक ऐसा मार्ग है जिसमें सभी किनारे अलग-अलग होते हैं।[1]
- एक पथ एक पगडंडी है जिसमें सभी कोने (और इसलिए सभी किनारे भी) अलग-अलग हैं।[1]
अगर w = (e1, e2, …, en − 1) वर्टेक्स अनुक्रम के साथ परिमित चलना है (v1, v2, …, vn) तो w को v से चलना कहा जाता है1 पत्र बीn. इसी प्रकार एक निशान या पथ के लिए। यदि दो अलग-अलग शीर्षों के बीच एक परिमित चाल है तो उनके बीच एक परिमित मार्ग और एक परिमित मार्ग भी है।
कुछ लेखकों की आवश्यकता नहीं है कि पथ के सभी कोने अलग-अलग हों और इसके बजाय ऐसे पथ को संदर्भित करने के लिए 'सरल पथ' शब्द का उपयोग करें जहां सभी कोने अलग-अलग हों।
एक भारित ग्राफ ग्राफ में प्रत्येक किनारे के साथ एक मान (वजन) को जोड़ता है। भारित ग्राफ़ में चलने (या पगडंडी या पथ) का भार ट्रैवर्स किए गए किनारों के भार का योग होता है। कभी-कभी वजन के स्थान पर लागत या लंबाई शब्दों का प्रयोग किया जाता है।
निर्देशित चलना, निर्देशित पगडंडी, और निर्देशित पथ
- एक निर्देशित चलना एज (ग्राफ सिद्धांत) का एक परिमित या अनंत अनुक्रम है जो उसी दिशा में निर्देशित होता है जो वर्टेक्स (ग्राफ सिद्धांत) के अनुक्रम में शामिल होता है।[1]
- होने देना G = (V, E, ϕ) एक निर्देशित ग्राफ बनें। एक परिमित निर्देशित चलना किनारों का एक क्रम है (e1, e2, …, en − 1) जिसके लिए वर्टिकल का एक क्रम है (v1, v2, …, vn) ऐसा है कि ϕ(ei) = (vi, vi + 1) के लिए i = 1, 2, …, n − 1. (v1, v2, …, vn) निर्देशित चलने का शीर्ष क्रम है। निर्देशित चलना बंद है अगर में1 = विn, और यह अन्यथा खुला है। एक अनंत निर्देशित चाल यहाँ वर्णित एक ही प्रकार के किनारों का एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंत निर्देशित चलना (या अंत (ग्राफ सिद्धांत)) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है।
- 'डायरेक्टेड ट्रेल' एक निर्देशित वॉक है जिसमें सभी किनारे अलग-अलग होते हैं।[1]
- एक निर्देशित पथ एक निर्देशित पथ है जिसमें सभी शीर्ष भिन्न होते हैं।[1]
अगर w = (e1, e2, …, en − 1) वर्टेक्स अनुक्रम के साथ एक परिमित निर्देशित चलना है (v1, v2, …, vn) तो w को v से चलना कहा जाता है1 पत्र बीn. इसी प्रकार एक निर्देशित निशान या पथ के लिए। यदि दो अलग-अलग शीर्षों के बीच एक परिमित निर्देशित चाल है तो एक परिमित निर्देशित मार्ग और उनके बीच एक परिमित निर्देशित मार्ग भी है।
एक सरल निर्देशित पथ एक ऐसा मार्ग है जहाँ सभी शीर्ष भिन्न होते हैं।
एक भारित ग्राफ़ निर्देशित ग्राफ़ में प्रत्येक किनारे के साथ एक मान (वजन) को जोड़ता है। भारित निर्देशित ग्राफ़ में एक निर्देशित चाल (या पगडंडी या पथ) का भार अनुप्रस्थ किनारों के भार का योग होता है। कभी-कभी वजन के स्थान पर लागत या लंबाई शब्दों का प्रयोग किया जाता है।
उदाहरण
- एक ग्राफ कनेक्टिविटी (ग्राफ सिद्धांत) है यदि प्रत्येक जोड़े के शीर्ष वाले पथ हैं।
- एक निर्देशित ग्राफ मजबूत रूप से जुड़ा हुआ डिग्राफ है यदि प्रत्येक जोड़े के कोने वाले विपरीत दिशा में निर्देशित पथ हैं।
- एक पथ ऐसा है कि कोई ग्राफ किनारा दो गैर-लगातार पथ के शीर्षों को जोड़ता है, एक प्रेरित पथ कहलाता है।
- एक पथ जिसमें बिना दोहराव के ग्राफ के प्रत्येक शीर्ष को शामिल किया जाता है, हैमिल्टनियन पथ के रूप में जाना जाता है।
- दो रास्ते वर्टेक्स-इंडिपेंडेंट (वैकल्पिक रूप से, आंतरिक रूप से वर्टेक्स-डिसजॉइंट) हैं यदि उनके पास कोई आंतरिक वर्टेक्स कॉमन नहीं है। इसी तरह, दो रास्ते एज-इंडिपेंडेंट (या एज-डिसजॉइंट) हैं, अगर उनमें कोई आंतरिक किनारा कॉमन नहीं है। दो आंतरिक रूप से वर्टेक्स-डिसजॉइंट पथ एज-डिसजॉइंट हैं, लेकिन इसका विलोम आवश्यक रूप से सत्य नहीं है।
- एक ग्राफ़ में दो शीर्षों के बीच की दूरी (ग्राफ़ सिद्धांत) उनके बीच सबसे छोटे पथ की लंबाई है, यदि कोई मौजूद है, और अन्यथा दूरी अनंत है।
- जुड़े हुए ग्राफ़ का व्यास, ग्राफ़ के शीर्षों के युग्मों के बीच की सबसे बड़ी दूरी (ऊपर परिभाषित) है।
पथ ढूँढना
ग्राफ़ में लघुतम पथ समस्या और सबसे लंबे पथ समस्या पथ को खोजने के लिए कई एल्गोरिदम मौजूद हैं, इस महत्वपूर्ण अंतर के साथ कि पूर्व की समस्या बाद की तुलना में कम्प्यूटेशनल रूप से बहुत आसान है।
दिज्क्स्ट्रा का एल्गोरिथ्म गैर-नकारात्मक एज वेट (या कोई एज वेट) के साथ निर्देशित और अप्रत्यक्ष ग्राफ़ में स्रोत वर्टेक्स से हर दूसरे वर्टेक्स तक सबसे छोटे रास्तों की एक सूची तैयार करता है, जबकि बेलमैन-फोर्ड एल्गोरिथ्म को नेगेटिव एज वेट के साथ निर्देशित ग्राफ़ पर लागू किया जा सकता है। . फ़्लॉइड-वॉर्शल एल्गोरिथम का उपयोग भारित निर्देशित ग्राफ़ में सभी जोड़े के बीच सबसे छोटा रास्ता खोजने के लिए किया जा सकता है।
यह भी देखें
- ग्राफ सिद्धांत की शब्दावली
- पथ ग्राफ
- बहुभुज श्रृंखला
- सबसे छोटा रास्ता समस्या
- सबसे लंबी पथ समस्या
- दिज्क्स्ट्रा का एल्गोरिथ्म
- बेलमैन-फोर्ड एल्गोरिथम
- फ्लोयड-वॉर्शल एल्गोरिथम
- स्वयं से परहेज करना
- सबसे छोटा पथ ग्राफ
संदर्भ
- Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability.
- Bondy, J. A.; Murty, U. S. R. (1976). Graph Theory with Applications. North Holland. p. 12-21. ISBN 0-444-19451-7.
- Diestel, Reinhard (2005). Graph Theory. Springer-Verlag. pp. 6–9. ISBN 3-540-26182-6.
- Gibbons, A. (1985). Algorithmic Graph Theory. Cambridge University Press. pp. 5–6. ISBN 0-521-28881-9.
- Korte, Bernhard; Lovász, László; Prömel, Hans Jürgen; Schrijver, Alexander (1990). Paths, Flows, and VLSI-Layout. Springer-Verlag. ISBN 0-387-52685-4.