पथ (ग्राफ सिद्धांत): Difference between revisions
mNo edit summary |
No edit summary |
||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
{{For|the family of graphs known as paths|Path graph}} | {{For|the family of graphs known as paths|Path graph}} | ||
[[File:Snake-in-the-box and Hamiltonian path.svg|thumb|right|एक त्रि-आयामी [[हाइपरक्यूब ग्राफ|अतिविम ग्राफ]]़ लाल रंग में [[हैमिल्टनियन पथ]] और गहरा काला रंग सबसे लंबा प्रेरित पथ दिखा रहा है।।]]ग्राफ़ सिद्धांत में, ग्राफ़ में एक पथ | [[File:Snake-in-the-box and Hamiltonian path.svg|thumb|right|एक त्रि-आयामी [[हाइपरक्यूब ग्राफ|अतिविम ग्राफ]]़ लाल रंग में [[हैमिल्टनियन पथ]] और गहरा काला रंग सबसे लंबा प्रेरित पथ दिखा रहा है।।]]ग्राफ़ सिद्धांत में, ग्राफ़ में एक पथ सिराओं का एक परिमित या अनंत अनुक्रम होता है जो शीर्षों के अनुक्रम में सम्मिलित होता है, जो कि अधिकांश परिभाषाओं के अनुसार, (और चूंकि कोने अलग होते हैं, इसलिए सिरा भी होते हैं) सभी अलग होते हैं। एक निर्देशित पथ (कभी-कभी द्विपथ {{sfn|Bender|Williamson|2010|p=162}} कहा जाता है) एक निर्देशित ग्राफ में सिराओं का एक परिमित या अनंत अनुक्रम होता है जो अलग-अलग शीर्षों के अनुक्रम में सम्मिलित होता है, लेकिन अतिरिक्त प्रतिबंध के साथ सिराओं को एक ही दिशा में निर्देशित किया जाता है। | ||
पथ ग्राफ सिद्धांत की मूलभूत अवधारणाएँ हैं, जिनका वर्णन अधिकांश ग्राफ सिद्धांत ग्रंथों के परिचयात्मक खंडों में वर्णित है। उदाहरण | पथ ग्राफ सिद्धांत की मूलभूत अवधारणाएँ हैं, जिनका वर्णन अधिकांश ग्राफ सिद्धांत ग्रंथों के परिचयात्मक खंडों में वर्णित है। उदाहरण के लिए बॉन्डी और मूर्ति (1976), गिबन्स (1985), या डायस्टेल (2005) कोर्टे एट अल (1990) रेखांकन में पथों से संबंधित अधिक उन्नत [[ कलन विधि |कलन विधि]] विषयों को कवर करते हैं। | ||
== परिभाषाएँ == | == परिभाषाएँ == | ||
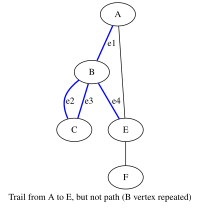
=== | === गति, निशान, और पथ === | ||
[[File:Trail but not path.svg|200px|thumb|right]] | [[File:Trail but not path.svg|200px|thumb|right]] | ||
* | * गति सिराओं का एक परिमित या अनंत क्रम है जो शीर्षों के अनुक्रम में सम्मिलित होता है{{sfn|Bender|Williamson|2010|p=162}} | ||
: मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित | : मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित गति सिराओं (e1, e2, …, en − 1) का एक क्रम है जिसके लिए शीर्ष का एक क्रम {{nowrap|(''v''<sub>1</sub>, ''v''<sub>2</sub>, …, ''v''<sub>''n''</sub>)}} है जैसे कि ϕ(ei) = {vi, vi 1} के लिए i = 1, 2, …, n − 1. (v1, v2, …, vn) गति का शीर्ष अनुक्रम है अगर v1 = vn,गति बंद है ,अन्यथा यह खुला है। एक अनंतगति यहाँ वर्णित एक ही प्रकार के सिराओं का एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंतगति (या किरण) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है। | ||
* निशान एक ऐसा | * निशान एक ऐसा गति है जिसके सभी सिरा अलग-अलग होते हैं।{{sfn|Bender|Williamson|2010|p=162}} | ||
* एक पथ एक निशान है जिसमें सभी कोने (और सभी | * एक पथ एक निशान है जिसमें सभी कोने (और सभी सिरा भी) अलग-अलग हैं।{{sfn|Bender|Williamson|2010|p=162}} | ||
इसी प्रकार एक निशान या पथ के लिए यदि w = (e1, e2, …, en − 1) शीर्ष अनुक्रम (v1, v2, …, vn) के साथ एक | इसी प्रकार एक निशान या पथ के लिए यदि w = (e1, e2, …, en − 1) शीर्ष अनुक्रम (v1, v2, …, vn) के साथ एक परिमितगति है, तो w को v1 से vn तक कीगति कहा जाता है। यदि दो अलग-अलग शीर्षों के बीच एक परिमितगति है तो एक परिमित निशान और उनके बीच एक परिमित पथ भी है। | ||
कुछ लेखकों के लिए यह आवश्यक नहीं है कि पथ के सभी शीर्ष भिन्न हों और इसके बजाय ऐसे पथ को संदर्भित करने के लिए 'सरल पथ' शब्द का उपयोग करें जहां सभी कोने अलग-अलग हों। | कुछ लेखकों के लिए यह आवश्यक नहीं है कि पथ के सभी शीर्ष भिन्न हों और इसके बजाय ऐसे पथ को संदर्भित करने के लिए 'सरल पथ' शब्द का उपयोग करें जहां सभी कोने अलग-अलग हों। | ||
एक भारित ग्राफ में प्रत्येक | एक भारित ग्राफ में प्रत्येक सिरा के साथ एक मान (वजन) को जोड़ता है। भारित ग्राफ़ में चलने (या निशान या पथ) का भार पार किए हुए सिरा के भार का योग होता है। कभी-कभी वजन के स्थान पर लागत या लंबाई शब्दों का प्रयोग किया जाता है। | ||
=== निर्देशित | === निर्देशित गति, निर्देशित निशान, और निर्देशित पथ === | ||
* एक निर्देशित | * एक निर्देशित गति छोर (ग्राफ सिद्धांत) का एक परिमित या अनंत अनुक्रम है जो उसी दिशा में निर्देशित होता है जो शीर्ष (ग्राफ सिद्धांत) के अनुक्रम में सम्मिलित होता है।{{sfn|Bender|Williamson|2010|p=162}} | ||
: मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित | : मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित निर्देशितगति सिराओंका एक क्रम है {{nowrap|(''e''<sub>1</sub>, ''e''<sub>2</sub>, …, ''e''<sub>''n'' − 1</sub>)}} जिसके लिए शीर्ष का एक क्रम {{nowrap|(''v''<sub>1</sub>, ''v''<sub>2</sub>, …, ''v''<sub>''n''</sub>)}} है जैसे कि {{nowrap|1=''ϕ''(''e''<sub>''i''</sub>) = (''v''<sub>''i''</sub>, ''v''<sub>''i'' + 1</sub>)}} के लिए {{nowrap|1=''i'' = 1, 2, …, ''n'' − 1}}. {{nowrap|(''v''<sub>1</sub>, ''v''<sub>2</sub>, …, ''v''<sub>''n''</sub>)}} निर्देशितगति का शीर्ष क्रम है। अगर v1 = vn, निर्देशितगति बंद है ,अन्यथा यह खुला है। एक अनंत निर्देशित गति यहाँ वर्णित एक ही प्रकार के सिराओंका एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंत निर्देशितगति (या किरण) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है। | ||
* एक निर्देशित निशान एक निर्देशित मार्ग है जिसमें सभी | * एक निर्देशित निशान एक निर्देशित मार्ग है जिसमें सभी सिरा अलग-अलग होते हैं। {{sfn|Bender|Williamson|2010|p=162}} | ||
* एक निर्देशित पथ एक निर्देशित पथ है जिसमें सभी शीर्ष भिन्न होते हैं।{{sfn|Bender|Williamson|2010|p=162}} | * एक निर्देशित पथ एक निर्देशित पथ है जिसमें सभी शीर्ष भिन्न होते हैं।{{sfn|Bender|Williamson|2010|p=162}} | ||
इसी प्रकार एक निर्देशित निशान या पथ के लिए यदि w = (e1, e2, …, en − 1) शीर्ष अनुक्रम (v1, v2, …, vn) के साथ एक परिमित निर्देशित | इसी प्रकार एक निर्देशित निशान या पथ के लिए यदि w = (e1, e2, …, en − 1) शीर्ष अनुक्रम (v1, v2, …, vn) के साथ एक परिमित निर्देशित गति है, तो w को v1 से vn तक की गति कहा जाता है। यदि दो अलग-अलग शीर्षों के बीच एक परिमित निर्देशित गति है तो एक परिमित निर्देशित निशान और उनके बीच एक परिमित निर्देशित पथ भी है। | ||
एक सरल निर्देशित पथ एक ऐसी | एक सरल निर्देशित पथ एक ऐसी गति है जहाँ सभी शीर्ष भिन्न होते हैं। | ||
एक भारित ग्राफ़ निर्देशित ग्राफ़ में | एक भारित ग्राफ़ निर्देशित ग्राफ़ में प्रत्येकसिरा के साथ एक मान (वजन) को जोड़ता है। भारित निर्देशित ग्राफ़ में एक निर्देशितगति (या निशान या पथ) का भार अनुप्रस्थ सिराओं के भार का योग होता है। कभी-कभी वजन के स्थान पर लागत या लंबाई शब्दों का प्रयोग किया जाता है। | ||
== उदाहरण == | == उदाहरण == | ||
* एक ग्राफ जुड़ा हुआ है यदि प्रत्येक जोड़े के शीर्ष वाले पथ हैं। | * एक ग्राफ जुड़ा हुआ है यदि प्रत्येक जोड़े के शीर्ष वाले पथ हैं। | ||
*एक निर्देशित ग्राफ दृढ़ता से जुड़ा हुआ है यदि विपरीत दिशा में निर्देशित पथ जिनमें प्रत्येक जोड़ी के कोने हैं। | *एक निर्देशित ग्राफ दृढ़ता से जुड़ा हुआ है यदि विपरीत दिशा में निर्देशित पथ जिनमें प्रत्येक जोड़ी के कोने हैं। | ||
* एक पथ ऐसा है कि कोई भी ग्राफ | * एक पथ ऐसा है कि कोई भी ग्राफ छोर दो अपरिचित-सतत पथ के शीर्षों को जोड़ता है,वह एक प्रेरित पथ कहलाता है। | ||
*एक पथ जिसमें दोहराए बिना ग्राफ़ के प्रत्येक शीर्ष को | *एक पथ जिसमें दोहराए बिना ग्राफ़ के प्रत्येक शीर्ष को सम्मिलित किया गया है, हैमिल्टनियन पथ के रूप में जाना जाता है। | ||
* दो पथ शीर्ष स्वतंत्र (वैकल्पिक रूप से, आंतरिक रूप से शीर्ष -विभिन्न करना) हैं यदि उनके पास कोई आंतरिक शीर्ष उभयनिष्ठ नहीं है। इसी तरह, दो | * दो पथ शीर्ष स्वतंत्र (वैकल्पिक रूप से, आंतरिक रूप से शीर्ष -विभिन्न करना) हैं यदि उनके पास कोई आंतरिक शीर्ष उभयनिष्ठ नहीं है। इसी तरह, दो रास्तेसिरा से स्वतंत्र (यासिरा से विभिन्न करना) हैं, अगर उनमें कोई आंतरिक छोर समान नहीं है। दो आंतरिक रूप से शीर्ष-विभिन्न करना पथसिरा से विभिन्न करना हैं, लेकिन इसका विलोम आवश्यक रूप से सत्य नहीं है। | ||
*एक ग्राफ़ में दो शीर्षों के बीच की दूरी (ग्राफ़ सिद्धांत) उनके बीच सबसे छोटे पथ की लंबाई है, यदि कोई | *एक ग्राफ़ में दो शीर्षों के बीच की दूरी (ग्राफ़ सिद्धांत) उनके बीच सबसे छोटे पथ की लंबाई है, यदि कोई उपस्थित है, अन्यथा दूरी अनंत है। | ||
* जुड़े हुए ग्राफ़ का व्यास, ग्राफ़ के शीर्षों के युग्मों के बीच की सबसे बड़ी दूरी (ऊपर परिभाषित) है। | * जुड़े हुए ग्राफ़ का व्यास, ग्राफ़ के शीर्षों के युग्मों के बीच की सबसे बड़ी दूरी (ऊपर परिभाषित) है। | ||
== पथ ढूँढना == | == पथ ढूँढना == | ||
ग्राफ़ में सबसे छोटा और सबसे | ग्राफ़ में सबसे छोटा और सबसे लंबा पथ खोजने के लिए कई कलन विधि उपस्थित हैं, इस महत्वपूर्ण अंतर के साथ कि पूर्व की समस्या गणना रूप से बाद की मिलान में बहुत आसान है। | ||
दिज्क्स्ट्रा का कलन विधि गैर-नकारात्मक | दिज्क्स्ट्रा का कलन विधि गैर-नकारात्मक छोर वजन (या कोई छोर वजन) के साथ निर्देशित और अप्रत्यक्ष ग्राफ़ में स्रोत शिखर से हर दूसरे शिखर तक सबसे छोटे रास्तों की एक सूची तैयार करता है, जबकि बेलमैन-फोर्ड कलन विधि को नकारात्मक छोर वजन के साथ निर्देशित ग्राफ़ पर लागू किया जा सकता है। फ़्लॉइड-वॉर्शल कलन विधि का उपयोग भारित निर्देशित ग्राफ़ में सभी जोड़े के बीच सबसे छोटा रास्ता खोजने के लिए किया जा सकता है। | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 69: | Line 69: | ||
{{interwiki extra|qid=Q917421}} | {{interwiki extra|qid=Q917421}} | ||
{{Authority control}} | {{Authority control}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category: | |||
[[Category:Created On 19/05/2023]] | [[Category:Created On 19/05/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:ग्राफ कनेक्टिविटी]] | |||
[[Category:ग्राफ सिद्धांत वस्तुओं]] | |||
Latest revision as of 10:08, 7 June 2023

ग्राफ़ सिद्धांत में, ग्राफ़ में एक पथ सिराओं का एक परिमित या अनंत अनुक्रम होता है जो शीर्षों के अनुक्रम में सम्मिलित होता है, जो कि अधिकांश परिभाषाओं के अनुसार, (और चूंकि कोने अलग होते हैं, इसलिए सिरा भी होते हैं) सभी अलग होते हैं। एक निर्देशित पथ (कभी-कभी द्विपथ [1] कहा जाता है) एक निर्देशित ग्राफ में सिराओं का एक परिमित या अनंत अनुक्रम होता है जो अलग-अलग शीर्षों के अनुक्रम में सम्मिलित होता है, लेकिन अतिरिक्त प्रतिबंध के साथ सिराओं को एक ही दिशा में निर्देशित किया जाता है।
पथ ग्राफ सिद्धांत की मूलभूत अवधारणाएँ हैं, जिनका वर्णन अधिकांश ग्राफ सिद्धांत ग्रंथों के परिचयात्मक खंडों में वर्णित है। उदाहरण के लिए बॉन्डी और मूर्ति (1976), गिबन्स (1985), या डायस्टेल (2005) कोर्टे एट अल (1990) रेखांकन में पथों से संबंधित अधिक उन्नत कलन विधि विषयों को कवर करते हैं।
परिभाषाएँ
गति, निशान, और पथ
- गति सिराओं का एक परिमित या अनंत क्रम है जो शीर्षों के अनुक्रम में सम्मिलित होता है[1]
- मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित गति सिराओं (e1, e2, …, en − 1) का एक क्रम है जिसके लिए शीर्ष का एक क्रम (v1, v2, …, vn) है जैसे कि ϕ(ei) = {vi, vi 1} के लिए i = 1, 2, …, n − 1. (v1, v2, …, vn) गति का शीर्ष अनुक्रम है अगर v1 = vn,गति बंद है ,अन्यथा यह खुला है। एक अनंतगति यहाँ वर्णित एक ही प्रकार के सिराओं का एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंतगति (या किरण) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है।
- निशान एक ऐसा गति है जिसके सभी सिरा अलग-अलग होते हैं।[1]
- एक पथ एक निशान है जिसमें सभी कोने (और सभी सिरा भी) अलग-अलग हैं।[1]
इसी प्रकार एक निशान या पथ के लिए यदि w = (e1, e2, …, en − 1) शीर्ष अनुक्रम (v1, v2, …, vn) के साथ एक परिमितगति है, तो w को v1 से vn तक कीगति कहा जाता है। यदि दो अलग-अलग शीर्षों के बीच एक परिमितगति है तो एक परिमित निशान और उनके बीच एक परिमित पथ भी है।
कुछ लेखकों के लिए यह आवश्यक नहीं है कि पथ के सभी शीर्ष भिन्न हों और इसके बजाय ऐसे पथ को संदर्भित करने के लिए 'सरल पथ' शब्द का उपयोग करें जहां सभी कोने अलग-अलग हों।
एक भारित ग्राफ में प्रत्येक सिरा के साथ एक मान (वजन) को जोड़ता है। भारित ग्राफ़ में चलने (या निशान या पथ) का भार पार किए हुए सिरा के भार का योग होता है। कभी-कभी वजन के स्थान पर लागत या लंबाई शब्दों का प्रयोग किया जाता है।
निर्देशित गति, निर्देशित निशान, और निर्देशित पथ
- एक निर्देशित गति छोर (ग्राफ सिद्धांत) का एक परिमित या अनंत अनुक्रम है जो उसी दिशा में निर्देशित होता है जो शीर्ष (ग्राफ सिद्धांत) के अनुक्रम में सम्मिलित होता है।[1]
- मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित निर्देशितगति सिराओंका एक क्रम है (e1, e2, …, en − 1) जिसके लिए शीर्ष का एक क्रम (v1, v2, …, vn) है जैसे कि ϕ(ei) = (vi, vi + 1) के लिए i = 1, 2, …, n − 1. (v1, v2, …, vn) निर्देशितगति का शीर्ष क्रम है। अगर v1 = vn, निर्देशितगति बंद है ,अन्यथा यह खुला है। एक अनंत निर्देशित गति यहाँ वर्णित एक ही प्रकार के सिराओंका एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंत निर्देशितगति (या किरण) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है।
- एक निर्देशित निशान एक निर्देशित मार्ग है जिसमें सभी सिरा अलग-अलग होते हैं। [1]
- एक निर्देशित पथ एक निर्देशित पथ है जिसमें सभी शीर्ष भिन्न होते हैं।[1]
इसी प्रकार एक निर्देशित निशान या पथ के लिए यदि w = (e1, e2, …, en − 1) शीर्ष अनुक्रम (v1, v2, …, vn) के साथ एक परिमित निर्देशित गति है, तो w को v1 से vn तक की गति कहा जाता है। यदि दो अलग-अलग शीर्षों के बीच एक परिमित निर्देशित गति है तो एक परिमित निर्देशित निशान और उनके बीच एक परिमित निर्देशित पथ भी है।
एक सरल निर्देशित पथ एक ऐसी गति है जहाँ सभी शीर्ष भिन्न होते हैं।
एक भारित ग्राफ़ निर्देशित ग्राफ़ में प्रत्येकसिरा के साथ एक मान (वजन) को जोड़ता है। भारित निर्देशित ग्राफ़ में एक निर्देशितगति (या निशान या पथ) का भार अनुप्रस्थ सिराओं के भार का योग होता है। कभी-कभी वजन के स्थान पर लागत या लंबाई शब्दों का प्रयोग किया जाता है।
उदाहरण
- एक ग्राफ जुड़ा हुआ है यदि प्रत्येक जोड़े के शीर्ष वाले पथ हैं।
- एक निर्देशित ग्राफ दृढ़ता से जुड़ा हुआ है यदि विपरीत दिशा में निर्देशित पथ जिनमें प्रत्येक जोड़ी के कोने हैं।
- एक पथ ऐसा है कि कोई भी ग्राफ छोर दो अपरिचित-सतत पथ के शीर्षों को जोड़ता है,वह एक प्रेरित पथ कहलाता है।
- एक पथ जिसमें दोहराए बिना ग्राफ़ के प्रत्येक शीर्ष को सम्मिलित किया गया है, हैमिल्टनियन पथ के रूप में जाना जाता है।
- दो पथ शीर्ष स्वतंत्र (वैकल्पिक रूप से, आंतरिक रूप से शीर्ष -विभिन्न करना) हैं यदि उनके पास कोई आंतरिक शीर्ष उभयनिष्ठ नहीं है। इसी तरह, दो रास्तेसिरा से स्वतंत्र (यासिरा से विभिन्न करना) हैं, अगर उनमें कोई आंतरिक छोर समान नहीं है। दो आंतरिक रूप से शीर्ष-विभिन्न करना पथसिरा से विभिन्न करना हैं, लेकिन इसका विलोम आवश्यक रूप से सत्य नहीं है।
- एक ग्राफ़ में दो शीर्षों के बीच की दूरी (ग्राफ़ सिद्धांत) उनके बीच सबसे छोटे पथ की लंबाई है, यदि कोई उपस्थित है, अन्यथा दूरी अनंत है।
- जुड़े हुए ग्राफ़ का व्यास, ग्राफ़ के शीर्षों के युग्मों के बीच की सबसे बड़ी दूरी (ऊपर परिभाषित) है।
पथ ढूँढना
ग्राफ़ में सबसे छोटा और सबसे लंबा पथ खोजने के लिए कई कलन विधि उपस्थित हैं, इस महत्वपूर्ण अंतर के साथ कि पूर्व की समस्या गणना रूप से बाद की मिलान में बहुत आसान है।
दिज्क्स्ट्रा का कलन विधि गैर-नकारात्मक छोर वजन (या कोई छोर वजन) के साथ निर्देशित और अप्रत्यक्ष ग्राफ़ में स्रोत शिखर से हर दूसरे शिखर तक सबसे छोटे रास्तों की एक सूची तैयार करता है, जबकि बेलमैन-फोर्ड कलन विधि को नकारात्मक छोर वजन के साथ निर्देशित ग्राफ़ पर लागू किया जा सकता है। फ़्लॉइड-वॉर्शल कलन विधि का उपयोग भारित निर्देशित ग्राफ़ में सभी जोड़े के बीच सबसे छोटा रास्ता खोजने के लिए किया जा सकता है।
यह भी देखें
- ग्राफ सिद्धांत की शब्दावली
- पथ ग्राफ
- बहुभुज श्रृंखला
- सबसे छोटा पथ समस्या
- सबसे लंबी पथ समस्या
- दिज्क्स्ट्रा का कलन विधि
- बेलमैन-फोर्ड कलन विधि
- फ्लोयड-वॉर्शल कलन विधि
- स्वयं से परहेज करना
- सबसे छोटा पथ ग्राफ
संदर्भ
- Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability.
- Bondy, J. A.; Murty, U. S. R. (1976). Graph Theory with Applications. North Holland. p. 12-21. ISBN 0-444-19451-7.
- Diestel, Reinhard (2005). Graph Theory. Springer-Verlag. pp. 6–9. ISBN 3-540-26182-6.
- Gibbons, A. (1985). Algorithmic Graph Theory. Cambridge University Press. pp. 5–6. ISBN 0-521-28881-9.
- Korte, Bernhard; Lovász, László; Prömel, Hans Jürgen; Schrijver, Alexander (1990). Paths, Flows, and VLSI-Layout. Springer-Verlag. ISBN 0-387-52685-4.