क्रिस-क्रॉस कलन विधि: Difference between revisions
(Created page with "{{Short description|Method for mathematical optimization}} {{About|an algorithm for mathematical optimization||Criss-cross (disambiguation){{!}}Criss-cross}} {{Use dmy dates|d...") |
(text) |
||
| Line 1: | Line 1: | ||
{{Short description|Method for mathematical optimization}} | {{Short description|Method for mathematical optimization}} | ||
{{About| | {{About|गणितीय अनुकूलन के लिए एक कलन विधि||क्रिस-क्रॉस (विसंदिग्धीकरण){{!}}क्रिस-क्रॉस}} | ||
{{Use dmy dates|date=December 2013}} | {{Use dmy dates|date=December 2013}} | ||
<!-- {{Context|date=May 2012}} --> | <!-- {{Context|date=May 2012}} --> | ||
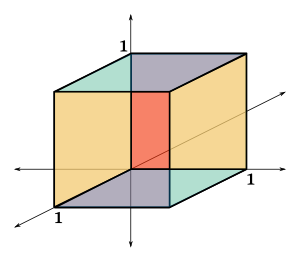
[[File:Unitcube.svg|thumb|right|alt=A three-डायमेंशनल क्यूब|क्रिस-क्रॉस | [[File:Unitcube.svg|thumb|right|alt=A three-डायमेंशनल क्यूब|क्रिस-क्रॉस कलन विधि सबसे खराब स्थिति में क्ले-मिन्टी घन के सभी 8 कोनों पर जाता है। यह औसतन 3 अतिरिक्त कोनों का दौरा करता है। क्ले-मिन्टी घन यहाँ दिखाए गए घन का एक क्षोभ है।]]इष्टमीकरण (गणित) में, क्रिस-क्रॉस [[ कलन विधि |कलन विधि]] [[रैखिक प्रोग्रामिंग|रैखिक क्रमादेशन]] के लिए कलन विधि के परिवार में से कोई है। क्रिस-क्रॉस कलन विधि के परिवर्त्य भी रैखिक क्रमादेशन और गैर-रैखिक क्रमादेशन [[अनुकूलन (गणित)]] के साथ अधिक सामान्य समस्याओं को हल करते हैं; [[रैखिक-आंशिक प्रोग्रामिंग|रैखिक-आंशिक क्रमादेशन]] समस्याओं के लिए क्रिस-क्रॉस कलन विधि हैं,<ref name="LF99Hyperbolic">{{harvtxt|Illés|Szirmai|Terlaky|1999}}</ref><ref name="Bibl" >{{cite journal|first=I. M.|last=Stancu-Minasian|title=आंशिक प्रोग्रामिंग की छठी ग्रंथ सूची|journal=Optimization|volume=55|number=4|date=August 2006|pages=405–428|doi=10.1080/02331930600819613|mr=2258634|s2cid=62199788}}</ref> [[द्विघात प्रोग्रामिंग|द्विघात क्रमादेशन]] समस्याएं, और रैखिक संपूरकता समस्याएं हैं।<ref name="FukudaTerlaky" >{{harvtxt|Fukuda|Terlaky|1997}}</ref> | ||
जॉर्ज बी. डेंटजिग के [[सिंप्लेक्स एल्गोरिदम|प्रसमुच्चय कलन विधि]] की तरह, रेखीय क्रमादेशन के लिए बहुपद-समय कलन विधि एक [[समय जटिलता]] नहीं है। दोनों कलन विधि सबसे खराब स्थिति में आयाम D, क्ले-मिन्टी घन (विक्टर क्ले और जॉर्ज जे मिंटी के बाद) में एक घन के सभी 2<sup>D</sup> कोनों पर जाते हैं। <ref name="Roos" >{{harvtxt|Roos|1990}}</ref><ref name="KleeMinty"/> हालांकि, जब इसे एक यादृच्छिक कोने पर प्रारम्भ किया जाता है, तो क्रिस-क्रॉस कलन विधि औसत आगमन पर केवल डी अतिरिक्त कोनों पर जाता है।<ref name="FTNamiki"/><ref name="FukudaNamiki"/><ref name="Borgwardt">The simplex algorithm takes on average ''D'' steps for a cube. {{harvtxt|Borgwardt|1987}}: {{cite book|last=Borgwardt|first=Karl-Heinz|title=The simplex method: A probabilistic analysis|series=Algorithms and Combinatorics (Study and Research Texts)|volume=1|publisher=Springer-Verlag|location=Berlin|year=1987|pages=xii+268|isbn=978-3-540-17096-9|mr=868467}}</ref> इस प्रकार, त्रि-आयामी घन के लिए, कलन विधि सबसे खराब स्थिति में सभी 8 कोनों और औसतन ठीक 3 अतिरिक्त कोनों पर जाता है। | |||
== इतिहास == | == इतिहास == | ||
क्रिस-क्रॉस | क्रिस-क्रॉस कलन विधि स्वतंत्र रूप से [[तमस टेरलाकी]] और जेड-मिन वांग द्वारा प्रकाशित किया गया था <ref>{{harvtxt|Terlaky|1985}} and {{harvtxt|Terlaky|1987}}</ref> <ref name="Wang" >{{harvtxt|Wang|1987}}</ref> संबंधित कलन विधि अन्य लेखकों द्वारा अप्रकाशित वर्णन में दिखाई दिए।<ref name="FukudaTerlaky"/> | ||
== रैखिक अनुकूलन के लिए | == रैखिक अनुकूलन के लिए प्रसमुच्चय कलन विधि के साथ तुलना == | ||
{{See also| | {{See also|रैखिक क्रमादेशन|प्रसमुच्चय कलन विधि|ब्लैंड का नियम}} | ||
[[File:Simplex description.png|thumb|240px|अपने दूसरे चरण में, | [[File:Simplex description.png|thumb|240px|अपने दूसरे चरण में, प्रसमुच्चय कलन विधि पॉलीटॉप के किनारों पर तब तक सरकन करता है जब तक कि यह अंत में एक इष्टतम शीर्ष (ज्यामिति) तक नहीं पहुंच जाता। क्रिस-क्रॉस कलन विधि उन आधारों पर विचार करता है जो शीर्षों से संबद्ध नहीं हैं, ताकि कुछ पुनरावृत्त संभव क्षेत्र के आंतरिक भाग में हो सकें, जैसे आंतरिक-बिंदु कलन विधि; क्राइस-क्रॉस कलन विधि संभव क्षेत्र के बाहर अव्यवहार्य पुनरावृति भी कर सकता है।]]रैखिक क्रमादेशन में, क्रिस-क्रॉस कलन विधि आधारों के अनुक्रम के बीच धुराग्र करता है लेकिन प्रसमुच्चय कलन विधि से भिन्न होता है। प्रसमुच्चय कलन विधि पहले चरण-एक समस्या को हल करके एक (प्राथमिक-) व्यवहार्य आधार पाता है; चरण दो में, प्रसमुच्चय कलन विधि बुनियादी व्यवहार्य समाधानों के अनुक्रम के बीच धुराग्र करता है ताकि उद्देश्य फलन प्रत्येक धुराग्र के साथ घटता न हो, एक इष्टतम समाधान के साथ समाप्त हो (अंत में एक दोहरी व्यवहार्य समाधान भी ढूंढ रहा है)।<ref name="FukudaTerlaky"/><ref name="TerlakyZhang">{{harvtxt|Terlaky|Zhang|1993}}</ref> | ||
क्रिस-क्रॉस | क्रिस-क्रॉस कलन विधि प्रसमुच्चय कलन विधि की तुलना में सरल है, क्योंकि क्रिस-क्रॉस कलन विधि में केवल एक चरण होता है। इसके धुरी नियम ब्लैंड के न्यूनतम-सूचकांक धुरी नियम के समान हैं। <ref name="Bland"> | ||
{{cite journal|title=New finite pivoting rules for the simplex method|first=Robert G.|last=Bland|journal=Mathematics of Operations Research|volume=2|number=2|date=May 1977|pages=103–107|doi=10.1287/moor.2.2.103|jstor=3689647|mr=459599}}</ref> योग्य | {{cite journal|title=New finite pivoting rules for the simplex method|first=Robert G.|last=Bland|journal=Mathematics of Operations Research|volume=2|number=2|date=May 1977|pages=103–107|doi=10.1287/moor.2.2.103|jstor=3689647|mr=459599}}</ref> योग्य धुराग्र तय करते समय ब्लैंड का नियम उनके वास्तविक संख्या के स्थान पर गुणांकों के केवल संकेत कार्यों का उपयोग करता है। ब्लैंड का नियम योग्य धुराग्र के वास्तविक-संख्या क्रम का उपयोग करके कम लागत के मूल्यों की तुलना करके एक प्रवेश चर का चयन करता है।<ref name="Bland"/><ref>Bland's rule is also related to an earlier least-index rule, which was proposed by Katta G. Murty for the [[linear complementarity problem]], according to {{harvtxt|Fukuda|Namiki|1994}}.</ref> ब्लैंड के नियम के विपरीत, क्रिस-क्रॉस कलन विधि विशुद्ध रूप से संयोजी है, एक प्रवेश चर और एक छोड़ने वाले चर का चयन करते हुए उनके वास्तविक-संख्या क्रम के स्थान पर केवल गुणांक के संकेतों पर विचार करके किया जाता है। <ref name="FukudaTerlaky"/><ref name="TerlakyZhang"/> क्रिस-क्रॉस कलन विधि को रैखिक बीजगणित में बुनियादी परिणामों के रचनात्मक प्रमाण प्रस्तुत करने के लिए लागू किया गया है, जैसे कि [[भेड़िया लेम्मा|फ़र्कस की लेम्मा।]] <ref name="KT91" >{{harvtxt|Klafszky|Terlaky|1991}}</ref> | ||
जबकि अधिकांश | |||
जबकि अधिकांश प्रसमुच्चय परिवर्ती उद्देश्य में एकदिष्ट होते हैं (कठोरता से गैर-पतित स्तिथि में), क्रिस-क्रॉस कलन विधि के अधिकांश परिवर्त्य में एक एकदिष्ट श्रेष्ठता फलन की कमी होती है जो व्यवहार में हानि हो सकती है। | |||
== विवरण == | == विवरण == | ||
{{Expand section|date=April 2011}} | {{Expand section|date=April 2011}} | ||
क्रिस-क्रॉस | क्रिस-क्रॉस कलन विधि एक मानक धुरी झांकी पर काम करता है (या झांकी के ऑन-द-फ्लाई परिकलित भागों, यदि संशोधित प्रसमुच्चय विधि की तरह लागू किया जाता है)। एक सामान्य चरण में, यदि झांकी प्रारंभिक या दोहरी अव्यवहार्य है, तो यह अनुक्रमणिका चयन नियम का उपयोग करके धुरी पंक्ति/स्तंभ के रूप में अव्यवहार्य पंक्तियों/स्तंभों में से एक का चयन करती है। एक महत्वपूर्ण संपत्ति यह है कि चयन अव्यवहार्य सूचकांकों के मिलन पर किया जाता है और कलन विधि का मानक संस्करण स्तंभ और पंक्ति सूचकांकों में अंतर नहीं करता है (अर्थात, स्तंभ सूचकांक पंक्तियों में बुनियादी हैं)। यदि एक पंक्ति का चयन किया जाता है तो कलन विधि दोहरे प्रकार के धुरी की स्थिति की पहचान करने के लिए सूचकांक चयन नियम का उपयोग करता है, जबकि यदि एक स्तंभ का चयन किया जाता है तो यह पंक्ति की स्थिति खोजने के लिए सूचकांक चयन नियम का उपयोग करता है और एक मूल प्रकार की धुरी करता है। | ||
== कम्प्यूटेशनल जटिलता: सबसे खराब और औसत | == कम्प्यूटेशनल जटिलता: सबसे खराब और औसत स्तिथि == | ||
[[File:Ellipsoid 2.png|thumb|right<!-- 400px -->|खाचियान के दीर्घवृत्त एल्गोरिथम की सबसे खराब स्थिति कम्प्यूटेशनल जटिलता एक बहुपद है। क्रिस-क्रॉस एल्गोरिथम में घातीय जटिलता है।]] | [[File:Ellipsoid 2.png|thumb|right<!-- 400px -->|खाचियान के दीर्घवृत्त एल्गोरिथम की सबसे खराब स्थिति कम्प्यूटेशनल जटिलता एक बहुपद है। क्रिस-क्रॉस एल्गोरिथम में घातीय जटिलता है।]]कलन विधि की समय जटिलता समस्या को हल करने के लिए कलन विधि के लिए पर्याप्त अंकगणितीय परिचालनों की संख्या की गणना करती है। उदाहरण के लिए, D<sup>3</sup> के अनुक्रम पर गॉसियन उन्मूलन संचालन की आवश्यकता होती है, और इसलिए इसे बहुपद समय-जटिलता कहा जाता है, क्योंकि इसकी जटिलता एक [[घन बहुपद]] से बंधी है। ऐसे कलन विधि के उदाहरण हैं जिनमें बहुपद-समय की जटिलता नहीं है। उदाहरण के लिए, गॉसियन उन्मूलन के एक सामान्यीकरण को बुचबर्गर के कलन विधि कहा जाता है, इसकी जटिलता के लिए एक समस्या डेटा का घातीय कार्य ([[एक बहुपद की डिग्री]] और [[बहुभिन्नरूपी बहुपद]] के चर की संख्या) है। क्योंकि घातीय कार्य अंततः बहुपद कार्यों की तुलना में बहुत तेजी से बढ़ते हैं, एक घातीय जटिलता का तात्पर्य है कि एक कलन विधि का बड़ी समस्याओं पर धीमा प्रदर्शन होता है। | ||
रेखीय क्रमादेशन के लिए कई कलन विधि—खाचियान का [[दीर्घवृत्त एल्गोरिथ्म|दीर्घवृत्त कलन विधि]], [[करमरकर]] का प्रक्षेपीय कलन विधि, और [[ आंतरिक-बिंदु विधि |आंतरिक-बिंदु विधि]] — में बहुपद समय-जटिलता होती है (सबसे खराब स्थिति में जटिलता और इस प्रकार औसत जटिलता)। दीर्घवृत्ताकार और प्रक्षेपी कलन विधि को क्रिस-क्रॉस कलन विधि से पहले प्रकाशित किया गया था। | |||
हालांकि, डेंटज़िग के | हालांकि, डेंटज़िग के प्रसमुच्चय कलन विधि की तरह, क्रिस-क्रॉस कलन विधि रैखिक क्रमादेशन के लिए बहुपद-समय कलन विधि नहीं है। 2<sup>D</sup> रूस के एक लेख के अनुसार, टेरलकी का क्रिस-क्रॉस कलन विधि आयाम D में एक (अशान्त) घन के सभी 2D कोनों पर जाता है। जिस पर प्रसमुच्चय कलन विधि 2<sup>''D''</sup> कदम लेता है।<ref name="FukudaTerlaky"/><ref name="Roos"/><ref name="KleeMinty">{{cite book|title=Inequalities III (Proceedings of the Third Symposium on Inequalities held at the University of California, Los Angeles, Calif., September 1–9, 1969, dedicated to the memory of Theodore S. Motzkin)|editor-first=Oved|editor-last=Shisha|publisher=Academic Press|location=New York-London|year=1972|mr=332165|last1=Klee|first1=Victor|author-link1=Victor Klee|last2=Minty|first2= George J.|author-link2=George J. Minty|chapter=How good is the simplex algorithm?|pages=159–175}}</ref> प्रसमुच्चय कलन विधि की तरह, क्रिस-क्रॉस कलन विधि सबसे खराब स्थिति में त्रि-आयामी घन के सभी 8 कोनों पर जाता है। | ||
जब इसे घन के एक यादृच्छिक कोने में प्रारंभ किया जाता है, तो क्रिस-क्रॉस | जब इसे घन के एक यादृच्छिक कोने में प्रारंभ किया जाता है, तो क्रिस-क्रॉस कलन विधि हालांकि, [[फुकुदा, पुराना नाम]] और नमिकी द्वारा 1994 के लेख के अनुसार केवल D अतिरिक्त कोनों पर जाता है। <ref name="FTNamiki" >{{harvtxt|Fukuda|Terlaky|1997|p=385}}</ref><ref name="FukudaNamiki" >{{harvtxt|Fukuda|Namiki|1994|p=367}}</ref> तुच्छ रूप से, प्रसमुच्चय कलन विधि घन के लिए औसत D चरण लेता है। <ref name="Borgwardt"/><ref>More generally, for the simplex algorithm, the expected number of steps is proportional to ''D'' for linear-programming problems that are randomly drawn from the [[Euclidean metric|Euclidean]] [[unit sphere]], as proved by Borgwardt and by [[Stephen Smale|Smale]].</ref> प्रसमुच्चय कलन विधि की तरह, क्रिस-क्रॉस कलन विधि औसतन तीन आयामी घन के ठीक 3 अतिरिक्त कोनों पर जाता है। | ||
== | == परिवर्त्य == | ||
रेखीय | रेखीय क्रमादेशन समस्याओं की तुलना में अधिक सामान्य समस्याओं को हल करने के लिए क्रिस-क्रॉस कलन विधि का विस्तार किया गया है। | ||
=== रैखिक बाधाओं के साथ अन्य अनुकूलन समस्याएं === | === रैखिक बाधाओं के साथ अन्य अनुकूलन समस्याएं === | ||
रैखिक | रैखिक क्रमादेशन के लिए, द्विघात क्रमादेशन के लिए, और रैखिक पूरकता समस्या के लिए क्रिस-क्रॉस कलन विधि के परिवर्त्य हैं। पर्याप्त मैट्रिसेस के साथ रैखिक-पूरक समस्या;<ref name="FukudaTerlaky"/><ref name="FTNamiki"/><ref name="FukudaNamikiLCP" >{{harvtxt|Fukuda|Namiki|1994|}}</ref><ref name="OMBook" >{{cite book|last1=Björner|first1=Anders|last2=Las Vergnas|first2=Michel|author2-link=Michel Las Vergnas|last3=Sturmfels|first3=Bernd|author-link3=Bernd Sturmfels|last4=White|first4=Neil|last5=Ziegler|first5=Günter|author-link5=Günter M. Ziegler|title=ओरिएंटेड मैट्रोइड्स|chapter=10 Linear programming|publisher=Cambridge University Press|year=1999|isbn=978-0-521-77750-6|pages=417–479|doi=10.1017/CBO9780511586507|mr=1744046}}</ref><ref name="HRT">{{cite journal|first1=D. |last1=den Hertog|first2=C.|last2=Roos|first3=T.|last3=Terlaky|title=रैखिक संपूरकता समस्या, पर्याप्त मैट्रिक्स और क्रिस-क्रॉस विधि|journal=Linear Algebra and Its Applications|volume=187|date=1 July 1993|pages=1–14|url=http://core.ac.uk/download/pdf/6714737.pdf|doi=10.1016/0024-3795(93)90124-7|doi-access=free}}</ref><ref name="CIsufficient">{{cite journal|first1=Zsolt|last1=Csizmadia|first2=Tibor|last2=Illés|title=पर्याप्त मैट्रिसेस के साथ रैखिक संपूरकता समस्याओं के लिए नए क्रिस-क्रॉस प्रकार के एल्गोरिदम|journal=Optimization Methods and Software|volume=21|year=2006|number=2|pages=247–266|doi=10.1080/10556780500095009 |url=http://www.cs.elte.hu/opres/orr/download/ORR03_1.pdf|format=pdf<!--|eprint=http://www.tandfonline.com/doi/pdf/10.1080/10556780500095009-->|mr=2195759|s2cid=24418835}}</ref> इसके विपरीत, रैखिक संपूरकता समस्याओं के लिए, क्रिस-क्रॉस कलन विधि केवल तभी समाप्त होता है जब आव्यूह एक पर्याप्त आव्यूह हो।<ref name="HRT"/><ref name="CIsufficient"/>एक पर्याप्त आव्यूह एक [[सकारात्मक-निश्चित मैट्रिक्स|सकारात्मक-निश्चित आव्यूह]] और एक [[पी-मैट्रिक्स|P-आव्यूह]] दोनों का एक सामान्यीकरण है, जिसके सिद्धांत लघु प्रत्येक सकारात्मक हैं।<ref name="HRT"/><ref name="CIsufficient"/><ref>{{cite journal|last1=Cottle|first1=R. W.|author-link1=Richard W. Cottle|last2=Pang|first2=J.-S.|last3=Venkateswaran|first3=V.|title=पर्याप्त मैट्रिक्स और रैखिक संपूरकता समस्या|journal=Linear Algebra and Its Applications|volume=114–115|date=March–April 1989|pages=231–249|doi=10.1016/0024-3795(89)90463-1|mr=986877|doi-access=free}}</ref> क्रिस-क्रॉस कलन विधि को रैखिक-भिन्नात्मक क्रमादेशन के लिए भी अनुकूलित किया गया है।<ref name="LF99Hyperbolic"/><ref name="Bibl"/> | ||
=== | === कोणबिंदु गणना === | ||
क्रिस-क्रॉस | क्रिस-क्रॉस कलन विधि का उपयोग [[ वर्टेक्स गणना समस्या |कोणबिंदु गणना समस्या]] के लिए एक कलन विधि में किया गया था, जिसे 1992 में[[ डेविड समीक्षाएं ]]और कोमेई फुकुदा द्वारा प्रकाशित किया गया था। <ref>{{harvtxt|Avis|Fukuda|1992|p=297}}</ref> एविस और फुकुदा ने एक कलन विधि प्रस्तुत किया जो D आयाम (सदिश समष्टि) में n [[रैखिक असमानता]] की अनपभ्रष्ट प्रणाली द्वारा परिभाषित एक [[ बहुतल |बहुतल]] के v कोने ढूंढता है (या, दोहरे रूप से, D आयामों में n बिंदुओं के उत्तल पतवार के v [[पहलू]], जहां प्रत्येक फलक में सटीक रूप से दिए गए D बिंदु होते हैं) समय में [[बिग ओह नोटेशन|O]] (nDv) और O (nD) [[अंतरिक्ष जटिलता|स्थल]] है। <ref>The ''v'' vertices in a simple arrangement of ''n'' [[hyperplane]]s in ''D'' dimensions can be found in O(''n''<sup>2</sup>''Dv'') time and O(''nD'') [[space complexity]].</ref> | ||
=== | === उन्मुख मैट्रोइड्स === | ||
[[File:max-flow min-cut example.svg|frame|right|[[मैक्स-फ्लो मिन-कट प्रमेय]] बताता है कि | [[File:max-flow min-cut example.svg|frame|right|[[मैक्स-फ्लो मिन-कट प्रमेय|अधिकतम प्रवाह-न्यूनतम कटौती प्रमेय]] बताता है कि संजाल के माध्यम से अधिकतम प्रवाह इसकी न्यूनतम कट की क्षमता है। उन्मुख मैट्रोइड्स के लिए क्रिस-क्रॉस कलन विधि का उपयोग करके इस प्रमेय को सिद्ध किया जा सकता है।]]क्रिस-क्रॉस कलन विधि का अध्ययन प्रायः [[उन्मुख matroid|उन्मुख मैट्रोइड]] (ओएम) के सिद्धांत का उपयोग करके किया जाता है, जो कि रैखिक-अनुकूलन सिद्धांत का एक संयोजी सार है। <ref name="OMBook"/><ref>The theory of [[oriented matroid]]s was initiated by [[R. Tyrrell Rockafellar]]. {{harv|Rockafellar|1969}}:<p>{{cite book | ||
|first=R. T. | |first=R. T. | ||
|last=Rockafellar | |last=Rockafellar | ||
| Line 57: | Line 58: | ||
|mr=278972 | |mr=278972 | ||
|chapter-url=http://www.math.washington.edu/~rtr/papers/rtr-ElemVectors.pdf |id=[http://www.math.washington.edu/~rtr/papers/rtr-ElemVectors.pdf PDF reprint]}}</p><p>Rockafellar was influenced by the earlier studies of [[Albert W. Tucker]] and [[George J. Minty]]. Tucker and Minty had studied the sign patterns of the matrices arising through the pivoting operations of Dantzig's simplex algorithm.</p> | |chapter-url=http://www.math.washington.edu/~rtr/papers/rtr-ElemVectors.pdf |id=[http://www.math.washington.edu/~rtr/papers/rtr-ElemVectors.pdf PDF reprint]}}</p><p>Rockafellar was influenced by the earlier studies of [[Albert W. Tucker]] and [[George J. Minty]]. Tucker and Minty had studied the sign patterns of the matrices arising through the pivoting operations of Dantzig's simplex algorithm.</p> | ||
</ref> दरअसल, ब्लैंड का पिवोटिंग नियम | </ref> दरअसल, ब्लैंड का पिवोटिंग नियम उन्मुख-मैट्रॉइड सिद्धांत पर उनके पिछले लेख पर आधारित था। हालाँकि, ब्लैंड का नियम कुछ उन्मुख-मैट्रोइड रैखिक-क्रमादेशन समस्याओं पर साइकिल चलाना प्रदर्शित करता है।<ref name="OMBook"/> रेखीय क्रमादेशन के लिए पहला विशुद्ध रूप से मिश्रित कलन विधि माइकल जे. टॉड (गणितज्ञ) द्वारा तैयार किया गया था। <ref name="OMBook"/><ref name="Todd"/> टोड के कलन विधि को न केवल उन्मुख मैट्रोइड्स की समायोजन में रैखिक-क्रमादेशन के लिए विकसित किया गया था, बल्कि द्विघात क्रमादेशन समस्याओं और रैखिक-पूरक समस्याओं के लिए भी विकसित किया गया था।<ref name="OMBook"/><ref name="Todd" >{{cite journal|last=Todd|first=Michael J.|author-link=Michael J. Todd (mathematician)|title=ओरिएंटेड मैट्रोइड्स में रैखिक और द्विघात प्रोग्रामिंग|journal=Journal of Combinatorial Theory|series=Series B|volume=39|year=1985|number=2|pages=105–133|mr=811116|doi=10.1016/0095-8956(85)90042-5|doi-access=free}}</ref> टोड का कलन विधि यहां तक कि स्तिथि के लिए जटिल है, दुर्भाग्य से, और इसके परिमित-अभिसरण प्रमाण कुछ जटिल हैं। <ref name="OMBook"/> | ||
क्रिस-क्रॉस | क्रिस-क्रॉस कलन विधि और इसके परिमित समाप्ति के प्रमाण को सरलता से कहा जा सकता है और उन्मुख मैट्रोइड्स की समायोजन को आसानी से बढ़ाया जा सकता है। रैखिक व्यवहार्यता समस्याओं के लिए कलन विधि को और सरल बनाया जा सकता है, जो कि रैखिक असमानताओं के साथ रैखिक प्रणालियों के लिए है; इन समस्याओं को उन्मुख मैट्रोइड्स के लिए तैयार किया जा सकता है। <ref name="KT91"/> क्राइस-क्रॉस कलन विधि को उन समस्याओं के लिए अनुकूलित किया गया है जो रैखिक क्रमादेशन की तुलना में अधिक जटिल हैं: द्विघात-क्रमादेशन समस्या और रैखिक-पूरक समस्या के लिए उन्मुख-मैट्रॉइड परिवर्त्य भी हैं।<ref name="FukudaTerlaky"/><ref name="FukudaNamikiLCP"/><ref name="OMBook"/> | ||
== सारांश == | == सारांश == | ||
क्रिस-क्रॉस | क्रिस-क्रॉस कलन विधि रैखिक क्रमादेशन के लिए सरल रूप से वर्णित कलन विधि है। यह रेखीय क्रमादेशन के लिए दूसरा पूरी तरह से सांयोगिक कलन विधि थी। कुछ (अवास्तविक) उन्मुख मैट्रोइड्स पर नरम चक्रों का आंशिक रूप से संयोजी प्रसमुच्चय कलन विधि है। टोड द्वारा पहली पूरी तरह से मिश्रित कलन विधि प्रकाशित किया गया था, और यह प्रसमुच्चय कलन विधि की तरह भी है जिसमें यह पहले व्यवहार्य आधार उत्पन्न होने के बाद व्यवहार्यता को संरक्षित करता है; हालाँकि, टॉड का नियम जटिल है। क्रिस-क्रॉस कलन विधि एक प्रसमुच्चय-जैसी कलन विधि नहीं है, क्योंकि इसे व्यवहार्यता बनाए रखने की आवश्यकता नहीं है। हालाँकि, क्रिस-क्रॉस कलन विधि में बहुपद समय-जटिलता नहीं है। | ||
शोधकर्ताओं ने रेखीय-भिन्नात्मक | शोधकर्ताओं ने रेखीय-भिन्नात्मक क्रमादेशन सहित कई अनुकूलन-समस्याओं के लिए क्रिस-क्रॉस कलन विधि का विस्तार किया है। क्रिस-क्रॉस कलन विधि उन्मुख मैट्रोइड्स की समायोजन में भी द्विघात क्रमादेशन समस्याओं और रैखिक पूरकता समस्याओं को हल कर सकता है। सामान्यीकृत होने पर भी, क्रिस-क्रॉस कलन विधि सरल रूप से कहा जाता है। | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[जैक एडमंड्स]] ( | * [[जैक एडमंड्स]] (सांयोगिक इष्टमीकरण और उन्मुख-मैट्रॉइड सिद्धांतवादी के अग्रणी; कोमेई फुकुदा के डॉक्टरेट सलाहकार) | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
| Line 94: | Line 95: | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
* [https://web.archive.org/web/20110728105602/http://www.ifor.math.ethz.ch/~fukuda/ Komei Fukuda (ETH Zentrum, Zurich)] with [https://web.archive.org/web/20110728105643/http://www.ifor.math.ethz.ch/~fukuda/publ/publ.html publications] | * [https://web.archive.org/web/20110728105602/http://www.ifor.math.ethz.ch/~fukuda/ Komei Fukuda (ETH Zentrum, Zurich)] with [https://web.archive.org/web/20110728105643/http://www.ifor.math.ethz.ch/~fukuda/publ/publ.html publications] | ||
* [http://coral.ie.lehigh.edu/~terlaky/ Tamás | * [http://coral.ie.lehigh.edu/~terlaky/ Tamás टेर्लाकी (Lehigh University)] with [http://coral.ie.lehigh.edu/~terlaky/publications publications] | ||
{{Mathematical programming|state=expanded}} | {{Mathematical programming|state=expanded}} | ||
Revision as of 16:13, 25 May 2023
इष्टमीकरण (गणित) में, क्रिस-क्रॉस कलन विधि रैखिक क्रमादेशन के लिए कलन विधि के परिवार में से कोई है। क्रिस-क्रॉस कलन विधि के परिवर्त्य भी रैखिक क्रमादेशन और गैर-रैखिक क्रमादेशन अनुकूलन (गणित) के साथ अधिक सामान्य समस्याओं को हल करते हैं; रैखिक-आंशिक क्रमादेशन समस्याओं के लिए क्रिस-क्रॉस कलन विधि हैं,[1][2] द्विघात क्रमादेशन समस्याएं, और रैखिक संपूरकता समस्याएं हैं।[3]
जॉर्ज बी. डेंटजिग के प्रसमुच्चय कलन विधि की तरह, रेखीय क्रमादेशन के लिए बहुपद-समय कलन विधि एक समय जटिलता नहीं है। दोनों कलन विधि सबसे खराब स्थिति में आयाम D, क्ले-मिन्टी घन (विक्टर क्ले और जॉर्ज जे मिंटी के बाद) में एक घन के सभी 2D कोनों पर जाते हैं। [4][5] हालांकि, जब इसे एक यादृच्छिक कोने पर प्रारम्भ किया जाता है, तो क्रिस-क्रॉस कलन विधि औसत आगमन पर केवल डी अतिरिक्त कोनों पर जाता है।[6][7][8] इस प्रकार, त्रि-आयामी घन के लिए, कलन विधि सबसे खराब स्थिति में सभी 8 कोनों और औसतन ठीक 3 अतिरिक्त कोनों पर जाता है।
इतिहास
क्रिस-क्रॉस कलन विधि स्वतंत्र रूप से तमस टेरलाकी और जेड-मिन वांग द्वारा प्रकाशित किया गया था [9] [10] संबंधित कलन विधि अन्य लेखकों द्वारा अप्रकाशित वर्णन में दिखाई दिए।[3]
रैखिक अनुकूलन के लिए प्रसमुच्चय कलन विधि के साथ तुलना

रैखिक क्रमादेशन में, क्रिस-क्रॉस कलन विधि आधारों के अनुक्रम के बीच धुराग्र करता है लेकिन प्रसमुच्चय कलन विधि से भिन्न होता है। प्रसमुच्चय कलन विधि पहले चरण-एक समस्या को हल करके एक (प्राथमिक-) व्यवहार्य आधार पाता है; चरण दो में, प्रसमुच्चय कलन विधि बुनियादी व्यवहार्य समाधानों के अनुक्रम के बीच धुराग्र करता है ताकि उद्देश्य फलन प्रत्येक धुराग्र के साथ घटता न हो, एक इष्टतम समाधान के साथ समाप्त हो (अंत में एक दोहरी व्यवहार्य समाधान भी ढूंढ रहा है)।[3][11]
क्रिस-क्रॉस कलन विधि प्रसमुच्चय कलन विधि की तुलना में सरल है, क्योंकि क्रिस-क्रॉस कलन विधि में केवल एक चरण होता है। इसके धुरी नियम ब्लैंड के न्यूनतम-सूचकांक धुरी नियम के समान हैं। [12] योग्य धुराग्र तय करते समय ब्लैंड का नियम उनके वास्तविक संख्या के स्थान पर गुणांकों के केवल संकेत कार्यों का उपयोग करता है। ब्लैंड का नियम योग्य धुराग्र के वास्तविक-संख्या क्रम का उपयोग करके कम लागत के मूल्यों की तुलना करके एक प्रवेश चर का चयन करता है।[12][13] ब्लैंड के नियम के विपरीत, क्रिस-क्रॉस कलन विधि विशुद्ध रूप से संयोजी है, एक प्रवेश चर और एक छोड़ने वाले चर का चयन करते हुए उनके वास्तविक-संख्या क्रम के स्थान पर केवल गुणांक के संकेतों पर विचार करके किया जाता है। [3][11] क्रिस-क्रॉस कलन विधि को रैखिक बीजगणित में बुनियादी परिणामों के रचनात्मक प्रमाण प्रस्तुत करने के लिए लागू किया गया है, जैसे कि फ़र्कस की लेम्मा। [14]
जबकि अधिकांश प्रसमुच्चय परिवर्ती उद्देश्य में एकदिष्ट होते हैं (कठोरता से गैर-पतित स्तिथि में), क्रिस-क्रॉस कलन विधि के अधिकांश परिवर्त्य में एक एकदिष्ट श्रेष्ठता फलन की कमी होती है जो व्यवहार में हानि हो सकती है।
विवरण
This section needs expansion. You can help by adding to it. (April 2011) |
क्रिस-क्रॉस कलन विधि एक मानक धुरी झांकी पर काम करता है (या झांकी के ऑन-द-फ्लाई परिकलित भागों, यदि संशोधित प्रसमुच्चय विधि की तरह लागू किया जाता है)। एक सामान्य चरण में, यदि झांकी प्रारंभिक या दोहरी अव्यवहार्य है, तो यह अनुक्रमणिका चयन नियम का उपयोग करके धुरी पंक्ति/स्तंभ के रूप में अव्यवहार्य पंक्तियों/स्तंभों में से एक का चयन करती है। एक महत्वपूर्ण संपत्ति यह है कि चयन अव्यवहार्य सूचकांकों के मिलन पर किया जाता है और कलन विधि का मानक संस्करण स्तंभ और पंक्ति सूचकांकों में अंतर नहीं करता है (अर्थात, स्तंभ सूचकांक पंक्तियों में बुनियादी हैं)। यदि एक पंक्ति का चयन किया जाता है तो कलन विधि दोहरे प्रकार के धुरी की स्थिति की पहचान करने के लिए सूचकांक चयन नियम का उपयोग करता है, जबकि यदि एक स्तंभ का चयन किया जाता है तो यह पंक्ति की स्थिति खोजने के लिए सूचकांक चयन नियम का उपयोग करता है और एक मूल प्रकार की धुरी करता है।
कम्प्यूटेशनल जटिलता: सबसे खराब और औसत स्तिथि
कलन विधि की समय जटिलता समस्या को हल करने के लिए कलन विधि के लिए पर्याप्त अंकगणितीय परिचालनों की संख्या की गणना करती है। उदाहरण के लिए, D3 के अनुक्रम पर गॉसियन उन्मूलन संचालन की आवश्यकता होती है, और इसलिए इसे बहुपद समय-जटिलता कहा जाता है, क्योंकि इसकी जटिलता एक घन बहुपद से बंधी है। ऐसे कलन विधि के उदाहरण हैं जिनमें बहुपद-समय की जटिलता नहीं है। उदाहरण के लिए, गॉसियन उन्मूलन के एक सामान्यीकरण को बुचबर्गर के कलन विधि कहा जाता है, इसकी जटिलता के लिए एक समस्या डेटा का घातीय कार्य (एक बहुपद की डिग्री और बहुभिन्नरूपी बहुपद के चर की संख्या) है। क्योंकि घातीय कार्य अंततः बहुपद कार्यों की तुलना में बहुत तेजी से बढ़ते हैं, एक घातीय जटिलता का तात्पर्य है कि एक कलन विधि का बड़ी समस्याओं पर धीमा प्रदर्शन होता है।
रेखीय क्रमादेशन के लिए कई कलन विधि—खाचियान का दीर्घवृत्त कलन विधि, करमरकर का प्रक्षेपीय कलन विधि, और आंतरिक-बिंदु विधि — में बहुपद समय-जटिलता होती है (सबसे खराब स्थिति में जटिलता और इस प्रकार औसत जटिलता)। दीर्घवृत्ताकार और प्रक्षेपी कलन विधि को क्रिस-क्रॉस कलन विधि से पहले प्रकाशित किया गया था।
हालांकि, डेंटज़िग के प्रसमुच्चय कलन विधि की तरह, क्रिस-क्रॉस कलन विधि रैखिक क्रमादेशन के लिए बहुपद-समय कलन विधि नहीं है। 2D रूस के एक लेख के अनुसार, टेरलकी का क्रिस-क्रॉस कलन विधि आयाम D में एक (अशान्त) घन के सभी 2D कोनों पर जाता है। जिस पर प्रसमुच्चय कलन विधि 2D कदम लेता है।[3][4][5] प्रसमुच्चय कलन विधि की तरह, क्रिस-क्रॉस कलन विधि सबसे खराब स्थिति में त्रि-आयामी घन के सभी 8 कोनों पर जाता है।
जब इसे घन के एक यादृच्छिक कोने में प्रारंभ किया जाता है, तो क्रिस-क्रॉस कलन विधि हालांकि, फुकुदा, पुराना नाम और नमिकी द्वारा 1994 के लेख के अनुसार केवल D अतिरिक्त कोनों पर जाता है। [6][7] तुच्छ रूप से, प्रसमुच्चय कलन विधि घन के लिए औसत D चरण लेता है। [8][15] प्रसमुच्चय कलन विधि की तरह, क्रिस-क्रॉस कलन विधि औसतन तीन आयामी घन के ठीक 3 अतिरिक्त कोनों पर जाता है।
परिवर्त्य
रेखीय क्रमादेशन समस्याओं की तुलना में अधिक सामान्य समस्याओं को हल करने के लिए क्रिस-क्रॉस कलन विधि का विस्तार किया गया है।
रैखिक बाधाओं के साथ अन्य अनुकूलन समस्याएं
रैखिक क्रमादेशन के लिए, द्विघात क्रमादेशन के लिए, और रैखिक पूरकता समस्या के लिए क्रिस-क्रॉस कलन विधि के परिवर्त्य हैं। पर्याप्त मैट्रिसेस के साथ रैखिक-पूरक समस्या;[3][6][16][17][18][19] इसके विपरीत, रैखिक संपूरकता समस्याओं के लिए, क्रिस-क्रॉस कलन विधि केवल तभी समाप्त होता है जब आव्यूह एक पर्याप्त आव्यूह हो।[18][19]एक पर्याप्त आव्यूह एक सकारात्मक-निश्चित आव्यूह और एक P-आव्यूह दोनों का एक सामान्यीकरण है, जिसके सिद्धांत लघु प्रत्येक सकारात्मक हैं।[18][19][20] क्रिस-क्रॉस कलन विधि को रैखिक-भिन्नात्मक क्रमादेशन के लिए भी अनुकूलित किया गया है।[1][2]
कोणबिंदु गणना
क्रिस-क्रॉस कलन विधि का उपयोग कोणबिंदु गणना समस्या के लिए एक कलन विधि में किया गया था, जिसे 1992 मेंडेविड समीक्षाएं और कोमेई फुकुदा द्वारा प्रकाशित किया गया था। [21] एविस और फुकुदा ने एक कलन विधि प्रस्तुत किया जो D आयाम (सदिश समष्टि) में n रैखिक असमानता की अनपभ्रष्ट प्रणाली द्वारा परिभाषित एक बहुतल के v कोने ढूंढता है (या, दोहरे रूप से, D आयामों में n बिंदुओं के उत्तल पतवार के v पहलू, जहां प्रत्येक फलक में सटीक रूप से दिए गए D बिंदु होते हैं) समय में O (nDv) और O (nD) स्थल है। [22]
उन्मुख मैट्रोइड्स

क्रिस-क्रॉस कलन विधि का अध्ययन प्रायः उन्मुख मैट्रोइड (ओएम) के सिद्धांत का उपयोग करके किया जाता है, जो कि रैखिक-अनुकूलन सिद्धांत का एक संयोजी सार है। [17][23] दरअसल, ब्लैंड का पिवोटिंग नियम उन्मुख-मैट्रॉइड सिद्धांत पर उनके पिछले लेख पर आधारित था। हालाँकि, ब्लैंड का नियम कुछ उन्मुख-मैट्रोइड रैखिक-क्रमादेशन समस्याओं पर साइकिल चलाना प्रदर्शित करता है।[17] रेखीय क्रमादेशन के लिए पहला विशुद्ध रूप से मिश्रित कलन विधि माइकल जे. टॉड (गणितज्ञ) द्वारा तैयार किया गया था। [17][24] टोड के कलन विधि को न केवल उन्मुख मैट्रोइड्स की समायोजन में रैखिक-क्रमादेशन के लिए विकसित किया गया था, बल्कि द्विघात क्रमादेशन समस्याओं और रैखिक-पूरक समस्याओं के लिए भी विकसित किया गया था।[17][24] टोड का कलन विधि यहां तक कि स्तिथि के लिए जटिल है, दुर्भाग्य से, और इसके परिमित-अभिसरण प्रमाण कुछ जटिल हैं। [17]
क्रिस-क्रॉस कलन विधि और इसके परिमित समाप्ति के प्रमाण को सरलता से कहा जा सकता है और उन्मुख मैट्रोइड्स की समायोजन को आसानी से बढ़ाया जा सकता है। रैखिक व्यवहार्यता समस्याओं के लिए कलन विधि को और सरल बनाया जा सकता है, जो कि रैखिक असमानताओं के साथ रैखिक प्रणालियों के लिए है; इन समस्याओं को उन्मुख मैट्रोइड्स के लिए तैयार किया जा सकता है। [14] क्राइस-क्रॉस कलन विधि को उन समस्याओं के लिए अनुकूलित किया गया है जो रैखिक क्रमादेशन की तुलना में अधिक जटिल हैं: द्विघात-क्रमादेशन समस्या और रैखिक-पूरक समस्या के लिए उन्मुख-मैट्रॉइड परिवर्त्य भी हैं।[3][16][17]
सारांश
क्रिस-क्रॉस कलन विधि रैखिक क्रमादेशन के लिए सरल रूप से वर्णित कलन विधि है। यह रेखीय क्रमादेशन के लिए दूसरा पूरी तरह से सांयोगिक कलन विधि थी। कुछ (अवास्तविक) उन्मुख मैट्रोइड्स पर नरम चक्रों का आंशिक रूप से संयोजी प्रसमुच्चय कलन विधि है। टोड द्वारा पहली पूरी तरह से मिश्रित कलन विधि प्रकाशित किया गया था, और यह प्रसमुच्चय कलन विधि की तरह भी है जिसमें यह पहले व्यवहार्य आधार उत्पन्न होने के बाद व्यवहार्यता को संरक्षित करता है; हालाँकि, टॉड का नियम जटिल है। क्रिस-क्रॉस कलन विधि एक प्रसमुच्चय-जैसी कलन विधि नहीं है, क्योंकि इसे व्यवहार्यता बनाए रखने की आवश्यकता नहीं है। हालाँकि, क्रिस-क्रॉस कलन विधि में बहुपद समय-जटिलता नहीं है।
शोधकर्ताओं ने रेखीय-भिन्नात्मक क्रमादेशन सहित कई अनुकूलन-समस्याओं के लिए क्रिस-क्रॉस कलन विधि का विस्तार किया है। क्रिस-क्रॉस कलन विधि उन्मुख मैट्रोइड्स की समायोजन में भी द्विघात क्रमादेशन समस्याओं और रैखिक पूरकता समस्याओं को हल कर सकता है। सामान्यीकृत होने पर भी, क्रिस-क्रॉस कलन विधि सरल रूप से कहा जाता है।
यह भी देखें
- जैक एडमंड्स (सांयोगिक इष्टमीकरण और उन्मुख-मैट्रॉइड सिद्धांतवादी के अग्रणी; कोमेई फुकुदा के डॉक्टरेट सलाहकार)
टिप्पणियाँ
- ↑ 1.0 1.1 Illés, Szirmai & Terlaky (1999)
- ↑ 2.0 2.1 Stancu-Minasian, I. M. (August 2006). "आंशिक प्रोग्रामिंग की छठी ग्रंथ सूची". Optimization. 55 (4): 405–428. doi:10.1080/02331930600819613. MR 2258634. S2CID 62199788.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Fukuda & Terlaky (1997)
- ↑ 4.0 4.1 Roos (1990)
- ↑ 5.0 5.1 Klee, Victor; Minty, George J. (1972). "How good is the simplex algorithm?". In Shisha, Oved (ed.). Inequalities III (Proceedings of the Third Symposium on Inequalities held at the University of California, Los Angeles, Calif., September 1–9, 1969, dedicated to the memory of Theodore S. Motzkin). New York-London: Academic Press. pp. 159–175. MR 0332165.
- ↑ 6.0 6.1 6.2 Fukuda & Terlaky (1997, p. 385)
- ↑ 7.0 7.1 Fukuda & Namiki (1994, p. 367)
- ↑ 8.0 8.1 The simplex algorithm takes on average D steps for a cube. Borgwardt (1987): Borgwardt, Karl-Heinz (1987). The simplex method: A probabilistic analysis. Algorithms and Combinatorics (Study and Research Texts). Vol. 1. Berlin: Springer-Verlag. pp. xii+268. ISBN 978-3-540-17096-9. MR 0868467.
- ↑ Terlaky (1985) and Terlaky (1987)
- ↑ Wang (1987)
- ↑ 11.0 11.1 Terlaky & Zhang (1993)
- ↑ 12.0 12.1 Bland, Robert G. (May 1977). "New finite pivoting rules for the simplex method". Mathematics of Operations Research. 2 (2): 103–107. doi:10.1287/moor.2.2.103. JSTOR 3689647. MR 0459599.
- ↑ Bland's rule is also related to an earlier least-index rule, which was proposed by Katta G. Murty for the linear complementarity problem, according to Fukuda & Namiki (1994).
- ↑ 14.0 14.1 Klafszky & Terlaky (1991)
- ↑ More generally, for the simplex algorithm, the expected number of steps is proportional to D for linear-programming problems that are randomly drawn from the Euclidean unit sphere, as proved by Borgwardt and by Smale.
- ↑ 16.0 16.1 Fukuda & Namiki (1994)
- ↑ 17.0 17.1 17.2 17.3 17.4 17.5 17.6 Björner, Anders; Las Vergnas, Michel; Sturmfels, Bernd; White, Neil; Ziegler, Günter (1999). "10 Linear programming". ओरिएंटेड मैट्रोइड्स. Cambridge University Press. pp. 417–479. doi:10.1017/CBO9780511586507. ISBN 978-0-521-77750-6. MR 1744046.
- ↑ 18.0 18.1 18.2 den Hertog, D.; Roos, C.; Terlaky, T. (1 July 1993). "रैखिक संपूरकता समस्या, पर्याप्त मैट्रिक्स और क्रिस-क्रॉस विधि" (PDF). Linear Algebra and Its Applications. 187: 1–14. doi:10.1016/0024-3795(93)90124-7.
- ↑ 19.0 19.1 19.2 Csizmadia, Zsolt; Illés, Tibor (2006). "पर्याप्त मैट्रिसेस के साथ रैखिक संपूरकता समस्याओं के लिए नए क्रिस-क्रॉस प्रकार के एल्गोरिदम" (pdf). Optimization Methods and Software. 21 (2): 247–266. doi:10.1080/10556780500095009. MR 2195759. S2CID 24418835.
- ↑ Cottle, R. W.; Pang, J.-S.; Venkateswaran, V. (March–April 1989). "पर्याप्त मैट्रिक्स और रैखिक संपूरकता समस्या". Linear Algebra and Its Applications. 114–115: 231–249. doi:10.1016/0024-3795(89)90463-1. MR 0986877.
- ↑ Avis & Fukuda (1992, p. 297)
- ↑ The v vertices in a simple arrangement of n hyperplanes in D dimensions can be found in O(n2Dv) time and O(nD) space complexity.
- ↑ The theory of oriented matroids was initiated by R. Tyrrell Rockafellar. (Rockafellar 1969):
Rockafellar, R. T. (1969). "The elementary vectors of a subspace of (1967)" (PDF). In R. C. Bose and T. A. Dowling (ed.). Combinatorial Mathematics and its Applications. The University of North Carolina Monograph Series in Probability and Statistics. Chapel Hill, North Carolina: University of North Carolina Press. pp. 104–127. MR 0278972. PDF reprint.
Rockafellar was influenced by the earlier studies of Albert W. Tucker and George J. Minty. Tucker and Minty had studied the sign patterns of the matrices arising through the pivoting operations of Dantzig's simplex algorithm.
- ↑ 24.0 24.1 Todd, Michael J. (1985). "ओरिएंटेड मैट्रोइड्स में रैखिक और द्विघात प्रोग्रामिंग". Journal of Combinatorial Theory. Series B. 39 (2): 105–133. doi:10.1016/0095-8956(85)90042-5. MR 0811116.
संदर्भ
- Avis, David; Fukuda, Komei (December 1992). "A pivoting algorithm for convex hulls and vertex enumeration of arrangements and polyhedra". Discrete and Computational Geometry. 8 (ACM Symposium on Computational Geometry (North Conway, NH, 1991) number 1): 295–313. doi:10.1007/BF02293050. MR 1174359.
- Csizmadia, Zsolt; Illés, Tibor (2006). "New criss-cross type algorithms for linear complementarity problems with sufficient matrices" (pdf). Optimization Methods and Software. 21 (2): 247–266. doi:10.1080/10556780500095009. MR 2195759. S2CID 24418835.
- Fukuda, Komei; Namiki, Makoto (March 1994). "On extremal behaviors of Murty's least index method". Mathematical Programming. 64 (1): 365–370. doi:10.1007/BF01582581. MR 1286455. S2CID 21476636.
- Fukuda, Komei; Terlaky, Tamás (1997). Liebling, Thomas M.; de Werra, Dominique (eds.). "Criss-cross methods: A fresh view on pivot algorithms". Mathematical Programming, Series B. 79 (Papers from the 16th International Symposium on Mathematical Programming held in Lausanne, 1997, number 1–3): 369–395. CiteSeerX 10.1.1.36.9373. doi:10.1007/BF02614325. MR 1464775. S2CID 2794181. Postscript preprint.
- den Hertog, D.; Roos, C.; Terlaky, T. (1 July 1993). "The linear complementarity problem, sufficient matrices, and the criss-cross method" (PDF). Linear Algebra and Its Applications. 187: 1–14. doi:10.1016/0024-3795(93)90124-7. MR 1221693.
- Illés, Tibor; Szirmai, Ákos; Terlaky, Tamás (1999). "The finite criss-cross method for hyperbolic programming". European Journal of Operational Research. 114 (1): 198–214. doi:10.1016/S0377-2217(98)00049-6. Zbl 0953.90055. Postscript preprint.
- Klafszky, Emil; Terlaky, Tamás (June 1991). "The role of pivoting in proving some fundamental theorems of linear algebra". Linear Algebra and Its Applications. 151: 97–118. doi:10.1016/0024-3795(91)90356-2. MR 1102142.
- Roos, C. (1990). "An exponential example for Terlaky's pivoting rule for the criss-cross simplex method". Mathematical Programming. Series A. 46 (1): 79–84. doi:10.1007/BF01585729. MR 1045573. S2CID 33463483.
- Terlaky, T. (1985). "A convergent criss-cross method". Optimization: A Journal of Mathematical Programming and Operations Research. 16 (5): 683–690. doi:10.1080/02331938508843067. ISSN 0233-1934. MR 0798939.
- Terlaky, Tamás (1987). "A finite crisscross method for oriented matroids". Journal of Combinatorial Theory. Series B. 42 (3): 319–327. doi:10.1016/0095-8956(87)90049-9. ISSN 0095-8956. MR 0888684.
- Terlaky, Tamás; Zhang, Shu Zhong (1993) [1991]. "Pivot rules for linear programming: A Survey on recent theoretical developments". Annals of Operations Research. 46–47 (Degeneracy in optimization problems, number 1): 203–233. CiteSeerX 10.1.1.36.7658. doi:10.1007/BF02096264. ISSN 0254-5330. MR 1260019. S2CID 6058077.
- Wang, Zhe Min (1987). "A finite conformal-elimination free algorithm over oriented matroid programming". Chinese Annals of Mathematics (Shuxue Niankan B Ji). Series B. 8 (1): 120–125. ISSN 0252-9599. MR 0886756.
बाहरी संबंध
- Komei Fukuda (ETH Zentrum, Zurich) with publications
- Tamás टेर्लाकी (Lehigh University) with publications
| group5 = Metaheuristics | abbr5 = heuristic | list5 =
| below =
}} | group5 =Metaheuuristic |abbr5 = heuristic | list5 =*विकासवादी एल्गोरिथ्म
| below =* सॉफ्टवेयर
}}