डीएफटी मैट्रिक्स: Difference between revisions
(Created page with "{{Use American English|date = March 2019}} {{Short description|Discrete Fourier Transform expressed as a matrix}} लागू गणित में, एक डीएफट...") |
No edit summary |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Discrete Fourier Transform expressed as a matrix}} | {{Short description|Discrete Fourier Transform expressed as a matrix}} | ||
प्रयुक्त गणित में, एक डीएफटी आव्यूह एक [[परिवर्तन मैट्रिक्स|परिवर्तन]] आव्यूह के रूप में [[असतत फूरियर रूपांतरण]] (डीएफटी) की अभिव्यक्ति है, जिसे [[मैट्रिक्स गुणन|आव्यूह गुणन]] के माध्यम से संकेत पर प्रयुक्त किया जा सकता है। | |||
== परिभाषा == | == परिभाषा == | ||
एक N-पॉइंट डीएफटी गुणा <math>X = W x</math> के रूप में व्यक्त किया जाता है, जहां <math>x</math> मूल इनपुट संकेत है, <math>W</math> N-बाय-N स्क्वायर डीएफटी आव्यूह है, और <math>X</math> संकेत का डीएफटी है। | |||
रूपांतरण आव्यूह <math>W</math> को <math>W = \left(\frac{\omega^{jk}}{{\sqrt{N}}}\right)_{j,k=0,\ldots,N-1} </math> के रूप में परिभाषित किया जा सकता है या समकक्ष: | |||
:<math> | :<math> | ||
| Line 18: | Line 17: | ||
</math>, | </math>, | ||
जहाँ <math>\omega = e^{-2\pi i/N}</math> एकता का आदिम <math>i^2=-1</math>रूट है जिसमें हम इस तथ्य का उपयोग करके <math>\omega</math> के लिए बड़े घातांक लिखने से बच सकते हैं कि किसी भी घातांक <math>x</math> के लिए हमारी पहचान <math>\omega^{x} = \omega^{x \bmod N}.</math> है यह वैंडरमोंड है एकता की जड़ों के लिए मैट्रिक्स, सामान्यीकरण कारक तक ध्यान दें कि योग के सामने सामान्यीकरण कारक <math>1/\sqrt{N}</math> और ω में घातांक का चिह्न केवल परंपराएं हैं, और कुछ उपचारों में भिन्न हैं। निम्नलिखित सभी चर्चा परिपाटी पर ध्यान दिए बिना प्रयुक्त होती है, अधिकतम सामान्य समायोजन के साथ एकमात्र महत्वपूर्ण बात यह है कि आगे और व्युत्क्रम परिवर्तनों में विपरीत-चिन्ह वाले घातांक होते हैं, और यह कि उनके सामान्यीकरण कारकों का गुणनफल 1/N होता है। चूँकि, यहाँ <math>1/\sqrt{N}</math> विकल्प परिणामी डीएफटी आव्यूह को एकात्मक बनाता है, जो कई परिस्थितियों में सुविधाजनक है। | |||
फास्ट फूरियर रूपांतरण एल्गोरिदम | फास्ट फूरियर रूपांतरण एल्गोरिदम आव्यूह के समरूपता का उपयोग इस आव्यूह द्वारा एक वेक्टर को गुणा करने के समय को कम करने के लिए करता है, सामान्य <math>O(N^2)</math> से हैडमार्ड आव्यूह और वॉल्श आव्यूह जैसे मैट्रिसेस द्वारा गुणन के लिए इसी तरह की विधियों को प्रयुक्त किया जा सकता है। | ||
== उदाहरण == | == उदाहरण == | ||
=== दो-बिंदु === | === दो-बिंदु === | ||
दो-बिंदु डीएफटी एक साधारण | दो-बिंदु डीएफटी एक साधारण स्थिति है, जिसमें पहली प्रविष्टि [[डीसी पूर्वाग्रह]] (योग) है और दूसरी प्रविष्टि [[एसी गुणांक]] (अंतर) है। | ||
:<math>W= | :<math>W= | ||
| Line 35: | Line 34: | ||
पहली पंक्ति योग करती है, और दूसरी पंक्ति अंतर करती है। | पहली पंक्ति योग करती है, और दूसरी पंक्ति अंतर करती है। | ||
<math>1/\sqrt{2}</math> का कारक परिवर्तन को एकात्मक बनाना है (नीचे देखें)। | |||
=== चार सूत्री === | === चार सूत्री === | ||
चार-बिंदु दक्षिणावर्त | चार-बिंदु दक्षिणावर्त डीएफटी आव्यूह इस प्रकार है: | ||
:<math> | :<math> | ||
| Line 54: | Line 53: | ||
1 & i & -1 & -i\end{bmatrix} | 1 & i & -1 & -i\end{bmatrix} | ||
</math> | </math> | ||
जहाँ <math>\omega = e^{-\frac{2 \pi i}{4}} = -i</math>. | |||
=== आठ-बिंदु === | === आठ-बिंदु === | ||
दो | दो स्थितियों की पहली गैर-तुच्छ पूर्णांक शक्ति आठ बिंदुओं के लिए है: | ||
:<math>W= \frac{1}{\sqrt{8}} | :<math>W= \frac{1}{\sqrt{8}} | ||
| Line 82: | Line 81: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
जहाँ | |||
:<math>\omega = e^{-\frac{2 \pi i}{8}} = \frac{1}{\sqrt{2}} - \frac{i}{\sqrt{2}}</math> | :<math>\omega = e^{-\frac{2 \pi i}{8}} = \frac{1}{\sqrt{2}} - \frac{i}{\sqrt{2}}</math> | ||
(ध्यान दें कि <math>\omega^{8 + n} = \omega^{n}</math>.) | (ध्यान दें कि <math>\omega^{8 + n} = \omega^{n}</math>.) | ||
निम्नलिखित छवि डीएफटी को | निम्नलिखित छवि डीएफटी को आव्यूह गुणन के रूप में दर्शाती है, जटिल घातांक के नमूनों द्वारा दर्शाए गए आव्यूह के तत्वों के साथ: | ||
[[File:Fourierop rows only.svg]] | [[File:Fourierop rows only.svg]] | ||
वास्तविक भाग (कोज्या तरंग) को एक ठोस रेखा और काल्पनिक भाग (साइन तरंग) को धराशायी रेखा द्वारा दर्शाया जाता है। | |||
शीर्ष पंक्ति सभी वाले हैं (द्वारा स्केल किया गया <math>1/\sqrt{8}</math> यूनिटारिटी के लिए), इसलिए यह इनपुट संकेत में डीसी पूर्वाग्रह को मापता है। अगली पंक्ति एक जटिल घातांक के ऋणात्मक एक चक्र के आठ नमूने हैं, अर्थात, −1/8 की भिन्नात्मक आवृत्ति वाला एक संकेत, इसलिए यह मापता है कि संकेत में भिन्नात्मक आवृत्ति +1/8 पर कितनी शक्ति है। याद रखें कि एक मेल खाने वाला फ़िल्टर संकेत की तुलना हम जो कुछ भी खोज रहे हैं उसके एक समय उलट संस्करण के साथ करते हैं, इसलिए जब हम आंशिक आवृत्ति की तलाश कर रहे हैं। 1/8 हम आंशिक आवृत्ति से तुलना करते हैं। −1/8 इसलिए यह पंक्ति ऋणात्मक बारंबारता है। अगली पंक्ति एक जटिल घातांक के ऋणात्मक दो चक्र हैं, जिन्हें आठ स्थानों पर नमूना लिया गया है, इसलिए इसमें -1/4 की भिन्नात्मक आवृत्ति है, और इस प्रकार उस सीमा को मापता है जिस तक संकेत की [[आंशिक आवृत्ति]] +1/4 है। | |||
निम्नलिखित सारांशित करता है कि 8-बिंदु डीएफटी भिन्नात्मक आवृत्ति के संदर्भ में पंक्ति दर पंक्ति काम करता है: | |||
समतुल्य रूप से अंतिम पंक्ति को +1/8 की भिन्नात्मक आवृत्ति कहा जा सकता है और इस प्रकार यह मापता है कि कितने | * 0 मापता है कि संकेत में कितना डीसी है | ||
* −1/8 मापता है कि कितने संकेत की आंशिक आवृत्ति +1/8 है | |||
* −1/4 मापता है कि कितने संकेत की आंशिक आवृत्ति +1/4 है | |||
* −3/8 मापता है कि कितने संकेत की भिन्नात्मक आवृत्ति +3/8 है | |||
* −1/2 मापता है कि कितने संकेत की आंशिक आवृत्ति +1/2 है | |||
* −5/8 मापता है कि कितने संकेत की भिन्नात्मक आवृत्ति +5/8 है | |||
* −3/4 मापता है कि कितने संकेत की आंशिक आवृत्ति +3/4 है | |||
* −7/8 मापता है कि कितने संकेत की भिन्नात्मक आवृत्ति +7/8 है | |||
समतुल्य रूप से अंतिम पंक्ति को +1/8 की भिन्नात्मक आवृत्ति कहा जा सकता है और इस प्रकार यह मापता है कि कितने संकेत की भिन्नात्मक आवृत्ति -1/8 है। इस तरह, यह कहा जा सकता है कि आव्यूह की शीर्ष पंक्तियाँ संकेत में सकारात्मक आवृत्ति सामग्री को मापती हैं और नीचे की पंक्तियाँ संकेत में [[नकारात्मक आवृत्ति|ऋणात्मक आवृत्ति]] घटक को मापती हैं। | |||
== एकात्मक परिवर्तन == | == एकात्मक परिवर्तन == | ||
डीएफटी (या स्केलिंग के उचित चयन के माध्यम से हो सकता है) एक एकात्मक परिवर्तन है, | डीएफटी (या स्केलिंग के उचित चयन के माध्यम से हो सकता है) एक एकात्मक परिवर्तन है, अर्थात, जो ऊर्जा को संरक्षित करता है। एकात्मकता प्राप्त करने के लिए स्केलिंग का उपयुक्त विकल्प <math>1/\sqrt{N}</math> है जिससे भौतिक डोमेन में ऊर्जा फूरियर डोमेन में ऊर्जा के समान हो, अर्थात पारसेवल के प्रमेय को संतुष्ट करने के लिए (अन्य, गैर-एकात्मक, स्केलिंग, सामान्यतः कम्प्यूटेशनल सुविधा के लिए भी उपयोग किए जाते हैं; उदाहरण के लिए, असतत फूरियर रूपांतरण लेख में दिखाए गए स्केलिंग के साथ [[कनवल्शन प्रमेय]] थोड़ा सरल रूप लेता है।) | ||
== अन्य गुण == | == अन्य गुण == | ||
डीएफटी | डीएफटी आव्यूह के अन्य गुणों के लिए, इसके आइजनवैल्यूज सहित, कनवल्शन से कनेक्शन, एप्लिकेशन, और इसी तरह, असतत फूरियर ट्रांसफॉर्म लेख देखें। | ||
== एक सीमित मामला: फूरियर ऑपरेटर == | == एक सीमित मामला: फूरियर ऑपरेटर == | ||
{{main article| | {{main article|फूरियर ऑपरेटर}} | ||
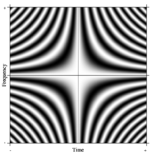
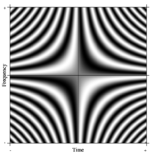
{{multiple image | {{multiple image | ||
| footer = The [[Fourier operator]] | | footer = The [[Fourier operator]] | ||
| Line 122: | Line 123: | ||
| caption2 = Imaginary part (sine) | | caption2 = Imaginary part (sine) | ||
}} | }} | ||
फूरियर रूपांतरण की धारणा आसानी से [[सामान्यीकृत फूरियर श्रृंखला]] है। एन-पॉइंट डीएफटी के ऐसे एक औपचारिक सामान्यीकरण की कल्पना एन को | फूरियर रूपांतरण की धारणा आसानी से [[सामान्यीकृत फूरियर श्रृंखला]] है। एन-पॉइंट डीएफटी के ऐसे एक औपचारिक सामान्यीकरण की कल्पना एन को इच्छानुसार से बड़ा करके की जा सकती है। सीमा में कठोर गणितीय मशीनरी ऐसे रैखिक ऑपरेटरों को तथाकथित [[ अभिन्न परिवर्तन |अभिन्न परिवर्तन]] के रूप में मानती है। इस स्थिति में, यदि हम पंक्तियों में जटिल घातांकों के साथ एक बहुत बड़ा आव्यूह बनाते हैं (अर्थात, कोज्या वास्तविक भाग और साइन काल्पनिक भाग), और बिना सीमा के रिज़ॉल्यूशन बढ़ाते हैं, तो हम दूसरी तरह के फ्रेडहोम इंटीग्रल समीकरण के कर्नेल तक पहुँचते हैं, अर्थात् [[फूरियर ऑपरेटर]] जो निरंतर फूरियर रूपांतरण को परिभाषित करता है। इस सतत फूरियर ऑपरेटर के एक आयताकार भाग को एक छवि के रूप में प्रदर्शित किया जा सकता है, जो डीएफटी आव्यूह के समान है, जैसा कि दाईं ओर दिखाया गया है, जहां ग्रेस्केल पिक्सेल मान संख्यात्मक मात्रा को दर्शाता है। | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[बहुआयामी परिवर्तन]] | * [[बहुआयामी परिवर्तन]] | ||
* पाउली मैट्रिसेस का सामान्यीकरण | * पाउली मैट्रिसेस का सामान्यीकरण या निर्माण: घड़ी और शिफ्ट मैट्रिसेस | ||
==संदर्भ== | ==संदर्भ== | ||
* [https://www.amazon.com/gp/reader/0849336929 The Transform and Data Compression Handbook by P. C. Yip, K. Ramamohan Rao] – See chapter 2 for a treatment of the | * [https://www.amazon.com/gp/reader/0849336929 The Transform and Data Compression Handbook by P. C. Yip, K. Ramamohan Rao] – See chapter 2 for a treatment of the डीएफटी based largely on the डीएफटी matrix | ||
| Line 137: | Line 138: | ||
{{Matrix classes}} | {{Matrix classes}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Collapse templates]] | |||
[[Category:Commons category link from Wikidata]] | |||
[[Category:Created On 13/05/2023]] | [[Category:Created On 13/05/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with empty portal template]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Portal-inline template with redlinked portals]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:अंकीय संकेत प्रक्रिया]] | |||
[[Category:फूरियर विश्लेषण]] | |||
[[Category:मैट्रिसेस]] | |||
Latest revision as of 17:06, 14 June 2023
प्रयुक्त गणित में, एक डीएफटी आव्यूह एक परिवर्तन आव्यूह के रूप में असतत फूरियर रूपांतरण (डीएफटी) की अभिव्यक्ति है, जिसे आव्यूह गुणन के माध्यम से संकेत पर प्रयुक्त किया जा सकता है।
परिभाषा
एक N-पॉइंट डीएफटी गुणा के रूप में व्यक्त किया जाता है, जहां मूल इनपुट संकेत है, N-बाय-N स्क्वायर डीएफटी आव्यूह है, और संकेत का डीएफटी है।
रूपांतरण आव्यूह को के रूप में परिभाषित किया जा सकता है या समकक्ष:
- ,
जहाँ एकता का आदिम रूट है जिसमें हम इस तथ्य का उपयोग करके के लिए बड़े घातांक लिखने से बच सकते हैं कि किसी भी घातांक के लिए हमारी पहचान है यह वैंडरमोंड है एकता की जड़ों के लिए मैट्रिक्स, सामान्यीकरण कारक तक ध्यान दें कि योग के सामने सामान्यीकरण कारक और ω में घातांक का चिह्न केवल परंपराएं हैं, और कुछ उपचारों में भिन्न हैं। निम्नलिखित सभी चर्चा परिपाटी पर ध्यान दिए बिना प्रयुक्त होती है, अधिकतम सामान्य समायोजन के साथ एकमात्र महत्वपूर्ण बात यह है कि आगे और व्युत्क्रम परिवर्तनों में विपरीत-चिन्ह वाले घातांक होते हैं, और यह कि उनके सामान्यीकरण कारकों का गुणनफल 1/N होता है। चूँकि, यहाँ विकल्प परिणामी डीएफटी आव्यूह को एकात्मक बनाता है, जो कई परिस्थितियों में सुविधाजनक है।
फास्ट फूरियर रूपांतरण एल्गोरिदम आव्यूह के समरूपता का उपयोग इस आव्यूह द्वारा एक वेक्टर को गुणा करने के समय को कम करने के लिए करता है, सामान्य से हैडमार्ड आव्यूह और वॉल्श आव्यूह जैसे मैट्रिसेस द्वारा गुणन के लिए इसी तरह की विधियों को प्रयुक्त किया जा सकता है।
उदाहरण
दो-बिंदु
दो-बिंदु डीएफटी एक साधारण स्थिति है, जिसमें पहली प्रविष्टि डीसी पूर्वाग्रह (योग) है और दूसरी प्रविष्टि एसी गुणांक (अंतर) है।
पहली पंक्ति योग करती है, और दूसरी पंक्ति अंतर करती है।
का कारक परिवर्तन को एकात्मक बनाना है (नीचे देखें)।
चार सूत्री
चार-बिंदु दक्षिणावर्त डीएफटी आव्यूह इस प्रकार है:
जहाँ .
आठ-बिंदु
दो स्थितियों की पहली गैर-तुच्छ पूर्णांक शक्ति आठ बिंदुओं के लिए है:
जहाँ
(ध्यान दें कि .)
निम्नलिखित छवि डीएफटी को आव्यूह गुणन के रूप में दर्शाती है, जटिल घातांक के नमूनों द्वारा दर्शाए गए आव्यूह के तत्वों के साथ:
वास्तविक भाग (कोज्या तरंग) को एक ठोस रेखा और काल्पनिक भाग (साइन तरंग) को धराशायी रेखा द्वारा दर्शाया जाता है।
शीर्ष पंक्ति सभी वाले हैं (द्वारा स्केल किया गया यूनिटारिटी के लिए), इसलिए यह इनपुट संकेत में डीसी पूर्वाग्रह को मापता है। अगली पंक्ति एक जटिल घातांक के ऋणात्मक एक चक्र के आठ नमूने हैं, अर्थात, −1/8 की भिन्नात्मक आवृत्ति वाला एक संकेत, इसलिए यह मापता है कि संकेत में भिन्नात्मक आवृत्ति +1/8 पर कितनी शक्ति है। याद रखें कि एक मेल खाने वाला फ़िल्टर संकेत की तुलना हम जो कुछ भी खोज रहे हैं उसके एक समय उलट संस्करण के साथ करते हैं, इसलिए जब हम आंशिक आवृत्ति की तलाश कर रहे हैं। 1/8 हम आंशिक आवृत्ति से तुलना करते हैं। −1/8 इसलिए यह पंक्ति ऋणात्मक बारंबारता है। अगली पंक्ति एक जटिल घातांक के ऋणात्मक दो चक्र हैं, जिन्हें आठ स्थानों पर नमूना लिया गया है, इसलिए इसमें -1/4 की भिन्नात्मक आवृत्ति है, और इस प्रकार उस सीमा को मापता है जिस तक संकेत की आंशिक आवृत्ति +1/4 है।
निम्नलिखित सारांशित करता है कि 8-बिंदु डीएफटी भिन्नात्मक आवृत्ति के संदर्भ में पंक्ति दर पंक्ति काम करता है:
- 0 मापता है कि संकेत में कितना डीसी है
- −1/8 मापता है कि कितने संकेत की आंशिक आवृत्ति +1/8 है
- −1/4 मापता है कि कितने संकेत की आंशिक आवृत्ति +1/4 है
- −3/8 मापता है कि कितने संकेत की भिन्नात्मक आवृत्ति +3/8 है
- −1/2 मापता है कि कितने संकेत की आंशिक आवृत्ति +1/2 है
- −5/8 मापता है कि कितने संकेत की भिन्नात्मक आवृत्ति +5/8 है
- −3/4 मापता है कि कितने संकेत की आंशिक आवृत्ति +3/4 है
- −7/8 मापता है कि कितने संकेत की भिन्नात्मक आवृत्ति +7/8 है
समतुल्य रूप से अंतिम पंक्ति को +1/8 की भिन्नात्मक आवृत्ति कहा जा सकता है और इस प्रकार यह मापता है कि कितने संकेत की भिन्नात्मक आवृत्ति -1/8 है। इस तरह, यह कहा जा सकता है कि आव्यूह की शीर्ष पंक्तियाँ संकेत में सकारात्मक आवृत्ति सामग्री को मापती हैं और नीचे की पंक्तियाँ संकेत में ऋणात्मक आवृत्ति घटक को मापती हैं।
एकात्मक परिवर्तन
डीएफटी (या स्केलिंग के उचित चयन के माध्यम से हो सकता है) एक एकात्मक परिवर्तन है, अर्थात, जो ऊर्जा को संरक्षित करता है। एकात्मकता प्राप्त करने के लिए स्केलिंग का उपयुक्त विकल्प है जिससे भौतिक डोमेन में ऊर्जा फूरियर डोमेन में ऊर्जा के समान हो, अर्थात पारसेवल के प्रमेय को संतुष्ट करने के लिए (अन्य, गैर-एकात्मक, स्केलिंग, सामान्यतः कम्प्यूटेशनल सुविधा के लिए भी उपयोग किए जाते हैं; उदाहरण के लिए, असतत फूरियर रूपांतरण लेख में दिखाए गए स्केलिंग के साथ कनवल्शन प्रमेय थोड़ा सरल रूप लेता है।)
अन्य गुण
डीएफटी आव्यूह के अन्य गुणों के लिए, इसके आइजनवैल्यूज सहित, कनवल्शन से कनेक्शन, एप्लिकेशन, और इसी तरह, असतत फूरियर ट्रांसफॉर्म लेख देखें।
एक सीमित मामला: फूरियर ऑपरेटर
फूरियर रूपांतरण की धारणा आसानी से सामान्यीकृत फूरियर श्रृंखला है। एन-पॉइंट डीएफटी के ऐसे एक औपचारिक सामान्यीकरण की कल्पना एन को इच्छानुसार से बड़ा करके की जा सकती है। सीमा में कठोर गणितीय मशीनरी ऐसे रैखिक ऑपरेटरों को तथाकथित अभिन्न परिवर्तन के रूप में मानती है। इस स्थिति में, यदि हम पंक्तियों में जटिल घातांकों के साथ एक बहुत बड़ा आव्यूह बनाते हैं (अर्थात, कोज्या वास्तविक भाग और साइन काल्पनिक भाग), और बिना सीमा के रिज़ॉल्यूशन बढ़ाते हैं, तो हम दूसरी तरह के फ्रेडहोम इंटीग्रल समीकरण के कर्नेल तक पहुँचते हैं, अर्थात् फूरियर ऑपरेटर जो निरंतर फूरियर रूपांतरण को परिभाषित करता है। इस सतत फूरियर ऑपरेटर के एक आयताकार भाग को एक छवि के रूप में प्रदर्शित किया जा सकता है, जो डीएफटी आव्यूह के समान है, जैसा कि दाईं ओर दिखाया गया है, जहां ग्रेस्केल पिक्सेल मान संख्यात्मक मात्रा को दर्शाता है।
यह भी देखें
- बहुआयामी परिवर्तन
- पाउली मैट्रिसेस का सामान्यीकरण या निर्माण: घड़ी और शिफ्ट मैट्रिसेस
संदर्भ
- The Transform and Data Compression Handbook by P. C. Yip, K. Ramamohan Rao – See chapter 2 for a treatment of the डीएफटी based largely on the डीएफटी matrix