लीवर नियम: Difference between revisions
(Created page with "{{short description|Formula for determining the mole or mass fraction of phases in a binary phase diagram}} रसायन विज्ञान में, लीवर...") |
No edit summary |
||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{ | [[रसायन विज्ञान]] में, '''लीवर नियम''' एक सूत्र होता है जिसका उपयोग द्विआधारी संतुलन चरण आरेख के प्रत्येक चरण के मोल अंश (''x<sub>i</sub>'') या ''[[द्रव्यमान अंश (रसायन विज्ञान)]]'' (''w<sub>i</sub>'') को निर्धारित करने के लिए किया जाता है। इसका उपयोग किसी दिए गए द्विआधारी संरचना और तापमान के लिए ''[[तरल]]'' और ''[[ठोस]]'' चरणों के अंश को निर्धारित करने के लिए किया जा सकता है जो तरल और ठोस रेखा के बीच होता है।''<ref name="smith">{{Citation | last = Smith.h | first = William F. halkias | last2 = Hashemi | first2 = Javad | title = Foundations of Materials Science and Engineering | edition = 4th | year = 2006 | publisher = McGraw-Hill | pages = 318–320 | isbn = 0-07-295358-6 | postscript =.}}</ref>'' | ||
एक [[मिश्र धातु]] या दो चरणों वाले [[मिश्रण]] में, α और β, जिसमें स्वयं दो [[रासायनिक तत्व]], A और B होते है, लीवर नियम बताता है कि α चरण का द्रव्यमान अंश है | |||
एक [[मिश्र धातु]] या दो चरणों वाले [[मिश्रण]] में, α और β, जिसमें स्वयं दो [[रासायनिक तत्व]], A और B होते | |||
:<math>w^\alpha = \frac{w_{\rm B}-w_{\rm B}^\beta}{w_{\rm B}^\alpha-w_{\rm B}^\beta}</math> | :<math>w^\alpha = \frac{w_{\rm B}-w_{\rm B}^\beta}{w_{\rm B}^\alpha-w_{\rm B}^\beta}</math> | ||
जहाँ | |||
* <math>w_{\rm B}^\alpha</math> α चरण में तत्व B का द्रव्यमान अंश है | * <math>w_{\rm B}^\alpha</math> α चरण में तत्व B का द्रव्यमान अंश है | ||
* <math>w_{\rm B}^\beta</math> β चरण में तत्व B का द्रव्यमान अंश है | * <math>w_{\rm B}^\beta</math> β चरण में तत्व B का द्रव्यमान अंश है | ||
* <math>w_{\rm B}</math> संपूर्ण मिश्रधातु या मिश्रण में तत्व B का द्रव्यमान अंश है | * <math>w_{\rm B}</math> संपूर्ण मिश्रधातु या मिश्रण में तत्व B का द्रव्यमान अंश है | ||
सब कुछ निश्चित तापमान या दबाव पर होता है। | |||
== व्युत्पत्ति == | == व्युत्पत्ति == | ||
मान | मान लेते है कि संतुलन तापमान T पर एक मिश्र धातु सम्मलित है <math>w_{\rm B}</math> तत्व B का द्रव्यमान अंश है। मान लेते है कि तापमान T पर मिश्र धातु में दो चरण होते है, α और β, जिसके लिए α में सम्मलित होते है <math>w_{\rm B}^\alpha</math>, और β में सम्मलित होते है <math>w_{\rm B}^\beta</math> मिश्रधातु में α चरण का द्रव्यमान होता है <math>m^\alpha</math> जिससे कि β चरण का द्रव्यमान होता है <math>m^\beta = m - m^\alpha</math>, जहाँ <math>m</math> मिश्र धातु का कुल द्रव्यमान होता है। | ||
परिभाषा के अनुसार, α चरण में तत्व B का द्रव्यमान है <math>m_{\rm B}^\alpha = w_{\rm B}^\alpha m^\alpha</math>, जबकि β चरण में तत्व B का द्रव्यमान है <math>m_{\rm B}^\beta = w_{\rm B}^\beta \left(m -m^\alpha\right)</math> | परिभाषा के अनुसार, α चरण में तत्व B का द्रव्यमान है <math>m_{\rm B}^\alpha = w_{\rm B}^\alpha m^\alpha</math>, जबकि β चरण में तत्व B का द्रव्यमान है <math>m_{\rm B}^\beta = w_{\rm B}^\beta \left(m -m^\alpha\right)</math> इन दोनों मात्राओं का योग मिश्रधातु में तत्व B के कुल द्रव्यमान का योग होता है, जो इसके द्वारा दिया गया है <math>m_{\rm B} = w_{\rm B}m</math> इसलिए, | ||
:<math> w_{\rm B}m = m_{\rm B} = m_{\rm B}^\alpha + m_{\rm B}^\beta = w_{\rm B}^\alpha m^\alpha + w_{\rm B}^\beta \left(m - m^\alpha\right)</math> | :<math> w_{\rm B}m = m_{\rm B} = m_{\rm B}^\alpha + m_{\rm B}^\beta = w_{\rm B}^\alpha m^\alpha + w_{\rm B}^\beta \left(m - m^\alpha\right)</math> | ||
पुनर्व्यवस्थित करके, | पुनर्व्यवस्थित करके, यह पाया जाता है | ||
:<math>w^\alpha \equiv \frac{m^\alpha}{m} = \frac{ w_{\rm B}-w_{\rm B}^{\beta} }{ w_{\rm B}^{\alpha}-w_{\rm B}^{\beta} }</math> | :<math>w^\alpha \equiv \frac{m^\alpha}{m} = \frac{ w_{\rm B}-w_{\rm B}^{\beta} }{ w_{\rm B}^{\alpha}-w_{\rm B}^{\beta} }</math> | ||
यह अंतिम अंश मिश्रधातु में α चरण का द्रव्यमान अंश है। | यह अंतिम अंश मिश्रधातु में α चरण का द्रव्यमान अंश होता है। | ||
== गणना == | == गणना == | ||
[[File:Lever rule.svg|thumb|400px|बाइनरी आइसोमॉर्फस | [[File:Lever rule.svg|thumb|400px|बाइनरी आइसोमॉर्फस प्रणाली के लिए टाई रेखा (एलएस) के साथ एक चरण आरेख। एक्स आयाम तत्वों ए और बी के द्रव्यमान अंश को परिभाषित करता है।]] | ||
=== बाइनरी चरण आरेख === | === बाइनरी चरण आरेख === | ||
किसी भी गणना से पहले, प्रत्येक तत्व के द्रव्यमान अंश को निर्धारित करने के लिए चरण आरेख पर एक रेखा खींची जाती है, चरण आरेख पर दाईं ओर यह [[रेखा खंड]] LS होती है। यह रेखा क्षैतिज रूप से संरचना के तापमान पर एक चरण से दूसरे तक खींची जाती है। तरल पदार्थ पर तत्व B का द्रव्यमान अंश ''w''<sub>B</sub><sup>l</sup> (इस चित्र में w<sub>l</sub> के रूप में दर्शाया गया है) द्वारा दिया गया है और ठोस पदार्थ पर तत्व B का द्रव्यमान अंश w<sub>B</sub><sup>s</sup> द्वारा दिया गया है (इस चित्र में w<sub>s</sub> के रूप में दर्शाया गया है)। ठोस और तरल के द्रव्यमान अंश की गणना निम्नलिखित लीवर नियम समीकरणों का उपयोग करके किया जा सकता है:<ref name="smith"/> | |||
:<math>w^{\rm s} = \frac{w_{\rm B} - w_{\rm B}^{\rm l}}{w_{\rm B}^{\rm s} - w_{\rm B}^{\rm l}}</math> | :<math>w^{\rm s} = \frac{w_{\rm B} - w_{\rm B}^{\rm l}}{w_{\rm B}^{\rm s} - w_{\rm B}^{\rm l}}</math> | ||
:<math>w^{\rm l} = \frac{w_{\rm B}^{\rm s} - w_{\rm B}}{w_{\rm B}^{\rm s} - w_{\rm B}^{\rm l}}</math> | :<math>w^{\rm l} = \frac{w_{\rm B}^{\rm s} - w_{\rm B}}{w_{\rm B}^{\rm s} - w_{\rm B}^{\rm l}}</math> | ||
जहाँ w<sub>B</sub> दी गई रचना के लिए तत्व B का द्रव्यमान अंश होता है (इस आरेख में w<sub>o</sub> के रूप में दर्शाया गया है)। | |||
प्रत्येक समीकरण का अंश मूल रचना है जिसमें हम रुचि रखते | प्रत्येक समीकरण का अंश मूल रचना होता है जिसमें हम रुचि रखते है +/- विपरीत लीवर बांह होता है। अर्थात अगर आप ठोस द्रव्यमान अंश चाहते है तो तरल संरचना और मूल संरचना के बीच का अंतर होता है। यदि आपको यह समझने में कठिनाई होती है कि ऐसा क्यों है, तो जब ''w''<sub>o</sub> ''w''<sub>l</sub> के पास आता है तो रचना की कल्पना करने का प्रयास करते है। तब द्रव की सघनता बढ़ने लगती है। | ||
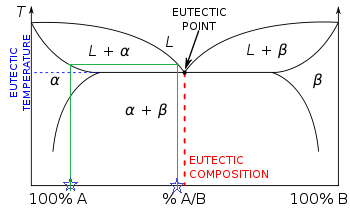
=== यूटेक्टिक चरण आरेख === | === यूटेक्टिक चरण आरेख === | ||
[[File:Eutectic phase diagram Tie Line.png|thumb|1500px|अल्फा प्लस लिक्विड दो चरण क्षेत्र में टाई | [[File:Eutectic phase diagram Tie Line.png|thumb|1500px|अल्फा प्लस लिक्विड दो चरण क्षेत्र में टाई रेखा]]अब एक से अधिक दो-चरण क्षेत्र होते है। खींची गई रेखा ठोस अल्फा से तरल तक होता है और इन बिंदुओं पर एक ऊर्ध्वाधर रेखा को नीचे गिराकर प्रत्येक चरण का द्रव्यमान अंश सीधे ग्राफ से पढ़ा जाता है, जो कि x अक्ष तत्व में द्रव्यमान अंश होता है। प्रत्येक चरण में मिश्र धातु के द्रव्यमान अंश को खोजने के लिए समान समीकरणों का उपयोग किया जाता है, अर्थात w<sup>l</sup> तरल चरण में पूरे नमूने का द्रव्यमान अंश होता है।<ref name="Callister">{{Citation | last = Callister | first = William D. | last2 = Rethwisch | first2 = David | title = Materials Science and Engineering An Introduction | edition = 8th | year = 2009 | publisher = Wiley | pages = 298–303 | isbn = 978-0-470-41997-7 | postscript =.}}</ref> | ||
==संदर्भ== | ==संदर्भ== | ||
{{reflist}} | {{reflist}} | ||
[[Category:Created On 23/05/2023]] | [[Category:Created On 23/05/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:चरण संक्रमण]] | |||
[[Category:चार्ट]] | |||
[[Category:चित्र]] | |||
[[Category:धातुकर्म]] | |||
[[Category:पदार्थ विज्ञान]] | |||
Latest revision as of 14:10, 15 June 2023
रसायन विज्ञान में, लीवर नियम एक सूत्र होता है जिसका उपयोग द्विआधारी संतुलन चरण आरेख के प्रत्येक चरण के मोल अंश (xi) या द्रव्यमान अंश (रसायन विज्ञान) (wi) को निर्धारित करने के लिए किया जाता है। इसका उपयोग किसी दिए गए द्विआधारी संरचना और तापमान के लिए तरल और ठोस चरणों के अंश को निर्धारित करने के लिए किया जा सकता है जो तरल और ठोस रेखा के बीच होता है।[1]
एक मिश्र धातु या दो चरणों वाले मिश्रण में, α और β, जिसमें स्वयं दो रासायनिक तत्व, A और B होते है, लीवर नियम बताता है कि α चरण का द्रव्यमान अंश है
जहाँ
- α चरण में तत्व B का द्रव्यमान अंश है
- β चरण में तत्व B का द्रव्यमान अंश है
- संपूर्ण मिश्रधातु या मिश्रण में तत्व B का द्रव्यमान अंश है
सब कुछ निश्चित तापमान या दबाव पर होता है।
व्युत्पत्ति
मान लेते है कि संतुलन तापमान T पर एक मिश्र धातु सम्मलित है तत्व B का द्रव्यमान अंश है। मान लेते है कि तापमान T पर मिश्र धातु में दो चरण होते है, α और β, जिसके लिए α में सम्मलित होते है , और β में सम्मलित होते है मिश्रधातु में α चरण का द्रव्यमान होता है जिससे कि β चरण का द्रव्यमान होता है , जहाँ मिश्र धातु का कुल द्रव्यमान होता है।
परिभाषा के अनुसार, α चरण में तत्व B का द्रव्यमान है , जबकि β चरण में तत्व B का द्रव्यमान है इन दोनों मात्राओं का योग मिश्रधातु में तत्व B के कुल द्रव्यमान का योग होता है, जो इसके द्वारा दिया गया है इसलिए,
पुनर्व्यवस्थित करके, यह पाया जाता है
यह अंतिम अंश मिश्रधातु में α चरण का द्रव्यमान अंश होता है।
गणना
बाइनरी चरण आरेख
किसी भी गणना से पहले, प्रत्येक तत्व के द्रव्यमान अंश को निर्धारित करने के लिए चरण आरेख पर एक रेखा खींची जाती है, चरण आरेख पर दाईं ओर यह रेखा खंड LS होती है। यह रेखा क्षैतिज रूप से संरचना के तापमान पर एक चरण से दूसरे तक खींची जाती है। तरल पदार्थ पर तत्व B का द्रव्यमान अंश wBl (इस चित्र में wl के रूप में दर्शाया गया है) द्वारा दिया गया है और ठोस पदार्थ पर तत्व B का द्रव्यमान अंश wBs द्वारा दिया गया है (इस चित्र में ws के रूप में दर्शाया गया है)। ठोस और तरल के द्रव्यमान अंश की गणना निम्नलिखित लीवर नियम समीकरणों का उपयोग करके किया जा सकता है:[1]
जहाँ wB दी गई रचना के लिए तत्व B का द्रव्यमान अंश होता है (इस आरेख में wo के रूप में दर्शाया गया है)।
प्रत्येक समीकरण का अंश मूल रचना होता है जिसमें हम रुचि रखते है +/- विपरीत लीवर बांह होता है। अर्थात अगर आप ठोस द्रव्यमान अंश चाहते है तो तरल संरचना और मूल संरचना के बीच का अंतर होता है। यदि आपको यह समझने में कठिनाई होती है कि ऐसा क्यों है, तो जब wo wl के पास आता है तो रचना की कल्पना करने का प्रयास करते है। तब द्रव की सघनता बढ़ने लगती है।
यूटेक्टिक चरण आरेख
अब एक से अधिक दो-चरण क्षेत्र होते है। खींची गई रेखा ठोस अल्फा से तरल तक होता है और इन बिंदुओं पर एक ऊर्ध्वाधर रेखा को नीचे गिराकर प्रत्येक चरण का द्रव्यमान अंश सीधे ग्राफ से पढ़ा जाता है, जो कि x अक्ष तत्व में द्रव्यमान अंश होता है। प्रत्येक चरण में मिश्र धातु के द्रव्यमान अंश को खोजने के लिए समान समीकरणों का उपयोग किया जाता है, अर्थात wl तरल चरण में पूरे नमूने का द्रव्यमान अंश होता है।[2]
संदर्भ
- ↑ 1.0 1.1 Smith.h, William F. halkias; Hashemi, Javad (2006), Foundations of Materials Science and Engineering (4th ed.), McGraw-Hill, pp. 318–320, ISBN 0-07-295358-6.
- ↑ Callister, William D.; Rethwisch, David (2009), Materials Science and Engineering An Introduction (8th ed.), Wiley, pp. 298–303, ISBN 978-0-470-41997-7.